Orthogonal Trajectories

Orthogonal Trajectories Of A Family Of Curves

Trajectory

Definition. If a carve C cuts every member of a given family of curves T according to some specified law, then the curve C is called the trajectory of the given family of curves T.

Orthogonal Trajectory

Definition. If a curve C cuts every member of a given family of curves T at a right angle, then the curve C is called an orthogonal trajectory of the family T.

example. Consider a family of concentric circles \(x^2+y^2=a^2\) with centre at the origin, where ‘a’ is a parameter. We know that the line y = x passing through the origin cuts each member of the above family of circles at a right angle. Therefore y = x is an orthogonal trajectory of the above family.

Infact y = mx where m is any real number is also an orthogonal trajectory.

Thus the family of straight lines y = mx where m is a parameter form orthogonal trajectories for the family of concentric circles.

Conversely, for the family of straight lines y = mx passing through the origin, the family of concentric circles \(x^2+y^2=a^2\) form orthogonal trajectories.

Orthogonal Trajectories Cartesian Coordinates

Theorem 1. The family of curves represented by the differential equation \(F\left(x, y,-1 / y^{\prime}\right)=0\) to form the orthogonal trajectories of the family of given curves represented by \(F\left(x, y, y^{\prime}\right)=0\).

Proof.

Let/(x,y,c) = 0 ….(1) be the equation of the family of curves, where c is the parameter.

Differentiating (1) w. r. t. x. and eliminating c from (1), we get the differential equation of the family (1).

Let the differential equation of the family (1) be F (x, y, y’) = 0.

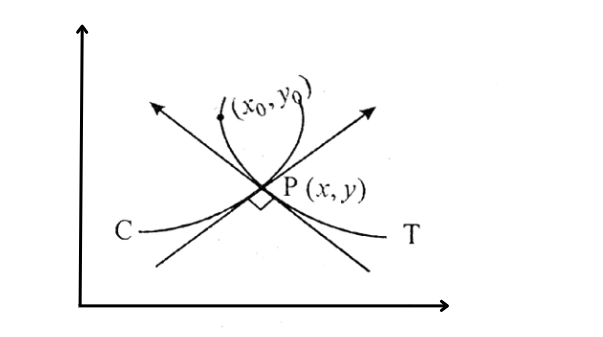
Let C be a member of the family of curves (1) and T be a member of the family of trajectories of (1).

Let \(\left(x_0, y_0\right)\) be any point on T.

Let two curves C and T intersect at P(x,y) at a right angle.

For each point on C, we associate an ordered triad (x,y,y’). where x,y are the coordinates of the point and y’ is the slope of the tangent line at that point to C.

Similarly, for each point on T we associate an ordered triad \(\left(x_0, y_0, y_0^{\prime}\right)\).

If \(\left(x, y, y^{\prime}\right) \text { and }\left(x_0, y_0, y_0^{\prime}\right)\) are ordered triads corresponding to P, we have \(x=x_0, y=y_0\) and \(y^{\prime}=-1 / y_0^{\prime}\)since the two curves C and T cut each other at a right angle at P.

Since the ordered triad (x,y,y’) = 0 satisfies F (x,y,y’) = 0, it implies that the ordered triad \(\left(x_0, y_0,-1 / y_0^{\prime}\right)\) satisfies the equation \(\mathrm{F}\left(x_0, y_0,-1 / y_0^{\prime}\right)=0\) …(2)

But the ordered triad \(\left(x_0, y_0-1 / y_0^{\prime}\right)\) represents any point on T. (2) is true for any point on T. Thus T is the locus of the point \(\left(x_0, y_0\right)\).

Hence the differential equation satisfying T is F (x,y,-1/ y’) = 0

∴ The family of curves of F (x,y,-1/y’) = 0 are the orthogonal trajectories of the family of F (x,y,y’) = 0.

Working Rule To Find The Orthogonal Trajectories Of A Given Family Of Curves

Let f(x,y,c) = 0 be the equation of the given family of curves. ………………..(1)

(1)Differentiate (1) w.r.t. x and obtain the differential equation F (x,y,y’) = 0 by eliminating the parameter c. …………………..(2)

Replace \(\frac{d y}{d x} \text { by }-\frac{1}{d y / d x}\) in (2)

Then the differential equation of the orthogonal trajectories if \(\mathrm{F}\left(x, y,-\frac{d x}{d y}\right)=0\) …………………..(3)

(3) Solve the equation (3) to get the equation of the orthogonal trajectories of (1).

Self Orthogonal Family Of Curves

Definition. If each member of a given family of curves cuts every other member of the family at right angle, then the given family of curves is said to be self-orthogonal.

Note. For self orthogonal family of curves, the differential equation of the family is the same as the differential equation of the family of orthogonal trajectories.

Orthogonal Trajectories Solved Problems

Example 1: Find the orthogonal trajectories of the family of curves \(y=\frac{1}{\log c_1 x}\) where \(c_1\) is the parameter.
Solution.

Given equation of the family of curves is \(y=\frac{1}{\log c_1 x} \Rightarrow \log c_1 x=\frac{1}{y}\) …………………..(1)

Differentiating (1) w. r. tx : \(x: \frac{1}{c_1 x} \cdot c_1=-\frac{1}{y^2} \frac{d y}{d x}\)

⇒ \(\Rightarrow \frac{1}{x}=-\frac{1}{y^2} \frac{d y}{d x} \Rightarrow \frac{d y}{d x}=-\frac{y^2}{x}\) …………………(2)

(2) is free from the parameter \(c_1\).

Hence (2) is the differential equation of the given family (1).

Replacing \(\frac{d y}{d x}\) by \(\frac{d x}{d y}\) in (2), the differential equation of the orthogonal trajectories is

⇒ \(-\frac{d x}{d y}=-\frac{y^2}{x} \Rightarrow y^2 d y=x d x \Rightarrow \int y^2 d y=\int x d x+c_2^{\prime}\)

⇒ \(\frac{y^3}{3}=\frac{x^2}{2}+c_2^{\prime} \Rightarrow 2 y^3=3 x^2+6 c_2^{\prime}=3 x^2+c_2\)

∴ The equation of the orthogonal trajectories of the given family is \(2 y^3=3 x^2+c_2\).

Orthogonal Trajectories Definition And Examples

Example. 2: Find the orthogonal trajectories of the family of curves \(y=\frac{x}{1+c_1 x}\)where \(c_1\) is the parameter.
Solution.

Given, the equation of the family of curves is \(y=\frac{x}{1+c_1 x}\) …………………(1)

Differentiating (1) i.e. \(1+c_1 x=x / y \text { w.r.t. } x: c_1=\frac{y \cdot 1-x y^{\prime}}{y^2}\) ……………………(2)

Eliminating \(\) from (1) and (2): \(1+x\left(\frac{y-x y^{\prime}}{y^2}\right)=\frac{x}{y} \Rightarrow 1+\frac{x}{y}-\frac{x^2}{y^2} \frac{d y}{d x}=\frac{x}{y}\)

⇒ \( 1=\frac{x^2}{y^2} \frac{d y}{d x}\) …………………….(3)

Now (3) is the differential equation of the given family (1).

Replacing \(\frac{d y}{d x}\) by \(-\frac{d x}{d y}\) in (3):

The Differential equation of the family of Orthogonal trajectories is

⇒ \(1=\frac{x^2}{y^2}\left(-\frac{d x}{d y}\right) \Rightarrow y^2 \frac{d y}{d x}=-x^2\)

⇒ \(\int y^2 d y=-\int x^2 d x+c_2^{\prime} \Rightarrow \frac{y^3}{3}=-\frac{x^3}{3}+c_2^{\prime} \Rightarrow x^3+y^3=3 c_2^{\prime}=c_2\)

∴ The equation of the orthogonal trajectories of the given family is \(x^3+y^3=c_2\).

Example. 3. Find the orthogonal trajectories of the family of curves \(\left(\frac{d y}{d x}\right)^2=\frac{a}{x}\)
Solution.

Given the differential equation of the family of curves is

⇒ \(\left(\frac{d y}{d x}\right)^2=\frac{a}{x}\) where a is any real number. ………………………(1)

Replacing \(\frac{d y}{d x}\) by \(-\frac{d x}{d y}\) in (1), the differential equation (D.E.) of the orthogonal trajectories

is \(\left(-\frac{d x}{d y}\right)^2=\frac{a}{x} \Rightarrow\left(\frac{d x}{d y}\right)^2=\frac{a}{x} \Rightarrow \frac{d x}{d y}=\pm \frac{\sqrt{a}}{\sqrt{x}} \Rightarrow d y=\pm \frac{\sqrt{x}}{\sqrt{a}} d x \Rightarrow \int d y=\pm \frac{1}{\sqrt{a}} \int \sqrt{x} d x-c\) ………………………..(2)

⇒ \(\Rightarrow y+c=\pm \frac{1}{\sqrt{a}} \frac{x^{3 / 2}}{(3 / 2)} \Rightarrow 3 \sqrt{a}(y+c)=\pm 2 x^{3 / 2} \Rightarrow 9 a(y+c)^2=4 x^3\) ……………………….(3)

∴ The equation of orthogonal trajectories is \(9 a(y+c)^2=4 x^3\) where c is the parameter.

Example. 4. Find the orthogonal trajectories of the family of carves \(x^{2 / 3}+y^{2 / 3}=a^{2 / 3}\), where ‘a’ is the parameter.
Solution.

Given equation of family of curves is x\(x^{2 / 3}+y^{2 / 3}=a^{2 / 3}\) …………………….(1)

Differentiating (1) w. r. t. \(x: \frac{2}{3} x^{-1 / 3}+\frac{2}{3} y^{-1 / 3} \frac{d y}{d x}=0\)

⇒ \(\Rightarrow x^{-1 / 3}+y^{-1 / 3} \frac{d y}{d x}=0 \Rightarrow x^{1 / 3} \frac{d y}{d x}+y^{1 / 3}=0\) ……………………….(2)

(2) is the differential equation of the given family (1).

Replacing \(\frac{d y}{d x}\) by \(\frac{d x}{d y}\) in (2), we get the D.E. of the orthogonal trajectories of (1) as \(y^{1 / 3}-x^{1 / 3} \frac{d x}{d y}=0 \Rightarrow y^{1 / 3} d y-x^{1 / 3} d x=0\).

Integrating: \(\int y^{1 / 3} d y-\int x^{1 / 3} d x=\frac{3}{4} c \Rightarrow \frac{y^{4 / 3}}{4 / 3}-\frac{x^{4 / 3}}{4 / 3}=\frac{c}{4 / 3}\)

⇒ \(y^{4 / 3}-x^{4 / 3}=c\) is the required equation of the orthogonal trajectories.

Solved Problems On Orthogonal Trajectories Step-By-Step

Example.5. Find the orthogonal trajectories of the family of parabolas through the origin and foci on the y-axis.
Solution.

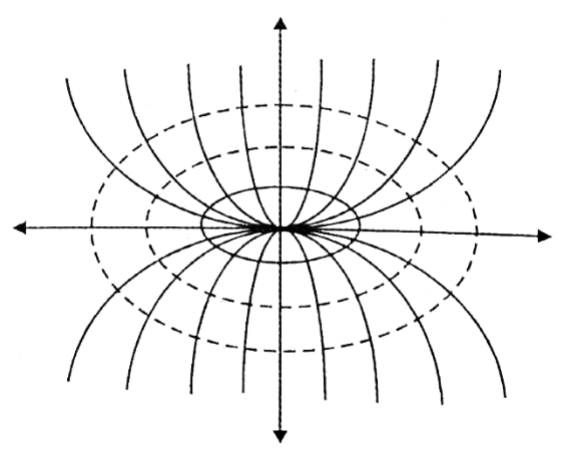
The equation of the family of parabolas through the origin and foci on the y-axis is \(x^2=4 a y\) …………………(1) where a is the parameter.

Differentiating (1) w. r. t. \(x: 2 x=4 a \frac{d y}{d x}\) ………………….(2)

Eliminating the parameter a from (1) and (2): \(\frac{d y}{d x}=\frac{2 y}{x}\) ………………………(3)

(3) is the differential equation of the family (1).

Replacing \(\frac{d y}{d x}\) by \(\left(-\frac{d x}{d y}\right)\) in (3), the D.E. of the orthogonal trajectories to (1) is

⇒ \(-\frac{d x}{d y}=\frac{2 y}{x} \Rightarrow \frac{d y}{d x}=\frac{-x}{2 y} \Rightarrow 2 y d y=-x d x\)

Integrating : \(\int 2 y d y=\int-x d x+c \Rightarrow y^2=-\left(\frac{x^2}{2}\right)+c\)

∴ The equation of the orthogonal trajectories of the family of curves (1) is

⇒ \(y^2=-\frac{x^2}{2}+c \Rightarrow \frac{y^2}{c}+\frac{x^2}{2 c}=1\) ……………………….(4)

Note. The orthogonal trajectories of the family of parabolas (1) are ellipses (4) with centres at the origin and with centres on x-axis

Example. 6. Find the orthogonal trajectories of the family of rectangular hyperbolas \(x y=a^2\) where a is the parameter.
Solution.

Given the equation of the family of curves is \(x y=a^2\) where a is the parameter. (1)

Differentiating (1) w.r. t. x : \(x \frac{d y}{d x}+y=0\) ……………………..(2) is free from ‘a’ the parameter.

Hence (2) is the differential equation of the given family of curves (1).

Replacing \(\frac{d y}{d x}\) by \(\left(-\frac{d x}{d y}\right)\) in (2), the differential equation of the orthogonal trajectories is: \(x\left(-\frac{d x}{d y}\right)+y=0 \Rightarrow y d y=x d x\).

Integrating: \(\int y d y=\int x d x+\frac{c}{2} \Rightarrow \frac{y^2}{2}=\frac{x^2}{2}+\frac{c}{2}\)

⇒ \(y^2-x^2=c \Rightarrow \frac{y^2}{c}-\frac{x^2}{c}=1, c \neq 0\)

∴ The equation of the orthogonal trajectories of the given family of rectangular hyperbolas is \(\frac{y^2}{c}-\frac{x^2}{c}=1(c \neq 0)\) which again represents a family of hyperbolas.

Step-By-Step Guide To Solving Orthogonal Trajectories Problems

Example. 7: Find the orthogonal trajectories of the family of curves \(4 y+x^2+1+c_1 e^{2 y}=0\) where \(c_1\) is the parameter.
Solution.

Given equation of family of curves is \(4 y+x^2+1+c_1 e^{2 y}=0\) ………………..(1)

Differentiating (1) w. r. t. \(x: 4 \frac{d y}{d x}+2 x+2 c_1 e^{2 y} \frac{d y}{d x}=0\) ……………………….(2)

Eliminating \(c_1\) from (1) and (2): \(4 \frac{d y}{d x}+2 x+2\left(-4 y-x^2-1\right) \frac{d y}{d x}=0\)

⇒ \(\left(4-8 y-2 x^2-2\right) \frac{d y}{d x}+2 x=0 \Rightarrow\left(1-4 y-x^2\right) \frac{d y}{d x}+x=0\) …………………………(3)

Now (3) is the differential equation of the given family (1).

Replacing \(\frac{d y}{d x}\) by \(-\frac{d x}{d y}\) in (3).

The Differential equation of the family of Orthogonal trajectories is

⇒ \(\left(1-4 y-x^2\right)\left(-\frac{d x}{d y}\right)+x=0 \Rightarrow x^2+4 y-1+x \frac{d y}{d x}=0 \Rightarrow x \frac{d y}{d x}+4 y=1-x^2\)

⇒ \(\frac{d y}{d x}+\left(\frac{4}{x}\right) y=\frac{1-x^2}{x}\)

This is a linear equation in y.

⇒ \(\text { I.F. }=e^{\int(4 / x) d x}=e^{4 \log x}=e^{\log x^4}=x^4\)

∴ The G.S is \(y x^4=\int\left(\frac{1-x^2}{x}\right) x^4 d x+c_2\)

⇒ \(y x^4=\int x^3 d x-\int x^5 d x+c_2=\frac{x^4}{4}-\frac{x^6}{6}+c_2 \Rightarrow y=\frac{1}{4}-\frac{x^2}{6}+c_2 x^{-4}\)

∴ The equation of the orthogonal trajectories of the given family is

⇒ \(y=(1 / 4)-(1 / 6) x^2+c_2 x^{-4}\)

Example. 8: Find the members of the orthogonal trajectories for the curve \(x+y=c e^y\) which passes through (0,5).
Solution.

Given family of curves is \(x+y=c e^y\) ……………………(1)

Differentiating (1) w. r. t. \(1+\frac{d y}{d x}=c e^y \frac{d y}{d x}\) ……………………..(2)

Eliminatingcfrom(1)and(2): \(1+\frac{d y}{d x}=(x+y) \frac{d y}{d x} \Rightarrow \frac{d y}{d x}(x+y-1)=1\) ………………………(3)

(3)is the differential equation of the given family of curves.

Replacing \(\frac{d y}{d x}\) by \(-\frac{d x}{d y}\) in (3):

The D. E. of the family of O. T. is \(-\frac{d x}{d y}(x+y-1)=1 \Rightarrow \frac{d y}{d x}=-x-y+1\)

⇒ \(\frac{d y}{d x}+y=1-x\) …………………..(4)

This is a linear equation in y.

I F = \(e^x\)

Solution is \(y e^x=e^x-\left(x e^x-e^x\right)+c_2 \Rightarrow y e^x=2 e^x-x e^x+c_2\)

∴ The equation of the O. T. of the given family of curves is \(y e^x=2 e^x-x e^x+c_2\).

Given this passes through (0,5) \(\Rightarrow 5=2-0+c_2 \Rightarrow c_2=3\)

∴ The equation of the orthogonal trajectories of the given family of curves is \(y e^x=2 e^x-x e^x+3 \Rightarrow y=2-x+3 e^{-x}\)

Example. 9. Find the orthogonal trajectories of the family of coaxial circles \(x^2+y^2+2 g x+c=0\), where g is a parameter.
Solution.

Given family of coaxial circles is \(x^2+y^2+2 g x+c=0\) …………………….(1)

Differentiating (1) w.r.t. \(x: 2 x+2 y \frac{d y}{d x}+2 g=0 \Rightarrow g=-x-y \frac{d y}{d x}\) …………………….(2)

Eliminating g from (1) and (2) :

⇒ \(x^2+y^2-2 x^2-2 x y \frac{d y}{d x}+c=0 \Rightarrow y^2-x^2-2 x y \frac{d y}{d x}+c=0\) ……………………..(3)

(3) is the differential equation of the given family of curves. Replacing \(\frac{d y}{d x}\) by \(-\frac{d x}{d y}\) in (3)

⇒ the D.E. of the family of orthogonal trajectories is \(y^2-x^2+(2 x y) \frac{d x}{d y}+c=0\)

⇒ \((2 x y) \frac{d x}{d y}-x^2=-y^2-c \Rightarrow 2 x \frac{d x}{d y}-\frac{1}{y} x^2=-y-\frac{c}{y}\) …………………..(4)

(4)is a linear equation.in x.

Putting \(x^2=v \Rightarrow 2 x \frac{d x}{d y}=\frac{d v}{d y}\) ……………………(5)

(4) and (5) \(frac{d v}{d y}-\frac{1}{y} v=-y-\frac{c}{y} \text { where } P=-\frac{1}{y}, Q=-y-\frac{c}{y}\) ……………………(6)

⇒ \(\text { I.F. }=\exp \left(\int-\frac{1}{y} d y\right)=e^{-\log y}=e^{\log y^{-1}}=\frac{1}{y}\)

General solution of (6) is v(I.F) = \(\int Q(\mathrm{I} . \mathrm{F}) d y+c \Rightarrow \frac{v}{y}=\int\left(-y-\frac{c}{y}\right) \frac{1}{y} d y+c_1\)

⇒ \(v\left(\frac{1}{y}\right)=-\int d y-\int \frac{c}{y^2} d y+c_1=-y+\frac{c}{y}+c_1\)

⇒ \(x^2+y^2-c_1 y-c=0\) is the equation of the orthogonal trajectories of the given family of circles where \(c_1\) is the parameter.

Aliter to solve : \(y^2-x^2+2 x y \frac{d x}{d y}+c=0 \Rightarrow y(2 x) d x-x^2 d y+\left(y^2+c\right) d y=0\)

⇒ \(\frac{y(2 x) d x-x^2 d y}{y^2}+d y+\frac{c}{y^2} d y=0 \Rightarrow\left(x^2 / y\right)+y-(c / y)+2 k=0 \Rightarrow x^2+y^2+2 k y-c=0\)

Worked Examples Of Orthogonal Trajectories In Mathematics

Example. 10. Find the orthogonal trajectories of the family of curves \(\frac{x^2}{a^2}+\frac{y^2}{a^2+\lambda}=1\), where λ is the parameter
Solution.

Given family of curves is \(\frac{x^2}{a^2}+\frac{y^2}{a^2+\lambda}=1\) ……………………(1) where λ is the parameter.

Differentiating (1) w.r.t. \(x: \frac{2 x}{a^2}+\frac{2 y}{a^2+\lambda} \cdot \frac{d y}{d x}=0\)

⇒ \(-\frac{x}{a^2}=\frac{y}{a^2+\lambda} \frac{d y}{d x} \Rightarrow \frac{1}{a^2+\lambda}=-\frac{x}{a^2 y} \frac{d x}{d y}\) ………………………(2)

Eliminating λ from (1) and (2): \(\frac{x^2}{a^2}+y^2\left(-\frac{x}{a^2 y} \frac{d x}{d y}\right)=1\)

⇒ \(\frac{x^2}{a^2}-\frac{x y}{a^2} \frac{1}{d y / d x}=1\) ……………………..(3)

(3) is the differential equation of the given family of curves (1).

Replacing \(\frac{d y}{d x}\) by \(\left(-\frac{d x}{d y}\right)\) in (3), the DE. of the orthogonal trajectories is:

⇒ \(\frac{x^2}{a^2}-\frac{x y}{a^2}\left(\frac{-1}{d x / d y}\right)=1 \Rightarrow \frac{x^2}{a^2}+\frac{x y}{a^2} \cdot \frac{d y}{d x}=1\)

⇒ \(\frac{x y}{a^2} \frac{d y}{d x}=1-\frac{x^2}{a^2}=\frac{a^2-x^2}{a^2} \Rightarrow y d y=\left(\frac{a^2}{x}-x\right) d x\)

Integrating: \(\int y d y=\int \frac{a^2}{x} d x-\int x d x+\frac{c}{2} \Rightarrow \frac{y^2}{2}=a^2 \log |x|-\frac{x^2}{2}+\frac{c}{2}\)

⇒ \(x^2+y^2-2 a^2 \log x=c\) where c is the parameter, is the required equation of the orthogonal trajectories.

Example. 11. Show that the family of confocal conics \(\frac{x^2}{a^2+\lambda}+\frac{y^2}{b^2+\lambda}=1\) is self-orthogonal, where λ is the parameter
Solution.

Given family of confocal conics is \(\frac{x^2}{a^2+\lambda}+\frac{y^2}{b^2+\lambda}=1\) ………………………..(1)

where λ is the parameter

Differentiating (1) w. r. t. \(x: \frac{2 x}{a^2+\lambda}+\frac{2 y}{b^2+\lambda} \cdot \frac{d y}{d x}=0\)

For convenience write \(\frac{d y}{d x}=p\).

Then \(\frac{x}{a^2+\lambda}+\frac{y}{b^2+\lambda} \cdot p=0\) …………………………(2)

⇒ \(x\left(b^2+\lambda\right)+y\left(a^2+\lambda\right) p=0\)

⇒ \(\lambda(x+y p)=-\left(a^2 y p+b^2 x\right) \Rightarrow \lambda=\frac{-\left(b^2 x+a^2 y p\right)}{x+y p}\)

⇒ \(a^2+\lambda=a^2-\frac{\left(b^2 x+a^2 y p\right)}{x+y p}=\frac{a^2 x+a^2 y p-b^2 x-a^2 y p}{x+y p} \Rightarrow a^2+\lambda=\frac{\left(a^2-b^2\right) x}{x+y p}\)

Also \(b^2+\lambda=\frac{-\left(a^2-b^2\right) y p}{x+y p}\) ………………………(3)

Eliminating λ from (1) and (3):

⇒ \(\frac{x(x+y p)}{a^2-b^2}-\frac{y(x+y p)}{\left(a^2-b^2\right) p}=1 \Rightarrow \frac{x+y p}{a^2-b^2}\left(x-\frac{y}{p}\right)=1\)

⇒ \((x+y p)\left(x-\frac{y}{p}\right)=a^2-b^2\) …………………….(4)

(4) is the differential equation of the given family of curves (1).

Replacing p by -1/ p in (4), the differential equation of the orthogonal trajectories is \(\left(x-\frac{y}{p}\right)(x+y p)=a^2-b^2\) ………………………..(5)

(5) is the same as the differential equation (4) of the given family of curves (1).

Hence the given family of confocal conics (1) is self-orthogonal. That is each member of the given family of curves intersects its own members orthogonally.

Orthogonal Trajectories Exercise 3(a)

1. Find the orthogonal trajectories of the following family of curves :

(1) y = cx where ‘c’ is the parameter.

Solution: \(x^2+y^2=k^2\)

(2) \(y=a x^n\) where ‘a’ is the parameter.

Solution: \(n y^2+x^2=c\)

(3) \(\sinh y=c_1 x\) where \(c_1\) is the parameter.

Solution: \(2 \log (\cosh y)+x^2=c_2\)

(4) \(c_1 x^2+y^2=1\) where \(c_1\) is the parameter.

Solution: \(2 \log |y|=x^2+y^2+c_2\)

(5) \(x^{1 / 3}+y^{1 / 3}=c_1\) where \(c_1\) is the parameter.

Solution: \(y^{5 / 3}-x^{5 / 3}=c_2\)

(6) \(y^3+3 x^2 y=c_1\) where \(c_1\) is the parameter.

Solution: \(y^2-x^2=c_2 x\)

(7) \(3 x y=x^3-a^3\) where ‘a’ is the parameter.

Solution: \(2 x^2=(2 y-1)+c e^{-2 y}\)

2. Find the orthogonal trajectories of

(1) the family of circles \(x^2+y^2=a^2\) where ‘a’ is the parameter.

Solution: \(x=c y\)

(2)the family of circles \(x^2+y^2=c x\), c being the parameter.

Solution: \(x^2+y^2=c_1 y\)

(3)the family of circles \(x^2+y^2+2 f y+1=0\), f being the parameter.

Solution: \(x^2+y^2+c x-1=0\)

(4)the family of semicubical parabolas \(a y^2=x^3\), ‘a’ being the parameter.

Solution: \(2 x^2+3 y^2=c\)

(5)the family of parabolas \(y^2=4 a x\) where ‘a’ is the parameter.

Solution: \(2 x^2+y^2=c\)

3. (1) Find the orthogonal trajectories of the family of rectangular hyperbolas \(y=c_1 / x\), \(c_1\) being the parameter.

Solution: \(y^2-x^2=c_2\)

(2) Find the orthogonal trajectories of the family of curves whose differential equation is \(\frac{d y}{d x}=\frac{y^2-x^2}{2 x y}\)

Solution: \(x^2+y^2=c y\)

4. (1) Find the orthogonal trajectories of the family of straight lines in a plane and passing through the origin.

Solution: \(x^2+y^2=c^2\)

(2) Find the orthogonal trajectories of the family of circles through the origin and with centres on x – axis.

Solution: \(x^2+y^2=c y\)

(3) Find the orthogonal trajectories of the family of parabolas opening in the y – direction with the vertex at (1,2).

Solution: \(2(y-2)^2+(x-1)^2=c_2^2\)

5. (1) Find the orthogonal trajectories of the family \(y=x+c e^{-x}\) and determine that particular member of each family that passes through (0,3).

Solution: \(y=x+3 e^{-x}, x-y+2+e^{3-y}\)

(2) Find the family orthogonal to the family \(y=c e^{-x}\) of exponential curves. Determine the member of each family passing through (0,4).

Solution: \(y=4 e^{-x}, y^2=2(x+8)\)

Orthogonal Trajectories: Polar Coordinates

Theorem 2. If f(r,θ,c) = 0, c being the parameter, is the polar equation of the family of curves, then the differential equation of the family of its orthogonal trajectories is \(\mathrm{F}\left(r, \theta,-r^2 \frac{d \theta}{d r}\right)=0\)

Proof.

Given equation of the family of curves is f(r,θ,c) = 0 …………………..(1)

where c is the parameter.

Differentiating (1) w. r. t. θ and eliminating c from (1), we get the differential equation of the family (1).

Let the differential equation of the family (1) be

⇒ \(\mathrm{F}\left(r, \theta, \frac{d r}{d \theta}\right)=0\) ……………………(2)

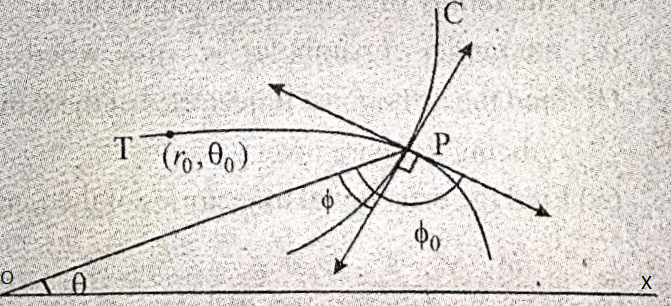
Let C be a member of the family of the curves (1) and T be a member of the family of the trajectories of (1).

Let \(\left(r_0, \theta_0\right)\) be any point on T. Let the two curves C and T intersect at P (r,θ). At P, let \(\phi\) and \(\phi_0\) be the angles which the tangets to the two curves C and T make with the common radius vector OP.

We have tan \(\tan \phi=r \frac{d \theta}{d r}, \tan \phi_0=r_0 \frac{d \theta_0}{d r_0}\)

Also \(\phi_0-\phi=\pi / 2 \Rightarrow \phi_0=(\pi / 2)+\phi\)

⇒ \(\tan \phi_0=\tan (\pi / 2+\phi)=-\cot \phi=-1 / \tan \phi \Rightarrow \tan \phi \tan \phi_0=-1 \Rightarrow\left(r \frac{d \theta}{d r}\right)\left(r_0 \frac{d \theta_0}{d r_0}\right)=-1\)

⇒ \(\frac{d r}{d \theta}=-r r_0 \frac{d \theta_0}{d r_0}\) ………………………(3)

Also at \(r=r_0 \Rightarrow \theta=\theta_0\) ………………………(4)

Eliminating \(r, \theta, \frac{d r}{d \theta}\), from (2), (3), (4) we get :

⇒ \(\mathrm{F}\left(r_0, \theta_0,-r_0^2 \frac{d \theta_0}{d r_0}\right)=0\) …………………….(5)

(5) is true for any point on T.

Thus T is the locus of the point \(\left(r_0, \theta_0\right)\).

Hence the differential equation satisfying T is \(\mathrm{F}\left(r, \theta,-r^2 \frac{d \theta}{d r}\right)=0\)

Working Rule To Find The Orthogonal Trajectories Of A Given Family Of Curves In Polar Coordinates

Let f(r.θ,c)=0 be the equation of the given family of curves …………………….(1)

(1) Differentiate (1) w. r. t. θ and obtain the differential equation \(\mathrm{F}\left(r, \theta, \frac{d r}{d \theta}\right)=0\) by eliminating the parameter c. ……………………………(2)

(2) Replace \(\frac{d r}{d \theta}\) by \(-r^2 \frac{d \theta}{d r}\) in (2)

Then the differential equation of the orthogonal trajectories is \(\mathrm{F}\left(r, \theta,-r^2 \frac{d \theta}{d r}\right)=0\) ……………………(3)

(3) Solve the equation (3) to get the equation of the orthogonal trajectories of (1).

Orthogonal Trajectories Solved Problems

Example. 1. Find the orthogonal trajectories of the family of curves r=aθ where a is the parameter.
Solution.

Given equation of family of curves is r = aθ ………………………..(1)

Differentiating (1) w. r. t. \(\theta \Rightarrow \frac{d r}{d \theta}=a\) …………………….(2)

Eliminating ‘a’ from (1) and (2) ⇒ \(r=\theta \frac{d r}{d \theta} \Rightarrow \frac{d r}{d \theta}=\frac{r}{\theta}\) ………………………(3)

(3) is the differential equation of the given family (1).

Changing \(\frac{d r}{d \theta}\) by \(\left(-r^2 \frac{d \theta}{d r}\right)\) in (3), the differential equation of required orthogonal trajectory is

⇒ \(-r^2 \frac{d \theta}{d r}=\frac{r}{\theta} \Rightarrow \frac{d r}{r}=-\theta d \theta \Rightarrow \int \frac{d r}{r}=-\int \theta d \theta+\log c \Rightarrow \log r=-\frac{\theta^2}{2}+\log c\)

⇒ \(\log r-\log c=-\frac{\theta^2}{2} \Rightarrow \log (r / c)=-\frac{\theta^2}{2} \Rightarrow r / c=\exp \left(-\theta^2 / 2\right)\)

∴ The required family of the orthogonal trajectories of the family (1) is \(\).

Example. 2. Find an equation of the orthogonal trajectory of the family of circles having a polar equation r = 2acosθ where ‘a’ is the parameter.
Solution.

Given equation of the family of circles is r = 2a cosθ ……………….(1)

where ‘a’ is the parameter

Differentiating (1) w. r. t. \(\theta \Rightarrow \frac{d r}{d \theta}=-2 a \sin \theta\) ………………….(2)

Eliminating ‘a’ from (1) and (2): \(r=-\frac{1}{\sin \theta} \cdot \frac{d r}{d \theta} \cdot \cos \theta \Rightarrow r=-(\cot \theta) \frac{d r}{d \theta}\) …………………..(3)

(3) is the differential equation of the given family (1).

Replace \(\frac{d r}{d \theta}\) by \(\left(-r^2 \frac{d \theta}{d r}\right)\) in (3), the differential equation of the required orthogonal trajectories is

⇒ \(r=(-\cot \theta)\left(-r^2 \frac{d \theta}{d r}\right) \Rightarrow \frac{d r}{d \theta}=r \cot \theta\)

⇒ \(\frac{d r}{r}=\cot \theta d \theta \Rightarrow \int \frac{d r}{r}=\int \cot \theta d \theta \Rightarrow \log r=\log \sin \theta+\log 2 c\)

⇒ \(\log r=\log 2 c \sin \theta \Rightarrow r=2 c \sin \theta\)

∴ The equation of the orthogonal trajectories of the given family is r = 2c sin θ.

Example. 3. Find the orthogonal trajectories of the family of curves \(r^2=a^2 \cos 2 \theta\) where ‘a’ is the parameter.
Solution.

Given equation of the family of curves \(r^2=a^2 \cos 2 \theta\) ……………………(1)

Differentiating (1) w.r.t. \(\theta \Rightarrow 2 r \frac{d r}{d \theta}=-2 a^2 \sin 2 \theta \Rightarrow \frac{d r}{d \theta}=-\frac{a^2}{r} \sin 2 \theta\) …………………….(2)

Eliminating \(\) from (1) and (2) \(\Rightarrow \frac{d r}{d \theta}=-\left(\frac{r^2}{\cos 2 \theta}\right) \frac{1}{r} \sin 2 \theta \Rightarrow \frac{d r}{d \theta}=-r \tan 2 \theta\) ……………………..(3)

(3) is the differential equation of the given family (1).

Replacing \(\frac{d r}{d \theta}\) by \(\left(-r^2 \frac{d \theta}{d r}\right)\) in (3), the differential equation of the required orthogonal trajectories is

⇒ \(-r^2 \frac{d \theta}{d r}=-r \tan 2 \theta \Rightarrow r \frac{d \theta}{d r}=\tan 2 \theta \Rightarrow \frac{d r}{r}=\cot 2 \theta d \theta\).

Integrating : \(\int \frac{d r}{r}=\int \cot 2 \theta d \theta+\log c \Rightarrow \log r=\frac{\log \sin 2 \theta}{2}+\log c\)

⇒ \(2 \log r=\log \sin 2 \theta+2 \log c \Rightarrow \log r^2=\log c^2 \sin 2 \theta\)

⇒ \(r^2=c^2\) sin 2θ is the equation of the orthogonal trajectories of the family (1).

Example. 4. Find the orthogonal trajectories of the family of curves r = a(1 – cos θ) where ‘a ‘is the parameter
Solution.

Given equation of the family of curves is

r = a(1 – cos θ) where a is the parameter. …………………..(1)

Differentiating (1) w.r.t. \(\theta: \frac{d r}{d \theta}=a \sin \theta \Rightarrow a=\frac{1}{\sin \theta} \frac{d r}{d \theta}\) ……………………….(2)

Eliminating a from (1) and (2)

⇒ \(r=\frac{1}{\sin \theta} \frac{d r}{d \theta}(1-\cos \theta) \Rightarrow r=\tan \frac{\theta}{2} \frac{d r}{d \theta} \Rightarrow \frac{d r}{d \theta}=r \cot \frac{\theta}{2}\) ………………………(3)

(3) is the differential equation of the given family (1).

Replacing \(\frac{d r}{d \theta}\) by \(\left(-r^2 \frac{d \theta}{d r}\right)\) in (3), the differential equation of the required orthogonal trajectories is

⇒ \(-r^2 \frac{d \theta}{d r}=r \cot \frac{\theta}{2} \Rightarrow \frac{d r}{r}=\left(-\tan \frac{\theta}{2}\right) d \theta\)

⇒ \(\int \frac{d r}{r}=-\int \tan \frac{\theta}{2} d \theta+\log c \Rightarrow \log r=2 \log \cos \left(\frac{\theta}{2}\right)+\log c\)

⇒ \(\log r=\log c \cos ^2\left(\frac{\theta}{2}\right) \Rightarrow r=c \cos ^2\left(\frac{\theta}{2}\right)=\left(\frac{c}{2}\right)(1+\cos \theta)\)

∴ The equation of the. orthogonal trajectories of the given family is r = k(1 + cos θ) where k = c/2.

Example. 5. Find the orthogonal trajectories of the families of curves \(r=\frac{2 a}{1+\cos \theta}\) a is a parameter.
Solution.

Given equation of the family of curves is \(r=\frac{2 a}{1+\cos \theta}\) where a is a parameter

⇒ \( r=\frac{2 a}{2 \cos ^2(\theta / 2)}=a \sec ^2 \frac{\theta}{2}\) …………………….(1)

Differentiating (1) w. r. t. \(\theta: \frac{d r}{d \theta}=2 a \sec \frac{\theta}{2} \cdot \sec \frac{\theta}{2} \tan \frac{\theta}{2} \cdot \frac{1}{2} \Rightarrow \frac{d r}{d \theta}=a \sec ^2 \frac{\theta}{2} \tan \frac{\theta}{2}\) …………….(2).

Eliminating a from (1) and (2) : \(\frac{d r}{d \theta}=r \tan \frac{\theta}{2}\) ………………….(3)

which is the differential equation of the family (1).

Replacing \(\frac{d r}{d \theta}\) by\(\left(-r^2 \frac{d \theta}{d r}\right)\) in (3), the differential equation of the required orthogonal trajectories is

⇒ \(-r^2 \frac{d \theta}{d r}=r \tan \frac{\theta}{2} \Rightarrow-r \frac{d \theta}{d r}=\tan \frac{\theta}{2} \Rightarrow \frac{d r}{r}=\left(-\cot \frac{\theta}{2}\right) d \theta\)

⇒ \(\int \frac{d r}{r}=-\int \cot \frac{\theta}{2} d \theta+\log c \Rightarrow \log r=-2 \log \sin (\theta / 2)+\log c \Rightarrow \log r \sin ^2(\theta / 2)=\log c\)

⇒ \(r \sin ^2(\theta / 2)=c \Rightarrow r=\frac{2 c}{1-\cos \theta}\) is the required family of orthogonal trajectories of the given family.

Example. 6. Find the orthogonal trajectories of the family of curves \(r^n \sin (n \theta)=a^n\) where a is the parameter.
Solution.

The given equation of the family of curves is \(r^n \sin (n \theta)=a^n\) where a is the parameter. …………………(1)

Taking log on both sides of (1) \(\Rightarrow n \log r+\log \sin (n \theta)=n \log a\) ……………….. (2)

Differentiating (2) w.r.t. \(\theta: \frac{n}{r} \frac{d r}{d \theta}+\frac{n \cos n \theta}{\sin n \theta}=0 \Rightarrow \frac{1}{r} \frac{d r}{d \theta}=-\cot n \theta \Rightarrow \frac{d r}{d \theta}=-r \cot n \theta\) ……………………..(3)

(3) is the differential equation of the given family of curves(1).

Replacing \(\frac{d r}{d \theta}\) by \(-r^2 \frac{d \theta}{d r}\) in (3), the differential equation of the required orthogonal trajectories is

⇒ \(-r^2 \frac{d \theta}{d r}=-r \cot n \theta \Rightarrow \frac{d r}{r}=\tan (n \theta) d \theta\)

Integrating: \(\int \frac{d r}{r}=\int \tan (n \theta) d \theta+\log c \Rightarrow \log r=-\frac{1}{n} \log \cos (n \theta)+\log c \Rightarrow n \log r\)\(+\log \cos (n \theta)=n \log c\)

⇒ \(r^n \cos n \theta=c^n\) is the required family of the orthogonal trajectories of (1).

Orthogonal Trajectories Exercise 3(b)

1. Find the orthogonal trajectories of the families of curves in polar coordinates :
(1) rθ = a, a being the parameter.

Solution: \(r^2=c e^{\theta^2}\)

(2) r = a( 1 + cos θ) where a is the parameter.

Solution: \(r=c(1-\cos \theta)\)

(3) r sin 2θ = λ, λ being the parameter.

Solution: \(r^4 \cos 2 \theta=c^2\)

(4) \(r^n=a^n \cos n \theta\) where a is the parameter.

Solution: \(r^n=c^n \sin (n \theta)\)

(5) \(r^n \cos n \theta=a^n\) where a is the parameter.

Solution: \(r^n \sin (n \theta)=c^n\)

2. Find the orthogonal trajectory of \(r=c_1(1-\sin \theta), c_1\) being the parameter.

Solution: \(r=c_2(1+\sin \theta)\)