Bessel’s Equations Exercise 5
Solved Exercise Problems On Bessel’S Equations
1. Define Bessel’s differential equation.
Solution:
The differential equation of the form \(\frac{d^2 y}{d x^2}+\frac{1}{x} \frac{d y}{d x}+\left(1-\frac{n^2}{x^2}\right) y=0\) is called Bessel’s differential equation or Bessel’s equation.
Bessel’s Equations step-by-step solutions
2. Prove that \(a_0 x^n\left[1+(-1) \frac{x^2}{2^2 \cdot 1 !(n+1)}+(-1)^2 \frac{x^4}{2^4 2 !(n+1)(n+2)}+\ldots\right]\)and \(a_0 x^{-n}\left[1+(-1) \frac{x^2}{2^2 \cdot 1 !(-n+1)}+(-1)^2 \frac{x^4}{2^4 2 !(-n+1)(-n+2)}+\ldots .\right]\) are solutions of Bessel’s differential equation:
Solution:
Given
The Bessel’s differential equation is \(\frac{d^2 y}{d x^2}+\frac{1}{x} \frac{d y}{d x}+\left(1-\frac{n^2}{x^2}\right) y=0 \rightarrow \text { (1) }\)
Let us assume that its series solution is \(y=\sum_{r=0}^{\infty} a_r x^{k+r}\).
∴ \(\frac{d y}{d x}=\sum_{r=0}^{\infty} a_r(k+r) x^{k+r-1}\) and \(\frac{d^2 y}{d x^2}=\sum_{r=0}^{\infty} a_r(k+r)(k+r-1) x^{k+r-2}\)
Substituting these values in (1) we have \(\sum_{r=0}^{\infty} a_r\left[(k+r)(k+r-1) x^{k+r-2}+\frac{1}{x}(k+r) x^{k+r-1}+\left(1-\frac{n^2}{x^2}\right) x^{k+r}\right]=0\)
⇒ \(\sum_{r=0}^{\infty}\left[a_r\left\{(k+r)^2-n^2\right\} x^{k+r-2}+x^{k+r}\right]=0 \rightarrow \text { (2) }\)
Since (2) is an identity, the coefficients of various powers of x must be zero.
∴ Equating to zero the coefficient of lowest power of x, i.e., of \(x^{k-2}\) in (2), we have \(a_0\left(k^2-n^2\right)=0 \text {. }\)
Now \(a_0 \neq 0\) as it is the coefficient of the first term with which we begin the series.
∴ \(k^2-n^2=0 \Rightarrow k= \pm n \rightarrow \text { (3) }\)
Now equating to zero the coefficient of \(x^{k-1}\) in (2), we have \(a_1\left\{(k+1)^2-n^2\right\}=0\)
Now \(k= \pm n \Rightarrow(k+1)^2-n^2 \neq 0 \Rightarrow a_1=0\).
Again equating to zero the coefficient of the general term i.e. of \(x^{k+r}\) in (2), we have
⇒ \(a_{r+2}\left\{(k+r+2)^2-n^2\right\}+a_r=0 \Rightarrow a_{r+2}(k+r+n+2)(k+r-n+2)=-a_r\)
⇒ \(a_{r+2}=-\frac{a_r}{(k+r+n+2)(k+r-n+2)} \rightarrow \text { (4) }\)
Putting r=1 in (4), we have \(a_3=\frac{a_1}{(k+n+3)(k-n+3)}=0\), since \(a_1=0\).
Similarly putting \(r=3,5, \ldots\) etc. in (4), we have \(a_1=a_3=a_5 \ldots=0\) (each).
Now two cases arise.
Case 1: When k=n, from (4), we have \(a_{r+2}=-\frac{a_r}{(2 n+r+2)(r+2)}\)
Putting r=0,2,4 etc, we have \(a_2=-\frac{a_0}{(2 n+2)(2)}=-\frac{a_0}{2^2 \cdot 1(n+1)}\)
⇒ \(a_4=-\frac{a_2}{(2 n+4)(4)}=-\frac{a_2}{2^2 \cdot 2!(n+2)}=\frac{a_0}{2^4 \cdot 2!(n+1)(n+2)} \text { etc. }\)
∴ y = \(a_0\left[x^n-\frac{x^{n+2}}{2^2 \cdot 1!(n+1)}+\frac{x^{n+4}}{2^4 2!(n+1)(n+2) \ldots}\right]\)
= \(a_0 x^n\left[1+(-1) \frac{x^2}{2^2 \cdot 1!(n+1)}+(-1)^2 \frac{x^4}{2^4 2!(n+1)(n+2)}+\cdots\right]\)
Case 2: When k=-i. The series solution is obtained by replacing n by -n as \(a_0 x^{-n}\left[1+(-1) \frac{x^2}{2^2 \cdot 1!(-n+1)}+(-1)^2 \frac{x^4}{2^4 2!(-n+1)(-n+2)}+\cdots\right]\)
Examples Of Bessel’s Equations Solved Problems
3. Define Bessel’s function of the first kind of order n.
Solution:
If \(a_0=\frac{1}{2^n \Gamma(n+1)}\), then the solution of the Bessel’s equation, \(y=a_0 x^n\left[1+(-1) \frac{x^2}{2^2 \cdot 1!(n+1)}+(-1)^2 \frac{x^4}{2^4 2!(n+1)(n+2)}+\cdots\right]\) is called
Bessel’s function of the first kind of order n and it is denoted by \(J_n(x)\).
∴ \(J_n(x)=\frac{x^n}{2^n \Gamma(n+1)}\left[1+(-1) \frac{x^2}{2^2 \cdot 1!(n+1)}+(-1)^2 \frac{x^4}{2^4 \cdot 2!(n+1)(n+2)}+.\right]\)
= \(\frac{x^n}{2^n \Gamma(n+1)} \sum_{r=0}^{\infty}(-1)^r \frac{x^{2 r}}{2^{2 r} r!(n+1)(n+2) \ldots(n+r)}=\sum_{r=0}^{\infty}(-1)^r\left(\frac{x}{2}\right)^{n+2 r} \frac{1}{r!\Gamma(n+r+1)}\)
Bessel’s Differential Equation Solved Problems
4. Show that
1) \(J_{-n}(x)=(-1)^n J_n(x)\) when n is a positive integer and
2) \(J_n(-x)=(-1)^n J_n(x)\) for + ve or – ve integers.
Solution:
1) We have \(\int_{-n}(x)=\sum_{r=0}^{\infty}(-1)^r\left(\frac{x}{2}\right)^{-n+2 r} \frac{1}{r!\Gamma(-n+r+1)^r}\)
Since if p is an integer, then \(\Gamma(-p)\) is infinity for p>0,
∴ we get terms in \(J_{-n}\) equal to zero till -n+r+1<1, i.e., r<n.
Hence \(J_{-n}(x)=\sum_{r=0}^{\infty} \frac{(-1)^r}{r!\Gamma(-n+r+1)}\left(\frac{x}{2}\right)^{-n+2 r}=\sum_{s=0}^{\infty} \frac{(-1)^{n+s}}{(n+s)!\Gamma(s+1)}\left(\frac{x}{2}\right)^{n+2 s}\)
= \((-1)^n \sum_{s=0}^{\infty} \frac{(-1)^s}{\Gamma(n+s+1) s!}\left(\frac{x}{2}\right)^{n+2 s}=(-1)^n J_n(x) \text {. }\)
2) We know that \(J_n(x)=\sum_{r=0}^{\infty}(-1)^r \frac{1}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r}\)
Case 1. Let n be a+v e integer. Replacing x bY -x, we have
⇒ \(J_n(-x)=\sum_{r=0}^{\infty}(-1)^r \frac{1}{r!\Gamma(n+r+1)}\left(\frac{-x}{2}\right)^{n+2 r}\)
= \((-1)^n \sum_{r=0}^{\infty}(-1)^r \frac{1}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r}\)
= \((-1)^n J_n(x)\)
Case 2. If n is – ve integer, say n=-m where m is a + ve integer:
∴ \(J_n(x)=J_{-m}(x)=(-1)^m J_m(x)\)
Replacing x by -x
⇒ \(J_n(-x)=(-1)^m J_m(-x)=(-1)^m(-1)^m J_m(x)=(-1)^m J_{-m}(x)=(-1)^{2 m}(-1)^{-m} J_{-m}(x)\)
= \((-1)^{-m} J_{-m}(x)=(-1)^n J_n(x)\)
Hence \(J_n(-x)=(-1)^n J_n(x)\) for + ve or – ve integers.
Step-By-Step Guide To Solving Bessel’s Equations
5. If \(Y_n(x)\) is defined by \(Y_n(x)=\frac{\cos n \pi J_n(x)-J_{-n}(x)}{\sin n \pi}\), when n is not an integer and \(Y_n(x)=\lim _{r \rightarrow n} \frac{\cos r \pi J_r(x)-J_{-r}(x)}{\sin r \pi}\), when n is an integer then show that \(J_n(x)\) and \(Y_n(x)\)are two independent solutions of Bessel’s equation.
solution:
Case 1. Suppose n is not an integer.
Since n is not an integer, \(\sin n \pi \neq 0\).
Hence \(Y_n(x)\) is a linear combination of \(J_n(x)\) and \(J_{-n}(x)\). But \(J_n(x)\) and \(J_{-n}(x)\) are two independent solutions of Bessel’s equation.
Thus \(J_n(x)\) and \(Y_n(x)\) are two independent solutions of Bessel’s equation.
Case 2. Suppose n is an integer.
Since n is an integer, \(\cos n \pi=(-1)^n, \cos n \pi=0\) and \(J_{-n}(x)=(-1)^n J_n\)
Hence \(Y_n(x)\) is undefined. To make it meaningful, we define \(Y_n(x)=\lim _{r \rightarrow n} Y_r(x)=\lim _{r \rightarrow n} \frac{\cos r \pi J_r(x)-J_{-r}(x)}{\sin r \pi}=\lim _{r \rightarrow n} \frac{\frac{\partial}{\partial r}\left[\cos r \pi J_r(x)-J_{-r}(x)\right]}{\frac{\partial}{\partial r}[\sin r \pi]}\)
= \(\left[\frac{-\pi \sin r \pi J_r(x)+\cos r \pi \frac{\partial}{\partial r} J_r(x)-\frac{\partial}{\partial r} J_{-r}(x)}{\pi \cos r \pi}\right]_{r=n}\)
= \(\frac{\cos n \pi\left[\frac{\partial}{\partial r} J_r(x)\right]_{r=n}-\left[\frac{\partial}{\partial r} J_{-r}(x)\right]_{r=n}}{\pi \cos r \pi}\)
= \(\frac{(-1)^n\left[\frac{\partial}{\partial r} J_r(x)\right]_{r=n}-(-1)^{2 n}\left[\frac{\partial}{\partial r} J_{-r}(x)\right]_{r=n}}{\pi(-1)^n}\)
= \(\frac{1}{\pi}\left[\frac{\partial}{\partial r} J_r(x)-(-1)^n \frac{\partial}{\partial r} J_{-r}(x)\right]_{r=n}\)
Since \(J_r(x)\) and \(J_{-r}(x)\) are two solutions of Bessel’s equation, it can be proved that \(Y_n(x)\) is a solution of Bessel’s equation and it is independent with \(J_n(x)\).
Bessel’s Equations Solutions With Applications
6. Define Bessel’s function of the second kind of order n.
Solution:
The function \(Y_n(x)\) defined by \(Y_n(x)=\frac{\cos n \pi J_n(x)-J_{-n}(x)}{\sin n \pi}\), when n is not an integer and \(Y_n(x)=\lim _{r \rightarrow n} \frac{\cos r \pi J_r(x)-J_{-r}(x)}{\sin r \pi}\), when n is an integer is called Bessel’s function of the second kind of order n.
7. Write the general solution of the following equations
1) \(x^2 \frac{d^2 y}{d x^2}+x \frac{d y}{d x}+\left(x^2-64\right) y=0\)
2) \(x^2 \frac{d^2 y}{d x^2}+x \frac{d y}{d x}+\left(x^2-\frac{9}{16}\right) y=0\).
Solution:
1) Given equation is \(x^2 \frac{d^2 y}{d x^2}+x \frac{d y}{d x}+\left(x^2-64\right) y=0\)
⇒ \(x^2 \frac{d^2 y}{d x^2}+x \frac{d y}{d x}+\left(x^2-8^2\right) y=0\), which is a Bessel’s equation of order 8 , an integer
∴ It’s solution is \(y=a J_8(x)+b Y_8(x)\), where a and b are arbitrary constants.
2) Given equation is \(x^2 \frac{d^2 y}{d x^2}+x \frac{d y}{d x}+\left(x^2-\frac{9}{16}\right) y=0\)
⇒ \(x^2 \frac{d^2 y}{d x^2}+x \frac{d y}{d x}+\left[x^2-\left(\frac{3}{4}\right)^2\right] y=0\), which is a Bessel’s equation of order 3/4, not an integer.
∴ It’s solution is \(y=a J_8(x)+b J_{-3 / 4}(x)\), where a and b are arbitrary constants.
8. \(y=a_0\left(1-\frac{x^2}{2^2}+\frac{x^4}{2^2 \cdot 4^2}-\frac{x^6}{2^2 \cdot 4^2 \cdot 6^2} \cdots\right)\) is a solution of Bessel’s differential equation for n=0.
Solution:
The Bessel’s differential equation for n=0 is \(\frac{d^2 y}{d x^2}+\frac{1}{x} \frac{d y}{d x}+y=0 \rightarrow\) (1).
Let us assume that its solution is \(y^{\prime}=\sum_{r=0}^{\infty} a_r x^{k+r}\)
∴ \(\frac{d y}{d x}=\sum_{n=0}^{\infty} a_r(k+r) x^{k+r-1} \text { and } \frac{d^2 y}{d x^2}=\sum_{r=0}^{\infty} a_r(k+r)(k+r-1) x^{r+r-2}\)
Substituting these values in (1), we get \(\sum_{r=0}^{\infty} a_r\left[(k+r)(k+r-1) x^{k+r-2}+\frac{1}{x}(k+r) x^{k+r-1}+x^{k+r}\right]=0\)
⇒ \(\sum_{r=0}^{\infty} a_r\left[(k+r)^2 x^{k+r-2}+x^{k+r}\right]=0 \rightarrow \text { (2) }\)
which is an identity.
Equating to zero, the coefficient of lowest power of x i.e. \(x^{k-2}\), we have \(a_0 k^2=0\).
Since \(a_0 \neq 0\) we get \(k^2=0 \Rightarrow k=0 \rightarrow(3)\)
Now equating to zero the coefficient of next power of x, i.e., \(x^{k-1}\), we have \(a_1(k+1)^2=0 \text {. }\)
Since \(k+1 \neq 0\) by virtue of (3), we have \(a_1=0\).
Again equating to zero the coefficient of the general term, i.e. \(x^{k-r}\), we have \(a_{r+2}(k+r+2)^2+a_r=0 \Rightarrow a_{r+2}=-\frac{a_r}{(k+r+2)^2}\).
When \(k=0, a_{r+2}=-\frac{a_r}{(r+2)^2}\).
Putting \(r=1,3,5, \ldots\) etc., we have \(a_1=a_3=a_5=\cdots=0\) (each).
Again putting r=0,2,4, etc., we have \(a_2=-\frac{a_0}{2^2}, a_4=-\frac{a_2}{4^2}=\frac{a_0}{2^2 \cdot 4^2}\) etc.
Since \(y=\sum_{r=0}^{\infty} a_r x^r\), when k=0, we have \(y=a_0\left(1-\frac{x^2}{2^2}+\frac{x^4}{2^2 \cdot 4^2}-\frac{x^6}{2^2 \cdot 4^2 \cdot 6^2} \cdots\right)\)
Advanced Solved Examples On Bessel’s Equations
9. Prove that \(\ Lt_{x \rightarrow 0} \frac{J_n(x)}{x^n}=\frac{1}{2^n \Gamma(n+1)}\).
Solution:
⇒ \(J_n(x)=\frac{x^n}{2^n \Gamma(n+1)}\left[1-\frac{x^2}{4(n+1)}+\frac{x^4}{4 \cdot 8(n+1)(n+2)}-\cdots\right]\)
⇒ \(\ Lt_{x \rightarrow 0} \frac{J_n(x)}{x^n}=L_{x \rightarrow 0} \frac{1}{2^n \Gamma(n+1)}\left[1-\frac{x^2}{4(n+1)}+\frac{x^4}{4 \cdot 8(n+1)(n+2)}-\ldots\right]=\frac{1}{2^n \Gamma(n+1)} .\)
10. Show that
1) \(J_{-1 / 2}(x)=\sqrt{\left(\frac{2}{\pi x}\right)} \cos x\),
2) \(J_{1 / 2}(x)=\sqrt{\left(\frac{2}{\pi x}\right)} \sin x\) and
3) \(\left[J_{1 / 2}(x)\right]^2+\left[J_{-1 / 2}(x)\right]^2=\frac{2}{\pi x}\)
Solution:
We know that \(J_n(x)=\frac{x^n}{2^n \Gamma(n+1)}\left[1-\frac{x^2}{2(2 n+2)}+\frac{x^4}{2 \cdot 4(2 n+2)(2 n+4)}+\cdots\right]\)
1) Putting \(n=-\frac{1}{2}\) in \(J_n(x)\), we get \(J_{-1 / 2}(x)=\frac{x^{-1 / 2}}{2^{-1 / 2} \Gamma(1 / 2)}\left[1-\frac{x^2}{2(-1+2)}+\frac{x^4}{2 \cdot 4(-1+2)(-1+4)}-\cdots\right]\)
= \(\sqrt{\left(\frac{2}{\pi x}\right)}\left[1-\frac{x^2}{2!}+\frac{x^4}{4!} \cdots\right]=\sqrt{\left(\frac{2}{\pi x}\right)} \cos x\)
2) Putting \(n=\frac{1}{2}\), in \(J_n(x)\), we have
⇒ \(J_{1 / 2}(x)=\frac{x^{1 / 2}}{2^{1 / 2} \Gamma(3 / 2)}\left[1-\frac{x^2}{2(1+2)}+\frac{x^4}{2 \cdot 4 \cdot(1+2)(1+4)} \cdots\right]\)
= \(\sqrt{\left(\frac{x}{2}\right)} \frac{1}{\frac{1}{2} \sqrt{\pi}} \frac{1}{x}\left[x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots\right]=\sqrt{\left(\frac{2}{\pi x}\right)} \sin x\)
3) \(\left[J_{1 / 2}(x)\right]^2+\left[J_{-1 / 2}(x)\right]^2=\left(\frac{2}{\pi x}\right) \cos ^2 x+\left(\frac{2}{\pi x}\right) \sin ^2 x=\frac{2}{\pi x}\)
11. Prove that \(\sqrt{\left(\frac{\pi x}{2}\right)} J_{3 / 2}(x)=\frac{1}{x} \sin x-\cos x\).
Solution:
We know that \(J_n(x)=\frac{x^n}{2^n \Gamma(n+1)}\left[1-\frac{x^2}{2(2 n+2)}+\frac{x^4}{2 \cdot 4(2 n+2)(2 n+4)} \cdots\right]\)
Putting n=3 / 2, we have \(J_{3 / 2}(x)=\frac{x^{3 / 2}}{2^{3 / 2} \Gamma(5 / 2)}[1-\frac{x^2}{2 \cdot 5}+\frac{x^4}{2 \cdot 4 \cdot 5 \cdot 7}\)
– \(\frac{x^6}{2 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 9} \cdots]\)
= \(\frac{x \sqrt{x}}{2 \sqrt{2}(3 / 2)(1 / 2) \sqrt{\pi}}\left[1-\frac{x^2}{2 \cdot 5}+\frac{x^4}{2 \cdot 4 \cdot 5 \cdot 7}-\frac{x^6}{2 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 9}+\cdots\right]\)
∴ \(\sqrt{\left(\frac{\pi x}{2}\right)} J_{\frac{3}{2}}(x)=\frac{1}{3}\left[x^2-\frac{x^4}{2 \cdot 5}+\frac{x^6}{2 \cdot 4 \cdot 5 \cdot 7}-\frac{x^8}{2 \cdot 4 \cdot 5 \cdot 6 \cdot 7 \cdot 9}\right]\)
= \(\frac{2 x^2}{3!}-\frac{4 x^4}{5!}+\frac{6 x^6}{7!}-\frac{8 x^8}{9!}+\cdots\)
= \(\left(\frac{1}{2!}-\frac{1}{3!}\right) x^2-\left(\frac{1}{4!}=\frac{1}{5!}\right) x^4+\left(\frac{1}{6!}-\frac{1}{7!}\right) x^6-\left(\frac{1}{8!}-\frac{1}{9!}\right) x^8 \cdots\)
= \(\left(\frac{x^2}{2!}-\frac{x^4}{4!}+\frac{x^6}{6!} \cdots\right)+\left(-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!} \cdots\right)\)
= \(-\left(1-\frac{x^2}{2!}+\frac{x^4}{4}-\frac{x^6}{6!} \cdots\right)+\frac{1}{x}\left[x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!} \cdots\right]=-\cos x+\frac{1}{x} \sin x .\)
Hence \(\sqrt{\left(\frac{\pi x}{2}\right)} J_{3 / 2}(x)=\frac{1}{x} \sin x-\cos x\)
Worked examples of Bessel’s equations problems
12. Show that
1) \(J_{-3 / 2}(x)=-\sqrt{\left(\frac{2}{\pi x}\right)}\left[\sin x+\frac{1}{x} \cos x\right]\).
2) \(J_{5 / 2}(x)=\left[\frac{2}{\pi x}\right]^{1 / 2}\left[\frac{3-x^2}{x^2} \sin x-\frac{3}{x} \cos x\right]\).
Solution
We know that \(J_n(x)=\frac{x^{\prime \prime}}{2^n \Gamma(n+1)}\left[1-\frac{x^2}{2(2 n+2)}+\frac{x^4}{2 \cdot 4(2 n+2)(2 n+4)}-\cdots\right]\) → (1)
1) Put n=-3 / 2 in (1). Then
Put n=-3 / 2 in (1).
⇒ \(J_{-3 / 2}(x)=\frac{x^{-3 / 2}}{2^{-3 / 2} \Gamma\left(-\frac{3}{2}+1\right)}\left[1-\frac{x^2}{2(-3+2)}+\frac{x^4}{2 \cdot 4 \cdot(-3+2)(-3+4)}-\cdots\right]\)
= \(\frac{2 \sqrt{2}}{x^{3 / 2} \Gamma \Gamma\left(\frac{-1}{2}\right)^2}\left[1+\frac{x^2}{2}-\frac{x^4}{8}+\frac{x^0}{144}-\cdots\right]\)
= \(\frac{2 \sqrt{2}}{x^{3 / 2}(-2 \sqrt{\pi})}\left[1+\frac{x^2}{2}-\frac{x^4}{8}+\frac{x^6}{144}-\cdots\right]\)
= \(-\sqrt{\frac{2}{\pi x}}\left[\frac{1}{x}+\frac{x}{2}-\frac{x^3}{8}+\frac{x^5}{144}-\cdots\right]\)
= \(-\sqrt{\frac{2}{\pi r}}\left[\frac{1}{x}\left(1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots\right)+\left(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots\right)\right]\)
= \(-\sqrt{\frac{2}{\pi x}}\left[\frac{1}{x} \cos x+\sin x\right]\)
2) Put n=5 / 2 in (1).
Then \(J_{5 / 2}(x)=\frac{x^{5 / 2}}{2^{5 / 2} \Gamma\left(\frac{5}{2}+1\right)}[1-\frac{x^2}{2 \cdot 7}\)
+ \(\frac{x^4}{2 \cdot 4 \cdot 7 \cdot 9}-\frac{x^6}{2 \cdot 4 \cdot 6 \cdot 7 \cdot 9 \cdot 11}+\cdots]\)
= \(\frac{x^{5 / 2}}{4 \sqrt{2}\left(\frac{5}{2}\right)\left(\frac{3}{2}\right)\left(\frac{1}{2}\right) \Gamma\left(\frac{1}{2}\right)}\left[1-\frac{x^2}{14}+\frac{x^4}{504}-\frac{x^6}{33264}+\cdots\right]\)
= \(\frac{x^2 \sqrt{2 x}}{15 \sqrt{\pi}}\left[1-\frac{x^2}{14}+\frac{x^4}{504}-\frac{x^6}{33264}+\cdots\right]\)
= \(\left[\frac{2}{\pi x}\right]^{1 / 2} \frac{1}{15}\left[x^3-\frac{x^5}{14}+\frac{x^7}{504}-\cdots\right]\)
= \(\left[\frac{2}{\pi x}\right]^{1 / 2}\left[\frac{x^3}{15}-\frac{x^5}{210}+\frac{x^7}{7560}-\cdots\right]\)
= \(\left[\frac{2}{\pi x}\right]^{1 / 2}\left[\frac{3}{x^2}\left(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots\right)-\left(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots\right)-\frac{3}{x}\left(1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots\right)\right]\)
= \(\left[\frac{2}{\pi x}\right]^{1 / 2}\left[\frac{3}{x^2} \sin x-\sin x-\frac{3}{x} \cos x\right]=\left[\frac{2}{\pi x}\right]^{1 / 2}\left[\frac{3-x^2}{x^2} \sin x-\frac{3}{x} \cos x\right]\)
13. Show that \(\int_0^1 \frac{u J_0(x u)}{\left(1-u^2\right)^{1 / 2}}=\frac{\sin x}{x}\).
Solution:
We have \(J_0(x)=1-\frac{x^2}{2^2}+\frac{x^4}{2^2 \cdot 4^2}-\frac{x^6}{2^2 \cdot 4^2 \cdot 6^2}+\cdots \rightarrow(1)\)
∴ \(\int_0^1 \frac{u J_0(x u)}{\left(1-u^2\right)^{1 / 2}} d u\)
= \(\int_0^1 \frac{u}{\left(1-u^2\right)^{1 / 2}}\left(1-\frac{x^2}{4} u^2+\frac{x^4}{4 \cdot 16} u^4 \ldots\right) d u^{\pi / 2}\)
= \(\int_0^\pi \frac{\sin \theta}{\cos \theta}\left(1-\frac{x^2}{4} \sin ^2 \theta+\frac{x^4}{64} \sin ^4 \theta-\cdots\right) \cos \theta d \theta\)
(On putting \(u=\sin \theta\) and \(u=\cos \theta d \theta\))
= \(\int_0^{\pi / 2} \sin \theta d \theta-\frac{x^2}{4} \int_0^{\pi / 2} \sin ^3 \theta d \theta+\frac{x^4}{64} \int_0^{\pi / 2} \sin ^5 \theta d \theta \ldots\)
= \([-\cos \theta]_0^{\pi / 2}-\frac{x^2}{4} \times \frac{2}{3}+\frac{x^4}{64} \times \frac{4 \cdot 2}{5 \cdot 3}-\cdots\)
= \(1-\frac{x^2}{3!}+\frac{x^4}{5!}-\cdots=\frac{1}{x}\left(x-\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots\right)=\frac{\sin x}{x}\)
Solutions for Bessel’s differential equation practice problems
14. Show that \(\int_0^{\pi / 2} J_1(z \cos \theta) d \theta=\frac{1-\cos z}{z}\).
Solution:
We have \(J_n(x)=\sum_{r=0}^{\infty} \frac{(-1)^r}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{2 r+n} \rightarrow(1)\)
(1) ⇒ \(J_1(z \cos \theta)=\sum_{r=0}^{\infty} \frac{(-1)^r}{r!\Gamma(1+r+1)}\left(\frac{z \cos \theta}{2}\right)^{2 r+1}\)
∴ \(\int_0^{\pi / 2} J_1(z \cos \theta) d \theta=\sum_{r=0}^{\infty} \frac{(-1)^r z^{2 r+1}}{r!(r+1)!2^{2 r+1}} \int_0^{\pi / 2} \cos ^{2 r+1} \theta d \theta\)
= \(\sum_{r=0}^{\infty} \frac{(-1)^r z^{2 r+1}}{r!(r+1)!2^{2 r+1}} \cdot \frac{2 r(2 r-2) \ldots 4 \cdot 2}{(2 r+1)(2 r-1) \ldots 5 \cdot 3}\)
= \(\sum_{r=0}^{\infty} \frac{(-1)^r z^{2 r+1}}{r!(r+1)!2^{2 r+1}} \cdot \frac{[2 r(2 r-2) \ldots 4 \cdot 2]^2}{(2 r+1) 2 r(2 r-1)(2 r-2) \ldots 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}\)
= \(\sum_{r=0}^{\infty} \frac{(-1)^r z^{2 r+1}}{r!(r+1)!2^{2 r+1}} \cdot \frac{2^2(r!)^2}{(2 r+1)!}=\sum_{r=0}^{\infty} \frac{(-1)^r z^{2 r+1}}{2(r+1)(2 r+1)!}\)
= \(\frac{1}{z}-\frac{1}{z}+\frac{z}{2!}-\frac{z^3}{4!}+\frac{z^5}{6!}-\cdots=\frac{1}{z}-\frac{1}{z}\left(1+\frac{z^2}{2!}-\frac{z^4}{4!}+\frac{z^6}{6!}-\cdots\right)=\frac{1-\cos z}{z}\)
15. Prove that Recurrence Formula I : \(x J_n^{\prime}(x)=n J_n(x)-x J_{n+1}(x)\).
Solution:
We have \(J_n(x)=\sum_{r=0}^{\infty}(=1)^r\left(\frac{x}{2}\right)^{n+2 r} \frac{1}{r!\Gamma(n+r+1)}\) where n is a positive integer.
Differentiating w.r.t. x, we have \(J_n^{\prime}(x)=\sum_{r=0}^{\infty}(-1)^r \frac{(n+2 r)}{r!\Gamma(n+r+1)} \frac{1}{2}\left(\frac{x}{2}\right)^{n+2 r-1}\)
∴ \(x J_n^{\prime}(x)=x \sum_{r=0}^{\infty}(-1)^r \frac{(n+2 r)}{r!\Gamma(n+r+1)} \frac{1}{2}\left(\frac{x}{2}\right)^{n+2 r-1}\)
= \(\sum_{r=0}^{\infty}(-1)^r \frac{(n+2 r)}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r}\)
= \(\sum_{r=0}^{\infty}(-1)^r \frac{n}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r}\)
+ \(\sum_{r=0}^{\infty}(-1)^r \frac{2 r}{r!\Gamma(n+r+1)} \frac{x}{2}\left(\frac{x}{2}\right)^{n+2 r-1}\)
= \(n J_n(x)+x \sum_{r=1}^{\infty}(-1)^r \frac{1}{(r-1)!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r-1}\) Putting r-1=s
= \(n J_n(x)-x \sum_{s=0}^{\infty}(-1)^s \frac{1}{s!\Gamma(n+1+s+1}\left(\frac{x}{2}\right)^{n+1+2 s}=n J_n(x)-x J_{n+1}(x) .\)
Hence \(x J_n^{\prime}=n J_n(x)-x J_{n+1}(x)\) which may also be written as \(\frac{d}{d x}\left(x^{-n} J_n\right)=-x^{-n} J_{n+1}\).
16. Prove that Recurrence Formula II : \(x J_n^{\prime}(x)=-n J_n(x)+x J_{n-1}(x)\).
Solution:
As in Recurrence Formula I, we have
⇒ \(x J_n^{\prime}(x)=\sum_{r=0}^{\infty}(-1)^r \frac{(n+2 r)}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r}\)
= \(\sum_{r=0}^{\infty}(-1)^r \frac{(2 n+2 r-n)}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2}\)
= \(-n \sum_{r=0}^{\infty}(-1)^r \frac{1}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r}\)
+ \(\sum_{r=0}^{\infty}(-1)^r \frac{(2 n+2 r)}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r}\)
= \(-n J_n(x)+\sum_{r=0}^{\infty}(-1)^r \frac{\dot{2}(n+r)}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r-1} \cdot\left(\frac{x}{2}\right)\)
= \(-n J_n(x)+x \sum_{r=0}^{\infty}(-1)^r \frac{1}{r!\Gamma(n+r)}\left(\frac{x}{2}\right)^{n+2 r-1}\)
= \(-n J_n(x)+x \sum_{r=0}^{\infty}(-1)^r \frac{1}{r!\Gamma(n-1+r+1)}\left(\frac{x}{2}\right)^{n-1+2 r}=-n J_n(x)+x J_{n-1}(x)\)
Hence \(x J_n^{\prime}(x)=-n J_n(x)+x J_{n-1}(x)\) which may also be written as \(\frac{d}{d x}\left(x^n J_n\right)=x^n J_{n-1}\)
17. Prove that Recurrence Formula 3: \(2 J_n^{\prime}(x)=J_{n-1}(x)-J_{n+1}(x)\).
Solution:
Recurrence formulas 1 and 2 are \(x J_n^{\prime}(x)=n J_n(x)-x J_{n+1}(x)\) and \(x J_n^{\prime}(x)=-n J_n(x)+x J_{n-1}(x) \text {. }\)
Adding we get \(2 x J_n^{\prime}(x)=x\left[J_{n-1}(x)-J_{n+1}(x)\right]\).
Hence \(2 J_n^{\prime}(x)=J_{n-1}(x)-J_{n+1}(x)\).
Aliter: \(J_n(x)=\sum_{r=0}^{\infty}(-1)^r \frac{1}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r}\)
⇒ \(2 J_n^{\prime}(x)=\sum_{r=0}^{\infty}(-1)^r \frac{2}{r!\Gamma(n+r+1)}(n+2 r) \frac{1}{2}\left(\frac{x}{2}\right)^{n+2 r-1}\)
= \(\sum_{r=0}^{\infty}(-1)^r \frac{(n+r+r)}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r-1}\)
= \(\sum_{r=0}^{\infty}(-1)^r \frac{(n+r)}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r-1}+\sum_{r=0}^{\infty}(-1)^r \frac{r}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r-1}\)
= \(\sum_{r=0}^{\infty}(-1)^r \frac{1}{r!\Gamma(n+r)}\left(\frac{x}{2}\right)^{n+2 r-1}-\sum_{r=0}^{\infty}(-1)^{r-1} \frac{1}{(r-1)!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r-1}\)
= \(\sum_{r=0}^{\infty}(-1)^r \frac{1}{r!\Gamma(n-1+r+1)}\left(\frac{x}{2}\right)^{n-1+2 r}-\sum_{s=0}^{\infty}(-1)^s \frac{1}{s!\Gamma(1+n+s+1)}\left(\frac{x}{2}\right)^{n+1+2 s}\)
by putting r-1=s.
= \(J_{n-1}(x)-J_{n+1}(x) \text {. Hence } 2 J_n^{\prime}(x)=J_{n-1}(x)-J_{n+1}(x) \text {. }\)
18. Prove that Recurrence Formula 4: \(2 n J_n(x)=x\left[J_{n-1}(x)+J_{n+1}(x)\right]\).
Solution:
Writing Recurrence formula 1 and 2, we have \(x J_n^{\prime}(x)=n J_n(x)-x J_{n+1}(x)\) and \(x J_n^{\prime}(x)=-n J_n(x)+x J_{n-1}(x) \text {. }\)
Subtracting, we have \(0=2 n J_n(x)-x\left[J_{n+1}(x)+J_{n-1}(x)\right]\).
Hence \(2 n J_n(x)=x\left[J_{n+1}(x)+J_{n-1}(x)\right]\)
Aliter: \(J_n(x)=\sum_{r=0}^{\infty}(-1)^r \frac{1}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r}\)
∴ \(2 n J_n(x)=\sum_{r=0}^{\infty}(-1)^r \frac{(2 n+2 r-2 r)}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r}\)
= \(\sum_{r=0}^{\infty}(-1)^r \frac{2(n+r)}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r}-\sum_{r=0}^{\infty}(-1)^r-\frac{2 r}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r}\)
= \(x \sum_{r=0}^x(-1)^r \frac{1}{r!\Gamma(n-1+r-1)}\left(\frac{x}{2}\right)^{n-1+2}+x \sum_{r=0}^{\infty}(-1)^{r-1} \frac{1}{(r-1)!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r-1}\)
= \(x J_{n-1}(x)+x \sum_{s=0}(-1)^s \frac{1}{s!\Gamma(n+1+s+1)} \times\left(\frac{x}{2}\right)^{n+1+2 s}\), by putting r-1=s
= \(x J_{n-1}(x)+x J_{n+1}(x)\)
Hence \(2 n J_n(x)=x\left[J_{n-1}(x)+J_{n+1}(x)\right]\).
19. Prove that Recurrence Formula 5: \(\frac{d}{d x}\left[x^{-n} J_n(x)\right]=x^{-n} J_{n+1}(x)\).
Solution:
⇒ \(\frac{d}{d x}\left[x^{-n} J_n(x)\right]=-n x^{-n-1} J_n(x)+x^{-n} J_n^{\prime}(x)=x^{-n-1}\left[-n J_n(x)+x J_n^{\prime}(x)\right]\)
= \(x^{-n-1}\left[-n J_n(x)+\left\{n J_n(x)-x J_{n+1}(x)\right\}\right]=x^{-n-1}\left[-x J_{n+1}(x)\right]=-x^{-n} J_{n+1}(x)\)
Hence \(\frac{d}{d x}\left[x^{-n} J_n(x)\right]=-x^{-n} J_{n+1}(x)\)
20. Prove that Recurrence Formula VI : \(\frac{d}{d x}\left[x^n J_n(x)\right]=x^n J_{n-1}(x)\).
Solution:
⇒ \(\frac{d}{d x}\left[x^n J_n(x)\right]=n x^{n-1} J_n(x)+x^n J_n^{\prime}(x)\)
= \(x^{n-1}\left[n J_n(x)+x J_n^{\prime}(x)\right]=x^{n-1}\left[n J_n(x)+\left\{-n J_n(x)+x J_{n-1}(x)\right\}\right]\)
= \(x^{n-1}\left[x J_{n-1}(x)\right]=x^n J_{n-1}(x)\)
Hence \(\frac{d}{d x}\left[x^n J_n(x)\right]=x^n J_{n-1}(x)\)
21. Prove that \(e^{x\left(z-\frac{1}{z}\right)}=\sum^{\infty} z^n J_n(x)\).
Solution:
⇒ \(e^{r(z-1 / z) / 2}=e^{n / 2} e^{-x / 2 z} \)
= \(\left[1+\frac{x z}{2}+\frac{1}{2!}\left(\frac{x z}{2}\right)^2+\cdots+\frac{1}{n!}\left(\frac{x z}{2}\right)^n+\frac{1}{(n+1)!}\left(\frac{x z}{2}\right)^{n+1}+\frac{1}{(n+2)!}\left(\frac{x z}{2}\right)^{n+2}+\cdots\right]\)
⇒ \({\left[1-\frac{x}{2 z}+\frac{1}{2!}\left(\frac{x}{2 z}\right)^2+\cdots+\frac{(-1)^n}{n!}\left(\frac{x}{2 z}\right)^n+\frac{(-1)^{n+1}}{(n+1)!}\left(\frac{x}{2 z}\right)^{n+1}+\frac{(-1)^{n+2}}{(n+2)!}\left(\frac{x}{2 z}\right)^{n+2}+\cdots\right]}\)
Coefficient of \(z^n\) in this product
= \(\frac{1}{n!}\left(\frac{x}{2}\right)^n-\frac{1}{(n+1)!}\left(\frac{x}{2}\right)\left(\frac{x}{2}\right)^{n+1}+\frac{1}{(n+2)!} \frac{1}{2!}\left(\frac{x}{2}\right)^2\left(\frac{x}{2}\right)^{n+2}+\cdots\)
= \(\frac{1}{n!}\left(\frac{x}{2}\right)^n-\frac{1}{(n+1)!}\left(\frac{x}{2}\right)^{n+2}+\frac{1}{2!(n+2)!}\left(\frac{x}{2}\right)^{n+4}+\cdots\)
= \(\frac{(-1)^0}{\Gamma(n+1)}\left(\frac{x}{2}\right)^n+\frac{(-1)}{1!\Gamma(n+2)}\left(\frac{x}{2}\right)^{n+2}+\frac{(-1)^2}{2!\Gamma(n+3)}\left(\frac{x}{2}\right)^{n+4}+\cdots\)
= \(\sum_{r=0}^{\infty}(-1)^r \frac{1}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r}=J_n(x)\)
Similarly, the coefficient of \(z^{-n}\) in the product
= \(\frac{(-1)^n}{n!}\left(\frac{x}{2}\right)^n+\frac{(-1)^{n+1}}{(n+1)!} \frac{x}{2}\left(\frac{x}{2}\right)^{n+1}+\frac{(-1)^{n+2}}{(n+2)!} \frac{1}{2!}\left(\frac{x}{2}\right)^2\left(\frac{x}{2}\right)^{n+2}+\cdots\)
= \((-1)^n\left[\frac{1}{n!}\left(\frac{x}{2}\right)^n+\frac{(-1)}{\Gamma(n+2)}\left(\frac{x}{2}\right)^{n+2}+\frac{(-1)^2}{2!\Gamma(n+3)}\left(\frac{x}{2}\right)^{n+4}+. .\right]=(-1)^n J_n(x) .\)
Hence \(e^{x\left(z-\frac{1}{2}\right)^2}=J_0+\left(z-\frac{1}{z}\right) J_1+\left(z^2+\frac{1}{z^2}\right)_2+\cdots\left[z^n+(-1)^n \frac{1}{z^n}\right] J_n+\cdots\)
= \(\sum_{-\infty}^{\infty} J_n(x), \text { since } J_{-n}(x)=(-1)^n J_n(x)\)
22. Prove that
1) \(\cos (x \sin \theta)=J_0+2 J_2 \cos 2 \theta+2 J_4 \cos 4 \theta+\ldots\)
2) \(\sin (x \sin \theta)=2 \sin \theta J_1+2 \sin 3 \theta J_3+\ldots+2 J_{2 m+1} \sin (2 m+1) \theta+\ldots\)
3) \(\cos x=J_0-2 J_2+2 J_4 \ldots\)
4) \(\sin x=2 J_1-2 J_3+2 J_5 \ldots\)
Solution:
We know that \(e^{(z-1 / z) / 2}=J_0+\left(z-\frac{1}{z}\right) J_1+\left(z^2+\frac{1}{z^2}\right) J_2+\left(z^3-\frac{1}{z^3}\right) J_3+\cdots\)
Putting \(z=e^{i \theta}\), we have
⇒ \(e^{x\left(\frac{e^{i \theta}-e^{-i \theta}}{2}\right)}=J_0+\left(e^{i \theta}-e^{-i \theta}\right) J_1+\left(e^{2 i \theta}+e^{-2 i \theta}\right) J_2+\left(e^{3 i \theta}-e^{-3 i \theta}\right) J_3+\cdots\)
⇒ \(e^{r i \sin \theta}=J_0+(2 i \sin \theta) J_1+(2 \cos 2 \theta) J_2+(2 i \sin 3 \theta) J_3+\cdots\)
⇒ \(\cos (x \sin \theta)+i \sin (x \sin \theta)\)
= \(\left(J_0+2 \cos 2 \theta J_2+2 \cos 4 \theta J_4+\cdots\right)+i\left(2 \sin \theta J_1+2 \sin 3 \theta J_3+\cdots\right)\)
Equating real and imaginary parts, we have
1) \(\cos (x \sin \theta)=J_0+2 J_2 \cos 2 \theta+2 J_4 \cos 4 \theta+\cdots+2 J_{2 m} \cos 2 m \theta+\cdots \rightarrow\) (1)
2) \(\sin (x \sin \theta)=2 \sin \theta J_1+2 \sin 3 \theta J_3+\cdots+2 J_{2 m+1} \sin (2 m+1) \theta+\cdots \rightarrow\) (2)
Putting \(\theta=\frac{\pi}{2}\) in (1) and (2) we have
3) \(\cos x=J_0-2 J_2+2 J_4+\cdots\) and
4) \(\sin x=2 J_1-2 J_3+2 J_5-\cdot\)
23. Express \(J_4(x)\) in terms of \(J_0 \text { and } J_1\).
Solution:
From recurrence relation 4, we have \(J_{n+1}(x)=\left(\frac{2 n}{x}\right) J_n(x)-J_{n-1}(x) \rightarrow\) (1)
Putting n=3 in (1), we get \(J_4(x)=\left(\frac{6}{x}\right) J_3(x)-J_2(x) \rightarrow(2)\)
Putting n=2 in (1), we get \(J_3(x)=\left(\frac{4}{x}\right) J_2(x)-J_1(x) \Rightarrow\) (3)
Substituting (3) in (2), we get \(J_4(x)=\frac{6}{x}\left[\frac{4}{x} J_2(x)-J_1(x)\right]-J_2(x)\)
⇒ \(J_4(x)=\left(\frac{24}{x^2}-1\right) J_2(x)-\frac{6}{x} J_1(x) \rightarrow(4)\)
Next, putting n=1 in (1) we get \(J_2(x)=\left(\frac{2}{x}\right) J_1(x)-J_0(x) \rightarrow\) (5)
Substituting (5) in (4), we get \(J_4(x)=\left(\frac{24}{x^2}-1\right)\left[\frac{2}{x} J_1(x)-J_0(x)\right]-\frac{6}{x} J_1(x)\)
⇒ \(J_4(x)=\left(\frac{48}{x^3}-\frac{8}{x}\right) J_1(x)-\left(\frac{24}{x^2}-1\right) J_0(x)\)
24. Prove that
1) \(J_0^{\prime}=-J_1\)
2) \(J_2=J_0^{\prime \prime}-x^{-1} J_0^{\prime}\) and
3) \(J_2-J_0=2 J_0^{\prime \prime}\).
Solution:
1) From Recurrence formula \(\mathrm{I}\), we have \(x J_n^{\prime}=n J_n-x J_{n+1}\).
Putting n=0, we have \(x J_0^{\prime}=-x J_1\)
∴ \(J_0^{\prime}=-J_1\)
2) From Recurrence formula {1}, we have \(x J_n^{\prime}=n J_n-x J_{n+1}\).
Putting n=1, we have \(x J_1^{\prime}=J_1-x J_2 \rightarrow\) (1).
But from (1): \(J_0^{\prime}=-J_1\).
∴ Differentiating, wehave \(J_0^{\prime \prime}=-J_1^{\prime}\).
Substituting these results in (1), we have \(-x J_0^{\prime \prime}=-J_0^{\prime}-x J_2 \Rightarrow x J_2=x J_0^{\prime \prime}-J_0^{\prime}\).
∴ \(J_2=J_0^{\prime \prime}-x^{-1} J_0^{\prime} \text {. }\)
3) From Recurrence formula 3, we have \(2 J_n^{\prime}=J_{n-1}-J_{n+1} \rightarrow(A)\)
Differentiating both sides w.r.t. x and multiplying by 2 we have \(2^2 J_n^{\prime \prime}=2 J^{\prime}{ }_{n-1}-2 J^{\prime}{ }_{n+1} \rightarrow(B)\)
From (A), replacing n by (n-1) and (n+1) respectively, we have \(2 J_{n-1}^{\prime}=J_{n-2}-J_n \text { and } 2 J_{n+1}^{\prime}=J_n-J_{n+2}\)
Substituting these values in (B), we have \(2^2 J_n^{\prime \prime}=\left(J_{n-2}-J_n\right)-\left(J_n-J_{n+2}\right)=J_{n-2}-2 J_n+J_{n+2}\)
Putting n=0, we get \(2^2 J_0^{\prime \prime}=J_{-2}-2 J_0+J_2=(-1)^2 J_2-2 J_0+J_2=2 J_2-2 J_0\) since \(J_{-n}=(-1)^n J_n\)
Hence \(2 J_0^{\prime \prime}=J_2-J_0\)
25. Prove that \(4 \frac{d^2}{d x^2}\left[J_n(x)\right]=J_{n-2}(x)-2 J_n(x)+J_{n+2}(x)\).
Solution:
Recurrence formula 3 is \(2 J_n^{\prime}(x)=J_{n-1}(x)-J_{n+1}(x) \rightarrow(1)\)
Replacing n by n-1 in (1), we get \(2 J_{n-1}^{\prime}(x)=J_{n-2}(x)-J_n(x) \rightarrow\) (2)
Replacing n by n+1 in (1), we get \(2 J_{n+1}^{\prime}(x)=J_n(x)-J_{n+2}(x) \rightarrow\) (3)
From (1), (2) and (3); \(4 \frac{d^2}{d x^2}\left[J_n(x)\right]=2 \frac{d}{d x}\left\{2 J_n^{\prime}(x)\right\}=2 \frac{d}{d x}\left\{J_{n-1}(x)-J_{n+1}(x)\right\}=2 J_{n-1}^{\prime}(x)-2 J_{n+1}^{\prime}(x)\)
= \(J_{n-2}(x)-J_n(x)-J_n(x)+J_{n+2}(x)=J_{n-2}(x)-2 J_n(x)+J_{n+2}(x)\)
26. Establish the differential formula \(x^2 J_n^{\prime \prime}(x)=\left(n^2-n-x^2\right) J_n(x)+x J_{n+1}(x) \text { for } n=0,1,2, \ldots\)
Solution:
Writing recurrence formula I, we have \(x J_n^{\prime}(x)=n J_n(x)-x J_{n+1}(x) \rightarrow(1)\)
Differentiating both sides w.r.t. x, we have
⇒ \(x J_n^{\prime \prime}(x)+J_n^{\prime}(x)=n J_n^{\prime}(x)-x J_{n+1}^{\prime}(x)-J_{n+1}(x)\)
⇒ \(x^2 J_n^{\prime \prime}(x)=(n-1) x J_n^{\prime}(x)-x \cdot x J_{n+1}^{\prime}(x)-x J_{n+1}(x) \rightarrow(2)\)
From recurrence formula 2, we have \(x J_n^{\prime}(x)=-n J_n(x)+x J_{n-1}(x)\).
Writing (n+1) for n; we have \(x J_{n+1}^{\prime}(x)=-(n+1) J_{n+1}(x)+x J_n(x) \rightarrow\) (3)
Substituting for \(x J_n^{\prime}(x)\) from (1) and for \(x J_{n+1}^{\prime}(x)\) from (3) in (2),
we have \(x^2 J_n^{\prime \prime}(x)=(n-1)[n J_n(x)-x J_{n+1}(x)-x\left[-(n+1) J_{n+1}(x)+x J_n(x)\right]-x J_{n+1}(x)]\)
= \(\left(n^2-n-x^2\right) J_n(x)+x J_{n+1}(x) .\)
27. Prove that
1) \(J_{n-1}=\frac{2}{x}\left[n J_n-(n+2) J_{n+2}+(n+4) J_{n+4} \cdots\right]\)
2) \(\frac{1}{2} x J_n=(n+1) J_{n+1}-(n+3) J_{n+3}+(n+5) J_{n+5}+\ldots\)
3) \(J_n^{\prime}=\frac{2}{x}\left[\frac{n}{2} J_n-(n+2) J_{n+2}+(n+4) J_{n+4} \cdots \cdots\right]\)
Solution:
1) From recurrence formula 4, we have \(x\left(J_{n-1}+J_{n+1}\right)=2 n J_n \Rightarrow J_{n-1}+J_{n+1}=\frac{2}{x} n J_n \rightarrow \text { (1). }\)
Replacing n by (n+2), and changing sign, we get \(-J_{n+1}-J_{n+3}=\frac{-2}{x}(n+2) J_{n+2} \rightarrow(2)\)
Again replacing n by (n+4) in (1), we have \(J_{n+3}+J_{n+5}=\frac{2}{x}(n+4) J_{n+4} \rightarrow\) (3)
Again replacing n by (n+6) in (1) and changing the sign, we have \(-J_{n+5}-J_{n+7}=\frac{2}{x}(n+6) J_{n+6} \rightarrow(4)\)
……..
……..
Adding (1), (2), (3), (4), etc., we have \(J_{n-1}=\frac{2}{x}\left[n J_n-(n+2) J_{n+2}+(n+4) J_{n+4}-(n+6) J_{n+6} \cdots\right]\)
2) Replacing n by (n+1), we have \(\frac{x}{2} J_n=(n+1) J_{n+1}-(n+3) J_{n+3}+(n+5) J_{n+5} \cdots\)
3) From recurrence formula II, we have \(J_n^{\prime}=-\frac{n}{x} J_n+J_{n-1}\).
Substituting the value of \(J_{n-1}\) from (1), we have \(J_n^{\prime}=-\frac{n}{x} J_n+\frac{2}{x}\left[n J_n-(n+2) J_{n+2}+(n+4) J_{n+4} \cdots\right]\)
= \(\frac{2}{x}\left[\frac{n}{2} J_n-(n+2) J_{n+2}+(n+4) J_{n+4} \cdots\right]\)
28. Prove that
1) \(\frac{d}{d x}\left[J_n^2+J_{n+1}^2\right]=2\left(\frac{n}{x} J_n^2-\frac{n+1}{x} J_{n+1}^2\right)\)
2) \(J_0^2+2\left(J_1^2+J_2^2+J_3^2+\ldots\right)=1\)
3) \(\left|J_0(x)\right| \leq 1,\left|J_n(x)\right| \leq 2^{-1 / 2},(n \geq 1)\)
Solution:
From recurrence formula 1, we have \(J_n^{\prime}=\frac{n}{x} J_n-J_{n+1} \rightarrow\) (1)
Also from recurrence formula 2, we have \(J_n^{\prime}=-\frac{n}{x} J_n+J_{n-1}\)
Replacing n by (n+1), we have \(J_{n+1}^{\prime}=-\frac{n+1}{x} J_{n+1}+J_n \rightarrow\) (3)
Substituting the values of \(J_n^{\prime}\) and \(J_{n+1}^{\prime}\) from (2) and (3), we have
⇒ \(\frac{d}{d x}\left(J_n^2+J_{n+1}^2\right)=2 J_n J_n^{\prime}+2 J_{n+1} J_{n+1}^{\prime}\)
= \(2 J_n\left(\frac{n}{\chi} J_n-J_{n+1}\right)+2 J_{n+1}\left(-\frac{n+1}{x} J_{n+1}+J_n\right)=2\left(\frac{n}{x} J_n^2-\frac{n+1}{x} J_{n+1}^2\right)\)
2) From (1), we have \(\frac{d}{d x}\left(J_n^2+J_{n+1}^2\right)=2\left(\frac{n}{x} J_n^2-\frac{n+1}{x} J_{n+1}^2\right)\)
Putting n=0,1,2,3, ….. etc., we have
⇒ \(\frac{d}{d x}\left(J_0^2+J_1^2\right)=2\left(0-\frac{1}{x} J_1^2\right)\)
⇒ \(\frac{d}{d x}\left(J_1^2+J_2^2\right)=2\left(\frac{1}{x} J_1^2-\frac{2}{x} J_2^2\right)\)
⇒ \(\frac{d}{d x}\left(J_2^2+J_3^2\right)=2\left(\frac{2}{x} J_2^2-\frac{3}{x} J_3^2\right)\)
………
………
Adding all these, we have \(\frac{d}{d x}\left[J_0^2+2\left(J_1^2+J_2^2+J_3^2+..\right)\right]=0\)
Integrating, we have \(J_0^2+2\left(J_1^2+J_2^2+J_3^2+\cdots\right)=c\) (constant), Putting x=0, we get \(\left(J_0^2\right)_{x=0}=c\), since
⇒ \(\left(J_1\right)_{x=0}=0,\left(J_2\right)_{x=0}=0\) etc.
⇒ \(\left(J_0^2\right)_{x=0}=c \Rightarrow 1=c\).
Hence \(J_0^2+2\left(J_1^2+J_2^2+J_3^2+\cdots\right)=1\).
3) We have proved that \(J_0^2+2\left(J_1^2+J_2^2+J_3^2 \cdots+J_n^2+\cdots\right)=1\)
Since \(J_1^2, J_2^2, J_3^2 \ldots\) are all positive or zero.
∴ \(J_0^2 \leq 1 \Rightarrow\left|J_0\right| \leq 1\), i.e.. \(\left|J_0(x)\right| \leq 1\).
Also \(|2 J_n^2| \leq 1 \Rightarrow W_n |\leq \frac{1}{\sqrt{2}}\), i.e., \(\left|J_n(x)\right| \leq 2^{-1 / 2}\) (for \(n \geq 1\)).
29. Prove that \(J_n(x)=0\) has no repeated roots except at x=0.
Solution:
If possible let α be a repeated root of \(J_n(x)=0\).
∴ \(J_n(\alpha)=0 \text { and } J_n^{\prime}(\alpha)=0 \rightarrow(1)\)
From Recurrence formulas 1 and 2, we have \(J_{n+1}(x)=\frac{n}{x} J_n-J_n^{\prime}(x)\) and \(J_{n-1}(x)=\frac{n}{x} J_n+J_n^{\prime}(x)\)
∴ \(J_{n+1}(\alpha)=0\) and \(J_{n-1}(\alpha)=0\) with the help of (1), i.e., for the same value of \(x, J_n(x), J_{n+1}(x)\) and \(J_{n-1}(x)\) are all zero, which is absurd as we cannot have two power series having the same sum function. Thus \(J_n(x)=0\) cannot have repeated roots except at x=0.
30. Show that \(\int_0^x x^n J_{n-1}(x) d x=x^n J_n(x)\).
Solution:
Recurrence formula VI is \(\frac{d}{d x}\left[x^n J_n(x)\right]=x^n J_{n-1}(x)\)
Integrate this between the limits 0 to x, we get
∴ \(\left[x^n J_n(x)\right]_0^x=\int_0^x x^n J_{n-1}(x) d x \Rightarrow \int_0^x x^n J_{n-1}(x) d x=x^n J_n(x) .\).
31. Show that \(\int_0^x x^{n+1} J_n(x) d x=x^{n+1} J_{n+1}(x)\).
Solution:
Recurrence formula VI is \(\frac{d}{d x}\left[x^n J_n(x)\right]=x^n J_{n-1}(x)\)
Replace n by n+1, we get \(\frac{d}{d x}\left[x^{n+1} J_{n+1}(x)\right]=x^{n+1} J_n(x)\)
Integrate this between the limits 0 to x we get
\(\left[x^{n+1} J_{n+1}(x)\right]=\int_0^x x^{n+1} J_n(x) d x \Rightarrow \int_0^x x^{n+1} J_n(x) d x=x^{n+1} J_{n+1}(x) .\).
32. Prove that \(\int_a^b J_0(x) J_1(x) d x=\frac{1}{2}\left[J_0^2(a)-J_0^2(b)\right]\).
Solution:
Recurrence relation VII is \(\frac{d}{d x}\left[x^{-n} J_n(x)\right]=-x^{-n} J_{n+1}(x) \Rightarrow \frac{d}{d x} J_0(x)=-J_1(x)\)
∴\(\int_a^b J_0(x) J_1(x) d x=-\int_a^b J_0(x) J_0^{\prime}(x) d x=-\left[\frac{\left[J_0(x)\right]^2}{2}\right]_a^b=\frac{1}{2}\left[J_0^2(a)-J_0^2(b)\right]\).
33. Prove that
1) \(\frac{d}{d x}\left(x J_n J_{n+1}\right)=x\left(J_n^2-J_{n+1}^2\right)\)
2) \(x=2 J_0 J_1+6 J_1 J_2+\ldots+2(2 n+1) J_n J_{n+1}+\ldots\)
Solution:
1) \(\frac{d}{d x}\left(x J_n J_{n+1}\right)=J_n J_{n+1}+x\left(J_n^{\prime} J_{n+1}+J_n J_{n+1}^{\prime}\right)\)
= \(J_n J_{n+1}+\left(x J_n^{\prime}\right) J_{n+1}+J_n\left(x J_{n+1}^{\prime}\right) \rightarrow \text { (1) }\)
From Recurrence formulas 1 and 2, we have \(x J_n^{\prime}=n J_n-x J_{n+1} \rightarrow\) (2)
and \(x J_n^{\prime}=-n J_n+x J_{n-1} \rightarrow \text { (3). }\)
Replacing n by (n+1) in (3), we have \(x J_{n+1}^{\prime}=-(n+1) J_{n+1}+x J_n \rightarrow\) (4)
Substituting the values of \(x J_n^{\prime}\) and \(x J_{n+1}^{\prime}\) from (2) and (4), in (1), we have
∴ \(\frac{d}{d x}\left(x J_n J_{n+1}\right)=J_n J_{n+1}+\left(n J_n-x J_{n+1}\right) J_{n+1}+J_n\left\{-(n+1) J_{n+1}+x J_n\right\}=x\left(J_n^2-J_{n+1}^2\right) \text {. }\)
2) From (1), we have \(\frac{d}{d x}\left(x J_n J_{n+1}\right)=x\left(J_n^2-J_{n+1}^2\right)\)
Putting n=0,1,2,3, ….. we have
⇒ \(\frac{d}{d x}\left(x J_0 J_1\right)=x\left(J_0^2-J_1^2\right) \rightarrow(1)\)
⇒ \(\frac{d}{d x}\left(x J_1 J_2\right)=x\left(J_1^2-J_2^2\right) \rightarrow(2)\)
⇒ \(\frac{d}{d x}\left(x J_2 J_3\right)=x\left(J_2^2-J_3^2\right) \rightarrow(3)\)
⇒ \(\frac{d}{d x}\left(x J_3 J_4\right)=x\left(J_3^2-J_4^2\right) \rightarrow(4)\)
………..
…….
Multiplying (1), (2), (3)… by 1,3,5, ………. respectively and adding we have
⇒ \(\frac{d}{d x} {\left[x\left(J_0 J_1+3 J_1 J_2+5 J_2 J_3+\cdots\right)\right]=x\left[\left(J_0^2-J_1^2\right)+3\left(J_1^2-J_2^2\right)+5\left(J_2^2-J_3^2\right)+\cdots\right] }\)
= \(x\left[J_0^2+2\left(J_1^2+J_2^2+\cdots\right)\right]=x \cdot 1=x\)
Integrating both sides, we have \(x\left(J_0 J_1+3 J_1 J_2+5 J_2 J_2+\cdots\right)=\frac{x^2}{2}+c\) (constant)
Putting x=0, we get 0=0+c ∴ c=0
Hence \(x\left(J_0 J_1+3 J_1 J_2+5 J_2 J_3+\cdots\right)=\frac{x^2}{2}\)
⇒ \(2 J_0 J_1+6 J_1 J_2+10 J_2 J_3+\cdots+2(2 n+1) J_n J_{n+1}+\cdots=x\)
34. Show that \(2^r J_n^r=J_{n-r}-r J_{n-r+2}+\frac{r(r-1)}{2 !} J_{n-r+4}-\cdots+(-1)^r J_{n+r}\)
Solution:
Recurrence formula 3 is \(2 J_n{ }^{\prime}=J_{n-1}-J_{n+1} \rightarrow\) (1)
Replacing n by (n-1) and (n+1) respectively in (1), we get \(2 J_{n-1}^{\prime}=J_{n-2}-J_n \rightarrow\) (2)
and \(2 J_{n+1}^{\prime}=J_n-J_{n+2} \rightarrow \text { (3) }\)
Differentiating (1), w.r.t. ‘ x ‘, we have \(2 J_n^{\prime \prime}=J_{n-1}^{\prime}-J^{\prime}{ }_{n+1} \Rightarrow 2^2 J_n^{\prime \prime}=2 J_{n-1}^{\prime}-2 J_{n+1}^{\prime} \rightarrow \text { (4) }\)
Substituting the values of \(2 J_{n-1}^{\prime}\) and \(2 J_{n+1}^{\prime}\) from (2) and (3) obtained in (4), we get \(2^2 J_n^{\prime \prime}=\left(J_{n-2}^{\prime}-J_n\right)-\left(J_n-J_{n+2}\right)=J_{n-2}-2 J_n+J_{n+2}^{\prime \prime} \text {. }\)
Differentiating (4) again, and multiplying by 2, we have \(2^3 J_n^{\prime \prime \prime}=2 J_{n-2}^{\prime}-2^2 J_n^{\prime}+2{ }_{n+2}^{\prime} \rightarrow \text { (5). }\)
Substituting in (5), the values of \(2 J_n^{\prime}, 2 J_{n-2}^{\prime}, 2 J_{n+2}^{\prime}\) from (1), the last two obtained by replacing n by (n-2) and (n+2) respectively in (1),
we get \(^3 J_n^{\prime \prime \prime}=\left(J_{n-3}-J_{n-1}\right)-2\left(J_{n-1}-J_{n+1}\right)+\left(J_{n+1}-J_{n+2}\right)\)
= \(J_{n-2}-3 J_{n-1}+3 J_{n+1}-J_{n+2}=J_{n-2}-{ }^3 C_1 J_{n-1}+{ }^2 C_2 J_{n+1}-{ }^3 C_3 J_{n+3}\)
Applying the same process again, and again, we have \(2^r J_n^r=J_{n-r}-{ }^r C_1 J_{n-r+2}+{ }^r C_2 J_{n-r+4}+\cdots+(-1)^r \cdot{ }^r C_r J_{n+r}\)
= \(J_{n-r}-r J_{n-r+2}+\frac{r(r-1)}{2!} J_{n-r+4}+\cdots+(-1)^r J_{n+r}\)
35. Prove that \(J_n J_{-n}^{\prime}-J_n^{\prime} J_{-n}=-\frac{2 \sin n \pi}{x \pi}\).
Solution:
We know that \(J_n\) and \(J_{-n}\) are solutions of Bessel’s equation \(y^{\prime \prime}+\frac{1}{x} y^{\prime}+\left(1-\frac{n^2}{x^2}\right) y=0\)
∴ \(J_n^{\prime \prime}+\frac{1}{x} J_n^{\prime}+\left(1-\frac{n^2}{x^2}\right) J_n=0 \rightarrow\) (1)
and \(J_{-n}^{\prime \prime}+\frac{1}{x} J_{-n}^{\prime}+\left(1-\frac{n^2}{x^2}\right) J_{-n}=0 \rightarrow \text { (2) }\)
Multiplying (1) by \(J_{-n}\) and (2) by \(J_n\) and then substracting. we get \(J_n^{\prime \prime} J_{-n}-J_{-n}^{\prime \prime} J_n+\frac{1}{x}\left(J_n^{\prime} J_{-n}-J_{-n}^{\prime} J_n\right)=0 \rightarrow (3)\)
Let \(J_n{ }^{\prime} J_{-n}-J_{-n}^{\prime} J_n=v \rightarrow(4)\)
Differentiating (4) w.r.t. x we get \(\left(J_n^{\prime \prime} J_{-n}+J_n^{\prime} J_{-n}^{\prime}\right)-\left(J_{-n}^{\prime \prime} J_n+J_{-n}^{\prime} J_n^{\prime}\right)=v^{\prime}\)
⇒ \(J_n^{\prime \prime} J_{-n}-J_{-n}^{\prime \prime} J_n=v^{\prime} \rightarrow \text { (5) }\)
Using (4) and (5), (3) becomes \(v^{\prime}+\left(\frac{1}{x}\right) v=0 \Rightarrow \frac{d v}{d x}+\frac{1}{x} v=0 \Rightarrow \frac{1}{v} d v+\frac{1}{x} d x=0\)
Integrating, we get \(\log v+\log x=\log c \Rightarrow v=\frac{c}{x} \Rightarrow J_n^{\prime} J_{-n}-J_{-n}^{\prime} J_n=\frac{c}{x} \rightarrow\) (6) by (4)
Now, \(J_n(x)=\frac{1}{2^n \Gamma(n+1)}\left[x^n-\frac{x^{n+2}}{4(n+1)}+\frac{x^{n+4}}{4 \cdot 8 \cdot(n+1)(n+2)}-\cdots\right]\)
and \(J_{-n}(x)=\frac{1}{2^{-n} \Gamma(-n+1)}\left[x^{-n}-\frac{x^{2-n}}{4(1-n)}+\frac{x^{4-n}}{4 \cdot 8 \cdot(1-n)(2-n)}-\cdots\right]\)
∴ Using the above values of \(J_n\) and \(J_{-n}\), and from (6) we have
⇒ \(\frac{1}{2^n \Gamma(n+1)}\left[n x^{n-1}-\frac{(n+2) x^{n+1}}{4(n+1)}+(n+4) \frac{x^{n+3}}{4 \cdot 8 \cdot(1-n)(2-n)}-\cdots\right]\)
x \(\frac{1}{2^{-n} \Gamma(-n+1)}\left[x^{-n}-\frac{x^{2-n}}{4(1-n)}+\frac{x^{4-n}}{4 \cdot 8 \cdot(1-n)(2-n)}-\cdots\right]\)
– \(\frac{1}{2^{-n} \Gamma(-n+1)}\left[-n x^{-n-1}-(2-n) \frac{x^{1-n}}{4(1-n)}+(4-n) \frac{x^{3-n}}{4 \cdot 8 \cdot(1-n)(2-n)}-\cdots\right]\)
x \(\frac{1}{2^n \Gamma(n+1)}\left[x^n-\frac{x^{n+2}}{4(n+1)}+\frac{x^{n+4}}{4 \cdot 8 \cdot(n+1)(n+2)}-\cdots\right]=\frac{c}{x}\)
Now comparing the coefficients of \(\frac{1}{x}\) from both sides, we get
⇒ \(\frac{n}{2^n \Gamma(n+1) \cdot 2^{-n} \Gamma(-n+1)}+\frac{n}{2^{-n} \cdot \Gamma(-n+1) 2^n \Gamma(n+1)}=c\)
⇒ \(c=\frac{2 n}{n \Gamma(n) \Gamma(1-n)} \Rightarrow c=\frac{2}{(\pi / \sin n \pi)}=\frac{2 \sin n \pi}{\pi}\)
(because \(\Gamma(n) \Gamma(1-n)=\frac{\pi}{\sin n \pi}\))
Putting this value of c in (6) and multiplying both sides by (-1), we get \(J_n J_{-n}^{\prime}-J_n^{\prime} J_{-n}=-\frac{2 \sin n \pi}{\pi x}\)
36. Prove that \(\frac{J_{n+1}}{J_n}=\frac{(x / 2)}{(n+1)-\frac{(x / 2)^2}{(n+2)-\frac{(x / 2)^2}{(n+3)} \cdots}}\)
Solution:
Since \(J_n\) and \(J_{-n}\) are the solutions of the Bessel’s differential equation.
⇒ \(\frac{d^2 y}{d x^2}+\frac{1}{x}-\frac{d y}{d x}+\left(1-\frac{n^2}{x^2}\right) y=0\), we have \(\frac{d^2 J_n}{d x^2}+\frac{1}{x} \frac{d J_n}{d x}+\left(1-\frac{n^2}{x^2}\right) J_n=0 \rightarrow(1)\) and \(\frac{d^2 J_{-n}}{d x^2}+\frac{1}{x} \frac{d J_{-n}}{d x}+\left(1-\frac{n^2}{x^2}\right) J_{-n}=0 \rightarrow (2)\)
Multiplying (1) by \(J_{-n}\) and (2) by \(J_n\) and subtracting, we have
⇒ \(\left(J_{-n} \frac{d^2 J_n}{d x^2}-J_n \frac{d^2 J_{-n}}{d x^2}\right)+\frac{1}{x}\left(J_{-n} \frac{d J_n}{d x}-J_n \frac{d J_{-n}}{d x}\right)=0\)
⇒ \(\frac{J_{-n} \frac{d^2 J_n}{d x^2}-J_n}{J_{-n} \frac{d J_n}{d x}-J_n}\) \(\frac{\frac{d^2 J_{-n}}{d x^2}}{\frac{d J_{-n}}{d x}}=-\frac{1}{x}\)
Integrating both the sides w.r.t x, we have \(\log \left(J_{-n} \frac{d J_n}{d x}-J_n \frac{d J_n}{x}\right)=-\log x+\log A\)
where A is an arbitrary constant. ∴ \({-n} \frac{d J_n}{d x}-J_n \frac{d J_{-n}}{d x}=\frac{A}{x} \rightarrow(3)\)
∴ \(\frac{1}{2^{-n} \Gamma(-n+1)}\left[x^{-n}-\frac{x^{-n+2}}{2(-2 n+2)}+\frac{x^{-n+4}}{2 \cdot 4(-2 n+2)(-2 n+4)} \cdots\right]\)
x \(\frac{1}{2^n \Gamma(n+1)}\left[n x^{n-1}-\frac{(n+2) x^{n+1}}{2 \cdot(2 n+2)}+\frac{(n+4) x^{n+3}}{2 \cdot 4(2 n+2)(2 n+4)} \cdots\right]\)
– \(\frac{1}{2^n \Gamma(n+1)} \cdot\left[x^n-\frac{x^{n+2}}{2(2 n+2)}+\frac{x^{n+4}}{2 \cdot 4(2 n+2)(2 n+4)}\right]\)
x \(\frac{1}{2^{-n} \Gamma(-n+1)}\left[-n x^{-n-1}-\frac{(-n+2) x^{-n+1}}{2 \cdot(-2 n+2)}+\frac{(-n+4) x^{-n+3}}{2 \cdot 4(-2 n+2)(-2 n+4)}\right]=\frac{A}{x}\).
Comparing coefficient of \(\frac{1}{x}\) on both the sides, we have \(\frac{1}{\Gamma(-n+1) \Gamma(n+1)}[n-(-n)]=A \Rightarrow A=\frac{2 n}{\Gamma(-n+1) \Gamma(n+1)}=\frac{2}{\Gamma(1-n) \Gamma(n)}\)
= \(\frac{2}{\frac{\pi}{\sin n \pi}}=\frac{2 \sin n \pi}{\pi}\), since \(\Gamma(n) \Gamma(1-n)=\frac{\pi}{\sin n \pi}\)
Hence from (3), we have \(J_{-n} \frac{d J_n}{d x}-J_n \frac{d J_{-n}}{d x}=\frac{2 \sin n \pi}{\pi x}\)
Dividing both sides by \(-J_n^2\), we get \(\frac{\frac{d J_{-n}}{d x} J_n-J_{-n} \frac{d J_n}{d x}}{J_n^2}=-\frac{2 \sin n \pi}{\pi x J_n^2} \Rightarrow \frac{d}{d x}\left(\frac{J_{-n}}{J_n}\right)=-\frac{2 \sin n \pi}{\pi x J_n^2}\).
37. Prove that \(\frac{d}{d x}\left(\frac{J_{-n}}{J_n}\right)=-\frac{2 \sin n \pi}{\pi x J_n^2}\).
Solution:
1) Recurrence relation 6 is \(\left.\frac{d}{d x}\left(x^n J_n\right)=x^n J_{n-1} \Rightarrow\left(\frac{1}{x} \frac{d}{d x}\right)\left(x^n J_n\right)=x^{n-1} J_{n-1}\right)\)
Now, \(\left(\frac{1}{x} \frac{d}{d x}\right)^m\left(x^n J_n\right)\)
= \(\left(\frac{1}{x} \frac{d}{d x}\right)^{m-1}\left(\frac{1}{x} \frac{d}{d x}\right)\left(x^n J_n\right)=\left(\frac{1}{x} \frac{d}{d x}\right)^{m-1}\left(x^{n-1} J_{n-1}\right) \cdots\)
= \(x^{n-m} J_{n-m}\), on preceeding as before m times more.
2) Recurrence relation 7 is \(\frac{d}{d x}\left(x^{-n} J_n\right)=-x^{-n} J_{n+1} \Rightarrow\left(\frac{1}{x} \frac{d}{d x}\right)\left(x^{-n} J_{n+1}\right)=(-1)^1 x^{-n-1} J_{n+1}\)
Now \(\left(\frac{1}{x} \frac{d}{d x}\right)^m\left(x^{-n} J_n\right)=\left(\frac{1}{x} \frac{d}{d x}\right)^{m-1}\left(\frac{1}{x} \frac{d}{d x}\right)\left(x^{-n} J_n\right)=\left(\frac{1}{x} \frac{d}{d x}\right)^{m-1}(-1)^1 x^{n-1} J_{n+1}\)
……. = \((-1)^m x^{-n-m} J_{n+m} \rightarrow(3)\), on proceeding as before m times more.
3) Replacing n by o and m by n in part \(\left(\frac{1}{x} \frac{d}{d x}\right)^m\left(x^{-n} J_n\right)=(-1)^m x^{-n-m} J_{n+m}\), we get
⇒ \(\left(\frac{1}{x} \frac{d}{d x}\right)^n J_0=(-1)^n x^{-n} J_n \Rightarrow J_n(x)=(-1)^n x^n\left(\frac{1}{x} \frac{d}{d x}\right)^n J_0(x)\)
38. Prove that
1) \(\left(\frac{1}{x} \frac{d}{d x}\right)^m\left(x^n J_n\right)=x^{n-m} J_{n-m}\), where m is positive integer and m<n.
2) \(\left(\frac{1}{x} \frac{d}{d x}\right)^m\left(x^{-n} J_n\right)=(-1)^m x^{-n-m} J_{n+m}\)
3) \(J_n(x)=(-1)^n x^n\left(\frac{1}{x} \frac{d}{d x}\right)^n J_0(x)\),n being positive integer
Solution:
From recurrence formula 4, we have \(J_{n-1}+J_{n+1}=\frac{2 n}{x} J_n \Rightarrow J_{n-1}=\frac{2 n}{x} J_n-J_{n+1}\).
Replacing n by (n+1), we have \(J_n=\frac{2(n+1)}{x} J_{n+1}-J_{n+2} \Rightarrow \frac{J_n}{J_{n+1}}=\frac{2(n+1)}{x}-\frac{J_{n+2}}{J_{n+1}} \rightarrow \text { (1). }\)
Replacing n by (n+1) in (1), we have \(\frac{J_{n+1}}{J_{n+2}}=\frac{2(n+2)}{x}-\frac{J_{n+3}}{J_{n+2}} \rightarrow\) (2) and etc.
⇒ \(\frac{J_{n+1}}{J_n}=\frac{1}{\frac{J_n}{J_{n+1}}}=\frac{1}{\frac{2(n+1)}{x}-\frac{J_{n+2}}{J_{n+1}}}\)
= \(\frac{1}{\frac{2(n+1)}{x}-\frac{1}{\frac{J n+1}{J n+2}}}=\frac{1}{\frac{2(n+1)}{x}-\frac{1}{\frac{2(n+2)}{x}-\frac{J_{n+3}}{J_{n+2}}}}\)
= \(\frac{1}{\frac{2(n+1)}{x}-\frac{1}{\frac{2(n+2)}{x}-\frac{1}{J n+2}}}=\frac{1}{\frac{2(n+1)}{x}-\frac{1}{\frac{2(n+2)}{x}-\frac{1}{\frac{2(n+3)}{x} \ldots}}}\)
= \(\frac{x / 2}{(n+1)-\frac{x / 2}{\frac{2(n+2)}{x}-\frac{1}{\frac{2(n+3)}{x}} \cdots}}=\frac{x / 2}{(n+1)-\frac{x}{(x / 2)^2}}\)
= \(\frac{(x / 2)}{(n+1)-\frac{(x / 2)^2}{(n+2)-\frac{(x / 2)^2}{(n+3)} \cdots}}\)
39. Show that \(x^n J_n(x)\) is a solution of \(x \frac{d^2 y}{d x^2}+(1-2 n) \frac{d y}{d x}+x y=0\).
Solution:
Given equation is \(x \frac{d^2 y}{d x^2}+(1-2 n) \frac{d y}{d x}+x y=0 \rightarrow\) (1)
Let \(y=x^n J_n(x) \rightarrow(2)\)
Recurrence relation 6 is \(\frac{d}{d x}\left[x^n J_n(x)\right]=x^n J_{n-1}(x) \Rightarrow \frac{d y}{d x}=x^n J_{n-1}\)
and hence \(\frac{d^2 y}{d x^2}=x^n J_{n-1}^{\prime}+n x^{n-1} J_{n-1}\)
From recurrence relation 1 we have \(J_n^{\prime}(x)=\frac{n}{x} J_n-J_{n+1}(x) \Rightarrow J_{n-1}^{\prime}-\frac{n-1}{x} J_{n-1}=-J_n(x) \rightarrow \text { (5) }\)
∴ \(x\left(x^n J_{n-1}^{\prime}+n x^{n-1} J_{n-1}\right)+(1-2 n) x^n J_{n-1}+x^{n+1} J_n\)
=\(x^{n+1} J_{n-1}^{\prime}-(n-1) x^n J_{n-1}+x^{n+1} J_n\)
= \(x^{n+1}\left[J_{n-1}^{\prime}-\frac{(n-1)}{x} J_{n-1}\right]+x^{n+1} J_n=x^{n+1} J_n-x^{n+1} J_n=0\)
Hence \(x^n J_n\) is a solution of \(x \frac{d^2 y}{d x^2}+(1-2 n) \frac{d y}{d x}+x y=0\).
40. Show that \(x^{-n} J_n(x)\) is a solution of \(x \frac{d^2 y}{d x^2}+(1+2 n) \frac{d y}{d x}+x y=0\).
Solution:
Given equation is \(x \frac{d^2 y}{d x^2}+(1+2 n) \frac{d y}{d x}+x y=0 \rightarrow\) (1)
Let \(y=x^{-n} J_n(x) \rightarrow(2)\)
Recurrence relation V is \(\frac{d}{d x}\left\{-x^n J_n(x)\right\}=-x^{-n} J_{n+1}(x) \Rightarrow \frac{d y}{d x}=-x^{-n} J_{n+1}\)
and hence \(\frac{d^2 y}{d x^2}=-x^{-n} J_{n+1}^{\prime}+n x^{-n-1} J_{n+1} \rightarrow\) (3)
From recurrence relation 2, we have \(J_n^{\prime}(x)=J_{n-1}(x)-\frac{n}{x} J_n \Rightarrow J_{n+1}^{\prime}+\frac{n+1}{x} J_{n+1}=J_n(x)\)
∴ \(x\left(-x^{-n} J_{n+1}^{\prime}+n x^{-n-1} J_{n+1}\right)+(1+2 n)\left(-x^{-n} J_{n+1}\right)+x^{-n+1} J_n\)
= \(-x^{-n+1} J_{n+1}^{\prime}-(n+1) x^{-n} J_{n+1}+x^{-n+1} J_n\)
=\(-x^{-n+1}\left[J_{n+1}^{\prime}+\frac{n+1}{x} J_{n+1}\right]+x^{-n+1} J_n=-x^{-n+1} J_n+x^{-n+1} J_n=0\)
Hence \(x^{-n} J_n\) is a solution of \(x \frac{d^2 y}{d x^2}+(1+2 n) \frac{d y}{d x}+x y=0\)
41. Show that \(y=x^{-n / 2} J_n(2 \sqrt{x})\) satisfies the differential equation \(x \frac{d^2 y}{d x^2}+(n+1) \frac{d y}{d x}+y=0\).
Solution:
Put \(2 \sqrt{x}=t\). Then \(x=\frac{t^2}{4} \Rightarrow \frac{d x}{d t}=\frac{t}{2}\)
Now \(y=x^{-n / 2} J_n(2 \sqrt{x})=\left(\frac{t^2}{4}\right)^{-n / 2} J_n(t)=\left(\frac{t}{2}\right)^{-n} J_n(t)\)
⇒ \( \frac{d y}{d x}=\frac{d y}{d t} \frac{d t}{d x}=\frac{2}{t} \frac{d}{d t}\left\{\left(\frac{t}{2}\right)^{-n} J_n(t)\right\}=\frac{2^{n+1}}{t} \frac{d}{d t}\left\{t^{-n} J_n(t)\right\}\)
= \(-\frac{2^{n+1}}{t} t^{-n} J_{n+1}(t)=-2^{n+1} t^{-n-1} J_{n+1}(t)\)
⇒ \(\frac{d^2 y}{d x^2}=\frac{d}{d x}\left\{\frac{d y}{d x}\right\}=\frac{d}{d t}\left\{\frac{d y}{d x}\right\} \frac{d t}{d x}=\frac{2}{t} \frac{d}{d t}\left\{-2^{n+1} t^{-n-1} J_{n+1}(t)\right\} \)
= \(-\frac{2^{n+2}}{t} \frac{d}{d t}\left\{t^{-(n+1)} J_{n+1}(t)\right\}=\frac{2^{n+2}}{t} t^{-(n+1)} J_{n+2}(t)=2^{n+2} t^{-n-2} J_{n+2}(t)\)
x \(\frac{d^2 y}{d x^2}+(n+1) \frac{d y}{d x}+y\)
= \(\frac{t^2}{4} 2^{n+2} t^{-n-2} J_{n+2}(t)+(n+1)\left(-2^{n+1}\right) t^{-n-1} J_{n+1}(t)+2^n t^{-n} J_n(t)\)
= \(2^n t^{-n-1}\left[t J_{n+2}(t)-2 J_{n+1}(t)(n+1)+t J_n(t)\right]=0\)
y = \(x^{-n / 2} J_n(2 \sqrt{x}) \text { satisfies } x \frac{d^2 y}{d x^2}+(n+1) \frac{d y}{d x}+y=0\) .
42. Show that \(y=\frac{1}{\pi} \int_0^\pi \cos (x \sin \phi) d \phi\) satisfies Bessel’s equation of zeroeth order.
Solution:
Let y = \(J_0(x)=\frac{1}{\pi} \int_0^\pi \cos (x \sin \phi) d \phi \rightarrow \text { (1) }\)
∴ \(\frac{d y}{d x}=-\frac{1}{\pi} \int_0^\pi \sin (x \sin \phi) \sin \phi d \phi \rightarrow(2)\)
and \(\frac{d^2 y}{d x^2}=-\frac{1}{\pi} \int_0^\pi \cos (x \sin \phi) \sin ^2 \phi d \phi \rightarrow \text { (3) }\)
Evaluating the R.H.S. of (2) by the method of integration by parts, we have \(\frac{d y}{d x}=-\frac{1}{\pi}\left[\{-\sin (x \sin \phi) \cos \phi\}_0^\pi+\int_0^\pi \cos (x \sin \phi) x \cos ^2 \phi d \phi\right]\)
= \(-\frac{x}{\pi} \int_0^\pi \cos (x \sin \phi) \cos ^2 \phi d \phi=-\frac{x}{\pi} \int_0^\pi \cos (x \sin \phi) \cdot\left(1-\sin ^2 \phi\right) d \phi\)
= \(-\frac{x}{\pi} \int_0^\pi \cos (x \sin \phi) d \phi+\frac{x}{\pi} \int_0^\pi \cos (x \sin \phi) \sin ^2 \phi d \phi=-x y-x \frac{d^2 y}{d x^2}\)
from (1) and (3)
∴ \(\frac{d^2 y}{d x^2}+\frac{1}{x} \frac{d y}{d x}+y=0\) which is Bessel’s equation for n=0
Hence \(y=\frac{1}{x} \int_0^\pi \cos (x \sin \phi) d \phi\) satisfies the Bessel’s equation of the zeroeth order.
43. Show that \(y=A J_n(x) \int_0^x \frac{d x}{x J_n^2(x)}+B J_n(x)\) is the complete solution of Bessel’s equation.
Solution:
The Bessel’s equation is \(y^{\prime \prime}+\frac{1}{x} y+\left(1-\frac{n^2}{x^2}\right) y=0 \rightarrow\) (1)
We know that a solution (1) is \(u=J_n(x) \rightarrow\) (2)
Let the complete solution of (1) be \(y=u v \rightarrow\)(3)
Comparing (1) with \(y^{\prime \prime}+P y^{\prime}+Q y=R\), we get \(P=\frac{1}{x}\) and Q = \(1-\frac{n^2}{x^2}, R=0\)
Then, we know that v is given by \(\frac{d^2 v}{d x^2}+\left(P+\frac{2}{u} \frac{d u}{d x}\right) \frac{d v}{d x}=\frac{R}{u}\)
⇒ \(\frac{d^2 v}{d x^2}+\left(\frac{1}{x}+\frac{2 J_n^{\prime}(x)}{J_n(x)}\right) \frac{d v}{d x}=0 \rightarrow(4)\)
Let \(\frac{d v}{d x}=q\) so that \(\frac{d^2 v}{d x^2}=\frac{d q}{d x} \rightarrow (5)\)
Then (4) ⇒ \(\frac{d q}{d x}+\left(\frac{1}{x}+\frac{2 J_n^{\prime}}{J_n}\right) q=0 \Rightarrow \frac{d q}{q}+\left(\frac{1}{x}+\frac{2 J_n^{\prime}}{J_n}\right) d x=0\).
Integrating, we get \(\log q+\log x+2 \log J_n=\log A \Rightarrow q x J_n^2=A\)
⇒ q = \(\frac{d v}{d x}=\frac{A}{\left(x J_n^2\right)} \Rightarrow d v=\left\{\frac{A}{\left(x J_n^2\right)}\right\} d x\)
Integrating, we get \(v=A \int_0^x \frac{d x}{x J_n^2}+B \rightarrow\) (6) where A and B are arbitrary constants.
From (2), (3) and (6) the required complete solution is
y = \(J_n(x)\left(A \int_0^x \frac{d x}{x J_n^2}+B\right) \Rightarrow y=A J_n(x) \int_0^x \frac{d x}{x J_n^2(x)}+B J_n(x)\)
44. If n>-1, show that \(\int_0^x x^{-n} J_{n+1}(x) d x=\frac{1}{2^n \Gamma(n+1)}-x^{-n} J_n(x)\).
Solution:
From recurrence formula V, we have \(x^{-n} J_{n+1}(x)=-\frac{d}{d x}\left\{x^{-n} J_n(x)\right\}\)
Integrating between the limits o and x, we have \(\int_0^x x^{-n} J_{n+1}(x) d x=-\left[x^{-n} J_n(x)\right]=-x^{-n} J_n(x)+L t \frac{J_n(x)}{x \rightarrow 0}\)
(Diffe. Nr. and Dr. n times)
= \(-x^{-n} J_n(x)+\underset{x \rightarrow 0}{ } \frac{J_n^n(x)}{n!}=-x^{-n} J_n(x)+\frac{n!}{2^n \Gamma(n+1) n!}=-x^{-n} J_n(x)+\frac{1}{2^n \Gamma(n+1)}\)
45. Show that when n is integral, 1) \(\pi J_n=\int_0^\pi \cos (n \theta-x \sin \theta) d \theta\)
2) \(\pi J_0=\int_0^\pi \cos (x \cos \phi) d \phi=\int_0^\pi \cos (x \sin \phi) d \phi\) and hence deduce that \(J_0(x)=1-\frac{x^2}{2^2}+\frac{x^4}{2^2 \cdot 4^2}-\frac{x^6}{2^2 \cdot 4^2 \cdot 6^2}+\ldots=\sum_{r=0}^{\infty} \frac{(-1)^r x^{2 r}}{\left(2^r r !\right)^2}\).
Solution:
We have \(\cos (x \sin \theta)=J_0+2 J_2 \cos 2 \theta+2 J_4 \cos 4 \theta+\cdots+2 J_{2 m} \cos 2 m \theta+\cdots \rightarrow (1)\)
and \(\sin (x \sin \theta)\) = \(2 \sin \theta J_1+2 \sin 3 \theta J_3+\cdots+2 J_{2 m+1} \sin (2 m+1) \theta+\cdots \rightarrow (2)\)
1. Multiplying both sides of (1) by \(\cos 2 m \theta\) and then integrating between the limits o to π, \(\int_0^\pi \cos (x \sin \theta) \cos 2 m \theta d \theta\)
= \(J_0 \int_0^\pi \cos 2 m \theta d \theta+2 J_2 \int_0^\pi \cos 2 \theta \cos 2 m \theta d \theta+\cdots\)
+ \(2 J_{2 m} \int_0^\pi \cos ^2 2 m \theta d \theta+\cdots=0+0+\cdots+J_{2 m} \int_0^\pi(1+\cos 4 m \theta) d \theta+\cdots=\pi J_{2 m}\).
Similarly we can prove that \(\int_0^\pi \cos (x \sin \theta) \cos (2 m+1) \theta d \theta=0\).
Again multiplying both sides of (2) by \(\sin (2 m+1) \theta\) and then integrating between the limits o to π,
⇒ \(\int_0^\pi \sin (x \sin \theta) \sin (2 m+1) \theta d \theta=2 J_1 \int_0^\pi \sin \theta \sin (2 m+1) \theta d \theta\)
+ \(2 J_3 \int_0^\pi \sin 3 \theta \sin (2 m+1) \theta d \theta+\cdots+2 J_{2 m+1} \int_0^\pi \sin ^2(2 m+1) \theta d \theta+\cdots\)
= \(0+0+\cdots+J_{2 m+1} \int_0^\pi\{1-\cos 2(2 m+1) \theta\} d \theta+\cdots=J_{2 m+1}(\theta)=\pi J_{2 m+1}\)
Similarly, \(\int_0^\pi \sin (x \sin \theta) \sin 2 m \theta d \theta=0\)
Therefore, \(\int_0^\pi \cos (2 \min \theta-x \sin \theta) d \theta\)
= \(\int_0^\pi \cos 2 m \theta \cos (x \sin \theta) d \theta+\int_0^\pi \sin 2 m \theta \sin (x \sin \theta) d \theta=\pi J_{2 m}\)
Also \(\int_0^\pi \cos [(2 m+1) \theta-x \sin \theta] d \theta\)
= \(\int_0^\pi \cos (2 m+1) \theta \cos (x \sin \theta) d \theta+\int_0^\pi \sin (2 m+1) \theta \sin (x \sin \theta) d \theta=\pi J_{2 m+1} \text {. }\)
Hence for all positive integral n, we have \(int_0^\pi \cos (n \theta-x \sin \theta) d \theta=\pi J_n\)
If n is negative, say n=-m,where m is +ve then \(\int_0^\pi \cos (n \theta-x \sin \theta) d \theta\)
= \(\int_0^\pi \cos \{-m(\pi-\phi)-x \sin (\pi-\phi)\} d \phi, \text { putting } \theta=\pi-\phi\)
= \(\int_0^\pi \cos \{-m \pi+(m \phi-x \sin \phi)\} d \phi\)
= \(\int_0^\pi\{\cos m \pi \cdot \cos (m \phi-x \sin \phi)+\sin m \pi \sin (m \phi-x \sin \phi)\} d \phi\)
= \((-1)^m \int \pi \cos (m \phi-x \sin \phi) d \phi=(-1)^m \pi J_m(x)=\pi J_{-m}(x)=\pi J_n(x)\)
Hence for all integral values of \(n, \int_0^\pi \cos (n \theta-x \sin \theta) d \theta=\pi J_n\).
2. Putting \(\theta=\frac{\pi}{2}+\phi\) in the value of \(\cos (x \sin \theta)\) from (1), we have
⇒ \(\cos (x \cos \phi)=J_0-2 J_2 \cos 2 \phi+2 J_4 \cos 4 \phi-\cdots\)
∴ \(\int_0^\pi \cos (x \cos \phi) d \phi=J_0 \int_0^\pi d \theta-2 J_2 \int_0^\pi \cos 2 \phi d \phi+\cdots\)
From (1) we have \(\cos (x \sin \phi)=J_0+2 J_2 \cos 2 \phi+2 J_4 \cos 4 \phi+\cdots\)
∴ \(\int_0^\pi \cos (x \sin \phi) d \phi=J_0 \int_0^\pi d \phi+2 J_2 \int_0^\pi \cos 2 \phi d \phi+\cdots=\pi J_0\)
Deduction: We have proved that \(J_0(x)=\frac{1}{\pi} \int_0^\pi \cos (x \cos \phi) d \phi\)
= \(\frac{1}{\pi} \int_0^\pi\left(1-\frac{x^2 \cos ^2 \phi}{2!}+\frac{x^4 \cos ^4 \phi}{4!}-\frac{x^6 \cos ^6 \phi}{6!}+\cdots\right) d \phi \rightarrow \text { (1) }\)
Since \(\int_0^\pi \cos ^{2 r} \phi d \phi=\frac{1 \cdot 3 \cdot 5 \cdot(2 r-1)}{2 \cdot 4 \cdot 6 \cdots(2 r)} \pi\) from definite integrals.
From (1) we have \(J_0(x)=\frac{1}{\pi}\left[\pi-\frac{x^2}{2!} \cdot \frac{1}{2} \pi+\frac{x^4}{4!} \cdot \frac{1 \cdot 3}{2 \cdot 4} \pi-\frac{x^6}{6!} \cdot \frac{1 \cdot 3 \cdot 5}{2 \cdot 4 \cdot 6} \pi+\cdots\right]\)
= \(1-\frac{x^2}{2^2}+\frac{x^4}{2^2 \cdot 4^2}-\frac{x^6}{2^2 \cdot 4^2 \cdot 6^2}+\cdots=1-\frac{x^2}{2^2}+\frac{x^4}{2^4(2!)^2}-\frac{x^6}{2^6(3!)^2}+\cdots\)
= \(\sum_{r=0}^{\infty} \frac{(-1)^r x^{2 r}}{\left(2^r r!\right)^2}\)
46. Show that \(J_{2 n}(x)=(-1)^n \frac{2}{\pi} \int_0^{\pi / 2} \cos 2 n \phi \cos (x \sin \phi) d \phi\).
Solution:
We have \(\cos (x \sin \theta)=J_0+2 J_2 \cos 2 \theta+2 J_4 \cos 4 \theta+\cdots+2 J_{2 m} \cos 2 m \theta+\cdots \rightarrow\) (1)
Multiplying both sides of (1) by \(\cos 2 m \theta\) and then integrating between the limits o to \(\pi\), \(\int_0^\pi \cos (x \sin \theta) \cos 2 m \theta d \theta=J_0^\pi \int_0^\pi \cos 2 m \theta d \theta+2 J_2 \int_0^\pi \cos 2 \theta \cos 2 m \theta d \theta+\cdots\)
+ \(2 J_{2 m} \int_0^\pi \cos ^2 2 m \theta d \theta+\cdots=0+0+\cdots+J_{2 m} \int_0^\pi(1+\cos 4 m \theta) d \theta+\cdots=\pi J_{2 m}\)
⇒ \(J_{2 m}=\frac{1}{\pi} \int_0^\pi \cos (x \sin \theta) \cos 2 m \theta d \theta \Rightarrow J_{2 n}=\frac{1}{\pi} \int_0^\pi \cos (x \sin \theta) \cos 2 n \theta d \theta\)
Put \(\theta=\phi+\frac{\pi}{2}\). Then \(d \theta=d \phi ; \theta=0, \pi \Rightarrow \phi=-\frac{\pi}{2}, \frac{\pi}{2}\)
∴ \(J_{2 n}=\frac{1}{\pi} \int_{-\pi / 2}^{\pi / 2} \cos (x \cos \phi) \cos (n \pi+2 n \phi) d \phi=\frac{(-1)^n}{\pi} \int_{-\pi / 2}^{\pi / 2} \cos (x \cos \phi) \cos 2 n \phi d \phi\)
= \((-1)^n \frac{2}{\pi} \int_0^{\pi / 2} \cos (x \cos \phi) \cos 2 n \phi d \phi\)
47. Show that \(J_{2 n-1}(x)=-(-1)^n \frac{2}{\pi} \int_0^{\pi / 2} \cos (2 n+1) \theta \sin (x \cos \theta) d \theta\).
Solution:
We have \(\sin (x \sin \theta)=2 \sin \theta J_1+2 \sin 3 \theta J_3+\cdots+2 J_{2 m+1} \sin (2 m+1) \theta+\cdots \rightarrow(1)\)
Multiplying both sides of (1) by sin (2 m+1)θ and then integrating between the limits o to π
⇒ \(\int_0^\pi \sin (x \sin \theta) \sin (2 m+1) \theta d \theta=2 J_1 \int_0^\pi \sin \theta \sin (2 m+1) \theta d \theta\)
+ \(J_3 \int_0^\pi \sin 3 \theta \sin (2 m+1) \theta d \theta+\cdots+2 J_{2 m+1} \int_0^\pi \sin ^2(2 m+1) \theta d \theta+\cdots\)
= \(0+0+\cdots+J_{2 m+1} \int_0^\pi\{1-\cos 2(2 m+1) \theta\} d \theta+\cdots=J_{2 m+1}(\theta)=\pi J_{2 m+1}\)
⇒ \(J_{2 m+1}=\frac{1}{\pi} \int_0^\pi \sin (x \sin \theta) \sin (2 m+1) \theta d \theta\)
⇒ \(J_{2 n+1}=\frac{1}{\pi} \int_0^\pi \sin (x \sin \theta) \sin (2 n+1) \theta d \theta\)
Put \(\theta=\phi+\frac{\pi}{2}\). Then \(d \theta=d \phi ; \theta=0, \pi \Rightarrow \phi=-\frac{\pi}{2}, \frac{\pi}{2}\)
∴ \(J_{2 n+1}=\frac{1}{\pi} \int_{-\pi / 2}^{\pi / 2} \sin (x \cos \phi) \sin \left[(2 n+1)\left(\phi+\frac{\pi}{2}\right)\right] d \phi\)
= \(\frac{1}{\pi} \int_{-\pi / 2}^{\pi / 2} \sin (x \cos \phi)(-1)^n \cos (2 n+1) \phi d \phi\)
= \((-1)^n \frac{2}{\pi} \int_{-\pi / 2}^{\pi / 2} \sin (x \cos \phi)(-1)^n \cos (2 n+1) \phi d \phi\)
48. Prove that \(J_n(x)=\frac{(x / 2)^n}{\sqrt{\pi} \Gamma(n+1 / 2)} \int_{-1}^{+1}\left(1-t^2\right)^{n-1 / 2} e^{i x t} d t,\left(n>-\frac{1}{2}\right)\). And deduce that \(\int_0^1\left(1-t^2\right)^{n-1 / 2} \cos (x t) d t=\frac{2^{n-1} \Gamma(1 / 2) \Gamma(n+1 / 2) J_n(x)}{x^n}\).
Solution:
Let I = \(\int_{-1}^{+1}\left(1-t^2\right)^{n-1 / 2} e^{i x t} d t=\int_{-1}^{+1}\left(1-t^2\right)^{n-1 / 2}\left(\sum_{r=0}^{\infty} \frac{\left(i x t^r\right.}{r!}\right) d t\)
= \(\sum_{r=0}^{\infty} \frac{(i x)^r}{r!} \int_{-1}^{+1}\left(1-t^2\right)^{n-1 / 2} r d t\)
Now, if r is odd, the integrand in $I$ is an odd function of t. ∴ I=0.
And if r is even, the integrand in I is an even function of t.
∴ I = \(\sum_{r=0}^{\infty} \frac{(i x)^{2 s}}{(2 s)!} 2 \int_0^1\left(1-t^2\right)^{n-1 / 2} t^{2 s} d t\)
= \(\sum_{t=0}^{\infty} \frac{(i x)^{2 s}}{(2 s)!} \int_0^1(1-v)^{n-1 / 2} \cdot v^{s-1 / 2} d v\) ; Putting \(t^2=v\) so that 2 t d t=d v
= \(\sum_{t=0}^{\infty} \frac{(i x)^{2 s}}{(2 s)!} B\left(n+\frac{1}{2}, s+\frac{1}{2}\right)\), since \(B(m, n)=\int_0^1(1-t)^{m-1} t^{n-1}\)
= \(\sum_{r=0}^{\infty} \frac{(i x)^2}{(2 s)!} \frac{\Gamma\left(-n+\frac{1}{2}\right) \Gamma\left(s+\frac{1}{2}\right)}{\Gamma\left(n+\frac{1}{2}+s+\frac{1}{2}\right)},\left(n>-\frac{1}{2}\right)\) since \(B(m, n)=\frac{\Gamma(m) \Gamma(n)}{\Gamma(m+n)}\)
= \(\Gamma\left(n+\frac{1}{2}\right)_{s=0}^{\infty} \frac{\left(i^2\right)^s x^{2 s}\{(2 s+1) / 2\}}{(2 s)!\Gamma(n+s+1)}\)
= \(\Gamma\left(n+\frac{1}{2}\right) \sum_{s=0}^{\infty} \frac{(-1)^s x^{2 s}}{(2 s)!\Gamma(n+s+1)} \frac{(2 s)!}{2^{2 s} s!} \sqrt{\pi}, \text { since } \Gamma \cdot\left(\frac{2 s+1}{2}\right)=\frac{(2 s)!\sqrt{\pi}}{2^{2 s} s!}\)
= \(\Gamma\left(n+\frac{1}{2}\right)\left(\frac{x}{2}\right)^{-n} \sum_{s=0}^{\infty} \frac{(-1)^s}{s!\Gamma(n+s+1)}\left(\frac{x}{2}\right)^{n+2 s} \sqrt{\pi}=\Gamma\left(n+\frac{1}{2}\right)\left(\frac{x}{2}\right)^{-n} \sqrt{\pi} J_n(x)\)
∴ \(J_n(x)=\frac{(x / 2)^n}{\sqrt{\pi} \Gamma\left(n+\frac{1}{2}\right)} \int_{-1}^{+1}\left(1-t^2\right)^{n-1 / 2} e^{i x t} d t \rightarrow(1)\)
Deduction: From (1), we have \(J_n(x)=\frac{x^n}{2^n \Gamma\left(\frac{1}{2}\right) \Gamma\left(n+\frac{1}{2}\right)} \int_{-1}^1\left(1-t^2\right)^{n-1 / 2}(\cos x t+i \sin x t) d t\)
Equating real parts from both sides, we get \(J_n(x)=\frac{x^n}{2^n \Gamma\left(\frac{1}{2}\right) \Gamma\left(n+\frac{1}{2}\right)} \int_{-1}^1\left(1-t^2\right)^{n-1 / 2} \cos (x t) d t\)
= \(\frac{x^n}{2^n \Gamma\left(\frac{1}{2}\right) \Gamma\left(n+\frac{1}{2}\right)} 2 \int_0\left(1-t^2\right)^{n-1 / 2} \cos (x t) d t\)
⇒ \(\int_0\left(1-t^2\right)^{n-1 / 2} \cos (x t) d t=\frac{2^{n-1} \Gamma\left(\frac{1}{2}\right) \Gamma\left(n+\frac{1}{2}\right) J_n(x)}{x^n}\)
49. Prove that \(J_n(x)=\frac{2(x / 2)^{n-m}}{\Gamma(n-m)} \int_0^1(1-t)^{n-m-1} t^{m+1} J_m(x t) d t\).
Solution:
Let I = \(\int_0^1\left(1-t^2\right)^{n-m-1} t^{m+1} J_m(x t) d t\)
= \(\int_0^1\left(1-t^2\right)^{n-m-1} t^{m+1} \sum_{r=0}^{\infty}(-1)^r \frac{1}{r!\Gamma(m+r+1)}\left(\frac{x t}{2}\right)^{2 r+m} d t\)
= \(\sum_{r=0}^{\infty} \frac{(-1)^r(x / 2)^{2 r+m}}{r!\Gamma(m+r+1)} \int_0^1\left(1-t^2\right)^{n-m-1} t^{2 r+2 m+1} d t\)
= \(\sum_{r=0}^{\infty} \frac{(-1)^r(x / 2)^{2 r+m}}{r!\Gamma(m+r+1)} \int_0^1\left(1-t^2\right)^{n-m-1}\left(t^2\right)^{m+r} t d t\)
= \(\sum_{r=0}^{\infty} \frac{(-1)^r(x / 2)^{2 r+m}}{r!\Gamma(m+r+1)} \frac{1}{2} \int_0^1(1-z)^{n-m-1} Z^{(m+r+1)-1} d z \text { on putting } t^2=z\)
= \(\sum_{r=0}^{\infty} \frac{(-1)^r(x / 2)^{2 r+m}}{r!\Gamma(m+r+1)} \frac{1}{2} B(n-m, m+r+1), \text { if } n-m>0, m+r+1>0\)
= \(\sum_{r=0}^{\infty} \frac{(-1)^r(x / 2)^{2 r+m}}{r!\Gamma(m+r+1)} \frac{1}{2} \frac{\Gamma(n-m) \Gamma(m+r+1)}{\Gamma(n+r+1)}\)
= \(\frac{\Gamma(n-m)}{2}\left(\frac{x}{2}\right)^{m-n} \sum_{r=0}^{\infty} \frac{(-1)^r}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{n+2 r}=\frac{\Gamma(n-m)}{2}\left(\frac{x}{2}\right)^{m-n} J_n(x)\)
∴ \( J_n(x)=\frac{2(x / 2)^{n-m}}{\Gamma(n-m)} \int_0^1\left(1-t^2\right)^{n-m-1} t^{m+1} J_m(x t) d t\)
50. Prove that \(J_n(x)=\frac{-x^n}{2^{n-1} \Gamma(n)} \int_0^{\pi / 2} \sin \theta \cos ^{2 n-1} \theta J_0(x \sin \theta) d \theta \text {, where } n>-\frac{1}{2}\).
Solution:
We have \(J_n(x)=\sum_{r=0}^{\infty} \frac{(-1)^r}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{2 r+n}\)
(1) ⇒ \(J_0(x \sin \theta)=\sum_{r=0}^{\infty} \frac{(-1)^r}{r!\Gamma(r+1)}\left(\frac{x \sin \theta}{2}\right)^{2 r} \text {. }\)…(2)
Let I = \(\int_0^{\pi / 2} \sin \theta \cos ^{2 n-1} \theta J_0(x \sin \theta) d \dot{\theta} \rightarrow(3)\)
∴ I = \(\int_0^{\pi / 2} \sin \theta \cos ^{2 n-1} \theta\left(\sum_{r=0}^{\infty} \frac{(-1)^r}{r!\Gamma(r+1)} \frac{x^{2 r}}{2^{2 r}} \sin ^{2 r} \theta\right) d \theta\)
= \(\sum_{r=0}^{\infty} \frac{(-1)^r x^{2 r}}{(r!)^2 \cdot 2^{2 r}} \int_0^{\pi / 2} \cos ^{2 n-1} \theta \sin ^{2 r+1} \theta d \theta\)
= \(\sum_{r=0}^{\infty} \frac{(-1)^r x^{2 r}}{(r!)^2 2^{2 r}} \frac{\Gamma(n) \Gamma(r+1)}{\Gamma(n+r+1)}=\frac{\Gamma(n)}{2} \sum_{r=0}^{\infty} \frac{(-1)^r}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{2 r}\)
⇒ \(\frac{x^n}{2^{n-1} \Gamma(n)} I=\left(\frac{x}{2}\right)^n \sum_{r=0}^{\infty} \frac{(-1)^r}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{2 r}=\sum_{r=0}^{\infty} \frac{(-1)^r}{r!\Gamma(n+r+1)}\left(\frac{x}{2}\right)^{2 r+n}\)
⇒ \(\frac{x^n}{2^{n-1} \Gamma(n)} \int_0^{\pi / 2} \sin \theta \cos ^{2 n-1} \theta J_0(x \sin \theta) d \theta=J_n(x)\), by (1) and (3).
51. Prove that \(J_n(x)=(-2)^n \cdot x^n \frac{d^n}{d\left(x^2\right)^n} J_0(x)\).
Solution:
Bessel’s equation for zeroeth order is \(y_2+\frac{1}{x} y_1+y=0 \rightarrow\) (1) whose solution is \(J_0(x)\)
Changing the independent variable from x to X, by the relation \(x^2=X\), so that
⇒ \(y_1=\frac{d y}{d x}=\frac{d y}{d X} \frac{d x}{d x}=2 x \frac{d y}{d x}=2 \sqrt{X} \frac{d y}{d X}\) and
⇒ \(y_2=\frac{d^2 y}{d x^2}=\frac{d}{d x}\left(2 \sqrt{X} \frac{d y}{d X}\right)\)
= \(\frac{d}{d x}\left(2 \sqrt{X} \frac{d y}{d X}\right) \frac{d x}{d x}=\left(2 \sqrt{X} \frac{d^2 y}{d X^2}+\frac{1}{\sqrt{X}} \frac{d y}{d X}\right) 2 \sqrt{X}\)
= \(4 X \frac{d^2 y}{d X^2}+2 \frac{d y}{d X}\)
Substituting in (1), we have \(\left(4 X \frac{d^2 y}{d X^2}+2 \frac{d y}{d X}\right)+\frac{1}{\sqrt{X}} 2 \sqrt{X} \frac{d y}{d X}+y=0\)
∴ \(4 X \frac{d^2 y}{d X^2}+4 \frac{d y}{d X}+y=0 \rightarrow \text { (4) }\)…..(4)
Differentiating (2), n times w.r.t. X by using Leibnitz’s theorem we have
4\(\left[X \frac{d^{n+2} y}{d X^{n+2}}+n 1 \frac{d^{n+1} y}{d X^{n+1}}\right]+4 \frac{d^{n+1} y}{d X^{n+1}}+\frac{d^n y}{d X^n}\)=0
⇒ \(4 X \frac{d^{n+2} y}{d X^{n+2}}+4(n+1) \frac{d^{n+1} y}{d X^{n+1}}+\frac{d^n y}{d X^n}=0\)
Putting \(y=\frac{d^n y}{d X^n}=\frac{d^n J_0(x)}{d X^n}\), it becomes \(4 X \frac{d^2 Y}{d X^2}+4(n+1) \frac{d Y}{d X}+Y=0\)
Again, \(J_n(x)\) is the solution of the Bessel’s equation \(\frac{d^2 y}{d x^2}+\frac{1}{x} \frac{d y}{d x}+\left(1-\frac{n^2}{x^2}\right) y=0 \rightarrow\) (4)
Putting \(y=x^n z\), so that \(\frac{d y}{d x}=x^n \frac{d z}{d x}+n x^{n-1} Z\)
and \(\frac{d^2 y}{d x^2}=x^n \frac{d^2 z}{d x^2}+2 n x^{n-1} \frac{d z}{d x}+n(n-1) x^{n-2} z\)=0
Substituting in (4), we have \(x^n \frac{d^2 z}{d x^2}+2 n x^{n-1} \frac{d z}{d x}+n(n-1) x^{n-2} z+\frac{1}{x}\left[x^n \frac{d z}{d x}+n x^{n-1} z\right]+\left[1-\frac{n^2}{x^2}\right] x^n z=0\)
⇒ \(x^n \frac{d^2 z}{d x^2}+(2 n+1) x^{n-1} \frac{d z}{d x}+x^n z=0 \Rightarrow \frac{d^2 z}{d x^2}+(2 n+1) \frac{1}{x} \frac{d z}{d x}+z=0 \rightarrow \text { (5). }\)
Comparing (3) and (5), we get \(z=Y=\frac{d^n J_0(x)}{d X^n}=\frac{d^n J_0(x)}{d\left(x^2\right)^n}\)
But y = \(x^n Z\)
Hence \(J_n(x)=c x^n \frac{d^n J_0(x)}{d\left(x^2\right)^n} \rightarrow(6)\) where c is a constant to be determined.
We know that \(J_0(x)=\sum_{r=0}^{\infty} \frac{(-1)^r x^{2 r}}{\left(2^r r!\right)^2}\)
∴ \(\frac{d^2 J_0(x)}{d\left(x^2\right)^n}=\frac{d^n}{d\left(x^2\right)^n} \sum_{r=0}^{\infty} \frac{(-1)^r x^{2 r}}{\left(2^r r!\right)^2}=\frac{d^n}{d\left(x^2\right)^n} \sum_{r=0}^{\infty} \frac{(-1)^{n+r}\left(x^2\right)^{n+r}}{\left[2^{n+r}(n+r)!\right]^2}\)
(Since all those terms in which the index of x is less than 2n will vanish on differentiation n times w.r.t. \(x^2\))
= \(\sum_{r=0}^{\infty} \frac{(-1)^{n+r}(n+r)(n+r-1) \ldots(r+1)\left(x^2\right)^r}{\left[2^{n+r} \cdot(n+r)!\right]^2}=(-1)^n \sum_{r=0}^{\infty}(-1)^r \frac{(n+r)!}{r!2^{3(n+r)} \cdot[(n+r)!]^2} x^{2 r}\)
∴ \(J_n(x)=c x^n(-1)^n \sum_{r=0}^{\infty}(-1)^r \frac{1}{r!2^{2 n+2 r}(n+r)!} x^{2 r}\)
= \(\frac{c(-1)^r}{2^n} \sum_{r=0}^{\infty}(-r)^r \frac{1}{r!\Gamma(n+r+1)}\left[\frac{x}{2}\right]^{n+2 r}=\frac{c}{(-2)^n} J_n(x)\) . ∴ \(c=(-2)^n\)
Hence \(J_n(x)=(-2)^n x^n \frac{d^n J_n(x)}{d\left(x^2\right)^n}\)
52. Prove that \(\int_0^{\infty} \frac{J_n(x)}{x} d x=\frac{1}{n}\).
Solution:
If n is a non-negative integer then we have \(\int_0^{\infty} J_n(x) d x=1\)
From recurrence relation 4, \(\frac{2 n}{x} J_n(x)=J_{n-1}^0(x)+J_{n+1}(x) \rightarrow\) (1)
Integrating (1) both sides with respect to x, from o to \(\infty\), we get
2n \(\int_0^{\infty} \frac{J_n(x)}{x}=\int_0^{\infty} J_{n-1}(x)+\int_0^{\infty} J_{n+1}(x) \Rightarrow 2 n \int_0^{\infty} \frac{J_n(x)}{x}\)=1+1
⇒ \(\int_0^{\infty} \frac{J_n(x)}{x}=1 \text {. }\)
53. Show that \(\int_0^{\pi / 2} \sqrt{(\pi x)} \cdot J_{1 / 2}(2 x) d x=1\).
Solution:
⇒ \(\int_0^{\pi / 2} \sqrt{\pi x} J_{1 / 2}(2 x) d x=\int_0^{\pi / 2} \sqrt{\pi x} \sqrt{\frac{2}{\pi(2 x)}} \sin 2 x d x=\int_0^{\pi / 2} \sin 2 x d x=\left[-\frac{1}{2} \cos 2 x\right]^{\pi / 2}\)
= \(-\frac{1}{2}[-1-1]=1\)
54. Show that \(\int_0^1 J_0[\sqrt{x(t-x)}] d x=2 \sin \frac{1}{2} t\).
Solution:
We know that \(J_n=\sum_{r=0}^{\infty}(-1)^r\left(\frac{x}{2}\right)^{n+2 r} \frac{1}{r!\Gamma(n+r+1)} \rightarrow(1)\)
Putting n=0 and \(x=\{x(t-x)\}^{1 / 2}\) in (1), we get
⇒ \(J_0(\{x(t-x)\}^{1 / 2}=\sum_{r=0}^{\infty}(-1)^r \frac{1}{r!\Gamma(r+1)}\left[\frac{x\{x(t-x)\}^{1 / 2}}{2}\right]^{2 r}=\sum_{r=0}^{\infty} \frac{(-1)^r x^r(t-x)^r}{2^{2 r} r!\Gamma(r+1)}\)
∴ \(\int_0^1 J_0\left(\{x(t-x)\}^{1 / 2}\right) d x=\int_0^1 \sum_{r=0}^{\infty} \frac{(-1)^r x^r(t-x)^r}{2^{2 r} r!\Gamma(r+1)} d x=\sum_{r=0}^{\infty} \frac{(-1)^r}{2^{2 r} r!\Gamma(r+1)} \int_0^1 x^r(t-x)^r d x\)
= \(\sum_{r=0}^{\infty} \frac{(-1)^r t^{2 r+1}}{2^{2 r} r!\Gamma(r+1)} \int_0^1 y^r(1-y)^r d y\), putting x = ty and d x=t dy
= \(\sum_{r=0}^{\infty} \frac{(-1)^r t^{2 r+1}}{2^{2 r} r!\Gamma(r+1)} B(r+1, r+1)=\sum_{r=0}^{\infty} \frac{(-1)^r t^{2 r+1}}{2^{2 r} r!\Gamma(r+1)} \frac{\Gamma(r+1) \Gamma(r+1)}{\Gamma(2 r+1)}\)
= \(\sum_{r=0}^{\infty} \frac{(-1)^r t^{2 r+1}}{2^{2 r} r!r!} \frac{r!r!}{\Gamma(2 r+1)}=\sum_{r=0}^{\infty} \frac{(-1)^r t^{2 r+1} r!}{2^{2 r} r!\Gamma(2 r+1)}=2 \sum_{r=0}^{\infty}(-1)^r \frac{(t / 2)^{2 r+1}}{(2 r+1)!}\)
= \(2\left\{\frac{t}{2}-\frac{(t / 2)^3}{3!}+\frac{(t / 5)^5}{5!}-. .\right\}=2 \sin \frac{t}{2}\)
55. Prove that \(\int_0^b x J_0(a x) d x=\frac{b}{a} J_1(a b)\).
Solution:
Put ax = t Then a dx=dt and x=0, b ⇒ t=0, a b
⇒ \(\int_0^b x J_0(a x) d x=\int_0^{a b} \frac{t}{a} J_0(t) \frac{d t}{a}=\frac{1}{a^2} \int_0^{a b} t J_0(t) d t=\frac{1}{a^2}\left[t J_1(t)\right]=\frac{a b}{a} J_1(a b) .\)
56. Evaluate \(\int J_3(x) d x\) and express the result in terms of \(J_0 \text { and } J_1\).
Solution:
Given
\(\int J_3(x) d x\)From recurrence 7, we have \(x^{-n} J_{n+1}=\frac{d}{d x}\left\{x^{-n} J_n(x)\right\}\).
Integrating it, \(\int x^{-n} J_{n+1}(x) d x=-x^{-n} J_n(x) \rightarrow\) (1)
Now \(\int J_3(x) d x=\int x^2\left[x^{-2} J_3(x)\right] d x=x^2\left[-x^{-2} J_2(x)\right]-\int 2 x\left[-x^{-2} J_2(x)\right] d x\)
= \(-J_2(x)+2 \int x^{-1} J_2(x) d x=-J_2(x)+2\left[-x^{-2} J_1(x)\right]+c\)
∴ \(\int J_3(x) d x=-J_2(x)-2 x^{-1} J_1(x)+c \rightarrow \text { (2) }\)
From recurrence relation 4, we have \(\left(\frac{2 n}{x}\right) J_n(x)=J_{n-1}(x)+J_{n+1}(x) \rightarrow(3)\)
Putting n=1 in (3), we get \(J_2(x)=\frac{2 J_1(x)}{x}-J_0(x) \rightarrow\) (4)
Substituting (4) in (2), we get \(\int J_3(x) d x=-\left(\frac{2 J_1(x)}{x}-J_0(x)\right)-2 x^{-1} J_2(x)+c\)
⇒ \(\int J_3(x) d x=J_0(x)-\frac{4 J_1(x)}{x}+c\), where c is an arbitrary constant.
57. Evaluate \(\int x^3 J_3(x) d x\).
Solution:
Given
\(\int x^3 J_3(x) d x\).
Since, \(\frac{d}{d x}\left\{x^{-n} J_n\right\}=-x^n J_{n+1}\), we have \(\int x^{-n} J_{n+1} d x=-x^{-n} J_n \rightarrow(1)\)
Now, \(\int x^3 J_3(x) d x=\int x^5\left(x^{-2} J_3\right) d x=x^5\left(-x^{-2} J_2\right)-\int 5 x^4\left(-x^{-2} J_2\right) d x\)
= \(-x^3 J_2+\int 5 x^2 J_2 d x=-x^3 J_2+5 \int x^3\left(x^{-1} J_2\right) d x\)
= \(-x^3 J_2+5\left[x^3\left(-x^{-1} J_1\right)-\int 3 x^2\left(-x^{-1} J_1\right) d x\right]\)
= \(-x^3 J_2-5 x^2 J_1+15 \int x J_1 d x=-x^3 J_2-5 x^2 J_1+15 \int x\left(-J_0^{\prime}\right) d x\)
= \(-x^3 J_2-5 x^2 J_1-15 \int x J_0^{\prime} d x=-x^3 J_2-5 x^2 J_1=15\left[x J_0-\int 1 J_0 d x\right]\)
= \(-x^3 J_2-5 x^3 J_1-15 x J_0+15 x \int J_0 d x\)
58. Evaluate \(\int x^4 J_1(x) d x\).
Solution:
Given
\(\int x^4 J_1(x) d x\).
Since, \(\frac{d}{d x}\left\{x^n J_n\right\}=x^n J_{n-1}\), we have \(\int x^n J_{n-1} d x=x^n J_n \rightarrow\) (1)
Now, \(\int x^4 J_1 d x=\int x^2\left(x^2 J_1\right) d x=x^2\left(x^2 J_2\right)-\int 2 x\left(x^2 J_2\right) d x\)
= \(x^4 J_2-2 \int x^3 J_2 d x=x^4 J_2-2 x^3 J_3+c\)
59. Express \(\int x^{-3} J_4(x) d x \text { in terms of } J_0 \text { and } J_1\).
Solution:
Putting n=3 in recurrence relation 7, we have \(\frac{d}{d x}\left\{x^{-n} J_n\right\}=-x^{-n} J_{n+1} \Rightarrow \frac{d}{d x}\left\{x^{-3} J_3\right\}=-x^{-3} J_4\)
Integrating, we get \(\int x^{-3} J_4(x) d x=-x^3 J_3+c \rightarrow\) (1), c being an arbitrary constant
From recurrence relation 6, we have \(J_{n+1}=\left(\frac{2 n}{x}\right) J_n-J_{n-1} \rightarrow\) (2)
Putting n=2 and n=1 successively in (2), we get \(J_3=\left(\frac{4}{x}\right) J_2-J_1 \rightarrow(3)\) and \(J_2=\left(\frac{2}{x}\right) J_1-J_0 \rightarrow \text { (4) }\)
Substituting (4) in (3), we get \(J_3=\left(\frac{4}{x}\right)\left[\left(\frac{2}{x}\right) J_1-J_0\right]-J_1=\left(\frac{8}{x^2}-1\right) J_1-\left(\frac{4}{x}\right) J_0 \rightarrow\) (5)
Substituting (5) in (1), we get \(\int x^{-3} J_4(x) d x=-x^{-3}\left[\left(\frac{8}{x^2}-1\right) J_1-\frac{4}{x} J_0\right]+c=\left(-\frac{1}{x^3}-\frac{8}{x^5}\right) J_1+\frac{4}{x^4} J_0 \text {. }\)
60. Prove that \(\int x^{-1} J_4(x) d x=-x^{-1} J_3(x)-2 x^{-2} J_2(x)+c\).
Solution:
Recurrence relation 7 is \(\frac{d}{d x}\left\{x^{-n} J_n(x)=-x^{-n} J_{n+i}(x)\right.\).
Integrating it, we get \(\int x^{-n} J_{n+1}(x) d x=-x^{-n} J_n(x) \rightarrow\) (1)
∴ \(x^{-1} J_4(x) d x=\int x^2\left[x^{-3} J_4(x)\right] d x=x^2\left[-x^{-3} J_3(x)\right]-\int 2 x \times\left[-x^{-3} J_3(x)\right] d x\)
= \(-x^{-1} J_3(x)+2 \int x^{-2} J_3(x) d x=-x^{-1} J_3(x)+2\left[-x^{-2} J_2(x)\right]+c\)
= \(-x^{-1} J_3(x)-2 x^{-2} J_2(x)+c\) .
61. Prove that \(\int J_3(x) d x=-J_2(x)-\frac{2}{x} J_0(x)+c\).
Solution:
⇒ \(\frac{d}{d x}\left\{x^{-n} J_n(x)\right\}=-x^{-n} J_{n+1}(x) \Rightarrow \int x^{-n} J_{n+1}(x) d x=-x^{-n} J_n(x) \rightarrow(1)\)
Now, \(\int J_3(x) d x=\int x^2\left\{x^{-2} J_3(x)\right\} d x=x^2 \int x^{-2} J_3(x) d x-\int 2 x\left(\int x^{-2} J_3(x) d x\right) d x\)
= \(x^2\left[-x^{-2} J_2(x)\right]-\int 2 x\left(-x^{-2} J_2(x)\right) d x\), using (1) for n=2
= \(-J_2(x)+2 \int x^{-1} J_2(x) d x=-J_2(x)-2 x^{-1} J_1(x)+c\), using (1) for n=1 .
62. Show that
1) \(\int_0^x x^3 J_0(x) d x=x^3 J_1(x)-2 x^2 J_2(x)\)
2) \(\int_0^1 x^3 J_0(x) d x=2 J_0(1)-3 J_1(1)\).
Solution:
1) \(\frac{d}{d x}\left\{x^n J_n(x)\right]=x^n J_{n-1}(x) \Rightarrow \int x^n J_{n-1}(x) d x=x^n J_n(x) \rightarrow \text { (1) }\)
∴ \(\int_0^x x^3 J_0(x) d x=\int_0^x x^2\left[x J_0(x)\right] d x=\left[x^2\left\{x J_1(x)\right\}\right]-\int_0^x 2 x\left\{x J_1(x)\right\} d x\) using (1) for n=1
= \(x^3 J_1(x)-2 \int_0^x x^2 J_1(x) d x=x^3 J_1(x)-2\left[x^2 J_2(x)\right]\), using (1) for n=2
= \(x^3 J_1(x)-2 x^2 J_2(x)\) as \(J_2(0)=0\).
2) From (1), we have \(\int_0^x x^3 J_0(x) d x=x^3 J_1(x)-2 x^2 J_2(x) \rightarrow\) (2)
Putting x=1 in (2), \(\int_0^1 x^3 J_0(x) d x=J_1(1)-2 J_2(1) \rightarrow\) (3)
Recurrence relation IV is \(J_{n-1}(x)+J_{n+1}(x)=\frac{2 n}{x} J_n(x)\).
Putting n=1 and x=1, we have \(J_2(1)=2 J_1(1)-J_0(1) \rightarrow(4)\)
Substituting the above value of \(J_2(1)\) in (3), we have \(\int_0^1 x^3 J_0(x) d x=J_1(1)-2\left[2 J_1(1)-J_0(1)\right]=2 J_0(1)-3 J_1(1) \text {. }\)
63. Prove that \(\int_0^{\infty} e^{-a x} J_0(b x) d x=\frac{1}{\sqrt{\left(a^2+b^2\right)}}, a>0\)
Solution:
We have \(J_0(x)=\frac{1}{\pi} \int_0^\pi \cos (x \sin \phi) d x\)
∴ \(\int_0^{\infty} e^{-a x} J_0(b x) d x=\int_0^{\infty} e^{-a x}\left\{\frac{1}{\pi} \int_0^\pi \cos (b x \sin \phi) d \phi\right\} d x\)
= \(\frac{1}{\pi} \int_0^\pi\left[\int_0^{\infty} e^{-a x} \cos (b x \sin \phi) d x\right] d \phi\)
= \(\frac{1}{\pi} \int_0^\pi\left[\int_0^{\infty} e^{-a x} \cdot \frac{e^{i(b x \sin \phi)}+e^{-i(b x \sin \phi)}}{2} d x\right] d \phi\)
= \(\frac{1}{2 \pi} \int_0^\pi\left[\int_0^{\infty}\left\{e^{-(a-i b \sin \phi) x}+e^{-(a+i b \sin \phi) x}\right\} d x\right] d \phi\)
= \(\left.\frac{1}{2 \pi} \int_0^\pi\left[\frac{e^{-(a-i b \sin \phi) x}}{-(a-i b \sin \phi)}-\frac{e^{-(a+i b \sin \phi) x}}{a+i b \sin \phi}\right] d \phi\right]\)
= \(\frac{1}{2 \pi} \int_0^\pi\left[\frac{1}{a-i b \sin \phi}+\frac{1}{a+i b \sin \phi}\right] d \phi\)
= \(\frac{1}{2 \pi} \int_0^\pi \frac{2 a d \phi}{a^2+b^2 \sin ^2 \phi}=2 \cdot \frac{a}{\pi} \int_0^{\pi / 2} \frac{\text{cosec}^2 \phi d \phi}{b^2+a^2 \text{cosec}^2 \phi}\)
= \(2 \frac{a}{\pi} \int_0^{\pi / 2} \frac{\text{cosec}^2 \phi d \phi}{\left(a^2+b^2\right)+a^2 \cot ^2 \phi}\)
= \(2 \frac{a}{\pi}\left(\frac{1}{a \sqrt{\left(a^2+b^2\right)}} \cot ^{-1} \frac{a \cot \phi}{\sqrt{\left(a^2+b^2\right)}}\right)_0^{\pi / 2}\)
= \(\frac{2}{\pi \sqrt{\left(a^2+b^2\right)}} \cdot\left(\cot ^{-1} 0-\cot ^{-1} \infty\right)=\frac{1}{\sqrt{\left(a^2+b^2\right)}}\)
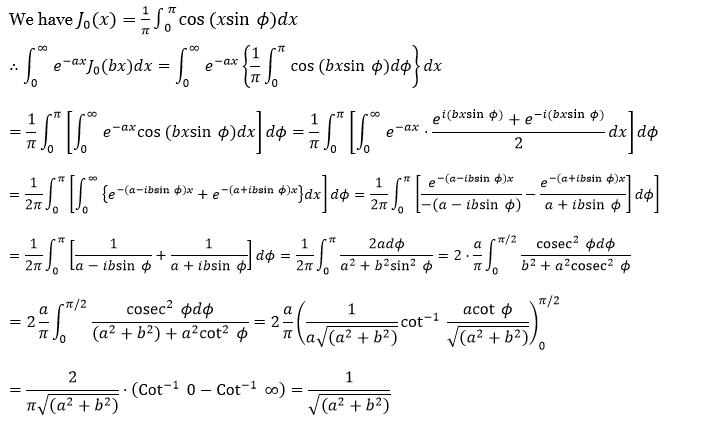
64. Prove that \(\int_0^x t\left\{J_n(t)\right\}^2 d t=\frac{x^2}{2}\left\{J_n^2(x)-J_{n-1}(x) J_{n+1}(x)\right\}\).
solution:
We have \(\frac{d}{d t}\left[\frac{t^2}{2}\left\{J_n^2(t)-J_{n=1}(t) J_{n+1}(t)\right\}\right]\)
= \(t\left(J_n^2-J_{n-1}^{\prime} J_{n+1}+\frac{t^2}{2}\left[2 J_n J_n^{\prime}-J_{n-1}^{\prime} J_{n+1}-J_{n-1} J_{n+1}^{\prime}\right]\right.\)
= \(t\left(J_n^2-J_{n-1} J_{n+1}\right)+\frac{t^2}{2}\left[J_n\left(J_{n-1}-J_{n+1}\right)-\left(\frac{n-1}{t} J_{n-1}-J_n\right) J_{n+1}-J_{n-1}\left(-\frac{n+1}{t} J_{n+1}+J_n\right)\right]\)
(Substituting the value of \(2 J_n^{\prime}\) from recurrence formula 3 and the value of \(2 J_{n-1}^{\prime}\) and \(J^{\prime} n+1\) obtained by replacing n by n-1 and n+1 in recurrence formula 1 and 2 respectively.
∴ \(\frac{d}{d t}\left[\frac{t^2}{2}\left\{J_n^2(t)-J_{n=1}(t) J_{n+1}(t)\right\}\right]=t J_n^2(t)\)
Integrating both sides from o to x, we have \(\int_0^x t\left\{J_n(t)\right\}^2 d t=\left[\frac{t^2}{2}\left\{J_n^2(t)-J_{n-1}(t) J_{n+1}(t)\right]_0^x=\frac{x^2}{2}\left\{J_n^2(x)-J_{n-1}(x) J_{n+1}(x)\right\} .\right.\)
