Differential Equations Introduction Solved Problems
Example 1: Form the differential equation corresponding to \(c(y+c)^2=x^2\) where c is a parameter.
Solution.
Given equation is \(c(y+c)^2=x^2\) ………………….(1)
Differentiating (1) w.r.t. x, we get: \(2 c(y+c) \frac{d y}{d x}=2 x \Rightarrow c(y+c) \frac{d y}{d x}=x\)
⇒ \(c(y+c)=\frac{x}{(d y / d x)}\) ……………………..(2)
⇒ \(\text { (1) } \div(2) \Rightarrow y+c=\frac{x^2}{x} \cdot \frac{d y}{d x}=x \frac{d y}{d x}\) ……………………..(3)
⇒ \(c=x \frac{d y}{d x}-y\) ……………………..(4)
Substituting the Values of (y + c) and c from (3) and (4) in (1), we get:
∴ \(\left(x \frac{d y}{d x}-y\right) \cdot\left(x \frac{d y}{d x}\right)^2=x^2 \Rightarrow\left(x \frac{d y}{d x}-y\right)\left(\frac{d y}{d x}\right)^2=1\) is the required differential equation.
Note: The given equation contains only one arbitrary constant. Hence we got only a first-order differential equation.
Example 2. Form the differential equation by eliminating the arbitrary constants A and B from the equation \(y=e^x(\mathrm{~A} \cos x+\mathrm{B} \sin x)\)
Solution.
Given equation is \(y=e^x(\mathrm{~A} \cos x+\mathrm{B} \sin x)\) ……………………(1)
Differentiating (1) w.r.t. x, we get: \(\frac{d y}{d x}=e^x(\mathrm{~A} \cos x+\mathrm{B} \sin x)+e^x(-\mathrm{A} \sin x+\mathrm{B} \cos x)\)
= \(y+e^x(-\mathrm{A} \sin x+\mathrm{B} \cos x)\) [Using (1)]………………….(2)
Differentiating (2) w.r.t. x, we get: \(\frac{d^2 y}{d x^2}=\frac{d y}{d x}+e^x(-\mathrm{A} \cos x-\mathrm{B} \sin x)+e^x(-\mathrm{A} \sin x+\mathrm{B} \cos x)=\frac{d y}{d x}-y+\frac{d y}{d x}-y\)
[Using (1) and (2)]
∴ The required differential equation is \(\frac{d^2 y}{d x^2}-2 \frac{d y}{d x}+2 y=0\)
Introduction To Differential Equations With Solved Problems
Example. 3. Form the differential equation whose solution is given by \(\) where A and α are arbitrary constants.
Solution.
Given equation is x = A cos(pt – α) …………………(1)
Differentiating (1) w.r.t. t, we get \(\frac{d x}{d t}\) = -Ap sin(pt-α) ……………….. (2)
Differentiating (2) w.r.t. t, we get: \(\frac{d^2 x}{d t^2}=-A p^2 \cos (p t-\alpha)=-p^2 x\) [Using (1)]
∴ The required differential equation is \(\frac{d^2 x}{d t^2}+p^2 x=0\)
Example. 4: By eliminating the arbitrary constants a,b obtain the differential equation of Which \(x y=a e^x+b e^{-x}+x^2\) is a solution.
Solution.
Given equation is \(x y=a e^x+b e^{-x}+x^2\) …………………..(1)
Differentiating (1) w.r.t. x, we get: \(x y^{\prime}+y=a e^x-b e^{-x}+2 x\) ……………….. (2)
Differentiating (2) w.r.t. x, we get \(x y^{\prime \prime}+y^{\prime}+y^{\prime}=a e^x+b e^{-x}+2\)
⇒ \(x y^{\prime \prime}+2 y^{\prime}-2=a e^x+b e^{-x} \Rightarrow x y^{\prime \prime}+2 y^{\prime}-2=\left(x y-x^2\right)\) [using (1)]
∴ The required differential equation is: \(x y^{\prime \prime}+2 y^{\prime}-x y+x^2-2=0\)
Example. 5. : Show that \(y=a e^{2 x}+b x e^{2 x}\) where a and b are arbitrary constants, is the solution of the differential equation \(y^{\prime \prime}-4 y^{\prime}+4 y=0\)
Solution.
Given differential equation is \(y^{\prime \prime}-4 y^{\prime}+4 y=0\)
Also given \(y=a e^{2 x}+b x e^{2 x}=(a+b x) e^{2 x}\) ……………………(1)
Differentiating (1) twice w.r.t. x: \(y^{\prime}=(a+b x) 2 e^{2 x}+b e^{2 x}, y^{\prime \prime}=(a+b x) 4 e^{2 x}+2 b e^{2 x}+2 b e^{2 x} \Rightarrow y^{\prime \prime}=4(a+b x) e^{2 x}+4 b e^{2 x}\)
Now, \(y^{\prime \prime}-4 y^{\prime}+4 y=4(a+b x) e^{2 x}+4 b e^{2 x}-8(a+b x) e^{2 x}-4 b e^{2 x}\)
+ \(4(a+b x) e^{2 x}=8(a+b x) e^{2 x}-8(a+b x) e^{2 x}+4 b e^{2 x}-4 b e^{2 x}=0 \text { for all, } x \in \mathrm{R}\)
∴ \(y=a e^{2 x}+b x e^{2 x}\) is the solution of \(y^{\prime \prime}-4 y^{\prime}+4 y=0\)
Examples Of Differential Equations With Family Of Curves
Example. 6. Find the differential equation of the family of circles having the centres on the x-axis and passing through the origin.
Solution.
The equation of the family of circles having the centres on the x-axis and passing through the origin is \(x^2+y^2+2 \lambda x=0\) where A, is the parameter ……………… (1)
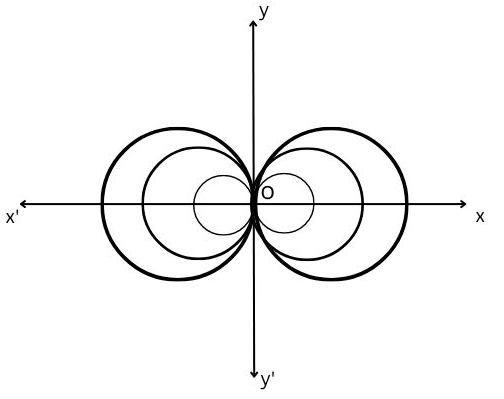
Differentiating (1) w.r.t. x, we get: \(2 x+2 y \frac{d y}{d x}+2 \lambda=0 \Rightarrow \lambda=-\left(x+y \frac{d y}{d x}\right)\) ………………….(2)
Eliminating λ from (1) and (2), we get: \(x^2+y^2-2 x\left(x+y \frac{d y}{d x}\right)=0\)
∴ The required differential equation of the family of circles is \(y^2-x^2-2 x y \frac{d y}{d x}=0\)
Example. 7: Find the differential equation of the family of parabolas having a vertex at the origin and foci on the y-axis.
Solution:
The equation of the family of parabolas with vertex at the origin and foci on the y-axis is \(\)ay where ‘a is the parameter of the family …………………. (1)
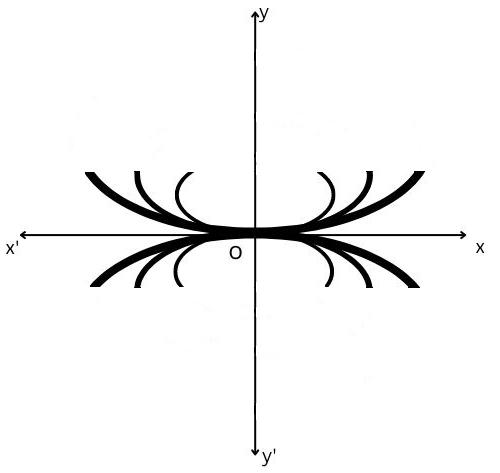
Differentiating (1) w.r.t. x, we get: \(2 x=4 a \frac{d y}{d x} \Rightarrow 4 a=2 x /\left(\frac{d y}{d x}\right)\) ………………..(2)
Eliminating ‘a’ from (1) and (2): \(x^2=\frac{2 x}{(d y / d x)} \cdot y\)
∴ The required differential equation is \(x \frac{d y}{d x}=2 y\)
Example. 8: Form the differential equation of the family of curves represented by the equation \(\frac{x^2}{a^2}+\frac{y^2}{a^2+\lambda}=1\) where λ is the parameter.
Solution.
Given equation of family of curves is \(\frac{x^2}{a^2}+\frac{y^2}{a^2+\lambda}=1\) ……………………(1)
Differentiating (1) w.r.t; x, we get: \(\frac{2 x}{a^2}+\frac{2 y y^{\prime}}{a^2+\lambda}=0 \Rightarrow \frac{y}{a^2+\lambda} \cdot y^{\prime}=-\frac{x}{a^2} \Rightarrow \frac{y^2}{a^2+\lambda}=\frac{-x y}{a^2 y^{\prime}}\) ……………………..(2)
Eliminating the parameter λ from (1) and (2): \(\frac{x^2}{a^2}-\frac{x y}{a^2 y^{\prime}}=1 \Rightarrow\left(x^2-a^2\right) y^{\prime}=x y\) is the required differential equation.
Example. 9. Form the differential equation of the family of circles of radius r.
Solution.
The equation of the family of all circles of radius r is given by \((x-h)^2+(y-k)^2=r^2\) where h and k are parameters.
Differentiating (1) w.r.t. x, we get: \(2(x-h)+2(y-k) y_1=0 \Rightarrow(x-h)+(y-k) y_1=0\) …………………..(2)
Differentiating (2) w.r.t. x, we get: \(1+(y-k) y_2+y_1^2=0\)
⇒ \((y-k) y_2=-1-y_1^2 \Rightarrow y-k=-\left(1+y_1^2\right) / y_2\) ………………………..(3)
From (2) and (3): \((x-h)=\frac{\left(1+y_1^2\right) y_1}{y_2}\) …………………….(4)
substituting the values (x-h) and (y-k) from (4) and (3) in (1) we get: \(\frac{\left(1+y_1^2\right)^2 y_1^2}{y_2^2}+\frac{\left(1+y_1^2\right)^2}{y_2^2}=r^2 \Rightarrow\left(1+y_1^2\right)^2\left(1+y_1^2\right)=r^2 y_2^2\)
∴ The required differential equation is \(\left(1+y_1^2\right)^3=r^2 y_2^2\).
Example. 10. Obtain the differential equation of the family of all ellipses whose axes coincide with the axes of coordinates and centre at the origin.
Solution.
The equation of the family of ellipses whose axes coincide with the axes of coordinates and centre at the origin is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
where a and b are parameters …………………….(1)
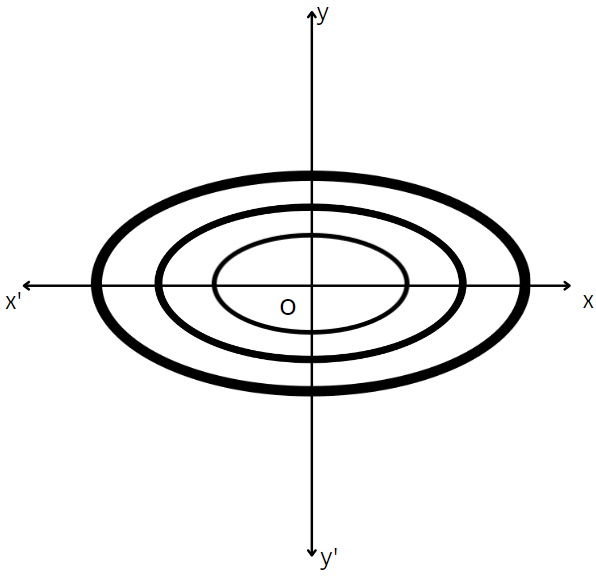
Differentiating (1) w.r.t. x, we get: \(\frac{2 x}{a^2}+\frac{2 y y_1}{b^2}=0 \Rightarrow \frac{x}{a^2}+\frac{y}{b^2} y_1=0 \Rightarrow \frac{y y_1}{x}=\frac{-b^2}{a^2}\) ………………………(2)
Differentiating (2) w.r.t. x, we get: \(\frac{y y_2}{x}+\frac{x y_1-y .1}{x^2} y_1=0\)
∴ The required differential equation is \(x y y_2+x y_1^2-y y_1=0\)
Solved Problems On Parabolas And Circles In Differential Equations
Example. 11: Form the differential equation of the family of circles given by \(x^2+y^2+2 a x+2 b y+c=0\) where a,b,c are arbitrary constants.
Solution.
Given equation is \(x^2+y^2+2 a x+2 b y+c=0\) …………………. (1)
Since a,b, and c are three arbitrary constants, we have to eliminate them between (1) and its, three derivatives.
Differentiating (1) w.r.t. x, successively, we get: \(2 x+2 y y_1+2 a x+2 b y_1=0\)
⇒ \(x+y y_1+a+b y_1=0\) …………………..(2)
⇒ \(1+y y_2+y_1^2=-b y_2\) ……………………(3)
⇒ \(y y_3+y_1 y_2+2 y_1 y_2=-b y_3 \Rightarrow y y_3+3 y_1 y_2=-b y_3\) …………………..(4)
∴ \((3) \div(4) \Rightarrow \frac{1+y y_2+y_1^2}{y y_3+3 y_1 y_2}=\frac{y_2}{y_3} \Rightarrow y_3\left(1+y y_2+y_1^2\right)=y_2\left(y y_3+3 y_1 y_2\right)\)
⇒ \(y_3+y y_2 y_3+y_3 y_1^2=y y_2 y_3+3 y_1 y_2^2\)
∴ The required differential equation is \(\frac{d^3 y}{d x^3}\left[1+\left(\frac{d y}{d x}\right)^2\right]=3\left(\frac{d y}{d x}\right)\left(\frac{d^2 y}{d x^2}\right)^2\)
Example. 12. Find the differential equation corresponding to \(y=a e^x+b e^{2 x}+c e^{3 x}\) where a, b,c. are parameters.
Solution.
Given equation is \(y=a e^x+b e^{2 x}+c e^{3 x}\) ……………………..(1)
Differentiating (1) w.r.t x, successively three times: \(y_1=a e^x+2 b e^{2 x}+3 c e^{3 x}=\left(a e^x+b e^{2 x}+c e^{3 x}\right)+b e^{2 x}+2 c e^{3 x}\)
⇒ \(y_1=y+b e^{2 x}+2 c e^{3 x}\) [Using (2)]
⇒ \(y_1-y=b e^{2 x}+2 c e^{3 x}\) …………………….(2)
Differentiating (2) w.r.t. x, we get: \(y_2-y_1=2 b e^{2 x}+6 c e^{3 x}=2\left(b e^{2 x}+2 c e^{3 x}\right)+2 c e^{3 x}\)
⇒ \(y_2-y_1=2\left(y_1-y\right)+2 c e^{3 x} \Rightarrow y_2-3 y_1+2 y=2 c e^{3 x}\) [from (2)] ……………………..(3)
Differentiating (3) w.r.t. x, we get: \(y_3-3 y_2+2 y_1=6 c e^{3 x}=3\left(2 c e^{3 x}\right)=3\left(y_2-3 y_1+2 y\right)\) [from (3)]
∴ The required differential equation is \(y_3-6 y_2+11 y_1-6 y=0\)
