Hermite Polynomials Exercise 3
Hermite Polynomials Solved Examples Step-By-Step
1. Define Hermite’s differential equation.
Solution: The differential equation \(\frac{d^2 y}{d x^2}-2 x \frac{d y}{d x}+2 \lambda y=0\), where λ is a constant, is called Hermite’s differential equation.
2. Find the general solution of Hermite’s differential equation. 3.
Solution:
The differential equation \(\frac{d^2 y}{d x^2}-2 x \frac{d y}{d x}+2 \lambda y=0\), where \(\lambda\) is a constant, is called Hermite’s differential equation.
The Hermite’s equation \(\frac{d^2 y}{d x^2}-2 x \frac{d y}{d x}+2 \lambda y=0 \rightarrow\) (1) is solved by series integration
Let us assume \(y=\sum_{n=0}^{\infty} a_n x^n \rightarrow\) (2) as the solution of the given equation (1)
∴ \(\frac{d y}{d x}=\sum_{n=1}^{\infty} n a_n x^{n-1}\) and\(\frac{d^2 y}{d x^2}=\sum_{n=2}^{\infty} n(n-1) a_n x^{n-2}\)
Substituting these in (1), we have \(\sum_{n=2}^{\infty} n(n-1) a_n x^{n-2}-2 x\left(\sum_{n=1}^{\infty} n a_n x^{n-1}\right)+2 \lambda\left(\sum_{n=0}^{\infty} a_n x^n\right)=0\)
⇒ \(\sum_{n=2}^{\infty} n(n-1) a_n x^{n-2}-\sum_{n=1}^{\infty} 2 n a_n x^n+\sum_{n=0}^{\infty} 2 \lambda a_n x^n=0\)
⇒ \(\sum_{n=0}^{\infty}(n+2)(n+1) a_{n+2} x^n-\sum_{n=1}^{\infty} 2 n a_n x^n+\sum_{n=0}^{\infty} 2 \lambda a_n x^n=0\)
⇒ \(\left(2 a_2+2 \lambda a_0\right)+\sum_{n=0}^{\infty}\left[(n+2)(n+1) a_{n+2}-2 n a_n+2 \lambda a_n\right] x^n=0 \rightarrow \text { (3) }\)
Now (3) being an identity. we can equate to zero the coefficients of various powers of x .
∴ We get \(2 a_2+2 \lambda a_0=0 \Rightarrow a_2=-\lambda a_0 \rightarrow \text { (4) }\)
(n+2)(n+1) \(a_{n+2}-2 n a_n+2 \lambda a_n=0 \Rightarrow(n+2)(n+1) a_{n+2}=(2 n-2 \lambda) a_n \rightarrow \text { (5) }\)
Putting \(n=1,2,3, \cdots\) in (5), we have
6 \(a_3=(2-2 \lambda) a_1 \Rightarrow a_3=-2(\lambda-1) \frac{a_1}{3!}\)
12 \(a_4 *(4-2 \lambda) a_2 \Rightarrow a_4=(2-\lambda)(-\lambda) \frac{a_0}{6}=\lambda(\lambda-2) \frac{a_0}{6}\)
20 \(a_5=(6-2 \lambda) a_3 \Rightarrow a_5=(3-\lambda)(1-\lambda) \frac{a_1}{30}=(\lambda-1)(\lambda-3) \frac{a_1}{30}\)
30 \(a_6=(8-2 \lambda) a_4 \Rightarrow a_6=(4-\lambda)(\lambda)(\lambda-2) \frac{a_0}{90}=-\lambda(\lambda-2)(\lambda-4) \frac{a_0}{90}\) and so on
Substituting these in (2), we get the solution as \(y=a_0+a_1 x-\lambda a_0 x^2-(\lambda-1) \frac{a_1}{3} x^3\)
+ \(\lambda(\lambda-2) \frac{a_0}{6} x^4+(\lambda-1)(\lambda-3) \frac{a_1}{30} x^5-\lambda(\lambda-2)(\lambda-4) \frac{a_0}{90} x^6+\cdots\)
⇒ \(y=a_0\left[1-\lambda x^2+\lambda(\lambda-2) \frac{x^4}{6}-\lambda(\lambda-2)(\lambda-4) \frac{x^6}{90}+\cdots\right]\)
+ \(a_1\left[x-(\lambda-1) \frac{x_3}{3}+(\lambda-1)(\lambda-3) \frac{x^5}{30}-\cdots\right]\)
⇒ y = \(a_0\left[1+\frac{(-2) \lambda x^2}{2!}+\frac{(-2)^2 \lambda(\lambda-2) x^4}{4!}+\frac{(-2)^3 \lambda(\lambda-2)(\lambda-4) x^6}{6!}+\cdots\right]\)
+ \(a_1\left[x+\frac{(-2)(\lambda-1) x^3}{3!}+\frac{(-2)^2(\lambda-1)(\lambda-3) x^5}{5!}+\cdots\right]\)
Hence the general solution of Hermite’s equation is \(y=a_0 y_1+a_1 y_2\)
where \(a_0\) and \(a_1\) are arbitrary constants and \(y_1, y_2\) are given by \(y_1=1+\frac{(-2) \lambda x^2}{2!}+\frac{(-2)^2 \lambda(\lambda-2) x^4}{4!}+\frac{(-2)^3 \lambda(\lambda-2)(\lambda-4) x^6}{6!}+\cdots\)
and \(y_2=x+\frac{(-2)(\lambda-1) x^3}{3!}+\frac{(-2)^2(\lambda-1)(\lambda-3) x^5}{5!}+\cdots\)
Solved Exercise Problems On Hermite Polynomials
3. Define Hermitte’s polynomial.
Solution:
Hermitte’s polynomial
The Hermite’s Polynomial \(H_n(x)\) of degree n is defined as \(H_n(x)=(2 x)^n\)
– \(\frac{n(n-1)}{1!}(2 x)^{n-2}+\frac{n(n-1)(n-2)(n-3)}{2!}(2 x)^{n-4}+\cdots+(-1)^{n / 2} \frac{n!}{(n / 2)!}\)
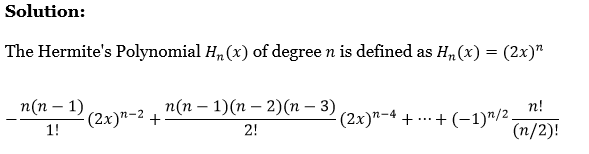
Applications Of Hermite Polynomials With Solved Problems
4. Prove that \(e^{2 l x-t^2}=\sum_{n=0}^{\infty} \frac{t^n}{n !} H_n(x)\).
Solution:
Here \(e^{2 x x-t^2}=e^{2 x x} e^{-1^2}=\sum_{r=0}^{\infty} \frac{(2 t x)^r}{r!} \sum_{s=0}^{\infty} \frac{\left(-t^2\right)^s}{s!}=\sum_{r, s=0}^{\infty}(-1)^s \frac{(2 x)^r}{r!s!} t^{r+2 s}\).
Coefficieent of \(t^n\) (for fixed value of s) = \((-1)^s \frac{(2 x)^{n-2 s}}{(n-2 s)!s!}\) obtained by putting r+2 s=n, i.e., r=n-2 s.
The total value of \(t^n\) is obtained by summing over all allowed values of s and since r=n-2 s.
∴ \(n-2 s \geq 0 \Rightarrow s \leq n / 2\).
Thus if n is even, s goes from o to n / 2 and if n is odd, s goes from o to (n-1) / 2.
∴ Coefficient of \(t^n=\sum_{s=0}^{(n / 2)}(-1)^s \frac{(2 x)^{n-2 s}}{(n-2 s)!s!}=\frac{H_n(x)}{n!}\).
Hence \(e^{2 x t-t^2}=\sum_{n=0}^{\infty} \frac{t^n}{n!} H_n(x)\)
5. Prove that \(H_n(x)=2^n\left\{\exp \left(-\frac{1}{4} \frac{d^2}{d x^2}\right)\right\} x^n .\).
Solution:
We have \(\frac{1}{2} \frac{d}{d x} e^{2 k x}=t e^{2 k x} \rightarrow\) (1)
Also \(\frac{d}{d x}\left(\frac{1}{2} \frac{d}{d x} e^{2 t x}\right)=2 t^2 e^{2 x x}\)
∴ \(\frac{1}{2} \frac{d}{d x}\left(\frac{1}{2} \frac{d}{d x} e^{2 \alpha x}\right)=t^2 e^{2 t x} \Rightarrow\left(\frac{1}{2} \frac{d}{d x}\right)^2 e^{2 t x}=t^2 e^{2 t x}\).
Hence \(\left(\frac{1}{2} \frac{d}{d x}\right)^n e^{2 x x}=t^n e^{2 t x} \rightarrow(2)\)
Thus \(\left\{\exp \left(-\frac{1}{4} \frac{d^2}{d x^2}\right)\right\} e^{2 x x}=\left[\sum_{n=0}^{\infty} \frac{1}{n!}\left(-\frac{1}{4} \frac{d^2}{d x^2}\right)^n\right] e^{2 x x}\)
= \(\sum_{n=0}^{\infty} \frac{(-1)^n}{n!}\left(\frac{1}{2} \frac{d}{d x}\right)^{2 n} e^{2 x x}\)
= \(\sum_{n=0}^{\infty} \frac{(-1)^n}{n!} t^{2 n} e^{2 x x}=e^{2 \alpha x} \sum_{n=0}^{\infty} \frac{(-1)^n}{n!} t^{2 n}\)
= \(e^{2 x x} \sum_{n=0}^{\infty} \frac{1}{n!}\left(-t^2\right)^n=e^{2 x x} e^{-t^2}=e^{-t^2+2 t x}\)
⇒ \(\left\{\exp \left(-\frac{1}{4} \frac{d^2}{d x^2}\right)\right\}_{n=0}^{\infty} \frac{1}{n!}(2 t x)^n=\sum_{n=0}^{\infty} \frac{t^n}{n!} H_n(x)\)
Equating the coefficient of \(t^n\) from the two sides, we have \(\left\{\exp \left(-\frac{1}{4} \frac{d^2}{d x^2}\right)\right\} \frac{1}{n!} 2^n x^n=\frac{1}{n!} H_n(x) \Rightarrow H_n(x)=2^n\left\{\exp \left(-\frac{1}{4} \frac{d^2}{d x^2}\right)\right\} x^n\)
Properties Of Hermite Polynomials With Solved Examples
6. Prove that \(H_n(x)=(-1)^n e^{x^2} \frac{d^n}{d x^n}\left(e^{-x^2}\right)\).
Solution:
⇒ \(e^{2 t x-t^2}=\sum_{n=0}^{\infty} \frac{H_n(x)}{n!} t^n\)
⇒ \(e^{x^2-(t-x)^2}=\frac{H_0(x)}{0!} t^0+\frac{H_1(x)}{1!} t+\frac{H_2(x)}{2!} t^2+\cdots+\frac{H_n(x)}{n!} t^n+\frac{H_{n+1}(x)}{(n+1)!} t^{n+1}+\cdots\)
Differentiating both sides, partially w.r.t ‘ t’, n times and then putting t=0, we have \(\left[\frac{\partial^n}{\partial t^n} e^{-(t-x)^2}\right]_{t=0} e^{x^2}=\frac{H_n(x)}{n!} n!\)
Now let t-x=u i.e., at t=0, x=-u.
∴ \(\frac{\partial}{\partial t}=\frac{\partial}{\partial u}\) and \(\left[\frac{\partial^n}{\partial t^n} e^{-(t-x)^2}\right]_{t=0}=\frac{\partial^n}{\partial u^n}\left(e^{-u^2}\right)\)
= \((-1)^n \frac{\partial^n}{\partial x^n}\left(e^{-x^2}\right)=(-1)^n \frac{d^n}{d x^n}\left(e^{-x^2}\right)\)
∴ \(H_n(x)=(-1)^n e^{x^2} \frac{d^n}{d x^n}\left(e^{-x^2}\right)\)
Exercises On Hermite Polynomials With Detailed Solutions
7. For what value of n,\(H_n(0)=0 \text {. }\).
Solution: \(H_n(0)=0 \Rightarrow(-1)^{n / 2} \frac{n !}{(n / 2) !}=0 \Rightarrow n \text { is odd. }\)
8. Prove that 1) \(H_0(x)=1\)
2) \(H_1(x)=2 x\)
3) \(H_2(x)=4 x^2-2\)
4) \(H_3(x)=8 x^3-12 x\)
Solution:
Putting \(n=0,1,2,3, \ldots\) in \(H_n(x)=(-1)^n e^{x^2} \frac{d^n}{d x^n}\left(e^{-x^2}\right)\), we have
⇒ \(H_0(x)=e^{x^2} e^{-x^2}=1\)
⇒ \(H_1(x)=(-1) e^{x^2} \frac{d}{d x}\left(e^{-x^2}\right)=2 x\)
⇒ \(H_2(x)=(-1)^2 e^{x^2} \frac{d^2}{d x^2}\left(e^{-x^2}\right)=e^{x^2} \frac{d}{d x}\left(-2 x e^{-x^2}\right)\)
= \(e^{x^2}\left(4 x^2 e^{-x^2}-2 e^{-x^2}\right)=4 x^2-2\)
⇒ \(H_3(x)=(-1)^3 e^{x^2} \frac{d^3}{d x^3}\left(e^{-x^2}\right)=-e^{x^2} \frac{d}{d x}\left\{\frac{d^2}{d x^2}\left(e^{-x^2}\right)\right\}\)
= \(-e^{x^2} \frac{d}{d x}{\left(4 x^2-2\right) e^{-x^2})}\)
= \(-e^{x^2}\left\{-2 x\left(4 x^2-2\right) e^{-x^2}+8 x e^{-x^2}\right\}=-e^{x^2}\left\{\left(-8 x^3+12 x\right) e^{-x^2}\right\}=8 x^3-12 x\)
Hermite Polynomial Problems In Quantum Mechanics Solve
9. Show that \(H_1(x)=2 x H_0(x)\).
Solution: We know \(H_0(x)=1, H_1(x)=2 x\). ∴ \(H_1(x)=2 x H_0(x) .\)
10. Prove that \(H_4(x)=16 x^4-48 x^2+12\).
Solution:
⇒ \(H_4(x)=(-1)^4 e^{x^2} \frac{d^4}{d x^4}\left(e^{-x^2}\right)\)
= \(e^{x^2} \frac{d}{d x}\left\{\frac{d}{d x}\left[\frac{d}{d x}\left(\frac{d}{d x}\left(e^{-x^2}\right)\right)\right]\right\}\)
= \(e^{x^2} \frac{d}{d x}\left\{\frac{d}{d x}\left[\frac{d}{x}\left(e^{-x^2}(-2 x)\right)\right]\right\}\)
= \(\left.e^{x^2} \frac{d}{d x}\left\{\frac{d}{d x} e^{-x^2}(-2)+(-2 x) e^{-x^2}(-2 x)\right]\right\}\)
= \(\left.e^{x^2} \frac{d}{d x}\left[\frac{d}{d x}\left\{\left(4 x^2-2\right) e^{-x^2}\right)\right\}\right]\)
= \(e^{x^2} \frac{d}{d x}\left\{-2 x\left(4 x^2-2\right) e^{-x^2}+8 x e^{-x^2}\right\}\)
= \(e^{x^2} \frac{d}{d x}\left\{\left(-8 x^3+12 x\right) e^{-x^2}\right\}\)
= \(e^{x^2} \frac{d}{d x}\left\{\left(-24 x^2+12\right) e^{-x^2}+\left(-8 x^3+12 x\right) e^{-x^2}(-2 x)\right\}\)
= \(e^{x^2}\left\{\left(-24 x^2+12+16 x^4-24 x^2\right) e^{-x^2}\right\}=16 x^4-48 x^2+12 .\)
Step-By-Step Guide To Solving Hermite Polynomial Exercises
11. Prove that \(H_5(x)=32 x^5-160 x^3+120 x\).
Solution:
⇒ \(H_5(x)=(-1)^5 e^{x^2} \frac{d^5}{d x^5}\left(e^{-x^2}\right)=-e^{x^2} \frac{d}{d x}\left[\frac{d}{d x}\left\{\frac{d}{d x}\left[\frac{d}{d x}\left(\frac{d}{d x}\left(e^{-x^2}\right)\right]\right]\right\}\right]\)
= \(-e^{x^2} \frac{d}{d x}\left[\frac{d}{d x}\left\{\frac{d}{d x}\left[\frac{d}{d x}\left(e^{-x^2}(-2 x)\right)\right]\right\}\right]\)
= \(-e^{x^2} \frac{d}{d x}\left[\frac{d}{d x}\left\{\frac{d}{d x}\left[e^{-x^2}(-2)+(-2 x) e^{-x^2}(-2 x)\right]\right\}\right]\)
= \(\left.=-e^{x^2} \frac{d}{d x}\left[\frac{d}{d x}\left\{\frac{d}{d x}\left\{\left(4 x^2-2\right) e^{-x^2}\right)\right\}\right\}\right]\)
= \(-e^{x^2} \frac{d}{d x}\left[\frac{d}{d x}\left\{-2 x\left(4 x^2-2\right) e^{-x^2}+8 x e^{-x^2}\right\}\right]\)
= \(-e^{x^2} \frac{d}{d x}\left[\frac{d}{d x}\left\{\left(-8 x^3+12 x\right) e^{-x^2}\right\}\right]\)
= \(-e^{x^2} \frac{d}{d x}\left\{\left(-24 x^2+12\right) e^{-x^2}+\left(-8 x^3+12 x\right) e^{-x^2}(-2 x)\right\}\)
= \(-e^{x^2} \frac{d}{d x}\left[\left(-24 x^2+12+16 x^4-24 x^2\right) e^{-x^2}\right]=-e^{x^2} \frac{d}{d x}\left[\left(16 x^4-48 x^2+12\right) e^{-x^2}\right]\)
= \(-e^{x^2}\left[\left(16 x^4-48 x^2+12\right) e^{-x^2}(-2 x)+\left(64 x^3-96 x\right) e^{-x^2}\right]\)
= \(-e^{x^2}\left(-32 x^5+160 x^3-120 x\right) e^{-x^2}=32 x^5-160 x^3+120 x\)
Worked Examples Of Hermite Polynomials In Physics And Mathematics
12. Show that \(x^4=\frac{1}{16} H_4(x)+\frac{3}{4} H_2(x)+\frac{3}{4} H_0(x)\).
Solution:
We know that \(H_0(x)=1, H_2(x)=4 x^2-2, H_4(x)=16 x^4-48 x^2+12\).
∴ \(16 x^4=H_4(x)+48 x^2-12=H_4(x)+12\left[H_2(x)+2\right]-12\)
= \(\mathrm{H}_4(x)+12 \mathrm{H}_2(x)+12 \mathrm{H}_0(x)\)
⇒ \(x^4=\frac{1}{16} H_4(x)+\frac{3}{4} H_2+\frac{3}{4} H_0(x) .\)
13. Show that \(x^5=\frac{1}{32} H_5(x)+\frac{5}{8} H_3+\frac{15}{4} H_1(x)\).
Solution:
We know that \(H_1(x)=2 x, H_3(x)=8 x^3-12 x, H_5(x)=32 x^5-160 x^3+120 x\)
∴ \(32 x^5=H_5(x)+160 x^3-120 x=H_5(x)+20\left[H_3(x)+12 x\right]\)
= \(H_5(x)+20 H_3(x)+240 x=H_5(x)+20 H_3(x)+120 H_1(x)\)
⇒ \(x^5=\frac{1}{32} H_5(x)+\frac{5}{8} H_3+\frac{15}{4} H_1(x)\)
14. Prove that \(\int_{-\infty}^{\infty} e^{-x^2} H_n(x) H_m(x) d x\)= 0 if m \(\neq\) n [atex]\sqrt{\pi} 2^n n ![/latex] if m=n[/latex]
Solution:
We have \(e^{-t^2+2 t x}=\sum_{n=0}^{\infty} H_n(x) \frac{t^n}{n!}\) and
⇒ \(e^{-s^2+2 s x}=\sum_{m=0}^{\infty} H_m(x) \frac{s^m}{m!}\)
∴ \(e^{-t^2+2 t x} e^{-s^2+2 s x}=\sum_{n=0}^{\infty} H_n(x) \frac{t^n}{n!} \sum_{m=0}^{\infty} H_m(x) \frac{s^m}{m!}\)
∴ \(\frac{1}{n!m!} H_n(x) H_m(x)=\)ncoeff. of \(l^n s^m\) in the expansion of \(e^{-t^2+2 k x} e^{-s^2+2 s x}\)
∴ \(\int_{-\infty}^{\infty} e^{-x^2} H_n(x) H_m(x) d x\)
= n!m! (coefficient of \(f^{\prime} s^m\) in the expansion of \(\left.\int_{-\infty}^{\infty} e^{-x^2} e^{-t^2+2 t x} e^{-s^2+2 s x} d x\right)\)
Now \(\int_{-\infty}^{\infty} e^{-x^2} e^{-t^2+2 t x} e^{-s^2+2 s x} d x=\int_{-\infty}^{\infty} e^{-\left[x^2-2(t+s) x+t^2+s^2\right]} d x\)
= \(\int_{-\infty}^{\infty} e^{\left.-[x-(t+s)]^2+2 t s\right]} d x=e^{2 t s} \int_{-\infty}^{\infty} e^{-[x-(t+s)]^2} d x=e^{2 t s} \int_{-\infty}^{\infty} e^{-u^2} d u\)
putting \(x-(t+s)=u\)
= \(e^{2 t s} \sqrt{\pi}=\sqrt{\pi}\left[1+2 t s+\frac{(2 t s)^2}{2!} \ldots+\frac{(2 t s)^n}{n!}+\cdots\right]\).
Since \(\int_{-\infty}^{\infty} e^{-u^2} d u=\sqrt{\pi}\)
Coefficient of \(t^{\prime} s^m\) in the expansion of \(\int_{-\infty}^{\infty} e^{-x^2} t^{-t^2+2 t x} e^{-s^2+2 s x} d x\) is o if \(m \neq n\) and \(\frac{2^n \sqrt{\pi}}{n!}\) if m=n
Hence \(\int_{-\infty}^{\infty} e^{-x^2} H_n(x) H_m(x) d x\)
= 0 if \(m \neq n\) \(\sqrt{\pi} 2^n n! \) if m=n
Hermite Polynomials Differential Equations Solved Examples
15. Prove that \(H_n^{\prime}(x)=2 n H_{n-1}(x), n \geq 1\).
Solution:
We have \(\sum_{n=0}^{\infty} \frac{H_n(x)}{n!} t^n=e^{-t^2+2 t x}\)
Differentiating both sides w.r.t. x, we have \(\sum_{n=0}^{\infty} \frac{H_n^{\prime}(x)}{n!} t^{\prime}\)
= \(e^{-t^2+2 x t} 2 t=2 t \sum_{n=0}^{\infty} \frac{H_n(x)}{n!} t^n=2 \sum_{n=0}^{\infty} \frac{H_n(x)}{n!} t^{n+1}=2 \sum_{n=1}^{\infty} \frac{H_{n-1}(x)}{(n-1)!} t^n\)
Equating the coefficient of \(t^{\prime \prime}\), on both sides, we have \(\frac{H_n^{\prime}(x)}{n!}=2 \frac{H_{n-1}(x)}{(n-1)!} \Rightarrow H_n^{\prime}(x)=2 n H_{n-1}(x)\)
16. Prove that \(2 x H_n(x)=2 n H_{n-1}(x)+H_{n+1}(x)\).
Solution:
We have \(\sum_{n=0}^{\infty} \frac{H_n(x)}{n!} t^n=e^{-t^2+2 t x}\).
Differentiating both sides w.r.t. t we have \(\sum_{n=0}^{\infty} \frac{H_n(x)}{n!} n t^{n-1}=e^{-t^2+2 t x}(-2 t+2 x)\)
⇒ \(\sum_{n=1}^{\infty} \frac{H_n(x)}{(n-1)!} t^{n-1}=-2 t e^{-t^2+2 t x}+2 x e^{-t^2+2 t x}\)
⇒ \(\sum_{n=1}^{\infty} \frac{H_n(x)}{(n-1)!} t^{n-1}=-2 t \sum_{n=0}^{\infty} \frac{H_n(x)}{n!} t^n+2 x \sum_{n=0}^{\infty} \frac{H_n(x)}{n!} t^n\)
⇒ \(2 x \sum_{n=0}^{\infty} \frac{H_n(x)}{n!} l^n=2 \sum_{n=0}^{\infty} \frac{H_n(x)}{n!} t^{n+1}+\sum_{n=1}^{\infty} \frac{H_n(x)}{(n-1)!} l^{n-1}\)
2 \(x \sum_{n=0}^{\infty} \frac{H_n(x)}{n!} t^n=2 \sum_{n=1}^{\infty} \frac{H_{n-1}(x)}{(n-1)!} t^n+\sum_{n=0}^{\infty} \frac{H_{n+1}(x)}{n!} t^n\)
Equating the coefficients of \(l^n\), on the two sides, we have 2 \(x \frac{H_n(x)}{n!}=2 \frac{H_{n-1}(x)}{(n-1)!}+\frac{H_{n+1}(x)}{n!} \Rightarrow 2 x H_n(x)=2 n H_{n-1}(x)+H_{n+1}(x) \text {. }\)
17. Prove that \(H_n^{\prime}(x)=2 x H_n(x)-H_{n+1}(x)\).
Solution:
Writing recurrence formulae 1 and 2, we have \(H_n^{\prime}(x)=2 n H_{n-1}(x)\)
and \(2 x H_n(x)=2 n H_{n-1}(x)+H_{n+1}(x) \rightarrow \text { (2) }\)
Subtracting (2) from (1), we have \(H_n^{\prime}(x)=2 x H_n(x)-H_{n+1}(x)\).
Hermite Polynomial Recursion Relation Examples Solved
18. Prove that \(H_n^{\prime \prime}(x)-2 x H_n^{\prime}(x)+2 n H_n(x)=0\).
Solution:
Hermite’s differential equation is \(\frac{d^2 y}{d x^2}-2 x \frac{d y}{d x}+2 n y=0 \rightarrow\) (1)
∴ \(H_n(x)\) is the solution of (1), therefore, we have \(H_n^{\prime \prime}(x)-2 x H_n^{\prime}(x)+2 n H_n(x)=0\).
19. Prove that \(H_n^{\prime \prime}=4 n(n-1) H_{n-2}\).
Solution:
From recurrence formula 1, we have \(H_n^{\prime}=2 n H_{n-1} \rightarrow\) (1)
Differentiating w.r.t. ‘x’ we have \(H_n^{\prime \prime}=2 n H_{n-1}^{\prime} \rightarrow\) (2)
Replacing n by (n-1) in (1), we have \(H_{n-1}^{\prime}=2(n-1) H_{n-2} \rightarrow\) (3)
∴ From (2) and (3), we have \(H_n^{\prime \prime}=4 n(n-1) H_{n-2}\)
20. Show that \(H_n{ }^n(x)=2^n n ! H_0(x)\).
Solution:
We know \(\sum_{n=0}^{\infty} \frac{t^n}{n !} H_n(x)=e^{-t^2+2 t x} \Rightarrow \sum_{n=0}^{\infty} \frac{t^n}{n !} \frac{d^n}{d x^n}\left\{H_n(x)\right\}=\frac{d^n}{d x^n}\left\{e^{-t^2+2 t x}\right\}\)
= \((2 t)^n \cdot e^{-t^2+2 t x}=(2 t)^n \sum_{n=0}^{\infty} \frac{t^n}{n !} H_n(x)=2^n \sum_{n=0}^{\infty} \frac{t^{2 n}}{n !} H_n(x)=2^n \sum_{r=0}^{\infty} \frac{t^r}{(r-n) !} H_{r-n}(x)\)
Equating the coefficient \(t^n\) of both sides, we get \(\frac{1}{n !} \frac{d^n}{d x^n}\left\{H_n(x)\right\}=2^n H_0(x) \Rightarrow H_n^n(x)=2^n n ! H_0(x)\)
Hermite Polynomials Orthogonality Property With Solved Problems
21. Show that \(H_n^{\prime \prime}(x)=\left(4 x^2-2 n\right) H_n(x)-2 x H_{n+1}(x)\).
Solution:
Recurrence formula 4 is \(H_n^{\prime \prime}(x)-2 x H_n^{\prime}(x)+2 n H_n(x)=0\)
⇒ \(H_n^{\prime \prime}(x)=2 x H_n^{\prime}(x)-2 n H_n(x)\)
⇒ \(H_n^{\prime \prime}(x)=2 x\left[2 x H_n(x)-H_{n+1}(x)\right]-2 n H_n(x)\), from recurrence formula III
⇒ \(H_n^{\prime \prime}(x)=\left(4 x^2-2 n\right) H_n^{\prime}(x)-2 x H_{n+1}(x) \text {. }\)
22. Show that \(H_n(x)=2 x H_{n-1}(x)-2(n-1) H_{n-2}(x)\).
Solution:
Recurrence formula 1 is \(H_n^{\prime}(x)=2 n H_{n-1}(x) \Rightarrow H_n^{\prime \prime}(x)=2 n H_{n-1}^{\prime}(x)\)
⇒ \(H_n^{\prime \prime}(x)=2 n 2(n-1) H_{n-2}(x)=4 n(n-1) H_{n-2}(x)\)
Recurrence formula 4 is \(H_n^{\prime \prime}(x)-2 x H_n^{\prime}(x)+2 n H_n(x)=0\)
4n(n-1) \(H_{n-2}(x)-2 x 2 n H_{n-1}(x)+2 n H_n(x)=0\)
2(n-1) \(H_{n-2}(x)-2 x H_{n-1}(x)+H_n(x)=0\)
⇒ \(H_n(x)=2 x H_{n-1}(x)-2(n-1) H_{n-2}(x)\)
23. Evaluate \(\int_{-\infty}^{\infty} x e^{-x^2} H_n(x) H_m(x) d x\).
Solution:
Given
\(\int_{-\infty}^{\infty} x e^{-x^2} H_n(x) H_m(x) d x\)From recurrence formula 2, we have \(x H_n(x)=n H_{n-\mathrm{j}}(x)+\frac{1}{2} H_{n+1}(x)\)
∴ \(\int_{-\infty}^{\infty} x e^{-x^2} H_n(x) H_m(x) d x=\int^{-e^2}\left[x H_n(x)\right] H_m(x) d x\)
= \(\int_{-\infty}^{\infty} e^{-x^2}\left\{n H_{n-1}(x)+\frac{1}{2} H_{n+1}(x)\right\} H_m(x) d x\)
= \(n \int_{-\infty}^{\infty} e^{-x^2} H_{n-1}(x) H_m(x) d x+\frac{1}{2} \int_{-\infty}^{\infty} e^{-x^2} H_{n+1}(x) H_m(x) d x\)
= \(n \sqrt{\pi} 2^{n-1}(n-1)!\delta_{n-1, m}+\frac{1}{2} \sqrt{\pi} 2^{n+1}(n+1)!\delta_{n+1, m}\)
= \(\sqrt{\pi} 2^{n-1} n!\delta_{n-1, m}+\sqrt{\pi} 2^n(n+1)!\delta_{n+1, m}\) where \(\delta\) is Kronecker delta.
24. Show that \(\int_{-\infty}^{\infty} x^2 e^{-x^2}\left\{H_n(x)\right\}^2 d x=\sqrt{\pi} 2^n n !\left(n+\frac{1}{2}\right)\).
Solution:
⇒ \(\int_{-\infty}^{\infty} x^2 e^{-x^2}\left\{H_n(x)\right\}^2 d x=\int_{-\infty}^{\infty} e^{-x^2}\left\{x H_n(x)\right\}^2 d x\)
= \(\int_{-\infty}^{\infty} e^{-x^2}\left[n H_{n-1}(x)+\frac{1}{2} H_{n+1}(x)\right]^2 d x\)
= \(\int_{-\infty}^{\infty} e^{-x^2}\left[n^2\left\{H_{n-1}(x)\right\}^2+\frac{1}{4}\left\{H_{n+1}(x)\right\}^2+n H_{n-1}(x) H_{n+1}(x)\right] d x\)
= \(n^2 \int_{-\infty}^{\infty} e^{-x^2}\left\{H_{n-1}(x)\right\}^2 d x+\frac{1}{4} \int_{-\infty}^{\infty} e^{-x^2}\left\{H_{n+1}(x)\right\}^2 d x+n \int_{-\infty}^{\infty} e^{-x^2} H_{n-1}(x) H_{n+1}(x) d x\)
= \(n^2 \sqrt{\pi} 2^{n-1}(n-1)!+\frac{1}{4} \sqrt{\pi} 2^{n+1}(n+1)!+0\)
= \(\sqrt{\pi} 2^n n!\left[\frac{n}{2}+\frac{1}{2}(n+1)\right]=\sqrt{\pi} 2^n n!\left(n+\frac{1}{2}\right)\)
25. If \(\psi_n(x)=e^{-x^2 / 2} H_n(x)\), where \(H_n(x)\) is a Hermites polynomial of degree n, then prove that \(I_{m, n}=\int_m^{\infty} \psi_m(x) \psi_n(x) d x=2^n n ! \sqrt{\pi} \delta_{m, n}\).
Solution:
Given
If \(\psi_n(x)=e^{-x^2 / 2} H_n(x)\), where \(H_n(x)\) is a Hermites polynomial of degree n
⇒ \(I_{m, n}=\int_{-\infty}^{\infty} \psi_m(x) \psi_n(x) d x=\int_{-\infty}^{\infty} e^{-x^2 / 2} H_m(x) e^{-x^2 / 2} H_n(x) d x\)
= \(\int_{-\infty}^{\infty} e^{-x^2} H_m(x) H_n(x) d x=2^n n ! \sqrt{\pi} \delta_{m, n}\)
26. Prove that 1) \(H_{2 n}(0)=(-1)^n \frac{(2 n) !}{n !}\) and 2) \(H_{2 n+1}(0)=0\).
Solution:
We have \(\sum_{n=0}^{\infty} \frac{t^n}{n!} H_n(x)=e^{-t^2+2 k x}\)
Putting x=0, we get \(\sum_{n=0}^{\infty} \frac{t^n}{n!} H_n(0)=e^{-t^2}=\left[1-t^2+\frac{\left(t^2\right)^2}{2!}+\cdots+(-1)^n \frac{\left(t^2\right)^n}{n!}+\cdots\right]\) → (1)
1) Equating the coefficients of \(2^{2 n}\), on the two sides, we have \(\frac{1}{(2 n)!} H_2,(0)=(-1)^n \frac{1}{n!}\)
∴ \(H_{2 n}(0)=(-1)^n \frac{(2 n)!}{n!}\)
2) Again equating the coefficients of \(t^{2 n+1}\), on the two sides of (1), we have \(\frac{1}{(2 n+1)!} H_{2 n+1}(0)=0\) (since R.H.S of (1) do not involve, odd powers of t.
∴ \(H_{2 n+1}(0)=0\)
27. Prove that if m<n, then \(\frac{d^m}{d x^m}\left\{H_n(x)\right\}=\frac{2^m n !}{(n-m) !} H_{n-m}(x)\).
Solution:
We have \(\sum_{n=0}^{\infty} \frac{t^n}{n!} H_n(x)=e^{-t^2+2 t x} \rightarrow\)
∴ \(\sum_{n=0}^{\infty} \frac{t^n}{n!} \frac{d^m}{d x^m}\left\{H_n(x)\right\}=\frac{d^m}{d x^m} e^{-t^2+2 t x}\)
= \((2 t)^m e^{-t^2+2 t x}=(2 t)^m \sum_{n=0}^{\infty} \frac{t^n}{n!} H_n(x)\)
= \(2^m \sum_{n=0}^{\infty} \frac{1}{n!} l^{n+m} H_n(x)=2^m \sum^{\infty} x \sum_{r=m}(r-m)!H_{r-m}(x) .\)
Putting \(n+m=r, n=r-m\). For n=0 ; r
Equating the coefficient of r from the two sides, we n=0; r=m, for n = \(\infty; r=\infty\).
∴ \(\frac{1}{n!} \frac{d^m}{d x^m}\left\{H_n(x)\right\}=2^m \frac{1}{(n-m)!} H_{n-m}(x) \Rightarrow \frac{d^m}{d x^m}\left\{H_n(x)\right\}=\frac{2^m n!}{(n-m)!} H_{n-m}(x)\)
28. If \(P_n(x)=\sum_{r=0}^{(n / 2)}(-1)^r \frac{(2 n-2 r) !}{2^n(r) !(n-2 r) !(n-r) !} x^{n-2 r}\) then, prove that \(P_n(x)=\frac{2}{\sqrt{\pi} n !} \int_0^{\infty} t^n e^{-t^2} H_n(x t) d t\).
Solution:
Given
If \(P_n(x)=\sum_{r=0}^{(n / 2)}(-1)^r \frac{(2 n-2 r) !}{2^n(r) !(n-2 r) !(n-r) !} x^{n-2 r}\)
We have \(H_n(x)=\sum_{r=0}^{(n / 2)}(-1)^r \frac{n!}{r!(n-2 r)!}(2 x)^{n-2 r}\)
∴ \(H_n(x t)=\sum_{r=0}(-1)^r \frac{n!}{r!(n-2 r)!}(2 x t)^{n-2 r}\)
∴ \(\frac{2}{\sqrt{\pi} n!} \int_0^{\infty} t^n e^{-t^2} H_n(x t) d t\)
= \(\frac{2}{\sqrt{\pi n!}} \int_0^{\infty} t^n e^{-t^{2(n / 2)}} \sum_{r=0}(-1)^r \underbrace{r-2 r)!}_{r!(n!}(2 x t)^{n-2 r} d t\)
= \(\sum_{r=0}^{(n / 2)} \frac{2^{n-2 r+1}(-1)^r x^{n-2 r}}{\sqrt{\pi r!(n-2 r)!}} \int_e^{-t^2} t^{2 n-2 r}\)
= \(\sum_{r=0}^{(n / 2)} \frac{2^{n-2 r+1}(-1)^r x^{n-2 r}}{\sqrt{\pi} r!(n-2 r)!} \int_0^{\infty} e^{-t^2} t^{2(n-r+1 / 2)-1} d t\)
= \(\sum_{r=0}^{(n / 2)} \frac{2^{n-2 r+1}(-1)^r x^{n-2 r}}{\sqrt{\pi} r!(n-2 r)!} \frac{1}{2} \Gamma\left(n-r+\frac{1}{2}\right)\), since \(2 \int_0^{\infty} e^{-t^2} t^{(2 n-1)} d t=\Gamma(n)\)
= \(\sum_{r=0}^{(n / 2)} \frac{2^{n-2 r}(-1)^r x^{n-2 r}[2(n-r)]!}{\sqrt{\pi} r!(n-2 r)!2^{2(n-r)}(n-r)!} \sqrt{\pi}\), since \(\Gamma\left(x+\frac{1}{2}\right)=\frac{(2 x)!}{2^{2 x} x!} \sqrt{\pi}\)
= \(\sum_{r=0}^{(n / 2)}(-1)^r \frac{(2 n-2 r)!}{2^n(r)!(n-2 r)!(n-r)!} x^{n-2 r}=P_n(x)\)
Hence \(P_n(x)=\frac{2}{\sqrt{\pi} r!} \int_0^{\infty} t^n e^{-t^2} H_n(x t) d t\)
29. Show that \(\sum_{k=0}^n \frac{H_k(x) H_k(z)}{2^k k !}=\frac{H_{n+1}(y) H_n(x)-H_{n+1}(x) H_n(y)}{2^{n+1} n !(y-x)}\).
Solution:
From recurrence formulae II, we have \(x H_n(x)=n H_{n-1}(x)+\frac{1}{2} H_{n+1}(x) \rightarrow\) (1)
∴ \(y H_n(y)=n H_{n-1}(y)+\frac{1}{2} H_{n+1}(y) \rightarrow(2)\).
Multiplying (2) by \(H_n(x)\) and (1) by \(H_n(y)\) and than subtracting, we have
(y-x) \(H_n(x) H_n(y)=\frac{1}{2}\left[H_{n+1}(y) H_n(x)-H_{n+1}(x) H_n(y)\right]\) – \(n\left[H_{n-1}(x) H_n(y)-H_{n-1}(y) H_n(x)\right] \rightarrow(3)\)
Putting n=0,1,2,3, ….,(n-1), n in (3) respectively, we have
(y-x) \(H_0(x) H_0(y)=\frac{1}{2}\left[H_1(y) H_0(x)-H_1(x) H_0(y)\right]-0 \ldots\left(A_0\right)\)
(y-x) \(H_1(x) H_1(y)=\frac{1}{2}\left[H_2(y) H_1(x)-H_2(x) H_1(y)\right]\) – \(1\left[H_0(x) H_1(x)-H_0(y) H_1(x)\right] \ldots\left(A_1\right)\)
(y-x) \(H_2(x) H_2(y)=\frac{1}{2}\left[H_3(y) H_2(x)-H_3(x) H_2(y)\right]\)– \(2\left[H_1(x) H_2(y)-H_1(y) H_2(x)\right] \ldots\left(A_2\right)\)
(y-x) \(H_3(x) H_3(y)=\frac{1}{2}\left[H_4(y) H_3(x)-H_4(x) H_3(y)\right]\)–\(3\left[H_2(x) H_3(y)-H_2(y) H_3(x)\right] \ldots\left(A_3\right)\)
….. ….. …… …… …… …… …… …… …… …… ….. ……
…. …… …… …… …… …… …… …… …… …… ….. ……
(y-x) \(H_{n-1}(x) H_{n-1}(y)=\frac{1}{2}\left[H_n(y) H_{n-1}(x)-H_n(x) H_{n-1}(y)\right]\)–\((n-1)\left[H_{n-2}(x) H_{n-1}(y)-H_{n-2}(y) H_{n-1}(x)\right] \ldots\left(A_{n-1}\right) \)
(y-x) \(H_n(x) H_n(y)=\frac{1}{2}\left[H_{n+1}(y) H_n(x)-H_{n+1}(x) H_n(y)\right]\)–\(n\left[H_{n-1}(x) H_n(y)-H_{n-1}(y) H_n(x)\right] \ldots\left(A_n\right)\)
Multiplying \(\left(A_0\right),\left(A_1\right),\left(A_2\right),\left(A_3\right), \ldots\left(A_{n-1}\right),\left(A_n\right)\) by \(1, \frac{1}{2 \cdot 1!}, \frac{1}{2^2 \cdot 2!}, \frac{1}{2^3 \cdot 3!}, \ldots, \frac{1}{2^{n-1} \cdot(n-1)!} \frac{1}{2^n \cdot n!}\) respectively and adding, we have
(y-x) \(\sum_{k=0}^n \frac{H_k(x) H_k(y)}{2^k k!}=\frac{H_{n+1}(y) H_n(x)-H_{n+1}(x) H_n(y)}{2^{n+1} n!}\)
∴ \(\sum_{k=0}^n \frac{H_k(x) H_k(y)}{2^k k!}=\frac{H_{n+1}(y) H_n(x)-H_{n+1}(x) H_n(y)}{2^{n+1} n!(y-x)}\)
