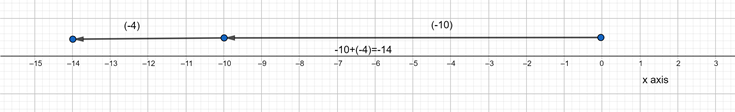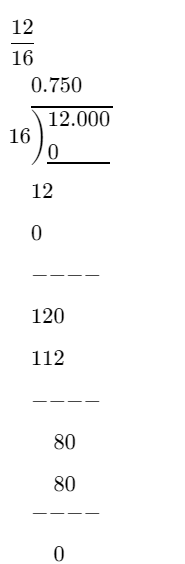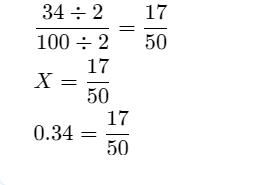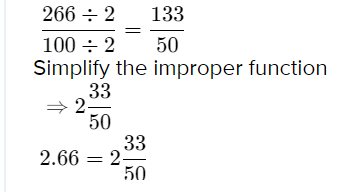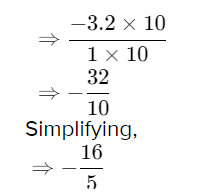Primary Mathematics Chapter 1 Whole Numbers
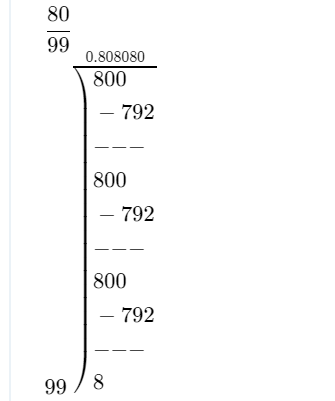
Chapter 1 Whole Numbers Exercises 1.1 Solutions Page 7 Exercise 1.1 Problem 1
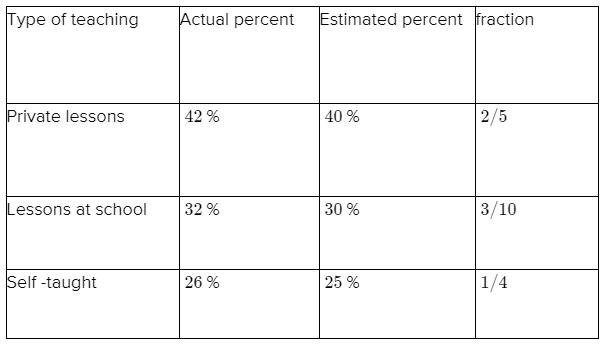
Given: Figure
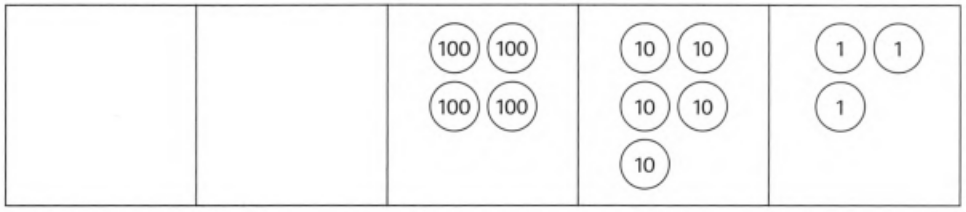
It is asked to write the number represented by the given image in figures.
Multiply the number of circles given in each column with its place value and then add all the obtained values form each places will give the required number.
Analyzing the given figure
There are no circles in the first column representing ten thousands.
⇒ 10000 × 0 = 0
Similarly, there are no circles in the second column representing thousands.
⇒ 1000 × 0 = 0
There are 4 circles in the third column representing hundreds.
⇒ 100 × 4 = 400
There are 5 circles in the fourth column representing tens.
⇒ 10 × 5 = 50
There are 3 circles in the fifth column representing ones.
⇒ 1 × 3 = 3
Add the total values of each places to obtain the given number in figures. so, we will get
0 + 0 + 400 + 50 + 3 = 453
Therefore, the required number represented by the given image in the figures is 453.
Page 7 Exercise 1.1 Problem 2
Given: Figure
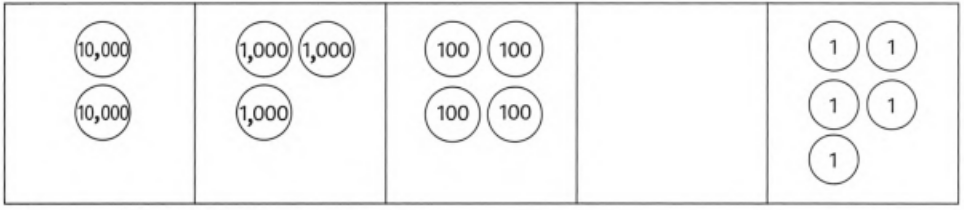
It is asked to write the number represented by the given image in figures.
Multiply the number of circles given in each column with its place value and then add all the obtained values form each places will give the required number.
Analyzing the given figure
There are 2 circles in the first column representing ten thousands.
⇒ 10000 × 2 = 20000
There are 3 circles in the second column representing thousands.
⇒ 1000 × 3 = 3000
There are 4 circles in the third column representing hundreds.
⇒ 100 × 4 = 400
There are zero circles in the fourth column representing tens.
⇒ 10 × 0 = 0
There are 5 circles in the fifth column representing ones.
⇒ 1 × 5 = 5
Add the total values of each places to obtain the given number in figures. so, we will get
20000 + 3000 + 400 + 0 + 5 = 23405
Therefore, the required number represented by the given image in the figures is 23405.
Page 7 Exercise 1.1 Problem 3
Given:
Mr. Royce sold his car for this amount of money represented by figure
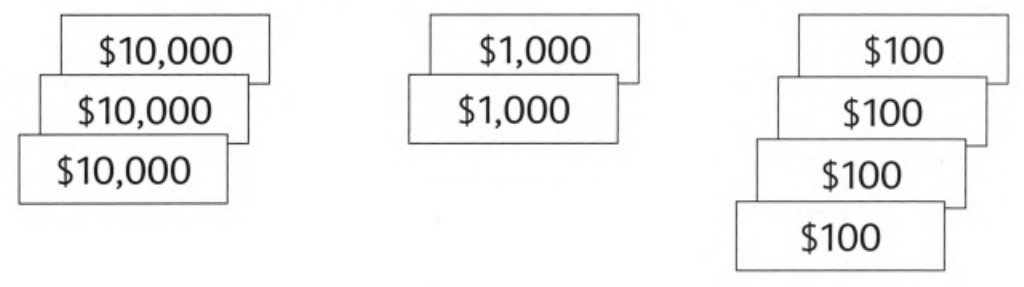
It is asked to write the total amount of money Mr. Royce in figures.
By multiplying the number of each type notes with its value and adding all the amount obtained in each type of note will get the total amount received by Mr. Royce.
By analyzing the figure, we get that Mr. Royce received 3 notes of $10000.
So, the total amount received in $10000 note will be
⇒ $10000 × 3 = $30000
Now, Mr. Royce also received 2 of $1000 notes and 4 of $100 notes.
So, the total amount received in $1000 note will be
⇒ $1000 ×2 = $2000
And total amount received in $100 will be
⇒ $100 × 4 = $400
So, the total amount received by Mr. Royce for the car is given by $30000 + $2000 + $400 = $32400
Therefore, the amount of money received by Mr. Royce for the car in figures is $32400.
Primary Mathematics 4A Chapter 1 Step-By-Step Solutions Page 7 Exercise 1.1 Problem 4
Given: Mr. Royce sold his car for this amount of money represented by figure
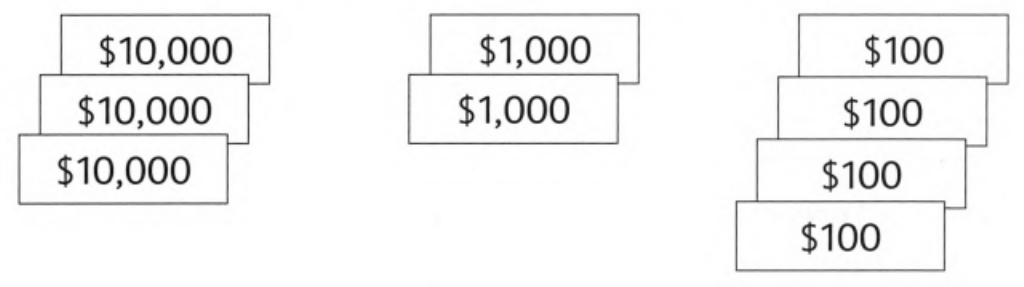
It is asked to write the total amount of money Mr. Royce in words.
By multiplying the number of each type notes with its value and adding all the amount obtained in each type of note will get the total amount received by Mr. Royce.
By referring to Exercise 1, Problem 2
We get that amount of money received by Mr. Royce for the car in figures is $32400.
To represent this amount in words, write this by specifying number of each values such as ten thousands, thousands, hundreds, etc.
So, $32400 is represented in words as Thirty two thousand four hundred Dollars.
Therefore, amount of money received by Mr. Royce for the car represented in words is ‘Thirty two thousand four hundred Dollars’.
Page 8 Exercise 1.1 Problem 5
Given: That there are 12 Thousands and 6 Hundreds.
The question is asked to write the given number in figures.
By multiplying the each number given with its place value and adding the total values of different place values together will give the required number
Given values are 12 thousands and 6 hundreds.
So, total place value of thousands gives
12 × 1000 = 12000
Now, total place value of hundreds gives
6×100=900
Now, by adding the total values obtained from different place values together will give the required number.
⇒ 12000 + 900 = 12900
Therefore, the given number can be represented in figures as 12900.
Whole Numbers Exercises Primary Mathematics Workbook 4A Answers Page 8 Exercise 1.1 Problem 6
Given: There are 45 Thousands, 9 tens and 3 ones.
The question is asked to write the given number in figures.
By multiplying the each number given with its place value and adding the total values of different place values together will give the required number.
Given values are 45 thousands, 9 tens and 3 ones.
So, total place value of thousands gives
45 × 1000 = 45000
Now, total place value of tens gives
9 × 10 = 90
And total place value of ones gives
3 × 1 = 3
Now, by adding the total values obtained from different place values together will give the required number.
⇒ 45000 + 90 + 3 = 45093
Therefore, the given number can be represented in figures as 45093
Page 8 Exercise 1.1 Problem 7
Given: There are 73 Thousand, 8 Hundreds, and 2 ones.
The question is asked to write the given number in figures.
By multiplying the each number given with its place value and adding the total values of different place values together will give the required number.
Given values are 73 thousand, 8 hundreds and 2 ones.
So, total place value of thousands gives
75 × 1000 = 75000
Now, total place value of hundreds gives
8 × 100 = 800 and, the total place value of ones gives
2 × 1=2
Now, by adding the total values obtained from different place values together will give the required number.
⇒ 75000 + 800 + 2 = 75802
Therefore, the given number can be represented in figures as 75802.
Common Core Primary Mathematics 4A Chapter 1 Solved Examples Page 8 Exercise 1.1 Problem 8
Given: There are twelve Thousands, seven Hundreds and ninety three.
The question is asked to write the given number in figures.
By multiplying the each number given with its place value and adding the total values of different place values together will give the required number.
Given values are twelve thousands and seven hundred ninety three.
So, total place value of thousands gives
12 × 1000 = 12000
And, another value given is seven hundred ninety three
⇒ 793
Now, by adding the total values obtained from different place values together will give the required number.
⇒ 12000 + 793= 12793
Therefore, the given number can be represented in figures as 12793.
Chapter 1 Whole Numbers Worked Solutions For Primary Mathematics 4A Page 8 Exercise 1.1 Problem 9
Given: There are ninety Thousand, five Hundred and eleven.
The question is asked to write the given number in figures.
By multiplying the each number given with its place value and adding the total values of different place values together will give the required number.
Given values are ninety thousand and five hundred eleven.
So, total place value of thousands gives
90 × 1000 = 90000
And another value given is five hundred-eleven.
⇒ 511
Now, by adding the total values obtained from different place values together will give the required number.
⇒ 90000 + 511 = 90511
Therefore, the given number can be represented in figures as 90511.
Primary Mathematics Workbook 4A Common Core Edition Practice Problems Page 8 Exercise 1.1 Problem 10
Given: There are eighty-eight Thousands and eight.
The question is asked to write the given number in figures.
By multiplying the each number given with its place value and adding the total values of different place values together will give the required number.
Given values are eighty-eight thousand and eight.
So, total place value of thousands gives
88 × 1000 = 88000
And another value given is eight
⇒ 8
Now, by adding the total values obtained from different place values together will give the required number.
⇒ 88000 + 8 = 88008
Therefore, the given number can be represented in figures as 88008.
Primary Mathematics Workbook 4A Chapter 1 Exercises Breakdown Page 8 Exercise 1.1 Problem 11
Given: There are 485 Thousand, 7 Hundred, and 2 ones.
The question is asked to write the given number in figures.
By multiplying the each number given with its place value and adding the total values of different place values together will give the required number.
Given values are 485 thousand 7 hundreds and 2 ones.
So, total place value of thousands gives
485 × 1000 = 485000
Now, total place value of hundreds gives
7 × 100 = 700
And total place value of ones gives
2 × 1 = 2
Now, by adding the total values obtained from different place values together will give the required number.
⇒ 485000 + 700 + 2 = 485702
Therefore, the given number can be represented in figures as 485702.
Step-By-Step Guide For Primary Mathematics Workbook 4a Chapter 1 Page 8 Exercise 1.1 Problem 12
Given: There are 600 Thousand and 3 Tens.
The question is asked to write the given number in figures.
By multiplying the each number given with its place value and adding the total values of different place values together will give the required number.
Given values are 600 thousand and 3 tens.
So, total place value of thousands gives
600 × 1000 = 600000
Now, the total place value of tens gives
3 × 10 = 30
Now, by adding the total values obtained from different place values together will give the required number.
⇒ 600000 + 30 = 600030
Therefore, the given number can be represented in figures as 600030.
Common Core 4A Chapter 1 Whole Numbers Answers Page 8 Exercise 1.1 Problem 13
Given: There are 999 Thousands, 9 tens and 9 ones.
Question is asked to write the given number in figures.
By multiplying the each number given with its place value and adding the total values of different place values together will give the required number.
Given values are 999 thousands, 9 tens and 9 ones.
So, total place value of thousands gives
999 × 1000 = 999000
Now, total place value of tens gives
9 × 10 = 90 and total place value of ones gives
9 × 1 = 9
Now, by adding the total values obtained from different place values together will give the required number.
⇒ 999000 + 90 + 9 = 999099
Therefore, the given number can be represented in figures as 999099
Page 8 Exercise 1.1 Problem 14
Given: That there are three hundred twelve Thousands and four hundred sixty.
The question is asked to write the given number in figures.
By multiplying the each number given with its place value and adding the total values of different place values together will give the required number.
Given values are three hundred twelve thousands and four hundred sixty.
So, total place value of thousands gives
312 × 1000 = 312000 and other value given is four hundred sixty
⇒ 460
Now, by adding the total values obtained from different place values together will give the required number.
⇒ 312000 + 460 = 312460
Therefore, the given number can be represented in figures as 312460.
Page 8 Exercise 1.1 Problem 15
Given: That there are eight hundred two Thousands and three.
The question is asked to write the given number in figures.
By multiplying the each number given with its place value and adding the total values of different place values together will give the required number.
Given values are 802 thousands and three.
So, total place value of thousands gives
802 × 1000 = 802000
And another value given is three.
⇒ 3
Now, by adding the total values obtained from different place values together will give the required number.
⇒ 802000 + 3 = 802003
Therefore, the given number can be represented in figures as 802003.
Page 8 Exercise 1.1 Problem 16
Given: That there are nine hundred Thousands and nine hundred nine.
The question is asked to write the given number in figures.
By multiplying the each number given with its place value and adding the total values of different place values together will give the required number.
Given values are 900 thousands and nine hundred nine.
So, total place value of thousands gives
900 × 1000 = 900000
And another value given is nine hundred nine.
⇒ 909
Now, by adding the total values obtained from different place values together will give the required number.
⇒ 900000 + 909 = 900909
Therefore, the given number can be represented in figures as 900909.
Page 9 Exercise 1.1 Problem 17
Given: Number is 2,080
Question is to express the given number in words.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.,
2080 = 2000 + 80
We can find the multiples of each place values from this expression.
⇒ 2080 = 2 × 1000 + 8 × 10
So, the number comprises of 2 thousands and 8 tens.
It can be expressed in words as ‘Two thousand eighty’.
Therefore, the given number can be represented in words as ‘Two thousand eighty’.
Page 9 Exercise 1.1 Problem 18
Given: The number is 9,215.
Question is to express the given number in words.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.,
9215 = 9000 + 200 + 10 + 5
We can find number of each place values from this expression.
9215 = 9 × 1000 + 2 × 100 + 1 × 10 + 5 × 1
So, the number comprises of 9 thousands, 2 hundreds, 1 ten and 5 ones.
It can be expressed in words as ‘Nine thousand two hundred fifteen’.
Therefore, the given number can be represented in words as ‘Nine thousand two hundred fifteen’.
Page 9 Exercise 1.1 Problem 19
Given: The number is 47,010.
Question is to express the given number in words.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.,
47010 = 40000 + 7000 + 10
We can find number of each place values from this expression.
47010 = 4 × 10000 + 7 × 1000 + 1 × 10
So, the number comprises of 4 ten thousands, 7 thousands and 1 ten.
It can be expressed in words as ‘Forty-seven thousand ten’.
Therefore, the given number can be represented in words as ‘Forty-seven thousand ten’.
Page 9 Exercise 1.1 Problem 20
Given: The Number is 89,102.
Question is to express the given number in words.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.,
89102 = 80000 + 9000 + 100 + 2
We can find number of each place values from this expression.
89102 = 8 × 10000 + 9 × 1000 + 1 × 100 + 2 × 1
So, the number comprises of 8 ten thousands, 9 thousands, 1 hundred and 2 ones.
It can be expressed in words as ‘Eighty-nine thousand one hundred two’.
Therefore, the given number can be represented in words as ‘Eighty-nine thousand one hundred two’.
Page 9 Exercise 1.1 Problem 21
Given: The Number is 40,900.
Question is to express the given number in words.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.,
40900 = 40000 + 900
We can find number of each place values from this expression.
40900 = 4 × 10000 + 9 × 100
So, the number comprises of 4 ten thousands and 9 hundreds.
It can be expressed in words as ‘Forty thousand nine hundred’.
Therefore, the given number can be represented in words as ‘Forty thousand nine hundred’.
Page 9 Exercise 1.1 Problem 22
Given: The Number is 78,999.
Question is to express the given number in words.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.,
78999 = 70000 + 8000 + 900 + 90 + 9
We can find number of each place values from this expression.
78999 = 7 × 10000 + 8 × 1000 + 9 × 100 + 9 × 10 + 9 × 1
So, the number comprises of 7 ten thousands, 8 thousands, 9 hundreds, 9 tens, and 9 ones.
It can be expressed in words as ‘Seventy-eight thousand nine hundred ninety-nine’.
Therefore, the given number can be represented in words as ‘Seventy-eight thousand nine hundred ninety-nine’.
Page 9 Exercise 1.1 Problem 23
Given: The number is 50,234.
Question is to express the given number in words.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.,
50234 = 50000 + 200 + 30 + 4
We can find number of each place values from this expression.
50234=5 × 10000 + 2 × 100 + 3 × 10 + 4 × 1
So, the number comprises of 5 ten thousands, 2 hundreds, 3 tens and 4 ones.
It can be expressed in words as ‘Fifty thousand two hundred thirty-four’.
Therefore, the given number can be represented in words as ‘Fifty thousand two hundred thirty-four’.
Page 9 Exercise 1.1 Problem 24
Given: The Number is 26,008.
Question is to express the given number in words.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.,
26,008 = 20000 + 6000 + 8
We can find number of each place values from this expression.
26,008 = 2 × 10000 + 6 × 1000 + 8 × 1
So, the number comprises of 2 ten thousands, 6 thousands and 8 ones.
It can be expressed in words as ‘Twenty-six thousand eight’.
Therefore, the given number can be represented in words as ‘Twenty-six thousand eight’.
Page 9 Exercise 1.1 Problem 25
Given: The Number is 73,506.
Question is to express the given number in words.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.,
73,506 = 70000 + 3000+ 500 + 6
We can find number of each place values from this expression.
73,506 = 7 × 10000 + 3 × 1000 + 5 × 100 + 6 × 1
So, the number comprises of 7 ten thousands, 3thousands, 5 hundreds and 6ones.
It can be expressed in words as ‘Seventy-three thousand five hundred six’.
Therefore, the given number can be represented in words as ‘Seventy-three thousand five hundred six’.
Page 9 Exercise 1.1 Problem 26
Given: The number is 367,450.
Question is to express the given number in words.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.,
367,450 = 300000 + 60000 + 7000 + 400 + 50
We can find number of each place values from this expression.
367,450 = 3 × 100000 + 6 × 10000 + 7 × 1000 + 4 ×100 + 5 × 10
So, the number comprises of 3 hundred thousands, 6 ten thousands, 7 thousands, 4 hundreds, and 5 tens.
It can be expressed in words as ‘Three hundred sixty-seven thousand four hundred fifty’.
Therefore, the given number can be represented in words as ‘Three hundred sixty-seven thousand four hundred fifty’.
Page 9 Exercise 1.1 Problem 27
Given: The Number is 506,009.
Question is to express the given number in words.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.,
506,009 = 500000 + 6000 + 9
We can find number of each place values from this expression.
506,009 = 5 × 100000 + 6 × 1000 + 9 × 1
So, the number comprises of 5 hundred thousands, 6 thousands, and 9 ones.
It can be expressed in words as ‘Five hundred-six thousand six’.
Therefore, the given number can be represented in words as ‘Five hundred-six thousand six
Page 9 Exercise 1.1 Problem 28
Given: Number is 430,016.
Question is to express the given number in words.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.,
430,016 = 400000 + 30000 + 10 + 6
We can find number of each place values from this expression.
430,016 = 4 × 100000 + 3 × 10000 + 1 × 10 + 6 × 1
So, the number comprises of 4 hundred thousands, 3 ten thousands, 1 ten and 6ones.
It can be expressed in words as ‘Four hundred thirty thousand sixteen’.
Therefore, the given number can be represented in words as ‘Four hundred thirty thousand sixteen’.
Page 9 Exercise 1.1 Problem 29
Given: Number is 800,550.
Question is to express the given number in words.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.,
800,550 = 800000 + 500 + 50
We can find number of each place values from this expression.
800,550 = 8 × 100000 + 5 × 100 + 5 × 10
So, the number comprises of 8 hundred thousands, 5 hundreds, and 5 tens.
It can be expressed in words as ‘Eight hundred thousand five hundred fifty’.
Therefore, the given number can be represented in words as ‘Eight hundred thousand five hundred fifty’.
Page 10 Exercise 1.2 Problem 1
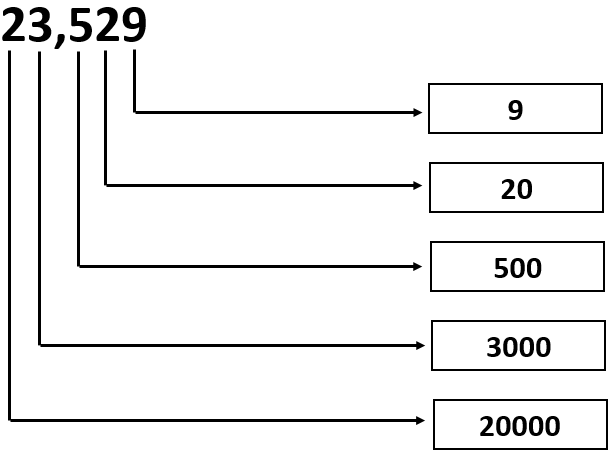
Given: The number is 23,529.
Question is to write the values of the digits.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.
23,529= 2 × 10000 + 3 × 1000 + 5 × 100 + 2 × 10 + 9 × 1 or
We can write it as
23,529 = 20000 + 3000 + 500 + 20 + 9
From the above expression, the values of the digits can be written in the given form as
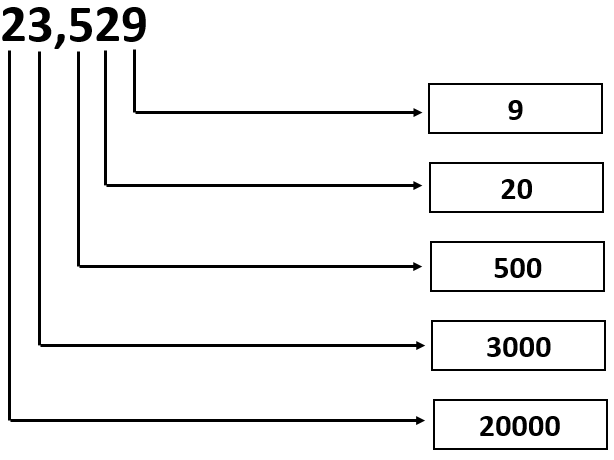
Therefore, the values of the digits in the given number 23,529 can be written as
Page 10 Exercise 1.2 Problem 2
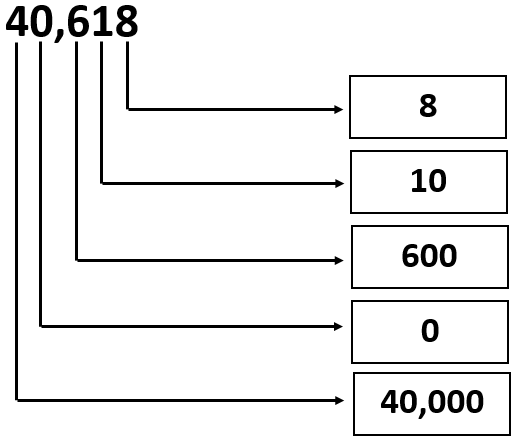
Given: The Number is 40618.
Question is to write the values of the digits.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.
40,618 = 4 × 10000 + 6 ×100+1 × 10 + 8 × 1 or
We can write it as
40,618 = 40000 + 600 + 10 + 8
From the above expression, the values of the digits can be written in the given form as
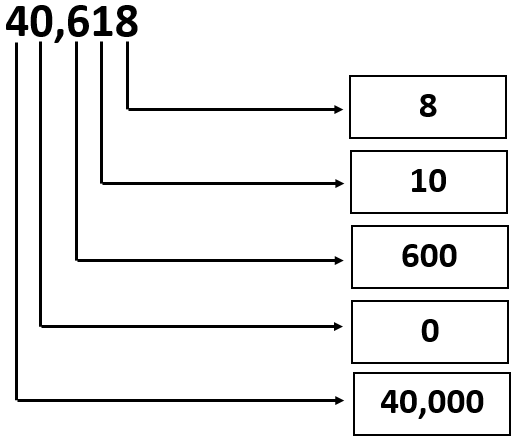
Therefore, the values of the digits in the given number 40,618 can be
Page 10 Exercise 1.2 Problem 3
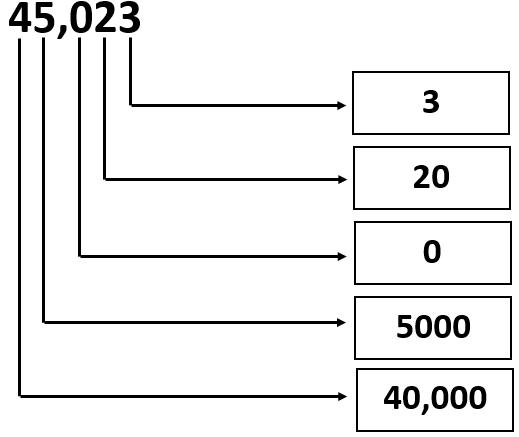
Given: The Number is 45023.
Question is to write the values of the digits.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.
45,023 = 4 × 10000 + 5 × 1000 + 2 × 10 + 3 × 1 or
We can write it as
45,023 = 40000 + 5000 + 20 + 3
From the above expression, the values of the digits can be written in the given form as
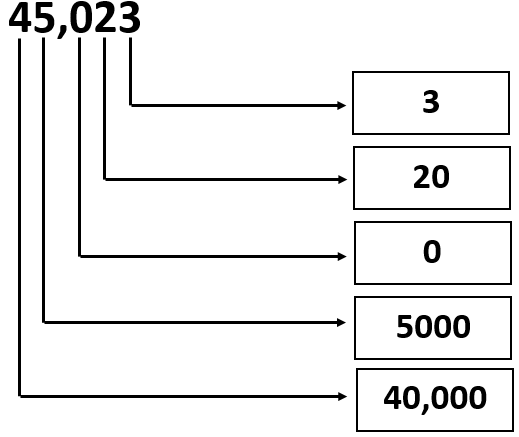
Therefore, the values of the digits in the given number 45,023 can be written as
Page 10 Exercise 1.2 Problem 4
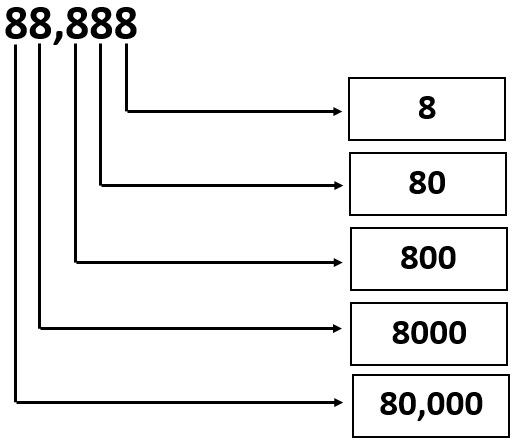
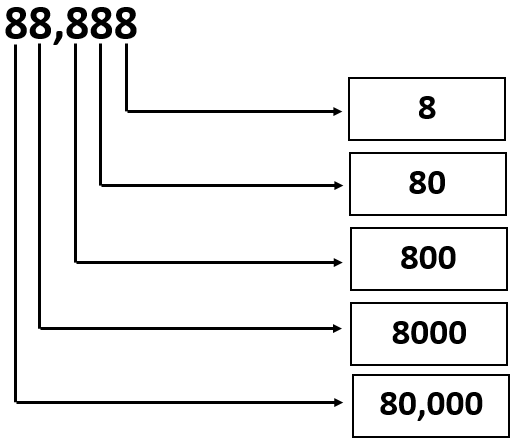
Given: The number is 88,888.
Question is to write the values of the digits.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.
88,888 = 8 × 10000 + 8 × 1000 + 8 × 100 + 8 × 10 + 8 × 1 or
We can write it as
88,888 = 80000 + 8000 + 800 + 80 + 8
From the above expression, the values of the digits can be written in the given form as
Therefore, the values of the digits in the given number 88,888 can be written as
Page 10 Exercise 1.2 Problem 5
Given: The number is 104,682.
Question is to write the values of the digits.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.
104682 = 100000 + 4000 + 600 + 80 + 2
We have
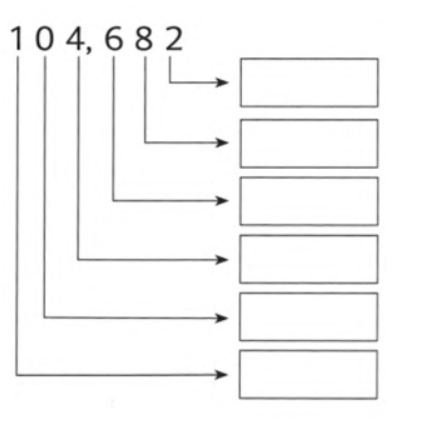
From the above expression, the values of the digits can be written in the given form as 2,80,600,4000,100000
Therefore, the values of the digits in the given number 104,682 can be written as 2,80,600,4000,100000.
Page 10 Exercise 1.2 Problem 6
Given: The number is 989,219.
Question is to write the values of the digits.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as the sum of multiples of each place values. i.e.
989219 = 9000000 + 800000 + 9000 + 200 + 10 + 9
We have
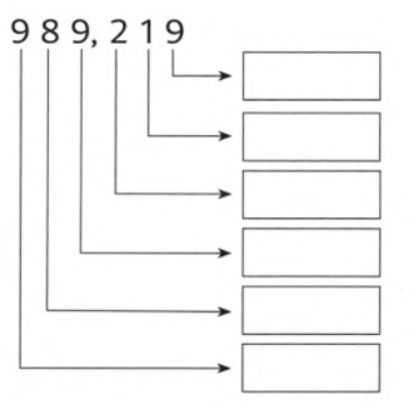
From the above expression, the values of the digits can be written in the given form as 9,10,200,9000,80000,900000
Therefore, the values of the digits in the given number 989,219 can be written as 9,10,200,9000,80000,900000
Page 11 Exercise 1.2 Problem 7
Given: The number is 78,243.
Question is to write the find the digit 7 stands for.
Split the given number according to place values and write it as an expression.
Analyze the table and find out the answer.
The given number can be written as the sum of multiples of each place values. i.e.
78,243 = 70000 + 8000 + 200 + 40 + 3
So, it is clear that digit 7 stands for ten thousands place in 700000.
In 78,243, the digit 7 stands for ten thousands place in 700000.
Page 11 Exercise 1.2 Problem 8
Given: The number is 78,243.
Question is to find the digit in hundreds place and its value.
Split the given number according to place values and write it as an expression.
Analyze the table and find out the answer.
The given number can be written as sum of multiples of each place values. i.e.
78,243 = 70000 + 8000 + 200 + 40 + 3
So, it is clear that the digit in hundreds place is 2.
The value of hundreds place is 200.
In 78,243, the digit 2 in hundreds place. The value of the digit is 200.
Page 11 Exercise 1.2 Problem 9
Given: The number is 78,243.
Question is to find the digit in tens place and thousands place.
Split the given number according to place values and write it as an expression.
Analyze the table and find out the answer.
From the table, it is clear that the digit in tens place is 4 and digit in thousands place 8.
Therefore, In 78,243, the tens digit is 4and the thousands digit is 8.
Page 11 Exercise 1.2 Problem 10
Given: Numbers are 78,243 and 8.243.
Question is to find the difference between given numbers..
Subtracting given two numbers gives the required answer.
⇒ 78,243 − 8,243 = 70,000
So, the difference is 70,000
Therefore, 78,243 is 70,000 more than 8,243.
Page 11 Exercise 1.2 Problem 11
Given: The number is 24,568.
Question is to find the place of the digit 4.
Split the given number according to place values and write it as an expression.
The given number can be written as sum of multiples of each place values. i.e.
24,568 = 20000 + 4000 + 500 + 60 + 8 or
We can write it as
24,568 = 2 × 10000 + 4 × 1000 + 5 × 100 + 6 × 10 + 8 × 1
From the above expression
At ten thousands place is the digit 2.
At thousands place is the digit 4.
At hundreds place is the digit 5.
At tens place is the digit 6.
At ones place is the digit 8.
So, the place of the digit 4is found to be Thousand.
Therefore, in 24,568 the digit 4 stands for thousands place.
Page 11 Exercise 1.2 Problem 12
Given: The number is 43,251.
Question is to find the digit in ten thousands place.
Split the given number according to place values and write it as an expression.
The given number can be written as sum of multiples of each place values. i.e.
43,251 = 40000 + 3000 + 200 + 50 + 1 or
We can write it as
43,251 = 4 × 10000 + 3 × 1000 + 2 × 100 + 5 × 10 + 1 × 1
From the above expression, the digit in the ten thousands place is found to be 4.
Therefore, in 43,251 the digit 4 is in the ten thousands place.
Page 11 Exercise 1.2 Problem 13
Given: 4,000 + 300 + 7 =_____
Question is to find the missing number and fill the blank.
Add the value of the given place values to obtain required number.
4,000 + 300 + 7 = 4,307
So, the required number is
Therefore, the solution of the given expression 4,000 + 300 + 7 = _____is 4,307.
Page 11 Exercise 1.2 Problem 14
Given: 50,000 + 6,000 + 400=_____
Question is to find the missing number and fill the blank.
Add the value of the given place values to obtain required number.
50,000+ 6,000 + 400 = 56,400
So, the required number is 56,400.
Therefore, the solution of the given expression 50,000 + 6,000 + 400 =_____ is 56,400
Page 11 Exercise 1.2 Problem 15
Given: 30,000 + 700 + 60 + 8 =_____
Question is to find the missing number and fill the blank.
Add the value of the given place values to obtain required number.
30,000 + 700 + 60 + 8 = 30,760
So, the required number is 30,760.
Therefore, the solution of the given expression 30,000 + 700 + 60 + 8 =_____is 30,760.
Page 11 Exercise 1.2 Problem 16
Given: 10,000 + 1,000 + 400 =_____
Question is to find the missing number and fill the blank.
Add the value of the given place values to obtain required number.
10,000 + 1,000 + 400 = 11,400
So, the required number is 11,400.
Therefore, the solution of the given expression 10,000 + 1,000 + 400 =_____is 11,400.
Page 11 Exercise 1.2 Problem 17
Given: The number 90,000 + 90 =_____
Question is to find the missing number and fill the blank.
Add the value of the given place values to obtain required number.
90,000 + 90 = 90,090
So, the required number is 90,090.
Therefore, the solution of the given expression 90,000 + 90 = _____is 90,090.
Page 12 Exercise 1.2 Problem 18
Given: The number is 127,685.
Question is to find the place of the digit 1.
Split the given number according to place values and write it as an expression
The given number can be written as sum of multiples of each place values. i.e.
127,685 = 100,000 + 20,000 + 7,000 + 600 + 80 + 5 or
We can write it as
127,685 = 1 × 100,000 + 2 × 10,000 + 7 × 1 ,000 + 6 × 100 + 8 × 10 + 5 × 1
From the above expression
At hundred thousands place is the digit 1.
At ten thousands place is the digit 2.
At thousands place is the digit 7.
At hundreds place is the digit 6.
At tens place is the digit 8.
At ones place is the digit 5.
So, the place of the digit 1 is hundred thousands.
Therefore, in 127,685, the digit 1 stands for hundred thousands place or 100,000.
Page 12 Exercise 1.2 Problem 19
Given: The number is 561,260.
Question is to find the digit in ten thousands place and to find the value of digit 1.
Split the given number according to place values and write it as an expression.
The given number can be written as sum of multiples of each place values. i.e.
561,260 = 500,000 + 60,000+1,000 + 200 + 60 + 0 or
We can write it as
561,260 = 5 × 100,000 + 6 × 10,000 + 1 × 1,000 + 2 × 100 + 6 × 10 + 0
From the above expression, the digit in the thousands place is found to be 1.
So, the value of the digit 1 is 1000.
Therefore, in 561,260, the digit 1 is in the thousands place, and the value of the digit 1 is 1,000
Page 12 Exercise 1.2 Problem 20
Given: The number is 432,091.
Question is to find the place of the digit 0.
Split the given number according to place values and write it as an expression.
The given number can be written as sum of multiples of each place values. i.e.
432,091 = 400,000 + 30,000 + 2,000 + 0 + 90 + 1 or
We can write it as
432,091 = 4 × 100,000 + 3 × 10,000 + 2 × 1,000 + 0 × 100 + 9 × 10 + 1 × 1
From the above expression
At hundred thousands place is the digit 4.
At ten thousands place is the digit 3.
At thousands place is the digit 2.
At hundreds place is the digit 0.
At tens place is the digit 9.
At ones place is the digit 1.
So, the place of the digit 0 is hundred.
Therefore, in 432,091, the digit 0 is in the hundreds place.
Page 12 Exercise 1.2 Problem 21
Given: The Number is 368,540.
Question is to value of the place of the digit 4.
Split the given number according to place values and write it as an expression.
The given number can be written as sum of multiples of each place values. i.e.
368,540 = 300,000 + 60,000 + 8,000 + 500 + 40 or
we can write it as
368,540 = 3 × 100,000 + 6 × 10,000 + 8 × 1,000 + 5 × 100 + 4 × 10
From the above expression, the values of the digits can be written as,.
The value at hundred thousands place is the digit is 300,000.
The value at ten thousands place is 60,000.
The value at thousands place is the digit is 8,000.
The value at hundreds place is the digit is 500.
The value at tens place is the digit 40.
So, the value of the digit 4 is 40.
Therefore, in 368,540 the digit 4 stands for tens place and its value is 40.
Page 12 Exercise 1.2 Problem 22
Given: The number is 760,835.
Question is to find how much more is 760,835 than 700,000
Finding the difference between the two numbers will give the required answer.
⇒ 760,835 − 700,000 = 60,835
So, the required answer is 60,835.
Therefore, 760,835 is 60,835 more than 700,000.
Page 12 Exercise 1.2 Problem 23
Given: The number is 40,000+2,000+100+8=_____
Question is to find the missing number and fill the blank.
Add the value of the given place values to obtain required number.
40,000 + 2,000 + 100 + 8 = 42,108
So, the required number is 42,108.
Therefore, the solution of the given expression 40,000 + 2,000 + 100 + 8= _____ is 42,108
Page 12 Exercise 1.2 Problem 24
Given: The number is 562,000 + 32 = _____
Question is to find the missing number and fill the blank.
Add the value of the given place values to obtain required number.
562,000 + 32 = 562,032
So, the required number is 562,032.
Therefore, the solution of the given expression 562,000 + 32=_____is 562,032.
Page 12 Exercise 1.2 Problem 25
Given: The number is 700,000 + 70,000 + 70 + 7 =_____
Question is to find the missing number and fill the blank.
Add the value of the given place values to obtain required number.
700,000 + 70,000 + 70 + 7 = 770,077
So, the required number is 770,077.
Therefore, the solution of the given expression 700,000 + 70,000 + 70 + 7 =_____is 770,077.
Page 12 Exercise 1.2 Problem 26
Given: The number is 900,000 + 214 =_____
Question is to find the missing number and fill the blank.
Add the value of the given place values to obtain required number.
900,000 + 214 = 900,214
So, the required number is 900,214.
Therefore, the solution of the given expression 900,000 + 214 =_____ is 900,214.
Page 12 Exercise 1.2 Problem 27
Given: The number is 25,830 = 25,000 + _____ + 30
Question is to find the missing number and fill the blank.
Subtract the sum of the given place values from the original number to obtain required number.
We have
25,830 = 25,000 + _____ + 30
Add the place values present at the right hand side.
25,830 = (25,000 + 30) +_____
From the above expression, bringing the number at right hand side to the left hand side and their difference will give the required number.
⇒ 25,830 − (25,000 + 30) =_____
⇒ 25,830 − 25,030 = 800
Therefore, the number missing in the given expression 25,830 = 25,000 + _____+ 30 is 800.
Page 12 Exercise 1.2 Problem 28
Given: The number is 370,049 =_____+ 70,000 + 40 + 9
Question is to find the missing number and fill the blank.
Subtract the sum of the given place values from the original number to obtain required number.
We have
370,049 =_____+ 70,000 + 40 + 9
Add the place values present at the right-hand side.
370,049 =_____+ (70,000 + 40 + 9)
From the above expression, bringing the number at right-hand side to the left-hand side and their difference will give the required number.
⇒ 370,049 − (70,000 + 40 + 9) =_____
⇒ 370,049 − 70,049 = 300,000
Therefore, the number missing in the given expression 370,049 =_____+ 70,000 + 40 + 9 is 300,000
Page 12 Exercise 1.2 Problem 29
Given: The number is 603,804 = 600,000+_____+ 800 + 4
Question is to find the missing number and fill the blank.
Subtract the sum of the given place values from the original number to obtain required number.
We have
603,804 = 600,000 +_____+ 800 + 4
Add the place values present at the right-hand side.
603,804 = (600,000 + 800 + 4) + _____
From the above expression, bringing the number at right-hand side to the left-hand side and their difference will give the required number.
⇒ 603,804−(600,000 +800 + 4) =_____
⇒ 603,804−600,804 = 3,000
Therefore, the number missing in the given expression 603,804 = 600,000 +_____+ 800 + 4 is 3,000.
Page 12 Exercise 1.2 Problem 30
Given: The number is 416,008 = 416,000 +_____
Question is to find the missing number and fill the blank.
Subtract the sum of the given place values from the original number to obtain required number.
⇒ 416,008−416,000 = 8
So, the required number is 8.
Therefore, the number missing in the given expression 416,008 = 416,000+_____ is 8.
Page 12 Exercise 1.2 Problem 31
Given: The number is 123,456.
Question is to find the number of ones.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.,
123,456 = 100,000 + 20,000 + 3,000 + 400 + 50 + 6
We can find number of each place values from this expression.
123,456 = 1 × 100,000 + 2 × 10,000 + 3 × 1,000 + 4 × 100 + 5 × 10 + 6 × 1
Analyzing the above expression
It can be concluded that there are 6 ones.
Therefore, the given number 123,456 has 6 ones.
Page 12 Exercise 1.2 Problem 32
Given: The Number is 123,456
Question is to find the number of tens.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.
123,456 = 100,000 + 20,000 + 3,000 + 400 + 50 + 6
We can find number of each place values from this expression.
123,456 = 1 × 100,000 + 2 × 10,000 + 3 × 1,000 + 4 × 100 + 5 × 10 + 6 × 1
Analyzing the above expression
It can be concluded that there are 5 tens.
Therefore, the given number 123,456 has 5 tens.
Page 12 Exercise 1.2 Problem 33
Given: The Number is 123,456
Question is to find the number of hundreds.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.
123,456 = 100,000 + 20,000 + 3,000 + 400 + 50 + 6
We can find number of each place values from this expression.
123,456 = 1 × 100,000 + 2 × 10,000 + 3 × 1,000 + 4 × 100 + 5 × 10 + 6 × 1
Analyzing the above expression
It can be concluded that there are 4 hundreds.
Therefore, the given number 123,456 has 4 hundreds.
Page 12 Exercise 1.2 Problem 34
Given: The number is 123,456.
Question is to find the number of thousands.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.
123,456 = 100,000 + 20,000 + 3,000 + 400 + 50 + 6
We can find number of each place values from this expression.
123,456 = 1 × 100,000 + 2 × 10,000 + 3 × 1,000 + 4 × 100 + 5 × 10 + 6 × 1
Analyzing the above expression
It can be concluded that there are 3 thousands.
Therefore, the given number 123,456 has 3 thousands.
Page 12 Exercise 1.2 Problem 35
Given: The number is 123,456.
Question is to find the number of ten thousands.
Split the given number according to place values and write it as an expression.
Analyze the expression and find the multiples of each place values.
The given number can be written as sum of multiples of each place values. i.e.
123,456 = 100,000 + 20,000 + 3,000 + 400 + 50 + 6
We can find number of each place values from this expression.
123,456 =1 × 100,000 + 2 × 10,000 + 3 × 1,000 + 4 × 100 + 5 × 10 + 6 × 1
Analyzing the above expression
It can be concluded that there are 2 ten thousands.
Therefore, the given number 123,456 has 2 ten thousands.
Page 12 Exercise 1.2 Problem 36
Given: The number 123,456
To calculate the number of hundred thousand.
Here, digit 1 is in the hundred thousand’s place so there is one hundred thousand in the given number.
Therefore, the number 123,456 has one hundred thousand.
Page 12 Exercise 1.2 Problem 37
Given: 50 ten thousand + 40 hundreds + 20 tens.
To write in standard form.
We have to write 20 at tens, 40 at hundreds and 50 at ten thousand’s place.
We will write the terms in numerical form. 50 ten thousand
=50×10000
40 hundreds = 40 × 100
20 tens = 20 × 10
Adding all the three terms we get:
50 × 10000 + 40 × 100 + 20 × 10 = 500,000 + 4,000 + 200
= 504,200
Hence, we have the standard form as 504,200.
Therefore, 50 ten thousand + 40 hundreds + 20 tens can be written in standard form as 504,200.
Page 12 Exercise 1.2 Problem 38
Given: 83 ten thousand + 4 tens + 7ones.
To write in standard form.
We have to write 7 at ones, 4 at tens and 83 at ten thousand’s place.
We will write the terms in numerical form. 83 ten thousand =83×10000
4tens = 4 × 10
7ones =7 × 1
Adding all the three terms we get:
83 × 10000 + 4 × 10 + 7 × 1= 830,000 + 40 + 7
= 8,30,047
Hence, we have the standard form as 8,30,047.
Therefore,83 ten thousand +4 tens + 7 ones can be written in standard form as 8,30,047.
Page 13 Exercise 1.3 Problem 1
Given: The number line.

To find – The number that each letter represents.
We will find the least count between the numbers and accordingly find the numbers.
First, we will find the number of divisions between 35,000 and 40,000.
There are 5 divisions which can be seen from the figure. Now, the difference between 35,000 and 40,000 can be calculated as 40,000−35,000=5,000.
Now dividing the difference by the number of divisions obtain the least count. Hence, the least count is given by
\(\frac{5,000}{5}\) = 1,000.
Now, the number that each letter represent can be found as follows
A is located two divisions before 35,000 so it can be calculated by subtracting 1,000 two times from 35,000.
Hence, A=35,000−1,000−1,000=33,000.
Now, B is located two divisions after 35,000 so it can be calculated by adding 1,000 two times to 35,000.
This implies, B = 35,000 + 1,000 + 1,000 = 37,000.
Solving further, no we find C.
C is located just after 40,000 so it can be calculated by adding 1,000 to 40,000.
Hence, A = 40,000 + 1,000 = 41,000.
Further, calculating D which is located before 45,000, we need to subtract 1,000 from 45,000.
So, D = 45,000 −1,000 = 44,000.
Therefore, the numbers that each letter represent are calculated as follows:
A=33,000
B=37,000
C=41,000
D=44,000
Page 13 Exercise 1.3 Problem 2
Given: The numbers 13,268 and 31,862.
To tell which number is greater.
We have to compare the digits on the extreme left.
We know that if two numbers have an equal number of digits, the number having a greater valued digit on the extreme left is greater.
Here, the digit on the extreme left is at ten thousand-place. So, we will compare the places.
From the given numbers, 13,268 and 31,862, 31,862 has a greater value digit at the ten thousand place as 3>1.
Hence, 31,862 is the greater number.
Therefore, 31,862 is greater as compared to 13,268
Page 13 Exercise 1.3 Problem 3
Given: The numbers 49,650 and 42,650.
To tell which number is smaller.
We have to compare the digits on the extreme left.
We know that if two numbers have an equal number of digits, the number having a smaller valued digit on the extreme left is smaller.
If the numbers’ digits on the extreme left are equal, the digits to the right of the extreme left digits are compared, and so on.
Here, the digit on the extreme left is 4 which is equal for both numbers so, we will take the next digit that is at the thousand place.
From the given numbers 49,650 and 42,650, 42,650 has a smaller value digit at the thousand place as 2<9.
Hence, 42,650 is a smaller number.
Therefore, 42,650 is smaller as compared to 49,650
Page 13 Exercise 1.3 Problem 4
Given: The numbers 33,856, 33,786, and 33,796.
To tell which number is greatest.
We have to compare the digits on the extreme left.
We know that if two numbers have an equal number of digits, the number having a greater valued digit on the extreme left is greater.
If the numbers’ digits on the extreme left are equal, the digits to the right of the extreme left digits are compared, and so on.
Here, the digits on the extreme left are equal. So, we will compare the places on the thousand-place.
Here too, the places are equal.
Moving on further, we will now compare hundreds place.
From the given numbers 33,856, 33,786, and 33,796,33,856 has a greater value digit at the hundreds place as 8>7.
Hence, 33,856 is the greatest number out of the three numbers.
Therefore, 33,856 is the greatest as compared to 33,786 & 33,796.
Page 13 Exercise 1.3 Problem 5
Given: The numbers 65,730, 65,703, and 66,730.
To tell which number is smallest.
We have to compare the digits on the extreme left.
We know that if two numbers have an equal number of digits, the number having a smaller valued digit on the extreme left is smaller.
If the numbers’ digits on the extreme left are equal, the digits to the right of the extreme left digits are compared, and so on.
Here, the digits on the extreme left are equal.
So, we will compare the places on the thousand-place.
Here, numbers 65,730 and 65,703 are smaller than 66,730 as 5<6.
Moving on further, we will now compare hundreds place which are equal for both 65,730 and 65,703.
Now, we compare the tens place.
From the numbers 65,730 and 65,703, 65,703 has a smaller value digit at the tens place as 0<3.
Hence, 65,703 is the smallest number out of the three numbers.
Therefore, 65,703 is the smallest as compared to 65,730 and 66,730.
Page 13 Exercise 1. 3 Problem 6
Given: The numbers 3,695, 3,956, 35,096, 30,965.
To arrange the numbers in increasing order.
We have to compare the numbers and arrange accordingly.
First, we count the number of digits in each number.
The number with the least number of digits is the smallest.
From the given numbers, 3,695 and 3,956 have fewer digits than 35,096 and 30,965.
Now we will compare the two smaller numbers.
We know that if the numbers’ digits on the extreme left are equal, the digits to the right of the extreme left digits are compared, and so on.
Here, the digits on the extreme left are equal. So, we will compare the places on the hundreds place.
From the given numbers, 3,695 and 3,956, 3,695 is smaller than 3,956 because it has a smaller value digit as 6<9.
Now, we compare the remaining two numbers which are 35,096 and 30,965.
Here, the digits on the extreme left are equal. So, we will compare the places on the thousands place.
From the numbers 35,096 and 30,965, 30,965 has a smaller value digit as 0<5.
Hence, we see that the numbers can be arranged from smallest to greatest as follows: 3,695<3,956<30,965<35,096.
Therefore, the numbers can be arranged in increasing order as follows: 3,695<3,956<30,965<35,096.
Page 13 Exercise 1. 3 Problem 7
Given: The numbers 435,760, 296,870, 503,140, 462,540.
To arrange the numbers in increasing order.
We have to compare the numbers and arrange accordingly.
First, we count the number of digits in each number.
For the numbers having the same number of digits, start with comparing the numbers from the leftmost digit.
Write the number with the smallest digit.
From the given numbers, 296,870 has the smallest leftmost digit that is 2 so it is the smallest of all four numbers.
Also, the number with the greatest leftmost digit is 503,140 so it is the greatest number.
Now, we compare the remaining two numbers which are 435,760 and 462,540.
We know that if the numbers’ digits on the extreme left are equal, the digits to the right of the extreme left digits are compared, and so on.
Here, the digits on the extreme left are equal. So, we will compare the ten thousand-place.
From the numbers 435,760 and 462,540, 435,760 has a smaller value digit at ten thousand-place as 3<6.
Hence, we see that the numbers can be arranged from smallest to greatest as follows:
296,870<435,760<462,540<503,140.
Therefore, the numbers can be arranged in increasing order as follows: 296,870<435,760<462,540<503,140.
Page 13 Exercise 1. 3 Problem 8
Given: The numbers 9,870 and 18,970.
To compare and write >,<, or =
The number having more digits is a greater number.
First, we need to count the number of digits in each number.
We see that 9,870 has four digits and 18,970 has five digits.
So, clearly, 18,970 has a greater number of digits and hence, it is greater.
Now, we will write the sign as follows: 9,870<18,970.
Therefore, we obtain the result as 9,870<18,970
Page 13 Exercise 1. 3 Problem 9
Given: The numbers 50,972 and 49,827…
To compare and write >,<, or =.
We have to compare the digits on the extreme left.
First, we need to count the number of digits in each number.
We see that the number of digits are equal in each number.
We know that if two numbers have an equal number of digits, the number having a greater valued digit on the extreme left is greater.
Here, the digit at extreme left is at ten thousand-place so we will compare the places.
From the given numbers, 50,972 has a greater valued digit at the extreme left as 5>4.
So, clearly, 50,972 is greater than 49,827.
Now, we will write the sign as follows: 50,972>49,827.
Therefore, we obtain the result as 50,972>49,827.
Page 13 Exercise 1. 3 Problem 10
Given: The numbers 326,548 and 326,593.
To compare and write >,<, or =.
We have to compare the digits on the extreme left.
First, we need to count the number of digits in each number.
We see that the number of digits are equal in each number.
We know that if two numbers have an equal number of digits, the number having a greater valued digit on the extreme left is greater.
If the numbers’ digits on the extreme left are equal, the digits to the right of the extreme left digits are compared, and so on.
Here, the digits at hundred thousand, ten thousand, thousand and hundreds place are equal so we will compare the places at tens place.
From the given numbers, 326,548 has a smaller valued digit at the tens place as 4<9.
So, clearly, 326,548 is smaller than 326,593.
Now, we will write the sign as follows: 326,548<326,593.
Therefore, we obtain the result as 326,548<326,593.
Page 14 Exercise 1.4 Problem 1
Given: The number 42,628.
To find which number is 1,000 more than 42,628.
We will obtain the new number by adding 1,000 to 42,628.
We can write it as − 1000 + 42628 = 43,628.
Therefore, the number which is 1000 more than 42,628 is 43,628.
Page 14 Exercise 1.4 Problem 2
Given: The number 2,63,240.
To find 2,63,240 is 10,000 more than that number.
We will obtain the new number by subtracting 10,00 from 2,63,240.
We can write it as − 2,63,240−10,000 = 2,53,240.
Therefore, 2,63,240 is 10,000 more than 2,53,240.
Page 14 Exercise 1.4 Problem 3
Given: The number 90,000.
To find which number is 100 less than 90,000.
We will obtain the new number by subtracting 100 from 90,000.
We can write it as− 90,000 − 100 = 89,900
Therefore, 89,990 is 100 less than 90,000.
Page 14 Exercise 1.4 Problem 4
Given: The number 86,000,000.
To find 86,000,000 is 100,000 less than which number.
We will obtain the new number by adding 100,000 to 86,000,000.
We can write it as 86,000,000 + 100,000 = 86,100,000.
Therefore, 86,000,000 is 100,000 less than 86,100,000.
Page 14 Exercise 1.4 Problem 5
Given: 45,500 is ____ more than 45,600.
Question is to fill the blank
We will obtain the number by subtracting 45,500 from 45,600.
We can write it as − 45,600 − 45,500 = 100.
Therefore, 45,500 is 100 more than 45,600.
Page 14 Exercise 1.4 Problem 6
Given: The numbers 384,000 and 39,400.
To find – 384,000 is a number less than 394,000.
We will obtain the number by subtracting 384,000 from 394,000.
We can write it as − 394,000 − 384,000 = 10,000.
Therefore, 384,000 is 10,000 less than 394,000.
Page 14 Exercise 1.4 Problem 7
Given: The numbers 29,409 and 39,409.
To find – The number which when added to 29,409 gives 39,409.
We will obtain the number by subtracting 29,409 from 39,409.
We can write it as − 39,409 − 29,409 = 10,000.
Therefore, the missing number which when added to 29,409 gives 39,409 is 10,000.
Page 14 Exercise 1.4 Problem 8
Given: The numbers 2,483,000 and 2,482,000.
To find the number which when subtracted from 2,483,000 gives 2,482,000.
We will obtain the number by subtracting 2,482,000 from 2,483,000.
We can write it as − 2,483,000 − 2,482,000 = 1,000.
Therefore, the missing number which when subtracted from 2,483,000 gives 2,482,000 is 1,000.
Page 14 Exercise 1.4 Problem 9
Given: The sequence 35,552;____;____;38,552;39,552.
To complete the given regular pattern.
We identify the certain sequence which is followed in the pattern and accordingly, fill the blanks.
We notice that the numbers 38,552 and 39,552 follow a certain sequence.
It can be seen that the difference between the numbers is 39,552−38,552=1,000.
Hence, the pattern follows a certain sequence which is a difference of 1,000 between numbers.
The first number is given as 35,552.
The second number will be 1000 added to the first number 35,552+1,000=36,552.
The third number will similarly be 36,552+1,000=37,552.
Therefore, the number pattern is completed as follows: 35,552; 36,552; 37,552; 38,552; 39,552
Page 14 Exercise 1.4 Problem 10
Given: The sequence 71,680;71,780;____;71,980;____.
To complete the given regular pattern.
We identify the certain sequence which is followed in the pattern and accordingly, fill the blanks.
We notice that the numbers 71,680 and 71,780 follow a certain sequence.
It can be seen that the difference between the numbers is 71,780−71,680=100.
Hence, the pattern follows a certain sequence which is a difference of 100 between numbers.
The first number is given as 71,680 and the second number is given as 71,780.
The third number will be 100added to the first number 71,780 + 100 = 71,880.
The fourth number is given as 71,980.
The fifth number will similarly be 100 added to the fourth number 71,980 + 100 = 72,080.
Therefore, the number pattern is completed as follows: 71,680; 71,780; 71,880; 71,980; 72,080.
Page 14 Exercise 1.4 Problem 11
Given: The sequence 283,610;293,610;____;____;323,610.
To complete the given regular pattern.
We identify the certain sequence which is followed in the pattern and accordingly, fill the blanks.
We notice that the numbers 283,610 and 293,610 follow a certain sequence.
It can be seen that the difference between the numbers is 293,610 − 283,610 = 10,000.
Hence, the pattern follows a certain sequence which is a difference of 10,000 between numbers.
The first number is given as 283,610 and the second number is 293,610.
The third number will be 10,000 added to the second number which is 293,610 + 10,000 = 303,610 and the fourth number will be 10,000 subtracted from the fifth number.
Hence, the fourth number is 323,610−10,000 = 313,610.
Therefore, the number pattern is completed as follows: 283,610; 293,610; 303,610; 313,610; 323,610.
Page 14 Exercise 1. 4 Problem 12
Given: A regular number pattern starts with 493,070 and increases each number by 10,000.
To create the regular number pattern.
We will create the pattern by adding 10,000 to the first number and so on.
We are given that the pattern starts with 493,070.
The next number will be 493,070+10,000 = 503,070.
The third number will be 503,070+10,000 = 513,070.
Continuing the sequence
The fourth number will be 513,070+10,000=523,070.
The next number will be 523,070+10,000=533,070.
And, the last number will be 533,070+10,000=543,070.
Therefore, the regular number pattern that starts with 493,070 and in which each number is increased by 10,000 is 493,070; 503,070;513,070; 523,070; 533,070; 543,070.
Page 14 Exercise 1.4 Problem 13
Given: A regular number pattern starts with 493,070 and decreases each number by 1,000.
To create the regular number pattern.
We will create the pattern by subtracting 1,000 from the first number and so on.
We are given that the pattern starts with 493,070.
The next number will be 493,070−1,000 = 492,070.
The third number will be 492,070−1,000 = 491,070.
Continuing the sequence
The fourth number will be 491,070−1,000 = 490,070.
The next number will be 490,070−1,000 = 489,070.
And, the last number will be 489,070−1,000 = 488,070.
Therefore, the regular number pattern that starts with 493,070 and in which each number is decreased by 1,000 is 493,070;492,070;491,070;490,070;489,070;488,070.
Page 15 Exercise 1. 4 Problem 14
Given the figures:
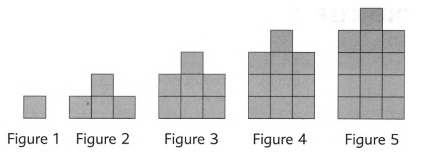
To draw figure 6.
We see that these figures follow a ceratain pattern.
Accordingly, we can draw figure 6 as follows:

Therefore, figure 6 is drawn below:

Page 15 Exercise 1. 4 Problem 15
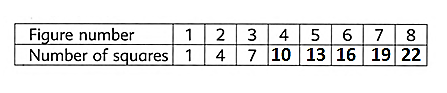
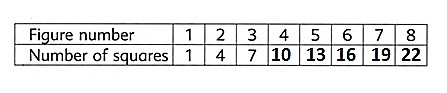
Given the table.

To complete the given table.
We identify the sequence of the pattern and accordingly solve it.
We can see that the difference between the numbers 4−1 =3 and 7−4 =3 is 3.
Moving on, the number of squares for figure 4 will be 7 + 3 = 10.
Accordingly, for figure 5 it will be 10 + 3 = 13.
Furthermore, the number of squares for figure 6 will be 13 + 3 = 16.
The number of squares for figure 7 and figure 8 will be 16 + 3 = 19 and 19 + 3 = 22 , respectively.
Therefore, the completed table is given below:
Page 15 Exercise 1. 4 Problem 16
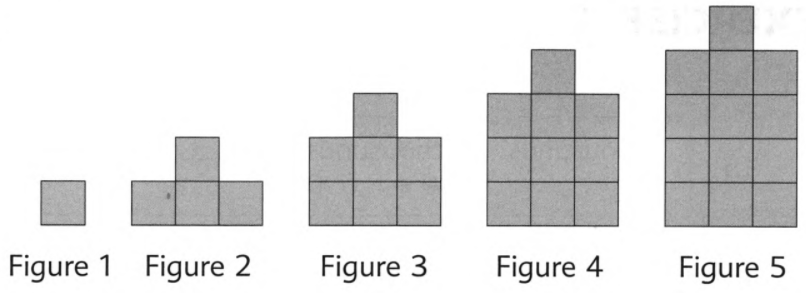
Given the figure and table as follows:
To tell the pattern that we notice in the number of squares.
From the figure, we can see that in figure 1, there is 1 square. In figure 2, the pattern changes to 1 + 2 + 1 = 4, in the next figure, it changes to 2 + 3 + 2 = 7, and so on.
Hence, we can notice that the pattern followed is 1 + 1 + 1 = 3 that is the difference between each number of squares is 3.
Therefore, the pattern that we notice in the number of squares is 1 + 1 + 1 = 3.
Page 16 Exercise 1.5 Problem 1
Given: The numbers 7 thousands and 9 thousands and the equation 7,000 + 9,000.
We have to add the numbers.
Using the place values, we add the numbers.
We are given the numbers 7 thousands and 9 thousands which are both at thousand-place.
Hence, we simply add the numbers 7 + 9 = 16
Hence, we obtain the sum of 7 thousands and 9 thousands is 16 thousands.
Also,7,000 + 9,000 = 16,000.
Therefore, we obtain the equation as 7 thousands + 9 thousands = 16 thousands.
Page 16 Exercise 1.5 Problem 2
Given: The numbers 23thousands and 14 thousands and the equation 23,000+14,000.
We have to add the numbers.
Using the place values, we add the numbers.
We are given the numbers 23 thousands and 14 thousands which are both at thousand-place.
Hence, we simply add the numbers 23 + 14 = 37.
Hence, we obtain the sum of 23 thousands and 14 thousands is 37 thousands.
Also,23,000 + 14,000 = 37,000.
Therefore, we obtain the equation as 23 thousands + 14 thousands = 37 thousands.
Page 16 Exercise 1.5 Problem 3
Given: The numbers 29,000&12,000.
We have to add the numbers.
Using the place values, we add the numbers.
We are given the numbers 29,000&12,000 which are both at thousand-place.
Hence, we simply add the numbers 29 + 12 = 41.
Hence, we obtain the sum of 29,000, and 12,000 is 41,000.
Therefore, we obtain the equation as 29,000 + 12,000 = 41,000.
Page 16 Exercise 1.5 Problem 4
Given: The numbers 3,46,000&24,000.
We have to add the numbers.
Using the place values, we add the numbers.
We are given the numbers 3,46,000&24,000.
We will add the numbers using their place values.
If we add ones, tens, and hundreds place we get 000.
Next, adding thousands place we have 6 + 4 = 10.
Now, adding ten thousands place 4 + 2 = 6.
Hence, we obtain the sum as 3,46,000+24,000=3,70,000.
Therefore, we obtain the equation as 3,46,000 + 24,000 = 3,70,000.
Page 16 Exercise 1.5 Problem 5
Given: The numbers 538,000&161,000.
We have to add the numbers.
Using the place values, we add the numbers.
We are given the numbers 538,000&161,000.
We will add the numbers using their place values.
If we add ones, tens, and hundreds place we get 000.
Next, adding thousands place we have 8+1=9.
Now, adding ten thousands place 3+6=9 and adding a hundred thousands place is 5 + 1 = 6.
Hence, we obtain the sum as 538,000 + 161,000 = 699,000.
Therefore, we obtain the equation as 538,000 + 161,000 = 699,000.
Page 17 Exercise 1.5 Problem 6
Given: The numbers 3 thousands & 2 and the equation 3000×2.
We have to multiply the numbers.
Using the place values, we multiply the numbers.
We are given the numbers 3 thousands & 2.
We multiply each digit of the number with 2.
Hence, we obtain the product of 3 thousands & 2 is 6 thousands as 3 × 2 = 6.
Also,3,000 × 2 = 6,000.
Therefore, we obtain the solution as 3 thousands & 2 = 6 Thousands.
Page 17 Exercise 1.5 Problem 7
Given: We have to multiply 8 thousands×6.
Solving
8 thousands × 6 = 24 thousands
8000 × 6 = 24000
By multiplying we get 8 thousands × 6 = 24 thousands and 8000 × 6 = 24000
Page 17 Exercise 1.5 Problem 8
Given: We have to multiply 14,000 × 3
Solving
14,000 × 3 = 42,000
On solving the given expression, we get 14,000 × 3 = 42,000
We have to multiply 18,000 × 5.
Solving
18,000 × 5 = 90,000
On solving the given expression, we get 18,000 × 5 = 90,000
Page 17 Exercise 1.5 Problem 9
Given: We have to multiply 60,000×7.
Solving
60,000 × 7 = 42,000
On solving the given expression, we get 60,000 × 7 = 42,000
Page 17 Exercise 1.5 Problem 10
Given: We have to divide \(\frac{\text 8 thousands }{4}\)
Solving
\(\frac{\text 8 thousands}{4}\)= 2 thousands and \(\frac{8,000}{4}\)= 2000
On solving the given expression, we get, \(\frac{\text 8 thousands}{4}\) = 2 thousands\(\frac{8,000}{4}\)= 2000
Page 17 Exercise 1.5 Problem 11
Given: We have to divide \(\frac{\text 72 thousands}{6}\)
Solving
\(\frac{\text 72 thousands}{6}\)= 12 thousands \(\frac{72,000}{6}\)
On solving the given expression, we get: \(\frac{\text 72 thousands}{6}\)= 12 thousands\(\frac{72,000}{6}\)
Page 17 Exercise 1.5 Problem 12
Given: We have to divide \(\frac{15,000}{5}\)
Solving
\(\frac{15,000}{5}\) = 3,000
On solving the given expression, we get \(\frac{15,000}{5}\) = 3,000
Page 17 Exercise 1.5 Problem 13
Given: We have to divide \(\frac{96,000}{8}\)
Solving
\(\frac{96,000}{8}\)= 12,000
On solving the given expression, we get \(\frac{96,000}{8}\)= 12,000
Page 17 Exercise 1.5 Problem 14
Given: We have to divide \(\frac{630,000}{7}\)
Solving
\(\frac{630,000}{7}\) = 90,000
On solving the given expression, we get\(\frac{630,000}{7}\) = 90,000
Page 18 Exercise 1. 5 Problem 15
Given: We have to add 120,000 + 340,000
Solving
120,000 + 340,000 = 460,000
On solving the given expression, we get 120,000+340,000=460,000
We have to subtract 120,000 − 34,000.
Solving
120,000 − 34,000 = 86,000
On solving the given expression, we get 120,000−34,000 = 86,000.
Page 18 Exercise 1. 5 Problem 16
Given: We have to multiply 120,000 × 2.
Solving
120,000 × 2 = 240,000
On solving the given expression, we get 120,000 × 2 = 240,000
Page 18 Exercise 1. 5 Problem 17
Given: We have to divide \(\frac{120,000}{2}\)
Solving
\(\frac{120,000}{2}\) = 60,000
On solving the given expression, we get \(\frac{120,000}{2}\) = 60,000
Page 18 Exercise 1.5 Problem 18
Given: We are given an expression 29,000 + n = 41,000.
We have to find the number represented by n.
Bringing n on one side
n = 41,000 − 29,000
n = 12,000
Therefore, the number represented is n=12,000.
Page 18 Exercise 1. 5 Problem 19
Given: We are given an expression n+24,000=100,000
We have to find the number represented by n
Bringing n on one side
n = 100,000 − 24,0000
n = 76,000
Therefore, the number represented is n = 76,000
Page 18 Exercise 1. 5 Problem 20
Given: We are given an expression 254,000 − n = 33,000
We have to find the number represented by n
Bringing n on one side
n = 254,000 − 33,000
n = 221,000
Therefore, the number represented is n = 221,000.
Page 18 Exercise 1. 5 Problem 21
Given: We are given an expression n−16,000 = 24,000
We have to find the number represented by n
Bringing n on one side
n = 24,000 − 16,000
n = 8,000
Therefore, the number represented is n = 8,000
Page 18 Exercise 1. 5 Problem 22
Given: We are given an expression 40,000 × n = 120,000
We have to find the number represented by n
Bringing n on one side
n= \(\frac{120,000}{40,000}\)
n = 3
Therefore, the number represented is n = 3.
Page 18 Exercise 1. 5 Problem 23
Given: We are given an expression n×5 = 40,000
We have to find the number represented by n
Brining n on one side
n = \(\frac{40,000}{5}\)
n = 8,000
Therefore, the number represented is n=8,000
Page 18 Exercise 1. 5 Problem 24
Given: We are given an expression \(\frac{15,000}{n}\)= 3,000
We have to find the number represented by n
Bringing n on one side
\(\frac{15,000}{3,000}\)
n = 5
Therefore, the number represented is n=5
Page 18 Exercise 1. 5 Problem 25
Given: We are given an expression \(\frac{n}{8}\)
We have to find the number represented by n
Bringing n on one side
n = 70,000×8
n = 560,000
Therefore, the number represented is n = 560,000
Page 18 Exercise 1.5 Problem 26
Given: We are given an expression with
LHS = 20,000 + 5,000 + 40 + 6 and
RHS=20,000 + 8,000 + 30 + 9.
We have to compare both sides of the expression, without finding the actual value.
As in the R.H.S 20,000 is added to 8,000, it is higher than in the L.H.S where it is added to 5,000
Therefore
20,000 + 5,000 + 40 + 6<20,000 + 8,000 + 30 + 9
Therefore, by comparing the sides of the expression we get: 20,000 + 5,000 + 40 + 6 < 20,000 + 8,000 + 30 + 9
Page 18 Exercise 1.5 Problem 27
Given: We are given an expression with
L.HS = 13,100 + 2000 and
R.HS = 13,100 + 200
We have to compare both sides of the expression, without finding the actual value.
As we add 2,000 in the L.H.S , which is higher than 200
Therefore
13,100 + 2000 > 13,100 + 200
Therefore, on comparing we get 13,100 + 2,000>13,100 + 200
Page 18 Exercise 1.5 Problem 28
Given: We are given an expression We have to compare both sides of the expression, without finding the actual value.
As a higher number 7000 is subtracted from 18,151 which is lower as compared to 19,151
18,151−7000<19,151−3,948
Therefore, by comparing we get 18,151−7000<19,151−3,948.
Page 18 Exercise 1.5 Problem 29
Given: We are given an expression with
L.HS = 700 × 6 and R.HS = 600 × 7
We have to compare both sides of the expression, without finding the actual value.
As 700>600
700×6>600×7
Therefore, by comparing we get 700 × 6>600 × 7
Page 18 Exercise 1.5 Problem 30
Given: We are given an expression with
L.HS = \(\frac{56,000}{2}\) and
R.HS = \(\frac{5,600}{2}\)
We have to compare both sides of the expression, without finding the actual value.
As 56,000>5,600 and both are divided by 2 Therefore
\(\frac{56,000}{2}\) > \(\frac{5,600}{2}\)
Therefore, by comparing we get \(\frac{56,000}{2}\) > \(\frac{5,600}{2}\)
Page 19 Exercise 1. 6 Problem 1
Given: We have to round 297 to the nearest ten.
As 297 is closer to 300 than 290 , 297 is 300 when rounded to the nearest ten.
Therefore, 297 is 300 when rounded to the nearest ten.
Page 19 Exercise 1. 6 Problem 2
Given: We have to round 1,315 to the nearest ten.
As 1,315 has to be rounded to the nearest ten, the next ten will be 1,320
Therefore, 1,315 is 1,320 when rounded to the nearest ten
Page 19 Exercise 1.6 Problem 3
Given: We have to round 5,982 to the nearest hundred.
As 6,000 is the nearest hundred to 5,982, 5,892 is 6,000 when rounded to the nearest hundred
Therefore, 5,982 is 6,000 when rounded to the nearest hundred
Page 19 Exercise 1.6 Problem 4
Given: We have to round 36,250 to the nearest hundred.
As 36,300 is the nearest hundred to 36,250, 36,250 is 36,300 when rounded to the nearest hundred.
Therefore, 36,250 is 36,300 when rounded to the nearest hundred.
Page 19 Exercise 1.6 Problem 5
Given:
We have to round 46,120 to the nearest thousand .
As 46,000 is nearest thousand to 46,120, 46,120 is 46,000 when rounded to the nearest thousand .
Therefore, 46,120 is 46,000 when rounded to the nearest thousand.
Page 19 Exercise 1.6 Problem 6
Given:
We have to round 235,870 to the nearest thousand.
As 236,000 is the nearest thousand to 235,870, 235,870 is 236,000 when rounded to the nearest thousand.
Therefore, 235,870 is 236,000 when rounded to the nearest thousand.
Page 20 Exercise 1. 6 Problem 7
Given:
We have to round 245,230 to the nearest thousand.
As 245,000 is the nearest thousand to 245,230, 245,230 is 245,000 when rounded to the nearest thousand.
Therefore, 245,230 is 245,000 when rounded to the nearest thousand.
Page 20 Exercise 1. 6 Problem 8
Given:
We have to round 247,826 to the nearest thousand .
As 248,000 is the nearest thousand to 247,826 .247,826 is 248,000 when rounded to the nearest thousand .
Therefore, 247,826 is 248,000 when rounded to the nearest thousand.
Page 20 Exercise 1. 6 Problem 9
Given:
We have to round 43,192 to the nearest ten.
As 43,190 is the nearest ten to 43,192, 43,192 is 43,190 when rounded to the nearest ten
Therefore, 49,192 is 43,190 when rounded to the nearest ten.
Page 20 Exercise 1. 6 Problem 10
Given:
We have to round 14,563 to the nearest hundred.
As 14,600 is the nearest hundred.14,563 is 14,600 when rounded to the nearest hundred.
Therefore, 14,563 is 14,600 when rounded to the nearest hundred.
Page 20 Exercise 1. 6 Problem 11
Given:
We have to round 82,926 to the nearest thousand.
As 83,000 is the nearest thousand to 82,926, 82,296 is 83,000 when rounded to the nearest thousand
Therefore, 82,926 is 83,000 when rounded to the nearest thousand.
Page 20 Exercise 1. 6 Problem 12
Given:
We have to round 964,250 to the nearest ten thousand.
As 960,000 is the nearest ten thousand, 964,520 is 960,000 when rounded to the nearest ten thousand.
Therefore, 964,520 is 960,000 when rounded to the nearest ten thousand.
Page 20 Exercise 1. 6 Problem 13
Given:
We have to round 754,000 to the nearest hundred thousand .
As 800,000 is the nearest hundred thousand , 754,000 is 800,000 when rounded to the nearest hundred thousand
Therefore, 754,000 is 800,000 when rounded to the nearest hundred thousand.
Page 20 Exercise 1. 6 Problem 14
Given:
We have to round $438,50 to the nearest ten thousand dollars.
As 440,000 is the nearest ten thousand to 438,50, $438,500 is $ 440,000 when rounded to the nearest ten thousand dollars.
After rounding $438,500 to the nearest ten thousand dollars we get $440,000
Page 20 Exercise 1. 6 Problem 15
Given:
$525,000
To round off the number to nearest ten thousand digit
First, identify the ten thousand digit
Check the previous digit is less than 5 or greater than equal to 5 and apply the rules.
Given the number is $525,000
The ten thousand digit in the number is 2 and the previous digit to it is 5
Since the previous digit to the ten thousand digit is equal to 5 So round up the ten thousand digit.
Therefore, the number $525,000 rounded off to the nearest ten thousand digit as $530,000 The round off answer will be $530,000.
Page 20 Exercise 1. 6 Problem 16
Given: $608,000
To round off the number to nearest ten thousand digit
First identify the ten thousand digit
Check the previous digit is less than 5 or greater than equal to 5 and apply the rules.
Given the number is $608,000
The ten thousand digit in the number is 0 and the previous digit to it is 8
Since the previous digit to the ten thousand digit is equal to 8 So round up the ten thousand digit.
The round-off answer will be $610,000.
Therefore, the number $608,000 rounded off to the nearest ten thousand digit is $610,000.
Page 20 Exercise 1. 6 Problem 17
Given: $974,500
To round off the number to nearest ten thousand digit
First, identify the ten thousand digit
Check the previous digit is less than 5 or greater than equal to 5 and apply the rules.
Given the number is $974,500
The ten thousand digit in the number is 7 and the previous digit to it is 4
Since the previous digit to the ten thousand digit is equal to 4 So round down the ten thousand digit. The round-off answer will be $970,000.
Therefore, the number $974,500rounded off to the nearest ten thousand digit is $970,000.
Page 20 Exercise 1. 6 Problem 18
Given: $990,400
To round off the number to nearest ten thousand digit
First, identify the ten thousand digit
Check the previous digit is less than 5 or greater than equal to 5 and apply the rules.
Given the number is $990,400
The ten thousand digit in the number is 9 and the previous digit to it is 0
Since the previous digit to the ten thousand digit is equal to 0 So round down the ten thousand digit.
The round-off answer will be $990,000.
Therefore, the number $990,400 rounded off to the nearest ten thousand digit is $990,000.
Page 20 Exercise 1. 6 Problem 19
Given: $226,300
To round off the number to nearest ten thousand digit
First, identify the ten thousand digit
Check the previous digit is less than 5 or greater than equal to 5 and apply the rules.
Given the number is $226,300
The ten thousand digit in the number is 2 and the previous digit to it is 6
Since the previous digit to the ten thousand digit is equal to 6 So round up the ten thousand digit.
The round-off answer will be $230,000.
Therefore, the number $226,300 rounded off to the nearest ten thousand digit is $230,000