Vector Differentiation- 3 Exercise 3 Solved Problems (Contd)
70. Find the angle between the surfaces x2yz = 3x + z2 and 3x2-y + 2z=1 at (1,-2, 1).
Solution:
Given
x2yz = 3x + z2 and 3x2-y + 2z=1 at (1,-2, 1)
A vector normal to the surfaces f=xy2z-3x-z2 is grad (xy2z-3x-z2)
=(y2z-3)i+2xyzj+(xy2+2z)k
A vector normal to g=3x-y+2z-1 is 6xi-2yj+2k
At(1,-2,1), grad g=6i+4j+2k:
If θ is the angle between the surfaces, then
cos θ \(=\frac{1(6)+(-4) 4+2 \cdot 2}{\sqrt{1+16+4} \sqrt{36+16+4}}\)
= \(\frac{-6}{\sqrt{21} \sqrt{56}}\)
⇒ θ =Cos-1\(\left(\frac{-3}{7 \sqrt{6}}\right)\)
Gradient And Divergence Vector Exercise Solutions
71. Find the cosine of the angle between the surfaces x2y + z = 3, x log z-y2 = 4 at P (- 1, 2, 1)The normal to the surfaces xy+z=3 is 2xyi+xj+k
Solution:
Given
x2y + z = 3, x log z-y2 = 4 at P (- 1, 2, 1)
The normal to the surfaces xy+z=3 is 2xyi+xj+k
At (-1,2,1), the normal is 4i+j+k
The normal to the surface x log z-y=4 is log zi-2yjj+(x/z)k
At(-1,2,1) the normal is -4j-k
The angle between the surfaces is equal to the angle between normal to the surfaces.
∴ cos θ \(=\left|\frac{4 \cdot 0+1(-4)+1(-1)}{\sqrt{4^2+1^2+1^2} \sqrt{(-4)^2+(-1)^2}}\right|\)
= \(\frac{5}{\sqrt{18} \sqrt{17}}\)
⇒ θ = cos-1\(\frac{5}{\sqrt{306}}\)
72. Define divergence of a vector point function.
Divergence: If F is continuously differentiable vector point function then \(\mathbf{i} \cdot \frac{\partial \boldsymbol{F}}{\partial x}+\mathbf{j} \cdot \frac{\partial \boldsymbol{F}}{\partial y}+\mathbf{k} \cdot \frac{\partial \boldsymbol{F}}{\partial z}\) is called divergence of F and it is denoted by div F or . F
73. If F1i+F2j+F3k then prove that div F = \(=\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}\).
Solution:
⇒ \({div} \mathbf{F}=\mathbf{i} \cdot \frac{\partial \mathbf{F}}{\partial x}+\mathbf{j} \cdot \frac{\partial \mathbf{F}}{\partial y}+\mathbf{k} \cdot \frac{\partial \mathbf{F}}{\partial z}\)
⇒ \(\mathbf{i} \cdot\left(\frac{\partial F_1}{\partial x} \mathbf{i}+\frac{\partial F_2}{\partial x} \mathbf{j}+\frac{\partial F_3}{\partial x} \mathbf{k}\right)+\mathbf{j} \cdot\left(\frac{\partial F_1}{\partial y} \mathbf{i}+\frac{\partial F_2}{\partial y} \mathbf{j}+\frac{\partial F_3}{\partial y} \mathbf{k}\right)+\mathbf{k} \cdot\left(\frac{\partial F_1}{\partial z} \mathbf{i}+\frac{\partial F_2}{\partial z} \mathbf{j}+\frac{\partial F_3}{\partial z} \mathbf{k}\right)\)
⇒ \(\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}\)
= \(\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
F_1 & F_2 & F_3
\end{array}\right|\)
74. If F and G are two vector point functions then prove that div (F ± G) = div F ± div G.
Solution:
⇒ \({div}(\mathbf{F}+\mathbf{G})=\mathbf{i} \cdot \frac{\partial}{\partial x}(\mathbf{F}+\mathbf{G})+\mathbf{j} \cdot \frac{\partial}{\partial y}(\mathbf{F}+\mathbf{G})+\mathbf{k} \cdot \frac{\partial}{\partial z}(\mathbf{F}+\mathbf{G})\)
⇒ \(\mathbf{i} \cdot\left(\frac{\partial \mathbf{F}}{\partial x}+\frac{\partial \mathbf{G}}{\partial x}\right)+\mathbf{j} \cdot\left(\frac{\partial \mathbf{F}}{\partial y}+\frac{\partial \mathbf{G}}{\partial y}\right)+\mathbf{k} \cdot\left(\frac{\partial \mathbf{F}}{\partial z}+\frac{\partial \mathbf{G}}{\partial z}\right)\)
⇒ \(\mathbf{i} \cdot \frac{\partial \mathbf{F}}{\partial x}+\mathbf{i} \cdot \frac{\partial \mathbf{G}}{\partial x}+\mathbf{j} \cdot \frac{\partial \mathbf{F}}{\partial y}+\mathbf{j} \cdot \frac{\partial \mathbf{G}}{\partial y}+\mathbf{k} \cdot \frac{\partial \mathbf{F}}{\partial z}+\mathbf{k} \cdot \frac{\partial \mathbf{G}}{\partial z}\)
⇒ \(\left(\mathbf{i} \cdot \frac{\partial \mathbf{F}}{\partial x}+\mathbf{j} \cdot \frac{\partial \mathbf{F}}{\partial y}+\mathbf{k} \cdot \frac{\partial \mathbf{F}}{\partial z}\right)+\left(\mathbf{i} \cdot \frac{\partial \mathbf{G}}{\partial x}+\mathbf{j} \cdot \frac{\partial \mathbf{G}}{\partial y}+\mathbf{k} \cdot \frac{\partial \mathbf{G}}{\partial z}\right)={div} \mathbf{F}+{div} \mathbf{G}\)
Similarly, we can prove that div(F-G)= div F-div G
75. If F = xyz i + x2y2z j + xyz3 k then find div F at (2, 1,- 3)
Solution: div F =\(\frac{\partial}{\partial x}\)(xyz)+\(\frac{\partial}{\partial y}\)(x2y2z)+\(\frac{\partial}{\partial z}\)(xyz3)
=yz+2x2yz+3xyz2 At (2,1,-3) , div F=-3-24+54=27.
76. Show that div r = 3
Solution: Let r=xi=yj+zk. Then \(\frac{\partial r}{\partial x}\)=i, \(\frac{\partial r}{\partial y}\)=j, \(\frac{\partial r}{\partial z}\)=k
div r=∇.r\(=\mathbf{i} \cdot \frac{\partial \mathbf{r}}{\partial x}+\mathbf{j} \cdot \frac{\partial \mathbf{r}}{\partial y}+\mathbf{k} \cdot \frac{\partial \mathbf{r}}{\partial z}\)=i.i+j.j+k.k= 1+1+1=3.
77. Show that div (r x a) = 0
Solution:
Let a = \(a_1 \mathbf{i}+a_2 \mathbf{j}+a_3 \mathbf{k}, \mathbf{r}=x \mathbf{i}+y \mathbf{j}+z \mathbf{k}\)
⇒ \(\mathbf{r} \times \mathbf{a}=\left|\begin{array}{ccc}
\mathbf{i} &\mathbf{j}& \mathbf{k} \\
x & y & z \\
a_1 & a_ 2 & a_3
\end{array}\right|=\mathbf{i}\left(a_3 y-a_2 z\right)-\mathbf{j}\left(a_3 x-a_1 z\right)+\mathbf{k}\left(a_2 x+a_1 y\right)\)
⇒ \({div}(\mathbf{r} \times \mathbf{a})=\nabla \cdot(\mathbf{r} \times \mathbf{a})=\frac{\partial}{\partial x}\left(a_3 y-a_2 y\right)+\frac{\partial}{\partial y}\left(a_1 z-a_3 x\right)+\frac{\partial}{\partial z}\left(a_2 x-a_1 y\right)\)
= 0+0+0 = 0
Divergence Of Vector Practice Problems
78. Show that div\(\frac{\underline{r}}{r}\)=\(\frac{2}{r}\)
Solution:
Let a = \(a_1 \mathbf{i}+a_2 \mathbf{j}+a_3 \mathbf{k}, \mathbf{r}=x \mathbf{i}+y \mathbf{j}+z \mathbf{k} .\)
⇒ \(\mathbf{r} \times \mathbf{a}=\left|\begin{array}{lll}
\mathbf{i} & \mathbf{j}& \mathbf{k} \\
x & y & z \\
a_ 1& a_ 2& a_ 3
\end{array}\right|=\mathbf{i}\left(a_3 y-a_2 z\right)-\mathbf{j}\left(a_3 x-a_1 z\right)+\mathbf{k}\left(a_2 x+a_1 y\right)\)
⇒ \({div}(\mathbf{r} \times \mathbf{a})=\nabla \cdot(\mathbf{r} \times \mathbf{a})=\frac{\partial}{\partial x}\left(a_3 y-a_2 y\right)+\frac{\partial}{\partial y}\left(a_1 z-a_3 x\right)+\frac{\partial}{\partial z}\left(a_2 x-a_1 y\right)\)
= 0+0+0 =0
79. Define solenoidal vector point function.
Solenoidal: A vector point function F is said to be solenoidal if div F=0
80. Show that F = 3y4 z2+ 4x3z2 j- 3x2y2 k is solenoidal.
Solution:
div F =\(\frac{\partial}{\partial x}\left(3 y^4 z^2\right)+\frac{\partial}{\partial y}\left(4 x^3 z^2\right)+\frac{\partial}{\partial z}\left(-3 x^2 y^2\right)\)=0
∴ F is solenoidal.
81. Prove that F =y3 z2 i-3x2z5 J- 15x5y4 k is solenoidal vector.
Solution:
div F \(=\frac{\partial}{\partial x}\left(3 y^4 z^2\right)+\frac{\partial}{\partial y}\left(4 x^3 z^2\right)+\frac{\partial}{\partial z}\left(-3 x^2 y^2\right)\)
= 0+0+0=0
∴ F is solenoidal.
82. If F = (x + 3y) i + (y-2z)y + (x+pz) k is solenoidal, find p.
Solution:
F is solenoidal div F =0 ⇒ ∇.F=0
⇒ \(\frac{\partial}{\partial x}\{x+3 y\}+\frac{\partial}{\partial y}\{y-2 z\}+\frac{\partial}{\partial z}\{x+p z\}\)=0 ⇒ 1+1+p=0 ⇒ p-2.
83. Define the curl of a vector point function.
Curl: If F is a continuously differentiable vector point function then \(\mathbf{i} \times \frac{\partial F}{\partial x}+j \times \frac{\partial F}{\partial y}+\mathbf{k} \times \frac{\partial F}{\partial z}\) is called curl of F. It is denoted by curl F or ∇×F.
84. If F = F1i+F2j+F3k then prove that curl F \(=\left|\begin{array}{ccc}\mathbf{1} & \mathbf{j} & \mathbf{k} \\\frac{\partial}{\partial x}& \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\F_1 & F_2 & F_3\end{array}\right|\)
Solution:
⇒ \({curl} \mathbf{F}=\mathbf{i} \times \frac{\partial \mathbf{F}}{\partial x}+\mathbf{j} \times \frac{\partial \mathbf{F}}{\partial y}+\mathbf{k} \times \frac{\partial \mathbf{F}}{\partial z}\)
⇒ \(\mathbf{i} \times\left(\frac{\partial F_1}{\partial x} \mathbf{i}+\frac{\partial F_2}{\partial x} \mathbf{j}+\frac{\partial F_3}{\partial x} \mathbf{k}\right)+\mathbf{j} \times\left(\frac{\partial F_1}{\partial y} \mathbf{i}+\frac{\partial F_2}{\partial y} \mathbf{j}+\frac{\partial F_3}{\partial y} \mathbf{k}\right)+\mathbf{k} \times\left(\frac{\partial F_1}{\partial z} \mathbf{i}+\frac{\partial F_2}{\partial z} \mathbf{j}+\frac{\partial F_3}{\partial z} \mathbf{k}\right)\)
⇒ \(\frac{\partial F_2}{\partial x} \mathbf{k}-\frac{\partial F_3}{\partial x} \mathbf{j}-\frac{\partial F_1}{\partial y} \mathbf{k}+\frac{\partial F_3}{\partial y} \mathbf{i}+\frac{\partial F_1}{\partial z} \mathbf{j}-\frac{\partial F_2}{\partial z} \mathbf{i}\)
⇒ \(\mathbf{i}\left(\frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z}\right)-\mathbf{j}\left(\frac{\partial F_3}{\partial x}-\frac{\partial F_1}{\partial z}\right)+\mathbf{k}\left(\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right)=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
F_1 & F_2 & F_3
\end{array}\right|\)
Gradient And Divergence Solved Examples
85. If F and G are two vector point functions then prove that curl (F ± G) = curl F ± curl G.
Solution:
⇒ \({curl}(\mathbf{F}+\mathbf{G})=\mathbf{i} \times \frac{\partial}{\partial x}(\mathbf{F}+\mathbf{G})+\mathbf{j} \times \frac{\partial}{\partial y}(\mathbf{F}+\mathbf{G})+\mathbf{k} \times \frac{\partial}{\partial z}(\mathbf{F}+\mathbf{G})\)
⇒ \(\mathbf{i} \times\left(\frac{\partial \mathbf{F}}{\partial x}+\frac{\partial \mathbf{G}}{\partial x}\right)+\mathbf{j} \times\left(\frac{\partial \mathbf{F}}{\partial y}+\frac{\partial \mathbf{G}}{\partial y}\right)+\mathbf{k} \times\left(\frac{\partial \mathbf{F}}{\partial z}+\frac{\partial \mathbf{G}}{\partial z}\right)\)
⇒ \(\mathbf{i} \times \frac{\partial \mathbf{F}}{\partial x}+\mathbf{i} \times \frac{\partial \mathbf{G}}{\partial x}+\mathbf{j} \times \frac{\partial \mathbf{F}}{\partial y}+\mathbf{j} \times \frac{\partial \mathbf{G}}{\partial y}+\mathbf{k} \times \frac{\partial \mathbf{F}}{\partial z}+\mathbf{k} \times \frac{\partial \mathbf{G}}{\partial z}\)
⇒ \(\left(\mathbf{i} \times \frac{\partial \mathbf{F}}{\partial x} + \mathbf{j} \times \frac{\partial \mathbf{F}}{\partial y}+\mathbf{k} \times \frac{\partial \mathbf{F}}{\partial z}\right)+\left(\mathbf{i} \times \frac{\partial \mathbf{G}}{\partial x}+\mathbf{j} \times \frac{\partial \mathbf{G}}{\partial y}+\mathbf{k} \times \frac{\partial \mathbf{G}}{\partial z}\right)={curl} \mathbf{F}+{curl} \mathbf{G}\)
Similarly, we can prove that curl (F-G) = curl G
Step-By-Step Guide To Solving Vector Differentiation Gradient Problems
86. If F = xyz i + zx2 j+ xy2 z k then find curl F at (1, 2,- 1).
Solution:
⇒ \({curl} \mathbf{F}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
x y z & z x^2 & x y^2 z
\end{array}\right|=\mathbf{i}\left(2 x y z-x^2\right)-\mathbf{j}\left(y^2 z-x y\right)+\mathbf{k}(2 x z-x z)\)
At (1,2,-1), curl F = -5i+6j-k
87. If F=x2yi- 2xzj + 2yz k, find curl F at (1, 1, 1)
Solution:
⇒ \({curl} \mathbf{F}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
x^2 y & -2 x z & 2 y z
\end{array}\right|=\mathbf{i}(2 z+2 x)-\mathbf{j}(0-0)+\mathbf{k}\left(-2 z-x^2\right)\)
At (1,1,1), curl F = 4i-3k
88. Find div F and curl F where F = xy2 i + 2x2yzj- 3yz2k at (1,-1, 1).
Solution:
⇒ \({div} \mathbf{F}=\frac{\partial}{\partial x}\left(x y^2\right)+\frac{\partial}{\partial y}\left(2 x^2 y z\right)+\frac{\partial}{\partial z}\left(-3 y z^2\right)=y^2+2 x^2 z-6 y z\)
⇒ \({At}(1,-1,1), {div} \mathbf{F}=(-1)^2+2(1)^2(1)-6(-1)(1)=1+2+6=9\)
⇒ \({curl} \mathbf{F}=\nabla \times \mathbf{F}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
x y^2 & 2 x^2 y z & -3 y z
\end{array}\right|=\mathbf{i}\left(-3 z^2-2 x^2 y\right)-\mathbf{j}(0-0)+\mathbf{k}(4 x y z-2 x y)\)
⇒ At (1,-1,1), curl F – i (-3+2) + k (-4+2) = -i-2k = -6i
Exercises On Vector Differentiation With Solutions
89. Iff =x2yi-2xzj + 2yzk, find (1) div f (2) curl f.
Solution: Given f=x2yi-2xyzj+2yzk
⇒ div f=\(\frac{\partial}{\partial x}\left\{x^2 y\right\}+\frac{\partial}{\partial y}\{-2 x z\}+\frac{\partial}{\partial z}\{2 y z\}\)=2xy+2y.
⇒ curl f=\(\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
x^2 y & -2 x z & 2 y z
\end{array}\right|\)
=i(2z+2x)-j(0-0)+k(-2z-x2)
=(2x+2z)i-(x2+2z)k.
90. If F =x2zi-2y3 z2 j+xy2zk find div F and curl F at (1,- 1, 1).
Solution:
⇒ \({div} \mathbf{F}=\frac{\partial}{\partial x}\left\{x^2 z\right\}+\frac{\partial}{\partial y}\left\{-2 y^3 z^2\right\}+\frac{\partial}{\partial z}\left\{x y^2 z\right\}=2 x z-6 y^2 z^2+x y^2\)
At (1,-1,1), div F = 2-6+1 -3
⇒ \({curl} \mathbf{F}=\nabla \times \mathbf{F}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
x^2 z & -2 y^3 z^2 & x y^2 z
\end{array}\right|=\mathbf{i}\left[2 x y z+4 y^3 z\right]-\mathbf{j}\left[y^2 z-x^2\right]+\mathbf{k}[0-0]\)
⇒ \({At}(1,-1,1),{curl} \mathbf{F}=\mathbf{i}\left[2(1)(-1)(1)+4(-1)^3(1)\right]-\mathbf{j}\left[(-1)^2(1)-(1)^2\right]=-6 \mathbf{i}\)
Vector Calculus Gradient And Divergence Problems Detailed Solutions
91. Show that curl r = 0
Solution:
Let r=xi+yj+zk.Then \(\frac{\partial \mathbf{r}}{\partial x}\)=i, \(\frac{\partial \mathbf{r}}{\partial y}\)=j, \(\frac{\partial \mathbf{r}}{\partial z}\)=k
⇒ curl r=∇× r=\(=\mathbf{i} \times \frac{\partial \mathbf{r}}{\partial x}+\mathbf{j} \times \frac{\partial \mathbf{r}}{\partial y}+\mathbf{k} \times \frac{\partial \mathbf{r}}{\partial z}\)=
i×i+j×j+k×k
=0+0+0=0.
Gradient Differentiation Tutorial
92. Show that curl (r x a) =- 2a
Solution:
⇒ \({curl}(\mathbf{r} \times \mathbf{a})=\nabla \times(\mathbf{r} \times \mathbf{a})=\mathbf{I} \times \frac{\partial}{\partial x}(\mathbf{r} \times \mathbf{a})+\mathbf{j} \times \frac{\partial}{\partial y}(\mathbf{r} \times \mathbf{a})+\mathbf{k} \times \frac{\partial}{\partial z}(\mathbf{r} \times \mathbf{a})\)
⇒ \(\mathbf{i} \times\left(\frac{\partial \mathbf{r}}{\partial x} \times \mathbf{a}\right)+\mathbf{j} \times\left(\frac{\partial \mathbf{r}}{\partial y} \times \mathbf{a}\right)+\mathbf{k} \times\left(\frac{\partial \mathbf{r}}{\partial z} \times \mathbf{a}\right)=\mathbf{i} \times(\mathbf{i} \times \mathbf{a})+\mathbf{j} \times(\mathbf{j} \times \mathbf{a})+\mathbf{k} \times(\mathbf{k} \times \mathbf{a})\)
= (i.a) i – (i.i) a + (j.a) j – (j.j) a+ (k.a) k – (k.k) a
= (i.a) i +(j.a) j + (k.a) K -3a = a-3a = -2a
93. If a and b are constant vectors then show that
- div {(r x a) x b} =- 2 (b . a)
- curl {(r x a) x b} = b x a .
Solution:
Let a \( =a_1 \mathbf{i}+a_2 \mathbf{j}+a_3 \mathbf{k}, \mathbf{b}=b_1 \mathbf{i}+b_2 \mathbf{j}+b_3 \mathbf{k} \text {. }\)
⇒ \(\mathbf{r} \times \mathbf{a}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
x & y & z \\
a_1 & a_2 & a_3
\end{array}\right|=\mathbf{i}\left(a_3 y-a_2 z\right)-\mathbf{j}\left(a_3 x-a_1 z\right)+\mathbf{k}\left(a_2 x-a_1 y\right)\)
⇒ \((\mathbf{r} \times \mathbf{a}) \times \mathbf{b}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
a_3 y-a_2 z & a_1 z-a_3 x & a_2 x-a_1 y \\
b_1 & b_2 & b_3
\end{array}\right|\)
⇒ \(\mathbf{i}\left(a_1 b_3 z-a_3 b_3 x-a_2 b_2 x+a_1 b_2 y\right)-\mathbf{J}\left(a_3 b_3 y-a_2 b_3 z-a_2 b_1 x+a_1 b_1 y\right)\)
+ \(\mathbf{k}\left(a_3 b_2 y-a_2 b_2 z-a_1 b_1 z-a_3 b_1 x\right)\)
1. \({div}[(\mathbf{r} \times \mathbf{a}) \times \mathbf{b}]=\frac{\partial}{\partial x}\left(a_1 b_3 z-a_3 b_3 x-a_2 b_2 x+a_1 b_2 y\right)\)
⇒ \(+\frac{\partial}{\partial y}\left(-a_3 b_3 y+a_2 b_3 z+a_2 b_1 x-a_1 b_1 y\right)+\frac{\partial}{\partial z}\left(a_3 b_2 y-a_2 b_2 z-a_1 b_1 z+a_3 b_1 x\right)\)
⇒ \(-a_3 b_3-a_2 b_2-a_3 b_3-a_1 b_1-a_2 b_2-a_1 b_1\)
⇒ \(-2\left(a_1 b_1+a_2 b_2+a_3 b_3\right)=-2(a \cdot b)=-2(b \cdot a)\)
2. curl [(r×a)×b]
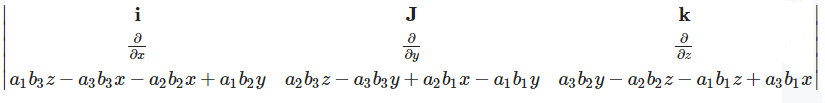
⇒ \(i\left(a_3 b_2-a_2 b_3\right)-\mathbf{j}\left(a_3 b_1-a_1 b_3\right)+\mathbf{k}\left(a_2 b_1-a_1 b_2\right)=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
b_1 & b_2 & b_3 \\
a_1 & a_2 & a_3
\end{array}\right|=\mathbf{b} \times \mathbf{a}\)
Solved Examples Of Gradient And Divergence Operations
94. Define the irrotational vector point function.
Irrotational: A vector point function F is said to be irrotational if curl F =0.
95. Show that F -yz i +zx j + xy k is irrotational
Solution:
curl F= \(=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
y z & z x & x y
\end{array}\right|\) =i(x-x)j(y-y)+k(z-z)=0
∴ F is irrotational.
96. Show that F = (sin y + z)i + (x cosy-z)j + (x – y)k is irrotational.
curl F\(=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
\sin y+z & x \cos y-z & x-y
\end{array}\right|\)=i(-1+1)-j(1-1)+k(cosy-cosy)=0
∴ F is irrotational.
97. Show that rn r is irrotational
Solution:
Let r=xi+yj+zk. Then \(\frac{\partial \mathbf{r}}{\partial x}\)=i, \(\frac{\partial \mathbf{r}}{\partial y}\)=j,\(\frac{\partial \mathbf{r}}{\partial z}\)= k
⇒ curl r=∇×r=\(\mathbf{i} \times \frac{\partial \mathbf{r}}{\partial x}+\mathbf{j} \times \frac{\partial \mathbf{r}}{\partial y}+\mathbf{k} \times \frac{\partial \mathbf{r}}{\partial z}=\)=i×i+j×j+k×k=
⇒ 0+0+0=0
Vector Differentiation Exercises For Beginners
98. Show that f(r) r is irrotational. Find when it is solenoidal.
Solution:
⇒ \(\mathbf{F}=r^n \mathbf{r}=r^n x \mathbf{i}+r^n y \mathbf{j}+r^n z \mathbf{k}\)
⇒ \({curl} \mathbf{F}=\nabla \times \mathbf{F}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{J} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
r^n x & r^n y & r^n z
\end{array}\right|\)
⇒ \(\mathbf{i}\left[\frac{\partial}{\partial y}\left(r^n z\right)-\frac{\partial}{\partial z}\left(r^n y\right)\right]-\mathbf{j}\left[\frac{\partial}{\partial x}\left(r^n z\right)-\frac{\partial}{\partial z}\left(r^n x\right)\right]+\mathbf{k}\left[\frac{\partial}{\partial x}\left(r^n y\right)-\frac{\partial}{\partial y}\left(r^n x\right)\right]\)
⇒ \(i\left[n r^{n-1} z \cdot \frac{y}{r}-n r^{n-1} \cdot y \cdot \frac{z}{r}\right]-j\left[n r^{n-1} z \cdot \frac{x}{r}-n r^{n-1} x \cdot \frac{z}{r}\right]+k\left[n r^{n-1} y \cdot \frac{x}{r}-n r^{n-1} x \cdot \frac{y}{r}\right]\)
= 0
∴ F is irrational
⇒ \(r^n \mathbf{r}=r^n x \mathbf{I}+r^n y \mathbf{j}+r^n z \mathbf{k} \text { is solenoidal }\)
⇒ \(r^n+x n r^{n-1} \frac{\partial r}{\partial x}+r^n+y n r^{n-1} \frac{\partial r}{\partial y}+r^n+z n r^{n-1} \frac{\partial r}{\partial z}=0\)
⇒ \(r^n+x n r^{n-1} \frac{\partial r}{\partial x}+r^n+y n r^{n-1} \frac{\partial r}{\partial y}+r^n+z n r^{n-1} \frac{\partial r}{\partial z}=0\)
⇒ \(3 r^n+n r^{n-1} \frac{x^2}{r}+n r^{n-1} \frac{y^2}{r}+n r^{n-1} \frac{z^2}{r}=0 \Rightarrow 3 r^n+n r^{n-2}\left(x^2+y^2+z^2\right)=0\)
⇒ \(3 r^n+n r^n=0 \Rightarrow n+3=0 \Rightarrow n=-3 .\)
99. Show that f(r) r is irrotational.
Solution:
⇒ \(\nabla \times \frac{\mathbf{r}}{r^2}=\nabla \times\left(\frac{x}{r^2} \mathbf{i}+\frac{y}{r^2} \mathbf{j}+\frac{z}{r^2} \mathbf{k}\right)=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
x / r^2 & y / r^2 & z / r^2
\end{array}\right|\)
⇒ \(i\left[\frac{\partial}{\partial y}\left(\frac{z}{r^2}\right)-\frac{\partial}{\partial z}\left(\frac{y}{r^2}\right)\right]-\mathbf{j}\left[\frac{\partial}{\partial x}\left(\frac{z}{r^2}\right)=\frac{\partial}{\partial z}\left(\frac{x}{r^2}\right)\right]+\mathbf{k}\left[\frac{\partial}{\partial x}\left(\frac{y}{r^2}\right)-\frac{\partial}{\partial y}\left(\frac{x}{r^2}\right)\right]\)
⇒ \(i\left[-2 r^{-3} \frac{\partial r}{\partial y} \cdot z+2 r^{-3} \frac{\partial r}{\partial z} y\right]-\mathbf{j}\left[-2 r^{-3} \frac{\partial r}{\partial x} z+2 r^{-3} \frac{\partial r}{\partial z} x\right]+\mathbf{k}\left[-2 r^{-3} \frac{\partial r}{\partial x} y+2 r^{-3} \frac{\partial r}{\partial y} x\right]\)
⇒ \(\mathbf{i}\left(-2 r^{-4} y z+2 r^{-4} z y\right)-\mathbf{j}\left(-2 r^{-4} x z+2 r^{-4} z x\right)+\mathbf{k}\left(-2 r^{-4} x y+2 r^{-4} y z\right)=\mathbf{0}\)
∴ \(r / r^2\) is irrational
Advanced Problems On Vector Gradient And Divergence Solutions
100. Show that r/r2 is always irrotational
Solution:
⇒ \(\nabla \times \frac{\mathbf{r}}{r^2}=\nabla \times\left(\frac{x}{r^2} \mathbf{i}+\frac{y}{r^2} \mathbf{j}+\frac{z}{r^2} \cdot \mathbf{k}\right)=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
x / r^2 & y / r^2 & z / r^2
\end{array}\right|\)
⇒ \(\mathbf{i}\left[\frac{\partial}{\partial y}\left(\frac{z}{r^2}\right)-\frac{\partial}{\partial z}\left(\frac{y}{r^2}\right)\right]-\mathbf{j}\left[\frac{\partial}{\partial x}\left(\frac{z}{r^2}\right)=\frac{\partial}{\partial z}\left(\frac{x}{r^2}\right)\right]+\mathbf{k}\left[\frac{\partial}{\partial x}\left(\frac{y}{r^2}\right)-\frac{\partial}{\partial y}\left(\frac{x}{r^2}\right)\right]\)
⇒ \(i\left[-2 r^{-3} \frac{\partial r}{\partial y} \cdot z+2 r^{-3} \frac{\partial r}{\partial z} y\right]-\mathbf{j}\left[-2 r^{-3} \frac{\partial r}{\partial x} z+2 r^{-3} \frac{\partial r}{\partial z} x\right]+\mathbf{k}\left[-2 r^{-3} \frac{\partial r}{\partial x} y+2 r^{-3} \frac{\partial r}{\partial y} x\right]\)
⇒ \(\mathbf{i}\left(-2 r^{-4} y z+2 r^{-4} z y\right)-\mathbf{j}\left(-2 r^{-4} x z+2 r^{-4} z x\right)+\mathbf{k}\left(-2 r^{-4} x y+2 r^{-4} y z\right)=\mathbf{0}\)
∴ \(\mathbf{r} / \boldsymbol{r}^2\) is irrational
101. Find the constants a, b, c so that (x + 2y + az)i + (bx −3y-z)j + (4x + cy + 2z) k is irrotational.
Solution:
Given
(x + 2y + az)i + (bx −3y-z)j + (4x + cy + 2z) k
⇒ \((x+2 y+a z) \mathbf{i}+(b x-3 y-z) \mathbf{j}+(4 x+c y+2 z) \mathbf{k} \text { is irrotational }\)
⇒ \(\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
x+2 y+a z & b x-3 y-z & 4 x+c y+2 z
\end{array}\right|=0\)
⇒ \(\mathbf{i}(c+1)-\mathbf{j}(4-a)+\mathbf{k}(b-2)=\mathbf{0} \Rightarrow c+1=0,4-a=0, b-2=0\)
⇒ a = 4, b = 2, c = 1
102. If A is a differentiable vector point function and φ is a differentiable scalar point function then prove that div (φA) = ( gradφ ).A + φ (div A).
Solution:
Given
A is a differentiable vector point function and φ is a differentiable scalar point function
curl (φA)=∇×(φA) =i×\(\frac{\partial}{\partial x}\)(φA)+j×\(\frac{\partial}{\partial y}\)(φA)+k× \(\frac{\partial}{\partial y}\) (φA)
⇒ \({div}(\varphi \mathbf{A})=\nabla \cdot(\varphi \mathbf{A})=\mathbf{i} \cdot \frac{\partial}{\partial x}(\varphi \mathbf{A})+\mathbf{j} \cdot \frac{\partial}{\partial y}(\varphi \mathbf{A})+\mathbf{k} \cdot \frac{\partial}{\partial z}(\varphi \mathbf{A})\)
⇒ \(\mathbf{i} \cdot\left[\frac{\partial \varphi}{\partial x} \mathbf{A}+\varphi \frac{\partial \mathbf{A}}{\partial x}\right]+\mathbf{j} \cdot\left[\frac{\partial \varphi}{\partial y} \mathbf{A}+\varphi \frac{\partial \mathbf{A}}{\partial y}\right]+\mathbf{k} \cdot\left[\frac{\partial \varphi}{\partial z} \mathbf{A}+\varphi \frac{\partial \mathbf{A}}{\partial z}\right]\)
⇒ \(\mathbf{i} \frac{\partial \varphi}{\partial x} \cdot \mathbf{A}+\varphi\left(\mathbf{i} \cdot \frac{\partial \mathbf{A}}{\partial x}\right)+\mathbf{j} \frac{\partial \varphi}{\partial y} \cdot \mathbf{A}+\varphi\left(\mathbf{j} \cdot \frac{\partial \mathbf{A}}{\partial y}\right)+\mathbf{k} \frac{\partial \varphi}{\partial z} \cdot \mathbf{A}+\varphi\left(\mathbf{k} \cdot \frac{\partial \mathbf{A}}{\partial z}\right)\)
⇒ \(\left[\mathbf{i} \frac{\partial \varphi}{\partial x}+\mathbf{J} \frac{\partial \varphi}{\partial y}+\mathbf{k} \frac{\partial \varphi}{\partial z}\right] \cdot \mathbf{A}+\varphi\left[\mathbf{i} \cdot \frac{\partial \mathbf{A}}{\partial x}+\mathbf{j} \cdot \frac{\partial \mathbf{A}}{\partial y}+\mathbf{k} \cdot \frac{\partial \mathbf{A}}{\partial z}\right]\)
⇒ \((\nabla \varphi) \cdot \mathbf{A}+\varphi(\nabla \cdot \mathbf{A})=({grad} \varphi) \cdot \mathbf{A}+\varphi({div} \mathbf{A})\)
103. If A is a differentiable vector point function and φ is a differentiable scalar point function then prove that curl (φA) = (grad φ)x A + φ ( curl A).
Solution:
⇒ curl (φA)=∇ × (φA)\(=\mathbf{i} \times \frac{\partial}{\partial x}(\varphi \mathbf{A})+\mathbf{j} \times \frac{\partial}{\partial y}(\varphi \mathbf{A})+\mathbf{k} \times \frac{\partial}{\partial z}(\varphi \mathbf{A})\)
⇒ \(\mathbf{i} \times\left[\frac{\partial \varphi}{\partial x} \mathbf{A}+\varphi \frac{\partial \mathbf{A}}{\partial x}\right]+\mathbf{j} \times\left[\frac{\partial \varphi}{\partial y} \mathbf{A}+\varphi \frac{\partial \mathbf{A}}{\partial y}\right]+\mathbf{k} \times\left[\frac{\partial \varphi}{\partial z} \mathbf{A}+\varphi \frac{\partial \mathbf{A}}{\partial z}\right]\)
⇒ \(\mathbf{i} \frac{\partial \varphi}{\partial x} \times \mathbf{A}+\varphi\left(\mathbf{i} \times \frac{\partial \mathbf{A}}{\partial x}\right)+\mathbf{j} \frac{\partial \varphi}{\partial y} \times \mathbf{A}+\varphi\left(\mathbf{j} \times \frac{\partial \mathbf{A}}{\partial y}\right)+\mathbf{k} \frac{\partial \varphi}{\partial z} \times \mathbf{A}+\varphi\left(\mathbf{k} \times \frac{\partial \mathbf{A}}{\partial z}\right)\)
⇒ \(\left[\mathbf{i} \frac{\partial \varphi}{\partial x}+\mathbf{j} \frac{\partial \varphi}{\partial y}+\mathbf{k} \frac{\partial \varphi}{\partial z}\right] \times \mathbf{A}+\varphi\left[\mathbf{i} \times \frac{\partial \mathbf{A}}{\partial x}+\mathbf{j} \times \frac{\partial \mathbf{A}}{\partial y}+\mathbf{k} \times \frac{\partial \mathbf{A}}{\partial z}\right]\)
⇒ \((\nabla \varphi) \times \mathbf{A}+\varphi(\nabla \times \mathbf{A})=({grad} \varphi) \times \mathbf{A}+\varphi({curl} \mathbf{A})\)
104. If A and B are two differentiable vector point functions then prove that
Solution:
grad (A.B) = (B.∇) A + (A.∇) B + B x (curl A) + A x (curl B)
⇒ \(\mathbf{A} \times({curl} \mathbf{B})=\mathbf{A} \times(\nabla \times \mathbf{B})=\mathbf{A} \times\left(\mathbf{i} \times \frac{\partial \mathbf{B}}{\partial x}+\mathbf{j} \times \frac{\partial \mathbf{B}}{\partial y}+\mathbf{k} \times \frac{\partial \mathbf{B}}{\partial z}\right)\)
⇒ \(\mathbf{A} \times\left(\mathbf{i} \times \frac{\partial \mathbf{B}}{\partial x}\right)+\mathbf{A} \times\left(\mathbf{j} \times \frac{\partial \mathbf{B}}{\partial y}\right)+\mathbf{A} \times\left(\mathbf{k} \times \frac{\partial \mathbf{B}}{\partial z}\right)\)
⇒ \(\left(\mathbf{A} \cdot \frac{\partial \mathbf{B}}{\partial x}\right) \mathbf{i}-(\mathbf{A} \cdot \mathbf{i}) \frac{\partial \mathbf{B}}{\partial x}+\left(\mathbf{A} \cdot \frac{\partial \mathbf{B}}{\partial y}\right) \mathbf{j}-(\mathbf{A} \cdot \mathbf{j}) \frac{\partial \mathbf{B}}{\partial y}+\left(\mathbf{A} \cdot \frac{\partial \mathbf{B}}{\partial z}\right) \mathbf{k}-(\mathbf{A} \cdot \mathbf{k}) \frac{\partial \mathbf{B}}{\partial z}\)
⇒ \(\mathbf{i}\left(\mathbf{A} \cdot \frac{\partial \mathbf{B}}{\partial x}\right)+\mathbf{j}\left(\mathbf{A} \cdot \frac{\partial \mathbf{B}}{\partial y}\right)+\mathbf{k}\left(\mathbf{A} \cdot \frac{\partial \mathbf{B}}{\partial z}\right)-\left[(\mathbf{A} \cdot \mathbf{i}) \frac{\partial \mathbf{B}}{\partial x}+(\mathbf{A} \cdot \mathbf{j}) \frac{\partial \mathbf{B}}{\partial y}+(\mathbf{A} \cdot \mathbf{k}) \frac{\partial \mathbf{B}}{\partial z}\right]\)
⇒ \(\mathbf{i}\left(\mathbf{A} \cdot \frac{\partial \mathbf{B}}{\partial x}\right)+\mathbf{j}\left(\mathbf{A} \cdot \frac{\partial \mathbf{B}}{\partial y}\right)+\mathbf{k}\left(\mathbf{A} \cdot \frac{\partial \mathbf{B}}{\partial z}\right)-(\mathbf{A} \cdot \nabla) \mathbf{B}\)
⇒ \(\text { Similarly } \mathbf{B} \times({curl} \mathbf{A})=\mathbf{i}\left(\mathbf{B} \cdot \frac{\partial \mathbf{A}}{\partial x}\right)+\mathbf{j}\left(\mathbf{B} \cdot \frac{\partial \mathbf{A}}{\partial y}\right)+\mathbf{k}\left(\mathbf{B} \cdot \frac{\partial \mathbf{A}}{\partial z}\right)-(\mathbf{B} \cdot \nabla) \mathbf{A}\)
∴ \(\mathbf{A} \times({curl} \mathbf{B})+\mathbf{B} \times({curl} \mathbf{A})\)
⇒ \(\mathbf{i}\left(\mathbf{A} \cdot \frac{\partial \mathbf{B}}{\partial x}+\mathbf{B} \cdot \frac{\partial \mathbf{A}}{\partial x}\right)+\mathbf{j}\left(\mathbf{A} \cdot \frac{\partial \mathbf{B}}{\partial y}+\mathbf{B} \cdot \frac{\partial \mathbf{A}}{\partial y}\right)+\mathbf{k}\left(\mathbf{A} \cdot \frac{\partial \mathbf{B}}{\partial z}+\mathbf{B} \cdot \frac{\partial \mathbf{A}}{\partial z}\right)-(\mathbf{A} \cdot \nabla) \mathbf{B}-(\mathbf{B} \cdot \nabla) \mathbf{A}\)
⇒ \(\mathbf{A} \times({curl} \mathbf{B})+\mathbf{B} \times({curl} \mathbf{A})+(\mathbf{A} \cdot \nabla) \mathbf{B}+(\mathbf{B} \cdot \nabla) \mathbf{A}\)
⇒ \(\mathbf{i} \frac{\partial}{\partial x}(\mathbf{A} \cdot \mathbf{B})+\mathbf{j} \frac{\partial}{\partial y}(\mathbf{A} \cdot \mathbf{B})+\mathbf{k} \frac{\partial}{\partial z}(\mathbf{A} \cdot \mathbf{B})=\nabla(\mathbf{A} \cdot \mathbf{B})={grad}(\mathbf{A} \cdot \mathbf{B})\)
Understanding Gradient And Divergence Through Solved Problems
105. If A and B are two differential vector point functions then prove that div(A×B)= B.(curl A)− A.(curl B)
Solution:
div (A×B) = \(\nabla \cdot(\mathbf{A} \times \mathbf{B})=\mathbf{i} \cdot \frac{\partial}{\partial x}(\mathbf{A} \times \mathbf{B})+\mathbf{j} \cdot \frac{\partial}{\partial y}(\mathbf{A} \times \mathbf{B})+\mathbf{k} \cdot \frac{\partial}{\partial z}(\mathbf{A} \times \mathbf{B})\)
⇒ \(\mathbf{i} \cdot\left(\frac{\partial \mathbf{A}}{\partial x} \times \mathbf{B}+\mathbf{A} \times \frac{\partial \mathbf{B}}{\partial x}\right)+\mathbf{j} \cdot\left(\frac{\partial \mathbf{A}}{\partial y} \times \mathbf{B}+\mathbf{A} \times \frac{\partial \mathbf{B}}{\partial y}\right)+\mathbf{k} \cdot\left(\frac{\partial \mathbf{A}}{\partial z} \times \mathbf{B}+\mathbf{A} \times \frac{\partial \mathbf{B}}{\partial z}\right)\)
⇒ \(\left(\mathbf{i} \cdot \frac{\partial \mathbf{A}}{\partial x} \times \mathbf{B}\right)+\mathbf{i} \cdot\left(\mathbf{A} \times \frac{\partial \mathbf{B}}{\partial x}\right)+\left(\mathbf{j} \cdot \frac{\partial \mathbf{A}}{\partial y} \times \mathbf{B}\right)+\mathbf{j} \cdot\left(\mathbf{A} \times \frac{\partial \mathbf{B}}{\partial y}\right)+\left(\mathbf{k} \cdot \frac{\partial \mathbf{A}}{\partial z} \times \mathbf{B}\right)+\mathbf{k} \cdot\left(\mathbf{A} \times \frac{\partial \mathbf{B}}{\partial z}\right)\)
⇒ \(\left(\mathbf{i} \times \frac{\partial \mathbf{A}}{\partial x}\right) \cdot \mathbf{B}+\left(\mathbf{j} \times \frac{\partial \mathbf{A}}{\partial y}\right) \cdot \mathbf{B}+\left(\mathbf{k} \times \frac{\partial \mathbf{A}}{\partial z}\right) \cdot \mathbf{B}-\mathbf{i} \cdot\left(\frac{\partial \mathbf{B}}{\partial x} \times \mathbf{A}\right)-\mathbf{j} \cdot\left(\frac{\partial \mathbf{B}}{\partial y} \times \mathbf{A}\right)-\mathbf{k} \cdot\left(\frac{\partial \mathbf{B}}{\partial z} \times \mathbf{A}\right)\)
⇒ \(\left(\mathbf{i} \times \frac{\partial \mathbf{A}}{\partial x}+\mathbf{j} \times \frac{\partial \mathbf{A}}{\partial y}+\mathbf{k} \times \frac{\partial \mathbf{A}}{\partial z}\right) \cdot \mathbf{B}-\left[\left(\mathbf{I} \times \frac{\partial \mathbf{B}}{\partial x}\right) \cdot \mathbf{A}+\left(\mathbf{j} \times \frac{\partial \mathbf{B}}{\partial y}\right) \cdot \mathbf{A}+\left(\mathbf{k} \times \frac{\partial \mathbf{B}}{\partial z}\right) \cdot \mathbf{A}\right]\)
⇒ \((\nabla \times \mathbf{A}) \cdot \mathbf{B}-\left[\mathbf{i} \times \frac{\partial \mathbf{B}}{\partial x}+\mathbf{j} \times \frac{\partial \mathbf{B}}{\partial y}+\mathbf{k} \times \frac{\partial \mathbf{B}}{\partial z}\right] \cdot \mathbf{A}=(\nabla \times \mathbf{A}) \cdot \mathbf{B}-(\nabla \times \mathbf{B}) \cdot \mathbf{A}\)
= B. (curl A) – A. (curl B).
106. If A and B are irrotational vector point functions then A×B is solenoidal.
Solution:
A, B are irrotational curl A=0, curl B
div(A×B)=B. (curl A)-A. (curl B)=B.0-A.0.
∴ A×B is solenoidal.
107. If A and B are two differentiable vector point functions then prove that.
Solution:
⇒ \({curl}(\mathbf{A} \times \mathbf{B})=\nabla \times(\mathbf{A} \times \mathbf{B})=\mathbf{i} \times \frac{\partial}{\partial x}(\mathbf{A} \times \mathbf{B})+\mathbf{j} \times \frac{\partial}{\partial y}(\mathbf{A} \times \mathbf{B})+\mathbf{k} \times \frac{\partial}{\partial z}(\mathbf{A} \times \mathbf{B})\)
⇒ \(\mathbf{i} \times\left(\frac{\partial \mathbf{A}}{\partial x} \times \mathbf{B}+\mathbf{A} \times \frac{\partial \mathbf{B}}{\partial x}\right)+\mathbf{j} \times\left(\frac{\partial \mathbf{A}}{\partial y} \times \mathbf{B}+\mathbf{A} \times \frac{\partial \mathbf{B}}{\partial y}\right)+\mathbf{k} \times\left(\frac{\partial \mathbf{A}}{\partial z} \times \mathbf{B}+\mathbf{A} \times \frac{\partial \mathbf{B}}{\partial z}\right)\)
⇒ \(\mathbf{i} \times\left(\frac{\partial \mathbf{A}}{\partial x} \times \mathbf{B}\right)+\mathbf{i} \times\left(\mathbf{A} \times \frac{\partial \mathbf{B}}{\partial x}\right)+\mathbf{j} \times\left(\frac{\partial \mathbf{A}}{\partial y} \times \mathbf{B}\right)\)
= \(+\mathbf{j} \times\left(\mathbf{A} \times \frac{\partial \mathbf{B}}{\partial y}\right)+\mathbf{k} \times\left(\frac{\partial \mathbf{A}}{\partial z} \times \mathbf{B}\right)+\mathbf{k} \times\left(\mathbf{A} \times \frac{\partial \mathbf{B}}{\partial z}\right)\)
⇒ \((\mathbf{i} \cdot \mathbf{B}) \frac{\partial \mathbf{A}}{\partial x}-\left(\mathbf{i} \cdot \frac{\partial \mathbf{A}}{\partial x}\right) \mathbf{B}+\left(\mathbf{i} \cdot \frac{\partial \mathbf{B}}{\partial x}\right) \mathbf{A}-(\mathbf{i} \cdot \mathbf{A}) \frac{\partial \mathbf{B}}{\partial x}+(\mathbf{j} \cdot \mathbf{B}) \frac{\partial \mathbf{A}}{\partial y}-\left(\mathbf{j} \cdot \frac{\partial \mathbf{A}}{\partial y}\right) \mathbf{B}\)
⇒ \(+\left(\mathbf{j} \cdot \frac{\partial \mathbf{B}}{\partial y}\right) \mathbf{A}-(\mathbf{j} \cdot \mathbf{A}) \frac{\partial \mathbf{B}}{\partial y}+(\mathbf{k} \cdot \mathbf{B}) \frac{\partial \mathbf{A}}{\partial z}-\left(\mathbf{k} \cdot \frac{\partial \mathbf{A}}{\partial z}\right) \mathbf{B}+\left(\mathbf{k} \cdot \frac{\partial \mathbf{B}}{\partial z}\right) \mathbf{A}-(\mathbf{k} \cdot \mathbf{A}) \frac{\partial \mathbf{B}}{\partial z}\)
⇒ \(\left[(\mathbf{B} \cdot \mathbf{i}) \frac{\partial \mathbf{A}}{\partial x}+(\mathbf{B} \cdot \mathbf{j}) \frac{\partial \mathbf{A}}{\partial y}+(\mathbf{B} \cdot \mathbf{k}) \frac{\partial \mathbf{A}}{\partial z}\right]-\mathbf{B}\left[\mathbf{i} \cdot \frac{\partial \mathbf{A}}{\partial x}+\mathbf{j} \cdot \frac{\partial \mathbf{A}}{\partial y}+\mathbf{k} \cdot \frac{\partial \mathbf{A}}{\partial z}\right]\)
⇒ \(+\mathbf{A}\left[\mathbf{i} \cdot \frac{\partial \mathbf{B}}{\partial x}+\mathbf{j} \cdot \frac{\partial \mathbf{B}}{\partial y}+\mathbf{k} \cdot \frac{\partial \mathbf{B}}{\partial z}\right]-\left[(\mathbf{A} \cdot \mathbf{i}) \frac{\partial \mathbf{B}}{\partial x}+(\mathbf{A} \cdot \mathbf{j}) \frac{\partial \mathbf{B}}{\partial y}+(\mathbf{A} \cdot \mathbf{k}) \frac{\partial \mathbf{B}}{\partial z}\right]\)
⇒ \((\mathbf{B} \cdot \nabla) \mathbf{A}-\mathbf{B}(\nabla \cdot \mathbf{A})+\mathbf{A}(\nabla \cdot \mathbf{B})-(\mathbf{A} \cdot \nabla) \mathbf{B}\)
⇒ \(\mathbf{A}({div} \mathbf{B})-\mathbf{B}({div} \mathbf{A})+(\mathbf{B} \cdot \nabla) \mathbf{A}-(\mathbf{A} \cdot \nabla) \mathbf{B}\)
108. If φ is a differentiable scalar function then prove that
Solution:
div grad φ=∇.∇φ\(=\frac{\partial^2 \varphi}{\partial x^2}+\frac{\partial^2 \varphi}{\partial y^2}+\frac{\partial^2 \varphi}{\partial z^2}\)
∇.∇φ=∇.\(\left(\mathbf{i} \frac{\partial \varphi}{\partial x}+\mathbf{j} \frac{\partial \varphi}{\partial y}+\mathbf{k} \frac{\partial \varphi}{\partial z}\right)\)
⇒ \(\frac{\partial}{\partial x}\left(\frac{\partial \varphi}{\partial x}\right)+\frac{\partial}{\partial y}\left(\frac{\partial \varphi}{\partial y}\right)+\frac{\partial}{\partial z}\left(\frac{\partial \varphi}{\partial z}\right)\)
= \(\frac{\partial^2 \varphi}{\partial x^2}+\frac{\partial^2 \varphi}{\partial y^2}+\frac{\partial^2 \varphi}{\partial z^2}\)
109. If φ is a differentiable scalar point function then the prove that curl (grad φ)=0
Solution:
⇒ \({grad} \varphi=\nabla \varphi=\mathbf{i} \frac{\partial \varphi}{\partial x}+\mathbf{j} \frac{\partial \varphi}{\partial y}+\mathbf{k} \frac{\partial \varphi}{\partial z}\)
⇒ \({curl}({grad} \varphi)=\nabla \times(\nabla \varphi)=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
\frac{\partial \varphi}{\partial x} & \frac{\partial \varphi}{\partial y} & \frac{\partial \varphi}{\partial z}
\end{array}\right|\)
⇒ \(\mathbf{I}\left(\frac{\partial^2 \varphi}{\partial y \partial z}-\frac{\partial^2 \varphi}{\partial y \partial z}\right)-\mathbf{J}\left(\frac{\partial^2 \varphi}{\partial x \partial z}-\frac{\partial^2 \varphi}{\partial z \partial x}\right)+\mathbf{k}\left(\frac{\partial^2 \varphi}{\partial x \partial y}-\frac{\partial^2 \varphi}{\partial y \partial x}\right)=\mathbf{0}\)
110. If φ is a differentiable scalar point function then this proves that grad φ is irrotational.
Solution:
φ is a differentiable scalar point function ⇒ curl (grad φ)=0
⇒ grad φ is irrotational.
Importance Of Divergence In Vector Calculus
111. If F is a differentiable vector point function then the prove that div (curl f)=0
Solution:
Let F = \(F_1 \mathbf{i}+F_2 \mathbf{j}+F_3 \mathbf{k}\)
⇒ \({curl} \mathbf{F}=\nabla \times \mathbf{F}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
F_1 & F_2 & F_3
\end{array}\right|=\mathbf{i}\left(\frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z}\right)-\mathbf{J}\left(\frac{\partial F_3}{\partial x}-\frac{\partial F_1}{\partial z}\right)+\mathbf{k}\left(\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right)\)
⇒ div (curl F) = \(\frac{\partial}{\partial x} \cdot\left(\frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z}\right)-\frac{\partial}{\partial y}\left(\frac{\partial F_3}{\partial x}-\frac{\partial F_1}{\partial z}\right)+\frac{\partial}{\partial z}\left(\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right)\)
⇒ \(\frac{\partial^2 F_3}{\partial x \partial y}-\frac{\partial^2 F_2}{\partial x \partial z}-\frac{\partial^2 F_3}{\partial y \partial x}+\frac{\partial^2 F_1}{\partial y \partial z}+\frac{\partial^2 F_2}{\partial z \partial x}-\frac{\partial^2 F_1}{\partial z \partial y}=0\)
Gradient And Divergence Exercise Problems For Beginners
112. If F is a differentiable vector point function then prove that curl F is solenoidal.
Solution: Fis differentiable vector point function ⇒ div (curl F)=0
⇒ curl F is solenoidal.
113. If F is a differentiable vector point function then prove that curl (curl F)=grad (div F)-∇2F.
Solution:
Curl (curl F) = \(\nabla \times(\nabla \times \mathbf{F})=\mathbf{i} \times \frac{\partial}{\partial x}(\nabla \times \mathbf{F})+\mathbf{j} \times \frac{\partial}{\partial y}(\nabla \times \mathbf{F})+\mathbf{k} \times \frac{\partial}{\partial z}(\nabla \times \mathbf{F})\)
⇒ \(\mathbf{i} \times \frac{\partial}{\partial x}\left(\mathbf{i} \times \frac{\partial \mathbf{F}}{\partial x}+\mathbf{j} \times \frac{\partial \mathbf{F}}{\partial y}+\mathbf{k} \times \frac{\partial \mathbf{F}}{\partial z}\right)\)
+\(\mathbf{j} \times \frac{\partial}{\partial y}\left(\mathbf{i} \times \frac{\partial \mathbf{F}}{\partial x}+\mathbf{j} \times \frac{\partial \mathbf{F}}{\partial y}+\mathbf{k} \times \frac{\partial \mathbf{F}}{\partial z}\right)\)
⇒ \(+\mathbf{k} \times \frac{\partial}{\partial z}\left(\mathbf{i} \times \frac{\partial \mathbf{F}}{\partial x}+\mathbf{j} \times \frac{\partial \mathbf{F}}{\partial y}+\mathbf{k} \times \frac{\partial \mathbf{F}}{\partial z}\right)\)
⇒ \(\mathbf{i} \times\left(\mathbf{i} \times \frac{\partial^2 \mathbf{F}}{\partial x^2}+\mathbf{j} \times \frac{\partial^2 \mathbf{F}}{\partial x \partial y}+\mathbf{k} \times \frac{\partial^2 \mathbf{F}}{\partial x \partial z}\right)\)
+ \(\mathbf{j} \times\left(\mathbf{i} \times \frac{\partial^2 \mathbf{F}}{\partial y \partial x}+\mathbf{j} \times \frac{\partial^2 \mathbf{F}}{\partial y^2}+\mathbf{k} \times \frac{\partial^2 \mathbf{F}}{\partial y \partial z}\right)\)
⇒ \(+\mathbf{k} \times\left(\mathbf{i} \times \frac{\partial^2 \mathbf{F}}{\partial z \partial x}+\mathbf{j} \times \frac{\partial^2 \mathbf{F}}{\partial z \partial y}+\mathbf{k} \times \frac{\partial^2 \mathbf{F}}{\partial z^2}\right)\)
⇒ \(\left(\mathbf{i} \cdot \frac{\partial^2 \mathbf{F}}{\partial x^2}\right) \mathbf{i}-(\mathbf{i} \cdot \mathbf{i}) \frac{\partial^2 \mathbf{F}}{\partial x}+\left(\mathbf{i} \cdot \frac{\partial^2 \mathbf{F}}{\partial x \partial y}\right) \mathbf{j}-(\mathbf{i} \cdot \mathbf{j}) \frac{\partial^2 \mathbf{F}}{\partial x \partial y}+\left(\mathbf{i} \cdot \frac{\partial^2 \mathbf{F}}{\partial x \partial z}\right) \mathbf{k}-(\mathbf{i} \cdot \mathbf{k}) \frac{\partial^2 \mathbf{F}}{\partial x \partial z}\)
⇒ \(+\left(\mathbf{j} \cdot \frac{\partial^2 \mathbf{F}}{\partial y \partial x}\right) \mathbf{i}-(\mathbf{j} \cdot \mathbf{i}) \frac{\partial^2 \mathbf{F}}{\partial y \partial x}+\left(\mathbf{j} \cdot \frac{\partial^2 \mathbf{F}}{\partial y^2}\right) \mathbf{j}-(\mathbf{j} \cdot \mathbf{j}) \frac{\partial^2 \mathbf{F}}{\partial y^2}+\left(\mathbf{j} \cdot \frac{\partial^2 \mathbf{F}}{\partial y \partial z}\right) \mathbf{k}\)
⇒ \(-(\mathbf{J} \cdot \mathbf{k}) \frac{\partial^2 \mathbf{F}}{\partial y \partial z}+\left(\mathbf{k} \cdot \frac{\partial^2 \mathbf{F}}{\partial z \partial x}\right) \mathbf{i}-(\mathbf{k} \cdot \mathbf{i}) \frac{\partial^2 \mathbf{F}}{\partial z \partial x}+\left(\mathbf{k} \cdot \frac{\partial^2 \mathbf{F}}{\partial z \partial y}\right) \mathbf{j}-(\mathbf{k} \cdot \mathbf{j}) \frac{\partial^2 \mathbf{F}}{\partial z \partial y}+\left(\mathbf{k} \cdot \frac{\partial^2 \mathbf{F}}{\partial z^2}\right) \mathbf{k}-(\mathbf{k} \cdot \mathbf{k}) \frac{\partial^2 \mathbf{F}}{\partial z^2}\)
⇒ \(\mathbf{i} \frac{\partial}{\partial x}\left(\mathbf{i} \cdot \frac{\partial \mathbf{F}}{\partial x}+\mathbf{j} \cdot \frac{\partial \mathbf{F}}{\partial y}+\mathbf{k} \cdot \frac{\partial \mathbf{F}}{\partial z}\right)+\mathbf{j} \frac{\partial}{\partial y}\left(\mathbf{i} \cdot \frac{\partial \mathbf{F}}{\partial x}+\mathbf{j} \cdot \frac{\partial \mathbf{F}}{\partial y}+\mathbf{k} \cdot \frac{\partial \mathbf{F}}{\partial z}\right)\)
⇒ \(+\mathbf{k} \frac{\partial}{\partial z}\left(\mathbf{i} \cdot \frac{\partial \mathbf{F}}{\partial x}+\mathbf{j} \cdot \frac{\partial \mathbf{F}}{\partial y}+\mathbf{k} \cdot \frac{\partial \mathbf{F}}{\partial z}\right)-\left(\frac{\partial^2 \mathbf{F}}{\partial x^2}+\frac{\partial^2 \mathbf{F}}{\partial y^2}+\frac{\partial^2 \mathbf{F}}{\partial z^2}\right)\)
⇒ \(\mathbf{i} \frac{\partial}{\partial x}(\nabla \cdot \mathbf{F})+\mathbf{j} \frac{\partial}{\partial x}(\nabla \cdot \mathbf{F})+\mathbf{k} \frac{\partial}{\partial z}(\nabla \cdot \mathbf{F})-\nabla^2 \mathbf{F}=\nabla(\nabla \cdot \mathbf{F})-\nabla^2 \mathbf{F}={grad}({div} \mathbf{F})-\nabla^2 \mathbf{F}\)
114.Show that ∇2 (rn)=n(n+1)rn-2
Solution:
⇒ \(\nabla^2\left(r^n\right)=\frac{\partial^2}{\partial x^2}\left(r^n\right)+\frac{\partial^2}{\partial y^2}\left(r^n\right)+\frac{\partial^2}{\partial z^2}\left(r^n\right)\)
⇒ \(\frac{\partial}{\partial x}\left[n r^{n-1} x / r\right]+\frac{\partial}{\partial y}\left[n r^{n-1} y / r\right]+\frac{\partial}{\partial z}\left[n r^{n-1} z / r\right]\)
⇒ \(n r^{n-2}+n(n-2) x \cdot r^{n-3} x / r+n r^{n-2}+n(n-2) y r^{n-3} y / r+n r^{n-2}\)
⇒ \(+n(n-2) z \cdot r^{n-3} z / r\)
⇒ \(3 n r^{n-2}+n(n-2) r^{n-4}\left(x^2+y^2+z^2\right)=3 n r^{n-2}+n(n-2) r^{n-2}\)
⇒ \(n(3+n-2) r^{n-2}=n(n+1) r^{n-2}\)
115. Show that ∇2 \(\left(\frac{1}{r}\right)\)=0
Solution:
⇒ \(\nabla^2\left(\frac{1}{r}\right)=\frac{\partial^2}{\partial x^2}\left(\frac{1}{r}\right)+\frac{\partial^2}{\partial y^2}\left(\frac{1}{r}\right)+\frac{\partial^2}{\partial z^2}\left(\frac{1}{r}\right)=\frac{\partial}{\partial x}\left\{-\frac{1}{r^2} \frac{x}{r}\right\}+\frac{\partial}{\partial y}\left\{-\frac{1}{r^2} \frac{y}{r}\right\}+\frac{\partial}{\partial z}\left\{-\frac{1}{r^2} \frac{z}{r}\right\}\)
⇒ \(\frac{r^3(-1)+x 3 r^2\left(\frac{x}{r}\right)}{r^6}+\frac{r^3(-1)+y 3 r^2\left(\frac{y}{r}\right)}{r^6}+\frac{r^3(-1)+z 3 r^2\left(\frac{z}{r}\right)}{r^6}\)
⇒ \(-\frac{1}{r^3}+\frac{3 x^2}{r^5}-\frac{1}{r^3}+\frac{3 y^2}{r^5}-\frac{1}{r^3}+\frac{3 z^2}{r^5}=-\frac{3}{r^3}+\frac{3}{r^5}\left(x^2+y^2+z^2\right)=-\frac{3}{r^3}+\frac{3}{r^3}=0\)
116. Prove that ∇2 (log r)=\(\frac{1}{r^2}\)
Solution:
⇒ \(\nabla^2(\log r)=\frac{\partial^2}{\partial x^2}(\log r)+\frac{\partial^2}{\partial y^2}(\log r)+\frac{\partial^2}{\partial z^2}(\log r)\)
⇒ \(\frac{\partial}{\partial x}\left\{\frac{1}{r} \cdot \frac{x}{r}\right\}+\frac{\partial}{\partial y}\left\{\frac{1}{r} \cdot \frac{y}{r}\right\}+\frac{\partial}{\partial z}\left\{\frac{1}{2} \cdot \frac{z}{r}\right\}\)
⇒ \(\frac{r^2 1-x 2 r\left(\frac{x}{r}\right)}{r^4}+\frac{r^2-y 2 r\left(\frac{y}{r}\right)}{r^4}+\frac{r^2-z 2 r\left(\frac{z}{x}\right)}{r^4}=\frac{3 r^2-2 x^2-2 y^2-2 z^2}{r^4}=\frac{3 r^2-2 r^2}{r^4}=\frac{1}{r^2}\)
117. Show that ∇2 \(\left(\frac{x}{r^3}\right)\)=0.
Solution:
⇒ \(\nabla^2\left(\frac{x}{r^3}\right)=\frac{\partial^2}{\partial x^2}\left(\frac{x}{r^3}\right)+\frac{\partial^2}{\partial y^2}\left(\frac{x}{r^3}\right)+\frac{\partial^2}{\partial z^2}\left(\frac{x}{r^3}\right)\)
⇒ \(\frac{\partial}{\partial x}\left[\frac{r^3-x \cdot 3 r^2 \cdot x / r}{r^6}\right]+\frac{\partial}{\partial y}\left[\frac{-3 x}{r^4} \cdot \frac{y}{r}\right]+\frac{\partial}{\partial z}\left[\frac{-3 x}{r^4} \cdot \frac{z}{r}\right]\)
⇒ \(\frac{\partial}{\partial x}\left[\frac{1}{r^3}-\frac{3 x^2}{r^5}\right]+\frac{\partial}{\partial y}\left[\frac{-3 x y}{r^5}\right]+\frac{\partial}{\partial z}\left[\frac{-3 x z}{r^5}\right]\)
⇒ \(-\frac{3}{r^4} \cdot \frac{x}{r}-\frac{r^5(6 x)-3 x^2 \cdot 5 r^4 x / r}{r^{10}}-\frac{r^5(3 x)-3 x y \cdot 5 r^4 \cdot y / r}{r^{10}}-\frac{r^5(3 x)-3 x z \cdot 5 r^4 \cdot z / r}{r^{10}}\)
⇒ \(-\frac{3 x}{r^5}-\frac{6 x}{r^5}+\frac{15 x^3}{r^7}-\frac{3 x}{r^5}+\frac{15 x y^2}{r^7}-\frac{3 x}{r^5}+\frac{15 x z^2}{r^7}\)
⇒ \(\frac{-15 x}{r^5}+\frac{15 x\left(x^2+y^2+z^2\right)}{r^7}=\frac{-15 x}{r^5}+\frac{15 x}{r^5}=0\)
Step-By-Step Gradient Differentiation Problems
118. Show that ∇2 \(\left(\frac{r}{r^3}\right)\)
Solution:
⇒ \(\nabla^2\left(\frac{\boldsymbol{r}}{r^3}\right)=\frac{\partial^2}{\partial x^2}\left(\frac{x}{r^3}\right)+\frac{\partial^2}{\partial y^2}\left(\frac{y}{r^3}\right)+\frac{\partial^2}{\partial z^2}\left(\frac{z}{r^3}\right)\)
⇒ \(\frac{r^3-x \cdot 3 r^2 \cdot x / r}{r^6}+\frac{r^3-y \cdot 3 r^2 \cdot y / r}{r^6}+\frac{r^3-z \cdot 3 r^2 \cdot z / r}{r^6}\)
⇒ \(\frac{3 r^3-3 r\left(x^2+y^2+z^2\right)}{r^6}=\frac{3 r^3-3 r^3}{r^6}=0\)
119. Show that ∇2 f(r) =\(=\frac{d^2 f}{\partial r^2}+\frac{2}{r} \frac{d f}{d r}\)
Solution:
⇒ \(\nabla^2 f(r)=\nabla \cdot\{\nabla f(r)\}={div}\{{grad} f(r)\}={div} .\left\{f^{\prime}(r){grad} r\right\}={div}\left\{\frac{1}{r} f^{\prime}(r) \mathbf{r}\right\}\)
⇒ \(\frac{1}{r} f^{\prime}(r){div} \mathbf{r}+\mathbf{r} \cdot{grad}\left\{\frac{1}{r} f^{\prime}(r)\right\}=\frac{3}{r} f^{\prime}(r)+\mathbf{r} \cdot\left[\frac{d}{d r}\left\{\frac{1}{r} f^{\prime}(r)\right\}{grad} r\right]\)
⇒ \(\frac{3}{r} f^{\prime}(r)+\mathbf{r} \cdot\left[\left\{-\frac{1}{r^2} f^{\prime}(r)+\frac{1}{r} f^{\prime \prime}(r)\right\} \frac{1}{r} \mathbf{r}\right]=\frac{3}{r} f^{\prime}(r)+\left[\frac{1}{r}\left\{-\frac{1}{r^2} f^{\prime}(r)+\frac{1}{r} f^{\prime \prime \prime}(r)\right\}\right](\mathbf{r} \cdot \mathbf{r})\)
⇒ \(\frac{3}{r} f^{\prime}(r)+\left[\frac{1}{r}\left\{-\frac{1}{r^2} f^{\prime}(r)+\frac{1}{r} f^{\prime \prime}(r)\right\}\right] r^2=\frac{3}{r} f^{\prime}(r)-\frac{1}{r} f^{\prime}(r)+f^{\prime \prime}(r)=f^{\prime \prime}(r)+\frac{2}{r} f^{\prime}(r)\)
120. Show that ∇\(\left[r \nabla\left(\frac{1}{r^3}\right)\right]\)\(=\frac{3}{r^4}\)
Solution:
⇒ \(\nabla\left(\frac{i}{r^3}\right)={grad} r^{-3}=\frac{\partial}{\partial x}\left(r^{-3}\right) \mathbf{i}+\frac{\partial}{\partial y}\left(r^{-3}\right) \mathbf{j}+\frac{\partial}{\partial z}+\left(r^{-3}\right) \mathbf{k}\)
⇒ \(-3 r^{-4}\left[\frac{\partial r}{\partial x} \mathbf{i}+\frac{\partial r}{\partial y} \mathbf{j}+\frac{\partial r}{\partial z} \mathbf{k}\right]=-3 r^{-4}\left[\frac{x}{r} \mathbf{i}+\frac{y}{r} \mathbf{j}+\frac{z}{r} \mathbf{k}\right]=-3 r^{-5} \mathbf{r}\)
∴ \(r \nabla\left(\frac{1}{r^3}\right)=-3 r^{-4}(x \mathbf{i}+y \mathbf{j}+z \mathbf{k})\)
∴ \(\nabla \cdot\left[r \nabla\left(\frac{1}{r^3}\right)\right]=\frac{\partial}{\partial x}\left(-3 r^{-4} x\right)+\frac{\partial}{\partial y}\left(-3 r^{-4} y\right)+\frac{\partial}{\partial z}\left(-3 r^{-4} z\right)\)
⇒ \(12 r^{-5} x \frac{\partial r}{\partial x}-3 r^{-4}+12 r^{-5} \frac{\partial r}{\partial y} y-3 r^{-4}+12 r^{-5} \frac{\partial r}{\partial y} z-3 r^{-4}\)
⇒ \(-9 r^{-4}+12 r^{-5}\left(\frac{x^2}{r}+\frac{y^2}{r}+\frac{z^2}{r}\right)=12 r^{-4}-9 r^{-4}=3 r^{-4}\)
121. If F=grad(x3+y3+z3-3xyz) then find div F, curl F.
Solution:
Given
F=grad(x3+y3+z3-3xyz)
F = grad \(\left(x^3+y^3+z^3-3 x y z\right)=\mathbf{i}\left(3 x^2-3 y z\right)+\mathbf{j}\left(3 y^2-3 x z\right)+\mathbf{k}\left(3 z^2-3 x y\right)\)
div F = \(\nabla \cdot \mathbf{F}=\frac{\partial}{\partial x}\left(3 x^2-3 y z\right)+\frac{\partial}{\partial y}\left(3 y^2-3 x z\right)+\frac{\partial}{\partial z}\left(3 z^2-3 x y\right)\)
⇒ 6x+6y+6z = 6 (x+y+z)
⇒ \({curl} \mathbf{F}=\nabla \times \mathbf{F}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
3 x^2-3 y z & 3 y^2-3 x z & 3 z^2-3 x y
\end{array}\right|\)
⇒ I (-3x+3x) -j (-3y + 3y )+k (-3z + 3z) = 0
122. If φ =2x3y2z4,find div(grad)
Solution:
Given
φ =2x3y2z4
⇒ \(\phi=2 x^3 y^2 z^4 \Rightarrow \frac{\partial \phi}{\partial x}=6 x^2 y^2 z^4, \frac{\partial \phi}{\partial y}=4 x^3 y z^4, \frac{\partial \phi}{\partial z}=8 x^3 y^2 z^3\)
⇒ \({grad} \phi=\nabla \phi=\mathbf{i} \frac{\partial \phi}{\partial x}+\mathbf{j} \frac{\partial \phi}{\partial y}+\mathbf{k} \frac{\partial \phi}{\partial z}=6 x^2 y^2 z^4
{i}+4 x^3 y z^4 \mathbf{j}+8 x^3 y^2 z^3 \mathbf{k}\)
⇒ \({div}{grad} \phi=\nabla \cdot(\nabla \phi)=\frac{\partial}{\partial x}\left(6 x^2 y^2 z^4\right)+\frac{\partial}{\partial y}\left(4 x^3 y z^4\right)+\frac{\partial}{\partial z}\left(8 x^3 y^2 z^3\right)\)
⇒ \(12 x y^2 z^4+4 x^3 z^4+24 x^3 y^2 z^2\)
123. If φ= 2x3y2z4 ,then show that
Solution:
⇒ \(\phi=2 x^3 y^2 z^4 \Rightarrow \frac{\partial \phi}{\partial x}=6 x^2 y^2 z^4, \frac{\partial \phi}{\partial y}=4 x^3 y z^4, \frac{\partial \phi}{\partial z}=8 x^3 y^2 z^3\)
⇒ \(\frac{\partial^2 \phi}{\partial x^2}=12 x y^2 z^4, \frac{\partial^2 \phi}{\partial y^2}=4 x^3 z^4, \frac{\partial^2 \phi}{\partial z^2}=24 x^3 y^2 z^2\)
⇒ \(\nabla \phi=\mathbf{i} \frac{\partial \phi}{\partial x}+\mathbf{j} \frac{\partial \phi}{\partial y}+\mathbf{k} \frac{\partial \phi}{\partial z}=6 x^2 y^2 z^4 \mathbf{i}+4 x^3 y z^4 \mathbf{j}+8 x^3 y^2 z^3 \mathbf{k}\)
⇒ \(\nabla \cdot(\nabla \phi)=\frac{\partial}{\partial x}\left(6 x^2 y^2 z^4\right)+\frac{\partial}{\partial y}\left(4 x^3 y z^4\right)+\frac{\partial}{\partial z}\left(8 x^3 y^2 z^3\right)=12 x y^2 z^4+4 x^3 z^4+24 x^3 y^2 z^2\)
⇒ \(\nabla^2 \phi=\frac{\partial^2 \phi}{\partial x^2}\left(6 x^2 y^2 z^4\right)+\frac{\partial^2 \phi}{\partial y^2}\left(4 x^3 y z^4\right)+\frac{\partial^2 \phi}{\partial z^2}\left(8 x^3 y^2 z^3\right)=12 x y^2 z^4+4 x^3 z^4+24 x^3 y^2 z^2\)
∴ \(\nabla \cdot(\nabla \phi)=\nabla^2 \phi\)
124.If u= x2+y2+z2,find curl ∇u
Solution:
⇒ \(\nabla u=\mathbf{i} \frac{\partial u}{\partial x}+\mathrm{j} \frac{\partial u}{\partial y}+\mathbf{k} \frac{\partial u}{\partial z}=2 x \mathbf{i}+2 y \mathrm{j}+2 z \mathbf{k}\)
⇒ \({curl} \nabla u=\left|\begin{array}{lll}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
2 x & 2 y & 2 z
\end{array}\right|=\mathbf{i}(0-0)-\mathbf{j}(0-0)+\mathbf{k}(0-0)=0\)
125. If φ =x2yz then find curl (grad φ).
Solution:
⇒ \({grad} \varphi=\nabla \varphi=\mathbf{i} \frac{\partial \varphi}{\partial x}+\mathbf{j} \frac{\partial \varphi}{\partial v}+\mathbf{k} \frac{\partial \varphi}{\partial z}=2 x y \mathbf{i}+x^2 z \mathbf{j}+x^2 y \mathbf{k}\)
⇒ \(\text { curl grad } \varphi=\nabla \times(\nabla \varphi)=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
2 x y z & x^2 z & x^2 y
\end{array}\right|=\mathbf{i}\left(x^2-x^2\right)-\mathbf{j}(2 x y-2 x y)+\mathbf{k}(2 x z-2 x z)\)
= 0
126. If A=2xz2 i-yzj+3xz3k then find curl (curlA) at (1,1,1).
Solution:
⇒ \({curl} \mathbf{A}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
2 x z^2 & -y z & 3 x z^3
\end{array}\right|=\mathbf{i}(0+y)-\mathbf{j}\left(3 z^3-4 x z\right)+\mathbf{k}(0-0)=y \mathbf{i}+\left(4 x z-3 z^3\right) \mathbf{j}\)
curl (curl A) = \(\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
y & 4 x z-3 z^3 & 0
\end{array}\right|=\mathbf{i}\left(0-4 x+9 z^2\right)-\mathbf{j}(0-0)+\mathbf{k}(4 z-1)\)
⇒ \(\left(9 z^2-4 x\right) \mathbf{i}+(4 z-1) \mathbf{k}=5 \mathbf{i}+3 \mathbf{k} \text { at }(1,1,1)\)
127. If f= x2yi-2xzj+2yzk a the point (1,-1,1) then find div f, curl (curl f).
Solution:
Given f = \(x^2 y \mathbf{i}-2 x z \mathbf{j}+2 y z \mathbf{k}\)
div f = \(\frac{\partial}{\partial x}\left\{x^2 y\right\}+\frac{\partial}{\partial y}\{-2 x z\}+\frac{\partial}{\partial z}\{2 y z\}=2 x y+2 y\)
= 2(1)(-1)+2(-1) = -4 at (1,-1,1)
curl f = \(\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
x^2 y & -2 x z & 2 y z
\end{array}\right|=\mathbf{i}(2 z+2 x)-\mathbf{j}(0-0)+\mathbf{k}\left(-2 z-x^2\right)=(2 x+2 z) \mathbf{i}-\left(x^2+2 z\right) \mathbf{k}\)
curl (curl f) = \(\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
2 x+2 z & 0 & -x^2-2 z
\end{array}\right|=\mathbf{i}(0-0)-\mathbf{J}(-2 x-2)+\mathbf{k}(0-0)=(2 x+2) \mathbf{j}\)
= 4j at (1,-1,1)
128.If f=x2yz, g=xy-3z2,find div (grad f× grad g).
Solution:
grad f = \(\mathbf{i} \frac{\partial f}{\partial x}+\mathbf{j} \frac{\partial f}{\partial y}+\mathbf{k} \frac{\partial f}{\partial z}=\mathbf{i} 2 x y z+\mathbf{j} x^2 z+\mathbf{k} x^2 y\)
grad g = \(\mathbf{i} \frac{\partial g}{\partial x}+\mathbf{j} \frac{\partial g}{\partial y}+\mathbf{k} \frac{\partial g}{\partial z}=\mathbf{i} y+\mathbf{j} x+\mathbf{k}(-6 z)\)
grad f × grad g = \(\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
2 x y z & x^2 z & x^2 y \\
y & x & -6 z
\end{array}\right|\)
⇒ \(\mathbf{i}\left(-6 x^2 z^2-x^3 y\right)-\mathbf{j}\left(-12 x y z^2-x^2 y^2\right)+\mathbf{k}\left(2 x^2 y z-x^2 y z\right)\)
⇒ \(\left(-6 x^2 z^2-x^3 y\right) \mathbf{i}+\left(12 x y z^2+x^2 y z\right) \mathbf{j}+\left(x^2 y z\right) \mathbf{k}\)
div (grad f × grad g) = \(\frac{\partial}{\partial x}\left(-6 x^2 z^2-x^3 y\right)+\frac{\partial}{\partial y}\left(12 x y z^2+x^2 y^2\right)+\frac{\partial}{\partial z}\left(x^2 y z\right)\)
⇒ \(-12 x z^2-3 x^2 y+12 x z^2+2 x^2 y+x^2 y=0\)
129.If φ =x2yz and A=2xz2i-yz-j+3xz3 K then find ∇×( φA)
Solution:
⇒ \(\nabla \times(\varphi \mathbf{A})={curl}\left(2 x^3 y z^2 \mathbf{i}-x^2 y^2 z^2 \mathbf{j}+3 x^3 y z^4 \mathbf{k}\right)=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
2 x^3 y z^2 & -x^2 y^2 z^2 & 3 x^3 y z^4
\end{array}\right|\)
⇒ \(\mathbf{i}\left(3 x^3 z^4+2 x^2 y^2 z\right)-\mathbf{j}\left(9 x^2 y z^4-4 x^3 y z\right)+\mathbf{k}\left(-2 x y^2 z^2-2 x^3 z^2\right)=5 \mathbf{i}-5 \mathbf{j}-4 \mathbf{k} \text { at }(1,1,1)\)
130. If F = 3xyzi+4xyj-xyzk the find ∇ ( ∇.F) and ∇× ( ∇×F) at (-1,2,1) .Also verify that ∇ ( ∇.F)=∇× ( ∇×F)+ ∇2F.
Solution:
⇒ \(\nabla \cdot \mathbf{F}=\frac{\partial}{\partial x}\left\{3 x y z^3\right\}+\frac{\partial}{\partial y}\left\{4 x^3 y\right\}-\frac{\partial}{\partial z}\left\{x y^2 z\right\}=3 y z^3+4 x^3-x y^2\)
⇒ \(\nabla(\nabla \cdot \mathbf{F})=\mathbf{i}\left(12 x^2-y^2\right)+\mathbf{j}\left(3 z^3-2 x y\right)+\mathbf{k}\left(9 y z^2\right)\)
⇒ \(\nabla \times \mathbf{F}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
3 x y z^3 & 4 x^3 y & -x y^2 z
\end{array}\right|=\mathbf{i}(-2 x y z-0)-\mathbf{j}\left(-y^2 z-9 x y z^2\right)+\mathbf{k}\left(12 x^2 y-3 x z^3\right)\)
⇒ \(\nabla \times(\nabla \times \mathbf{F})=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
-2 x y z & 9 x y z^2+y^2 z & 12 x^2 y-3 x z^3
\end{array}\right|\)
⇒ \(\mathbf{i}\left(12 x^2-18 x y z-y^2\right)-\mathbf{j}\left(24 x y-3 z^3+2 x y\right)+\mathbf{k}\left(9 y z^2+2 x z\right)\)
⇒ \(\mathbf{i} \times \frac{\partial}{\partial x}\left(\frac{\mathbf{a} \times \mathbf{r}}{r^3}\right)=-\frac{3 x}{r^5} \mathbf{i} \times(\mathbf{a} \times \mathbf{r})+\frac{i}{r^3} \mathbf{i} \times(\mathbf{a} \times \mathbf{i})\)
⇒ \(-\frac{3 x}{r^5}[(\mathbf{i} \cdot \mathbf{r}) \mathbf{a}-(\mathbf{i} \cdot \mathbf{a}) \mathbf{r}]+\frac{1}{r^3}[(\mathbf{i} \cdot \mathbf{i}) \mathbf{a}-(\mathbf{i} \cdot \mathbf{a}) \mathbf{i}]\)
⇒ \(-\frac{3 x}{r^5} x a+\frac{3 x}{r^5} a_1 \mathbf{r}+\frac{1}{r^3} \mathbf{a}-\frac{1}{r^3} a_1 \mathbf{i}\left[\text { where } \mathbf{a}=a_1 \mathbf{i}+a_2 \mathbf{j}+a_3 \mathbf{k}\right]\)
⇒ \(-\frac{3 x^2}{r^5} a+\frac{3}{r^5} a_1 x \mathbf{r}+\frac{1}{r^3} a-\frac{1}{r^3} a_1 \mathbf{i}\)
⇒ \(\Sigma\left\{\mathbf{i} \times \frac{\partial}{\partial x}\left(\frac{\mathbf{a} \times \mathbf{r}}{r^3}\right)\right\}=\left\{-\frac{3}{r^5} \Sigma x^2\right\} \mathbf{a}+\left\{\frac{3}{r^5} \Sigma a_1 x\right\} \mathbf{r}+\frac{3}{r^3} \mathbf{a}-\frac{1}{r^3} \Sigma a_1 \mathbf{i}\)
⇒ \(-\frac{3}{r^5} r^2 a+\frac{3}{r^5}(r \cdot a) r+\frac{3}{r^3} a-\frac{1}{r^3} a=-\frac{a}{r^3}+\frac{3}{r^5}(a \cdot r) r\)
131. If a is a constant vector then show that curl\(\frac{a \times r}{r^3}\) =\(\frac{-a}{r^3}+3 \frac{r}{r^5}\)(a.r).
Solution:
curl \(\frac{\mathbf{a} \times \mathbf{r}}{r^3}=\nabla \times\left(\frac{\mathbf{a} \times \mathbf{r}}{r^3}\right)=\Sigma\left\{\mathbf{i} \times \frac{\partial}{\partial x}\left(\frac{\mathbf{a} \times \mathbf{r}}{r^3}\right)\right\}\)
Now \(\frac{\partial}{\partial x}\left(\frac{\mathbf{a} \times \mathbf{r}}{r^3}\right)=-\frac{3}{r^4} \frac{\partial r}{\partial x}(\mathbf{a} \times \mathbf{r})+\frac{1}{r^3}\left(\mathbf{a} \times \frac{\partial \mathbf{r}}{\partial x}\right)+\frac{1}{r^3}\left(\frac{\partial \mathbf{a}}{\partial x} \times \mathbf{r}\right)\)
⇒ \(\frac{\partial}{\partial x}\left(\frac{\mathbf{a} \times \mathbf{r}}{r^3}\right)=-\frac{3}{r^4} \frac{x}{r}(\mathbf{a} \times \mathbf{r})+\frac{1}{r^3}(\mathbf{a} \times \mathbf{i})=-\frac{3 x}{r^5}(\mathbf{a} \times \mathbf{r})+\frac{1}{r^3}(\mathbf{a} \times \mathbf{i})\)
⇒ \(\mathbf{i} \times \frac{\partial}{\partial x}\left(\frac{\mathbf{a} \times \mathbf{r}}{r^3}\right)=-\frac{3 x}{r^5} \mathbf{i} \times(\mathbf{a} \times \mathbf{r})+\frac{1}{r^3} \mathbf{i} \times(\mathbf{a} \times \mathbf{i})\)
⇒ \(\mathbf{i} \times \frac{\partial}{\partial x}\left(\frac{\mathbf{a} \times \mathbf{r}}{r^3}\right)=-\frac{3 x}{r^5} \mathbf{i} \times(\mathbf{a} \times \mathbf{r})+\frac{1}{r^3} \mathbf{i} \times(\mathbf{a} \times \mathbf{i})\)
⇒ \(-\frac{3 x}{r^5}[(\mathbf{i} \cdot \mathbf{r}) \mathbf{a}-(\mathbf{i} \cdot \mathbf{a}) \mathbf{r}]+\frac{1}{r^3}[(\mathbf{i} \cdot \mathbf{i}) \mathbf{a}-(\mathbf{i} \cdot \mathbf{a}) \mathbf{i}]\)
⇒ \(-\frac{3 x}{r^5} x \mathbf{a}+\frac{3 x}{r^5} a_1 \mathbf{r}+\frac{1}{r^3} \mathbf{a}-\frac{1}{r^3} a_1 \mathbf{i}\left[\text { where } \mathbf{a}=a_1 \mathbf{i}+a_2 \mathbf{j}+a_3 \mathbf{k}\right]\)
⇒ \(-\frac{3 x^2}{r^5} a+\frac{3}{r^5} a_1 x \mathbf{r}+\frac{1}{r^3} a-\frac{1}{r^3} a_1 \mathbf{i}\)
⇒ \(\Sigma\left\{\mathbf{i} \times \frac{\partial}{\partial x}\left(\frac{\mathbf{a} \times \mathbf{r}}{r^3}\right)\right\}=\left\{-\frac{3}{r^5} \Sigma x^2\right\} \mathbf{a}+\left\{\frac{3}{r^5} \Sigma a_1 x\right\} \mathbf{r}+\frac{3}{r^3} \mathbf{a}-\frac{1}{r^3} \Sigma a_1 \mathbf{i}\)
⇒ \(-\frac{3}{r^5} r^2 a+\frac{3}{r^5}(r \cdot a) r+\frac{3}{r^3} a-\frac{1}{r^3} a=-\frac{a}{r^3}+\frac{3}{r^5}(a \cdot r)\)
132. If F is a vector point function, show that(F×∇).r=0.
Solution:
(F×∇).r \(=\left\{\boldsymbol{F} \times \Sigma \mathbf{i} \frac{\partial}{\partial x}\right\}\)
\(=\left\{\Sigma(\mathbf{F} \times \mathbf{i}) \cdot \frac{\partial \mathbf{r}}{\partial x}\right\}\)=∑(F×i).i=0.
133. If f is a vector point function, prove that(f×∇)×r=-2f.
Solution:
⇒ \((\mathbf{f} \times \nabla) \times \mathbf{r}=(\mathbf{f} \times \mathbf{i}) \times \frac{\partial \mathbf{r}}{\partial x}+(\mathbf{f} \times \mathbf{j}) \times \frac{\partial \mathbf{r}}{\partial y}+(\mathbf{f} \times \mathbf{j}) \times \frac{\partial \mathbf{r}}{\partial z}\)
⇒ (f × i) × i + (f × j × j + (f × k) × k
= (i.f) i – (i.i)f + (j.f) j – (j.j) f + (k.f) k – (k.k)f
= (i.f) i – (i.i) f + (j.f) j – (j.j)f + (k.f)k- (k.k) f
= (i.f)i+(j.f) j + (k.f) k – 3f = f – 3f = -2f
134. If F is a vector point function and a is a constant vector then show that
(1) ∇(a.F)=(a.∇)F+a×(curl f)
(2) ∇.(a×F)=-a.curlF
(3) ∇×(a×F) = a(div F)-(a.∇)F.
Solution:
⇒ \(\mathbf{a} \times({curl} \mathbf{F})=\mathbf{a} \times(\nabla \times \mathbf{F})=\mathbf{a} \times\left[\mathbf{i} \times \frac{\partial \mathbf{F}}{\partial x}+\mathbf{j} \times \frac{\partial \mathbf{F}}{\partial y}+\mathbf{k} \times \frac{\partial \mathbf{F}}{\partial z}\right]\)
⇒ \(=\mathbf{a} \times\left(\mathbf{i} \times \frac{\partial \mathbf{F}}{\partial x}\right)+\mathbf{a} \times\left(\mathbf{j} \times \frac{\partial \mathbf{F}}{\partial y}\right)+\mathbf{a} \times\left(\mathbf{k} \times \frac{\partial \mathbf{F}}{\partial z}\right)\)
⇒ \(\left(\mathbf{a} \cdot \frac{\partial \mathbf{F}}{\partial x}\right) \mathbf{i}-(\mathbf{a} \cdot \mathbf{i}) \frac{\partial \mathbf{F}}{\partial x}+\left(\mathbf{a} \cdot \frac{\partial \mathbf{F}}{\partial y}\right) \mathbf{j}-(\mathbf{a} \cdot \mathbf{j}) \frac{\partial \mathbf{F}}{\partial y}+\left(\mathbf{a} \cdot \frac{\partial \mathbf{F}}{\partial z}\right) \mathbf{k}-(\mathbf{a} \cdot \mathbf{k}) \frac{\partial \mathbf{F}}{\partial z}\)
⇒ \(i\left(\mathbf{a} \cdot \frac{\partial \mathbf{F}}{\partial x}\right)+\mathbf{j}\left(\mathbf{a} \cdot \frac{\partial \mathbf{F}}{\partial y}\right)+\mathbf{k}\left(\mathbf{a} \cdot \frac{\partial \mathbf{F}}{\partial z}\right)-\left[(\mathbf{a} \cdot \mathbf{i}) \frac{\partial \mathbf{F}}{\partial x}+(\mathbf{a} \cdot \mathbf{j}) \frac{\partial \mathbf{F}}{\partial y}+(\mathbf{a} \cdot \mathbf{k}) \frac{\partial \mathbf{F}}{\partial z}\right]\)
⇒ \(\mathbf{i} \frac{\partial}{\partial x}(\mathbf{a} \cdot \mathbf{F})+\mathbf{j} \frac{\partial}{\partial y}(\mathbf{a} \cdot \mathbf{F})+\mathbf{k} \frac{\partial}{\partial z}(\mathbf{a} \cdot \mathbf{F})-(\mathbf{a} \cdot \nabla) \mathbf{F}=\nabla(\mathbf{a} \cdot \mathbf{F})-(\mathbf{a} \cdot \nabla) \mathbf{F}\)
⇒ \(\nabla \cdot(\mathbf{a} \times \mathbf{F})=\mathbf{F} \cdot(\nabla \times \mathbf{a})-\mathbf{a} \cdot(\nabla \times \mathbf{F})=-\mathbf{a} \cdot({curl} \mathbf{F})\)
⇒ \(\nabla \times(\mathbf{a} \times \mathbf{F})=\mathbf{i} \times \frac{\partial}{\partial x}(\mathbf{a} \times \mathbf{F})+\mathbf{j} \times \frac{\partial}{\partial y}(\mathbf{a} \times \mathbf{F})+\mathbf{k} \times \frac{\partial}{\partial z}(\mathbf{a} \times \mathbf{F})\)
⇒ \(\mathbf{i} \times\left(\mathbf{a} \times \frac{\partial \mathbf{F}}{\partial x}\right)+\mathbf{j} \times\left(\mathbf{a} \times \frac{\partial \mathbf{F}}{\partial y}\right)+\mathbf{k} \times\left(\mathbf{a} \times \frac{\partial \mathbf{F}}{\partial z}\right)\)
⇒ \(\left.\left(\mathbf{i} \cdot \frac{\partial \mathbf{F}}{\partial x}\right) \mathbf{a}-(\mathbf{i} \cdot \mathbf{a}) \frac{\partial \mathbf{F}}{\partial x}+\left(\mathbf{j} \cdot \frac{\partial \mathbf{F}}{\partial y}\right) \mathbf{a}-\mathbf{j} \cdot \mathbf{a}\right) \frac{\partial \mathbf{F}}{\partial y}+\left(\mathbf{k} \cdot \frac{\partial \mathbf{F}}{\partial z}\right) \mathbf{a}-(\mathbf{k} \cdot \mathbf{a}) \frac{\partial \mathbf{F}}{\partial z}\)
⇒ \(\mathbf{a}\left[\mathbf{i} \cdot \frac{\partial \mathbf{F}}{\partial x}+\mathbf{j} \cdot \frac{\partial \mathbf{F}}{\partial y}+\mathbf{k} \cdot \frac{\partial \mathbf{F}}{\partial z}\right]-\left[(\mathbf{a} \cdot \mathbf{i}) \frac{\partial \mathbf{F}}{\partial x}+(\mathbf{a} \cdot \mathbf{j}) \frac{\partial \mathbf{F}}{\partial y}+(\mathbf{a} \cdot \mathbf{k}) \frac{\partial \mathbf{F}}{\partial z}\right]\)
⇒ \(\mathbf{a}(\nabla \cdot \mathbf{F})-(\mathbf{a} \cdot \nabla) \mathbf{F}=\mathbf{a}({div} \mathbf{F})-(\mathbf{a} \cdot \nabla) \mathbf{F}\)
135.Show that curl rn (a×r)=(n+2)rn a-nrn-2 (a.r)r.
Solution:
⇒ \({curl} r^n(\mathbf{a} \times \mathbf{r})=\nabla \times r^n(\mathbf{a} \times \mathbf{r})=\nabla r^n \times(\mathbf{a} \times \mathbf{r})+r^n \nabla \times(\mathbf{a} \times \mathbf{r})\)
⇒ \(n r^{n-2} \mathbf{r} \times(\mathbf{a} \times \mathbf{r})+r^n 2 \mathbf{a}=n r^{n-2}[(\mathbf{r} \cdot \mathbf{r}) \mathbf{a}-(\mathbf{r} \cdot \mathbf{a}) \mathbf{r}]+2 r^n \mathbf{a}\)
⇒ \(n r^n a+2 r^n a-n r^{n-2} r(\mathbf{r} \cdot \mathbf{a})=(n+2) r^n a-n r^{n-2} r(\mathbf{r} \cdot \mathbf{a})\)
136. If f and g are two scalar point functions then prove that div(f∇g)=f∇2 g+∇ f.∇ g
Solution:
⇒ \({div}(f \nabla g)={i} \cdot(f \nabla g)={i} \cdot \frac{\partial}{\partial x}(f \nabla g)+{j}\frac{\partial}{\partial y}(f \nabla g)+\mathbf{k} \cdot \frac{\partial}{\partial z}(f \nabla g)\)
⇒ \(\mathbf{i} \cdot\left(\frac{\partial f}{\partial x} \nabla g+f \frac{\partial}{\partial x} \nabla g\right)+\mathbf{j} \cdot\left(\frac{\partial f}{\partial y} \nabla g+f \frac{\partial}{\partial y} \nabla g\right)+\mathbf{k} \cdot\left(\frac{\partial f}{\partial z} \nabla g+f \frac{\partial}{\partial z} \nabla g\right)\)
⇒ \(\mathbf{i} \frac{\partial f}{\partial x} \cdot \nabla g+f\left(\mathbf{i} \cdot \frac{\partial}{\partial x} \nabla g\right)+\mathbf{j} \frac{\partial f}{\partial y} \cdot \nabla g+f\left(\mathbf{j} \cdot \frac{\partial}{\partial y} \nabla g\right)+\mathbf{k} \frac{\partial f}{\partial z} \cdot \nabla g+f\left(\mathbf{k} \cdot \frac{\partial}{\partial z} \nabla g\right)\)
⇒ \(\left(\mathbf{i} \frac{\partial f}{\partial x}+\mathbf{j} \frac{\partial f}{\partial y}+\mathbf{k} \frac{\partial f}{\partial z}\right) \cdot \nabla g+f\left(\mathbf{i} \cdot \frac{\partial}{\partial x} \nabla \dot{g}+\mathbf{j} \cdot \frac{\partial}{\partial y} \nabla g+\mathbf{k} \cdot \frac{\partial}{\partial z} \nabla g\right)\)
⇒ \(\nabla f \cdot \nabla g+f \nabla \cdot \nabla g=\nabla f \cdot \nabla g+f \nabla^2 g\)
137. Show that div (f∇g)-div(g∇f)=f∇2g-g∇2f.
Solution:
⇒ \(f \nabla g=\mathbf{i} f \frac{\partial g}{\partial x}+\mathbf{j} f \frac{\partial g}{\partial y}+\mathbf{k} f \frac{\partial g}{\partial z}\)
⇒ \({div}(f \nabla g)=\nabla \cdot(f \nabla g)=\frac{\partial}{\partial x}\left(f \frac{\partial g}{\partial x}\right)+\frac{\partial}{\partial y}\left(f \frac{\partial g}{\partial y}\right)+\frac{\partial}{\partial z}\left(f \frac{\partial g}{\partial z}\right)\)
⇒ \(f\left(\frac{\partial^2 g}{\partial x^2}+\frac{\partial^2 g}{\partial y^2}+\frac{\partial^2 g}{\partial z^2}\right)+\frac{\partial f}{\partial x} \frac{\partial g}{\partial x}+\frac{\partial f}{\partial y} \frac{\partial g}{\partial y}+\frac{\partial f}{\partial z} \frac{\partial g}{\partial z}\)
⇒ \(f \nabla^2 g+\left(\mathbf{i} \frac{\partial f}{\partial x}+\mathbf{j} \frac{\partial f}{\partial y}+\mathbf{k} \frac{\partial f}{\partial z}\right) \cdot\left(\mathbf{i} \frac{\partial g}{\partial x}+\mathbf{j} \frac{\partial g}{\partial y}+\mathbf{k} \frac{\partial g}{\partial z}\right)=f \nabla^2 g+\nabla f \cdot \nabla g\)
Similarly div \((g \nabla f)=g \nabla^2 f+\nabla g \cdot \nabla f\)
∴ \({div}(f \nabla g)-{div}(g \nabla f)=f \nabla^2 g-g \nabla^2 f\)