Marksparks

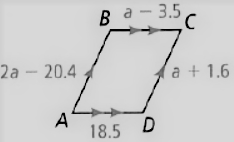
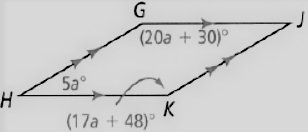
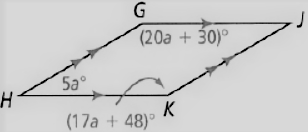
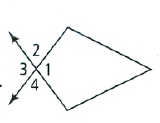
Savvas Learning Co Geometry Student Edition Chapter 8 Right Triangles And Trigonometry Exercise 8.1 The Pythagorean Theorem And Its Converse

Savvas Learning Co Geometry Student Edition Chapter 8 Exercise 8.1 The Pythagorean Theorem And Its Converse Solutions Page 495 Exercise 1 Problem 1

Given:

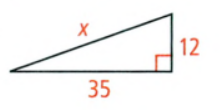
To find – The value of the variable.

Using the Pythagorean theorem find the value of the given variable.

We have

⇒ x² = 35² + 12²

⇒ x² = 1225 + 144

⇒ x²  = 1369

⇒ x = \(\sqrt{1369}\)

⇒ x = 37

The value is x = 37.

Read and Learn More Savvas Learning Co Geometry Student Edition Solutions

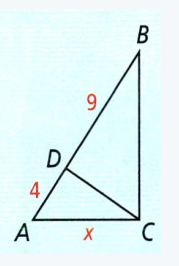
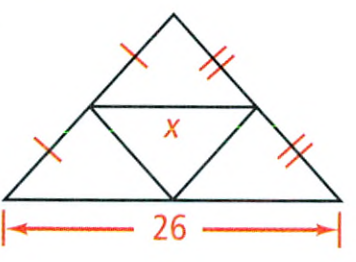
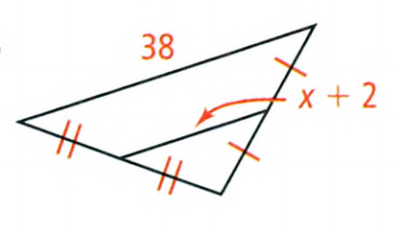
Exercise 8.1 The Pythagorean Theorem And Its Converse Savvas Geometry Answers Page 495  Exercise 2  Problem 2

Given:

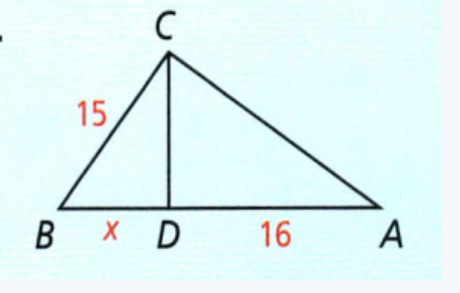
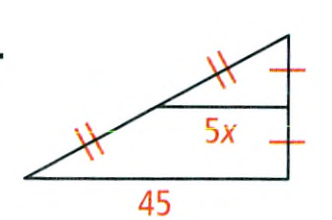
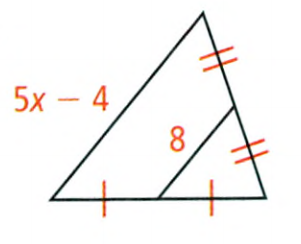
Exercise 8.1 The Pythagorean Theorem And Its Converse Savvas Geometry Answers Page 495  Exercise 3  Problem 3

Given:

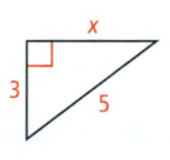
To find – The value of the variable.

Using the Pythagorean theorem find the value of the given variable.

We have

⇒ x² =  5² − 3²

⇒ x²  = 25 − 9

⇒ x = \(\sqrt{16}\)

⇒ x = 4

The value is x = 4.

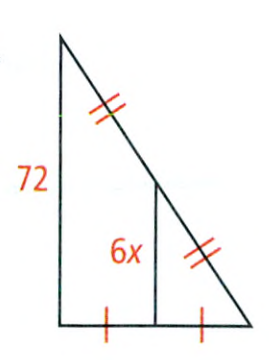
The Pythagorean Theorem And Its Converse Solutions Chapter 8 Exercise 8.1 Savvas Geometry Page 495 Exercise 4 Problem 4

Given:

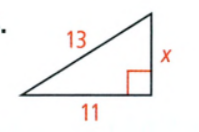
To find – The value of the variable.

Using the Pythagorean theorem find the value of the given variable.

We have

⇒ x² = 13² − 11²

⇒ x² = 169 − 121

⇒ x = \(\sqrt{48}\)

⇒ x = 4\(\sqrt{3}\).

The value is  x = 4\(\sqrt{3}\).

Chapter 8 Exercise 8.1 The Pythagorean Theorem And Its Converse Savvas Learning Co Geometry Explanation Page 495  Exercise 5  Problem 5

Given: Describe the conditions that a set of three numbers must meet in order to form a Pythagorean triple.

To find –  The condition for a Pythagorean triple.

The condition that must be met for three numbers to form a Pythagorean triple is that the sum of the squares of the two numbers should be equal to the square of the third number.

The condition that must be met for three numbers to form a Pythagorean triple is that the sum of the squares of the two numbers should be equal to the square of the third number.

Chapter 8 Exercise 8.1 The Pythagorean Theorem And Its Converse Savvas Learning Co Geometry Explanation Page 495  Exercise 6  Problem 6

Given:

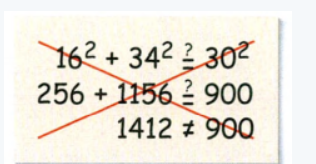
To find – Describe the error.

Friend made a mistake in choosing the hypotenuse. Instead of 30,34 should have been chosen for the hypotenuse.

Choose  34  as hypotenuse, and 16,30 for legs.

We have

⇒ 16² + 30² = 34²

⇒ 256 + 900 = 1156

⇒ 1156 = 1156

The friend made a mistake in choosing the hypotenuse. Instead of 30,34 should have been chosen for the hypotenuse. We see that the sum of the squares of the lengths of the legs is equal to the square of the hypotenuse. So the triangle is a right-angled triangle.

Solutions For The Pythagorean Theorem And Its Converse Exercise 8.1 In Savvas Geometry Chapter 8 Student Edition Page 495  Exercise 7  Problem 7

Given:

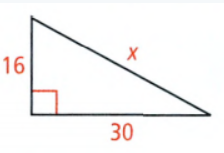
To find – The value of the variable.

Using the Pythagorean theorem find the value of the given variable.

We have

⇒ x² = 16² + 30² 

⇒ x²  = 256 + 900

⇒ x² = 1156

⇒ x = \(\sqrt{1156}\)

⇒ x = 34

The value is x = 34.

Solutions For The Pythagorean Theorem And Its Converse Exercise 8.1 In Savvas Geometry Chapter 8 Student Edition Page 495  Exercise 8  Problem 8

Given: A right-angle triangle

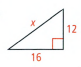
To Find – The value of x

We have, a or leg₁ = 16 and b or leg₂ = 12

So by applying the Pythagorean theorem

​⇒   a² + b²  = x²

⇒   16² + 12² =  x²

⇒   256 + 144 = x²

⇒   400 = x²

​⇒  \(\sqrt{400}\)

=  \(\sqrt{x^2}\)  (Take positive square root)

⇒  x =  20

So the length of the hypotenuse or the value of x is 20.

The length of the hypotenuse (value of x) of a right-angle triangle with the other two sides being 16 and 12 is 20.

Exercise 8.1 The Pythagorean Theorem And Its Converse Savvas Learning Co Geometry Detailed Answers Page 495  Exercise 9  Problem 9

Given: A right-angle triangle

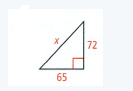
To Find – The value of x

We have, a or leg₁  = 65 and b or leg₂  = 72

So by applying the Pythagorean theorem

​⇒  a²  + b² =  x²

⇒  65² + 72² =  x²

⇒   4225 + 5184  =  x²

⇒  9409 = x²

⇒  x = 97    (Take positive square root)

So the value of x is 97.

The length of the hypotenuse (value of x) of a right-angle triangle with the other two sides being 65 and 72 is 97.

Exercise 8.1 The Pythagorean Theorem And Its Converse Savvas Learning Co Geometry Detailed Answers Page 495 Exercise 10 Problem 10

Given: A right-angle triangle

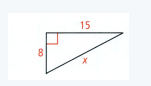
To Find – The value of x

We have, a or leg₁ = 15 and b or leg₂ =  8

So by applying the Pythagorean theorem

⇒  a²  + b² = x²

⇒  15² + 8² = x²

⇒  225 + 64 = x²

⇒  289 = x²

​⇒  x = 17 (Take positive square root)

So the value of x is 17.

The length of the hypotenuse (value of x) of a right-angle triangle with the other two sides being 15 and 8 is 17.

Geometry Chapter 8 The Pythagorean Theorem And Its Converse Savvas Learning Co Explanation Guide Page 495  Exercise 11  Problem 11

Given: A set of numbers- 4, 5, 6

To Find – Does the set of numbers form a Pythagorean triple

We have, a set of whole numbers- 4, 5, 6

Let, a = 4, b = 5, c = 6

Substituting the value of a, b, and c in a² + b² = c²

​⇒   4² + 5² = 6² 

⇒  16 + 25 = 36

⇒  41 ≠ 36
​
As L.H.S. is not equal to R.H.S., therefore, the sets 4, 5, 6 do not satisfy the equation a² + b²  = c²

So the set 4, 5, 6 is not a Pythagorean triple.

The set of numbers 4, 5, 6 is not a Pythagorean triple as it does not satisfy the equation a² + b²  = c².

Geometry Chapter 8 The Pythagorean Theorem And Its Converse Savvas Learning Co Explanation Guide Page 495  Exercise 12  Problem 12

Given: A set of numbers- 10, 24, 26.

To Find – Does the given set of numbers form a Pythagorean triple

We have, a set of numbers- 10, 24, 26

Let, a = 10,b = 24, c = 26

Substituting the values of a, b, c in the equation a² + b²  = c²

​⇒  a² + b²  = c² 

⇒  10²  + 24²  = 26²

⇒  100 + 576 = 676

⇒  676 = 676
​
As L.H.S. is equal to R.H.S. therefore, the set of numbers 10, 24, 26 satisfy the equation a² + b² = c²

Hence, the set of numbers 10, 24, 26 is a Pythagorean triple.

The set of numbers 10, 24, 26 is a Pythagorean triple because it satisfies the equation a² + b² = c²

Geometry Chapter 8 The Pythagorean Theorem And Its Converse Savvas Learning Co Explanation Guide Page 495  Exercise 13  Problem 13

Given: A set of numbers- 10, 24, 26.

To Find – Does the given set of numbers form a Pythagorean triple

We have, a set of numbers- 10, 24, 26

Let, a = 10, b = 24, c = 26

Substituting the values of a, b, and c in the equation a² + b² = c²

​⇒  a²  + b²  = c²

⇒  10² + 24² = 26²

⇒  100 + 576  =  676

⇒  676 = 676
​
As L.H.S. is equal to R.H.S., therefore, the set of numbers 10, 24, 26 satisfies the equation a² + b² = c²

Hence, the set of numbers 10, 24, 26 is a Pythagorean Triple.

The set of numbers 10, 24, 26 is a Pythagorean triple because it satisfies the equation a²+ b² = c².

Geometry Chapter 8 The Pythagorean Theorem And Its Converse Savvas Learning Co Explanation Guide Page 496  Exercise 14  Problem 14

Given: A set of numbers- 15, 20, 25

To Find – Does the given set of numbers form a Pythagorean triple

We have, a set of numbers- 15, 20, 25

Let, a = 15,b = 20,c = 25

Substituting the values of a, b, c in the equation a² + b² = c²

​⇒   a² + b²  = c²

⇒  15² + 20² =  25²

⇒  225 + 400 = 625

⇒  625 = 625
​
As L.H.S. is equal to R.H.S., therefore, the set of numbers 15, 20, 25 satisfies the equation a² + b² = c²

Hence, the set of numbers 15, 20, 25 is a Pythagorean Triple.

The set of numbers 15, 20, 25 is a Pythagorean Triple because it satisfies the equation  a² + b² = c²

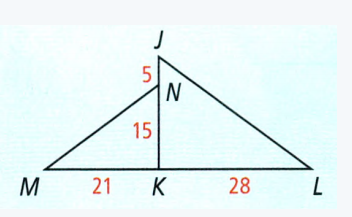
Exercise 8.1 The Pythagorean Theorem And Its Converse Savvas Geometry Answers Page 496  Exercise 15  Problem 15

Given: A right-angle triangle with two sides

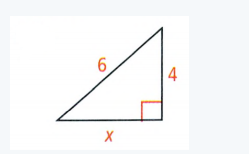
To Find – The value of x

In the given right-angle triangle

Base (a) = x units

Height (b) = 4 units

Hypotenuse (c) = 6 units

(leg₁ )²+(leg₂)² = (Hypotenuse)²               (Pythagorean theorem)

Substitute the values of a, b, c in the Pythagorean Theorem

​⇒   a² + b² = c²

⇒   x ²+ 4²  = 6²

⇒    x² + 16 = 36

⇒   x² + 16 − 16 = 36 − 16

⇒     x² = 20

⇒    x = \(\sqrt{20}\)

⇒    x = \(\sqrt{4(5)}\)

⇒   x = 2\(\sqrt{5}\)

The value of x in the simplest radical form is 2\(\sqrt{5}\).

Exercise 8.1 The Pythagorean Theorem And Its Converse Savvas Geometry Answers Page 496  Exercise 16  Problem 16

Given: A right-angle triangle with two sides

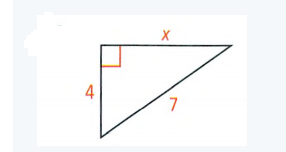
To Find – The value of x in simplest radical form

In the given right-angle triangle

Base (a) = x units

Height (b) = 4 units

Hypotenuse (c) = 7 units

Substituting the values in the Pythagorean theorem

(leg1)² + (leg2)² =(Hypotenuse)²

​⇒   x² + 4² = 7²

⇒   x² + 16 = 49

⇒   x²  + 16 − 16 = 49 − 16

⇒   x² = 33

⇒   x = \(\sqrt{33}\)

​The value of x in the simplest radical form is \(\sqrt{33}\).

The Pythagorean Theorem And Its Converse Solutions Chapter 8 Exercise 8.1 Savvas Geometry Page 496  Exercise 17  Problem 17

Given: A right-angle triangle with two sides

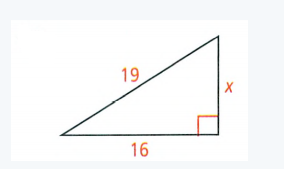
To Find  –  The value of x in simplest radical form

In the given right-angle triangle

leg₁ = 16, leg₂ = x,  Hypotenuse = 19

Substituting the values in the Pythagorean Theorem
(leg₁)² +(leg₂)² = (Hypotenuse)²

​⇒   16²  + x² = 19²

⇒   256 + x² = 361

⇒   x² = 361 − 256

⇒   x²  = 105

⇒  x = \(\sqrt{105}\)

​The value of x in the simplest radical form is \(\sqrt{105}\).

The Pythagorean Theorem And Its Converse Solutions Chapter 8 Exercise 8.1 Savvas Geometry Page 496  Exercise 18  Problem 18

Given: A right-angle triangle

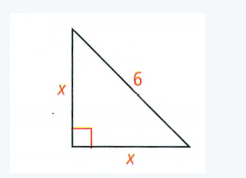
To Find –  The value of x in simplest radical form

In the given right-angle triangle

leg₁ = x, leg₂ = x, Hypotenuse = 6

Substituting the values in the Pythagorean Theorem

​⇒   (leg₁)²  + (leg₂ )² = (Hypotenuse)

⇒   x²  + x² = 6²

⇒  2x² = 36

⇒   \(\frac{2 x^2}{2}=\frac{36}{2}\)

⇒   x² = 18

⇒   x = \(\sqrt{18}\)

⇒   x  =  \(\sqrt{9(2)}\)

⇒   x =  3\(\sqrt{2}\)

The value of x in the simplest radical form is 3\(\sqrt{2}\)

The Pythagorean Theorem And Its Converse Solutions Chapter 8 Exercise 8.1 Savvas Geometry Page 496  Exercise 19  Problem 19

Given: A right-angle triangle

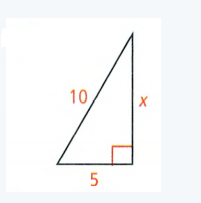
To find – The value of x in the simplest radical form

In the given right-angle triangle

leg₁ = 5, leg₂ = x , Hypotenuse = 10

Substituting the values in the Pythagorean Theorem

​⇒  (leg1)² + (leg2)² = (Hypotenuse)²

⇒   5² + x²  = 10²

⇒   25 + x²  = 100

⇒   25 − 25 + x² = 100 − 25

⇒    x² = 75

⇒    x = \(\sqrt{75}\)

⇒    x = \(\sqrt{25(3)}\)

⇒   x = 5\(\sqrt{3}\)

The value of x in the simplest radical form is 5\(\sqrt{3}\).

Solutions for The Pythagorean Theorem and Its Converse Exercise 8.1 in Savvas Geometry Chapter 8 Student Edition Page 496  Exercise 20  Problem 20

​Given: Length of the ladder is 15 -ft, Base of the ladder from the house is 5 -ft

To Find –  Height on the house that the ladder reach

As the ladder is leaning against the house so the height of the ladder will be the hypotenuse, i.e., 15 − ft.

The base of the ladder is 5 ft from the house, so the base will be  5 ft.  b = 5ft

Let the height on the house that the ladder reach be x ft.

So according to the Pythagorean Theorem

​⇒   Base²+ Height² =  Hypotenuse²

⇒   5² + x² = 152

⇒   25 + x² = 225

⇒  x² = 225 − 25

⇒  x = \(\sqrt{200}\)

⇒  x = 14.142
​
⇒  x = 14.1ft (Roud off to nearest tenth)

Hence the height on the house that the ladder reach is 14.1 ft.

When a 15 − ft ladder leans against the house and the base of the ladder is 5 − ft from the house then the height on the house that the ladder reach is 14.1 ft.

Solutions for The Pythagorean Theorem and Its Converse Exercise 8.1 in Savvas Geometry Chapter 8 Student Edition Page 496 Exercise 21 Problem 21

Given: A 24 m long walkway forms a diagonal of a square playground.

To Find –  Length of a side of the playground

As the walkway divides the square into two right-angle triangles, and the walkway (Diagonal) is 24 m long so the Pythagorean Theorem can be applied.

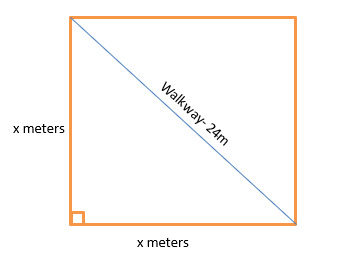
As each side of a square is equal so let leg₁  = leg₂ = x meters and the walkway will be the hypotenuse.

Substituting the values in the Pythagorean Theorem

⇒  (leg₁)² + (leg₂)² = (hypotenuse)²

⇒    x² + x² = 24²

⇒   2x² = 576

⇒   \(\frac{2 x^2}{2}=\frac{576}{2}\)

⇒   x²  = 288

⇒   x = \(\sqrt{288}\)

⇒   x≈16.97
​
⇒  x≈17.0 meters (Round off)

Hence, the length of each side of the playground is approximately 17 meters.

If a 24 m walkway forms one diagonal of a square playground then, the length of a side of the playground is approximately 17 meters.

Exercise 8.1 The Pythagorean Theorem And Its Converse Savvas Learning Co Geometry Detailed Answers Page 496  Exercise 22  Problem 22

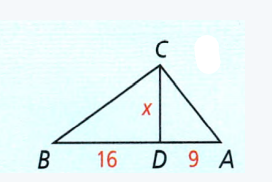
Given: A triangle

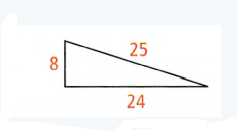
To Find – If the triangle is a right-triangle

Hypotenuse = 25, leg₁  = 24, leg₂ = 8

For checking, if the triangle is a right triangle apply the Pythagorean theorem

​⇒  (leg₁)² + (leg₂ )² = (Hypotenuse)²

⇒   24² + 8² = 25²

⇒  576 + 64 = 625

⇒   640 ≠ 625
​
As L.H.S. is not equal to R.H.S., therefore it does not satisfy the Pythagorean Theorem and hence it is not a right triangle.

The triangle is not a right triangle because it does not satisfy the Pythagorean theorem, 24² + 8² ≠25².

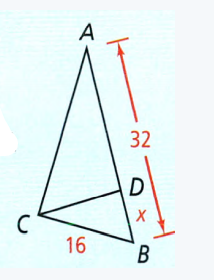
Exercise 8.1 The Pythagorean Theorem And Its Converse Savvas Learning Co Geometry Detailed Answers Page 496  Exercise 23  Problem 23

Given: The triangle.

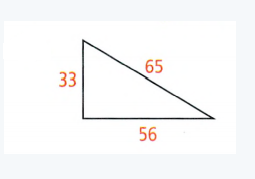
To Find – If the triangle is a right-angled triangle or not.

Using the Pythagoras theorem, we will find if the triangle is a right-angled triangle.

Consider the triangle

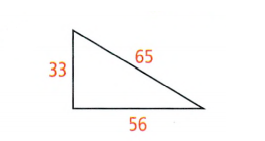
Pythagoras theorem states that the square of the hypotenuse is equal to the sum of the squares of other sides.

Let,​c = 65, a = 56 , b = 33

​Now, using Pythagoras theorem:

⇒ ​c² = 65²

⇒ c² = 4225
​
And,​a² + b² = 56² + 33²

⇒ a² + b² = 4225.
​
Since,c² = a2 + b²  the triangle is a right-angled triangle.

The triangle is a right triangle.

Exercise 8.1 The Pythagorean Theorem And Its Converse Savvas Learning Co Geometry Detailed Answers Page 496  Exercise 24  Problem 24

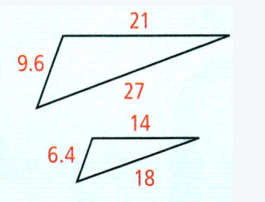
Given: The lengths of the sides of a triangle are 4,5,6.

To Find – The type of triangle.

In order to determine the type of triangle, we need to observe the inequality of the Pythagoras theorem

Consider the lengths of the three sides of a triangle , 4,5,6

Now, if  a² + b² = c² the triangle is a right angle, if a² + b² > c² triangle is acute, if a² + b² < c² triangle is obtuse.

Now, the highest length is the hypotenuse.

So, ​a = 4 , b = 5 , c = 6

​So, a² + b² = 4² + 5²

⇒ a² + b² =16 + 25

⇒ a² + b² = 41

⇒ ​c² = 6²

⇒ c² = 36.

As a² + b² >c² the triangle is an acute triangle.

Geometry Chapter 8 The Pythagorean Theorem And Its Converse Savvas Learning Co Explanation Guide Page 496  Exercise 25  Problem 25

Given: The length of the sides of a triangle is  0.3,0.4,0.6 .

To Find – The type of triangle.

In order to determine the type of triangle, we need to observe the inequality of the Pythagoras theorem.

Consider the lengths of the three sides of a triangle  , 0.3,0.4,0.6.

Now, if a2 + b2 = c2 the triangle is a right triangle, if a² + b² > c² triangle is acute, if a² + b² < c² triangle is obtuse.

The highest length is the hypotenuse. So,​a = 0.3 b = 0.4 c = 0.6
​
Now,​a² + b² = 0.3² + 0.4²

⇒ a² + b² = 0.25 and c² = 0.62

⇒ c² = 0.36
​
As a² + b² <c²  the triangle is an obtuse triangle.

The triangle with lengths with sides 0.3,0.4,0.6 is an obtuse triangle.

Geometry Chapter 8 The Pythagorean Theorem And Its Converse Savvas Learning Co Explanation Guide Page 496  Exercise 26  Problem 26

Given: The length of the sides of a triangle is11,12,15.

To Find – The type of triangle.

In order to determine the type of triangle, we need to observe the inequality of the Pythagoras theorem.

Consider the sides of the triangle , 11,12,15.

Now, if a²  + b²  = c² the triangle is a right-angle triangle, if a²  +b² > c²  triangle is acute, if a²+ b² <c²  triangle is obtuse.

The highest length is the hypotenuse. So,​a = 11 b = 12 c = 15

So,​a² + b² = 11² + 12²

⇒ a² + b² = 121 + 144

⇒ a² + b² = 265.
​
And,​c²= 15²

⇒ c² = 225

As a²  + b² > c² the triangle is an acute triangle.

The triangle with lengths of sides 11,12,15 is an acute triangle.

Geometry Chapter 8 The Pythagorean Theorem And Its Converse Savvas Learning Co Explanation Guide Page 496  Exercise 27  Problem 27

Given: The length of the sides of a triangle is \(\sqrt{3}\),2,3.

 To find – The type of triangle.

In order to determine the type of triangle, we need to observe the inequality of the Pythagoras theorem.

Consider the sides of the triangle ,  \(\sqrt{3}\),2,3.

Now, if a² + b² = c² triangle is a right angle triangle, if a² + b² > c² the triangle is an acute triangle and if a² + b² < c² the triangle is an obtuse triangle.

The highest length in a triangle is the hypotenuse.

So, a =   \(\sqrt{3}\) , b= 2, c= 3

Now, a² + b² = 7 and

⇒ ​c² = 3²

⇒ c² = 9

As a² + b² < c²  the triangle is an obtuse triangle.

The triangle with the sides  \(\sqrt{3}\) ,2,3 is an obtuse triangle.

Savvas Learning Co Geometry Student Edition Chapter 8 Right Triangles and Trigonometry Exercise

Savvas Learning Co Geometry Student Edition Chapter 8 Right Triangles And Trigonometry Exercise Solutions Page 487  Exercise 1  Problem 1

Given: 0.5858 = \(\frac{24}{x}\)

To Find: We have to solve the given expression.

Using algebraic identities.

Given

​⇒ 0.5858 = \(\frac{24}{x}\)

​⇒ x = \(\frac{24}{0.5858}\)

​⇒ 0.5858

∴ x = 40.9696
​
The value of x is 40.9696.

Chapter 8 Right Triangles And Trigonometry Exercise Savvas Geometry Answers Page 487  Exercise 2  Problem 2

Given: 0.8572 = \(\frac{5271}{x}\)

To Find – We have to solve the given expression.

Using algebraic identities.

Given

​⇒ ​0.8572 = \(\frac{5271}{x}\)

​⇒ 0.8572x = 5271

​⇒ x = \(\frac{5271}{0.8572}\)

∴ x = 6149.0900
​
The value of x is 6149.0900.

Read and Learn More Savvas Learning Co Geometry Student Edition Solutions

Chapter 8 Right Triangles And Trigonometry Exercise Savvas Geometry Answers Page 487  Exercise 3  Problem 3

Given: 0.5 = \(\frac{x}{3x+5}\)

To Find –  We have to solve the given expression.

Using algebraic identities.

Given , 0.5 = \(\frac{x}{3x+5}\)

​⇒ 1.5x + 2.5 = x

​⇒ 1.5x − x + 2.5 = 0

​⇒ 0.5x + 2.5 = 0

​⇒ 0.5x = −2.5

​⇒ x = −2.5

​⇒ 0.5

∴ x = −5

The value of x is −5.

How To Solve Right Triangles And Trigonometry Exercises In Savvas Geometry Chapter 8 Page 487  Exercise 4  Problem 4

Right Triangles And Trigonometry Exercises Solutions Chapter 8 Savvas Geometry Page 487  Exercise 5  Problem 5

Given: A pair of triangles.

To Find – We have to prove the given pair of triangles is similar.

Using the theorems and postulates of similarities.

From the given diagram
​
\(\frac{21}{27}\) = \(\frac{14}{18}\)

∴ \(\frac{7}{9}\) = \(\frac{7}{9}\)

And , \(\frac{21}{9.6}\) = \(\frac{14}{6.4}\)

∴ \(\frac{7}{3.2}\) = \(\frac{7}{3.2}\)

And , \(\frac{27}{9.6}\) = \(\frac{18}{6.4}\)

∴ \(\frac{9}{3.2}\) = \(\frac{9}{3.2}\)

Therefore, the given pair of triangles are similar.

By proving the ratio of the corresponding sides of the triangles are same we have proved that the given pair of triangles are similar.

Right Triangles And Trigonometry Exercises Solutions Chapter 8 Savvas Geometry Page 487  Exercise 6  Problem 6

Given: \(\overline{J K}\) ⊥ \(\overline{M L}\)

To Find –  We have to prove the given pair of triangles as similar.

Using the theorems and postulates of similarities.

In the given diagram that

Given  \(\overline{J K}\) ⊥ \(\overline{M L}\)

From the diagram we get

tan M =  \(\frac{15}{21}\)

M = tan^-1(\(\frac{5}{7}\))

​⇒ ∠M = 35.5°

tan L = \(\frac{20}{28}\)

L = tan^-1(\(\frac{5}{7}\))

∴ ∠L = 35.5°

Therefore ∠M = ∠L

The given pair of triangles are similar by ASA property of similarity.

By ASA property of similarity, we have proved that the given pair of triangles are similar.

Right Triangles And Trigonometry Exercises Solutions Chapter 8 Savvas Geometry Page 487  Exercise 7  Problem 7

Given: A diagram of a ΔABCb with right ∠C and altitude \(\overline{C D}\)

To Find – We have to find the value of x.

Using the rules of the right angles.

From the given diagram we get

​​⇒ BD = 16

​⇒ DA = 9
​
​tan∠B = tan∠ACD

⇒  \(\frac{16}{x} – {9}{x}\)

⇒  \(\frac{7}{x}\) = 0

∴ x = 7

​In ΔABC the value of x is 7.

Chapter 8 Right Triangles And Trigonometry Explanation Savvas Learning Co Geometry Page 487  Exercise 8  Problem 8

Given: A diagram of aΔABC with right ∠C and altitude \(\overline{C D}\)

To Find –We have to find the value of x.

Using the rules of the right angles.

From the given diagram we get

​⇒ AB = 32 [Given]

​⇒ BC = 16 [Given]

​⇒ ∠D = 90° [Given]

​⇒ ​Cos∠ABC = cos∠DBC

\(\frac{16}{32-x}\) = \(\frac{x}{16}\)

​⇒ 32x − x² = 256

​⇒ x² − 32x + 256 = 0

​⇒ x² − 16x − 16x + 256 = 0

​⇒ x(x − 16) − 16(x − 16) = 0

​⇒ (x−16)(x−16) = 0

∴ x = 16
​
In ΔABC the value of x is 16.

Solutions For Right Triangles And Trigonometry Exercises In Savvas Geometry Chapter 8 Student Edition Page 487  Exercise 9  Problem 9

Given: A diagram of a ΔABC with right ∠C and altitude \(\overline{C D}\)

To Find – We have to find the value of x.

Using the rules of the right angles.

From the diagram we get

​⇒ AD = 4 [Given]

​⇒ DB = 9 [Given]

​⇒ ∠D = 90°[Given]

​⇒ ∠C = 90° [Given]

​cos∠DAC = cos∠BAC

\(\frac{4}{x}\) = \(\frac{x}{13}\)

​⇒ x² =  52

∴ x = 7.211
​
In ΔABC the value of x is 7.211.

Right Triangles And Trigonometry Exercises Savvas Learning Co Geometry Detailed Answers Page 487  Exercise 10  Problem 10

Given:  The triangle

To find – The value of x.

We will use geometric form and calculate the value of x

The geometric means are as follows:

\(\frac{d}{b}\) = \(\frac{b}{e}\)

\(\frac{x+16}{15}\) = \(\frac{15}{x}\)

​⇒ x(x + 16) = 225x

​⇒ x² + 16x − 225x = 0

​⇒ x = 0,209

The value of x in △ABC with right ∠C and altitude is 209 \(\overline{C D}\)

Right Triangles And Trigonometry Exercises Savvas Learning Co Geometry Detailed Answers Page 487  Exercise 11  Problem 11

We have to describe how might you describe an angle of elevation in geometry.

We observe that the angle of elevation is the angle between the horizontal line of sight and the line of sight up to an object.

An angle of elevation is the angle between the horizontal line of sight to the object when looking up.

In geometry it is the angle of elevation is the angle between the horizontal line of sight and the line of sight up to an object.

An angle of elevation in geometry is the angle of elevation is the angle between the horizontal line of sight and the line of sight up to an object.

Geometry Chapter 8 Right Triangles And Trigonometry Savvas Learning Co Explanation Guide Page 487  Exercise 12  Problem 12

We have to describe how to calculate the magnitude of a line segment in the coordinate plane.

For a line segment AB containing the points, A, B the magnitude is the length of the line segment.

|AB| = \(\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}\)

The magnitude of a line segment in the coordinate plane can be calculated by the distance between the two points containing the formula and taking the magnitude

Geometry Chapter 8 Right Triangles And Trigonometry Savvas Learning Co Explanation Guide Page 487  Exercise 13  Problem 13

We have to what the prefix indicates in these words and what geometric figure you think is associated with the phrase trigonometric ratio.

We observe that tri represents three in quantity so the geometric figure associated with the phrase trigonometric ratio is a triangle.

The geometric figure is a triangle.

The prefix tri indicates three and the geometric figure you think is associated with the phrase trigonometric ratio is triangle.

Savvas Learning Co Geometry Student Edition Chapter 7 Similarity Exercise 7.1 Ratios And Proportions

Savvas Learning Co Geometry Student Edition Chapter 7 Exercise 7.1 Ratios And Proportions Solutions Page 436  Exercise 1  Problem 1

We are given that a cellphone is 46mm wide and stands 84mm long.

We are required to find the ratio of the width to its length.

Here, we will divide the width by the length to get the answer.

From the given information, we have

​​⇒ L = 84mm
​
​​⇒ W = 46mm
​
Since both the measures are in the same units, we find the ratio as

​Ratio = \(\frac{W}{L}\)

=  \(\frac{46 \mathrm{~mm}}{84 \mathrm{~mm}}\)

=  \(\frac{23}{42}\)

Hence the required ratio is 23:42.

​When, To The Nearest Millimeter, A Cell Phone Is 84mm Long And 46mm Wide, The Ratio Of The Width To The Length Is 23:42.

Read and Learn More Savvas Learning Co Geometry Student Edition Solutions

Savvas Learning Co Geometry Student Edition Chapter 7 Page 436  Exercise 2  Problem 2

We are given that two angle measures are in the ratio 5:9.

We are required to write expressions for the two angle measures in terms of the variable x.

Here, we will equate the given ratio to the variable to get the expression.

Let us equate the given ratio of angles to the variable, to get

\(\frac{5}{9}\) = x

Now, multiplying both sides by 9, we get

\(\frac{5}{9}\) × 9 = x × 9

​​⇒ 5 = 9x
​
Which is the required expression.

When Two Angle Measures Are In The Ratio 5:9, Expressions For The Two Angle Measures In Terms Of The Variable x Is 5 = 9x.

Exercise 7.1 Ratios And Proportions Savvas Geometry Answers Page 436  Exercise 3  Problem 3

​The solution of the given proportion \(\frac{5z}{5}\) = \(\frac{60}{5}\) is z = 12, obtained using cross multiplication and simple arithmetic operations.

Exercise 7.1 Ratios And Proportions Savvas Geometry Answers Page 436  Exercise 4  Problem 4

We are given the proportion \(\frac{a}{7}\) = \(\frac{13}{b}\)

We are required to find the ratio that completes the equivalent proportion

Here, we will use cross multiplication to the given proportion to get to the answer.

From the given proportion, using cross multiplication, we can write that

⇒  \(\frac{a}{7}\) = \(\frac{13}{b}\)

​​⇒ a × b = 13 × 7
​
Multiplying both sides of the equation by \(\frac{1}{13×b}\),we get

​​⇒ ​a × b × \(\frac{1}{13×b}\)

= 13 × 7 × \(\frac{1}{13×b}\)

⇒  \(\frac{a}{13}\) = \(\frac{7}{b}\)

The ratio that completes the given equivalent proportion is given by \(\frac{a}{13}\) = \(\frac{7}{b}\), which is obtained from the given value \(\frac{a}{7}\) = \(\frac{13}{b}\)

Ratios And Proportions Solutions Chapter 7 Exercise 7.1 Savvas Geometry Page 436  Exercise 4  Problem 5

We are given the proportion\(\frac{a}{7}\) = \(\frac{13}{b}\).

We are required to find the ratio that completes the equivalent proportion

Here, we will use subtraction from the given proportion to get to the answer.

The ratio that completes the given equivalent proportion is given by.  \(\frac{a-7}{7}=\frac{13-b}{b}\), which is obtained from the given value . \(\frac{a}{7}\) = \(\frac{13}{b}\)

Ratios And Proportions Solutions Chapter 7 Exercise 7.1 Savvas Geometry Page 436  Exercise 4  Problem 6

We are given the proportion \(\frac{a}{7}\) = \(\frac{13}{b}\).

We are required to find the ratio that completes the equivalent proportion

Here, we will take the reciprocal of the given proportion to get to the answer.

For the given proportion

\(\frac{a}{7}\) = \(\frac{13}{b}\)

We can take the reciprocal to get

\(\frac{7}{a}\) = \(\frac{b}{13}\)

Which is the required equivalent proportion.

The ratio that completes the given equivalent proportion is given by \(\frac{7}{a}\) = \(\frac{b}{13}\) , which is obtained from the given value  \(\frac{7}{a}\) = \(\frac{b}{13}\)

Ratios And Proportions Solutions Chapter 7 Exercise 7.1 Savvas Geometry Page 436  Exercise 5  Problem 7

In the given question, we have been given that the length of the sides of the triangle are in the extended ratio 3:6:7.

We need to find two possible sets of side lengths, in inches, for the triangle.

First, we will assume the length side and then put it into the expended ratio.

Let us assume that x is the length of the sides of the triangle.

Then we get the length of the sides of the triangle as 3x,6x,7x.

Let we assume x = 1 , then the sides of the triangle will be 3(1),(6(1),7(1) = 3,6,7(all in inches).

Let we assume x = 2 , then the sides of the triangle will be 3(2),6(2),7(2)=6,12,14 (all in inches).

So, the two sets will be 3,6,7​ and​ 6,12,14 (all in inches).

The lengths of the sides of a triangle are in the extended ratio 3:6:7 then two possible sets of side lengths, in inches, for the triangle will be: 3in,​6in,​7in 6in,​12in,​14in

Chapter 7 Exercise 7.1 Ratios And Proportions Savvas Learning Co Geometry Explanation Page 436  Exercise 6  Problem 8

In the given question, we have been given the solution of the proportion shown below.

We need to tell the error in the solution of the proportion.

We will do the proportion and then multiply numbers diagonally to find the error.

Here we will find the proportion of \(\frac{7}{3}\) = \(\frac{4}{x}\).

We will multiply the numbers diagonally, we will get

​​⇒ ​7x = 12

​​⇒ x = \(\frac{12}{7}\)

So the correct answer is x = \(\frac{12}{7}\).

And the error is in multiplying the number diagonally.

The correct solution is x = \(\frac{12}{7}\) not \(\frac{28}{3}\)  which is the error in the solution of the proportion shown.

Chapter 7 Exercise 7.1 Ratios And Proportions Savvas Learning Co Geometry Explanation Page 436  Exercise  7  Problem 9

We have been asked what is a proportion that has means 6​and ​18 and extremes 9​ and ​12.

Since we know that when the proportion is stated with colons, the means are the two words that are closest together and when the proportion is stated with colons.

The extremes are the words in the proportion that are the farthest apart.

Thus the proportion will be 9:6 = 18:12.

As the first and the last numbers in a proportion are extremes and the middle two are the means.

A proportion that has means 6​ and ​18 and extremes 9 ​and ​12 is 6:9 = 18:12.

Savvas Learning Co Geometry Student Edition Chapter 7 Page 436  Exercise 8  Problem 10

In the question, we have been given that the height of a table tennis net is 6​in. and the height of a tennis net is 3​ft.

We have been asked to write the ratio of the first measurement to the second measurement.

We will convert the height into inches and then divide them.

We have been given that the height of a table tennis net is 6​in and the height of a tennis net is 3​ft.

We know that 1​ft = ​12​in.

Thus, we will get ​3​ft ​= 3 × 12​in = 36​in

Now for the ratio, we will divide the height, we will get 6​in

​​⇒ 36​ in = \(\frac{1}{6}\)

= 1:6
​
So, the ratio is 1:6.

The ratio of the first measurement to the second measurement of the height of a table tennis net is 6​in and the height of a tennis net is 3​ft is 1:6.

Solutions For Ratios And Proportions Exercise 7.1 In Savvas Geometry Chapter 7 Student Edition Page 436  Exercise 9  Problem 11

We have been given that a baseball team played 154 regular-season games and the ratio of the number of games they won to the number of games they lost was \(\frac{5}{2}\)

We have been asked how many games did they win and also how many games did they lose.

We will assume x and then use the given ratio to find the result.

Given to us that a baseball team played 154 regular-season games the ratio of the number of games they won to the number of games they lost was 5:2.

Let the number of games be x, then the number of games they won will be 5x and the number of games they lose will be 2x.

Then we can write

​​​⇒ 5x + 2x = 154

​​⇒ 7x = 154

​​⇒ x = \(\frac{154}{7}\)

​​⇒ x = 22
​
Then the number of games they won will be 5 × 22 = 110.

And the number of games they lose will be 2 × 22 = 44.

A baseball team played 154 regular-season games and the ratio of the number of games they won to the number of games they lost was \(\frac{5}{2}\) then 110 games did they win and 44 games did they lose.

Solutions For Ratios And Proportions Exercise 7.1 In Savvas Geometry Chapter 7 Student Edition Page 436  Exercise 10  Problem 12

We have been given that the measures of two supplementary angles are in the ratio 5:7

We need to find the measure of the larger angle.

By using the sum of supplementary angles, we will find the result.

The measure of two supplementary angles is in the ratio 5:7.

Let us assume the measure of angle is x.

Then we can write 5x + 7x = 180°

Solving it, we will get

​​​⇒ 12x = 180

​​⇒ x = \(\frac{180}{12}\)

​​⇒ x = 15
​
Then the measure of angles will be

​​⇒ ​5 × 15 = 75

​​⇒ 7 × 15 = 95
​
So, the measure of the angle of the larger angle is 95°.

The measures of the two supplementary angles are in the ratio 5:7 then the measure of the larger angle is 95°.

Solutions For Ratios And Proportions Exercise 7.1 In Savvas Geometry Chapter 7 Student Edition Page 436  Exercise 11  Problem 13

In the given question, we have been given a proportion \(\frac{1}{3}\)= \(\frac{x}{12}\).

We have e  been asked to solve the given proportion.

Using cross multiplication, we will solve it.

Given to us a proportion \(\frac{1}{3}\)= \(\frac{x}{12}\).

By using the cross-multiplication, we can write

​​⇒ ​1 × 12 = 3 × x

​​⇒ 12 = 3x

​​⇒ \(\frac{12}{3}\) = x

​​⇒ 4 = x  or  x = 4
​
So, the solution of the given proportion is x = 4.

The solution of the given proportion \(\frac{1}{3}\)= \(\frac{x}{12}\) is x = 4

Exercise 7.1 Ratios And Proportions Savvas Learning Co Geometry Detailed Answers Page 436  Exercise 12 Problem 14

From the given question, we have a proportion \(\frac{9}{5}\)= \(\frac{3}{x}\).

We have e been asked to solve the given proportion.

Using cross multiplication, we will solve it.

Given to us a proportion \(\frac{9}{5}\)= \(\frac{3}{x}\).

By using the cross-multiplication, we can write

​​⇒ ​9 × x = 3 × 5

​​⇒ 9x = 15

​​⇒ x = \(\frac{15}{9}\)

​​⇒ x = \(\frac{5}{3}\)

So, the solution of the given proportion is x = \(\frac{5}{3}\)

The solution of the given proportion \(\frac{9}{5}\)= \(\frac{3}{x}\) is x = \(\frac{5}{3}\)

Exercise 7.1 Ratios And Proportions Savvas Learning Co Geometry Detailed Answers Page 436  Exercise 13  Problem 15

In the given question, we have been given a proportion \(\frac{4}{x}\)= \(\frac{5}{9}\).

We have e been asked to solve the given proportion.

Using cross multiplication, we will solve it.

Given to us a proportion \(\frac{4}{x}\)= \(\frac{5}{9}\)

By using the cross-multiplication, we can write

​​​⇒ 4 × 9 = 5 × x

​​⇒ 36 = 5x

\(\frac{36}{5}\) = x
​
So, the solution of the given proportion is \(\frac{36}{5}\).

The solution of the given proportion \(\frac{4}{x}\)= \(\frac{5}{9}\) is \(\frac{36}{5}\).

Savvas Learning Co Geometry Student Edition Chapter 7 Page 436  Exercise 14  Problem 16

We have been given a proportion \(\frac{y}{10}\)= \(\frac{15}{25}\).

We have e been asked to solve the given proportion.

Using cross multiplication, we will solve it.

Given to us a proportion \(\frac{y}{10}\)= \(\frac{15}{25}\).

By using the cross-multiplication, we can write

​​⇒ ​y × 25 = 15 × 10

​​⇒ 25y = 150

​​⇒ y = \(\frac{150}{25}\)

​​⇒ y = 6

So, the solution of the given proportion is 6.

The solution of the given proportion \(\frac{y}{10}\)= \(\frac{15}{25}\).

Geometry Chapter 7 Ratios And Proportions Savvas Learning Co Explanation Guide Page 436  Exercise 15  Problem 17

In this question, we are given the proportion \(\frac{9}{24}\) = \(\frac{12}{n}\)

We need to solve each proportion.

We multiply the numerator of the first fraction with the denominator of the second fraction and the numerator of the second fraction with the denominator of the first fraction.

We are given the proportion \(\frac{9}{24}\) = \(\frac{12}{n}\)

We will solve by cross multiplication, and we get the value of n \(\frac{9}{24}\) = \(\frac{12}{n}\)

​​⇒ 12 × 24 = 9 × n

\(\frac{288}{9}\) = n

​​⇒ 32 = n or n = 32

The solution of the given proportion \(\frac{9}{24}\) = \(\frac{12}{n}\) after solving using cross multiplication got the value of n = 32.

Geometry Chapter 7 Ratios And Proportions Savvas Learning Co Explanation Guide Page 436  Exercise 16  Problem 18

In this question, we are given the proportion \(\frac{11}{14}\) = \(\frac{b}{21}\).

We need to solve each proportion.

We multiply the numerator of the first fraction with the denominator of the second fraction and the numerator of the second fraction with the denominator of the first fraction.

We are given the proportion \(\frac{11}{14}\) = \(\frac{b}{21}\)

We will solve by cross multiplication, we get the value of b.

\(\frac{11}{14}\) = \(\frac{b}{21}\)

​​⇒ 11 × 21 = 14 × b

\(\frac{231}{14}\) = b

​​⇒ 16.5 = b

​The solution of the given proportion \(\frac{11}{14}\) = \(\frac{b}{21}\) after solving using cross multiplication got the value of b = 16.5.

Savvas Learning Co Geometry Student Edition Chapter 7 Page 436  Exercise 17  Problem 19

In this question, we are given the proportion \(\frac{3}{5}\) = \(\frac{6}{x+3}\)

We need to solve each proportion.

We multiply the numerator of the first fraction with the denominator of the second fraction and the numerator of the second fraction with the denominator of the first fraction.

We are given the proportion \(\frac{3}{5}\) = \(\frac{6}{x+3}\)

We will solve proportion using cross multiplication, we get the value of x

\(\frac{3}{5}\) = \(\frac{6}{x+3}\)

​​⇒ (x + 3)3 = 6 × 5 3x + 9 = 30
​
After simplifying, we get

​​⇒ ​3x = 30 − 9

​​⇒ x = \(\frac{30−9}{3}\)

​​⇒ x = \(\frac{21}{3}\)

​​⇒ x = 7

​The solution of the given proportion \(\frac{3}{5}\) = \(\frac{6}{x+3}\) after solving using cross multiplication got the value of x = 7.

Ratios And Proportions Solutions Chapter 7 Exercise 7.1 Savvas Geometry Page 436  Exercise 18  Problem 20

In this question, we are given the proportion \(\frac{y+7}{9}=\frac{8}{5}\)

We need to solve each proportion.

We multiply the numerator of the first fraction with the denominator of the second fraction and the numerator of the second fraction with the denominator of the first fraction.

We are given the proportion \(\frac{y+7}{9}=\frac{8}{5}\)

We will solve by cross multiplication, we get the value of y

⇒  \(\frac{y+7}{9}=\frac{8}{5}\)

​​⇒ (y + 7)5 = 8 × 9

​​⇒ 5y + 35 = 72
​
After solving this, we get

​​⇒ ​5y = 72 − 35

​​⇒ 5y = 37

​​⇒ y = \(\frac{37}{5}\)

​​⇒ y = 7.4

​The solution of the given proportion \(\frac{y+7}{9}=\frac{8}{5}\) after solving using cross multiplication got the value of y = 7.4.

Ratios And Proportions Solutions Chapter 7 Exercise 7.1 Savvas Geometry Page 436  Exercise 19  Problem 21

In this question, we are given the proportion \(\frac{5}{x-3}=\frac{10}{x}\)

We need to solve each proportion.

We multiply the numerator of the first fraction with the denominator of the second fraction and the numerator of the second fraction with the denominator of the first fraction.

We are given the proportion \(\frac{5}{x-3}=\frac{10}{x}\)

We will solve by cross multiplication, we get the value of x

⇒ \(\frac{5}{x-3}=\frac{10}{x}\)

​​⇒ 5 × x = 10(x − 3)

​​⇒ 5x = 10x − 30

​​⇒ 30 = 10x − 5x

​After solving this, we get

​​⇒ ​30 = 5x

​​⇒ \(\frac{30}{5}\) = x

​​⇒ 6 = x or x = 6
​
The solution of the given proportion \(\frac{5}{x-3}=\frac{10}{x}\)after solving using cross multiplication got the value of x = 6.

Solutions For Ratios And Proportions Exercise 7.1 In Savvas Geometry Chapter 7 Student Edition Page 437  Exercise 20  Problem 22

In this question, we are given the diagram \(\frac{a}{b}=\frac{3}{4}\)

We need to complete each statement \(\frac{b}{4}=\frac{?}{?}\)

We multiply the numerator of the first fraction with the denominator of the second fraction and the numerator of the second fraction with the denominator of the first fraction.

We are given the following information

⇒  \(\frac{a}{b}=\frac{3}{4}\)

To find the value of \(\frac{b}{4}\) we must multiply the numbers diagonally, we get

⇒  \(\frac{a}{b}=\frac{3}{4}\)

​​⇒ 4 × a = 3 × b
​
Now we need to divide the equation by 4, and we get
​
\(\frac{4a}{4}\) = \(\frac{3b}{4}\)
​
a = \(\frac{3b}{4}\)

And now with 3, we get

​\(\frac{a}{3}=\frac{3 b}{4 \times 3}\)

⇒ \(\frac{a}{3}=\frac{b}{4}\)

The solution of the given expression \(\frac{a}{b}\) = \(\frac{3}{4}\) using multiply the numbers diagonally is\(\frac{b}{4}=\frac{a}{3}\).

Solutions For Ratios And Proportions Exercise 7.1 In Savvas Geometry Chapter 7 Student Edition Page 437  Exercise 21  Problem 23

In this question, we are given the diagram \(\frac{a}{b}=\frac{3}{4}\)

We need to complete each statement \(\frac{7}{4}=\frac{?}{?}\)

We multiply the numerator of the first fraction with the denominator of the second fraction and the numerator of the second fraction with the denominator of the first fraction.

We are given the following information

⇒ \(\frac{a}{b}=\frac{3}{4}\)

To find the value of \(\frac{7}{4}\)

We need to add 1 to both sides of the equation, and we get

⇒ \(\frac{a}{b}=\frac{3}{4}\)

⇒  \(\frac{a}{b}+1=\frac{3}{4}+1\)

⇒  \(\frac{a+b}{b}=\frac{3+4}{4}\)

⇒  \(\frac{a+b}{b}=\frac{7}{4}\)

The solution of the given expression \(\frac{a}{b}=\frac{3}{4}\) by adding1 to both sides of the equation is \(\frac{7}{4}=\frac{a+b}{b}\).

Savvas Learning Co Geometry Student Edition Chapter 7 Similarity Exercise

Savvas Learning Co Geometry Student Edition Chapter 7 Similarity Exercise Solutions Page 429  Exercise 1  Problem 1

In this question, we have been given a diagram and an angle ∠1.

We need to find the measure of an angle.

By using Supplementary angles, we will calculate the result.

When two angles add up to 180 degrees, they are considered to be supplementary angles.

A straight line is formed by the intersection of two angles, but the angles do not have to be the same.

So, we find the angle by subtracting 110 to the 180 degrees

⇒ ​∠1 + 110° = 180°

⇒ ∠1 = 180° − 110°

⇒ ∠1 = 70°

​By using Supplementary angles, the measure of the given angle ∠1 is 70°

Chapter 7 Similarity Exercise Savvas Geometry Answers Page 429  Exercise 2  Problem 2

In this question, we have been given a diagram and an angle ∠2.

We need to find the measure of an angle.

By using Supplementary angles, we will calculate the result.

Read and Learn More Savvas Learning Co Geometry Student Edition Solutions

When two angles add up to 180 degrees, they are considered to be supplementary angles.

A straight line is formed by the intersection of two angles, but the angles do not have to be the same.

Since the previous exercise 1 , we have the value ∠1=70°.

So, we find the angle by subtracting 70 to the 180 degrees

​⇒ ∠2+70° = 180°

⇒ ∠2 = 180° − 70°

⇒ ∠2 = 110°
​
By using Supplementary angles, the measure of the given angle ∠2 is 110°.

Chapter 7 Similarity Exercise Savvas Geometry Answers Page 429  Exercise 3  Problem 3

In this question, we have been given a diagram and an angle ∠3.

We need to find the measure of an angle.

By using Supplementary angles, we will calculate the result.

When two angles add up to 180 degrees, they are considered to be supplementary angles.

A straight line is formed by the intersection of two angles, but the angles do not have to be the same.

So, we find the angle by subtracting 110 to the 180 degrees

⇒ ​∠3 + 110° =  180°

⇒ ∠3 = 180°− 110°

⇒ ∠3 = 70°

By using Supplementary angles, the measure of the given angle ∠3 is 70°.

Similarity Exercises Solutions Chapter 7 Savvas Geometry Page 429  Exercise 4  Problem 4

In this question, we have been given a diagram and an angle ∠4.

We need to find the measure of an angle.

By using Supplementary angles, we will calculate the result.

​
By using Supplementary angles, the measure of the given angle∠4 is 70°.

Similarity Exercises Solutions Chapter 7 Savvas Geometry Page 429  Exercise 5  Problem 5

In this question, we have been given ΔPAC ≅ ΔDHL.

We need to complete the congruence statement.

By using the properties of Congruence of Triangles, we will calculate the result.

We have given the two congruent triangles ΔPAC and ΔDHL.

The two triangles are said to be congruent if all three sides of one triangle are comparable to the corresponding three sides of the second triangle by SSS using rule
​
⇒ PA = DH

⇒ AC = HL

⇒ PC = DL
​
Therefore, \(\overline{P C} \cong \overline{D L}\).

By using the properties of Congruence of Triangles, the complete congruence statement is \(\overline{P C} \cong \overline{D L}\).

Chapter 7 Similarity Savvas Learning Co Geometry Explanation Page 429  Exercise 6  Problem 6

In this question, we have been given ΔPAC ≅ ΔDHL.

We need to complete the congruence statement.

By using the properties of Congruence of Triangles, we will calculate the result.

The two triangles are said to be congruent if any two sides and the angle included between the sides of one triangle are equivalent to the corresponding two sides and the angle between the sides of the second triangle by using SAS rule.

⇒ ​PA = DH

⇒ AC = HL
​
Therefore, ∠H ≅ ∠A

By using the properties of Congruence of Triangles, the complete congruence statement is ∠H≅∠A

Chapter 7 Similarity Savvas Learning Co Geometry Explanation Page 429  Exercise 7  Problem 7

In this question, we have been given ΔPAC ≅ ΔDHL.

We need to complete the congruence statement.

By using the properties of Congruence of Triangles, we will calculate the result.

We have given the two congruent triangles  ΔPAC and ΔDHL

The two triangles are said to be congruent if any two angles and the side included between the angles of one triangle are comparable to the corresponding two angles and sides included between the angles of the second triangle by using ASA rule.

From the previous Page 429  Exercise 6 Problem 6  we have the angle ∠A ≅ ∠H, PC ≅ DL

Therefore, ∠PCA ≅ DLH

By using the properties of Congruence of Triangles, the complete congruence statement is ∠PCA ≅ DLH.

Solutions For Similarity Exercises In Savvas Geometry Chapter 7 Student Edition Page 429  Exercise 8  Problem 8

In this question, we have been given ΔPAC ≅ ΔDHL.

We need to complete the congruence statement.

By using the properties of Congruence of

Triangles, we will calculate the result.

Since all the sides of the ΔDHL when we find the congruence for ΔHDL so, the triangles are congruent by SSS rule.

The two triangles are said to be congruent if all three sides of one triangle are comparable to the corresponding three sides of the second triangle.

Therefore, ΔHDL ≅ ΔAPC

By using the properties of Congruence of Triangles, the complete congruence statement is ΔHDL ≅ ΔAPC.

​
Solutions For Similarity Exercises In Savvas Geometry Chapter 7 Student Edition Page 429  Exercise 9  Problem 9

In this question, we have been given a triangle.We need to write a congruence statement for each pair of triangles.

By using the SSS rule, we will calculate the result.

The two triangles are said to be congruent if all three sides of one triangle are comparable to the corresponding three sides of the second triangle.

We have given the two triangles ΔHUG and ΔBUG in which we have given three equal sides

⇒ ​HU = BU

⇒ HG = BG

⇒ UG=UG​(same​side)

Therefore, ΔHUG ≅ ΔBUG by SSS rule

A congruence statement for the pair of triangles is “The two triangles are said to be congruent if all three sides of one triangle are comparable to the corresponding three sides of the second triangle”. by SSS rule the triangles are congruent ΔHUG ≅ ΔBUG.

Solutions For Similarity Exercises In Savvas Geometry Chapter 7 Student Edition Page 429  Exercise 10  Problem 10

In this question, we have been given a triangle, and the value of

​⇒ BC = 12

⇒ EF = 4.7

We need to find the value of BF and DE.

By using the properties of the triangle, we will calculate the result.

As we know from the triangle diagram the side BC = BF + CF and BF = CF so to calculate the value of BF we substitute the value

⇒ ​12 = BF + BF

⇒ 12 = 2BF

\(\frac{12}{2}\)= BF

6 = BF or BF = 6
​
We know the value of EF which is equal to DE

By using the properties of the triangle, the value of BF is 6 . the value of EF is 4.7

Solutions For Similarity Exercises In Savvas Geometry Chapter 7 Student Edition Page 429  Exercise 11  Problem 11

In this question, we have been given a triangle, and the value of

⇒ ​BC = 12

⇒ EF = 4.7
​
We need to find the value of AD and AC.

By using the properties of the triangle, we will calculate the result.

We can calculate the value of BE by Pythagoras theorem by substituting the values from the previous  Page 429  Exercise 10  Problem 10 in triangle ΔBEF

​⇒ BE² = BF² − EF²

⇒ BE² = 62 − 4.72

⇒ BE² = 13.91

⇒ BE = 3.72
​
Now, we calculate the value of AD by Pythagoras theorem by substituting the values from the previous  Page 429  Exercise 10  Problem 10  in triangle ΔADE

⇒ ​AD² = 4.72 − 3.72

⇒ AD² = 4.72 − 3.72

⇒ AD = \(\sqrt{8.4}\)

⇒ AD = 2.9
​
By using the properties of the triangle, the value of BE is 3.72  the value of AD is 2.9.

Similarity Exercises Savvas Learning Co Geometry Detailed Answers Page 429  Exercise 12  Problem 12

In this question, we have been given an artist sketches a person.

She is careful to draw the different parts of the person’s body in proportion.

We need to find the meaning of proportion in this situation By using the proportion, we will calculate the result.

The meaning of proportion in this situation is the proper or suitable relationship between the size, shape, and orientation of different portions of anything

An artist creates a portrait of a person. She takes great care to draw the various sections of a person’s physique in proportion. The meaning of proportion in this situation is the proper or suitable relationship between the size, shape, and orientation of different portions of anything.

Similarity Exercises Savvas Learning Co Geometry Detailed Answers Page 429  Exercise 13  Problem 13

In this question, we have been given Siblings often look similar to each other.

We need to find the two geometric figures to be similarBy using the Geometric figures, we will calculate the result.

As we know Geometric figures are similar if they have the same shape but not necessarily the same size.

Siblings are frequently mistaken for one another. Geometric figures are similar if they have the same shape but not necessarily the same size.

Geometry Chapter 7 Similarity Savvas Learning Co Explanation Guide Page 429  Exercise 14  Problem 14

In this question, we have been given a road map that has a scale on it that tells us how many miles are equivalent to a distance of 1 inch on the map.

We need to estimate the distance between the two cities on the map.

By using the Distance, we will calculate the result.

We first measure the distance between the two cities in inches, then using the given scale, we convert the distance to miles.

On a road map, there is a scale that shows how many miles are comparable to 1 inch on the map. To measure the distance between the two cities in inches, then using the given scale, convert the distance to miles.

Savvas Learning Co Geometry Student Edition Chapter 6 Polygons And Quadrilaterals Exercise 6.2 Properties of Parallelograms

Savvas Learning Co Geometry Student Edition Chapter 6 Exercise 6.2 Properties Of Parallelograms Solutions Page 363  Exercise 1  Problem 1

Given: The parallelogram as 

To find –  The value of m∠A.

We will be using the properties of the parallelogram to find the above asked.

From the figure, we have ∠B = 127°.

Now as the opposite angles of the parallelogram are equal so we have 

⇒ ∠B = ∠D

⇒ ∠A = ∠C
​
By angle sum property we have

⇒ ​∠A + ∠B + ∠C + ∠D = 360°

⇒ ∠A + 127o + ∠A + 127°

=  360°

⇒ 2∠A + 254°  =  360°

⇒ 2∠A  =  106°

⇒ ∠A  =  \(\frac{63}{2}\)

⇒ ∠A  =  53°

The value of m∠A is 53°.

Read and Learn More Savvas Learning Co Geometry Student Edition Solutions

Exercise 6.2 Properties Of Parallelograms Savvas Geometry Answers Page 363  Exercise 2  Problem 2

Given: The parallelogram as 

To find –  The value of m∠D.

We will be using the properties of the parallelogram to find the above asked.

From the given figure we have ∠B = 127°.

Now as the opposite angles of the parallelogram are equal so, we have 

⇒ ∠B = ∠D

⇒ ∠D = 127°

​The value of m∠D is 127°.

Exercise 6.2 Properties Of Parallelograms Savvas Geometry Answers Page 363  Exercise 3  Problem 3

Given: The parallelogram as 

To find  – The value of x.

We will be using the properties of the parallelogram to find the above asked.

From the given figure, we have ​AB = x + 2

⇒ CD = 2x − 3.

Mow in a parallelogram the opposite sides are equal so, we have 

⇒ ​AB = CD

⇒ x + 2 = 2x − 3

⇒ 2x − x = 3 + 2

⇒ x = 5

The value of x is 5.

Properties Of Parallelograms Solutions Chapter 6 Exercise 6.2 Savvas Geometry Page 363  Exercise 4  Problem 4

Given: The parallelogram as 

To find – The value of AB.

We will be using the properties of the parallelogram to find the above asked.

Now as we have that ABCD is a parallelogram, so the opposite sides are parallel and equal, that is AB = CD.

So, we have :

​⇒ x + 2 = 2x − 3

⇒ 2x − x = 3 + 2

⇒  x = 5
​
From the given figure, we have AB = x + 2.

And we have x = 5, which gives

⇒ ​AB = x + 2

⇒ AB = 5 + 2

⇒ AB = 7

​The value of AB is 7.

Properties Of Parallelograms Solutions Chapter 6 Exercise 6.2 Savvas Geometry Page 363  Exercise 5  Problem 5

Given: The figure as 

Since, AB = BC so we know by theorem 6−7 that is three or more parallel lines cut off congruent segments on one transversal then they cut off congruent segments on every transversal.

So we have

⇒  ​FE = ED

⇒ ED = 12

​⇒ FD = FE + ED

= 12 + 12

= 24
​
The value of ED = 12 and FD = 24.

Chapter 6 Exercise 6.2 Properties Of Parallelograms Savvas Learning Co Geometry Explanation Page 363  Exercise 6  Problem 6

If we know one measure of angle, we can find the other three angles by using the angle sum property of a quadrilateral, which says that the sum of all the angles is 360o

Also, in the parallelogram the opposite angles are equal so, we can easily find the measure of three angles if we have the measure of one angle.

For example if in a parallelogram one angle is x , then the opposite angle will also be x and suppose the adjacent angle to x is y , so the opposite angle will also be y.

So by angle sum property we have x + x + y + y = 360°.

So if we have one known value of angle of a parallelogram, then we can find the other three by using angle sum property of the quadrilateral and by using the property of parallelogram that opposite angles are equal.

Chapter 6 Exercise 6.2 Properties Of Parallelograms Savvas Learning Co Geometry Explanation Page 363  Exercise 7  Problem 7

We may have the difference between quadrilateral and parallelogram written as -Quadrilaterals are polygons with four sides while parallelogram is a special type of a quadrilateral that has some special properties.

The four sides of quadrilateral cannot be equal or parallel but in a parallelogram the opposite sides are equal and parallel.

The angles in a Quadrilateral may vary and may not be all equal but in a parallelogram the opposite angles are equal.

The diagonals of a parallelogram divides the parallelogram into two congruent triangles, but this may not be necessary in a quadrilateral.

The diagonals of a parallelogram bisect each other but this is not necessary in a quadrilateral.

The difference between quadrilateral and parallelogram is given below :

⇒  Quadrilaterals are polygons with four sides while parallelogram is a special type of a quadrilateral that has some special properties.

⇒  The four sides of quadrilateral cannot be equal or parallel but in a parallelogram the opposite sides are equal and parallel.

⇒  The angles in a Quadrilateral may vary and may not be all equal but in a parallelogram the opposite angles are equal.

⇒  The diagonals of a parallelogram divides the parallelogram into two congruent triangles, but this may not be necessary in a quadrilateral.

⇒  The diagonals of a parallelogram bisect each other but this is not necessary in a quadrilateral.

Chapter 6 Exercise 6.2 Properties Of Parallelograms Savvas Learning Co Geometry Explanation Page 363  Exercise 8  Problem 8

Consider the figure given to us as

Now we are given that

​PR ≅ RT

QS = 5cm
​
PT and QV ae transversals of the lines PQ, RS,TV.

The classmate has applied the following theorem

Theorem: If three ( or more) parallel lines cut off congruent segments on one transversal, then they cut off congruent segments on every transversal.

Since, the lines PQ,RS and TV are not given to be parallel, therefore, the statement QV = 10 may not be correct.

The statement given by our classmate that is QV = 10 may not be correct because we are not given any lines to be parallel.

Savvas Learning Co Geometry Student Edition Chapter 6 Page 364  Exercise 9  Problem 9

Given: We have the parallelogram with one angle as 53° and one as x°

The figure for the same is given below

To find – The value of x.

We will be using the properties of parallelogram to find the value of the given variable.

We have one angle of parallelogram as 53° as the opposite angles are equal in a parallelogram so the opposite angle will also be 53°.

Similarly, we have two angles measuring as x°.

By angle sum property of a quadrilateral we have

⇒ ​53 + x + 53 + x = 360

⇒ 2x + 106 = 360

⇒ 2x = 360 − 106

⇒ 2x = 254

⇒ x = \(\frac{254}{2}\)

⇒ x = 127°

​The value of x is given as 127°.

Solutions For Properties Of Parallelograms Exercise 6.2 In Savvas Geometry Chapter 6 Student Edition Page 364  Exercise 10  Problem 10

Given: We have the parallelogram with two angles given as 113° and x°.

The figure for the same is given below

To find –  The value of x.

We will be using the concept of properties of parallelogram to find the value of the unknown variable.

We are given one angle as 113°.

As opposite angles in parallelogram are equal to the other opposite angle will be 113°

Similarly, we have two angles as x°.

By angle sum property of quadrilateral, we have

⇒ ​113 + x + 113 + x  =  360

⇒ 2x + 226 = 360

⇒ 2x = 134

⇒ x = \(\frac{134}{2}\)

⇒ x = 67°

​The value of x is given as 67°.

Solutions For Properties Of Parallelograms Exercise 6.2 In Savvas Geometry Chapter 6 Student Edition Page 364  Exercise 11  Problem 11

Given: The figure of the parallelogram is

To find –  We have to find the value of x.

We will analyze the given data and then apply the condition to solve the problem.

Given, The figure of the parallelogram is

As we now that, the opposite angles of a parallelogram are equal.

Thus , ​∠D = ∠B , ∠A = ∠B

​The angle sum property of a parallelogram tells that

​⇒ ∠A + ∠B ∠C + ∠D = 180°

⇒ 80° + x°+ 80° + x° = 180°

⇒ 2x = 180° − 160°

⇒ x =\(\frac{20^{\circ}}{2}\)

⇒ x = 10°

Hence, the value of x = 10°.

The value of x in given parallelogram is 10°.

Exercise 6.2 Properties Of Parallelograms Savvas Learning Co Geometry Detailed Answers Page 364  Exercise 12  Problem 12

Given: The figure of the parallelogram is

To find – We have to find the value of x.

We will analyze the given data and then apply the condition to solve the problem.

Given, The figure of the parallelogram is

As we now that, the opposite angles of a parallelogram are equal.

Thus , ​∠D = ∠B , ∠A = ∠C

​The angle sum property of a parallelogram tells that

​⇒ ∠A + ∠B + ∠C + ∠D = 180°

⇒ 62° + x + 62° + x = 180°

⇒ 2x  = 180° − 124°

⇒ x  =  \(\frac{56^{\circ}}{2}\)

⇒ x = 28°

Hence, the value of x  =  28°.

The value of x in given parallelogram is 28°.

Exercise 6.2 Properties Of Parallelograms Savvas Learning Co Geometry Detailed Answers Page 364  Exercise 13  Problem 13

Given: The figure of the parallelogram is

To find –  We have to complete the given table.

We will analyze the given data and then apply the condition to solve the problem.

Given, The figure of the parallelogram is

Since, ABCD is a parallelogram, which means.

Its opposite sides are parallel

Thus, AB ∥ CD

And ∠1  =  ∠4  (Alternate Interior angle Property)

Similarly ∠2 = ∠3

Since, opposite sides of a parallelogram are equal.

Thus, AB ≈ CD

In triangle AED & BEC

∠1  =  ∠4     (Alternate Interior Angle Property)

AD  =  BC   (Opposite Sides of a parallelogram are equal)

∠AED  =  ∠BEC   (Vertically Opposite Angle Property)

Hence, by ASA Congruency ΔAED ≅ ΔBEC.

The diagonals of a parallelogram bisects each other.

Thus, ​AE = CE, BE = DE

The bisector is a ray or a segment which divides the geometry in two identical halves.

In the parallelogram ABCD ,AC and BD bisects each other at E.

Exercise 6.2 Properties Of Parallelograms Savvas Learning Co Geometry Detailed Answers Page 364  Exercise 14  Problem 14

Given: The side lengths given are

​⇒ PT = 2x

⇒ TR = y + 4

⇒ QT = x + 2

⇒ TS = y
​
The figure of the parallelogram is

To find – We have to find the value of x and y.

We will analyze the given data and then apply the condition to solve the problem.

Given,  The side lengths given are

⇒ ​PT = 2x

⇒ TR = y + 4

⇒ QT = x + 2

⇒ TS = y
​
The figure of the parallelogram is

Since, the diagonals of a parallelogram bisects each other.

So, PT = TR , QT = TS
​
Thus, the equation obtained are

⇒ 2x = y + 4 and x + 2 = y

On solving the above equations, we get

⇒ ​2x = (x + 2) + 4

⇒ 2x − x = 4 + 2

⇒ x = 6

⇒  y = 6 + 2

⇒  y = 8
​
Hence, the value of  x = 6 and y = 8.

The value of x and y in given parallelogram is 6 and 8.

Geometry Chapter 6 Properties Of Parallelograms Savvas Learning Co Explanation Guide Page 364  Exercise 15  Problem 15

Given: The given sides are​

⇒ PT = x + 2

⇒ TR = y

⇒ QT = 2x

⇒ TS = y + 3
​
The figure of the parallelogram is

To find – We have to find the value of x and y.

We will analyze the given data and then apply the condition to solve the problem.

Given, The given side lengths are

⇒ ​PT = x + 2

⇒ TR = y

⇒ QT = 2x

⇒ TS = y + 3
​
The figure of the parallelogram is

Since, the diagonals of a parallelogram bisects each other.

⇒ ​PT = TR

⇒ QT = TS
​
So, the equations obtained are x + 2 = y and 2x = y + 3

On solving the above equations, we get

​⇒ 2x = (x + 2) + 3

⇒ 2x − x = 2 + 3

⇒ x = 5

⇒  y = 5 + 2

⇒  y = 7

Hence, the value of x = 5 and y = 7.

The value of x and y in given parallelogram is 5 and 7.

Geometry Chapter 6 Properties Of Parallelograms Savvas Learning Co Explanation Guide Page 364   Exercise 16  Problem 16

Given: The relation between the segments are PQ = QR = RS

The diagram given is

To find –  We have to find the length of XZ.

We will analyze the given data and then apply the condition to solve the problem.

Given, The side length given are

PQ = QR = RS

The diagram given is

Since, the if a line cuts the parallel lines of pair of three or more, then

Those parallel lines will divide the cutting lines in equal segments.

So, XT = XZ = ZU

As it is given that, the length of the segment is

XT = 3

Thus , ​XT = XZ

⇒  XZ = 3
​
Hence, the value of XZ = 3.

The value of XZ in the given figure is 3.

Exercise 6.2 Properties Of Parallelograms Savvas Geometry Answers Page 364  Exercise 17  Problem 17

Given: The relation given is PQ = QR = RS

The diagram given is

To find – We have to find the length of TU.

We will analyze the given data and then apply the condition to solve the problem.

Given, The relation given is

PQ = QR = RS

The diagram given is

Since, the if a line cuts the parallel lines of pair of three or more, then

Those parallel lines will divide the cutting lines in equal segments.

So , XT = XZ = ZU

As it known that, the length of the segment XT = 3

Thus, TU = XT + ZX + ZU

⇒ TU = 3(XT)

⇒ TU = 3(3)

⇒ TU = 9
​
Hence, the value of TU = 9.

The value of TU in the given figure is 9.

Exercise 6.2 Properties Of Parallelograms Savvas Geometry Answers Page 364  Exercise 18  Problem 18

Given:  The relation given is  PQ = QR = RS

The diagram given is

To find – We have to find the length of XV.

We will analyze the given data and then apply the condition to solve the problem.

Given, The relation given is

PQ = QR = RS

The diagram given is

Since, the if a line cuts the parallel lines of pair of three or more, then

Those parallel lines will divide the cutting lines in equal segments.

So, WY = YX = XV

As we know that, the length of the segment is

⇒ WY  =  2.25

Thus ,WY = XV

⇒  XV  =  2.25
​
Hence, the value of  XV  =  2.25.

The value of XV in the given figure is 2.25.

Properties Of Parallelograms Solutions Chapter 6 Exercise 6.2 Savvas Geometry Page 364  Exercise 19  Problem 19

Given: The given relation is PQ = QR = RS

The diagram given is

To find –  We have to find the length of YV.

We will analyze the given data and then apply the condition to solve the problem.

Given, The given relation is, PQ = QR = RS

The diagram given is

Since, the if a line cuts the parallel lines of pair of three or more, then

Those parallel lines will divide the cutting lines in equal segments.

So , WY = YX = XV

As we know that, the length of the segment is

WY = 2.25

Thus , ​YV  =  YX + XV

⇒ YV  =  2XV

⇒ YV  =  2WY

⇒ YV  =  2(2.25)

⇒ YV  =  4.5
​
Hence, the value of YV = 4.5.

The value of YV in the give figure is 4.5.

Properties Of Parallelograms Solutions Chapter 6 Exercise 6.2 Savvas Geometry Page 364  Exercise 20  Problem 20

Given: The given relation is PQ = QR = RS

The diagram given is

To find –  We have to find the length of WV.

We will analyze the given data and then apply the condition to solve the problem.

Given, The given relation is, PQ = QR = RS

The diagram given is

Since, the if a line cuts the parallel lines of pair of three or more, then

Those parallel lines will divide the cutting lines in equal segments.

So, WY = YX = XV

As we know that, the length of the segment is

⇒ WY = 2.25

Thus , ​WV = WY + YX + XV

⇒ WV  =  3WY

⇒ WV  =  3(2.25)

⇒ WV  =  6.75
​
Hence, the value of WV = 6.75.

The value of WV in the given figure is 6.75.

Savvas Learning Co Geometry Student Edition Chapter 6 Page 364  Exercise 21  Problem 21

Given: The parallelogram given is

To find –  We have to find the values of each variables in the given parallelogram.

We will analyze the given data and then apply the condition to solve the problem.

Given, The parallelogram given is

As we now that, the opposite angles of a parallelogram are equal.

Thus , ∠A = ∠C

So, the angles are related as

⇒ 4a − 4  =  2a + 30

⇒ 4a − 2a  =  30 + 4

⇒ 2a  =  34

⇒ a  =  \(\frac{34}{2}\)

⇒ a  =  17
​
Hence, the value of a  =  17.

The value of a in the given parallelogram is 17.

Properties Of Parallelograms Solutions Chapter 6 Exercise 6.2 Savvas Geometry Page 365  Exercise 22  Problem 22

Given: The parallelogram given is

To find – We have to find the values of x and y and we have to find the relation between the angles.

We will analyze the given data and then apply the condition to solve the problem.

Given, The parallelogram given is

As we now that, the opposite angles of a parallelogram are equal.

So, ∠D = ∠B, ∠A = ∠C

​Thus, the angles are related as y = 3x, ∠C = 3y

​As we know the angle sum property of a parallelogram

⇒ ​∠A + ∠B + ∠C + ∠D = 360°

⇒ 3y + 3x + 3y + y = 360°

⇒ 3y + y + 3y + y = 360°

⇒ 8y  =  360°

⇒ y = \(\frac{360^{\circ}}{8}\)

⇒ y  =  45°

⇒   x = \(\frac{45^{\circ}}{3}\)

⇒   x = 15°

Hence, the value of x = 15°  and y = 45°.

The relation between angles in the given parallelogram is y = 3x and ∠C = 3y and the values of x andy are 15° and 45°.

Chapter 6 Exercise 6.2 Properties Of Parallelograms Savvas Learning Co Geometry Explanation Page 365  Exercise 22  Problem 23

Given: The parallelogram given is

To find – We have to find the values of x and y and also have to tell which variable is going to be solved first.

We will analyze the given data and then apply the condition to solve the problem

Given, The parallelogram given is

As we now that, the opposite angles of a parallelogram are equal.

So, ∠D = ∠B , ∠A = ∠C
​
Thus, the angles are related as y = 3x, ∠C = 3y
​
As we know the angle sum property of a parallelogram

​⇒ ∠A + ∠B + ∠C + ∠D  =  360°

⇒ 3y + 3x + 3y + y  =  360°

⇒ 3y + y + 3y + y  =  360°

⇒ 8y  =  360°

⇒ y = \(\frac{360^{\circ}}{8}\)

⇒ y  =  45°

⇒  x = \(\frac{45^{\circ}}{3}\)

⇒  x  =  15°

​Hence, the value of x  =  15° and y = 45°.

The variable first going to be solve is y m and the values of x and y are 15° and 45°.

Chapter 6 Exercise 6.2 Properties Of Parallelograms Savvas Learning Co Geometry Explanation Page 365  Exercise 23  Problem 24

Given: The parallelogram given is

To find – We have to find the length of given parallelogram.

We will analyze the given data and then apply the condition to solve the problem.

Given, The parallelogram given is

Since, the length of opposite sides of parallelogram are equal.

So, AD = BC , AB = CD
​
Thus, the sides are related as

​⇒ 18.5  =  a − 3.5

⇒ a  =  18.5 + 3.5

⇒ a = 22

​The length of sides are

​⇒ CD = a + 1.6

⇒  22 + 16

⇒  38
​
​BC  =  a − 3.5

⇒  22.0 − 3.5

⇒  18.5
​
​AB = 2a − 20.4

⇒  2(22.0) − 20.4

⇒  44.0 − 20.4

⇒  23.6

Hence, the length of sides are​

CD = 38

BC = 18.5

AB = 23.6

AD 18.5.

​The length of sides of the given parallelogram are CD = 38, BC = 18.5, AB = 23.6, AD = 18.5.

Savvas Learning Co Geometry Student Edition Chapter 6 Page 365  Exercise 24  Problem 25

Given: The parallelogram given is

To find – We have to find the value of a angle measure of given parallelogram.

We will analyze the given data and then apply the condition to solve the problem.

Given, The parallelogram given is

As we now that, the opposite angles of a parallelogram are equal.

So, ∠G = ∠K ∠H = ∠J

​Thus, the angles are related as

⇒ ​20a + 30 = 17a + 48

⇒ 20a − 17a = 48 − 30

⇒ 3a = 18

⇒ a = 6
​
The angle measures are

​∠G  =  (20a + 30)°

⇒  (20(6) + 30)°

⇒  150°

​∠H = 5a°

⇒  5(6)°

⇒  30°

​∠J = ∠H

⇒ ∠J = 30°

​∠K = ∠G

⇒  ∠K = 150°

Chapter 6 Exercise 6.2 Properties Of Parallelograms Savvas Learning Co Geometry Explanation

Hence, the angle measure are​

⇒ ∠G = 150°

⇒ ∠H = 30°

⇒ ∠J = 30°

⇒ ∠K = 150°.

​The values of angle measure of given parallelogram is​ ∠G = 150°, ∠H = 30°, ∠J = 30°, ∠K = 150°.

Savvas Learning Co Geometry Student Edition Chapter 6 Polygons And Quadrilaterals Exercise 6.1 The Polygon – Sum Theorems

Savvas Learning Co Geometry Student Edition Chapter 6 Exercise 6.1 The Polygon-Sum Theorems Solutions Page 356  Exercise 1  Problem 1

Given:  We have given a regular decagon.

To find –  Measures of an interior angle and an exterior angle of a regular decagon.

We will be using the concept of finding the sum of interior angles of the polygon with a given number of sides and the polygon exterior angle sum theorem.

We are given a regular decagon, that is the number of sides are n = 10.

The measure of the exterior angle of a decagon is given by

\(\frac{360^{\circ}}{10}\) = 36°

The sum of interior angles is given by:

⇒ ​S  =  180 (n − 2)

⇒ S  =  180 (10 − 2)

⇒ S  =  180 (8)

⇒ S  =  1440°

So, we have the measure of an interior angle as

\(\frac{1440^{\circ}}{10}\) = 144°

The measures of an interior angle is 144° and an exterior angle is 36° of a regular decagon

Read and Learn More Savvas Learning Co Geometry Student Edition Solutions

Exercise 6.1 The Polygon-Sum Theorems Savvas Geometry Answers Page 356  Exercise 2  Problem 2

An equiangular polygon means a polygon with the same measure of each interior angle.

Yes, we can draw an equiangular polygon that is not equilateral. For example we may draw a rectangle, that has all the angles as right angles but not all the sides of same measure.

Exercise 6.1 The Polygon-Sum Theorems Savvas Geometry Answers Page 356  Exercise 3  Problem 3

We have the given figure as 

We know that an exterior angle is an angle which is formed by one of the sides of any closed shape structure such as polygon and the extension of its adjacent side.

From the given figure, we may see that the exterior angle of ∠1 can be given by ∠2,∠4

We see that ∠1,∠2 makes a linear pair and ∠1,∠4 also make linear pair. So the measure of the exterior angle ∠2, ∠4 can be given by 180° −∠1.

The exterior angles of ∠1 are given by ∠2, ∠4.

The measure of these angles can be given by 180° −∠1 as both the exterior angle makes a linear pair with the given interior angle.

Exercise 6.1 The Polygon-Sum Theorems Savvas Geometry Answers Page 356  Exercise 4  Problem 4

Given:  We have given a 35 – polygon.

To find –  The sum of interior angles.

We will be using the concept of finding the sum of interior angles of the polygon with a given number of sides.

We have the given polygon with total number of sides as n = 35.

The sum of interior angles of a polygon can be given by

S = 180 (n − 2), where n is the number of sides.

So, we have

​⇒ S  =  180 (35 − 2)

⇒ S  =  180 (33)

⇒ S  =  5940°

The sum of the interior angle measures of the given polygon is 5940°.

The Polygon-Sum Theorems Solutions Chapter 6 Exercise 6.1 Savvas Geometry Page 356  Exercise 5  Problem 5

Given:  A  14 − polygon.

To find –  The sum of interior angles.

We will be using the concept of finding the sum of interior angles of the polygon with a given number of sides.

We have the given polygon with total number of sides as n = 14.

The sum of interior angles of a polygon can be given by

S = 180 (n−2), where n is the number of sides.

So, we have

⇒ ​S  =  180 (14 − 2)

⇒ S  =  180 (12)

⇒ S  =  2160°

The sum of the interior angle measures of the given polygon is 2160°.

The Polygon-Sum Theorems Solutions Chapter 6 Exercise 6.1 Savvas Geometry Page 356   Exercise 6   Problem 6

Given: The regular polygon as

To find – The measure of one interior angle in regular polygon.

We will be using the concept of finding the sum of interior angles of the polygon with a given number of sides.

From the given figure, we have the number of sides of the given regular polygon as n = 8.

The sum of all interior angles is given by:

⇒ ​S  =  180 (n − 2)

⇒ S  =  180 (8 − 2)

⇒ S  =  180 (6)

⇒ S  =  1080°

Measure of one interior angle is given by

=  \(\frac{1080^{\circ}}{8}\)

=  135°

The measure of one interior angle is 135° in the given regular polygon.

The Polygon-Sum Theorems Solutions Chapter 6 Exercise 6.1 Savvas Geometry Page 356  Exercise 7  Problem 7

Given: The figure as showing a quadrilateral as follows

To find –  The missing angles.

We will be using the concept of sum of all interior angles to find the measure of missing angle.

We are given a quadrilateral with angle measures as – 2h°, 2h°, h°, h°.

By angle sum property of quadrilateral, we have:

⇒ ​2h + h + 2h + h = 360°

⇒ 6h = 360°

⇒ h = 60°

So we have

⇒ ​2h  =  2 (60°)

​⇒ 2h  =  120°

⇒ h  =  \(\frac{120^{\circ}}{2}\)

⇒ h  =  60°

​The angle measure of the given quadrilateral are 120°,120°,60°, 60.

Chapter 6 Exercise 6.1 The Polygon-Sum Theorems Savvas Learning Co Geometry Explanation Page 356  Exercise 8  Problem 8

Given: The figure representing a pentagon as follows 

To find –  The missing angles.

We will be using the concept of sum of all interior angles to find the measure of missing angle.

​We are given a pentagon with some angle measures as – 117°,100°,105°,115°,x°.

By angle sum property of a pentagon, we have:

⇒ 117° + 100° + 105° + 115° + x  =  540°

⇒ x + 437° = 540°

⇒ x  =  540° − 437°

⇒ x  =  103°

The measure of missing angle is 103° for the given pentagon.

Solutions For The Polygon-Sum Theorems Exercise 6.1 In Savvas Geometry Chapter 6 Student Edition Page 356  Exercise 9  Problem 9

Given: We have given a pentagon.

To find  – The measure of an exterior angle of the given regular polygon.

We will be using the concept of polygon exterior angle-sum theorem.

We are given a pentagon, that means the number of sides are n = 5.

By polygon exterior angle sum theorem, we have that the measure of an exterior angle of a regular polygon is the ratio of the whole angle by the number of sides of the polygon.

So, we have the measure of an exterior angle of given polygon as

\(\frac{360^{\circ}}{5}\)  =  72°

The measure of an exterior angle is 72° of the given pentagon.

Exercise 6.1 The Polygon-Sum Theorems Savvas Learning Co Geometry Detailed Answers Page 356  Exercise 10  Problem 10

Given:  We have given a 36 −polygon.

To find  – The measure of an exterior angle of the given regular polygon.

We will be using the concept of polygon exterior angle-sum theorem.

We are given a 36 − polygon, that means the number of sides are n =  36.

By polygon exterior angle sum theorem, we have that the measure of an exterior angle of a regular polygon is the ratio of the whole angle by the number of sides of the polygon.

So, we have the measure of an exterior angle of given polygon as

\(\frac{360^{\circ}}{36}\) = 10°

The measure of an exterior angle is 10o of the given 36 –  polygon.

Exercise 6.1 The Polygon-Sum Theorems Savvas Learning Co Geometry Detailed Answers Page 356  Exercise 11  Problem 11

Given: We have given a 100 − polygon.

To find –  The measure of an exterior angle of the given regular polygon.

We will be using the concept of polygon exterior angle-sum theorem.

We are given a 100 − polygon, that means the number of sides are  n   = 100.

By polygon exterior angle sum theorem, we have that the measure of an exterior angle of a regular polygon is the ratio of the whole angle by the number of sides of the polygon.

So, we have the measure of an exterior angle of given polygon as

\(\frac{360^{\circ}}{100}\) = 3.6°

The measure of an exterior angle is 3.6° of the given 100 − polygon.

Geometry Chapter 6 The Polygon-Sum Theorems Savvas Learning Co Explanation Guide Page 356  Exercise 12  Problem 12

Given: The sum of interior angles of a polygon is given as 180°.

To find – The number of sides of the polygon.

We will be using the concept of finding the sum of interior angles of the polygon with a given number of sides.

We are given the sum of interior angles of the polygon as S = 180°

By using the formula for finding the sum, we have:

S = 180 (n−2), where is n the number of sides.

So we have

⇒ ​180 = 180 (n − 2)

⇒ 1  =  n − 2

⇒ n  =  2 + 1

⇒ n  =  3
​
The number of sides are 3 when the sum of interior angles is given as 180° for a polygon.

Geometry Chapter 6 The Polygon-Sum Theorems Savvas Learning Co Explanation Guide Page 356  Exercise 13 Problem 13

Given:  The sum of interior angles of a polygon is given as 1080°.

To find –  The number of sides of the polygon.

We will be using the concept of finding the sum of interior angles of the polygon with a given number of sides.

We are given the sum of interior angles of the polygon as S = 1080°.

By using the formula for finding the sum, we have:

S = 180 (n − 2), where n is the number of sides.

So we have

​1080 = 180 (n − 2)

\(\frac{1080}{180}\) = n − 2

⇒ 6 = n − 2

⇒ n = 6 + 2

⇒ n = 8

​The number of sides are 8 when the sum of interior angles is given as 1080° for a polygon.

Solutions For The Polygon-Sum Theorems Exercise 6.1 In Savvas Geometry Chapter 6 Student Edition Page 356  Exercise 14  Problem 14

Given:  The sum of interior angles of a polygon is given as 1980°.

To find – The number of sides of the polygon.

We will be using the concept of finding the sum of interior angles of the polygon with a given number of sides.

We are given the sum of interior angles of the polygon as 1980°.

By using the formula for finding the sum, we have:

S = 180 (n − 2), where nis the number of sides.

So we have

​⇒ 1980 = 180 (n − 2)

\(\frac{1980}{180}\) = n − 2

⇒ 11 = n − 2

⇒ n = 11 + 2

⇒ n = 13
​
The number of sides are 13 when the sum of interior angles is given as 1980° for a polygon.

Solutions For The Polygon-Sum Theorems Exercise 6.1 In Savvas Geometry Chapter 6 Student Edition Page 356  Exercise 15  Problem 15

Given: The sum of interior angles of a polygon is given as 2880°.

To find – The number of sides of the polygon.

We will be using the concept of finding the sum of interior angles of the polygon with a given number of sides.

We are given the sum of interior angles of the polygon as 2880°.

By using the formula for finding the sum, we have:

S = 180 (n − 2), where n is the number of sides.

So we have

​2880 = 180 (n − 2)

\(\frac{2880}{180}\) = n − 2

⇒ 16 = n − 2

⇒ n = 16 + 2

⇒ n = 18
​
The number of sides are 18 when the sum of interior angles is given as 2880° for a polygon.

Exercise 6.1 The Polygon-Sum Theorems Savvas Learning Co Geometry Detailed Answers Page 357  Exercise 16  Problem 16

We know that Polygon is a representation of the surface and is formed using a collection of lines.

An polygon that can is equilateral but not equiangular can be given by a rhombus.

As a rhombus have all equal sides, but the angles of the rhombus are not equal.

We may sketch the rhombus as follows:

The sketch of an equilateral polygon that is not equiangular is a rhombus that is given below: 

Exercise 6.1 The Polygon-Sum Theorems Savvas Learning Co Geometry Detailed Answers Page 357   Exercise 17   Problem 17

We are given that a triangle has two congruent interior angles and an exterior angle that measures 100°.

So, we may draw the diagram for the triangle as:

Now, here we see that the two interior angles that are congruent to each other are given by y, and other interior angle is given by x.

Diagram thus helps us to find the values of the missing angle in any polygon.

The diagram helps us to find the missing angles in a polygon, which is only possible if we have the diagram with the given values of angles and the missing values as variables.

Exercise 6.1 The Polygon-Sum Theorems Savvas Learning Co Geometry Detailed Answers Page 357  Exercise 17  Problem 18

We are given a triangle has two congruent interior angles and an exterior angle that measures 100°

Also, we have the diagram for the given triangle as follows:

Now by angle sum property of a triangle we know that the sum of all the interior angles of a triangle is always 180°.

We can also verify this by the formula S = 180(n − 2), where n is the number of sides and we will get :

⇒ ​S = 180 (3 − 2)

⇒ S = 180° (1)

⇒ S =  180°

The sum of the angle measures in a triangle is always 180°.

​

Exercise 6.1 The Polygon-Sum Theorems Savvas Geometry Answers Page 357  Exercise 18  Problem 19

Given: The figure as

To find  – The value of each variable.

We will be using the angle sum property of the polygon and the linear pair property to find the missing values.

From the given figure as, we see that z,110o form a linear pair, so we have :

⇒ z +110° = 180°

⇒ z = 180° − 110°

⇒ z = 70°

Now by angle sum property of a quadrilateral, we have:

​⇒ z + y + 100° + 87° =  360°

⇒ 70° + y + 100°+ 87° = 360°

⇒ y + 257°  = 360°

⇒ y = 360° − 257°

⇒ y = 103°

The value of variable are ​y = 103°, z = 70°.

Exercise 6.1 The Polygon-Sum Theorems Savvas Geometry Answers ​Page 357  Exercise 19  Problem 20

Given: The figure as 

To find –The value of each variable.

We will be using the angle sum property of the polygon and the linear pair property to find the missing values.

We know by polygon exterior angle sum property that the sum of all exterior angles is 360°, so here we have:

⇒ ​z + (z − 13°) + (z + 10°) = 360°

⇒ z + z + z − 13°+ 10° =  360°

⇒ 3z = 360° + 3

⇒ z  =  \(\frac{363}{3}\)

⇒ z  =  121°

​Now, we that each each interior angle makes linear pair with the exterior angle, so we have:
​
⇒ z + x = 180°

⇒ x = 180° − z

⇒ x = 180° − 121°

⇒ x = 59°

As, (z − 13° ) makes linear pair with w so we have:

⇒ ​z − 13° + w = 180°

⇒ w = 180° − 13° − 121°

⇒ w = 46°

Again (z​ + 10o) makes a linear pair with y, so we have:

⇒ z + 10° + y = 180°

⇒ y = 180° − 10°− 121°

⇒ y = 49°

​The values of the variables are :- ​x = 59° ,y = 49° ,z = 121° ,w = 46°

Savvas Learning Co Geometry Student Edition Chapter 6 Polygons And Quadrilaterals Exercise

Savvas Learning Co Geometry Student Edition Chapter 6 Polygons And Quadrilaterals Exercise Solutions Page 349  Exercise 1  Problem 1

Given: The figure as 

To find  – The value of x.

We will be using the concept of co-interior angles to find the value of the unknown variables.

From the given figure, we see that since the opposite sides of the given parallelogram are equal, so the angles formed are co-interior angles.

As co-interior angles are supplementary, so we have:

⇒ ​(3x − 14) + (2x − 16) = 18

⇒ 5x − 30 = 180

⇒ 5x = 180 + 30

⇒ 5x = 210

⇒ x = \(\frac{210}{5}\)

⇒ x = 42°

​The value of x = 42°

Read and Learn More Savvas Learning Co Geometry Student Edition Solutions

Chapter 6 Polygons And Quadrilaterals Exercise Savvas Geometry Answers Page 349  Exercise 2  Problem 2

Given: The figure as 

To find –  The value of x.

We will be using the concept of corresponding angles to find the value of unknown variable.

From the given figure, we have the lines parallel to each other, so the corresponding angles will be equal.

So, we have

⇒ ​5x  = 176 − 3x

⇒ 5x + 3x  =  176

⇒ 8x = 176

⇒ x  =  \(\frac{176}{8}\)

⇒ x  =  22°

​The value of x = 22°.

Polygons And Quadrilaterals Exercises Solutions Chapter 6 Savvas Geometry Page  349  Exercise 3  Problem 3

We have the given figure as

Polygons And Quadrilaterals Exercises Solutions Chapter 6 Savvas Geometry Page 349  Exercise 4  Problem 4

Given: The figure as

To check  –  If AB ∥ CD.

We will be using the concept of corresponding angles, to check the above asked.

Now, we know that AB is parallel to CD if the corresponding angles formed by these lines are equal, that is if

∠CDF = ∠FAB

Let us consider the ΔCFD by angles sum property, we have:

⇒ ​2x + 4x + 3x = 180

⇒ 9x = 180

⇒ x =  \(\frac{180}{9}\)

⇒ x  =  20°

So we have

⇒ ∠CDF = 4x

=   4 × 20

=   80°

⇒ ∠FAB = (3x + 18)

=  3 × 20 + 18

=  60 + 18

=  78°

As ∠CDF ≠ ∠FAB, thus the lines are not parallel.

The line AB is not parallel to CD.

Chapter 6 Polygons And Quadrilaterals Explanation Savvas Learning Co Geometry Page 349  Exercise 5  Problem 5

Given: The figure as

To check:  If AB ∥ CD.

We will be using the concept of co-interior angles to check if the two lines are parallel or not.

From the figure, we have the pair of vertically opposite angles as

​⇒ 2x + 11 = 3x − 9

⇒ 3x − 2x = 11 + 9

⇒ x = 20°

So, now we know that AB ∥ CD if the co-interior angles are supplementary

⇒ ​3x − 9 = 3 × 20 − 9

=  60 − 9

=  51°

⇒ 6x + 9 = 6 × 20 + 9

=  120 + 9

=  129°

​This gives

⇒ (3x − 9) + (6x + 9) = 180

⇒ 51°+ 129° = 180°

⇒ 180° = 180°

Which is true.

Thus, the lines are parallel.

The line AB is parallel to CD.

Chapter 6 Polygons And Quadrilaterals Explanation Savvas Learning Co Geometry Page 349  Exercise 6  Problem 6

Given:  The lines as

⇒  ​y = −2x

⇒  y − 2x + 4
​
To check: Is the lines are parallel, perpendicular or neither.

We will be calculating the slope of each line and check if they are equal than the slopes are parallel and if the product of the slopes is −1 then they are perpendicular.

We have the line as

⇒ y = −2x

Now, comparing the equation with the slope-intercept form y = mx + c gives the slope as:

⇒ m₁ = −2

The other line is

⇒ y = −2x + 4

Now, we have the slope for this as

⇒ m₂ = −2

This implies

⇒ m₁ = m₂

Thus, the lines are parallel.

The given lines ​y = −2x, y = −2x + 4 are parallel.

Solutions For Polygons And Quadrilaterals Exercises In Savvas Geometry Chapter 6 Student Edition Page 349  Exercise 7  Problem 7

Given: The lines as

⇒ ​y  =  \(\frac{−3}{5}\)  x + 1

⇒  y  = \(\frac{5}{3}\) x − 3
​
To check:  Is the lines are parallel, perpendicular or neither.

We will be calculating the slope of each line and check if they are equal than the slopes are parallel and if the product of the slopes is −1 then they are perpendicular

We have the line as

⇒  ​y = \(\frac{−3}{5}\)  x + 1

This gives us the slope as m₁ = \(\frac{−3}{5}\)

Now the other line is given as

⇒  y = \(\frac{5}{3}\) x − 3

So we have the slope as m₂  =  \(\frac{5}{3}\)

Now since the two slopes are not equal this means the lines are not parallel.

Now, we have

m₁ m₂  = \(\frac{−3}{5}\) × \(\frac{5}{3}\)

= −1

Thus, the lines are perpendicular.

The given lines ​y = \(\frac{−3}{5}\) x + 1 , y =\(\frac{5}{3}\) x − 3 are perpendicular.

Polygons And Quadrilaterals Exercises Savvas Learning Co Geometry Detailed Answers Page 349  Exercise 8  Problem 8

We are given the following figure as

From the given figure, we see that we have a parallelogram with two triangles as  ΔABC, ΔADC

Now, in the two triangles we see that the opposite sides of the parallelogram are equal and the one is the diagonal that is common between the two triangles.

That means, the two triangles are congruent using the SSS congruence rule.

The postulate or theorem that makes each pair of triangles congruent in the given figure is the Side-Side-Side (SSS) congruence rule.

Polygons And Quadrilaterals Exercises Savvas Learning Co Geometry Detailed Answers Page 349   Exercise 9   Problem 9

We are given the following figure as

From the given figure, we see that we have two triangles.

The base of both the triangles are given to be equal and the perpendicular is common in both the triangles.

Now, we see that the angle formed by the perpendicular is right angle angle in both the triangles, which gives that hypotenuse must be equal in both the triangles.

Thus, both the triangles are congruent by Right angle-Hypotenuse-Side (RHS) rule.

The postulate or theorem that makes each pair of triangles congruent is Right angle-Hypotenuse-Side (RHS) congruence rule.

Geometry Chapter 6 Polygons And Quadrilaterals Savvas Learning Co Explanation Guide Page 349  Exercise 10  Problem 10

We are given the figure ass

From the given figure, we see that we have two triangles.

The base of both the triangles are given to be equal and the angle formed on the base is right angle.

Since in both the triangles, angles are equal and length of both the angles are equal, this implies that the other leg of the angle must be equal.

Thus, both the triangles are congruent by Side Angle Side (SAS) rule.

The postulate or theorem that makes each pair of triangles congruent is Side-Angle-Side (SAS) congruence rule.

Geometry Chapter 6 Polygons And Quadrilaterals Savvas Learning Co Explanation Guide Page 349  Exercise 11  Problem 11

The word or the term “equilateral” means having all its sides of the same length.

For Example: An equilateral triangle, which means that the triangle where all the sides are of same measure or the same length.

Similarly, if we think about an equilateral polygon, we know that it is such a kind of polygon where all the sides of the it are equal.

Suppose let us take and example of polygon that is – a pentagon. The figure given below have all the sides of same measure, thus forming a pentagon with five equal sides.

The word “equilateral” means having all its sides of the same length. The equilateral polygon is the polygon where all the sides are of same length or measure.

Chapter 6 Polygons And Quadrilaterals Exercise Savvas Geometry Answers Page 349  Exercise 12  Problem 12

Now, we see that a Kite is a flat shape with straight sides. The kite is a quadrilateral with four sides.

Kite is diamond shape quadrilateral.

The geometrical characteristics of the kite are given below:

⇒  Two pair of adjacent sides are equal

⇒  The intersection of the diagonals of a kite form 90o (right) angles.  This means that they are perpendicular.

⇒  The longer diagonal of a kite bisects the shorter one.  This means that the longer diagonal cuts the shorter one in half.

⇒  The angles between the two pairs of equal adjacent sides are equal to each other.

A kite can be defines as a diamond shaped quadrilateral. The geometrical characteristics of the kite are as follows :- there are two pair of adjacent sides that are equal, the diagonals are perpendicular to each other, the longer diagonal bisects the shorter diagonal and the angles between the two pair of adjacent sides are equal.

Chapter 6 Polygons And Quadrilaterals Exercise Savvas Geometry Answers Page 349  Exercise 13  Problem 13

We know that when a team wins two consecutive gold medals, it means they have won two gold medals in a row.

This gives us the meaning of the term or the word “consecutive” as following each other continuously without interruption.

If we talk about a quadrilateral, then two consecutive angle will be one after the other, which means if one angle is ∠A, then the consecutive angle can be given by its adjacent angle ∠B
and so on.

Thus, the consecutive angle in a quadrilateral are the angles following each other without the interruption of any other angle.

The consecutive angle in a quadrilateral are the angles following each other without the interruption of any other angle.

Savvas Learning Co Geometry Student Edition Chapter 5 Relationships Within Triangles Exercise 5.1 Midsegments Of Triangles

Savvas Learning Co Geometry Student Edition Chapter 5 Exercise 5.1 Midsegments Of Triangles Solutions Page 288  Exercise 1 Problem 1

From the given figure we can see that \(\overline{N O}\) is parallel to \(\overline{J K} \)

The segment \(\overline{N O}\) is parallel to \(\overline{J K} \).

Exercise 5.1 Midsegments Of Triangles Savvas Geometry Answers Page 288  Exercise 2  Problem 2

Given: Length of the side of the triangle.

To Find – Length of NM.

Use the relationship between the length of a midsegment and the length of the side of a triangle.

We have,LK = 46

Using the relationship

Length of a midsegment = \(\frac{1}{2}\) (length of the third side)

⇒ NM  =  \(\frac{1}{2}\)(46)

⇒ NM = 23

The length of the midsegment NM is 23.

Read and Learn More Savvas Learning Co Geometry Student Edition Solutions

Exercise 5.1 Midsegments Of Triangles Savvas Geometry Answers Page 288  Exercise 3  Problem 3

A line segment that connects two midpoints of the sides of a triangle is called a midsegment.

It is a line that is drawn from one side to another, parallel to the other side.

A midsegment connects two mid points of the side of a triangle.

Exercise 5.1 Midsegments Of Triangles Savvas Geometry Answers Page 288  Exercise 4  Problem 4

The two noncollinear segments in the coordinate plane have the same slope, which means that the segments are neither perpendicular nor intersecting.

Thus, the two segments are parallel to each other which is the reason that the slopes of both the noncollinear segments are the same.

The two noncollinear segments are parallel to each other in the coordinate plane.

Midsegments Of Triangles Solutions Chapter 5 Exercise 5.1 Savvas Geometry Page 288  Exercise 5  Problem 5

In the given figure, we know that NP = PT.

Which means that P is the midpoint of the side NT.

On the other hand, there is no information if OL is equal to LT, so we can say that L is not the midpoint of the side OT.

Thus, we can say that the conclusion given by the student is not correct and PL is not parallel to NO.

The error in the student’s reasoning is that L is not the midpoint of the side OT.

Midsegments Of Triangles Solutions Chapter 5 Exercise 5.1 Savvas Geometry Page 288  Exercise 6  Problem 6

Chapter 5 Exercise 5.1 Midsegments Of Triangles Savvas Learning Co Geometry Explanation Page 288  Exercise 7  Problem 7

Given: A segment of the triangle.

To Find – The segment that is parallel to the given segment.

Use the triangle midsegment theorem.

We have the given segment,BC of the triangle

Using the triangle midsegment theorem, BC ∥ GF

The segment that is parallel to the segment BC is the segment GF.

Chapter 5 Exercise 5.1 Midsegments Of Triangles Savvas Learning Co Geometry Explanation Page 288  Exercise 8  Problem 8

Given: A segment of the triangle.

To Find – The segment that is parallel to the given segment.

Use the triangle midsegment theorem.

We have the given segment,EF of the triangle ABC.

Using the triangle midsegment theorem, EF ∥ AB

The segment parallel to the segment EF is the segment AB.

Chapter 5 Exercise 5.1 Midsegments Of Triangles Savvas Learning Co Geometry Explanation Page 288  Exercise 9  Problem 9

Given: A segment of the triangle ABC.

To Find – The segment parallel to the given segment.

Use the triangle midsegment theorem.

We have the given segment,CA of the triangle ABC.

Using the triangle midsegment theorem, CA ∥ EG

The segment parallel to the segment CA is the segment EG.

Solutions For Midsegments Of Triangles Exercise 5.1 In Savvas Geometry Chapter 5 Student Edition Page 288  Exercise 10  Problem 10

Given: A segment of the triangle ABC.

To Find –  The segment parallel to the given segment.

Use the triangle midsegment theorem.

We have the segment,EG of the triangle FGE

Using the triangle midsegment theorem, EG ∥ CA

The segment parallel to the segment EG is the segment CA.

Solutions For Midsegments Of Triangles Exercise 5.1 In Savvas Geometry Chapter 5 Student Edition Page 288  Exercise 11  Problem 11

Given: Midpoints and lengths of the sides of the ΔTUV.

To Find – The length of HE.

Use the triangle midsegment theorem.

We have

⇒ UV = 80

⇒ TV = 100 and HD = 80 also,E,D and H are the midpoints of ΔTUV

Using the triangle midsegment theorem

⇒ HE = \(\frac{1}{2}\) VU

⇒ HE = \(\frac{1}{2}\) (80)

⇒ HE = 40

The length of HE is 40 units.

Exercise 5.1 Midsegments Of Triangles Savvas Learning Co Geometry Detailed Answers Page 288  Exercise 12  Problem 12

Given: Midpoints and lengths of the sides of the ΔTUV.

To Find –  The length of ED.

Use the triangle midsegment theorem.

We have

UV = 80, TV = 100 and HD = 80 also E,D and H are the midpoints of the sides of the ΔTUV

Using the triangle midsegment theorem

⇒ ED = \(\frac{1}{2}\) TV

⇒ ED = \(\frac{1}{2}\) (100)

⇒ ED = 50

The length of ED is 50 units.

Exercise 5.1 Midsegments Of Triangles Savvas Learning Co Geometry Detailed Answers Page 288  Exercise 13  Problem 13

Given: HD = 80

To Find  –  The length of TU

In triangle TUV by midpoint theorem.

⇒ ​HD = \(\frac{1}{2}\) TU

⇒ 80 = \(\frac{1}{2}\) TU

⇒ TU = 160

​The value of TU = 160

Geometry Chapter 5 Midsegments of Triangles Savvas Learning Co explanation guide Page 288  Exercise 14  Problem 14

Given: HD = 80

To Find – The length of TE

In triangle TUV by mid point theorem.

​HD = \(\frac{1}{2}\) TU

80 = \(\frac{1}{2}\) TU

⇒ TU = 160

⇒ TU = 2 TE

⇒ TE = \(\frac{TU}{2}\)

⇒ TE = \(\frac{160}{2}\)

⇒ TE = 80

The value of TE = 80

Geometry Chapter 5 Midsegments Of Triangles Savvas Learning Co Explanation Guide Page 288  Exercise 15  Problem 15

Given:  A diagram

To Find – The value of x

In the triangle by midpoint theorem, segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side

SO,  x = \(\frac{1}{2}\) × 26

⇒  x = 13
​
The value of x = 13

Geometry Chapter 5 Midsegments of Triangles Savvas Learning Co explanation guide Page 288  Exercise 16  Problem 16

Given: A diagram

To Find  – The value of x

In the triangle by midpoint theorem, segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side

SO,  5x = \(\frac{1}{2}\) × 45

⇒  x  = 4.5

The value of x = 4.5

Savvas Learning Co Geometry Student Edition Chapter 5 Page 288  Exercise 17  Problem 17

Given: A diagram

To Find – The value of x

In the triangle by midpoint theorem, segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side

So​, 6x = \(\frac{72}{2}\)

⇒  x  =  6
​
The value of x = 6

Midsegments Of Triangles Solutions Chapter 5 Exercise 5.1 Savvas Geometry Page 289  Exercise 18  Problem 18

Given: A diagram

To Find – The value of x

In the triangle by midpoint theorem, segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side

So ​x − 4  =  \(\frac{1}{2}\) × 17

⇒  x  =  \(\frac{17}{2}\) + 4

⇒  x  =  12.5
​
The value of x = 12.5

Savvas Learning Co Geometry Student Edition Chapter 5 Page 289  Exercise 19  Problem 19

Given: A diagram

To Find –  The value of x

In the triangle by midpoint theorem, segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side

So​ x + 2 =   \(\frac{1}{2}\)  × 38

⇒ x = 19 − 2

⇒  x = 17

​The value of x = 17

Midsegments Of Triangles Solutions Chapter 5 Exercise 5.1 Savvas Geometry Page 289  Exercise 20 Problem 20

Given: A diagram

To Find –  The value of x

In the triangle by midpoint theorem, segment joining two sides of a triangle at the midpoints of those sides is parallel to the third side and is half the length of the third side.

So, ​5x − 4 = \(\frac{1}{2}\) × 8

⇒  5x = 8

⇒  x = \(\frac{8}{5}\)

⇒  x = 1.6
​
The value of x = 1.6.

Savvas Learning Co Geometry Student Edition Chapter 5 Page 289  Exercise 21  Problem 21

Given: The number of strides is shown in the triangle and the average stride is 3.5 ft

To Find  – The length of the longest side of the triangle.

In the triangle, the longest side will be in which maximum strides are paddled so the maximum number of strides is 250

The length of the longest side ​= 3.5 × 250

⇒  875ft
​
The length of the longest side is 875ft

Midsegments Of Triangles Solutions Chapter 5 Exercise 5.1 Savvas Geometry Page 289  Exercise 21  Problem 22

Given: The sides of the triangle.To find: Distance to be paddled across the lake.

Let ,a,b, c be sides of the triangle.

⇒ a = 80 + 80 = 160  (Say)

⇒ b = 250  (Say)

⇒ c = 150 + 150 = 300 (Say)

Distance to be paddled across the lake = The perimeter of the triangle × 3.5

=  (a + b + c) × 3.5

=  (160 + 250 + 300) × 3.5

=  710 × 3.5

=  2485 ft

The distance to be paddled across the lake is 2485ft.

Savvas Learning Co Geometry Student Edition Chapter 5 Page 289  Exercise 22  Problem 23

Given: The following triangular face of the Rock and Roll Hall of Fame in Cleveland, Ohio, that is isosceles is provided with congruent red segments and the length of the base is 229 feet 6 Inches or 229 ft 6 in.

Converting the given measurement of the base into inches 229 ft 6 in

=  (229 × 12) + 6 in

=  2748  +  6 in

=  2754 in

The red segments divide the legs into four congruent parts and the white segment divides each leg into two congruent parts. The white segment is a midsegment of the triangular face of the building, so its length is half the length of the base.

So, the length of the white segment

=  \(\frac{2754}{2}\)

=  1377 in

Converting to feet and inches

Length of the white segment

=   \(\frac{1377}{12}\) ft

=   114. 75 ft

=   114 ft (0.75 × 12) in

=  114 ft 9 in

The length of the white segment is 114 ft 9in.

Midsegments Of Triangles Solutions Chapter 5 Exercise 5.1 Savvas Geometry Page 289  Exercise 23  Problem 24

Given: A figure.

To find –  m ∠ QPR

S is the mid-point of QP

T is the mid-point of QR

Using the mid-point theorem, we get  ST ∥ PR

QP is a transversal and  ST ∥ PR

Therefore,∠QPR = ∠QST  (Corresponding angles)

∠QPR = 40°  (Since,∠QST  =  40°)

Using the mid-point theorem,m ∠QPR = 40°.

Savvas Learning Co Geometry Student Edition Chapter 5 Page 289  Exercise 24  Problem 25

Given: The coordinates of the vertices of a triangle  EFG.

To find – The coordinates of H & J.

Since, H is the mid-point of EG

Therefore, coordinates of

H = \(\left(\frac{1+3}{2}, \frac{2-2}{2}\right)\)

H = (2,0)

Since, J is the mid-point of FG

Therefore, coordinates of

J = \(\left(\frac{5+3}{2}, \frac{6-2}{2}\right)\)

J = (4,2)

The coordinates of H = (2,0) and of J = (4,2).

Chapter 5 Exercise 5.1 Midsegments Of Triangles Savvas Learning Co Geometry Explanation Page 289  Exercise 24  Problem 26

Given:  H,  J are the mid-points of the sides EG, FG respectively.

To prove – HJ ∥ EF

Since, H,J are the mid-points of the sides EG, FG respectively.

Therefore, using the mid-point theorem we get, HJ ∥ EF

Using the mid-point theorem we get, HJ ∥ EF

Chapter 5 Exercise 5.1 Midsegments Of Triangles Savvas Learning Co Geometry Explanation Page 289  Exercise 24  Problem 27

Given: H,J are the mid-points of the sides EG, FG respectively.

To prove –  HJ = \(\frac{1}{2}\) EF

Since, H,J  are the mid-points of the sides EG,FG, respectively.

Therefore, using the mid-point theorem we get

⇒ HJ = \(\frac{1}{2}\) EF

Using the mid-point theorem we get,HJ = \(\frac{1}{2}\) EF

Savvas Learning Co Geometry Student Edition Chapter 5 Page 289  Exercise 25  Problem 28

Given: X,Y are the mid-points of the sides UV, UW respectively.m∠UXY = 60

To find – m∠V

Since, X, Y are the mid-points of the sides UV, UW respectively.

Therefore, using the mid-point theorem we get, XY ∥ VW

Hence,∠V = ∠UXY (Corresponding angles)

⇒ m∠V = 60 (Since m∠UXY = 60)

According to the question,m∠V = 60°.

Chapter 5 Exercise 5.1 Midsegments Of Triangles Savvas Learning Co Geometry Explanation Page 289  Exercise 26  Problem 29

Given: X,Y are the mid-points of the sides UV,UW respectively.

To find –  m∠UYX

Since ,X,Y are the mid-points of the sides UV, UW respectively.

Therefore, using the mid-point theorem we get, XY ∥ VW

Hence,∠UYX = ∠W (Corresponding angles)

⇒ m∠UYX = 45 (Since m∠W = 45)

According to the given condition, m∠UYX = 45°

Savvas Learning Co Geometry Student Edition Chapter 5 Relationships Within Triangles Exercise

Savvas Learning Co Geometry Student Edition Chapter 5 Relationships Within Triangles Exercise Solutions Page 281  Exercise 1  Problem 1

Given: Use a compass and straightedge

To find –  Construct the perpendicular bisector of a segment.

Open the compass more than half of the distance between A and B n, and scribe arcs of the same radius centered at A and B.

Call the two points where these two arcs meet C and D. Draw the line between C and D.

CD is the perpendicular bisector of the line segment AB.

We have

The perpendicular bisector of a segment:

Chapter 5 Relationships Within Triangles Exercise Savvas Geometry Answers Page 281  Exercise 2  Problem 2

Given: A(5,1),B(−3,3),C(1,−7).

To find –  Find the coordinates of the midpoints of the sides and then find the lengths of the three sides of the triangle.

Find the coordinates using the midpoint formula and length using the distance formula.

We have

Read and Learn More Savvas Learning Co Geometry Student Edition Solutions

We have,the​distance​between​(x₁,​y₁),​(x₂,​y₂) : \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

To find AB, use A(5,1)and B(−3,3)

⇒  \(\sqrt{(-3-5)^2+(3-1)^2}\)

= 2\(\sqrt{17}\)

To find BC, use B(−3,3)and C(1,−7)

⇒  \(\sqrt{(1-(-3))^2+(-7-3)^2}\)

= 2\(\sqrt{29}\)

To find AC, use A(5,1)and C(1,−7)

⇒  \(\sqrt{(1-5)^2+(-7-1)^2}\)

= 4\(\sqrt{5}\)

The coordinates of the midpoint of the sides of AB, BC, AC are(1,2),(−1,−2), (3,−3)  respectively.  The length of the sides AB, BC, AC  are 2\(\sqrt{17}\), 2\(\sqrt{29}\),4 \(\sqrt{5}\) respectively.

Chapter 5 Relationships Within Triangles Exercise Savvas Geometry Answers Page 281  Exercise 3  Problem 3

Given: A(−1,2), B(9,2), C(−1,8)

To find – Find the coordinates of the midpoints of the sides and then find the lengths of the three sides of the triangle.

Find the coordinates using midpoint formula and length using distance formula.

We have

Midpoint​of​ (x₁,​y₁),​(x₂,​y₂):  \(\left(\frac{x_2+x_1}{2}, \frac{y_2+y_1}{2}\right)\)

To find AB, use A(−1,2) and B(9,2)

\(\left(\frac{9-1}{2}, \frac{2+2}{2}\right)\) = (4,2)

To find BC, use B(9,2)and C(−1,8)

\(\left(\frac{-1+9}{2}, \frac{8+2}{2}\right)\) = (4,5)

To find AC, use A(−1,2)and C(−1,8)

\(\left(\frac{-1-1}{2}, \frac{8+2}{2}\right)\) = (−1,5)

We have,the ​distance​between (x₁,​y₁),​(x₂,​y₂): \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
​
To find AB , use A(−1,2) and B(9,2)

⇒  \(\sqrt{(9-(-1))^2+(2-2)^2}\)

= 10

To find BC, use B(9,2) and C(−1,8)

⇒  \(\sqrt{(-1-9)^2+(8-2)^2}\)

= 2\(\sqrt{34}\)

To find AC, use A(−1,2)and C(−1,8)

⇒  \(\sqrt{(-1-(-1))^2+(8-2)^2}\)

= 6

The coordinates of the midpoint of the sides of AB, BC, AC are (4,2),(4,5),(−1,5) respectively. The length of the sides AB, BC, AC are 10, 2\(\sqrt{34}\), 6 respectively.

Relationships Within Triangles Exercises Solutions Chapter 5 Savvas Geometry Page 281  Exercise 4  Problem 4

Given: A(−2,−3), B(2,−3), C(0,3).

To find – Find the coordinates of the midpoints of the sides and then find the lengths of the three sides of the triangle.

Find the coordinates using the midpoint formula and length using the distance formula.

We have

Midpoint ​of (x₁,​y₁),​(x₂,​y₂): \(\left(\frac{x_2+x_1}{2}, \frac{y_2+y_1}{2}\right)\)

The midpoint of AB using A(−2,−3) and B(2,−3) is

\(\left(\frac{2-2}{2}, \frac{-3-3}{2}\right)\) = (0,−3)

The midpoint of BC using B(2,−3) and C(0,3) is

\(\left(\frac{0+2}{2}, \frac{3-3}{2}\right)\) = (1, 0)

The midpoint of AC using A(−2,−3) and C(0,3) is

\(\left(\frac{0-2}{2}, \frac{3-3}{2}\right)\) = (−1, 0)

We have the​ distance​between​ (x₁,​y₁),​(x₂,​y₂): \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
​
To find AB, use A(−2,−3) and B(2,−3) is

⇒  \(\sqrt{(2-(-2))^2+(-3-(-3))^2}\)

= 4

To find BC, use B(2,−3)and C(0,3)

⇒  \(\sqrt{(0-2)^2+(3-(-3))^2}\)

=  2\(\sqrt{10}\)

To find AC, use A(−2,−3) and C(0,3)

⇒  \(\sqrt{(0-(-2))^2+(3-(-3))^2}\)

=  2\(\sqrt{10}\)

The coordinates of midpoint of the sides of AB, BC, AC are (0,−3),(1,0),(−1,0) respectively. The length of the sides AB, BC, AC are 4, 2\(\sqrt{10}\),  2\(\sqrt{10}\) respectively.

Relationships Within Triangles Exercises Solutions Chapter 5 Savvas Geometry Page 281  Exercise 5  Problem 5

Given:  It is not too late.

To find –  The negation of a statement.

The negation of a statement is the opposite of the given mathematical statement.

It is too late is the negation of It is not too late.

The negation of the given statement is it is too late.

Chapter 5 Relationships Within Triangles Savvas Learning Co Geometry Explanation Page 281  Exercise 6 Problem 6

Given:  m∠R > 60

To find –  The negation of a statement.

The negation of a statement is the opposite of the given mathematical statement.

he measure of the angle R is not greater than 60.

The measure of the ∠R  is not greater than 60.

Solutions For Relationships Within Triangles Exercises In Savvas Geometry Chapter 5 Student Edition Page 281  Exercise 7  Problem 7

Given:  A(9,6), B(8,12)

To find – The slope of the line passing through the given points.

Slope between two points:

Slope = \(\frac{y_2-y_1}{x_2-x_1}\)

We have

⇒ (x₁,y₁) = (9,6)

⇒ (x₂,y₂) = (8,-12)

⇒ m = \(\frac{12-6}{8-9}\)

⇒ m = -6

The slope of the line passing through the given points is m =−6.

Relationships Within Triangles Exercises Savvas Learning Co Geometry Detailed Answers  Page 281  Exercise 8  Problem 8

Given: The distance between your home and your school is the length of the shortest path connecting them.

To find – How might you define the distance between a point and a line in geometry?

Distance is a numerical measurement of how far apart objects or points are.

The distance from a point to a line is the shortest distance from a given point to any point on an infinite straight line.

It is the perpendicular distance of the point to the line, the length of the line segment which joins the point to the nearest point on the line.

The distance from a point to a line is the shortest distance from a given point to any point on an infinite straight line. It is the perpendicular distance of the point to the line, the length of the line segment which joins the point to the nearest point on the line.

Savvas Learning Co Geometry Student Edition Chapter 5 Page 281  Exercise 9  Problem 9

Given:  A midpoint of a segment.

To find – What do you think a midsegment of a triangle is?

The midpoint is the middle point of a line segment.

It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints.

A midsegment of a triangle is a segment that connects the midpoints of two sides of a triangle.

A midsegment of a triangle is a segment that connects the midpoints of two sides of a triangle.

Relationships Within Triangles Exercises Savvas Learning Co Geometry Detailed Answers Page 281  Exercise 10  Problem 10

Given: If two parties are happening at the same time, they are concurrent.

To find –  What would it mean for three lines to be concurrent?

Lines in a plane or higher-dimensional space are said to be concurrent if they intersect at a single point.

Three or more lines in a plane passing through the same point are concurrent lines.

When a third line also passes through the point of intersection made by the first two lines then these three lines are said to be concurrent lines.

The point of intersection of all these lines is called the ‘Point of Concurrency’.

Three or more lines in a plane passing through the same point are concurrent lines. When a third line also passes through the point of intersection made by the first two lines then these three lines are said to be concurrent lines. The point of intersection of all these lines is called the ‘Point of Concurrency’.

Savvas Learning Co Geometry Student Edition Chapter 4 Congruent Triangles Exercise 4.2 Triangles Congruence By SSS And SAS

Savvas Learning Co Geometry Student Edition Chapter 4 Exercise 4.2 Triangles Congruence by SSS and SAS solutions Page 230  Exercise 1  Problem 1

In the given situation, we need to name the angle that is included between the given sides.

Let us draw a figure of the triangle with given information

According to the above figure

1. The angle that is included between the sides, \(\overline{\mathrm{PE}} \text { and } \overline{\mathrm{EN}}\) is ∠PEN.

2. The angle that is included between the sides, \(\overline{N P} \text { and } \overline{P E}\) is ∠NPE.

1. The angle that is included between the sides \(\overline{\mathrm{PE}} \text { and } \overline{\mathrm{EN}}\) is ∠PEN.

2. The angle that is included between the sides,  \(\overline{N P} \text { and } \overline{P E}\) is ∠NPE.

Read and Learn More Savvas Learning Co Geometry Student Edition Solutions

Exercise 4.2 Triangles Congruence By Side Side Side And Side Angle Side Savvas Geometry Answers
Page 230  Exercise 2  Problem 2

In the given situation, we need to name the sides between which given angles are included.

Let us draw a figure of the triangle with given information,

According to the above figure

1. The sides which includes  \(\angle H \text { are } \overline{A H} \text { and } \overline{\mathrm{HT}}\)

2.The sides which includes  \(\angle T \text { are } \overline{H T} \text { and } \overline{T A}\)

Exercise 4.2 Triangles Congruence By Side Side Side And Side Angle Side Savvas Geometry Answers
Page 230  Exercise 3  Problem 3

In the given situation, we need to name the postulate that will be used to prove the triangles congruent.

The diagram shows that  \(\overline{\mathrm{BC}} \cong \overline{E C}\) and also  \(\overline{A C} \cong \overline{D C}\).

As  \(\angle A C B \cong \angle D C E\)  by vertically opposite angle.

Therefore Δ ABC≅ Δ DEC by using the Side Angle Side postulate (SAS).

Side Angle Side postulate (SAS) postulate would be used to prove the given triangles congruent.

Triangles Congruence By Sss And Sas Solutions Chapter 4 Exercise 4.2 Savvas Geometry Page 230  Exercise 4  Problem 4

In the given situation, we need to find the postulate that would be used to prove the triangles congruent.

The diagram shows that \(\overline{A B} \cong \overline{C D}\) and \(\overline{A D} \cong \overline{B C}\)

Also by the Reflexive Property of Congruence. \(\overline{B D} \cong \overline{B D}\)

Therefore, the given triangles are congruent by using Side-Side-Side (SSS) theorem.

The given triangles are congruent by using Side-Side-Side (SSS) theorem.

Savvas Learning Co Geometry Student Edition Chapter 4 Page 230  Exercise 5  Problem 5

In the given question, we need to find what are the similarities and differences between SAS and SSS postulates.

How are the SAS Postulate and SSS Postulate​ alike?

1. They both require three congruency statements.

2. They both use two sides and one angle.

3. They both use one side and two angles.

4. They both can be used to prove that triangles are congruent.

5. They both use three sides.

How are the SAS Postulate and SSS Postulate​ different?

1. They require different numbers of congruency statements.

2. They apply to different kinds of triangles​ (acute or​ obtuse).

3. They use different numbers of sides​ and/or angles.

4. SSS can be used to prove two triangles are​ congruent, while SAS can be used to prove that corresponding angles are congruent.

The SSS and SAS Postulates are different and alike as well.

Chapter 4 Exercise 4.2 Triangles Congruence By Side Side Side And Side Angle Side Savvas Learning Co Geometry Explanation Page 230  Exercise 6  Problem 6

In the given situation, we need to find that the able triangles are congruent by which theorem.

Let us re-draw the given triangles

The diagram shows that,  \(\overline{A B} \cong \overline{P Q}\)  and  \(\overline{\mathrm{BC}} \cong \overline{Q R}\)

Also, ∠BAC ≅ ∠QPR

Therefore, the given triangles can be proven right congruent by using the Side Angle Side postulate (SAS).

The given triangles can be proven congruent by using the Side Angle Side postulate (SAS).

Solutions For Triangles Congruence By Sss And Sas Exercise 4.2 In Savvas Geometry Chapter 4 Student Edition Page 230  Exercise 7  Problem 7

Given: The side length of the first triangle is 7 ft and the side length of the second triangle is 21 ft.

To Find –  If two triangles are congruent.

Proof: According to the question,

∵  Side length of Δ ABC = 7 ft and side length of Δ PQR = 21 ft

Since, side length if both the triangles are in ratio1:3

Therefore Δ ABC ≅ ΔPQR, by using Side-Side-Side (SSS) theorem.

Triangles with side 7 ft and  21 ft are congruent by SSS theorem.

Exercise 4.2 Triangles Congruence By Side Side Side And Side Angle Side Savvas Learning Co Geometry Detailed Answers Page 230  Exercise 8  Problem 8

Given: \(\overline{J K}\) ≅ \(\overline{L M}\),\(\overline{J M}\) ≅ \(\overline{K K}\)

Proof:

 \(\overline{J K}\) ≅ \(\overline{L M}\)  (Given)

\(\mathrm{J} \overline{\mathrm{M}} \cong \overline{K K}\)  (Given)

\(\overline{K M} \cong \overline{K M}\) (Reflexive property of congruence )

Therefore, ΔJKM≅ m ΔLMK, by SSS theorem.

ΔJKM and ΔLMK are congruent using the SSS theorem.

Savvas Learning Co Geometry Student Edition Chapter 4 Page 230  Exercise 9  Problem 9

Given:    \(\overline{I E} \cong \overline{G H}\),   \(\overline{E F}\) ≅ \(\overline{H F}\)  and F is the midpoint of GI

The figure:

To Find – Prove EFI ≅ HFG

When we compare these two triangles, we get that they have equal corresponding sides as we can see from the figure.

⇒  \(\overline{I E} \cong \overline{G H}\)

⇒  ​\(\overline{E F} \cong \overline{H F}\)

⇒  \(\overline{F I} \cong \overline{F G}\)

We know, that F is the midpoint of \(\overline{G I}\)

The midpoint divides the side into two equal parts.

Based on the SSS congruence theorem, these two triangles are congruent.

Hence, proved.

By the SSS Congruence theorem, the given triangles are congurent.

Geometry Chapter 4 Triangles Congruence By Side Side Side And Side Angle Side Savvas Learning Co Explanation Guide Page 230  Exercise 10  Problem 10

Given: \(\overline{W Z}\) ≅ \(\overline{S D}\) ≅ \(\overline{D W}\)

The figure:

To find –  Prove \(\mathrm{WZD} \cong S D Z\)

When we compare these two triangles WZD and SDZ we get that they have equal corresponding sides, as we can see from the given figure

⇒  \(\overline{W Z}\) ≅ \(\overline{S D}\) ≅ \(\overline{D W}\)

⇒  \(\overline{Z D} \cong \overline{Z D}\)

⇒  \(\overline{Z D}\)

Is the common side for both triangles based on the SSS Congruence theorem , these two traiangles are congruent.

Hence , proved

\(\overline{Z D}\) common side for both triangles. Based on the SSS congruence theorem thes two triangles are congruent.

Savvas Learning Co Geometry Student Edition Chapter 4 Page 231  Exercise 11  Problem 11

Given: 

The figure

To Find – What other information, if any, do you need to prove the two triangles congruent by SAS? Explain.

When we compare these two triangles RTS and WVU we get that they have equal corresponding sides, as we see that the figure.

⇒   \(T R\) ≅   \(\overline{V W}\)

⇒  \(\angle R \cong \angle W\)

⇒  \(\overline{T S} \cong \overline{V U}\)

∠R are the included angles for sides \(\overline{T R}\), \(\overline{T S}\)

∠W are the included angles for sides  \(\overline{V W}\), and  \(\overline{V U}\)

Now, we have to find the included angles for the sides.

When we compare these two triangles we get that they have equal corresponding angles, as we can see from the figure.

⇒  \(\angle T \cong \angle V\)

∠T are the included angles for sides   \(\overline{T R}\), \(\overline{T S}\)

∠V are the included angles for sides \(\overline{V W}\), and \(\overline{V U}\)

The additional information that we need to prove that these two triangles are congruent using the SAS Congruence theorem is

⇒    ∠T ≅ ∠V

Now, we will find corresponding sides for the included angles R and W.

∠R are the included angles for sides \(\overline{T R}\), \(\overline{T S}\)

∠W are the included angles for sides \(\overline{V W}\), and  \(\overline{V U}\)

The additional information that we need to prove that these two triangles are congruent using the SAS Congruence theorem is

⇒  \(R S\)   ≅  \(\overline{W U}\).

The additional information we need is   ∠T ≅ ∠V,  \(R S\) ≅  \(\overline{W U}\)

The additional information we need is   ∠T ≅ ∠V,  RS ≅  \(\overline{W U}\)

Page 231  Exercise 12  Problem 12

Given: 

The figure

To Find – Would you use SSS or SAS to prove the triangles congruent? If there is not enough information to prove the triangles congruent by SSS or SAS, write not enough information. Explain your answer.

When we compare these two triangles PQT and SQR we get that they have equal corresponding sides, as we see that the figure

⇒  \(P T \cong \overline{S R}\)

⇒  \(Q T \cong \overline{Q R}\)

⇒ ∠PQT and ∠SQR are vertical angles.

So,∠PQT≅∠SQR

∠PQT is not the included for sides \(\overline{P T}\) and \(\overline{Q T}\)

∠SQR is not the included angles for sides \(\overline{S R}\) and \(\overline{Q R}\)

There is not enough information to prove that triangles PQT and SQR are congruent using the SSS and the SAS Congruence Theorem.

There is not enough information to prove that triangles PQT and SQR are congruent using the SSS and the SAS Congruence Theorem.

Savvas Learning Co Geometry Student Edition Chapter 4 Page 231  Exercise 13  Problem 13

Given:

The figure

To Find –  Would you use SSS or SAS to prove the triangles congruent? If there is not enough information to prove the triangles congruent by SSS or SAS, write not enough information.

Explain your answer.  When we compare these two triangles ABC and CDA we get that they have equal corresponding sides, as we see that the figure

⇒  \(A B\)  ≅ \(\overline{D C}\)

∠BAC ≅ ∠DCA

⇒  \(A C \cong \overline{A C}\)

∠AC are the common side for both triangles.

∠BAC are the included angles for sides \(\overline{A B} \text { and } \overline{A C}\)

∠DCA are the included angles for the sides \(\overline{D C} \text { and } \overline{A C}\)

Based on SAS Congruence Theorem, these two triangles ABC and CDA are congruent.

We would use the SAS Congruence theorem.

By the SAS Congruence Theorem, these two triangles are congruent.

Savvas Learning Co Geometry Student Edition Chapter 4 Page 231  Exercise 14  Problem 14

Given: Each triangle should have two 5inches sides and an angle of 40degrees

To find – Which postulate, SSS or SAS, are you likely to apply to the given situation?

SAS postulate says that two triangles are congruent if two sides of one triangle are congruent with the corresponding sides of the other triangle and the angle that overlaps those two sides are congruent with the corresponding angle of the other triangle.

These two triangles have two equal corresponding sides of 5 inches and 40 degrees angle.

Based on the SAS congruence theorem, these two triangles are congruent.

Diagram:

The SAS congruence theorem, prove two triangles are congruent. The diagram

Savvas Learning Co Geometry Student Edition Chapter 4 Page 231  Exercise 15  Problem 15

Given:  \(B C \cong \overline{D A}\),  \(\angle \bar{C} B \bar{D} \cong \angle A D B\)

The figure

To find – Prove BCD ≅ DAB

When we compare these two triangles BCD and DAB we get that they have equal corresponding sides, as we see that the figure:

⇒  \(B C \cong \overline{D A}\)

⇒  \(\angle C B D \cong \angle A D B\)

⇒  \(B D \cong \overline{B D}\)

∠CBD are the included angles for side \(\overline{B C} \text { and } \overline{B D}\)

∠ADB are the included angles for sides \(\overline{D A} \text { and } \overline{B D}\)

Based on the SAS Congruence Theorem, these two triangles BCD and DAB are congruent.

The SAS Congruence Theorem probe triangle BCD and DAB congruent.

Savvas Learning Co Geometry Student Edition Chapter 4 Page 231  Exercise 16  Problem 16

Given: The pairs A(1,4), B(5,5), C(2,2), D(−5,1), E(−1,0), F(−4,3)​

To find – Use the Distance Formula to determine whether ABC and DEF are congruent. Justify your answer.

The distance formula:

AB = \(\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}\)

Now, we will calculate the side length of triangles ABC based on this formula

Now calculate for AB, BC, AC

A(1,4) , B(5,4)

⇒ AB = \(\sqrt{(1-5)^2+(4-5)^2}\)

⇒ AB = \(\sqrt{16+7}\)

⇒ AB = \(\sqrt{17}\)

B (5,5), C(2,2)

⇒ BC = \(\sqrt{(5-2)^2+(5-2)^2}\)

⇒ BC = \(\sqrt{9+9}\)

⇒ BC = \(\sqrt{18}\)

A(1,40, C(2,2)

⇒ AC = \(\sqrt{(1-2)^2+(4-2)^2}\)

⇒ AC = \(\sqrt{1+4}\)

⇒ AC = \(\sqrt{5}\)

Now, we know the length of the sides of a triangle DEF.

Now, we will calculate the length of the sides of a triangle DEF.

Calculate for DE, EF, DF.

D (-5, 1), E(-1,0)

⇒ DE = \(\sqrt{(-5-(-1))^2+(1-0)^2}\)

⇒ DE = \(\sqrt(16+1)\)

⇒ DE = \(\sqrt{17}\)

E (-1,0), F (-4,30

⇒ EF = \(\sqrt{\left(-1-(-4)^2+(0-3)^2\right.}\)

⇒ EF = \(\sqrt{9+9}\)

⇒ EF = \(\sqrt{18}\)

D (-5,1), F (-4,3)

⇒ DF = \(\sqrt{\left(-5-(-4)^2+(1-3)^2\right.}\)

⇒ DF = \(\sqrt{1+4}\)

⇒ DF = \(\sqrt{5}\)

When we compare the length of the sides of these two triangles we get that:

⇒ ​AB = DE

⇒ BC = EF

⇒ AC = DF

Based on SSS Congruence Theorem, these two triangles are congruent.

The SSS Congruence Theorem proves that the two triangles are congruent.

Savvas Learning Co Geometry Student Edition Chapter 4 Page 231  Exercise 17  Problem 17

Given: The A(3,8), B(8,12), C(10,5), D(3,−1), E(7,−7), F(12,−2)

To find – Use the Distance Formula to determine whether ABC and DEF are congruent. Justify your answer.

Given,A(3,8), B(8,12), C(10,5)​,D(3,−1), E(7,−7)F(12,−2)
​
Now use the distance formula:

Formula: \(\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}\)

Now substitute for AB, BC, CA, DE, EF, FD

⇒ AB = \(\sqrt{(8-3)^2+(12-8)^2}\) = \(\sqrt{41}\)

⇒ BC =  \(\sqrt{(10-8)^2+(5-12)^2}\) = \(\sqrt{53}\)

⇒ CA = \(\sqrt{(10-3)^2+(5-8)^2}\)= \(\sqrt{58}\)

⇒ DE =  \(\sqrt{(7-3)^2+\left(-7-(-1)^2\right.}\)= \(\sqrt{52}\)

⇒ EF =  \(\sqrt{(12-7)^2+\left(-2-(-7)^2\right.}\)= \(\sqrt{50}\)

⇒ FD =  \(\sqrt{(12-3)^2+\left(-2-(-1)^2\right.}\)= \(\sqrt{82}\)

We compute the lengths of each triangle’s edges, using the formula of distance.

So, Triangle ABC ≅ DEF

Since the triangles have different lengths of edges, they are not congruent.

The triangle ABC and DEF are not congruent.

Savvas Learning Co Geometry Student Edition Chapter 4 Page 231  Exercise 18  Problem 18

Given: The pairs A(2,9), B(2,4), C(5,4), D(1,−3), E(1,2), F(−2,2)

To find – Use the Distance Formula to determine whether ABC and DEF are congruent. Justify your answer.

The distance formula:

AB = \(\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}\)

Now, we will calculate the side length of triangles ABC based on this formula:

Now calculate for AB, BC, AC

A(2,9) , B(2,4)

⇒ AB =  \(\sqrt{(2-2)^2+(9-4)^2}=\sqrt{25}\) = 5

⇒ BC =  \(\sqrt{(2-5)^2+(4-4)^2}=\sqrt{9}\)= 3

⇒ AC =  \(\sqrt{(2-5)^2+(9-4)^2}=\sqrt{34}\)

Now , we caculated for DE, EF, DF

⇒ DE =  \(\sqrt{(1-1)^2+\left(-3-2)^2\right.}=\sqrt{25}\) = 5

⇒ EF =  \(\sqrt{(1-(-2))^2+\left(-2-2)^2\right.}=\sqrt{9}\)= 3

⇒ DF= \(\sqrt{(-1)-2)^2+\left(-3-2)^2\right.}=\sqrt{34}\).

We compare  the lengths of the sides of these triangles we get that

⇒ AB= DE

⇒ BC = EF

⇒ AC= DF

Based on SSS Congruence theorem.. these two triangles are congruent.

The  SSS Congruence theorem.. these two triangles are congruent. 

Savvas Learning Co Geometry Student Edition Chapter 4 Page 231  Exercise 19  Problem 19

Given: Congruent triangles.

To find – List three real-life uses of congruent triangles.

For each real-life use, describe why you think congruence is necessary.

Two triangles are said to be congruent if they are of the same size and same shape.

Two congruent triangles have the same area and perimeter.

When we consider the application of congruent triangles in real life, the first thing I remember is toys for children can be in the shape of triangles that are congruent.

Congruent triangles are used in the construction to reinforce the structure.

Jewelry can also consist of congruent triangles.

When we consider the application of congruent triangles in real life, toys for children can be in the shape of triangles that are congruent. Congruent triangles are used in the construction to reinforce the structure. Jewelry can also consist of congruent triangles.

Savvas Learning Co Geometry Student Edition Chapter 4 Page 232  Exercise 20  Problem 20

Given: Use a straightedge to draw any triangle JKL

To find –   ΔMNP ≅ ΔJKL using SSS and SAS theoremThe SSS theorem states that two triangles are congruent if three sides of one are equal respectively to three sides of the other The SAS theorem states that two triangles are equal if two sides and the angle between those two sides are equal.

To prove ΔMNP ≅ ΔJKL using SSS theorem

We’ll start by drawing a triangle JKL, then a line adjacent to it with the point M marked on it.

The length of the line JL will then be measured with the opening of the compass and transferred from point M to the line.

The point P is obtained by intersecting the arc with the line.

Then we’ll use a compass to transfer the distance JK from point M to point P, and then we’ll use the compass to transfer the distance LK from point P to point M.

The point N is formed by the intersection of these two arcs.

Finally, we shall connect these points to form the triangle MNP.

We have

To prove using SAS theorem.

We’ll start by drawing a triangle JKL , then a line adjacent to it with the point M marked on it.

Then, using the opening of the compass, we’ll measure the length of the line JK and transfer it from point M to the line.

The point N is found at the intersection of the arc and the line.

Then, from the point M , we’ll transfer the arc with the angle at the vertex J and its length, and then, from the point M , we’ll transfer the distance JL via the compass’s opening, and finally, from the point M , we’ll transmit the distance JL

The point P is formed by the intersection of these two arcs.

Finally, we’ll connect these points to form the MNP triangle.

We have

By SSS theorem ΔMNP ≅ ΔJKL

By SAS theorem ΔMNP≅ΔJKL

Savvas Learning Co Geometry Student Edition Chapter 4 Page 232  Exercise 21  Problem 21

Given: Two triangle ΔYHD AND ΔKPT

​YH = KP

HD = PT
​
To find – Triangles are congruent to each other.

Equate the corresponding sides of the one triangle to the second triangle.

In the above figure

As Given

YH = KP

HD = PT
​
As We are missing the third information for congruency criteria to be applied

We need a side to apply SSS or an angle to apply SAS.

NO, We can not.

We need third information to apply congruency criteria which can be a side or an angle to the corresponding sides

Page 232  Exercise 22  Problem 22

Given: Two triangles ΔGJK and ΔGMK

GJ = GM

∠IGK = ∠MGK

To find: Triangles are congruent to each other.

Equate the corresponding sides of the one triangle to the second triangle.

In the above figure

As Given In ΔGJK and ΔGMK

​GJ = GM

∠IGK = ∠MGK

GK = GK
​
Using SAS congruency criterion ΔGJK ≅ ΔGMK

Using SAS congruency criterion ΔGJK ≅ ΔGMK

Savvas Learning Co Geometry Student Edition Chapter 4 Page 232  Exercise 23  Problem 23

Given: Two triangles where AE and BD bisect each other.

To find –  Triangles are congruent to each otherEquate the corresponding sides of the one triangle to the second triangle.

In ΔACB and ΔECD

It is given that AE and BD biscet each other so

​AC = CE

BC = CD

Also, ∠ACB = ECD (Vertically opposite angle)

By using SAS congruency criterion

ΔACB ≅ ΔECD

Using SAS congruency criterion,ΔACB ≅ ΔECD

Page 232  Exercise 24  Problem 24

Given: Two triangles where AB⊥CM, AB⊥DB, CM = DB

To find –  Triangles are congruent to each other.

Equate the corresponding sides of the one triangle to the second triangle.

Mid-pointIn ΔAMC and ΔMBD

It is given that CM = AB
​
As ∠AMC = ∠MBD

= 90

Also as m is the mid -point AM = MB

By using the SAS congruency criterion ΔAMC ≅ ΔMBD

Using SAS congruency criterion, ΔAMC ≅ ΔMBD

Savvas Learning Co Geometry Student Edition Chapter 4 Page 232  Exercise 25  Problem 25

Given: polygon ABCD whose four sides are congruent.

To find –  EFGH and ABCD and EFGH are congruent or not Using the definition of congruent polygons, ABCD and EFGH are congruent of the corresponding angles are also congruent.

A quadrilateral is not rigid because, for the same side lengths, the interior angles can be different

Using the definition of congruent polygons, ABCD and EFGH are congruent of the corresponding angles are also congruent A quadrilateral is not rigid because, for the same side lengths, the interior angles can be different

Page 232  Exercise 26  Problem 26

Given: Two triangles where HK = LG, HF = LJ, FG = JK

To find –  Triangles are congruent to each otherEquate the corresponding sides of the one triangle to the second triangle.

In ΔFGH and ΔJKL

It is given that

⇒ HK = LG,HF = LJ,FG = JK

⇒ As HK = LG

Adding both sides GK we get

⇒ HK + GK = LG + GK

⇒ HG = KL

By using SSS congruency criteria We get  ΔFGH ≅ ΔJKL

By using SSS congruency Criterion ΔFGH ≅ ΔJKL

Savvas Learning Co Geometry Student Edition Chapter 4 Page 232  Exercise 27  Problem 27

Given: Two triangles where ∠N = ∠L,MN = OL,NO = LM

To find – Prove MN ∥ OL

Equate the corresponding sides of the one triangle to the second triangle.

In ΔONM and ΔMLO

It is given that

⇒ ∠N = ∠L,MN = OL,NO = LM

By using the SAS congruency criterion we can say that, ΔONM ≅ ΔMLO

Also Using CPCT in the congruent triangles

∠NOM = ∠LMO which is a pair of alternate interior angles.

So MN ∥ OL

MN ∥ OL as ∠NOM = ∠LMO is pair of alternate interior angles.

Page 232  Exercise 28  Problem 28

Given: Two Triangles ΔVWY and ΔVWZ where ∠VWY = ∠VWZ

To find  –  Conditions for the triangles to be congruent by SAS.

As given ∠VWY = ∠VWZ also, we have a common side VW = VW

So we need another side to apply the SAS congruency criterion which can be YW = ZW and no other option can satisfy it

The correct answer  is  which is YW = ZW to satisfy SAS congruency criterion

Savvas Learning Co Geometry Student Edition Chapter 4 Page 232 Exercise 29 Problem 29

Given: Two angles of a triangle equal to 43 and 38.

To find – Measure of third angle

Let The third angle be ∠A.

Then we know that sum of all interior angles is 180

So, according to question

​⇒ 43 + 38 + ∠A = 180

⇒ 81 + ∠A = 180

⇒ ∠A = 180 − 81

⇒ ∠A = 99

​The right anser is ∠A = 99

The correct answer is which is equal to 99

Page 232  Exercise 30  Problem 30

Given: ABCD ≅ EFGH

To find –  Side 9s de that corresponds to BC

So, given here ABCD ≅ EFGH both are congruent. And the rule for writing congruency is to write the corresponding same angles and sides of shapes.

For eg; if in ΔABC and ΔDEF, ∠A = ∠E, AB = DE, and BC = DF. Then congruency will be written as ΔABC ≅ ΔEDF.

So, according to the given congruency here, we can figure out a few points.

Angles: ∠A = ∠E,∠B = ∠F,∠C = ∠G and ∠D = ∠H

Sides: AB = EF,BC = FG,CD = GH and DA = HE

Side corresponding to BC in congruency relation ABCD ≅ EFGH is FG.

Savvas Learning Co Geometry Student Edition Chapter 4 Page 232  Exercise 3 1 Problem 31

Given: If x  = 3, then x² = 9

To find: Converse of statement and determine if true or false.

Here hypothesis is x = 3 and conclusion is  x²  = 9.

So, the converse of the given statement will be “If x² = 9, then x = 3″.

Simplifying the conclusion in the given statement by taking root both sides, we get x = ±3.

So, there are two solutions for the conclusion.

The statement is true, Converse is false.