Marksparks

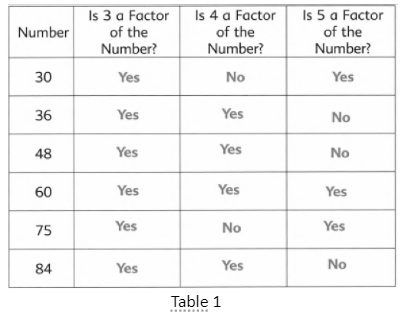
Primary Mathematics Chapter 3 Fractions

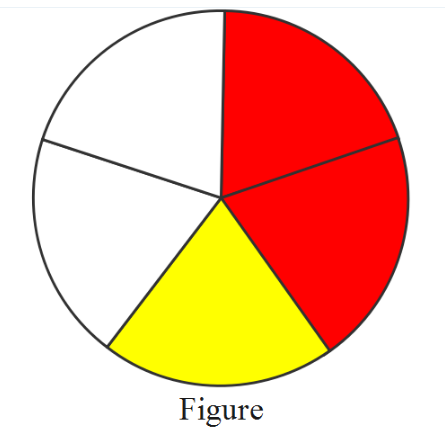
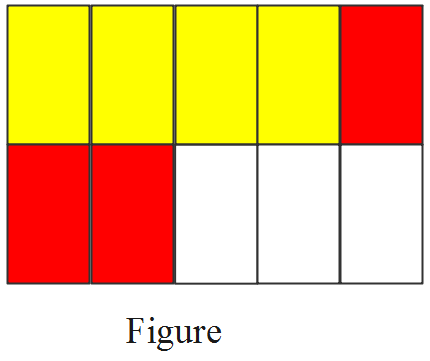
Primary Mathematics Workbook 4A Common Core Solutions Chapter 3 Fractions Exercise 3.4 Page 91  Exercise 3.4  Problem 1

Given:  Expression \(\frac{4}{5}\)–\(\frac{1}{5}\)= ______

Question is to find the difference between the given numbers.

Subtraction of a fractional number can be done by making their denominators same.

As the denominators are same here, just by adding directly, answers can be obtained.

The answer can be obtained by analyzing the given figure also.

The difference can be found by subtracting the numerators directly as the denominators are same.

⇒ \(\frac{4}{5}\)–\(\frac{1}{5}\)

⇒ \(\frac{4}{5}\)–\(\frac{1}{5}\)= \(\frac{3}{5}\)

So the difference between given numbers is found to be \(\frac{3}{5}\)

Also, by analyzing the figure, out of4 shaded part, 1 is subtracted. So, 3 shaded parts out of 5 parts remain.

Therefore, solution for the given expression=_______ is \(\frac{3}{5}\).

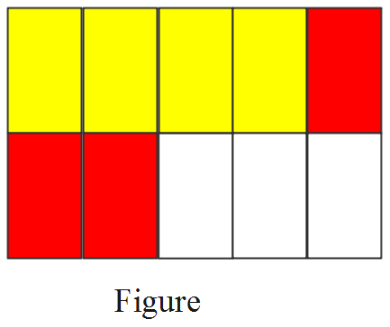
Chapter 3 Fractions Exercise 3.4 Answers Workbook 4A Common CorePage 91  Exercise 3.4 Problem 2

Given:  Expression \(\frac{4}{6}\)–\(\frac{3}{6}\)= \(\frac{3}{5}\)= ______

Question is to find the difference between the given numbers.

Subtraction of a fractional number can be done by making their denominators same.

As the denominators are same here, just by adding directly, answers can be obtained.

The answer can be obtained by analyzing the given figure also.

The difference can be found by subtracting the numerators directly as the denominators are same.

⇒ \(\frac{4}{6}\)–\(\frac{3}{6}\)= \(\frac{3}{5}\)= \(\frac{4-3}{6}\)

⇒ \(\frac{4}{6}\)–\(\frac{3}{6}\)= \(\frac{3}{5}\)= \(\frac{1}{6}\)

Therefore, solution for the given expression \(\frac{4}{6}\)− \(\frac{3}{6}\)=____ is  \(\frac{3}{5}\)= \(\frac{1}{6}\).

Primary Mathematics 4A Fractions Exercise 3.4 Step-By-Step Solutions Page 91  Exercise 3.4  Problem 3

Given:  Expression \(\frac{5}{8}\)–\(\frac{2}{8}\)=____

The question is to find the difference between the given numbers.

Subtraction of a fractional number can be done by making their denominators same.

As the denominators are the same here, just by adding directly, answers can be obtained.

The answer can be obtained by analyzing the given figure also.

The difference can be found by subtracting the numerators directly as the denominators are the same.

⇒ \(\frac{5}{8}\)–\(\frac{2}{8}\)= =\(\frac{5-2}{8}\)

⇒ \(\frac{5}{8}\)–\(\frac{2}{8}\)= =\(\frac{3}{8}\)

So the difference between given numbers is found to be\(\frac{3}{8}\)

Also, by analyzing the figure, out of 5 shaded parts, 2 is subtracted. So, 3 shaded parts out of 8 parts remain.

Therefore, solution for the given expression \(\frac{5}{8}\)–\(\frac{2}{8}\)=_____ is \(\frac{5-2}{8}\).

Fractions Exercise 3.4 Explanation Common Core Workbook 4A Page 91 Exercise 3.4  Problem 4

Given:  Expression \(\frac{7}{10}\)–\(\frac{4}{10}\)=____

The question is to find the difference between the given numbers.

Subtraction of a fractional number can be done by making their denominators same.

As the denominators are same here, just by adding directly, answers can be obtained.

The answer can be obtained by analyzing the given figure also.

The difference can be found by subtracting the numerators directly as the denominators are same.

⇒ \(\frac{7}{10}\)–\(\frac{4}{10}\)=\(\frac{7-4}{10}\)

⇒ \(\frac{7}{10}\)–\(\frac{4}{10}\)=\(\frac{3}{10}\)

So the difference between given numbers is found to be \(\frac{3}{10}\)

Also, by analyzing the figure, out of 7 shaded parts, 4 is subtracted. So, 3 shaded parts out of 10 parts remains.

Therefore, solution for the given expression ⇒ \(\frac{7}{10}\)−\(\frac{4}{10}\)=____ is \(\frac{3}{10}\)

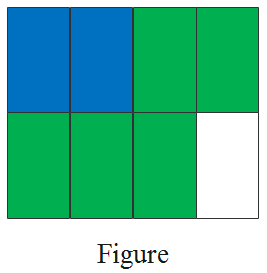
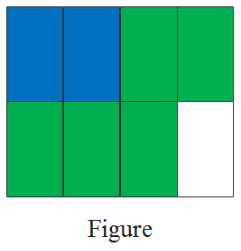
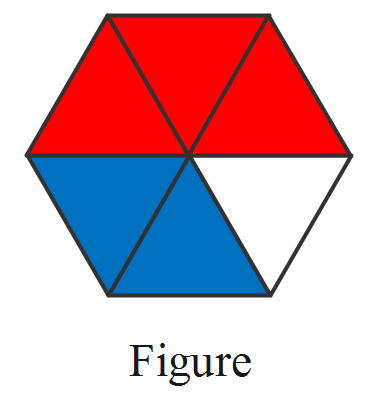
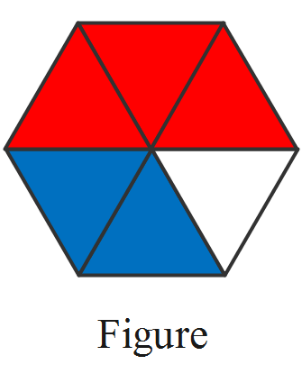
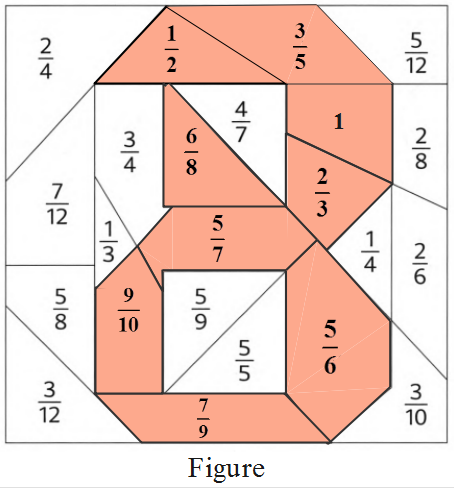
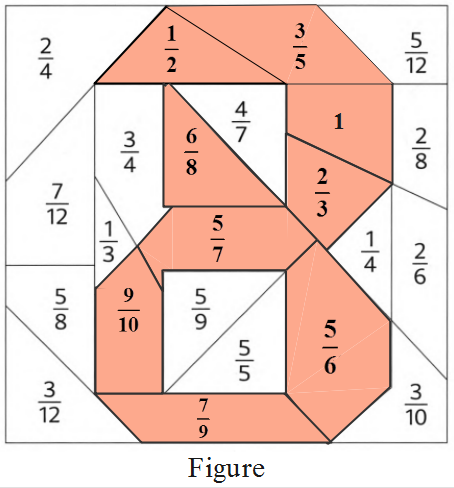
Exercise 3.4 Fractions Detailed Explanation Workbook 4A Page 92  Exercise 3.4 Problem  5

Given:  A set of additions and a figure.

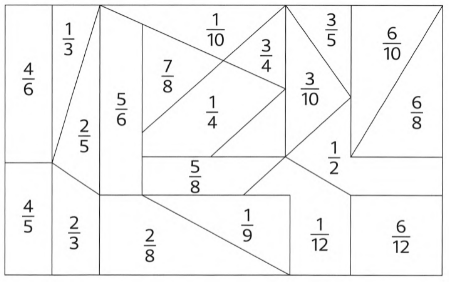
Question is to color the given figures that contain the answers of the given Subtractions.

Subtraction of a fractional number can be done by making their denominators same.

As the denominators are same here, just by Subtracting directly, answers can be obtained.

Subtraction of the given expression can be done as

1)\(\frac{2}{3}-\frac{1}{3}\)=\(\frac{1}{3}\)

2)\(\frac{4}{5}-\frac{2}{5}\)=\(\frac{4}{5}\)

3)\(\frac{5}{6}-\frac{1}{6}\)=\(\frac{4}{6}\)

4)\(\frac{7}{8}-\frac{2}{8}\)=\(\frac{5}{8}\)

5)\(\frac{5}{8}-\frac{3}{8}\)=\(\frac{2}{8}\)

6)\(\frac{7}{8}-\frac{1}{8}\)=\(\frac{6}{8}\)

7)\(\frac{9}{10}-\frac{3}{10}\)=\(\frac{6}{109}\)

8)\(\frac{7}{10}-\frac{4}{10}\)=\(\frac{3}{10}\)

9)\(\frac{7}{12}-\frac{6}{12}\)=\(\frac{1}{12}\)

So, the answers of the given subtractions  are\(\frac{1}{3}\),\(\frac{4}{5}\),\(\frac{4}{6}\),\(\frac{5}{8}\),\(\frac{2}{8}\),\(\frac{6}{8}\),\(\frac{6}{109}\), and \(\frac{1}{12}\)

Now, the two times seven can be found by coloring the figures that contain the answers.

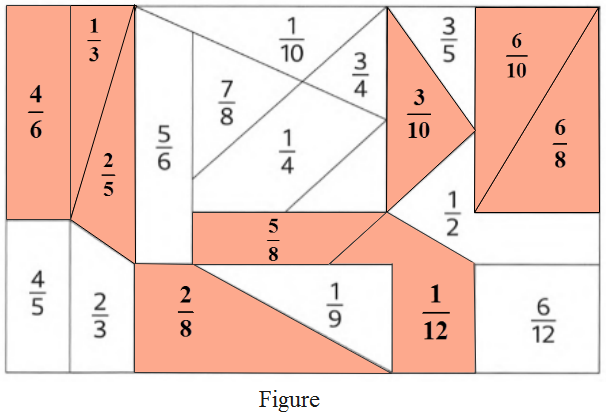
From the figure, after coloring, the number appearing is 14. So, two times seven is 14

Therefore, the answers in their simplest form for the given expressions are \(\frac{1}{3}\),\(\frac{4}{5}\),\(\frac{4}{6}\),\(\frac{5}{8}\),\(\frac{2}{8}\),\(\frac{6}{8}\),\(\frac{6}{109}\), and \(\frac{1}{12}\) respectively. After coloring the figures that contain the answers, two times seven is obtained as 14.

Common Core Primary Mathematics Workbook 4A Fractions Help Chapter 3 Page 93  Exercise 3.4  Problem 6

Given:  Expression \(1-\frac{1}{4}-\frac{1}{4}\)=________

Question is to find the difference between the given numbers.

Subtraction of a fractional number can be done by making their denominators same.

As the denominators are not same here, by finding the LCM and making the denominator same, answers can be obtained.

The answer can be obtained by analyzing the given figure also.

As denominators are different, LCM is needed to make the denominator same.

LCM = 1×4

LCM = 4 Then the numbers will become

\(\frac{1 \times 4}{1 \times 4}-\frac{1}{4}-\frac{1}{4}\)=_______

Now, the difference can be found by subtracting the numerators directly as the denominators are same.

⇒ \(\frac{4}{4}-\frac{1}{4}-\frac{1}{4}\)= \(\frac{4-1-1}{4}\)

⇒ \(\frac{4}{4}-\frac{1}{4}-\frac{1}{4}\)= \(\frac{2}{4}\)

⇒ \(\frac{4}{4}-\frac{1}{4}-\frac{1}{4}\)= \(\frac{1}{2}\)

So the difference between given numbers is found to be \(\frac{1}{2}\)

Therefore, the solution for the given expression 1−1 \(1-\frac{1}{4}-\frac{1}{4}\)=________in its shortest form is \(\frac{1}{2}\)

Primary Mathematics 4A Exercise 3.4 Common Core Fraction Problems Page 93   Exercise 3.4  Problem 7

Given:  Expression 1-\(\frac{3}{5}\)=_______

Question is to find the difference between the given numbers.

Subtraction of a fractional number can be done by making their denominators same.

As the denominators are not same here, by finding the LCM and making the denominator same, answers can be obtained.

The answer can be obtained by analyzing the given figure also.

As d e nominators are different, LCM is needed to make the denominator same.

LCM = 1  ×5

LCM  = 5

Then the numbers will become

\(\frac{1 \times 5}{1 \times 5}-\frac{3}{5}\)=_______

Now, the difference can be found by subtracting the numerators directly as the denominators are same.

⇒ \(\frac{5}{5}-\frac{3}{5}\)=\(\frac{5-3}{5}\)

⇒ \(\frac{5}{5}-\frac{3}{5}\)=\(\frac{2}{5}\)

So the difference between given numbers is found to be \(\frac{5}{5}-\frac{3}{5}\)=\(\frac{2}{5}\).

Therefore, the solution for the given expression \(\frac{1 \times 5}{1 \times 5}-\frac{3}{5}\)=_______in its shortest form is \(\frac{2}{5}\)

Fractions Exercise 3.4 Primary Mathematics Workbook 4A Worksheet Help Page 93  Exercise 3.4  Problem 8

Given:  Expression\(\frac{4}{5}\)−\(\frac{3}{5}\)−\(\frac{1}{5} \)=______

Question is to find the difference between the given numbers.

Subtraction of a fractional number can be done by making their denominators same.

As the denominators are same here, just by adding directly, answers can be obtained.

The answer can be obtained by analyzing the given figure also.

The difference can be found by subtracting the numerators directly as the denominators are same.

⇒ \(\frac{4}{5}−\frac{3}{5}\)−\(\frac{1}{5}\)= \(\frac{4-3-1}{5}\)

⇒ \(\frac{4}{5}−\frac{3}{5}\)−\(\frac{1}{5}\)= \(\frac{0}{5}\)

⇒ \(\frac{4}{5}−\frac{3}{5}\)−\(\frac{1}{5}\) = 0

So the difference between given numbers is found to be 0.

Therefore, the solution for the given expression \(\frac{4}{5}−\frac{3}{5}\)−\(\frac{1}{5}\)=______ in its shortest form is

Page 93 Exercise 3.4 Problem  9

Given: Gwen bought 1 kg of potatoes in which she used \(\frac{4}{7}\) Kg to make some potasto salad and another \(\frac{2}{7}\) Kg to make some mashed potato.

Question is to find how many kilograms of potatoes she have left and write the answer in its simplest form.

By subtracting the used potatoes from total potatoes bought will give the required answer.

Subtraction of a fractional number can be done by making their denominators same.

As the denominators are not same here, by finding the LCM and making the denominator same, answers can be obtained.

Now, to make some mashed potato, Gwen uses\(\frac{2}{7}\) Kg out of the remaining\(\frac{3}{7}\) Kg of potatoes left.

Then, net potatoes left can be obtained by subtracting potatoes used for making mashed potatoes from potatoes left after making salad.

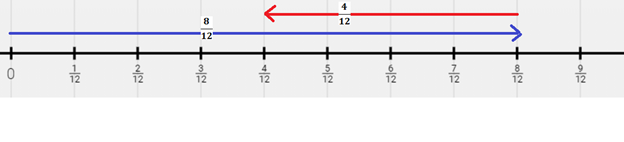
⇒  \(\frac{3}{7}\) −  \(\frac{2}{7}\)= \(\frac{1}{7}\)

So, the total potatoes left is \(\frac{1}{7}\) kg.

 Page 94  Exercise 3.5  Problem 1

In the problem, the figure is given with a note 3 wholes 1 half

It is required to write a mixed number.

As it is given there are 3 wholes and 1 half.

This can be written as,

1+1+1+\(\frac{1}{2}\)= 3 + \(\frac{1}{2}\)

The mixed number obtained for 3 wholes and 1 half is 3 \(\frac{1}{2}\)

 Page 94  Exercise 3.5  Problem 2

In the problem, the figure is given with note 2 wholes 4 fifths.

It is required to write a mixed number.

As it is given there are 2 wholes and 4 fifths.

This can be written as

1+1+\(\frac{4}{5}\)= 2+\(\frac{4}{5}\)

1+1+\(\frac{4}{5}\) = 2\(\frac{4}{5}\)

The mixed number obtained for 2 wholes and 4 fifths is 2\(\frac{4}{5}\)

Page 94  Exercise 3.5  Problem 3

In the problem, the figure is given with note 2 wholes 4 fifths.

It is required to write a mixed number.

As it is given there are 2 wholes and 4 fifths.

This can be written as

1+1+\(\frac{4}{5}\)= 2+\(\frac{4}{5}\)

1+1+\(\frac{4}{5}\)= 2 \(\frac{4}{5}\)

The mixed number obtained for 2 wholes and 4 fifths is 2 \(\frac{4}{5}\).

 Page 94  Exercise 3.5  Problem 4

In the problem, the figure is given with a note 2 wholes 1 sixth.

It is required to write a mixed number.

As it is given there are 2 wholes and 1 sixth.

This can be written as

1+1+\(\frac{1}{6}\)= 2+\(\frac{1}{6}\)

1+1+\(\frac{1}{6}\)= 2\(\frac{1}{6}\)

The mixed number obtained for 2 wholes and 1 sixth is 2\(\frac{1}{6}\)

Page 94  Exercise 3.5  Problem 5

In the problem, the figure is given with a note 3 wholes 7 eighths.

It is required to write a mixed number

As it is given there are 3 wholes an6 7 eighths.

This can be written as

1+1+1+\(\frac{7}{8}\)= 3+\(\frac{7}{8}\)

1+1+1+\(\frac{7}{8}\)= 3\(\frac{7}{8}\)

The mixed number obtained for 3 wholes and 7 eighths is  3\(\frac{7}{8}\)

Page 95  Exercise 3.5  Problem 6

In the problem, a figure is with 3 strings and their lengths are given.

It is required to fill the blanks with a length of string B and C.

So solve this, first consider string B there are 1 whole and 3 fifth.

This can be written as

1+ \(\frac{3}{5}\)= 1\(\frac{3}{5}\)

Consider string C there are 2 wholes and 2 fifth.

This can be written as

1 + 1 + \(\frac{2}{5}\)= 2\(\frac{2}{5}\).

The length of B is  1\(\frac{3}{5}\)M, The length of C is  2\(\frac{2}{5}\)

Page 95  Exercise 3.5  Problem 7

In the problem, a figure is given where 3 wholes and 1fifth liters are represented.

It is required to find the total amount of water.

As it is given there are 3 wholes and 1 fifth liter.

This can be written as a mixed number

1+1+1+\(\frac{1}{5}\)= 3+\(\frac{1}{5}\)

1+1+1+\(\frac{1}{5}\)= 3\(\frac{1}{5}\)

The total amount of water is  3\(\frac{1}{5}\)

Page 95  Exercise 3.5  Problem 8

In the problem, a figure with a note 2+\(\frac{3}{4}\)is given

It is required to fill the blanks, find 2+\(\frac{3}{4}\)

As it is given, 2 wholes and 3 fourth will give a mixed number

2 + \(\frac{3}{4}\) = 2\(\frac{3}{4}\)

For given  2 + \(\frac{3}{4}\), the mixed number is obtained  2\(\frac{3}{4}\)

Page 95  Exercise 3.5  Problem 9

In the problem, a figure with a note 3-\(\frac{1}{3}\) is given.

It is required to fill the blanks, find 3-\(\frac{1}{3}\).

As it is given, 2 wholes and 2 third will give a mixed number 1 + 1 + \(\frac{2}{3}\)= 2\(\frac{2}{3}\) that means,

3 – \(\frac{1}{3}\) =  2\(\frac{2}{3}\)

For the given 3-\(\frac{1}{3}\) the mixed number is obtained as 2\(\frac{2}{3}\).

Page 97  Exercise 3.6  Problem 1

In the problem, a figure is given where 2 wholes and 5 sixths are represented.

It is required to write a mixed number and an improper fraction.

To solve this, there are 2 wholes and 5 sixths.

This can be written as

1 + 1 + \(\frac{5}{6}\)= 2+\(\frac{5}{6}\)

1 + 1 + \(\frac{5}{6}\) = 2\(\frac{5}{6}\)

As it is given there are 2 wholes and 5 sixths.

The count of the total shaded portion will give the numerator and the number of separations made in one single shape will give the denominator.

Here the numerator is 17 and the denominator is 6 so the improper fraction is  \(\frac{17}{6}\)

The mixed number obtained for 2 wholes and 5 sixths is  2\(\frac{5}{6}\) and the improper fraction obtained is \(\frac{17}{6}\)

Page 97 Exercise 3.6 Problem 2

In the problem, a figure is given where 2 wholes and 4 ninths are represented.

It is required to write a mixed number and an improper fraction.

To solve this, there are 2 wholes and 4 ninths.

The mixed number can be written as

1 + 1 + \(\frac{4}{9}\)  = 2 + \(\frac{4}{9}\)

1 + 1 + \(\frac{4}{9}\) = 2\(\frac{4}{9}\)

As it is given there are 2 wholes and 4 ninths.

The count of the total shaded portion will give the numerator and the number of separations made in one single shape will give the denominator.

Here the numerator is 22 and the denominator is 9 so the improper fraction is\(\frac{22}{9}\).

The mixed number obtained for 2 wholes and 4 ninths is  2\(\frac{4}{9}\) and the improper fraction obtained is \(\frac{22}{9}\).

Page 97 Exercise 3.6 Problem 3

In the problem, a figure is given where 1 wholes and 2 nthirds are represented.

It is required to write a mixed number and an improper fraction.

To solve this, there are 1 wholes and 2 thirds. The mixed number can be written as,

1 + \(\frac{2}{3}\) =1 +\(\frac{2}{3}\)

1 + \(\frac{2}{3}\) = 1\(\frac{2}{3}\)

As it is given there are 1 wholes and 2 thirds.

The count of the total shaded portion will give the numerator and the number of separations made in one single shape will give the denominator.

Here the numerator is 5 and the denominator is 3 so the improper fraction is  \(\frac{5}{3}\).

The mixed number obtained for 1 wholes and 2 thirds is  1\(\frac{2}{3}\) and the improper fraction obtained is  \(\frac{5}{3}\).

Page 97 Exercise 3.6 Problem 4

In the problem, a figure is given where 3 wholes and 3 fourth are represented.

It is required to write a mixed number and an improper fraction.

To solve this, there are 3 wholes and 3 fourth.

The mixed number can be written as,

1 + 1 + 1 + \(\frac{3}{4}\) = 3 + \(\frac{3}{4}\)

1 + 1 + 1 + \(\frac{3}{4}\) = 3\(\frac{3}{4}\)

As it is given there are 3 wholes and 3 fourth.

The count of the total shaded portion will give the numerator and the number of separations made in one single shape will give the denominator.

Here the numerator is 15 and the denominator is 4 so the improper fraction is  \(\frac{15}{4}\).

The mixed number obtained for 3 wholes and 3 fourth is  3\(\frac{3}{4}\) and the improper fraction obtained is  \(\frac{15}{4}\).

Page 97  Exercise 3.6  Problem 5

In the problem, a figure is given where 2 wholes and 3 fifths are represented.

It is required to write a mixed number and an improper fraction.

To solve this, there are 2 wholes and 3 fifths.

The mixed number can be written as,

1 + 1 + \(\frac{3}{5}\)= 2+\(\frac{3}{5}\)

1 + 1 + \(\frac{3}{5}\) =  2\(\frac{3}{5}\)

As it is given there are 2 wholes and 3 fifths.

The count of the total shaded portion will give the numerator and the number of separations made in one single shape will give the denominator.

Here the numerator is 13 and the denominator is 5 so the improper fraction is \(\frac{13}{5}\).

The mixed number obtained for 2 wholes and 3 fifths is  2\(\frac{3}{5}\) and the improper fraction obtained is \(\frac{13}{5}\).

Page 97  Exercise 3.6  Problem 6

In the problem, a figure is given where 2 wholes and 7 eighths are represented.

It is required to write a mixed number and an improper fraction.

To solve this, there are 2 wholes and 7 eighths.

The mixed number can be written as

1 + 1 + \(\frac{7}{8}\) = 2 + \(\frac{7}{8}\)

1 + 1 + \(\frac{7}{8}\) = 2\(\frac{7}{8}\)

As it is given there are 2 wholes and 7 eighths.

The count of the total shaded portion will give the numerator and the number of separations made in one single shape will give the denominator.

Here the numerator is 23 and the denominator is 8 so the improper fraction is \(\frac{23}{8}\).

The mixed number obtained for 2 wholes and 7 eighths is  2\(\frac{7}{8}\)and the improper fraction obtained is \(\frac{23}{8}\).

Page 98  Exercise 3.7  Problem 1

In the problem, it is given an improper fraction \(\frac{11}{4}\).

The picture representations are also given. It is required to express

In the problem, it is given an improper fraction \(\frac{11}{4}\)as a mixed number.

To solve this, rewrite the given improper fraction as the sum of two fractions.

Where the first fraction will give a whole number and the second one is a proper fraction. Then obtain the mixed number.

\(\frac{11}{4}\)= \(\frac{8}{4}\)+ \(\frac{3}{4}\)

\(\frac{11}{4}\) = 2 + \(\frac{3}{4}\)

\(\frac{11}{4}\)= 2\(\frac{3}{4}\)

The improper fraction  \(\frac{11}{4}\) is expressed as a mixed number  2\(\frac{3}{4}\).

Page 98  Exercise 3.7  Problem 2

In the problem, it is given an improper fraction \(\frac{18}{5}\)

The picture representations are also given.It is required to express \(\frac{18}{5}\) as a mixed number.

To solve this, rewrite the given improper fraction as the sum of two fractions.

Where the first fraction will give a whole number and the second one is a proper fraction. Then obtain the mixed number.

\(\frac{18}{5}\) = \(\frac{15}{5}\)+\(\frac{3}{5}\)

\(\frac{18}{5}\) = 3 + \(\frac{3}{5}\)

\(\frac{18}{5}\) = 3\(\frac{3}{5}\)

The improper fraction  \(\frac{18}{5}\) is expressed as a mixed number  3\(\frac{3}{5}\).

Page 98  Exercise 3.7  Problem 3

In the problem, a figure of improper fractions is given .

It is required to fill each box with a mixed number or a whole number.

To solve this, rewrite the given improper fraction as the sum of two fractions.

Where the first fraction will give a whole number and the second one is a proper fraction.

Then obtain the mixed number or a whole number.

Improper fraction \(\frac{5}{3}\)

\(\frac{5}{3}\)= \(\frac{3}{3}\)+\(\frac{2}{3}\)

\(\frac{5}{3}\)=1+\(\frac{2}{3}\)

\(\frac{5}{3}\)= 1\(\frac{2}{3}\)

Improper fraction \(\frac{7}{3}\) to mixed fraction

\(\frac{7}{3}\) =\(\frac{6}{3}\) +\(\frac{1}{3}\)

\(\frac{7}{3}\)  = 2 + \(\frac{1}{3}\)

\(\frac{7}{3}\) = 2\(\frac{1}{3}\)

Improper fraction \(\frac{9}{3}\) to a whole number.

\(\frac{9}{3}\)= 3

Improper fraction \(\frac{11}{3}\) to a mixed number.

\(\frac{11}{3}\)= \(\frac{9}{3}\)+ \(\frac{2}{3}\)

3 +\(\frac{2}{3}\)

\(\frac{11}{3}\) = 3\(\frac{2}{3}\)

 Therefore: The box for \(\frac{5}{3}\) can be filled with a mixed number 1\(\frac{2}{3}\).

The box for \(\frac{7}{3}\)can be filled with a mixed number 2\(\frac{1}{3}\).

The box for\(\frac{9}{3}\) can be filled with a mixed number 3.

The box for\(\frac{11}{3}\) can be filled with a mixed number 3\(\frac{2}{3}\).

Page 99  Exercise 3.7  Problem 4

In the problem, it is given an improper fraction

It is required to change the improper fraction to a mixed number or a whole number.

To solve this, rewrite the given improper fraction as the sum of two fractions with the same denominator.

Where the first fraction will give a whole number and the second one is a proper fraction.

Then obtain the mixed number.

= 2 + \(\frac{1}{2}\)

= 2\(\frac{1}{2}\)

The improper fraction \(\frac{5}{2}\)  is changed to a mixed number  2\(\frac{1}{2}\)

Page 99  Exercise 3.7  Problem 5

In the problem, it is given an improper fraction

It is required to change the improper fraction to a mixed number or a whole number.

To solve this, rewrite the given improper fraction as the sum of two fractions with the same denominator.

Where the first fraction will give a whole number and the second one is a proper fraction.

Then obtain the mixed number.

= 1+\(\frac{7}{10}\)

= 1\(\frac{7}{10}\)

The improper fraction  \(\frac{17}{10}\)  is changed to a mixed number  1\(\frac{7}{10}\)

Page 99 Exercise 3.7 Problem 6

In the problem, it is given an improper fraction\(\frac{7}{6}\)

It is required to change the improper fraction to a mixed number or a whole number.

To solve this, rewrite the given improper fraction as the sum of two fractions with the same denominator.

Where the first fraction will give a whole number and the second one is a proper fraction. Then obtain the mixed number.

\(\frac{7}{6}\) =\(\frac{6}{6}\)+\(\frac{1}{6}\)

= 1 + \(\frac{1}{6}\)

= 1\(\frac{1}{6}\)

The improper fraction \(\frac{7}{6}\)  is changed to a mixed number 1\(\frac{1}{6}\)

Page 99 Exercise 3.7 Problem 7

In the problem, it is given an improper fraction \(\frac{7}{3}\)

It is required to change the improper fraction to a mixed number or a whole number.

To solve this, rewrite the given improper fraction as the sum of two fractions.

Where the first fraction will give a whole number and the second one is a proper fraction. Then obtain the mixed number.

\(\frac{7}{3}\) = \(\frac{6}{3}\)=\(\frac{1}{3}\)

= 2  + \(\frac{1}{3}\)

= 2\(\frac{1}{3}\)

The improper fraction  \(\frac{7}{3}\)  is changed to a mixed number 2\(\frac{1}{3}\).

Page 100  Exercise 3.8  Problem 1

Given:  An image of the circles – whole circles and also circles divided into portions of equal size.

Find the improper fraction from the image.

Given that, 2 whole circles are there.

Each circle is divided into 3 parts.

Then

2 =  \(\frac{2×3}{3}\)

\(\frac{6}{3}\)= 2

​Therefore, the improper fraction for 2 whole circles divided into 3 parts is \(\frac{6}{3}\).

Page 100 Exercise 3.8 Problem 2

Given:  An image of the circles – whole circles and also circles divided into portions of equal size.

Find the improper fraction from the image.

Given that, 2 whole circles and \(\frac{2}{3}\) circles.

Two of the circles are divided into 3 parts.

Then

2\(\frac{2}{3}\) = 2 + \(\frac{2}{3}\)

=  \(\frac{2×3}{3}\) + \(\frac{2}{3}\)

​=  \(\frac{6}{3}\) + \(\frac{2}{3}\)

=  \(\frac{8}{3}\)

Therefore, the improper fraction for  2\(\frac{2}{3}\)  is  \(\frac{8}{3}\)

Page 100 Exercise 3.8 Problem 3

Given:  An image of the circles – whole hexagons and also hexagon divided into portions of equal size.

Find the improper fraction from the image.

Therefore, we can do the calculation as

1\(\frac{5}{6}\) = 1 + \(\frac{5}{6}\)

= \(\frac{1×6}{6}\) + \(\frac{5}{6}\)

=\(\frac{6}{6}\) + \(\frac{5}{6}\)

= \(\frac{11}{6}\)

Therefore, the improper fraction for  1\(\frac{5}{6}\)  is  \(\frac{11}{6}\)

Page 100  Exercise 3.8 Problem 4

Given:  An image of the circles – whole squares and also squares divided into portions of equal size.

Find the improper fraction from the image.

We can calculate and write as

2\(\frac{3}{8}\)= 2+\(\frac{3}{8}\)

= \(\frac{2×8}{6}\) + \(\frac{3}{8}\)

= \(\frac{16}{8}\) + \(\frac{3}{8}\)

= \(\frac{19}{8}\)

Therefore, the improper fraction for  2\(\frac{3}{8}\)  is  \(\frac{19}{8}\).

Page 101  Exercise 3.8  Problem 5

Given: 1\(\frac{2}{5}\)

Convert the given mixed fraction into improper fraction.

Represent it as the sum of a whole number and improper fraction.

Then add them up to get a single improper fraction.

Given ,  1\(\frac{2}{5}\)

Converting it

1\(\frac{2}{5}\) = 1+ \(\frac{2}{5}\)

= \(\frac{1×5}{5}\) +\(\frac{2}{5}\)

= \(\frac{5}{5}\)+\(\frac{2}{5}\)

= \(\frac{7}{5}\)

Therefore, the improper fraction for = 1 + \(\frac{2}{5}\) is \(\frac{7}{5}\)

Page 101  Exercise 3.8  Problem 6

Given: 1\(\frac{1}{4}\)

Convert the given mixed fraction into improper fraction.

Represent it as the sum of a whole number and improper fraction.

Then add them up to get a single improper fraction.

Given ,  1\(\frac{1}{4}\)

Converting it

1\(\frac{1}{4}\)= 1 + \(\frac{1}{4}\)

= \(\frac{1×4}{4}\) + \(\frac{1}{4}\)

= \(\frac{4}{4}\) + \(\frac{1}{4}\)

= \(\frac{5}{4}\)

Therefore, the improper fraction for 1\(\frac{1}{4}\) is = \(\frac{5}{4}\)

Page 101 Exercise 3.8 Problem 7

Given: 2\(\frac{3}{8}\).

Convert the given mixed fraction into improper fraction.

Represent it as the sum of a whole number and improper fraction.

Then add them up to get a single improper fraction.

Given ,  2\(\frac{3}{8}\)

Converting it

2\(\frac{3}{8}\) =  2+\(\frac{3}{8}\)

= \(\frac{2×8}{4}\) + \(\frac{3}{8}\)

= \(\frac{16}{8}\) + \(\frac{3}{8}\)

= \(\frac{19}{8}\)

Therefore, the improper fraction for  2\(\frac{3}{8}\) is \(\frac{19}{8}\).

Page 101 Exercise 3.8  Problem 8

Given: 2\(\frac{1}{10}\)

Convert the given mixed fraction into improper fraction.

Represent it as the sum of a whole number and improper fraction.

Then add them up to get a single improper fraction.

Given, 2\(\frac{1}{10}\)

Converting it

2\(\frac{1}{10}\)= 2 + \(\frac{1}{10}\)

= \(\frac{2×10}{10}\) + \(\frac{1}{10}\)

= \(\frac{20}{10}\) + \(\frac{1}{10}\)

= \(\frac{21}{10}\)

Therefore, the improper fraction for  2\(\frac{1}{10}\) is \(\frac{21}{10}\).

Page 102 Exercise 3.8  Problem 9

Given: \(\frac{3}{5}\)+\(\frac{2}{5}\)

Add the given fractions and simplify it.

Denominator is the same.

So adding numerators and writing the denominator will give the result.

\(\frac{3}{5}\)+\(\frac{2}{5}\)=\(\frac{3+2}{5}\)

= \(\frac{5}{5}\)

This can be further simplified as 1.

Therefore, the simplest form for \(\frac{3}{5}\)+\(\frac{2}{5}\) is \(\frac{5}{5}\) or 1.

Page 102  Exercise 3.8  Problem 10

Given: \(\frac{1}{3}\)+\(\frac{2}{3}\).

Add the given fractions and simplify it.

Denominator is the same.

So adding numerators and writing the denominator will give the result.

\(\frac{1}{3}\)+\(\frac{2}{3}\)

= \(\frac{3}{3}\)

This can be further simplified as 1

Therefore, the simplest form for \(\frac{1}{3}\)+\(\frac{2}{3}\) is\(\frac{3}{3}\) or 1.

Page 102  Exercise 3.8  Problem 11

Given: \(\frac{3}{4}\)+\(\frac{3}{4}\)

Add the given fractions and simplify it.

Denominator is the same.

So adding numerators and writing the denominator will give the result.

\(\frac{3}{4}\)+\(\frac{3}{4}\)= \(\frac{3+3}{4}\)

= \(\frac{6}{4}\)

= \(\frac{3}{2}\)

There is a common factor of 2, so the simplest form is obtained as \(\frac{3}{2}\).

Therefore, the simplest form for  \(\frac{3}{4}\)+\(\frac{3}{4}\) is  \(\frac{3}{2}\).

Page 102  Exercise 3.8  Problem 12

Given: \(\frac{4}{7}\)+\(\frac{5}{7}\)

Add the given fractions and simplify it.

Denominator is the same.

So adding numerators and writing the denominator will give the result.

\(\frac{4}{7}\)+\(\frac{5}{7}\)= \(\frac{4+5}{7}\)

= \(\frac{9}{7}\)

Therefore, the simplest form for  \(\frac{4}{7}\)+\(\frac{5}{7}\)  is  \(\frac{9}{7}\).

Page 102  Exercise 3.8  Problem 13

Given: 1 \(\frac{1}{2}\) and \(\frac{7}{8}\)

Find whether given fractions are equal to, or less than, or greater than the other.

First, convert the mixed fraction into an improper fraction.

Make them like fractions for comparing them easily.

Then compare the fractions and write the proper symbol.

Given , 1 \(\frac{1}{2}\) and \(\frac{7}{8}\)

Convert the given mixed fraction into improper fraction as follows.

1 \(\frac{1}{2}\) = \(\frac{2+1}{1}\)

= \(\frac{3}{2}\)

Now making them like fractions.

The denominator of the fractions is different so multiply the number to get the same denominator.
​
\(\frac{3}{2}\) =\(\frac{3×4}{2×4}\)

= \(\frac{12}{8}\)

Now , 1 \(\frac{1}{2}\) = \(\frac{12}{8}\).

So, we have to compare \(\frac{12}{8}\) and \(\frac{7}{8}\)

Since 12>7

\(\frac{12}{8}\) is greater than \(\frac{7}{8}\)

Or we can say that

1 \(\frac{1}{2}\) > \(\frac{7}{8}\).

Therefore, after making them like fractions and comparing, we can write as 1 \(\frac{1}{2}\) > \(\frac{7}{8}\).

Page 102  Exercise 3.8  Problem 14

Given: \(\frac{6}{7}\) and 1.

Find whether given fractions are equal to, or less than, or greater than the other.

First, convert the whole number into an improper fraction.

Make them like fractions for comparing them easily.

Then compare the fractions and write the proper symbol.

Given, \(\frac{6}{7}\) and 1.

Convert the given whole number into improper fraction as follows.

Multiply and divide 7 to get a fraction,
​
​1=1×\(\frac{7}{7}\)

= \(\frac{7}{7}\)

= 1 ​Now making them like fractions.

Now, 1 = \(\frac{7}{7}\)

So, we have to compare \(\frac{6}{7}\) and \(\frac{7}{7}\)

Since 6<7

\(\frac{6}{7}\) is lesser than \(\frac{7}{7}\).

Or we can say that\(\frac{6}{7}\)<1.

Therefore, after making them like fractions and comparing, we can write as \(\frac{6}{7}\)<1.

Page 102  Exercise 3.8  Problem 15

Given: \(\frac{10}{11}\) and \(\frac{11}{3}\)

Find whether given fractions are equal to, or less than, or greater than the other.

Make them like fractions for comparing them easily.

Then compare the fractions and write the proper symbol.

Given, \(\frac{10}{11}\) and \(\frac{11}{3}\)

Now making them like fractions.

The denominator of the fractions isdifferent so multiply the number to get the same denominator.
​
\(\frac{10}{11}\) = \(\frac{10×3}{11×3}\)

= \(\frac{30}{33}\)

\(\frac{11}{3}\) = \(\frac{11×11}{3×11}\)

= \(\frac{121}{33}\)

Now

\(\frac{10}{11}\)= \(\frac{30}{33}\) and

\(\frac{11}{3}\)]= \(\frac{121}{33}\)

So, we have to compare \(\frac{30}{33}\) and \(\frac{121}{33}\)

Since 30<121

\(\frac{30}{33}\) is lesser than \(\frac{121}{33}\)

Or we can say that \(\frac{10}{11}\)< \(\frac{11}{3}\)

Therefore, after making them like fractions and comparing them, we can write as  \(\frac{10}{11}\)< \(\frac{11}{3}\)

​Page 102 Exercise 3.8 Problem 16

Given: \(\frac{10}{3}\) and 3 \(\frac{1}{3}\)

Find whether given fractions are equal to, or less than, or greater than the other.

First, convert the mixed fraction into an improper fraction.

Make them like fractions for comparing them easily.

Then compare the fractions and write the proper symbol.

Given, \(\frac{10}{3}\) and 3 \(\frac{1}{3}\)
​
Convert the given mixed fraction into improper fraction as follows.
​
3 \(\frac{1}{3}\)

=\(\frac{(3×3)+1}{3}\)

= \(\frac{9+1}{3}\)

= \(\frac{10}{3}\)

​Now making them like fractions.

Now,3 \(\frac{1}{3}\)= \(\frac{10}{3}\)

So, we have to compare\(\frac{10}{3}\) and \(\frac{10}{3}\)

Since 10 = 10

\(\frac{10}{3}\) is equal to \(\frac{10}{3}\)

Or we can say that \(\frac{10}{3}\) = 3\(\frac{1}{3}\)

Therefore, after making them like fractions and comparing, we can write as  \(\frac{10}{3}\)= 3\(\frac{1}{3}\)

Page 103  Exercise 3.8  Problem 17

Given:

A figure with various mixed fractions.

To convert these mixed fractions into standard form.

Firstly, Convert all mixed fractions into standard form.

Finally, represent this in a figure.

From the figure various mixed fractions are-

The improper form of these fractions is given as-

\(1 \frac{3}{4}\)= \(\frac{7}{4}\)

\(2 \frac{1}{4}\)= \(\frac{9}{4}\)

\( 2 \frac{3}{4}\)= \(\frac{11}{4}\)

\(3 \frac{2}{4}\)= \(\frac{14}{4}\)

Now, for whole number 1.

Since its a number line of denominator 4.

Therefore, multiply and dividing 1 by 4.

So

1×\(\frac{4}{4}\)= \(\frac{4}{4}\)

Hence 1 can be written \(\frac{4}{4}\).

Representing these in a figure-

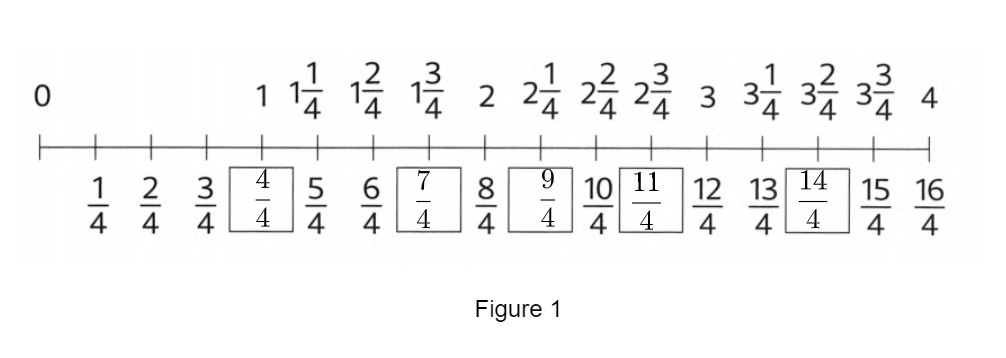
The figure filling each box with an improper fraction is given as-

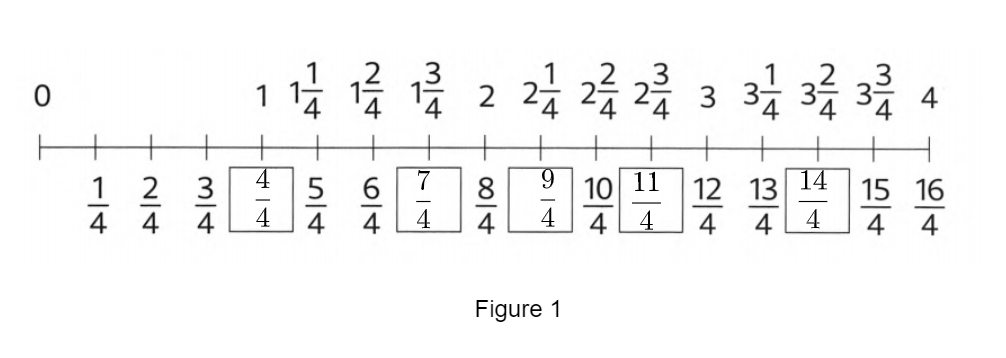
Page 103  Exercise 3.8  Problem 18

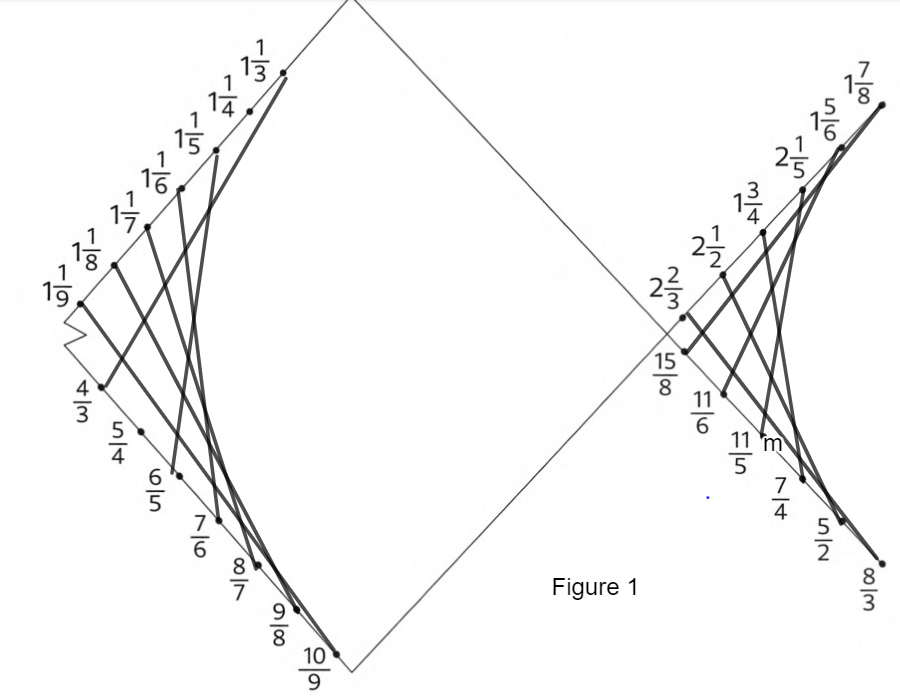
Given:

Various mixed fractions.

To match equal fractions after converting these mixed fractions into standard form.

Firstly, Convert all mixed fractions into standard form.

Then, match equal fractions with each other.

Finally, represent this in a figure.

From the figure given mixed fractions are-

And \(2 \frac{2}{3}, 2 \frac{1}{2}, 1 \frac{3}{4}, 2 \frac{1}{5}, 1 \frac{5}{6}, 1 \frac{7}{8}\)

These fraction in improper fraction are as follows-

1\(\frac{1}{9}\)= \(\frac{10}{9}\)

1\(\frac{1}{8}\)= \(\frac{9}{8}\)

1\(\frac{1}{7}\)= \(\frac{8}{7}\)

1\(\frac{1}{6}\)= \(\frac{7}{6}\)

And

1\(\frac{1}{5}\)= \(\frac{6}{5}\)

1\(\frac{1}{4}\)= \(\frac{5}{4}\)

1\(\frac{1}{3}\)=\(\frac{4}{3}\)

Remaining are-

2\(\frac{2}{3}\)= \(\frac{8}{3}\)

2\(\frac{1}{2}\)= \(\frac{5}{2}\)

1\(\frac{3}{4}\)=\(\frac{7}{4}\)

2\(\frac{1}{5}\)= \(\frac{11}{5}\)

And

1\(\frac{5}{6}\)= \(\frac{11}{5}\)

1\(\frac{7}{8}\)= \(\frac{15}{8}\)

Matching equal fractions in the figure –

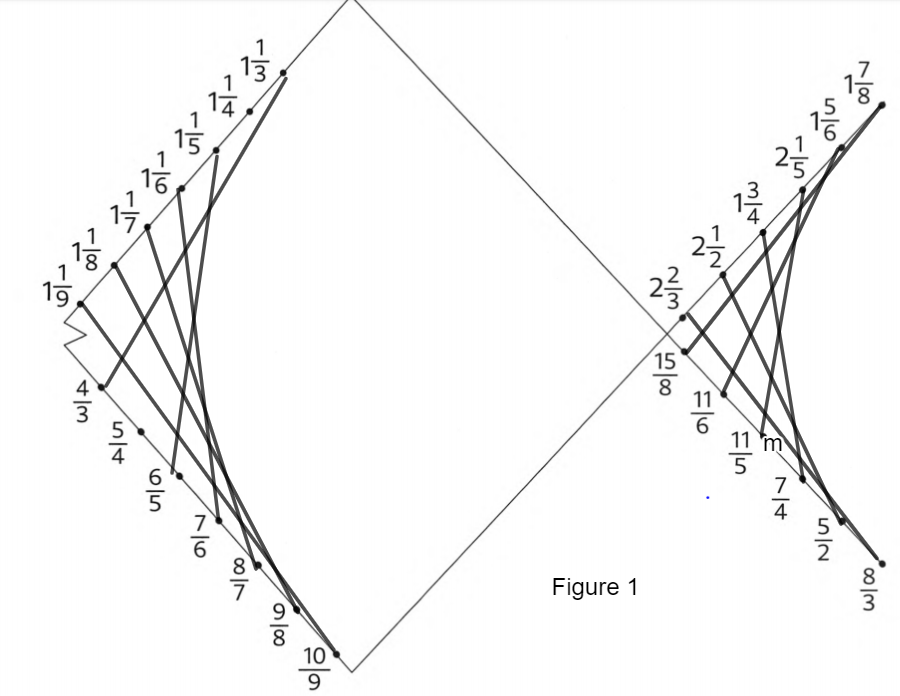
The figure joining equal fractions is as follows-

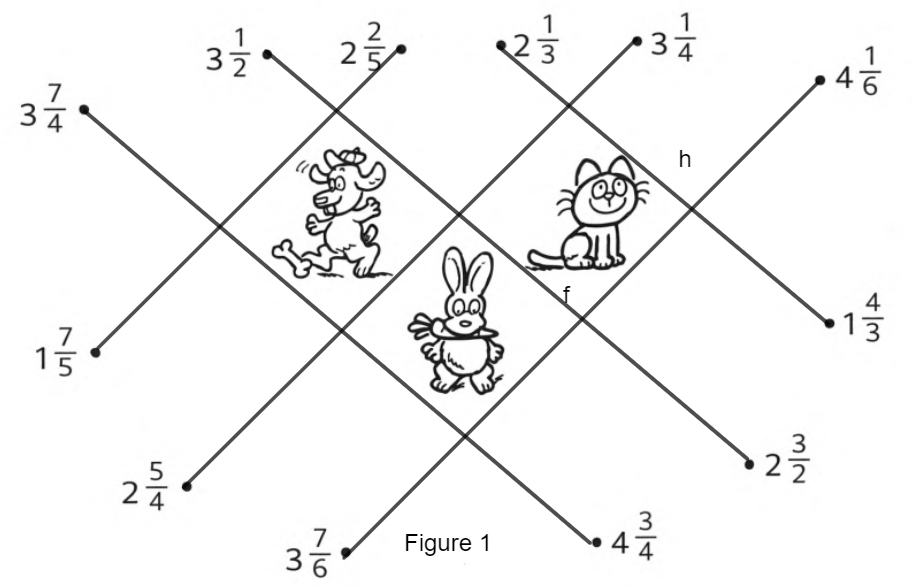
Page 104 Exercise3.8 Problem 19 

Given:

Various mixed fractions.

To match equal fractions after converting these mixed fractions into standard form such that animals can be trapped.

Firstly, Convert all mixed fractions into standard form.

Then, match equal fractions with each other.

Finally, represent this so that animals can be trapped.

From figure given mixed fractions are-

These fractions in improper fraction are as follows-

\(3 \frac{7}{4}\)= \(\frac{19}{4}\)

\(3 \frac{1}{2}\)=\(\frac{7}{2}\)

\( 2 \frac{2}{5}\)=\(\frac{12}{5}\)

\( 2 \frac{1}{3}\)=\(\frac{7}{3}\)

\( 3 \frac{1}{4}\)=\(\frac{13}{4}\)

\( 4 \frac{1}{6}\)=\( \frac{25}{6}\)

\( 1 \frac{4}{3}\)=\(\frac{7}{3}\)

\(2 \frac{3}{2}\)=\(\frac{7}{2}\)

Remaining are-

\(4 \frac{3}{4}\)=\(\frac{19}{4}\)

\(3 \frac{7}{6}\)=\(\frac{25}{6}\)

\(2 \frac{5}{4}\)=\(\frac{13}{4}\)

\(1 \frac{7}{5}\)=\(\frac{12}{5}\)

Thus, after converting from mixed fraction to improper fraction equal values are-

\(2 \frac{3}{2}\)=\(3 \frac{1}{2}\)=\(\frac{7}{2}\)

\( 2 \frac{2}{5}\)=\(1 \frac{7}{5}\)=\(\frac{12}{5}\)

\( 1 \frac{4}{3}\)=\( 2 \frac{1}{3}\)=\(\frac{7}{3}\)

\(2 \frac{5}{4}\)=\( 3 \frac{1}{4}\) =\(\frac{13}{4}\)

And

\(3 \frac{7}{6}\)=\( 4 \frac{1}{6}\)=\(\frac{25}{6}\)

\(4 \frac{3}{4}\)=\(3 \frac{7}{4}\)=\(\frac{19}{4}\)

Matching equal fractions in the figure –

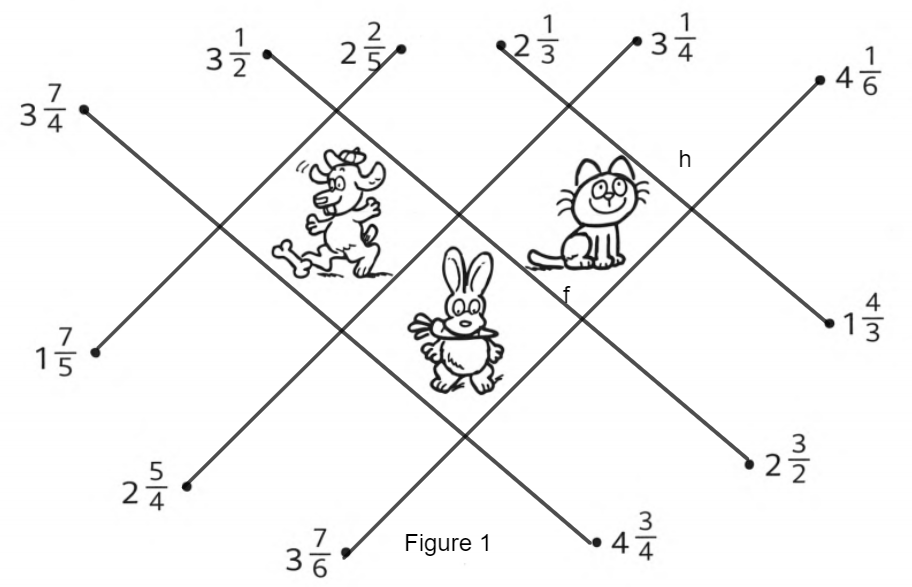
The figure joining equal fractions such that animals are trapped is as follows-

Page 105  Exercise 3.9  Problem 1

We are asked to convert the given figure into an improper fraction.

As it is given 3 full circles with 2 parts equally.

We have 1 Full circle and then we have a half circle which implies

= 1+ \(\frac{1}{2}\)

= \(\frac{3}{2}\)

Therefore, by converting the given figure into the improper fraction, we get \(\frac{3}{2}\).

Page 105  Exercise 3.9  Problem 2

We are asked to convert the given figure into an improper fraction.

As it is given 5 full circles with 3 parts equally.

We have 1 full circle and then one circle with 3 parts which implies

= 1+ \(\frac{2}{3}\)

= \(\frac{5}{3}\)

Therefore, by converting the given figure into the improper fraction, we get \(\frac{5}{3}\).

We are asked to convert the given figure into an improper fraction.

As it is given 7 full circl es with 4 parts equally.

We have 1 full circle and then one circle with 3 parts which implies

​=1+ \(\frac{3}{4}\)

=\(\frac{7}{4}\)

Therefore, by converting the given figure into the improper fraction, we get  \(\frac{7}{4}\)

Page 106  Exercise 3.9 Problem 3

We are given to convert given improper fraction into mixed fraction.

Given – \(\frac{8}{3}\)

To con- vert an improper fraction into mixed fraction let us divide the given fraction and then we have to write the divisor as whole number and quotient as the numerator and remainder as the denominator.

So, for 8÷3 we get 2 as quotient and 2 as remainder.

So, Mixed fraction = 3\(\frac{2}{2}\)

Therefore, by converting the improper fraction into mixed fraction we get 3\(\frac{2}{2}\)

Page 106 Exercise 3.9 Problem 4

We are given to convert given improper fractions into a mixed fraction.

Given – \(\frac{10}{3}\)

To convert improper fractions into mixed fractions let us divide the given fraction and then we have to write the divisor as whole number and quotient as the numerator and the remainder as the numerator.

So, for 10 ÷ 3 we get 3 as quotient and 1 as remainder.

So, Mixed fraction = 3\(\frac{1}{3}\).

Therefore, by converting the improper fraction into mixed fraction we get 3\(\frac{1}{3}\)

Page 106  Exercise 3.9  Problem 5

We are given to convert given improper fractions into a mixed fraction.

Given –  \(\frac{12}{5}\)

To convert improper fractions into mixed fractions let us divide the given fraction and then we have to write the divisor as whole number and quotient as the numerator and remainder as numerator.

So, for 12÷5 we get 3 as quotient and 2 as remainder.

So, Mixed fraction = 2\(\frac{2}{5}\).

Therefore, by converting the improper fraction into mixed fraction we get 2\(\frac{2}{5}\)

Page 106  Exercise 3.9  Problem 6

We are given to convert given improper fraction into a mixed fraction.

Given –  \(\frac{11}{4}\)

To convert improper fractions into mixed fractions let us divide the given fraction and then we have to write the divisor as whole number and quotient as the numerator and the remainder as the numerator.

So, for 11÷4 we get 2 as quotient and 3 as remainder.

So, Mixed fraction = 2 \(\frac{3}{4}\).

Therefore, by converting the improper fraction into mixed fraction we get \(\frac{3}{4}\)

Page 106  Exercise 3.9  Problem 7

We are given an improper fraction to convert into mixed fraction or a whole number.

Given – \(\frac{8}{2}\).

As we- can see that 8 is divisible by 2 at 4th time.

So, \(\frac{8}{2}\) is 4.

Therefore, we can say that by converting \(\frac{8}{2}\) into whole number we get.

Page 106  Exercise 3.9  Problem 8

We are given to convert given improper fractions into a mixed fractions or whole numbers.

Given –  \(\frac{11}{5}\)

To convert improper fractions into mixed fractions let us divide the given fraction and then we have to write the divisor as whole number and quotient as the numerator and the remainder as the numerator.

So, fo – r 11÷5 we get 2 as quotient and 1 as remainder.

So, Mixed fraction = 2\(\frac{1}{5}\).

Therefore, by converting the improper fraction into a mixed fraction we get 2\(\frac{1}{5}\).

Page 106  Exercise 3.9  Problem 9

We are given to convert given improper fractions into mixed fractions or whole numbers.

Given – 2 \(\frac{17}{8}\)

To convert improper fractions into mixed fractions let us divide the given fraction and then we have to write the divisor as whole number and quotient as the numerator and the remainder as the numerator.

So, for 17÷8 we get 2 as quotient and 1 as remainder.

So, Mixed fraction = 2 \(\frac{1}{8}\).

Therefore, by converting the improper fraction into mixed fraction we get2 \(\frac{1}{8}\).

Page 106 Exercise 3.9 Problem 10

We are given an improper fraction to convert into mixed fraction or a whole number.

Given – \(\frac{27}{3}\).

As we can see that 27 is divisible by 3 at 9th time.

So,\(\frac{27}{3}\) is 9.

Therefore, we can say that by converting \(\frac{27}{3}\) into whole number we get 9.

Primary Mathematics Chapter 3 Fractions

Chapter 3 Fractions Exercise 3.1 Solutions Page 81 Exercise 3.1 Problem 1

Given: \(\frac{1}{2}\)= \(\frac{4}{8}\)

To find –  The numerator by observing the given figure.

Here the number of black boxes denotes the numerator.

The number of black boxes + a number of white boxes denotes the denominator. (i.e. total number of boxes)

By observing the figure , \(\frac{1}{2}\)= \(\frac{4}{8}\)

The numerator by observing the given figure.\(\frac{1}{2}\)= \(\frac{4}{8}\)

Page 81 Exercise 3.1 Problem 2

Given: \(\frac{6}{10}=\frac{}{5}\)

To find the numerator by observing the given figure.

Here the number of black boxes denotes the numerator.

The number of black boxes + a number of white boxes denotes the denominator. (i.e. total number of boxes)

By observing the figure , \(\frac{6}{10}=\frac{3}{5}\)

The numerator by observing the given figure: \(\frac{6}{10}=\frac{3}{5}\)

Page 81  Exercise 3.1 Problem 3

Given: \(\frac{2}{3}=\frac{6}{}\)

To find -The denominator by observing the given figure.

Here the number of black boxes denotes the numerator.

The number of black boxes + a number of white boxes denotes the denominator. (i.e. total number of boxes)

By observing the figure \(\frac{2}{3}=\frac{6}{9}\)( Here the LHS is multiplied and divided by 3 to obtain the RHS)

The numerator by observing the given figure: \(\frac{2}{3}=\frac{6}{9}\)

Page 81  Exercise 3.1 Problem 4

Given: \(\frac{9}{12} = \frac{3}{}\)

To find – The denominator by observing the given figure.

Here the number of black boxes denotes the numerator.

The number of black boxes + a number of white boxes denotes the denominator. (i.e. total number of boxes)

By observing the figure, \(\frac{9}{12}=\frac{3}{4}\)

The numerator by observing the given figure: \(\frac{9}{12}=\frac{3}{4}\)

Primary Mathematics 4A Chapter 3 Step-By-Step Solutions For Exercise 3.1 Page 81  Exercise 3.1 Problem 5

Given: \(\frac{1}{4}\)

To find – The equivalent fraction by observing the given figure.

Here the number of black boxes denotes the numerator.

The number of black boxes + a number of white boxes denotes the denominator. (i.e. total number of boxes)

By observing the figure, \(\frac{1}{4}\)= \(\frac{3}{12}\) ( Here the LHS is multiplied and divided by 3 to obtain the RHS)

The numerator by observing the given figure: \(\frac{1}{4}\)= \(\frac{3}{12}\)

Page 81  Exercise 3.1 Problem 6

Given: \(\frac{4}{5}\)

To find – The equivalent fraction by observing the given figure.

Here the number of black boxes denotes the numerator.

The number of black boxes + a number of white boxes denotes the denominator. (i.e. total number of boxes)

By observing the figure, \(\frac{4}{5}\)= \(\frac{8}{10}\)( Here the LHS is multiplied and divided by 2 to obtain the RHS)

The numerator by observing the given figure: \(\frac{4}{5}\)= \(\frac{8}{10}\)

Page 81  Exercise 3.1 Problem 7

Given: \(\frac{6}{12}\)

To find – The equivalent fraction by observing the given figure.

Here the number of black boxes denotes the numerator.

The number of black boxes + a number of white boxes denotes the denominator. (i.e. total number of boxes)

By observing the figure, \(\frac{6}{12}\)= \(\frac{1}{2}\) ( Here the RHS is multiplied and divided by 6 to obtain the LHS)

The equivalent fraction:\(\frac{6}{12}\)= \(\frac{1}{2}\)

Page 81  Exercise 3.1 Problem 8

Given: \(\frac{12}{6}\)

To find – The equivalent fraction by observing the given figure.

Here the number of black boxes denotes the numerator.

The number of black boxes + a number of white boxes denotes the denominator. (i.e. total number of boxes)

By observing the figure, \(\frac{12}{6}\)= \(\frac{3}{4}\) ( Here the RHS is multiplied and divided by 4 to obtain the LHS)

The equivalent fraction \(\frac{12}{6}\)= \(\frac{3}{4}\)

Fractions Exercise 3.1 Primary Mathematics Workbook Answers  Page 82  Exercise 3.1 Problem 9

Given: Eight pairs of equivalent fractions have been given.

We have to join each pair with a straight line.

If we do it correctly, we will get four rectangles.

The eight pair of equivalent fractions joined:

Page 83  Exercise 3.1  Problem 10

Given: \(\frac{1}{3}=\frac{2}{6}=\frac{3}{-}=\frac{}{12}\)

To find –  The missing numerator and denominator in each set of equivalent fractions.

Let the missing denominator be x

Let the missing numerator be y.

The equation can be rewritten as \(\frac{1}{3}=\frac{2}{6}=\frac{3}{x}=\frac{y}{12}\)

Equating the first and the third fraction.
​
​⇒ \(\frac{1}{3}\)= \(\frac{3}{x}\)

⇒ x = 9

Equating the first and the fourth fraction.

​​⇒ \(\frac{1}{3}\)=\(\frac{y}{12}\)

​​⇒ y \(\frac{12}{3}\)

​​⇒ y = 4

Substituting values of x and y

⇒ \(\frac{1}{3}=\frac{2}{6}=\frac{3}{x}=\frac{y}{12}\)

⇒ \(\frac{1}{3}=\frac{2}{6}=\frac{3}{9}=\frac{4}{12}\)

The missing numerator and denominator in each set of equivalent fractions ⇒   \(\frac{1}{3}=\frac{2}{6}=\frac{3}{9}=\frac{4}{12}\)

Common Core Primary Mathematics 4A Chapter 3 Solved Examples For 3.1 Page 83  Exercise 3.1  Problem 11

Given: \(\frac{5}{10}=\frac{4}{6}=\frac{4}{-}\)

To find – The missing numerator and denominator in each set of equivalent fractions.

Let the missing denominator be y

Let the missing numerator be x.

The equation can be rewritten as \(\frac{5}{10}=\frac{x}{6}=\frac{4}{y}\)

Equating the first and the second fraction.

​​⇒ \(\frac{5}{10}\)= \(\frac{x}{6}\)

​​⇒  x \(=\frac{6(5)}{10}\)

​​⇒ x =  3

Equating the first and the third fraction.

​​⇒ \(\frac{5}{10}\)\(=\frac{4}{y}\)

​​⇒ y \(=\frac{4(10)}{5}\)

​​⇒ y = 8

Substituting values of x and y

⇒ \(\frac{5}{10}=\frac{x}{6}=\frac{4}{y}\)

⇒ \(\frac{5}{10}=\frac{3}{6}=\frac{4}{8}\)

The missing numerator and denominator in each set of equivalent fraction

⇒ \(\frac{5}{10}=\frac{3}{6}=\frac{4}{8}\)

Solutions For Fractions Exercise 3.1 In Primary Mathematics 4A Page 83 Exercise 3.1 Problem 12

Given: \(\overline{12}=\frac{4}{-}=\frac{1}{4}\)

To find the missing numerator and denominator in each set of equivalent fractions.

Let the missing denominator be y

Let the missing numerator be x.

The equation can be rewritten as \(\frac{x}{12}=\frac{4}{y}=\frac{1}{4}\)

Equating the first and the third fraction.

⇒ \(\frac{x}{12}\) = \(\frac{1}{4}\)

⇒ x = \(\frac{12}{4}\)

⇒ x = 3

Equating the second and the third fraction.

⇒  \(\frac{4}{y}\)= \(\frac{1}{4}\)

⇒  y = 4(4)

⇒ y = 16

Substituting values of x and y

⇒ \(\frac{x}{12}=\frac{4}{y}=\frac{1}{4}\)

⇒ \(\frac{3}{12}=\frac{4}{16}=\frac{1}{4}\)

The missing numerator and denominator in each set of equivalent fractions ⇒\(\frac{3}{12}=\frac{4}{16}=\frac{1}{4}\)

Detailed Solutions For Exercise 3.1 Fractions In 4A Workbook Page 83  Exercise 3.1 Problem 13

Given: \(\frac{3}{-}=\frac{6}{8}=\frac{}{12}\)

To find – The missing numerator and denominator in each set of equivalent fractions.

Let the missing denominator be y

Let the missing numerator be x.

The equation can be rewritten as \(\frac{3}{y}=\frac{6}{8}=\frac{x}{12}\)

Equating the first and the second fraction.

​​⇒ \(\frac{3}{y}\)= \(\frac{6}{8}\)

​⇒ y = \(\frac{3(8)}{6}\)

⇒ y = 4

Equating the second and the third fraction.
​
​⇒  \(\frac{6}{8}\) = \(\frac{x}{12}\)

⇒ x = \(\frac{12(6)}{8}\)

⇒x = 9
​
Substituting values of x and y

⇒ \(\frac{3}{y}=\frac{6}{8}=\frac{x}{12}\)

⇒ \(\frac{3}{4}=\frac{6}{8}=\frac{9}{12}\)

The missing numerator and denominator in each set of equivalent fractions ⇒\(\frac{3}{4}=\frac{6}{8}=\frac{9}{12}\)

Page 83  Exercise 3.1 Problem 14

Given: \(\frac{12}{10}=\frac{10}{10}=\frac{}{8}\)

To find – The missing numerator and denominator in each set of equivalent fractions.

Let the missing denominator be y

Let the missing numerator be x.

The equation can be rewritten as \(\frac{12}{y}=\frac{10}{10}=\frac{x}{8}\)

Equating the first and the second fraction.

⇒  \(\frac{12}{y}\) = \(\frac{10}{10}\)

y = 12

Equating the second and the third fraction.

⇒ \(\frac{10}{10}\)= \(\frac{x}{8}\)

⇒ \(\frac{12}{12}\)=\(\frac{10}{10}\)=\(\frac{8}{8}\)

The missing numerator and denominator in each set of equivalent fractions ⇒ \(\frac{12}{12}\)=\(\frac{10}{10}\)=\(\frac{8}{8}\)

Page 84  Exercise 3.1 Problem 15

Given: \(\frac{9}{12}\)

To write – The fractions in their simplest form.

The given fraction can be written as ⇒ \(\frac{9}{12}\)= \(\frac{3×3}{3×4}\)

Canceling 3 in the numerator and the denominator

⇒ \(\frac{9}{12}\)= \(\frac{3}{4}\)

Therefore, the simplest form of ⇒ \(\frac{9}{12}\)= \(\frac{3}{4}\)

Step-By-Step Guide For Fractions Exercise 3.1 In 4A Workbook Page 84  Exercise 3.1 Problem 16

Given: \(\frac{8}{10}\)

To write – The fractions in their simplest form.

The given fraction can be written as

⇒ \(\frac{8}{10}\) = \(\frac{4×2}{5×2}\)

Canceling 2 in the numerator and the denominator

⇒ \(\frac{8}{10}\)= \(\frac{4}{5}\)

Therefore, the simplest form of ⇒ \(\frac{8}{10}\)= \(\frac{4}{5}\)

Page 84  Exercise 3.1 Problem 17

Given: \(\frac{10}{15}\)

To write – The fractions in their simplest form.

The given fraction can be written as

⇒ \(\frac{10}{15}\)= \(\frac{5×2}{5×3}\)

Canceling 5 in the numerator and the denominator

⇒ \(\frac{10}{15}\)= \(\frac{2}{3}\)

Therefore, the simplest form of \(\frac{10}{15}\)= \(\frac{2}{3}\)

Primary Mathematics Workbook 4A Exercise 3.1 Fractions Page 84  Exercise 3.1 Problem 18

Given: \(\frac{9}{18}\)

To write  – The fractions in their simplest form.

The given fraction can be written as

⇒ \(\frac{9}{18}\) = \(\frac{9}{9(2)}\)

Canceling 2 in the numerator and the denominator

⇒ \(\frac{9}{18}\) = \(\frac{1}{2}\)

Therefore, the simplest form of ⇒ \(\frac{9}{18}\) = \(\frac{1}{2}\)

Page 84  Exercise 3.1 Problem 19

Given: \(\frac{8}{20}\)

To write –  The fractions in their simplest form.

The given fraction can be written as

⇒ \(\frac{8}{20}\)= \(\frac{4×2}{4×5}\)

Canceling 2 in the numerator and the denominator,

⇒\(\frac{8}{20}\)= \(\frac{2}{5}\)

Therefore, the simplest form of ⇒\(\frac{8}{20}\)= \(\frac{2}{5}\)

Chapter 3 Fractions Exercise 3.1 Breakdown With Solutions Page 84 Exercise 3.1 Problem 20

Given: \(\frac{18}{24}\)

To write –  The fractions in their simplest form.

The given fraction can be written as

⇒ \(\frac{18}{24}\)= \(\frac{6×3}{6×4}\)

Canceling 2 in the numerator and the denominator

⇒ \(\frac{18}{24}\)= \(\frac{3}{4}\)

Therefore, the simplest form of ⇒ \(\frac{18}{24}\)= \(\frac{3}{4}\)

Page 84  Exercise 3.1 Problem 21

Given: \(\frac{12}{30}\)

To write – The fractions in their simplest form.

The given fraction can be written as;

⇒ \(\frac{12}{30}\)= \(\frac{6×2}{6×5}\)

Canceling 6 in the numerator and the denominator,

⇒ \(\frac{12}{30}\)= \(\frac{2}{5}\)

Therefore, the simplest form of \(\frac{12}{30}\)= \(\frac{2}{5}\)

Page 84 Exercise 3.1 Problem 22

Given: \(\frac{20}{60}\)

To write  – The fractions in their simplest form.

The given fraction can be written as;

⇒ \(\frac{20}{60}\)= \(\frac{10×2}{6×5×3}\)

Canceling 10 and 2 in the numerator and the denominator

⇒ \(\frac{20}{60}\) = \(\frac{2}{3}\)

Therefore, the simplest form of ⇒ \(\frac{20}{60}\) = \(\frac{2}{3}\)

Page 85  Exercise 3.2  Problem 1

Given:  Fractional numbers \( \frac{5}{7}, \frac{5}{12}, \frac{11}{18}, \frac{12}{25}\)

The question is to find which of the fractions are greater than \(\frac{1}{2}\)

Compare the numerator and denominator. The fraction will be greater than \(\frac{1}{2}\) , If and only if the denominator is greater than 2×numerator

If we compare the numerator and denominator of each fraction

For, \(\frac{5}{7}\) denominator 7 is not greater than 2 × numerator

∴ So, it is not greater than \(\frac{1}{2}\)

For ,\(\frac{5}{12}\) , denominator 12 is greater than 2 × numerator

∴ So, it is greater than \(\frac{1}{2}\).

For , \(\frac{11}{18}\) denominator 18 is not greater than 2 × numerator

∴ So, it is not greater than \(\frac{1}{2}\).

\(\frac{12}{25}\) denominator 25 is greater than 2 × numerator

∴ So, it is greater than \(\frac{1}{2}\).

From the above step, it is clear that there are two numbers among the given fractions which are greater than \(\frac{1}{2}\)

They are \(\frac{5}{12}\) and \(\frac{12}{25}\)

Therefore, out of the given fractional numbers ,\( \frac{5}{7}, \frac{5}{12}, \frac{11}{18}, \frac{12}{25}\),the numbers that are greater than are circled.

Common Core 4A Chapter 3 Exercise 3.1 Solutions Page 85 Exercise 3.2  Problem 2

Given:  Fractional numbers \(\frac{1}{3}, \frac{1}{5}, \frac{12}{25}, \frac{5}{12}\)

The question is to find which of the fractions are greater than \(\frac{1}{4}\)

Compare the numerator and denominator. If the denominator is greater than 4 × numerator, then that value of the fraction will be greater than \(\frac{1}{4}\)

If we compare the numerator and denominator of each fraction

For \(\frac{1}{3}\), denominator 3 is not greater than 4 × numerator

∴  So, it is not greater than \(\frac{1}{4}\)

For, \(\frac{1}{5}\) , denominator 5 is greater than 4 × numerator

∴ So, it is greater than\(\frac{1}{4}\)

For, \(\frac{12}{25}\) , denominator 25 is not greater than 4 × numerator

∴ So, it is not greater than \(\frac{1}{4}\)

For , \(\frac{5}{12}\), denominator 12 is not greater than 4×numerator

∴ So, it is not greater than \(\frac{1}{4}\)

From the above step, it is clear that there are only one number among the given fractions which are greater than \(\frac{1}{4}\) It is \(\frac{1}{5}\)

Therefore, out of the given fractional numbers \(\frac{1}{3}, \frac{1}{5}, \frac{12}{25}, \frac{5}{12}\) the numbers that are greater than \(\frac{1}{4}\) are circled.

Page 85  Exercise 3.2 Problem 3

Given: Fractional numbers \(\frac{6}{7}, \frac{6}{8}, \frac{8}{9}, \frac{7}{8}\)

The question is to find which of the fractions are closer to 1.

Write the fraction in decimals and compare the answers.

Finding the decimal value of each fraction will give,

⇒ \(\frac{6}{7}\) = 0.8571

⇒ \(\frac{6}{8}\) = 0.75

⇒ \(\frac{8}{9}\) = 0.8889

⇒ \(\frac{7}{8}\) = 0.875

From the above values, the closest to 1 is 0.8889.

So, the fraction closest to 1 among the given fractional numbers is \(\frac{8}{9}\)

Therefore the fraction closest to 1 is \(\frac{8}{9}\)

Page 86  Exercise 3.2   Problem 4

Given:  Fractional numbers \(\frac{3}{13}, \frac{8}{13}, \frac{5}{13}, \frac{11}{13}\)

The question is to arrange the given fractions in ascending order.

As all the denominators are the same, by comparing the numerator, the numbers can be arranged.

If all the denominators of the given numbers are same then the number with least numerator will be the smallest number.

While comparing the given numbers, they can be arranged in increasing order as,

⇒ \(\frac{3}{13}<\frac{5}{13}<\frac{8}{13}<\frac{11}{13}\)

Therefore, the given numbers can be arranged in increasing order as  ⇒ \(\frac{3}{13}<\frac{5}{13}<\frac{8}{13}<\frac{11}{13}\)

Page 86 Exercise 3.2 Problem 5

Given:  Fractional numbers \(\frac{2}{3}, \frac{2}{9}, \frac{2}{7}, \frac{2}{5}\)

Question is to arrange the given fractions in ascending order.

As all the numerators are same, by comparing the denominators, the numbers can be arranged.

If all the numerator of the given numbers are same then the number with the greatest denominator will be the smallest number.

While comparing the given numbers, they can be arranged in increasing order as,

⇒ \(\frac{2}{9}<\frac{2}{7}<\frac{2}{5}<\frac{2}{3}\)

Therefore, the given numbers can be arranged in increasing order as ⇒  \(\frac{2}{9}<\frac{2}{7}<\frac{2}{5}<\frac{2}{3}\)

Exercise 3.2 Page 86 Problem 6

Given:  Fractional numbers \(\frac{2}{5}, \frac{3}{10}, \frac{7}{10}\)

The question is to arrange the given fractions in ascending order.

By finding LCM, make the denominators of all given fractions equal.

As all the denominators are the same, by comparing the numerator, the numbers can be arranged.

Make the denominators the same by finding the LCM.

LCM = 10

⇒  \(\frac{2×2}{5×2}\)\(\frac{3}{10}\), \( \frac{7}{10}\)

⇒  \(\frac{4}{10}\), \(\frac{3}{10}\), \( \frac{7}{10}\)

If all the denominators of the given numbers are the same then the number with the least numerator will be the smallest number.

While comparing the given numbers, they can be arranged in increasing order as,

⇒ \(\frac{3}{10}<\frac{4}{10}<\frac{7}{10}\)

⇒ \(\frac{3}{10}<\frac{4}{10}<\frac{7}{10}\)

Therefore, the given numbers can be arranged in increasing order  ⇒ \(\frac{3}{10}<\frac{4}{10}<\frac{7}{10}\)

 Page 86  Exercise 3.2 Problem 7

Given:  Fractional numbers \(\frac{1}{2}, \frac{3}{4}, \frac{5}{12}\)

The question is to arrange the given fractions in ascending order.

By finding LCM, make the denominators of all given fractions equal.

As all the denominators are the same, by comparing the numerator, the numbers can be arranged.

Make the denominators the same by finding the LCM.

LCM = 2 × 2 × 3

LCM=12

Then the numbers will become

⇒ \(\frac{1×6}{2×6}\), \(\frac{3×3}{4×3}\), \(\frac{5}{12}\)

⇒ \(\frac{6}{12}\), \(\frac{9}{12}\), \(\frac{5}{12}\)

If all the denominators of the given numbers are same then the number w ⇒ ith least numerator will be the smallest number.

While comparing the given numbers, they can be arranged in increasing order as,

⇒ \(\frac{5}{12}<\frac{6}{12}<\frac{9}{12}\)

⇒ \(\frac{5}{12}<\frac{6}{12}<\frac{9}{12}\)

Therefore, the given numbers can be arranged in increasing order as ⇒ \(\frac{5}{12}<\frac{6}{12}<\frac{9}{12}\)

 Page 86 Exercise 3.2 Problem  8

Given: Fractional numbers\(\frac{1}{8}\),\(\frac{2}{10}\), \(\frac{11}{12}\),\(\frac{3}{4}\)

The question is to arrange the given fractions in ascending order.

By finding LCM, make the denominators of all given fractions equal. As all the denominators are the same, by comparing the numerator, the numbers can be arranged.

Make the denominators the same by finding the LCM.

LCM =2 × 2 × 2 × 3 × 5

LCM = 120

Then the numbers will become

⇒ \(\frac{1×15}{8×15}\),\(\frac{2×12}{10×12}\),\(\frac{11×10}{12×10}\), \(\frac{3×30}{4×30}\)

⇒ \(\Rightarrow \frac{15}{120}, \frac{24}{120}, \frac{110}{120}, \frac{90}{120}\)

If all the denominators of the given numbers are the same then the number with the least numerator will be the smallest number.

While comparing the given numbers, they can be arranged in increasing order as,

⇒ \(\frac{15}{120}<\frac{24}{120}<\frac{90}{120}<\frac{110}{120}\)

⇒ \(\Rightarrow \frac{1}{8}<\frac{2}{10}<\frac{3}{4}<\frac{11}{12}\)

Therefore, the given numbers can be arranged in increasing order as ⇒ \(\frac{1}{8}<\frac{2}{10}<\frac{3}{4}<\frac{11}{12}\)

Exercise 3.2 Page 86 Problem 9

Given: Fractional numbers \(\frac{12}{15}, \frac{3}{5}, \frac{7}{15}, \frac{3}{7}\)

The question is to arrange the given fractions in ascending order.

By finding LCM, make the denominators of all given fractions equal

As all the denominators are the same, by comparing the numerator, the numbers can be arranged.

Make the denominators the same by finding the LCM.

LCM = 7 × 5 × 3

LCM = 105

Then the numbers will become

⇒ \(\frac{12×7}{15×7}\), \(\frac{3×21}{5×21}\), \(\frac{7×7}{15×7}\), \(\frac{3×15}{7×15}\)

⇒ \(\frac{84}{105}, \frac{63}{105}, \frac{49}{105}, \frac{45}{105}\)

If all the denominators of the given numbers are same then the number with least numerator will be the smallest number.

While comparing the given numbers, they can be arranged in increasing order as

⇒ \(\frac{45}{105}<\frac{49}{105}<\frac{63}{105}<\frac{84}{105}\)

⇒ \(\frac{3}{7}<\frac{7}{15}<\frac{3}{5}<\frac{12}{15}\)

Therefore, the given numbers can be arranged in increasing order as  ⇒ \(\frac{3}{7}<\frac{7}{15}<\frac{3}{5}<\frac{12}{15}\)

Page 87  Exercise 3.3 Problem 1

Given:  Margery has a 1 yd long ribbon that she wants to cut it into equal lengths that are either \(\frac{1}{6}\) yd, \(\frac{2}{6}\) yd, \(\frac{3}{6}\) y long.,

The question is to color the given figure to show different ways of getting it done and write addition equations.

The addition of a fractional number can be done by making their denominators same.

As the denominators are same here, just by adding directly, answers can be obtained.

There are 3 ways that Margery can cut this 1 yd ribbon into equal pices of length.

The first way is to cut the ribbon into 6 pieces of \(\frac{1}{6}\) yd length.

⇒ \(\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}=1\)

The second way is to cut the ribbon into 3 pieces of \(\frac{2}{6}\) yd length.

⇒ \(\frac{2}{6}\)+\(\frac{2}{6}\)+\(\frac{2}{6}\)= 1

The third way is to cut the ribbon into 3 pieces of \(\frac{3}{6}\) yd length.

⇒ \(\frac{3}{6}\)+ \(\frac{3}{6}\)= 1

It can be represented as

Therefore, Margery can cut the 1 yd ribbon into equal pieces of length in 3 different ways.

⇒ By cutting the ribbon into 6 pieces of \(\frac{1}{6}\) yd length.

⇒ By cutting the ribbon into 3 pieces of \(\frac{2}{6}\) yd length.

⇒ By cutting the ribbon into 2 pieces of \(\frac{3}{6}\) yd length.

Page 88  Exercise 3.3  Problem 2

Given:  Figure

Question is to color the figure as \(\frac{2}{5}\) red and \(\frac{1}{5}\) yellow and add them.

Color the figure accordingly and add them by following properties of addition of fractional numbers.

Given figure colored according to the given fraction latex]\frac{2}{5}[/latex] red and \(\frac{1}{5}\) yellow Will be as follows

The denominator of the given numbers are equal. So, addition can be don directly.

Adding the numbers will give

⇒ \(\frac{2}{5}\) + \(\frac{1}{5}\)= \(\frac{3}{5}\)

Therefore, the sum of the given fractional numbers ⇒  \(\frac{2}{5}\) red and \(\frac{1}{5}\) yellow is \(\frac{3}{5}\).The figure is colored accordingly as

Page 88  Exercise 3.3 Problem 3

Given:  Figure

Question is to color the figure as \(\frac{2}{8}\) blue and \(\frac{5}{8}\)green and add them.

Color the figure accordingly and add them by following properties of addition of fractional numbers.

Given figure colored according to the given fraction \(\frac{2}{8}\) blue and \(\frac{5}{8}\)green Will be as follows

The denominator of the given numbers are equal.

So, addition can be don directly.

Adding the numbers will give

⇒ \(\frac{2}{8}\)+\(\frac{5}{8}\)= \(\frac{7}{8}\)

Therefore, the sum of the given fractional numbers\(\frac{2}{8}\) blue and \(\frac{5}{8}\)green is \(\frac{7}{8}\) The figure is colored accordingly as

Page 88  Exercise 3.3 Problem 4

Given:  Figure

Question is to color the figure as \(\frac{3}{6}\) red and \(\frac{2}{6}\) blue and them.

Color the figure accordingly and add them by following properties of addition of fractional numbers.

Given figure colored according to the given fraction \(\frac{3}{6}\) red and \(\frac{2}{6}\) blue will be as follows

The denominator of the given numbers are equal. So, addition can be don directly.

Adding the numbers will give

⇒ \(\frac{3}{6}\)+ \(\frac{2}{6}\)= \(\frac{5}{6}\)

Therefore, the sum of the given fractional numbers ⇒  \(\frac{3}{6}\) red and \(\frac{2}{6}\) blue The figure is colored accordingly as

Page 88  Exercise 3.3 Problem 5

Given:  Figure

Question is to color the figure as \(\frac{4}{10}\) yellow and \(\frac{3}{10}\) red and add them.

Color the figure accordingly and add them by following properties of addition of fractional numbers.

Given figure colored according to the given fraction \(\frac{4}{10}\) yellow and \(\frac{3}{10}\) red will be as follows

The denominator of the given numbers are equal. So, addition can be don directly.

Adding the numbers will give

\(\frac{4}{10}\) +\(\frac{3}{10}\)= \(\frac{7}{10}\)

Therefore, the sum of the given fractional numbers \(\frac{4}{10}\) yellow and \(\frac{3}{10}\) red is\(\frac{7}{10}\) The figure is colored accordingly as

Page 89  Exercise 3.3 Problem 6

Given:  A set of additions and a figure.

Question is to color the given figures that contain the answers of the given additions.

Addition of a fractional number can be done by making their denominators same.

As the denominators are same here, just by adding directly, answers can be obtained.

Addition of the given expression can be done a

1) \(\frac{1}{2}+\frac{1}{2}\)= 1

2) \(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{1}{2}\)

3) \(\frac{1}{3}\) + \(\frac{1}{3}\) = \(\frac{2}{3}\)

4) \(\frac{1}{5}\) + \(\frac{2}{5}\) = \(\frac{3}{5}\)

5) \(\frac{3}{6}\) + \(\frac{2}{6}\) = \(\frac{5}{6}\)

6) \(\frac{1}{7}\) + \(\frac{4}{7}\) = \(\frac{5}{7}\)

7) \(\frac{5}{8}\) + \(\frac{1}{8}\) = \(\frac{6}{8}\)

8) \(\frac{2}{9}\) + \(\frac{5}{9}\) = \(\frac{7}{9}\)

9) \(\frac{2}{10}+\frac{7}{10}\)= \(\frac{9}{10}\)

So, the answers of the given additions are 1, \(\frac{1}{2}\),\(\frac{2}{3}\),\(\frac{3}{5}\),= \(\frac{5}{6}\), \(\frac{5}{7}\) , \(\frac{7}{9}\), \(\frac{9}{10}\) and respectively.

Now, the number of legs of a spider can be found by coloring the figures that contain the answers.

From the figure, after coloring, the number appearing is 8 . So, number of legs of a spider is 8.

Therefore, the answers of the given additions are 1, \(\frac{1}{2}\),\(\frac{2}{3}\),\(\frac{3}{5}\),= \(\frac{5}{6}\), \(\frac{5}{7}\), \(\frac{7}{9}\), \(\frac{9}{10}\) and respectively.

After coloring the figures that contain the answers, the number of legs of a spider is obtained as 8.

Page 90  Exercise 3.3 Problem 7

Given: Expression

\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\) = ______

The question is to find the missing number by adding the given numbers.

The addition of a fractional number can be done by making their denominators the same.

As the denominators are the same here, just by adding directly, answers can be obtained.

The missing number can be found by adding the numerators directly as the denominators are the same.

⇒\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)=\(\frac{1+1+1}{5}\)

⇒ \(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)= \(\frac{3}{5}\)

So the missing number is found to be \(\frac{3}{5}\).

Therefore, the missing number in the given expression\(\frac{1}{5}\)+\(\frac{1}{5}\)+\(\frac{1}{5}\)=______ is found to be ⇒  \(\frac{3}{5}\)

Page 90  Exercise 3.3  Problem 8

Given: Expression \(\frac{1}{5}\)+\(\frac{3}{5}\)+\(\frac{1}{5}\) =_____

The question is to find the missing number by adding the given numbers.

The addition of a fractional number can be done by making their denominators the same.

As the denominators are the same here, just by adding directly, answers can be obtained.

The missing number can be found by adding the numerators directly as the denominators

⇒ \(\frac{1}{5}\)+\(\frac{3}{5}\)+\(\frac{1}{5}\)=\(\frac{1+3+1}{5}\)

⇒ \(\frac{1}{5}\)+\(\frac{3}{5}\)+\(\frac{1}{5}\)= \(\frac{5}{5}\)

⇒ \(\frac{1}{5}\)+\(\frac{3}{5}\)+\(\frac{1}{5}\)=1

So the missing number is found to be 1.

Therefore, the missing number in the given expression \(\frac{1}{5}\)+\(\frac{3}{5}\)+\(\frac{1}{5}\)______ is found to be 1.

Page 90  Exercise 3.3 Problem 9

Given: Expression \(\frac{3}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\)=______

The question is to find the missing number by adding the given numbers.

The addition of a fractional number can be done by making their denominators the same.

As the denominators are the same here, just by adding directly, answers can be obtained.

The missing number can be found by adding the numerators directly as the denominators are the same.

⇒ \(\frac{3}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\)=\(\frac{3+1+1}{8}\)

⇒ \(\frac{3}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\)= \(\frac{5}{8}\)

So the missing number is found to be \(\frac{5}{8}\)

Therefore, the missing number in the given expression \(\frac{3}{8}\)+\(\frac{1}{8}\)+\(\frac{1}{8}\)=______ is found to be ⇒  \(\frac{5}{8}\).

Page 90  Exercise 3.3 Problem 10

Given:  Expression \(\frac{1}{9}\)+\(\frac{2}{9}\)+\(\frac{4}{9}\)=______

The question is to find the missing number by adding the given numbers.

The addition of a fractional number can be done by making their denominators the same.

As the denominators are the same here, just by adding directly, answers can be obtained.

The missing number can be found by adding the numerators directly as the denominators are the same.

⇒ \(\frac{1}{9}\)+\(\frac{2}{9}\)+\(\frac{4}{9}\)= \(\frac{1+2+4}{9}\)

⇒ \(\frac{1}{9}\)+\(\frac{2}{9}\)+\(\frac{4}{9}\) = \(\frac{7}{9}\)

Therefore, the missing number in the given expression \(\frac{1}{9}\)+\(\frac{2}{9}\)+\(\frac{4}{9}\)=______ is found to be ⇒  \(\frac{7}{9}\)

Page 90 Exercise 3.3 Problem 11

Given: Expression \(\frac{2}{7}\)+ \(\frac{2}{7}\) + \(\frac{2}{7}\)=_______

The question is to find the missing number by adding the given numbers.

Addition of a fractional number can be done by making their denominators same.

As the denominators are same here, just by adding directly, answers can be obtained.

The missing number can be found by adding the numerators directly as the denominators are same.

⇒ \(\frac{2}{7}\)+ \(\frac{2}{7}\)+ \(\frac{2}{7}\)=\(\frac{2+2+2}{7}\)

⇒ \(\frac{2}{7}\)+ \(\frac{2}{7}\)+ \(\frac{2}{7}\) = \(\frac{6}{7}\)

So the missing number is found to be \(\frac{6}{7}\)

Therefore, the missing number in the given expression \(\frac{2}{7}\)+ \(\frac{2}{7}\)+ \(\frac{2}{7}\)=______ is found to be  ⇒ \(\frac{6}{7}\)

Page 90  Exercise 3.3  Problem 12

Given: Expression \(\frac{5}{9}\)+ \(\frac{2}{9}\)+ \(\frac{2}{9}\)=______

The question is to find the missing number by adding the given numbers.

Addition of a fractional number can be done by making their denominators the same.

As the denominators are the same here, just by adding directly, answers can be obtained.

The missing number can be found by adding the numerators directly as the denominators are the same.

⇒\(\frac{5}{9}\)+ \(\frac{2}{9}\)+ \(\frac{2}{9}\)=\(\frac{5+2+2}{9}\)

⇒\(\frac{5}{9}\)+ \(\frac{2}{9}\)+ \(\frac{2}{9}\)= \(\frac{9}{9}\)

⇒\(\frac{5}{9}\)+ \(\frac{2}{9}\)+ \(\frac{2}{9}\)=1

So the missing number is found to be 1.

Therefore, the missing number in the given expression \(\frac{5}{9}\)+ \(\frac{2}{9}\)+ \(\frac{2}{9}\)=______ is found to be 1.

Page 90 Exercise 3.3 Problem 13

Given: Expression \(\frac{3}{10}\)+ \(\frac{2}{10}\)+ \(\frac{1}{10}\)=______

The question is to find the missing number by adding the given numbers.

Addition of a fractional number can be done by making their denominators same.

As the denominators are same here, just by adding directly, answers can be obtained.

The missing number can be found by adding the numerators directly as the denominators are same.

⇒\(\frac{3}{10}\)+ \(\frac{2}{10}\)+ \(\frac{1}{10}\)=\(\frac{3+2+1}{10}\)

⇒\(\frac{3}{10}\)+ \(\frac{2}{10}\)+ \(\frac{1}{10}\)= \(\frac{6}{10}\)

So the missing number is found to be \(\frac{6}{10}\)

Therefore, the missing number in the given expression \(\frac{3}{10}\)+ \(\frac{2}{10}\)+ \(\frac{1}{10}\)=______ is found to be \(\frac{6}{10}\)

Page 90  Exercise 3.3  Problem 14

Given: Expression \(\frac{5}{12}\)+ \(\frac{1}{12}\)+ \(\frac{3}{12}\)=______

The question is to find the missing number by adding the given numbers.

Addition of a fractional number can be done by making their denominators same.

As the denominators are same here, just by adding directly, answers can be obtained.

The missing number can be found by adding the numerators directly as the denominators are same.

⇒ \(\frac{5}{12}\)+ \(\frac{1}{12}\)+ \(\frac{3}{12}\)= \(\frac{5+1+3}{12}\)

⇒ \(\frac{5}{12}\)+ \(\frac{1}{12}\)+ \(\frac{3}{12}\)=\(\frac{9}{12}\)

So the missing number is found to be \(\frac{9}{12}\)

Therefore, the missing number in the given expression \(\frac{5}{12}\)+ \(\frac{1}{12}\)+ \(\frac{3}{12}\)=______ is found to be ⇒  \(\frac{9}{12}\)

Page 90  Exercise 3.3  Problem 15

Given: Figure

The question is to find the missing numbers by addition.

Addition of a fractional number can be done by making their denominators the same.

As the denominators are the same here, just by adding directly, answers can be obtained.

Finding the missing numbers in clockwise direction

let the missing numbers be denoted as x

1)  x + \(\frac{1}{3}\) = 1

⇒  x = 1- \(\frac{1}{3}\)

⇒ x = \(\frac{2}{3}\)

2) x  + \(\frac{1}{4}\)  =1

⇒ x = 1− \(\frac{1}{4}\)

⇒ x = \(\frac{3}{4}\)

Similarly, the next missing numbers can be found by subtracting the given number from 1.

3)  x = 1− \(\frac{2}{5}\)

⇒  x = \(\frac{3}{5}\)

4)  x = 1− \(\frac{1}{6}\)

⇒ x = \(\frac{5}{6}\)

Further calculating

5) x = 1− \(\frac{5}{8}\)

x = \(\frac{3}{8}\)

6)  x = 1\(\frac{7}{10}\)

x = \(\frac{3}{10}\)

7) x = 1− \(\frac{2}{9}\)

x = \(\frac{7}{9}\)

As all the answers are in their simplest form, the figure will look like

Therefore, the missing numbers in the given figure is obtained as

Primary Mathematics Chapter 2 The Four Operations Of Whole Numbers

Chapter 2 The Four Operations Of Whole Numbers Exercise 2.1 Solutions Page 40  Exercise 2.1  Problem 1

To find – The sum of

7 ​ 4  2  3
+ 6  5  2
_________

Place the digits under respective place values.

Add the digits in each place value, and continue this process till we add the digits in all the place values.

Referring to the question and placing digits under respective place values

7  4  2  3
+ 6  5  2
___________

Adding the digits in each place value

Th H ​ T O
7  4  2  3
+  6  5  2
___________
8 0 7 5

Hence, the sum of ⇒ 7 4 2 3 + 6 5 2 =  8075.

Page 40  Exercise 2.1  Problem 2

To find – The sum of

2  3  5  7
+ 6  5  2
__________

Place the digits under respective place values.

Add the digits in each place value taking the carryover, if any, to the next column to the left, and add it along with the digit in that place value.

Continue this process till we add the digits in all the place values.

Referring to the question and placing digits under respective place values,

Th H ​ T O
2   3  5  7
+  6  5  2
___________

Adding the digits in each place value

Th H ​ T  O
2   3  5   7
+  6  5   2
_____________
3 0 0 9

Hence, the sum of ⇒ 2 3 5 7 + 6 5 2 =  3009.

Primary Mathematics 4A Chapter 2 Step-By-Step Solutions For Exercise 2.1 Page 41  Exercise 2.1  Problem 3

Given: Some numbers.

To find – The difference between the given numbers.

The difference between two numbers is nothing but the subtraction of the smallest number from the largest number.

Follow the steps given below.

Complete the subtractions in the first row.

The first difference (subtraction) is given by
​
​ 5  6  7  8
1  2  3  4
−
____________
4 4 4 4
​
The second difference (subtraction) is given by
​
​ 8 4 3 2

− 9 7 6
_________
7 4 5 6
​
The third difference (subtraction) is given by
​
​ 5  1  2  3
1  2  3  4
−
_________
3 8 8 9
​
Complete the subtractions in the second row.

The first difference (subtraction) is given by
​
​ 3  0  0  0
2  8  7  4
−
__________
1 2 6
​
The second difference (subtraction) is given by
​
​ 9 0 0 1
− 1 2 8
__________
8 8 7 3
​
The third difference (subtraction) is given by
​
​ 6  0  6  0
3  6  8  7
−
__________
2 3 7 3
​

Complete the subtractions in the third row.

The first difference (subtraction) is given by
​
​ 5  2  6  2
4  9  0  8
−
__________
3 5 4

​The second difference (subtraction) is given by
​
​ 1 0 0 6
− 8 9 7
___________
1 0 9
​
The third difference (subtraction) is given by
​
​ 9  0  2  2
1  1  3  4
−
__________
7 8 8 8
​
Complete the subtractions in the fourth row.

The first difference (subtraction) is given by
​
​4 2 0 0
1 5 3 2
−
_________
2 6 6 8
​
The second difference (subtraction) is given by
​
​ 1 9 8 2
− 9 9 9
_________
9 8 3
​
The third difference (subtraction) is given by
​
​ 7 2 5 8

6 1 8 9
_
__________
1 0 6 9
​
The complete difference for each expression is given below.

The Four Operations Exercise 2.1 Primary Mathematics Workbook Answers Page 41  Exercise 2.1  Problem 4

Given: Some numbers in a box.

To find – The name of the city which is a landmark of Golden Bridge.

Referring to Exercise 2.1 above table it is obtained that

Observe that, the first given number 109 corresponds to the letter “S” in the above table.

The second given number 1069 corresponds to the letter “A “ in the above table.

The third given number 3889 corresponds to the letter “N “ in the above table, and so on…

Finally, in this way, all the letters will form the word “SAN FRANCISCO” as shown in the table below.

The city that is the landmark of Golden Bridge is “SAN FRANCISCO” which is represented by the following table.

Common Core Primary Mathematics 4A Chapter 2 Solved Examples For 2.1 Page 42   Exercise 2.2  Problem 1

To find – The sum of

⇒ ​8 + 2

⇒ 28 + 2

⇒ 328 + 2

⇒ 6,328 + 2
​
Place the digits under respective place values.

Add the digits in each place value, and continue this process till we add the digits in all the place values.

Referring to the question and placing digits under respective place values for each sum

Adding the digits in each place value

​
Hence, the addition is  ⇒  8 + 2 = 10 28 + 2 = 30 328 + 2 = 330, and 6,328 + 2 = 6330.

Solutions For The Four Operations Exercise 2.1 In Primary Mathematics 4A Page 42  Exercise 2.2  Problem 2

To find – The sum of

⇒ ​4 + 6

⇒ 54 + 6

⇒ 254 + 6

⇒ 3,254 + 6
​
Place the digits under respective place values.

Add the digits in each place value, and continue this process till we add the digits in all the place values.

Referring to the question and placing digits under respective place values for each sum

Adding the digits in each place value,

​

Hence, the addition is ⇒  4 + 6 = 10 , 54 + 6 = 60,  254 + 6 = 260, and 3,254 + 6 = 3260.

Detailed Solutions For Exercise 2.1 The Four Operations In 4A Workbook Page 42  Exercise 2.2  Problem 3

To find – The sum of 2,457 + 4

Place the digits under the respective place values.

Add the digits in each place value, and continue this process till we add the digits in all the place values.

Referring to the question and placing digits under respective place values for each sum

​Th  H  T  O
​​​​​​​​​​2   4   5  7
​​​​​​​​​​​​​​​​​​​+           4
​____________

Adding the digits in each place value

​Th H  T  O
​​​​​​​​​​ 2  4  5  7
​​​​​​​​​​​​​​​​​​​ +         4
_________
​​​​​​​​​​​​2 4 6 1
​

Hence, the addition is ⇒ 2,457 + 4 = 2461.

Page 42  Exercise 2.2  Problem 4

Given: 2,839 + 6

We have to find the sum of these numbers.

Place the digits under respective place values.

Add the digits in each place value, and continue this process till we add the digits in all the place values.

Referring to the question and placing digits under respective place value for each sum

Th  ​H  T  ​ O
2    8   3  9
+            6
___________

Adding the digits in each place value and taking carry over

Th  ​H ​ T ​O
2   8  3  9
+          6
____________
2  8  4  5

Hence, the addition will be ⇒  2,839 + 6 = 2845.

Step-By-Step Guide For The Four Operations Exercise 2.1 In 4A Workbook Page 43  Exercise 2.2  Problem 5

To subtract

⇒ ​10 − 6

⇒ 40 − 6

⇒ 250 − 6

⇒ 5,230 − 6
​
Place the digits under respective place values.

Beginning with the ones, we go on subtracting place value wise borrowing if necessary, from the next place value to the left.

Referring to the question and placing digits under respective place value for each sum

​TO    TO ​​   HTO   ​​ThHTO
10     40    250      5230
−6    −6     −6         −6
_________________________

Subtracting the digits in each place value

​TO  TO  ​​ HTO ​​ ThHTO
10   40    250    5230
−6  −6     −6       −6
______________________
4     34     244    5224

Hence, the result of subtraction is ⇒ 10 − 6 = 4, 40 − 6 = 34, 250 − 6 = 244, and  5,230 − 6 = 5224.

Page 43  Exercise 2.2  Problem 6

To subtract

⇒ 10 − 9

⇒ 100 − 9

⇒ 1,000 − 9

⇒ 2,000 − 9
​
Place the digits under respective place values.

Beginning with the ones, we go on subtracting place value wise, borrowing if necessary, from the next place value to the left.

Referring to the question and placing digits under respective place value for each sum
​
​TO  HTO ​​ ThHTO  ​​ThHTO
10   100    1000      2000
−9    −9       −9         −9
_____________________________

Subtracting the digits in each place value

​
​TO  HTO ​​ ThHTO  ​​ThHTO
10   100    1000       2000
−9    −9       −9          −9
______________________________
1      91        991         1991

Hence, the result of subtraction is ⇒  10 − 9 = 1, 100 − 9 = 91, 1,000 − 9 = 991 and, 2,000 − 9 = 1991.

Primary Mathematics Workbook 4A Exercise 2.1 The Four Operations Page 43  Exercise 2.2  Problem 7

To subtract – 2,570 − 68.

Place the digits under respective place value.

Beginning with the ones, we go on subtracting place value wise, borrowing if necessary, from the next place value to the left.

Referring to the question and placing digits under respective place value for each sum

​Th  H  T O
​​​​​​​​​ 2   5   7 0
​​​​​​​​​​​​        −6 8
​___________

Subtracting the digits in each place value

​Th   H  T  O
​​​​​​​​​2    5   7  0
​​​​​​​​​​​​          −6 8
​_______________
2 5 0 2

Hence, the result of subtraction is 2,570 − 68 = 2,502.

Chapter 2 The Four Operations Exercise 2.1 Breakdown With Solutions Page 43  Exercise 2.2  Problem 8

To subtract – 3,410 − 9.

Place the digits under respective place value.

Beginning with the ones, we go on subtracting place value wise, borrowing if necessary, from the next place value to the left.

Referring to the question and placing digits under respective place value for each sum

​Th  H  T O
​​​​​​​​​3   4   1 0
​​​​​​​​​​​​           −9
​____________

Subtracting the digits in each place value

​Th H T O
​​​​​​​​​3   4  1 0
​​​​​​​​​​​​         −9
​____________
3 4 0 1

Hence, the result of subtraction is 3,410 − 9 = 3,401.

Common Core 4A Chapter 2 Exercise 2.1 Solutions Page 44  Exercise 2.3  Problem 1

To add

⇒ ​1,582 + 9

⇒ 1,582 + 99

⇒ 1,582+999
​
Place the digits under respective place values.

Add the digits in each place value, and continue this process till we add the digits in all the place values.

Referring to the question and placing digits under respective place value for each sum

Subtracting the digits in each place value

Hence, the result of addition is  ⇒  1,582 + 9 =1,591, 1,582 + 99 = 1,681 and 1,582 + 999 = 2,581.

Page 44  Exercise 2.3  Problem 2

To add

​⇒ 2,756+8

⇒ 2,756+98

⇒ 2,756+998
​
Place the digits under respective place values.

Add the digits in each place value, and continue this process till we add the digits in all the place values.

Referring to the question and placing digits under respective place value for each sum

Subtracting the digits in each place value

Hence, the result of addition is ⇒ 2,756 + 8 = 2,764, 2,756 + 98 = 2,854 and 2,756 + 998 = 3,754.

Page 44  Exercise 2.3  Problem 3

Given: 1963 + 98

To find: Add or subtract. By using mathematical operation we can add it or solve it.

First, we perform operation that is given

Adding 1963 and 98 ⇒ 1963 + 98 = 2061

Addition is 1963 + 98 = 2061

Page 44  Exercise 2.3  Problem 4

Given: 7981 − 99

To find – Subtract.By using given operation we can solve it.

Subtracting 99 into 7981 ⇒ 7981 − 99 = 7882

Subtraction is 7981 − 99 = 7882

Page 44  Exercise 2.3  Problem 5

Given: 9405 − 998

To find –  Subtract

We can write, 9405 − 998 = 8407 (Subtracting)

Subtraction is 9405− 998 = 8407

Page 44  Exercise 2.3  Problem 6

Given: 3824+997

To find –  Find addition.

By using mathematical operation, we can write

3824 + 997 = 4821 (Adding 3824 and 997)

Addition is 3824 + 997 = 4821

Page 44  Exercise 2.3  Problem 7

Given: 6448 + 199

To find – Solve addition.

First, we write, 6448 + 199 = 6647 (Adding 6448 and 199, and simplify)

The addition is 6448 + 199 = 6647

Page 44  Exercise 2.3  Problem 8

Given: 5832 − 598

To find – Subtract the given number.

By using mathematical operation we can solve it.

5832−598 = 5234 (Subtracting 598 from 5832, and simplify)

Subtraction is 5832−598 = 5234

Page 45  Exercise 2.3  Problem 9

Given: 2100 − 80

To find –  Subtract.

By using mathematical operation we can solve it.

2100 − 80 = 2020  (Subtracting 80from 2100, and simplify)

Subtraction is 2100 − 80 = 2020

Page 45  Exercise 2.3  Problem 10

Given: 2700 − 98

To find – Subtract 2700 and 98

By using mathematical operation we can solve it.

2700 − 98 = 2602  (Subtracting 98from 2700, and simplify)

Subtraction is 2700 − 98 = 2602

Page 45  Exercise 2.3  Problem 11

Given: 3200 − 54

To find – Subtract the given numbers.

By using mathematical operation we can solve it.

3200−54 = 3146    (Subtracting 54 from 3200, and simplify)

Subtraction is 3200 − 54 = 3146

Page 45  Exercise 2.3  Problem 12

Given: 3900−99

To find – SubtractBy using mathematical operation

3900 − 99 = 3801 (Subtracting 99 from 3900, and simplify)

Subtraction is 3900 − 99 = 3801

Page 45  Exercise 2.3  Problem 13

Given: 4200 − 98

To find – SubtractWe have

4200 − 98 = 4102 (Subtracting 98 from 4200, and simplify)

Subtraction is 4200 − 98 = 4102

Page 45  Exercise 2.3  Problem  14

Given: 3000 − 400

To find – Subtract 400 from 3000

First, we can write

3000−400=2600(Subtracting and simplify)

Subtraction is  3000 − 400 = 2600

Page 45  Exercise 2.3  Problem 15

Given: 3000 − 750

To find – Subtract

We can solve it by using the operation,

3000 − 750 = 2250    (Subtracting 750 from 3000 and simplify)

Subtraction is  3000 − 750 = 2250

Page 45  Exercise 2.3  Problem 16

Given: 3000−530

To find –  Subtract

By using mathematical operation we can solve it

3000−530 = 2470  (Subtracting 530from 3000, and simplify)

Subtraction is 3000−530 = 2470

Page 45  Exercise 2.3  Problem 17

Given: 3000−999

To find –  Subtract

We have, 3000−999 = 2001 (Subtracting 999 from 3000 , and simplify)

Subtraction is 3000 − 999 = 2001

Page 45  Exercise 2.3  Problem 18

Given: 4000−998

To find – Subtract

We have, 4000 − 998 = 3002 (Subtracting 998 from 4000 , and simplify)

Subtraction is 4000 − 998 = 3002

Page 46  Exercise 2.4  Problem 1

Given: 3890+14

To find – Add 3890 and 14

By using mathematical operation (addition) we can solve it.

We have

3890+14 = 3904 (Add 3890 and 14, and simplify)

Addition is 3890+14 = 3904

Page 46  Exercise 2.4  Problem 2

Given: 3598+42

To find – Add 3598 and 42

By solving mathematical operation we can solve it

3598 + 42 = 3640 (Add 3598 and 42, and simplify)

Addition is 3598 + 42 = 3640

Page 46  Exercise 2.4  Problem 3

Given: 4264 + 38

To find – Add 4264  and 38

We first write given operation and then solve

4264 + 38 = 4302 (Add 4264 and 38, and simplify)

Addition is 4264 + 38 = 4302

Page 46  Exercise 2.4  Problem 4

Given: 2700 + 324

To find – Add 2700 + 324

By using addition we can solve it

2700 + 324 = 3024 (Add 2700 and 324, and simplify)

Addition is 2700 + 324 = 3024

Page 46  Exercise 2.4  Problem 5

Given: 2997+203

To find – Add 2997+203

By using addition we can solve it

2997 + 203 = 3200 (Add 2997 and 203, and simplify)

Addition is 2997 + 203 = 3200

Page 46  Exercise 2.4  Problem 6

Given: 2998 + 275

To find – Add 2998 and 275

By using addition we can solve it

2998 + 275 = 3273 (Add 2998 and 275, and simplify)

Addition is 2998275 = 3273

Page 47  Exercise 2.4  Problem 7

Given: 2543 + 68 =​_____

To find –  Write the missing numbers.

By using mathematical operations we can solve it

2543 + 60 = 2603

2603 + 8 = 2611

First, we add  +60 into 2543 and then we add +8  into 2603

Answer is ⇒ 2543+ 60 = 2603, 2603 + 8 = 2611, 2543 + 68 = 2611

Page 47  Exercise 2.4  Problem 8

Given: 3276 + 2040​ =​ __​_____

To find – Write the missing numbers.

First, we add 2000 and then we add 40 into 5276

3276 + 2000 = 5276

5276 + 40 = 5316

3276 + 2040 = 5316

Missing numbers are ⇒ 3276 + 2000 = 5276, 5276 + 40 = 5316, 3276 + 2040 = 5316

Page 47  Exercise 2.4  Problem 9

Given:  3524 − 630 = ​______

To find – Write the missing number.

By using mathematical operations we can solve.

First, we subtract 600 and then subtract 30 from 3524

3524−600 = 2924

2924−30 = 2894

3524−630 = 2894

Missing numbers are ⇒  3524 − 600 = 2924, 2924 − 30 = 2894,  3524 − 630 = 2894

Page 47  Exercise 2.4  Problem 10

Given: 4261−2500=?

To find – Write missing numbers.

By using mathematical operations we can solve it.

4261- 2500 = 1761

The missing numbers are  ⇒ \(4261 \stackrel{-2000}{\longrightarrow} 2261 \stackrel{-500}{\longrightarrow} 1761\), \(4261-2500\)= 1761

Page 47  Exercise 2.4  Problem 11

Given: 3423 − 607

To find – Subtract 607 from 3423

Subtracting 607 from 3423 we get, 3423−607 = 2816

The subtraction is 2816.

Page 47  Exercise 2.4  Problem 12

Given: 5697 − 2700

To find – Subtract 2700 from 5697

Subtracting 2700 from 5697 we get, 5697−2700=2997

Subtraction is 2997.

Page 48  Exercise 2.5  Problem 1

Given: 319  + 589

To find –  Round each number to the nearest hundred then estimate it.

First, we round each number to the nearest hundred then we solve it.

​319 + 589
↓
300 + 600 = 900
​
The estimate value of expression is 900.

Page 48  Exercise 2.5  Problem 2

Given: 782 − 509

To find – Round the number to nearest hundred then estimate it.

First, we write round the number to nearest hundred then solve it.

​780  −  ​509
↓          ↓
800 ​−  500 = 300

The estimate value of expression is 300.

Page 48  Exercise 2.5  Problem 3

Given: 792 + 204

To find – Round the number to nearest hundred then estimate expression.

First, we round the number to nearest hundred then solve.

792  ​+  204
↓           ↓
800  +  200 = 1000

The estimate value of expression is 1000.

Page 48 Exercise 2.5  Problem 4

​Given: 903 − 288

To find – Round the number to nearest hundred then estimate expression.

First, we round the number to nearest hundred then solve.

903   −   288
↓            ↓
900   −  300 = 600

The estimate value of expression is 600.

Page 48  Exercise 2.5  Problem 5

Given: 612 + 589

To find – Round the number to nearest hundred then estimate expression.

First, we round the number to nearest hundred then solve.

612  ​+  ​589
↓           ↓
600 ​ +  600 = 1200

The estimate value of expression  is 1200.

Page 48  Exercise 2.5  Problem 6

Given: 892−328

To find – Round the number to nearest hundred then estimate expression.

First, we round the number to nearest hundred then estimate expression.

892 ​ − ​ 328
↓           ↓
900  ​−  300 = 600

The estimate value of expression is 600.

Page 48  Exercise 2.5  Problem 7

Given: 1798 + 416

To find – Round the number to nearest hundred then estimate it.

First, we round the number to nearest hundred then solve.

​1798 ​ +   416
↓              ↓
​1800  +   400 = 2200

The estimate value of expression is 2200.

Page 48  Exercise 2.5  Problem 8

Given: 2304−996

To find – Round the number to nearest hundred then estimate value of expression.

First, we round the number to nearest hundred then solve.

2304  ​−  996 ​
↓            ↓
2300 ​−  1000 = 1300

​The estimate value of expression is 1300.

Page 49  Exercise 2.5  Problem 9
​
Given: 296 + 109 + 394

To find – Round the number to nearest hundred then solve.

First, we round the number to nearest hundred then solve it.

296 ​ +  ​109  ​+  ​  394
↓           ↓            ↓
300  +  100   +  400 = 800

The estimate value of expression is 800.

Page 49  Exercise 2.5  Problem 10

Given: 704 − 196 − 312

To find –  Round the number to nearest hundred then solve it.

First, we round the number to nearest hundred then solve it.

704  −​ 196  −  ​312
↓          ↓          ↓
700​ −  200  −  300 = 200

The estimate value of expression is 200.

Page 49  Exercise 2.5  Problem 11

Given: 998 − 194 + 97

To find – Round the number to nearest hundred then solve it.

First, we round the number to nearest hundred then solve it.

998   ​−  ​194   + ​97
↓            ↓            ↓
1000 ​−  200  + 100 = 900

​The estimate value of expression is 900.

Page 49  Exercise 2.5  Problem 12

Given: 499 + 301 − 29

To find – Round the number to nearest hundred then solve it.

First, we round the number to nearest hundred then solve it.

499  +  ​301 −  29
↓           ↓         ↓
500 +  300  − 30 = 770

The estimate value of expression is 770.

​

Page 49  Exercise 2.5  Problem 13

Given: 1992 − 67 + 489

To find – Round the number to nearest hundred then solve it.

First, we round the number to nearest hundred then solve it.

2000 − 70 + 500 = 2430

The estimate value of expression is 2430.

Page 49  Exercise 2.5  Problem 14

Given: 2409 + 593 − 708

To find – Round the number to nearest hundred then solve it.

First, we round the number to nearest hundred then solve it.

2400 + 600 − 700 = 2300

The estimate value of expression is 2300.

Page 49  Exercise 2.5  Problem 15

Given: 1109 − 98 + 392

To find – Round the number to nearest hundred then solve it.

First, we round the number to nearest hundred then solve it.

1100 − 100 + 400 = 1410

The estimate value of expression is 1410.

Page 49  Exercise 2.5  Problem 16

Given: 3012 + 62 + 402

To find – Round the number to nearest hundred then solve it.

First, we round the number to nearest hundred then solve it.

3010 + 70 + 400 = 3480

The estimate value of expression is 3480.

Page 50  Exercise 2.6  Problem 1

Given: 4670

European stamps and 698 African stamps more than European stamps.

To find – Total stamps altogether.

First, we write given stamps and then we add all stamps.

​European − Stamps ​ →   African − stamps ​   →      Total−stamps
4670         +                        4670    +   698        =

4670         +                              5368                 =       10038

​Sarah have 10038 total stamps.

Page 50  Exercise 2.6  Problem 2

​Given: I Drove 325 miles on Saturday.

To find – How many miles did she travels on two days?

First, we add 49 miles to 325 miles for Sunday drove then we calculate for both days drove.

325miles + 49miles = 374miles on Sunday.

For two days travel is:

325miles + 374miles = 699miles

Mrs. Charles did travels on both days are 699 miles.

Page 51  Exercise 2.6  Problem 3

Given: Cost $3225 for Piano.

To find – How much more money does she need?

First, we add total money then we subtract total money from the Piano cost.

Total money,  $1950 + $625 = $2575

Now she needs money more

$3225 − $2575 = $650

Mrs. Gina need $650 more money.

Page 51  Exercise 2.6  Problem 4

Given: Earned $2365 in January, $2740 in February.

To find –  How much did he saved?

First, we calculate both months earned money then we subtract spend money from earned money.

Earned in January = $2365

Earned in February ($2365+$375) = $2740

Total = $2365 + $2740

= $5105

He spent $4250, Now we calculate saving $5105 − $4250=$855, Mr. Mudley save $855.

Page 52  Exercise 2.7  Problem 1

We are given to estimate and multiply for  82 × 6.

So, the nearest round figure for 82 is 80.

So, the estimation will be  80 × 6 = 480.

Therefore, the estimated product is  80 × 6 = 480.

Page 52  Exercise 2.7  Problem 2

We are given to estimate and multiply for  79 × 6.

So, the nearest round figure for  79 is 80.

So, the estimation will be  80 × 7 = 560.

Therefore, the estimated product is  80 × 7 = 560.

Page 52  Exercise 2.7  Problem 3

We are given to estimate and multiply for 83 × 8.

So, the nearest round figure for 83 is 80.

So, the estimation will be 80 × 8 = 640.

Therefore, the estimated product is 80 × 8 = 640

Page 52  Exercise 2.7  Problem 4

We are given to estimate and multiply for 96 × 9.

So, the nearest round figure for 96  is 100.

So, the estimation will be 100 × 9 = 900.

Therefore, the estimated product is 100 × 9 = 900.

Page 53  Exercise 2.7  Problem 5

We are given to estimate and multiply for  213 × 5.

So, the nearest round figure for  213 is 200.

So, the estimation will be 200 × 5 = 1000.

Therefore, the estimated product is 200 × 5 = 1000.

Page 53  Exercise 2.7  Problem 6

We are given to estimate and multiply for 497 × 4.

So, the nearest round figure for 497 is 500.

So, the estimation will be 500 × 4 = 2000.

Therefore, the estimated product is 500 × 4 = 2000.

Page 53  Exercise 2.7  Problem 7

We are given to estimate and multiply for 706 × 8.

So, the nearest round figure for 706 is 700.

So, the estimation will be 700 × 8 = 5600.

Therefore, the estimated product is 700 × 8= 5600.

Page 53  Exercise 2.7  Problem 8

We are given to estimate and multiply for 898 × 7.

So, the nearest round figure for 898 is 900.

So, the estimation will be 900 × 7 = 6300.

Therefore, the estimated product is 900 × 7 = 6300.

Page 54  Exercise 2.7   Problem  9

We are given to multiply the given numbers:

By multiplying, we get

⇒ 34 × 4 = 136

⇒ 47 × 5 = 235

⇒ 228 × 3 = 684

⇒ 219 × 6 = 1314

⇒ 357 × 7 = 2499

⇒ 285 × 9 = 2565

⇒ 356 × 8 = 2848

⇒ 489 × 9 = 4401

Therefore, by multiplying the given numbers we get the below answers.

⇒ 34 × 4 = 136

⇒ 47 × 5 = 235

⇒ 228 × 3 = 684

⇒ 219 × 6 = 1314

⇒ 357 × 7 = 2499

⇒ 285 × 9 = 2565

⇒ 356 × 8 = 2848

⇒ 489 × 9 = 4401

Primary Mathematics Chapter 2 The Four Operations Of Whole Numbers

Chapter 2 The Four Operations Of Whole Numbers Exercise 2.8 Solutions Page 55  Exercise 2.8  Problem 1

We are given to estimate and multiply for 1893 × 4.

So, the nearest round figure for 1893 is 2000.

So, the estimation will be 2000 × 4 = 8000.

Therefore, the estimated product is 2000 × 4 = 8000.

Page 55  Exercise 2.8  Problem 2

We are given to estimate and multiply for 4036×7.

So, the nearest round figure for 4036 is 4000

So, the estimation will be 4000×7=28000

Therefore, the estimated product is 4000×7=28000.

Page 55  Exercise 2.8  Problem 3

We are given to estimate and multiply for 5987×8.

So, the nearest round figure for 6000 is 5987.

So, the estimation will be 4000 × 7 = 28000.

Therefore, the estimated product is 6000 × 8 = 48000.

Primary Mathematics 4A Chapter 2 Step-By-Step Solutions For Exercise 2.8 Page 55  Exercise 2.8  Problem 4

We are given to estimate and multiply for 8195 × 9.

So, the nearest round figure for 8000 is 8195.

So, the estimation will be 8000 × 9 = 72000.

Therefore, the estimated product is 8000 × 9 = 72000.

Page 56  Exercise 2.9  Problem 1

We are given that the hotel received 1320 stems of flowers each month and it is also given that the hotel received for 6 months.

We have to find the total number of stems of flowers did manager received.

Which is the product of a number of stems received per month and a number of months.
​
​= 1320 × 6

= 7920
​
Therefore, the total number of flowers that the hotel received altogether is 7920.

The Four Operations exercise 2.8 Primary Mathematics Workbook answers Page 56  Exercise 2.9 Problem 2

We are given that a bottle contains red beads and white beads.

The number of red beads is three times the number of white beads.

If there are 1875 red beads then we have to find white beads.

Which is three times of red beads.
​
​= 1875 × 3

= 5625
​
Therefore, the total number of white beads are 5625.

Page 57  Exercise 2.9  Problem 3

We are given that Mrs Wiley earned $2350 in January.

She earned $500 in February.

In March, she earned twice as much as in February.

We have to find the amount earned by Wiley in March.

Money earned in February is = $2350 + $500 = $2850.

Hence money earned in March is = 2 × $2850 = $5700.

Therefore, the money earned by Wiley in March is $5700.

Common Core Primary Mathematics 4A Chapter 2 Solved Examples For 2.8 Page 58  Exercise 2.9  Problem 4

It is given David bought 2 computers at $3569 each.

He had $2907 left with the money.

We are asked how much money he have at first.

The total money that he have at first is the sum of cost of the computers and the remaining amount.

Cost of two computers is = 2 × 3569

= $7138

The total money that he have at first is  = 7138 + 2907

= $10045

Therefore, the total money that he have at first is $10045.

Solutions For The Four Operations Exercise 2.8 In Primary Mathematics 4A Page 58  Exercise 2.9  Problem 5

It is given that 5 people shared a sum of money.

2 of them received Others received

We are asked to find the sum of the money.

Sum of the money is the sum of the two people’s money and the other’s people money.

Two people’s money is = 2 × 4356 = 8712.

Other people’s money is = 3 × 3807 = 11421.

Therefore, total money is = 8712 + 11421 = 20133.

Therefore, the sum of money is $20133.

Page 59  Exercise 2.10 Problem 1

We are given to estimate and then divide for the given numbers.

Given: 292 ÷ 4

We have to round of the large number to the nearest second number’s multiple for estimating.

By rounding off, 292 will become 280.

So

= 280 ÷ 4 = 70

Therefore, by estimating and dividing the given number, we get 70.

Detailed Solutions For Exercise 2.8 The Four Operations In 4A Workbook Page 59  Exercise 2.10 Problem 2

We are given to estimate and then divide for the given numbers.

Given:  378 ÷ 6

We have to round of the large number to nearest second number’s multiple for estimating.

By rounding off, 378 will become 360.

So

= 360 ÷ 6 = 60

Therefore, by estimating and dividing the given number, we get 70.

Page 59  Exercise 2.10 Problem 3

We are given to estimate and then divide for the given numbers.

Given:  651 ÷ 7

We have to round of the large number to nearest second number’s multiple for estimating.

By rounding off, 651 will become 630.

So

= 630 ÷ 7 = 90

Therefore, by estimating and dividing the given number, we get 90.

Step-By-Step Guide For The Four Operations Exercise 2.8 In 4A Workbook Page 59  Exercise 2.10 Problem 4

We are given to estimate and then divide for the given numbers.

Given:  801 ÷ 9

We have to round of the large number to nearest second number’s multiple for estimating.

By rounding off, 801 will become 810.

So

= 810 ÷ 9 = 90

Therefore, by estimating and dividing the given number, we get 90.

Page 60  Exercise 2.10  Problem 5

We are asked to fill the empty cells in the given table using the answers.

Let us find the quotients and remainders.

After that let us fill the table with the correct divisors.

Let us solve the divisions

For  68 ÷ 4, the remainder is 0 and the quotient is 17.

For  96 ÷ 8  remainder is 0 and the quotient is 12.

For  98 ÷ 7  remainder is 0 and the quotient is 14.

For  635 ÷ 5 remainder is 0 and the quotient is 127.

For 963 ÷ 9 remainder is 0 and the quotient is 107.

Therefore the filled table is

Primary Mathematics Workbook 4A Exercise 2.8 The Four Operations Page 61  Exercise 2.11  Problem 1

We are given to estimate and then divide for the given numbers.

Given:  2475÷5

We have to round of the large number to nearest second number’s multiple for estimating.

By rounding off, 2475 will become 2500.

So

= 2500 ÷ 5 = 500

Therefore, by estimating and dividing the given number, we get 500

Page 61  Exercise 2.11  Problem 2

We are given to estimate and then divide for the given numbers.

Given:  3594÷6

We have to round of the large number to nearest second number’s multiple for estimating.

By rounding off, 3594 will become 3600.

So

= 3600 ÷ 6 = 600

Therefore, by estimating and dividing the given number, we get 600.

Chapter 2 The Four Operations Exercise 2.8 Breakdown With Solutions  Page 61  Exercise 2.11  Problem 3

We are given to estimate and then divide for the given numbers.

Given:  4214 ÷ 7

We have to round of the large number to nearest second number’s multiple for estimating.

By rounding off, 4214 will become 4200.

So

= 4200 ÷ 7 = 600

Therefore, by estimating and dividing the given number, we get 600.

Page 61  Exercise 2.11  Problem 4

We are given to estimate and then divide for the given numbers.

Given:  6480 ÷ 9

We have to round of the large number to nearest second number’s multiple for estimating.

By rounding off, 6490 will become 6300.

So

= 6300 ÷ 9 = 700

Therefore, by estimating and dividing the given number, we get 700.

Common Core 4A Chapter 2 exercise 2.8 Solutions Page 62  Exercise 2.11  Problem 5

We are given to multiple or divide the given numbers.

Multiplication:
​
⇒ ​4023 × 3 = 12069

⇒ ​2370 × 5 = 11850

⇒ ​3208 × 9 = 28872

⇒ ​7248 × 6 = 43488
​
Division:
​
​⇒ ​5208 ÷ 4 = 1302

⇒ ​9207 ÷ 8 = 3069

⇒ ​1936 ÷ 8 = 242

⇒ ​2520 ÷ 10 = 252
​
Therefore, by doing multiplication and division, we get

Multiplication:
​
⇒ ​​4023 × 3 = 12069

⇒ ​2370 × 5 = 11850

⇒ ​3208 × 9 = 28872

⇒ ​7248 × 6 = 43488
​
Division:
​
⇒ ​​5208 ÷ 4 = 1302

⇒ ​9207 ÷ 8 = 3069

⇒ ​1936 ÷ 8 = 242

⇒ ​2520 ÷ 10 = 252

Common Core 4A Chapter 2 exercise 2.8 solutions Page 63  Exercise 2.11  Problem 6

We are given to replace letter n with a number to make equation true.

Given:  n × 6 = 6474

To find – The value of n .

Divide both sides by  6, and we get
​
​⇒ \(\frac{n \times 6}{6}\) = \(\frac{6474}{6}\)

⇒ n = 1079
​
Therefore, value of n is 1079.

Page 63  Exercise 2.11  Problem 7

We are given to replace letter n with a number to make equation true.

Given: n × 7 = 8904.

To find – The value of n .

Divide both sides by 7, and we get
​
​⇒  \(\frac{n \times 7}{7}\)= \(\frac{8904}{7}\)

⇒  n = 1272
​
Therefore, value of n is 1272.

Page 63  Exercise 2.11  Problem 8

We are given to replace letter n with a number to make equation true.

Given:  n × 5 = 3290.

To find – The value of n.

Divide both sides by 5, and we get

​⇒  \(\frac{n \times 5}{5}\)= \(\frac{3290}{5}\)

⇒  n = 658

Therefore, the value of n is 658.

Page 63  Exercise 2.11  Problem 9

We are given to replace letter n with a number to make equation true.

Given:  n ÷ 2 = 3845.

To find  – The value of n.

Multiply both sides by 2, and we get

\(\frac{n \times 2}{2}\)= 3845 × 2

⇒  n= 7690

Therefore, the value of n is 7690.

Page 63  Exercise 2.11  Problem  10

We are given to replace letter n with a number to make equation true.

Given:  n ÷ 3 = 4095.

To find –  The value of n.

Multiply both sides by 3, and we get

\(\frac{n \times 3}{3}\) = 4095 × 3

⇒  n = 12285

Therefore, the value of n is 12285.

Page 64  Exercise 2.12  Problem 1

It is given that a baker made meat pies 4

Times the number of vegetable pies.

It is given that there are 4864 meat pies.

We are asked to find how many meat pies are made more than vegetable pies.

For that we have to do number of meat pies – number of vegetable pies.

Let us consider x for vegetable pies.

Hence, from the question

4x = 4864

Or  x  = \(\frac{4864}{4}\)= 1216

Number of meat pies made more than vegetable pies are
​
​⇒ 4864 − 1216

⇒ 3648
​
Therefore, 3648 meat pies are made more than vegetable pies.

Page 64  Exercise 2.12 Problem 2

It is given that Margo sold three times as many pears as apples in a week.

She sold 3456 apples.

We are asked to find the number of pears did she sell.

Let us consider number of pears as x.

From the question

3x = 3456

Or  x= \(\frac{3456}{3}\)

x = 1152

Therefore, 1152 pears are sold.

Page 65  Exercise 2.12  Problem 3

It is given sue, Pat and Jerry shared $387 equally among themselves.

Sue gave $42 and Pat gave $28.

We are asked to find the money did Pat have in the end.

It is given that $387 is shared equally which means

=  \(\frac{387}{3}\)

=  129

Therefore, everyone have $129 with them at start.

Now, Sue gave Pat $42 means

= $129+$42

= 172

And now pat sent $28 back.

= $172 − $28 = 144

Therefore, P at have $144 at the end.

Page 65  Exercise 2.12  Problem 4

It is given that a sum of 1040 was divided into 8 equal parts.

It is given that Alice got 4 parts and bob got 1 part and remaining are shared equally to the other 5 members,

By dividing 8 parts, we get

=  \(\frac{1040}{8}\)

= 130

From the question we can say that Bob gets 130.

The remaining are 3 × 130 = 390.

Now Gloria have ​ \(\frac{390}{5}\)

= 78

​The amount that shared between them is 78 per each.

The number that bob exceeded than Gloria is

​= 130 − 78

= 52
​
Therefore, Bob has 52 more than Gloria.

Page 67   Exercise  2.13  Problem 1

We are given to find the multiplications for the given numbers.

For up:

B  −   21 × 13 = 273.

D  −   17 × 39 = 663

F  −    37 × 24 = 888.

G  −   83 × 79 = 6557.

For down:

A −  28 × 31 = 868.

B −   53 × 45 = 2385.

C −  59 × 63 = 3717.

E −  49 × 14 = 686.

Therefore the products of the given numbers will be

For up:

B  −   21 × 13 = 273.

D  −   17 × 39 = 663

F  −    37 × 24 = 888.

G  −   83 × 79 = 6557.

For down:

A −  28 × 31 = 868.

B −   53 × 45 = 2385.

C −  59 × 63 = 3717.

E −  49 × 14 = 686.

Page 69  Exercise 2.14  Problem  1 

We are given to estimate and multiply for 52 × 39.

So, the nearest round figure for 52 and 39 is 50 and 40 respectively.

So, the estimation will be 50 × 40=2000.

Therefore, the estimated product is 50 × 40 = 2000.

Page 69  Exercise 2.14  Problem  2 

We are given to estimate and multiply for 78 × 33.

So, the nearest round figure for 78 and 33 is 80 and 30 respectively.

So, the estimation will be 80 × 30 = 2400.

Therefore, the estimated product is 80 × 30 = 2400.

Page 69  Exercise 2.14  Problem  3

We are given to estimate and multiply for 29 × 87.

So, the nearest round figure for 29 and 87 is 30 and 90 respectively.

So, the estimation will be 30 × 90 = 2700.

Therefore, the estimated product is 30 × 90 = 2700

Page 69  Exercise 2.14  Problem  4

We are given to estimate and multiply for 92 × 71.

So, the nearest round figure for 92 and 71 is 90 and 70 respectively.

So, the estimation will be 90 × 70 = 6300.

Therefore, the estimated product is 90 × 70 = 6300.

Page 70  Exercise 2.14  Problem  5

We are given to estimate and multiply for 218 × 37.

So, the nearest round figure for 218 and 37 is 200 and 40 respectively.

So, the estimation will be 200 × 40 = 8000.

Therefore, the estimated product is 200 × 40 = 8000.

Page 70  Exercise 2.14  Problem  6

We are given to estimate and multiply for 483×59.

So, the nearest round figure for 483 and 59 is 500 and 60 respectively.

So, the estimation will be 500 × 60 = 30000.

Therefore, the estimated product is 500 × 60 = 30000.

Page 70  Exercise 2.14  Problem  7

We are given to estimate and multiply for 372 × 64.

So, the nearest round figure for 372 and 64 is 400 and 60 respectively.

So, the estimation will be 400 × 60 = 24000.

Therefore, the estimated product is 400 × 60 = 24000.

Page 70  Exercise 2.14  Problem  8

We are given to estimate and multiply for 648 × 78.

So, the nearest round figure for 648 and 78 is 600 and 80 respectively.

So, the estimation will be 600 × 80 = 48000.

Therefore, the estimated product is 600 × 80 = 48000.

Page 71  Exercise  2.15  Problem 1

We are asked to find the value of 36 × 9.

Which means 9 times of 36.

So, now let us find 10 times of 36 and then we can subtract 36 from it.

​= 36 × 10 − 36

= 360 − 36

= 324
​
Therefore, the product of 36 × 9 is 324.

Page 71  Exercise  2.15  Problem 2

We are asked to find the value of 58 × 99.

Which means 99 times of 58.

So, now let us find 100 times of 58 and then we can subtract 58 from it.
​
​= 58 × 100 − 58

= 5800 − 58

= 5742

Therefore, the product of 58 × 99 is 5742.

Page 71  Exercise  2.15  Problem 3

We are asked to find the value of 69×99

Which means 99 times of 69.

So, now let us find 100 times of 69 and then we can subtract 69 from it.
​
​= 69 × 100 − 69

= 6900 − 69

= 6831
​
Therefore, the product of 69 × 99 is 6831.

Page 71  Exercise  2.15  Problem 4

We are asked to find the value of 87×99.

Which means 99 times of 87.

So, now let us find 100 times of 87 and then we can subtract 87 from it.
​
​= 87 × 100 − 87

= 8700 − 87

= 8613
​
Therefore, the product of 87 × 99 is 8631.

Page 71  Exercise 2.15  Problem 5

We are asked to find the value of 68 × 50.

Which means 68 times of 50.

Now let us make 50 as 100 by rewriting 68 as 34×2.

We get
​
​= 34 × 2 × 50

= 34 × 100

= 3400
​
Therefore, the product of 68 × 50 is 3400.

Page 71  Exercise 2.15  Problem 6

We are asked to find the value of 32 × 25.

Which means 32 times of 25.

Now let us make 25 as 100 by rewriting 32 as 4 × 8.

We get
​
​= 8 × 4 × 25

= 8 × 100

= 800
​
Therefore, the product of 32 × 25 is 800.

Page 71  Exercise 2.15  Problem 7

We are asked to find the value of 84 × 25.

Which means 84 times of 25.

Now let us make 25 as 100 by rewriting 84 as 4 × 21.

We get
​
​= 21 × 4 × 25

= 21 × 100

= 2100
​
Therefore, the product of 84 × 25 is 2100.

Page 71  Exercise 2.15  Problem 8

We are asked to find the value of 25 × 56 .

Which means 56 times of 25.

Now let us make 25 as 100 by rewriting 84 as 4 × 14.

We get
​
​= 14 × 4 × 25

= 14 × 100

= 1400
​

Therefore, the product of 25 × 56 is 1400.

Page 72  Exercise 2. 15 Problem 9

We are asked to answer for the given multiplications.

Across:

⇒ ​118 × 23 = 2714

⇒ ​249 × 31 = 7719

⇒ ​329 × 18 = 5922

⇒ ​167 × 17 = 2839

⇒ ​138 × 11 = 1518

⇒ ​249 × 25 = 6225

Down:

⇒ ​895 × 31 = 27745

⇒ ​676 × 62 = 7719

⇒ ​346 × 28 = 9688

⇒ ​406 × 53 = 21518

⇒ ​119 × 29 = 3451

⇒ ​135 × 65 = 8775

Therefore, the product of the given numbers is:

Across:

⇒ ​118 × 23 = 2714

⇒ ​249 × 31 = 7719

⇒ ​329 × 18 = 5922

⇒ ​167 × 17 = 2839

⇒ ​138 × 11 = 1518

⇒ ​249 × 25 = 6225

Down:

⇒ ​895 × 31 = 27745

⇒ ​676 × 62 = 7719

⇒ ​346 × 28 = 9688

⇒ ​406 × 53 = 21518

⇒ ​119 × 29 = 3451

⇒ ​135 × 65 = 8775

Page 73  Exercise 2.16  Problem 1

It is given that Natalie made 14 jars of butter biscuits and 16 jars of jam biscuits.

And it is also given that they are 48 biscuits in each jar.

We have to find the total number of biscuits she made which is equal to product of number of jars and number of biscuits.

The total number of jars is

14 + 16 = 30

Therefore, the total no of biscuits are 30 × 48 = 1440.

Therefore, Natalie made 1440 biscuits altogether.

Page 73  Exercise 2.16  Problem 2

It is given that William bought 12 packets of yoghurt.

Each pack contains 465ml of yoghurt. He used 2500ml of yoghurt.

We have to find the remaining yoghurt.

The remaining yoghurt is equal to subtraction of total yoghurt and used yoghurt.

Total yoghurt is
​
​= 12 × 465

= 5580
​
Therefore, the remaining is
​
​= 5580 − 2000

= 3580ml
​
Therefore, 3580ml of yoghurt is left after usage.

Primary Mathematics Chapter 2 The Four Operations Of Whole Numbers

Chapter 2 The Four Operations Of Whole Numbers Exercise 2.17 Solutions Page 74  Exercise 2.17  Problem 1

Given: Holly’s savings  = ​312

Leigh’s savings  = ​998

To find – How much Holly saved more than Leigh.

Here, we have the subtracted Leigh’s savings from Holly’s savings to find how much more was saved by Holly

Amount saved =  Holly’s savings – Leigh’s savings

​⇒ 10312 − 7998

⇒ 2314

Holly saved more than Leigh.

Page 74   Exercise 2.17  Problem 2

Given: To find the quotient and remainder when 2490 is divided by 4.

Let’s divide 2490 by 4

Quotient  = 622

Remainder = 2

When 2490 is divided by 4

Quotient = 622

Remainder = 2

Primary Mathematics 4A Chapter 2 Step-By-Step Solutions For Exercise 2.17 Page 74  Exercise 2.17  Problem 3

Given: 1548,​397,​621

First round off the numbers to its nearest hundred.

Then, add all the numbers.

Rounding off 1548 to its nearest hundred  = 1500

Rounding off 397 to its nearest hundred = 400

Rounding off 621 to its nearest hundred = 600

Now, add all the rounded numbers.
​
​⇒ 1500 + 400 + 600

⇒ 2500

​Required estimate = 2500

The Four Operations Exercise 2.17 Primary Mathematics Workbook Answers Page 74  Exercise 2.17  Problem 4

Given: 459,24

First, find the product of the given numbers

Then, round it off to the nearest ten.

Product of 459,24:
​
​⇒ 459 × 24

⇒ 11016
​
Now, rounding off to the nearest ten.

⇒ 11020

Required estimate  ⇒ 11020

Page 74  Exercise 2.17  Problem 5

Given: To subtract 238 from the product of 23 and 80

First, find the product of 23 and 80

Then subtract 238 from the product.

Product of 23 and 80 :
​
​⇒ 23 × 80

⇒ 1840
​
Now, subtract 238 from the product of 23 and 80.
​
​⇒ 1840−238

⇒ 1602
​
Required answer = 1602

Page 75  Exercise 2.17  Problem 6

Given: Divide the sum of 352 and 698 by 5

First, find the sum of 352 and 698

Then divide by 5

Sum of 352 and 698

​⇒  352 + 698

⇒  1050
​
Now, divide by 5

​​⇒ \(\frac{1050}{5}\)

⇒ 210
​
Required answer = 210

Common Core Primary Mathematics 4A Chapter 2 Solved Examples For 2.17 Page 75  Exercise 2.17   Problem 7

Given:  4345 + 998​​ ◯​​ 5345 − 98

To fill – The circle with either <,> or =.

First, find the left-hand side (LHS) of the circle, and then find the right-hand side (RHS) of the circle.

If LHS is greater than RHS, use >

If LHS is smaller than RHS, use <

If LHS is equal than RHS, use =

LHS:
​
​⇒ 4345 + 998

⇒ 5343
​

RHS:
​
​⇒ 5345 − 98

⇒ 5247
​

Here, LHS is greater than RHS. 5343 is greater than 5247

Therefore, 5343>5247

The required solution is  4345+998​​>5345−98

Solutions for The Four Operations Exercise 2.17 In Primary Mathematics 4A Page 75  Exercise 2.17  Problem 8

Given: (600 × 8) + (5 × 8) + (3 × 8) ​​◯​​ 654 × 8

To fill – The circle with either <,> or =.

First, find the left-hand side (LHS) of the circle, and then find the right-hand side (RHS) of the circle.

If LHS is greater than RHS, use >

If LHS is smaller than RHS, use <

If LHS is equal than RHS, use =

LHS:

First, multiply the terms in the bracket and then add.

​⇒  (600 × 8) + (5 × 8) + ( 3 × 8)​​

⇒ (4800) + (5 × 8) + (3 × 8)​​

⇒ (4800) + (40) + (3 × 8)​​

⇒ (4800) + (40) + (24)​​

⇒ 4864
​

RHS:

​⇒  654 × 8

⇒ 5232
​
Here, LHS is smaller than RHS.

4864 is smaller than 5232

Therefore, 4864<5232

The required solution is (600 × 8) + (5 × 8) + (3 × 8)< 654 × 8

Detailed Solutions For Exercise 2.17 The Four Operations In 4A Workbook Page 75  Exercise 2.17  Problem 9

Given: 7191 ÷ ​9​​ ◯​​ 5994 ÷ 6

To fill – The circle with either <,> or =.

First, find the left-hand side (LHS) of the circle, and then find the right-hand side (RHS) of the circle.

If LHS is greater than RHS, use >

If LHS is smaller than RHS, use <

If LHS is equal than RHS, use =

LHS:
​
​⇒ \(\frac{7191}{9}\)

⇒ 799

LHS = 799
​
RHS:
​
​⇒ ​5994 ÷ 6

⇒ 999

RHS = 999
​
Here, LHS is smaller than RHS.

799 is smaller than 999

Therefore, 799<999

The required solution is 7191 ÷ 9 < 5994 ÷ 6

Step-By-Step Guide For The Four Operations Exercise 2.17 In 4A Workbook Page 75  Exercise 2.17  Problem  10

Given: 605 × 40​ ◯​​ 505 × 30

To fill – The circle with either <,> or =.

First, find the left-hand side (LHS) of the circle, and then find the right-hand side (RHS) of the circle.

If LHS is greater than RHS, use >

If LHS is smaller than RHS, use <

If LHS is equal than RHS, use =

LHS:
​
​⇒ 605 × 40

⇒ 24200

LHS = 24200
​
RHS:
​
​⇒ 505 × 30

⇒ 15150

RHS = 15150
​
Here, LHS is greater than RHS.

24200 is greater than 15150

Therefore, 24200>15150

The required solution is 605 × 40 > 505 × 30

Primary Mathematics Workbook 4A Exercise 2.17 The Four Operations Page 75  Exercise 2.17  Problem 11

Given: 1000−750 + 480 ÷ 3 =

To find – The value of the given expression.

By BODMAS, first, divide the expression.

Then add and subtract.

First, divide the expression.
​
​⇒ 1000 − 750 + 480 ÷ 3

⇒ 1000−750 + 160
​
Now add all the same sign terms.
​
​⇒ 1160 − 750

⇒ 410
​
The required solution is 1000 − 750 + 480 ÷ 3 = 410

Chapter 2 The Four Operations Exercise 2.17 Breakdown With Solutions Page 75  Exercise 2.17  Problem 12

Given: 9000−(6000−1430)

To find – The value of the given expression.

By BODMAS, first, subtract the expression in the bracket.

Then add and subtract.

First, subtract the expression in the bracket.
​
​⇒  9000 − (6000 − 1430)

⇒  9000 − (4570)
​
Now subtract the terms.
​
​⇒ 9000 − 4570

⇒ 4430

​The required solution is 9000 −(6000 −1430) = 4430

Page 75  Exercise 2.17  Problem 13

Given: 1475−(18×21)

To find –  The value of the given expression.

By BODMAS, first, multiply the expression inside brackets.

Then subtract.

First, multiply the expression inside brackets.
​
​⇒ 1475 − (18 × 21)

⇒ 1475 − (378)
​
Now subtract the terms.
​
​⇒ 1475 − 378

⇒ 1097
​
The required solution is 1475 − (18 × 21) = 1097

Page 75  Exercise 2.17  Problem 14

Given:  40 + 13 × (12 + 6)=

To find – The value of the given expression.

By BODMAS, first, add the expression in the brackets.

Then multiply and add.

First, add the expression in the brackets.
​
​⇒ 40 + 13 × (12 + 6)

⇒ 40 + 13 × (18)
​
Now multiply the last two terms.
​
​⇒ 40 + 234

⇒ 274
​
Therefore,40 + 13 × (12 + 6) = 274

Common Core 4A Chapter 2 Exercise 2.17 Solutions Page 75  Exercise 2.17  Problem 15

Given: 30 × (40 + 50)

To match the correct expression.

Here, 30 is multiplied with both 40​​and​​50

The above expression can be rewritten as ([30×40]+[30×50])

Therefore, the correct match is the price of forty 30-cent red pencils and fifty 30-cent blue pencils.

(Here ‘and’ indicate addition)

Hence,30×(40+50): The price of forty 30-cent red pencils and fifty 30-cent blue pencils.

Page 75  Exercise 2.17  Problem 16

Given: 30 + 40 × 50

To match the correct expression.

Here, 40​ is multiplied 50 and add 30

The above expression can be rewritten as ([1×30]+[40×50])

Therefore, the correct match is the price of one 30-cent pencils and fifty 40-cent erasers. (Here ‘and’ indicates addition)

30+40×50: The price of one 30-cent pencil and fifty 40-cent erasers.

Page 75  Exercise 2.17  Problem 17

Given: 30 × 40 + 50

To match the correct expression.

Here, 30 is multiplied with 40​ and then 50 is added.

The above expression can be rewritten as ([30×40]+[50×1])

Therefore, the correct match is the price of forty 30-cent red pencils and a 50-cent eraser. (Here ‘and’ indicate addition)

30+40×50: The price of forty 30-cent red pencils and a 50-cent eraser.

Page 76  Exercise 2.17  Problem 18

Given: Lucas made 1192 muffins. He wants to put them in bags that can hold 6 muffins each.

To find – The least number of bags he needs.

Here, we have to find how 1192 muffins can be divided into 6 muffins in each bag.

Here, divide 1192 by 6

​​⇒  \(\frac{1192}{6}\)

⇒ 198.67
​
So, from the above calculation, we can conclude that

Least number of bags needed =198

Therefore, the least number of bags needed = 198

Page 76 Exercise 2.17  Problem 19

Given: A computer costs $1857.

It costs 3 times as much as a printer.

To find – How much the computer and the printer cost altogether.

Let the cost of the printer be x

Here, the cost of the computer $1857 is 3 times the cost of the printer.

∴ 1857 = 3x

Dividing both sides by 3

x =  \(\frac{1857}{3}\)

x =  619

Therefore, the cost of the printer is $619

Page 77  Exercise 2.17  Problem 20

Given: Nicole and Tasha have 2000 stickers altogether. Nicole has 600 more stickers than Tasha.

To find –  Number of stickers Nicole has.

Let x be the number of stickers Nicole has.

Let y be the number of stickers Tasha has.

Nicole has 600 more stickers than Tasha.

Therefore, the number of Nicole stickers = 600+ number of Tasha stickers.

⇒  x = 600 + y

Nicole and Tasha have 2000 stickers altogether.

Number of Nicole’s stickers + Number of Tasha’s stickers = 2000

x + y = 2000

Substitute x = 600 + y in the above equation.

600 + y + y = 2000

600 + 2y = 2000

2y = 2000 − 600

2y = 1400

​y = 700
​
Therefore, the number of stickers Nicole have x = 600 + 700 = 1300

Therefore, the number of stickers Nicole have are  = 1300

Page 77   Exercise 2.17  Problem 21

Given: 2500 people took part in a cross-country race.

The number of adults was 4 times the number of children. There were 1200 men.

To find – The number of women.

Let x be the number of adults.

Let y be the number of children

2500 people took part in a cross-country race. Therefore, number of adults + number of children = 2500

x + y = 2500……. (1)

The number of adults was 4 times the number of children. ⇒  x = 4y ……….(2)

Substitute 2 in (1)

x + y = 2500

4y + y = 2500

5y = 2500
​
​y = 500

Therefore, number of adults  ⇒  x = 4y = 4(500) = 2000

Number of men +number of women=number of adults

⇒ 1200 +  Number of women =  2000

⇒  Number of women = 2000−1200

⇒ Number of women = 800

Therefore, the number of women are = 800

Page 78  Exercise 2.17  Problem 22

Given: the cost of a stereo set and a television set was shared equally among 4 people.

The television set cost $1980

The stereo set cost $1200 more than the television set.

To find – How much each person should pay.

Let the cost of the stereo set be x

The television set cost = $1980

The stereo set cost $1200 more than the television set.

Therefore, cost of stereo set = $1200 + $1980

​⇒ x = 1200 + 1980

⇒ x = 3180
​
The total cost of stereo set and television:
​
​⇒ 1980 + 3180

⇒ 5160
​
The cost of a stereo set and a television set was shared equally among 4 people.

∴  Amount each person should pay =\(\frac{5160}{4}\)

= 1290

Therefore the amount each person should pay is = $1290

Page 78  Exercise 2.17  Problem 23

Given: Jared bought a table and 12 chairs for $2400

Each chair cost $165

Let the cost of a table be x

Let the cost of a chair be y

To find – The cost of a table.

Jared bought a table and 12 chairs for $ 2400.

⇒ x + 12y = 2400

Each chair cost

Therefore, y = 165

​⇒  x + 12(165) = 2400

⇒ x + 1980 = 2400

⇒ x = 2400−1980

⇒ x = 420
​
Therefore, the cost of a table is $ 420

Page 79  Exercise 2.17  Problem 24

Given: A shopkeeper has 50 boxes of apples. There were 24 apples in each box.

He sold all the apples for $1.

To find –  How much money he received.

A shopkeeper has 50 boxes of apples.

There were 24 apples in each box.

Therefore, the total number of apples = 50 × 24 = 1200

He sold the apples for $1.

Therefore, the money he received = $1200

Therefore, the money he received is = $1200

Page 79  Exercise 2.17  Problem 25

Given: A greengrocer had 25 crates of grapefruit.

There were 36 grapefruit in each crate.

She threw away 28 rotten grapefruit and sold 786 of the rest.

To find – The number of grapefruit left.

First, find the total number of grapefruits.

Then subtract the number of rotten grapefruit and sold fruit from the total to find the number of grapefruit left.

A greengrocer had 25 crates of grapefruit.

There were 36 grapefruit in each crate.

Total number of grapefruit = 25 × 36 = 900

She threw away 28 rotten grapefruit and sold 786 of the rest.
​
​⇒ 900 − 28 − 786

⇒ 900 − 814

⇒ 86

​Therefore, the number of grapefruit left is = 86

Page 80  Exercise 2.17  Problem 26

Given: There are 14 blocks of apartments in an estate.

There are 25 floors in each block of apartments. There are 4 apartments on each floor.

To find – The number of apartments altogether.

Using the given information, the total number of apartments is equal to

⇒ 14 × 25 × 4

= 1400

Therefore, the total number of apartments = 1400

Primary Mathematics Chapter 1 Whole Numbers

Chapter 1 Whole Numbers Exercises 1.13 Solutions Page 35   Exercise 1.13  Problem 1

Given: 14 thousands 6 tens.

To write:  The sentence in the standard form.

Use the strategy of BODMAS to simplify the thousands and tens separately.

Then add both tens and thousands with standard form.

Solve the sentence using parentheses wherever necessary.

Given sentence is written as
​
​14 thousands = 14 × 1000

= 14000
​
​6 tens = 6 × 10 = 60
​
Further adding both the solutions

​14 thousands + 6 tens = 14000 + 60

​14 thousands + 6 tens= 14 × 1000 + 6 × 10

​14 thousands + 6 tens = (14 × 1000) + (6 × 10)
​
​14 thousands + 6 tens = 14060

Therefore the standard form is 14060.

Hence, the standard form of 14 thousands and 6 tens is 14060.

Page 35   Exercise 1.13  Problem 2

Given: 32 thousands 5 hundreds 2 tens.

To write:  The sentence in the standard form.

Use the strategy of BODMAS to simplify the thousands, hundreds, and tens separately.

Then add tens, hundreds, and thousands with standard form.

Solve the sentence using parentheses where ever necessary.

Given sentence is written as
​
​32 thousands = 32 × 1000

= 32000
​
​5 hundreds = 5 × 100

= 500

​2 tens = 2 × 10

= 20
​
Further adding the standard forms
​
​32 thousands + 5 hundreds + 2 tens = 32000 + 500 + 20

​32 thousands + 5 hundreds + 2 tens  = 32 × 1000 + 5 × 100 + 2 × 10

​32 thousands + 5 hundreds + 2 tens  =(32×1000) + (5 × 100) + (2 × 10)
​
​32 thousands + 5 hundreds + 2 tens  = 32520

Therefore the standard form is 32520.

Hence, the standard form of 32 thousands, 5 hundreds, and 2 tens is 32520.

Page 35   Exercise 1.13  Problem 3

Given:​ 4 hundred thousands  6 tens  9 ones

To write:  The sentence in the standard form.

Use the strategy of BODMAS to simplify the hundred thousands, ones, and tens separately

Then add tens, hundred thousands, and ones with standard form.

Solve the sentence Using parentheses wherever necessary.

Given sentence is written as

4 hundred thousands = 4 × 100 × 1000

9 ones = 9 × 1

6 tens = 6 × 10

Further adding the standard forms
​
​4 hundred thousands+6 tens+9 ones=4×100×1000+6×10+9×1

=(4 × 100 × 1000) + (6 × 10) + (9 × 1)
​
Therefore the standard form is (4 × 100 × 1000) + (6 × 10) + (9 × 1)

Hence, the standard form of 4 hundred thousands , 6 tens, and 9 ones is (4 × 100 × 1000) + (6 × 10) + (9 × 1)

Page 35   Exercise 1.13  Problem 4

Given:  ​55 thousands  3 hundred  82

To write:  The sentence in the standard form.

Use the strategy of BODMAS to simplify the hundred , thousands, ones separately

Then add tens, hundred, thousands, and ones with standard form.

Solve the sentence Using parentheses wherever necessary.

Given sentence is written as

55 thousands = 55 × 1000

3 hundred = 3 × 100

Eighty two = 82

Further adding the standard forms
​
​55 thousands + 3 hundred + 82 = 55 × 1000 + 3 × 100 + 82

​55 thousands + 3 hundred + 82 = (55 × 1000) + (3 × 100) + 82
​
Therefore the standard form is (55 × 1000) + (3 ×1 00) + 82

Hence, the standard form of 55 thousands 3 hundred and 82 is (55 × 1000) + (3 × 100) + 82

Primary Mathematics 4A Chapter 1 Step-By-Step Solutions For Exercise 1.13 Page 35   Exercise 1.13  Problem 5

Given: 2 hundred thousands Twelve

To write:  The sentence in the standard form.

Use the strategy of BODMAS to simplify the hundred thousand and twelve separately.

Then add twelve, hundred thousand with standard form.

Solve the sentence Using parentheses wherever necessary.

Given sentence is written as

2 hundred thousands = 2 × 100 × 1000

Twelve = 12

Further adding the standard forms

2 hundred thousands+twelve = 2 × 100 × 1000 + 12

= (2 × 100 × 1000) + 12

Therefore the standard form is (2 × 100 × 1000) + 12

Hence, the standard form of 2 hundred thousands twelve is (2 × 100 × 1000) + 12

Page 35   Exercise 1.13  Problem 6

Given:  ​12, 025

To write:  The sentence in the expanded form.

Use the strategy of BODMAS to expand the hundreds thousands tens and ones separately

Then write the number in the sentence form as words in expanded form

Solve the sentence Using parentheses where ever necessary.

Expand the given number
​
​12025 = 12000 + 25

= (12 × 1000) + 25

​Further writing the number in expanded sentence forms as words
​
​12025 = (12 × 1000) + 25

= Twelve thousand twenty-five
​
Therefore the expanded form is twelve thousand twenty-five

Hence, the expanded form of 12025 in words is twelve thousand twenty-five

Whole Numbers Exercise 1.13 Primary Mathematics Workbook 4A Answers Page 35   Exercise 1.13  Problem 7

Given: ​ ​500,006

To write:  The sentence in the expanded form.

Use the strategy of BODMAS to expand the hundreds thousands tens and ones separately

Then write the number in the sentence form as words in expanded form

Solve the sentence Using parentheses where ever necessary.

Expand the given number
​
​500,006 = 500000 + 6

= (5 × 100 × 1000) + 6
​
Further writing the number in expanded sentence forms as words
​
​500,006 = (5 × 100 × 1000) + 6

= Five hundred thousand six
​
Therefore the expanded form is five hundred thousand six

Hence, the expanded form of 500,006 in words is five hundred thousand six

Page 35   Exercise 1.13  Problem 8

Given: 34,120.

To write:  The sentence in the expanded form.

Use the strategy of BODMAS to expand the hundreds thousands tens and ones separately.

Then write the number in the sentence form as words in expanded form.

Solve the sentence using parentheses wherever necessary.

Expand the given number
​
​34120 = 30000 + 4000 + 100 + 20

= 3 × 10,000 + 4 × 1000 + 1 × 100 + 2 × 10
​
Further writing the number in expanded sentence forms as words
​
​34120 = 3 × 10,000 + 4 × 1000 + 1 × 100 + 2 × 10

= Thirty four thousand one hundred twenty
​
Therefore the expanded form is thirty-four thousand one hundred twenty

Hence, the expanded form of 34120 is  3 × 10,000 + 4 × 1000 + 1 × 100 + 2 × 10. In words it will bethirty four thousand one hundred twenty.

Common Core Primary Mathematics 4A Chapter 1 Solved Examples For 1.13 Page 36   Exercise 1.14  Problem 1

Given: ​385,270

To write:  The sentence in the expanded form.

Use the strategy of BODMAS to expand the hundreds thousands tens and ones separately

Then write the number in the sentence form as words in expanded form

Solve the sentence Using parentheses wherever necessary.

Check for the digit to fill the blank.

Expand the given number

​385,270 = 300,000 + 85000 + 200 + 70

= 3 × 100 × 1000 + 85 × 1000 + 2 × 100 + 70

= (3 × 100 × 1000) + (8 × 10 × 000) + (5 × 1000) + (2 × 100) + 70
​
Further writing the number in expanded sentence forms as words
​
​385,270 = (3 × 100 × 1000) + (8 × 10 × 000) + (5 × 1000) + (2 × 100) + 70

=  Three hundred thousand eight-ten thousands five thousand two hundreds seventy
​Referring to the expanded form the digit 8 in 385,270 stands for (8×10×000) that is eight-ten thousands

Hence, the digit 8 in 385,270 stands for (8×10×000) that is eight-ten thousands

Page 36   Exercise 1.14  Problem 2

Given: ​396,048

To write:  The sentence in the expanded form.

Use the strategy of BODMAS to expand the hundreds thousands tens and ones separately

Then write the number in the sentence form as words in expanded form

Solve the sentence Using parentheses wherever necessary.

Check for the digit to fill the blank.

Expand the given number

​396,048 = 300,000 + 96000 + 40 + 8

= 3 × 100 × 1000 + 96 × 1000 + 40 + 8

= (3 × 100 × 1000) + (96 × 1000) + ( 4 × 10) + 8
​

Further writing the number in expanded sentence forms as words
​
​396,048 = (3 × 100 × 1000) + (96 × 1000) + (4 × 10) + 8

= Three hundred thousands ninety-six thousands four tens eight
​
Referring to the expanded form the digit 3 in 396,048 stands for (3 × 100 × 000) that is three hundred thousands

Hence, the digit 3 in 396,048 stands for (3 × 100 × 000) that is three hundred thousands

Chapter 1 Whole Numbers Worked Solutions For Exercise 1.13 In 4A  Page 36   Exercise 1.14  Problem 3

Given:​ 98,406

To write:  The sentence in the expanded form.

Use the strategy of BODMAS to expand the hundreds thousands tens and ones separately

Then write the number in the sentence form as words in expanded form

Solve the sentence Using parentheses wherever necessary.

Check for the digit to fill the blank.

Expand the given number

​98,406 = 90000 + 8000 + 400 + 6

= 9 × 10 × 1000 + 8 × 1000 + 400 + 6

= (9 × 10 × 1000) + (8 × 1000) + (4 × 100) + 6
​
Further writing the number in expanded sentence forms as words
​
​98,406=(9 × 10 × 1000) + (8 × 1000) + (4 × 100) + 6

= Nine ten thousands eight thousands four hundreds six
​
Referring to the expanded form of 98,406 the blank is 8000 or (8 × 1000)

Hence, the missing number of the number 98,406 is 8000 or (8 × 1000)

Page 36   Exercise 1.14  Problem 4

Given: 10,501

To write:  The sentence in the expanded form.

Use the strategy of BODMAS to expand the hundreds thousands tens and ones separately

Then write the number in the sentence form as words in expanded form

Solve the sentence Using parentheses wherever necessary.

Check for the digit to fill the blank.

Expand the given number
​
10,501​= 10000 + 500 + 1

= 10 × 1000 + 5 × 100 + 1

= (10 × 1000) + (5 × 100) + 1
​
Further writing the number in expanded sentence forms as words
​
10,501​= (10 × 1000) + (5 × 100) + 1

= 10,501

= Ten thousands five hundreds and one
​
Referring to the expanded form the blank is 10,501

Hence, the missing number is 10,501

How to solve Primary Mathematics 4A Chapter 1 Whole Numbers 1.13 problems Page 36   Exercise 1.14  Problem 5

Given: ​67,014

To write:  The sentence in the expanded form.

Use the strategy of BODMAS to expand the hundreds thousands tens and ones separately

Then write the number in the sentence form as words in expanded form

Solve the sentence Using parentheses wherever necessary.

Check for the digit to fill the blank.

Expand the given number
​
​67014 = 67000 + 14
​
= 67 × 1000 + 14

Further writing the number in expanded sentence forms as words

​67014 = (67 × 1000) + 14

= Sixty seven thousands fourteen

​Referring to the expanded form of 67014 the blank is 67000 or (67 × 1000)

Hence, the missing number of the number 67014 is 67000 or (67 × 1000)

Primary Mathematics Workbook 4A Chapter 1 Exercise 1.13 Breakdown Page 36   Exercise 1.14  Problem 6

Given:  10,000 more than 46,952 is _____.

Question is to fill the blank with the number which is 10,000 more than 46,952

So, by adding 10,000 to 46,952 will give the required number.

⇒ 46,952 + 10,000 = 56,952

Hence the required number is obtained.

Therefore, it is found that 10,000 more than 46,952 is 56,952.

Exercise 1.13 Whole Numbers Primary Mathematics Workbook Step-By-Step Page 36   Exercise 1.14  Problem 7

Given:100,000 less than 999,998 is____.

Question is to fill the blank with the number which is 100,000 lesser than 999,998

So, finding difference between 999,998 and 100,000 will give the required number.

⇒ 999,998−100,000 = 899,998

Hence the required number is obtained.

Therefore, it is found that 100,000 less than 999,998 is 899,998.

Primary Mathematics Workbook 4A Common Core Edition 1.13 Practice Page 36   Exercise 1.14  Problem 8

Given: 79,049 is ____ less than 80,049

Question is to fill the blank with the number whose difference from 80,049 gives 79,049

So, finding the difference will give

80,049−x = 79,049

x = 80,049 − 79,049

x = 1000

Hence the required number is obtained.

Therefore, it is found that 79,049 is 1000 less than 80,049.

Common Core 4A Chapter 1 Whole Numbers 1.13 Solutions Page 36   Exercise 1.14  Problem 9

Given: 300,561 is _____more than 290,561

Question is to fill in the blank with the number whose addition to 290,561 will make it 300,561

So, adding x with 290,561 will give 300,561

290,561 + x = 300,561

x = 300,561 − 290,561

x = 10,000

Hence the required number is obtained.

Therefore, it is found that 300,561 is 10,000 more than 290,561.

Page 36   Exercise 1.14  Problem 10

Given: A number pattern _____ ; 48,615 ; 58,615 ; ______ ; 78,615

Question is to fill the blanks according to the pattern.

Identify the sequence that which mathematical operation is carried out through out the pattern and accordingly solve it.

The difference between the third number and second number can be found by  58,615 − 48,615 = 10,000

This difference must be the common factor in this sequence.

So, the sequence is designed in a manner that the succeeding number will be 10,000 more than the preceding number.

So, the first term will be 10,000 Less than the second term.

⇒  48,615−10,000 = 38,615

And the fourth term will be 10,000 more than the third.

⇒ 58,615 + 10,000 = 68,615

Then, the pattern will be, 38,615; 48,615; 58,615; 68,615; 78,615

Therefore, the given number pattern is completed as 38,615; 48,615; 58,615;68,615; 78,615.

Page 36   Exercise 1.14  Problem 11

Given: A number pattern 103,840 ; 102,840 ; 101,840; _____ ; _______ ; _______

Question is to fill the blanks according to the pattern.

Identify the sequence that which mathematical operation is carried out through out the pattern and accordingly solve it.

The difference between the first number and second number can be found by

⇒ 103,840−102,840 = 1000

Similarly, the difference between the first number and second number can be found by

102,840 − 101,840 = 1000

So, the common difference is 1000

So, the sequence is designed in a manner that the succeeding number will be 1000 less than the preceding number.

So, the fourth term will be less than the third term.

101,840 − 1000 = 100,840

The third term will be less than the fourth term.

100,840 − 1000 = 99,840

And, the fourth term will be less than the sixth term.

99,840 − 1000 = 98,840

Then, the pattern will be, 103,840;102,840;101,840; 100,840;99,840; 98,840

Therefore, the given number pattern is completed as 103,840;102,840;101,840; 100,840; 99,840; 98,840.

Page 36   Exercise 1.14  Problem 12

Use the strategy of BODMAS wherever necessary.

Check LHS = RHS

Solve LHS and RHS by expanding them to thousands, hundreds, tens, and ones to identify the inequality.

Compare LHS and RHS to find the answer/solution.

Expand the numbers to identify the inequality

LHS = 85928

= 80000 + 5000 + 900 + 20 + 8

RHS = 85892

​= 80000 + 5000 + 800 + 90 + 2
​
Further comparing LHS = RHS

Clearly, the hundreds place of 85928 is greater than 85892

So, 85928>85892

Hence, by comparing the both the numbers we conclude that 85928>85892

Page 36   Exercise 1.14  Problem 13

Use the strategy of BODMAS wherever necessary.

Check LHS = RHS

Solve LHS and RHS by expanding them to thousands, hundreds, tens, and ones to identify the inequality.

Compare LHS and RHS to find the answer/solution.

Expand the numbers to identify the inequality

LHS = 630,109

= 600,000 + 30,000 + 100 + 9

RHS = 603,901

​= 600,000 + 3000 + 900 + 1

​Further comparing LHS = RHS

Clearly, the thousands place of 630,109 is greater than 603,901

So, 630,109>603,901

Hence, by comparing the both the numbers we conclude that 630,109>603,901

Page 36   Exercise 1.14   Problem 14

Given data: 4569 − 999____3569 + 999

To write: <,​> or = in each blank.

Calculate the L.H.S (left-hand side) of the blank as shown below

 ∴   4569−999 = 3570

Again calculate the R.H.S (right-hand side) of the blank as shown below

∴ 3569  +  999  =  4568

It can be clearly observed that the term on R.H.S  is greater than the term on the L.H.S and therefore the sign to be used is <.

Thus, it can be clearly concluded that 4569 − 999 < 3569 + 999.

Page 36   Exercise 1.14  Problem 15

Given data: 54100_____ 541 × 1000

To write: <,​> more = in each blank.

Calculate the L.H.S (left-hand side) if necessary, of the blank as shown below

 ∴ 54100

Again calculate the R.H.S (right-hand side) of the blank as shown below

∴ 541 × 1000 = 541000

It can be clearly observed that the term on R.H.S  is greater than the term on the L.H.S and therefore the sign to be used is <.

Thus, it can be clearly concluded that  54100<541 × 1000.

Page 36   Exercise 1.14  Problem 16

Given data: 42000 ÷ 7 ____ 3600 ÷ 6

To write: <,​> or = in each blank.

Calculate the L.H.S (left-hand side) if necessary, of the blank as shown below

 ∴ 42000 ÷ 7 = 6000

Again calculate the R.H.S (right-hand side) of the blank as shown below

 ∴ 3600 ÷ 600

It can be clearly observed that the term on L.H.S  is greater than the term on the R.H.S and therefore the sign to be used is >.

Thus, it can be clearly concluded that  42000 ÷ 7 > 3600 ÷ 6.

Page 36   Exercise 1.14  Problem 17

Given data: 50000 × 7 ____ 400000

To write:<,​> or = in each blank.

Calculate the L.H.S (left-hand side) if necessary, of the blank as shown below

 ∴ 50000×7=350000

Again calculate the R.H.S (right-hand side) if necessary, of the blank as shown below

∴ 400000

It can be clearly observed that the term on R.H.S  is greater than the term on the L.H.S and therefore the sign to be used is <.

Thus, it can be clearly concluded that 50000 × 7 < 400000.

Page 36   Exercise 1.14  Problem 18

Given data: 23000 + 40000 ___ 87000−24000

To write: <,​> or,  =,  in each blank.

Calculate the L.H.S (left-hand side) if necessary, of the blank as shown below

∴ 23000 + 40000 = 63000

Again calculate the R.H.S (right-hand side) if necessary, of the blank as shown below

 ∴ 87000 − 24000 = 63000

It can be clearly observed that the term on L.H.S  is equal to the term on the R.H.S and therefore the sign to be used is =.

Thus, it can be clearly concluded that 23000 + 40000 = 87000 − 24000.

Page 37  Exercise 1.15  Problem 1

Given data: $460000 + a = 480000$

To find – The missing number represented by each a.

Solve the equation as shown below

∴ 460000 + a = 480000

a = 480000 − 460000

a = 20000

​Thus, it can be clearly concluded that the missing number represented by a, in the equation 460000 + a = 480000 is, 20000.

Page 37   Exercise 1.15  Problem 2

Given data: 48000 ÷ a = 6000

To find – The missing number represented by each a.

Solve the equation as shown below

∴ 48000 ÷ a = 6000

48000 ÷ 6000 = a

a = 8
​
Thus, it can be clearly concluded that the missing number represented by a, in the equation 48000 ÷ a = 6000 is, 8.

Page 37  Exercise 1.15  Problem 3

Given data: 48000 − a = 6000

To find – The missing number represented by each a.

Solve the equation as shown below

∴ ​48000 − a = 6000

48000 − 6000 = a

a = 42000
​
Thus, it can be clearly concluded that the missing number represented by a, in the equation 48000 − a = 6000 is, 42000

Page 37  Exercise 1.15  Problem 4

Given data: 4000 × a = 32000

To find –  The missing number represented by each a.

Solve the equation as shown below

 ∴ ​4000 × a = 32000

a = \(\frac{32000}{4000}\)

a = 8
​
Thus, it can be clearly concluded that the missing number represented by a, in the equation 4000 × a = 32000 is, 8.

Page 37  Exercise 1.15  Problem 5

Given data: 22906,​28609,​82096,​28069,​8209

To arrange: The numbers in increasing order.

Observe that 8209 is the whole number which is the lowest in value and now on arranging it with increasing values, the following can be obtained as shown below

 ∴ 8209,​226906,​28069,​28609,​82096

Thus, it can be clearly concluded that the numbers, 22906,​28609,​82096,​28069,​and 8209 can be arranged in increasing order as 8209,​22906,​28069,​28609,​and 82096.

Page 37  Exercise 1.15  Problem 6

Given data: 435260,​296870,​503140,​463540

To arrange: The numbers in increasing order.

Observe that 296870 is the whole number which is the lowest in value and now on arranging it with increasing values, the following can be obtained as shown below

 ∴ 296870,​435260,​463540,​503140

Thus, it can be clearly concluded that the numbers 435260,​296870,​503140,​and 463540 can be arranged in increasing order as 296870,​435260,​463540,​and 503140.

Page 37  Exercise 1.15  Problem 7

Given data: Some figures are given.

To fill – In Figure 4.

Observe that the number of circles in the first figure is 4, then 9, and then 16, and therefore, in the fourth figure it again increased to 25

Thus, in the fourth figure, one line of circles will increase like in the fourth line of figure 3 with 2 more circles in it.

Therefore, the fourth figure can be filled in as shown below

Thus, it can be clearly concluded that figure 4 can be filled in as shown below

Page 38  Exercise 1.16  Problem 1

Given data: Some figures are given.

To find – The pattern that we notice in the number of circles.

Observe that the number of circles in the first figure is 4, then 9 and then 16 and therefore, in the fourth figure it again increased to 25

Thus, the difference in the number of circles is increasing by 2 after being 4 and 9 in the first and second figures respectively.

Thus, there is an increasing pattern with the number of circles in the n^th figure being (n+1)².

Thus, it can be clearly concluded that the pattern that we notice in the number of circles is an increasing pattern with the number of circles in the n^th figure being (n+1)².

Page 38  Exercise 1.16  Problem 2

Given data: The digits are 0,​1,​9,​and 5,8.

To find – The greatest 5 -digit number that can be formed using all of the given five digits.

Observe that digit greatest in value, that is, 9, and now arrange the digits in order of decreasing values to obtain as shown below

Therefore,98510

Thus, it can be clearly concluded that the greatest 5 -digit number that can be formed using all of the given five digits that are, 0,​1,​9,​5, and 8 is, 98510.

Page 38  Exercise 1.16  Problem 3

Given data: The multiples of 8.

To find – The first 5 multiples of 8.

Observe that the first five multiples of 8 are including 8 itself and as shown below

Therefore 8,​16,​24,​32 and 40

Thus, it can be clearly concluded that the first 5 multiples of 8 are 8,​16,​24,​32, and 40.

Page 38  Exercise 1.16  Problem 4

Given data: The common multiples of 4 and 5.

To find – The first2 common multiples of 4 and 5.

Observe that the first two common multiples of  4 and 5 can be calculated as shown below

Therefore

​L.C.M = 2.2.5

= 20
​
[where L.C.M represents the lowest common multiple]

And also, 20.2 = 40

Thus, it can be clearly concluded that the first 2 common multiples of 4 and 5 are 20,​and 40.

Page 38  Exercise 1.16  Problem 5

Given data: The given number is 4598.

To find –  If 6 is a factor of 4598.

Observe that on dividing 4598 by 6, the following is obtained as shown below

Therefore \(\frac{4598}{6}\) = 766.334

Which shows that 6 is not a factor of 4598.

Thus, it can be clearly concluded that 6 is not a factor of 4598.

Page 38  Exercise 1.16  Problem 6

Given data: The given number is 54.

To find –  All the factors of 54.

Observe that the various numbers which can be divided by 54 are obtained as shown below

Therefore;  1,​2,​3,​6,​9,​18,​27,​54,​−1,​−2,​−3,​−6,​−9,​−18,​−27,​−54 are all factors of 54.

Thus, it can be clearly concluded that all the factors of 54 are 1,​2,​3,​6,​9,​18,​27,​54,​−1,​−2,​−3,​−6,​−9,​−18,​−27,​−54.

Page 38 Exercise 1.16   Problem 7

Given data: The given numbers are 4,​6,​8, and 12.

To find – The common factor of 18 and 36 from these numbers.

Observe that the various numbers which can be divided by 18 and 36 are obtained as shown below

Therefore; 1,​2,​3,​6,​9,​18,​−1,​−2,​−3,​−6,​−9,​−18 are all factors of 18.

1,​2,​3,​4,​6,​9,​12,​18,​36,​​−1,​−2,​−3,​−4,​−6,​−9,​−12,​−18,​−36 are all factors of 36.

Now, observe that the common factors of 18 and 36 are 1,​2,​3,​6,​9,​18,​−1,​−2,​−3,​−6,​−9,​−18, and out of the given four numbers it is 6

Thus, it can be clearly concluded that the common factor of 18 and 36 from the numbers, 4,​6,​8, and 12 is 6.

Page 39   Exercise 1.17  Problem  1

Given data: The given numbers are 25 and 30.

To find – A prime number between 25 and 30.

Observe that a prime number between 25 and 30 is 29 as it is divisible by 1 and itself only.

Thus, it can be clearly concluded that a prime number between 25 and 30 is 29.

Page 39   Exercise 1.17  Problem  2

Given data: 5 × 24 = 5 × 6 × n

To find – The missing factor represented by each n.

Solve the equation as shown below

∴ ​5×24 = 5 × 6 × n

\(\frac{5×24}{5×6}\) = n

n = 4
​
Thus, it can be clearly concluded that the missing factor represented by n, in the equation  5 × 24 = 5 × 6 × n is, 4.

Page 39   Exercise 1.17  Problem  3

Given data: 2 × 180 = 4 × n

To find – The missing factor represented by each n.

Solve the equation as shown below

∴ ​2 × 180 = 4 × n

\(\frac{2×180}{4}\)  = n

n = 90
​
Thus, it can be clearly concluded that the missing factor represented by n, in the equation 2 × 180 = 4 × n is, 90

Page 39   Exercise 1.17  Problem  4

Given data: 26 × 55 = 26 × n × 5

To find –  The missing factor represented by each n.

Solve the equation as shown below

∴  26 × 55 = 26 × n × 5

\(\frac{26×55}{26×5}\)  = n

n = 11
​
Thus, it can be clearly concluded that the missing factor represented by n, in the equation 26×55 = 26×n×5, is 11.

Page 39   Exercise 1.17  Problem  5

Given data: 15 × 250 = 15 × 5 × n

To find – The missing factor represented by each n.

Solve the equation as shown below

∴  15 × 250 = 15 × 5 × n

\(\frac{15×250}{15×5}\) = n

n = 50
​
Thus, it can be clearly concluded that the missing factor represented by n, in equation 15 × 250 = 15 × 5 × n is, 50.

Page 39   Exercise 1.17  Problem  6

Given data: 18 × 35 = 9 × 2 × n × 7

To find – The missing factor represented by each n.

Solve the equation as shown below

∴  ​18 × 35 = 9 × 2 × n × 7

\(\frac{18×35}{9×2×7}\) = n

n = 5
​
Thus, it can be clearly concluded that the missing factor represented by n, in the equation 18 × 35 = 9 × 2 × n × 7 is, 5.

Page 39   Exercise 1.17  Problem  7

Given data: The given equation is 67−(100−52) = ____

To solve: The following equation that is given.

Solve the equation using the BODMAS (Bracket, Of, Division Multiplication Addition and Subtraction) rule as shown below

∴  ​67−(100−52) = 67 − 100 + 52

​67−(100−52)  = 67−48

​67−(100−52)  = 19
​
Thus, it can be clearly concluded that the given equation that is, 67−(100−52) =_____can be solved as  67−(100−52) = 19.

Page 39   Exercise 1.17  Problem  8

Given data: The given equation is (84−32) ÷ 4 =_____.

To solve: The following equation that is given.

Solve the equation using the BODMAS (Bracket, Of, Division Multiplication Addition and Subtraction) rule as shown below

∴  ​(84−32) ÷ 4 = 52 ÷ 4

​(84−32) ÷ 4 = 13
​
Thus, it can be clearly concluded that the given equation that is, (84−32) ÷ 4 =____can be solved as (84−32) ÷ 4 = 13.

Page 39   Exercise 1.17  Problem  9

Given data: The given equation is 72 ÷6 + 18 ÷ 3 =____.

To solve: The following equation that is given.

Solve the equation using the BODMAS (Bracket, Of, Division Multiplication Addition and Subtraction) rule as shown below

∴  72 ÷ 6 + 18 ÷ 3 = 12 + 6

= 18
​
Thus, it can be clearly concluded that the given equation that is, 72 ÷ 6 + 18 ÷ 3=_____can be solved as 72 ÷ 6 + 18 ÷ 3 = 18.

Page 39   Exercise 1.17  Problem  10

Given data: The given equation is  47−28 ÷ 7 × 8 =____.

To solve: The following equation that is given.

Solve the equation using the BODMAS (Bracket, Of, Division Multiplication Addition and Subtraction) rule as shown below

∴  ​47−28 ÷ 7 × 8 = 47 − 4 × 8

= 47−32

= 15
​
Thus, it can be clearly concluded that the given equation that is, 47 − 28 ÷  7 × 8=____ can be solved as  47−28 ÷ 7 × 8 = 15.

Page 39   Exercise 1.17  Problem  11

Given data: (37−15) × (5 + 3)______ 22 × 9

To write: >,​< or = in each blank.

Calculate the L.H.S (left-hand side) of the blank using BODMAS as shown below

∴  (37−15) × (5 + 3) = 22 × 8

= 176
​
Again calculate the R.H.S (right-hand side) of the blank using BODMAS  as shown below

∴  22 × 9 = 198

It can be clearly observed that the term on R.H.S  is greater than the term on the L.H.S and therefore the sign to be used is <.

Thus, it can be clearly concluded that (37−15) × (5 + 3) < 22 × 9.

Page 39   Exercise 1.17  Problem  12

Given data: 40 ÷ (12−4) + 2_____ 40 ÷ 10

To write: >,​< or = in each blank.

Calculate the L.H.S (left-hand side) of the blank using BODMAS as shown below

∴  ​40 ÷ (12−4) + 2 = 40 ÷ 8 + 2

= 5 + 2

= 7

Again calculate the R.H.S (right-hand side) of the blank using BODMAS  as shown below

∴  40 ÷ 10 = 4

It can be clearly observed that the term on R.H.S  is less than the term on the L.H.S and therefore the sign to be used is >.

Thus, it can be clearly concluded that  40 ÷ (12 − 4) + 2 > 40 ÷ 10.

Page 39   Exercise 1.17  Problem  13

Given data: 16 + 2×_____= 20

To fill: In the blank to make the equation true.

Let the blank or the missing value be represented by x

Solve the equation as shown below

Therefore

​16 + 2×__ = 20

20−16 = 2x

\(\frac{4}{2}\) = x

2 = x  (or)  x = 2
​
Thus, it can be clearly concluded that the equation, that is, 16 + 2×___= 20 can be made true by filling in the blank with 2.

Page 39   Exercise 1.17  Problem  14

Given data:  48÷(4 × 2)−2 = 2×______

To fill: In the blank to make the equation true.

Let the blank or the missing value be represented by x

Solve the equation as shown below

∴  ​48 ÷ (4 × 2) − 2 = 2 × x

48 ÷ 8 − 2 = 2x

6 − 2 = 2x

2 = x  (or)  x = 2
​
Thus, it can be clearly concluded that the equation, that is, 48 ÷ (4 × 2)−2 = 2×___can be made true by filling the blank with 2.

Page 39   Exercise 1.17  Problem  15

Given data: 18 − (10 − 6) = 10 +______

To fill: In the blank to make the equation true.

Let the blank or the missing value be represented by x

Solve the equation as shown below

∴ ​18−(10−6) = 10 + x

18 − 4 − 10 = x

4 = x (or)  x = 4
​
Thus, it can be clearly concluded that the equation, that is, 18−(10−6) = 10 +____can be made true by filling in the blank with 4.

Page 39   Exercise 1.17  Problem  16

Given data: (7 + 5) × (15−12) =_____× 12

To fill: In the blank to make the equation true.

Let the blank or the missing value be represented by x

Solve the equation as shown below

∴  ​(7 + 5) × (15−12) = x × 12

12 × 3 = x

\(\frac{12×3}{12}\) = x

3 = x (or)  x = 3
​
Thus, it can be clearly concluded that the equation, that is, (7 + 5) × (15 − 12)=___× 12 can be made true by filling in the blank with 3.

Page 39   Exercise 1.17  Problem  17

Given data: 16 + 4 × 8 =______+ 32

To fill: In the blank to make the equation true.

Let the blank or the missing value be represented by x

Solve the equation as shown below

∴  ​16 + 4 × 8 = x + 32

16 + 32−32 = x

16 = x (or)  x = 16
​
Thus, it can be clearly concluded that the equation, that is, 16 + 4 × 8 =___+ 32 can be made true by filling in the blank with 16.

Page 39   Exercise 1.17  Problem  18

Given data: 9 + 12 ÷ 3 − 2 = 4+____

To fill: In the blank to make the equation true.

Let the blank or the missing value be represented by x

Solve the equation as shown below

∴  9 + 12 ÷ 3 − 2 = 4 + x

9 + 4 − 2−4 = x

7=x  (or)  x = 7
​
Thus, it can be clearly concluded that the equation, that is, 9 + 12 ÷ 3 − 2 = 4 +___can be made true by filling in the blank with 7.

Page 39   Exercise 1.17 Problem  19

Given data: 12 − 3 × 2 + 9 = 15

To insert: Parentheses, where necessary, to make the given equation true.

Solve the equation by inserting the parentheses as shown below

∴ 12−3 × 2 + 9 = 15

Observe that no parentheses is required to be inserted in this equation as it is already true.

Thus, it can be clearly concluded that the equation, that is, 12 − 3 × 2 + 9 = 15 can be made true by inserting no parentheses as 12−3 × 2 + 9 = 15.

Page 39   Exercise 1.17  Problem  20

Given data: 12 − 3 × 2 + 9 = 99

To insert: Parentheses, where necessary, to make the given equation true.

Solve the equation by inserting the parentheses as shown below

∴ 12 − 3 × 2 + 9 = 99

⇒ (12−3) × (2 + 9) = 99
​
Thus, it can be clearly concluded that the equation, that is, 12 − 3 × 2 + 9 = 99 can be made true by inserting no parentheses as (12 − 3) × (2 + 9) = 99.

Primary Mathematics Chapter 1 Whole Numbers

Chapter 1 Whole Numbers Exercises 1.7 Solutions Page 21  Exercise  1.7  Problem 1

Given: Multiples of 6

To find – Several multiples of 6

Put different values of k to find different multiples

Given: Multiples of 6

Multiples of 6 can be written as 6k

For the first multiple of 6 (k=1)

​⇒ 6 × 1

⇒ 6
​
For second multiple of  6( k = 2 )

​⇒ 6 × 2

⇒ 12

​For the third multiple of 6 (k = 3)

​⇒ 6 × 3

⇒ 18
​

For the fourth multiple of 6 (k=4)

​⇒ 6 × 4

⇒ 24
​
The first, second, third, and fourth multiple of 6 is 6,12,18, and 24.

Primary Mathematics 4A Chapter 1 Step-By-Step Solutions For Exercise 1.7 Page 21   Exercise  1.7   Problem 2

Given: Multiples of 7

To find – Several multiples of 7

Put different values of K to find different multiples

Given: Multiples of 7

Multiples of 7 can be written as 7k

For the first multiple of 7 (k = 1)

​⇒ 7 × 1

⇒ 7
​
For the second multiple of 7 (k = 2)

​⇒ 7 × 2

⇒ 14
​

For the third multiple of 7 (k = 3)

​⇒ 7 × 3

⇒ 21
​

For the fourth multiple of 7 (k = 4)

​⇒ 7 × 4

⇒ 28
​

For the fifth multiple of 7 (k = 5)

​⇒ 7 × 5

⇒ 35
​
First, five multiples of 7 are 7,14,21,28,35.

Page 21  Exercise 1.7   Problem 3

Given: Multiples of 2,3,4,6,8,10

To find –  Next five multiples of 2,3,4,6,8,10

Put different values of k to find different multiples

Multiples of 2

Multiples of 2 can be written as 2k

For the third multiple of 2 (k = 3)

​⇒ 2 × 3

⇒ 6
​
For the fourth multiple of 2 (k = 4)

​⇒ 2 × 4

⇒ 8
​
For the fifth multiple of 2 (k = 5)

​⇒ 2 × 5

⇒ 10
​

For the sixth multiple of 2 (k=6)

​⇒ 2 × 6

⇒ 12
​
For seventh multiple of 2(k = 7)

​⇒ 2 × 7

⇒ 14

Multiples of 3

Multiples of 3 can be written as 3k

For the third multiple of 3 (k = 3)

​⇒ 3 × 3

⇒ 9
​
For the fourth multiple of 3 (k = 4)

​⇒ 3 × 4

⇒ 12
​

For the fifth multiple of 3 (k = 5)

​⇒ 3 × 5

⇒ 15
​

For the sixth multiple of 3 (k = 6)

​⇒ 3 × 6

⇒ 18
​

For the seventh multiple of 3 (k = 7)

​⇒ 3 × 7

⇒ 21

Multiples of 4

Multiples of 4 can be written as 4k

For the third multiple of 4 (k = 3)

​⇒  4 × 3

⇒ 12
​

For the fourth multiple of 4 (k = 4)

​⇒ 4 × 4

⇒ 16
​

For the fifth multiple of 4 (k = 5)

​⇒ 4 × 5

⇒ 20
​
For the sixth multiple of 4 (k = 6)

​⇒ 4 × 6

⇒ 24
​
For the seventh multiple of 4 (k = 7)

​⇒ 4 × 7

⇒ 28

Multiples of 6

Multiples of 6 can be written as 6k

For the third multiple of 6 (k = 3)

​⇒ 6 × 3

⇒ 18

​For the fourth multiple of 6 (k = 4)

​⇒ 6 × 4

⇒ 24
​

For the fifth multiple of 6 (k = 5)

​⇒ 6 × 5

⇒ 30
​

For the sixth multiple of 6(k = 6)

​⇒ 6 × 6

⇒ 36
​

For the seventh multiple of 6 (k = 7)

​⇒ 6 × 7

⇒ 42

Multiples of 8

Multiples of 8 can be written as 8k

For the third multiple of 8 (k = 3)

​⇒ 8 × 3

⇒ 24
​
For the fourth multiple of 8 (k = 4)

​⇒ 8 × 4

⇒ 32
​
For the fifth multiple of 8 (k = 5)

​⇒ 8 × 5

⇒ 40
​

For the sixth multiple of 8 (k = 6)

​⇒ 8 × 6

⇒ 48
​
For the seventh multiple of 8 (k = 7)

​⇒ 8 × 7

⇒ 56

Multiples of 10

Multiples of 10 can be written as 10k

For the third multiple of 10 (k = 3)

​⇒ 10 × 3

⇒ 30
​
For the fourth multiple of 10 (k = 4)

​⇒ 10 × 4

⇒ 40
​

For the fifth multiple of 10 (k = 5)

​⇒ 10 × 5

⇒ 50
​

For the sixth multiple of 10 (k = 6)

​⇒ 10 × 6

⇒ 60
​
For the seventh multiple of 10 (k = 7)

​⇒ 10 × 7

⇒  70
​

Therefore

The next five multiples of 2 is 6,8,10,12,14

The next five multiples of 3 is 9,12,15,18,21

The next five multiples of 4 is 12,16,20,24,28

The next five multiples of 6 is 18,24,30,36,42

The next five multiples of 8 is 24,32,40,48,56

The next five multiples of 10 is 30,40,50,60,70.

Whole Numbers Exercise 1.7 Primary Mathematics Workbook 4A Answers Page 22   Exercise 1.7   Problem  4

Given: Random digits and numbers

To check that digits are multiples of number

Check the pattern of numbers multiple and mark it YES or NO

Statement: 57 is a multiple of 3

Multiple of 3 have digits add up to multiple of 3.

Sum of digits of 57 is 12 which is a multiple of 3.

YES, 57 is a multiple of 3.

Statement: 57 is a multiple of 6

Multiple of 6 are even and have digits add up to multiple of 3.

Sum of digits of 57 is 12 which is a multiple of 3 but 57 is not even.

No, 57 is not a multiple of 6.

Statement: 78 is a multiple of 2

Multiple of 2 are even and have last digit as 0,2,4,6,8, last digit of 78 is 8

YES, 78 is a multiple of 2.

Statement: 33,450 is a multiple of 10

Multiple of 10 have 0 at the ones place. 33,450 has 0 at the ones place.

YES, 33,450 is a multiple of 10.

Statement: 452 is a multiple of 3

Multiple of 3 have 3 has digits add up to multiple of 3.

The sum of digits of 452 is 11 which is not a multiple of 3.

No, 452 is not a multiple of 3.

Statement: 4985 is a multiple of 2

Multiple of 2 have the last digit as 0,2,4,6,8.

The last digit of 4985 is 5.

No, 4985 is not a multiple of 2.

Statement: 4985 is a multiple of 5

Multiple of 5 have the last digit as 0,5.

Last digit of 4985 is 5.

YES, 4985 is a multiple of 5.

So, we can conclude the table as

YES, 57 is a multiple of 3.

No, 57 is not a multiple of 6.

YES, 78 is a multiple of 2.

YES, 33,450 is a multiple of 10.

No, 452 is not a multiple of 3.

No, 4985 is not a multiple of 2.

YES, 4985 is a multiple of 5.

Common Core Primary Mathematics 4A Chapter 1 Solved Examples For 1.7 Page 22   Exercise 1.7   Problem 5

Given: Multiple of 100.

To find – Rule for multiples of 100.

Check the pattern of the multiple.

Multiples of 100 can be written as 100k

⇒ 100 × k = k00

The first multiple of 100 is 100

The second multiple of 100 is 200 and so on.

Each multiple 100 of has 0 at its ones and tenth place.

Therefore, the rule of multiples of 100 is found that each multiple of 100 has 0 at its ones and tenth place.

Chapter 1 Whole Numbers Worked Solutions For Exercise 1.7 In 4A Page 23  Exercise  1.8  Problem  1

Given: Integer 20

To find-  The factors of 20

Find the factors of 20 from the shown above.

Given: Integer 20

We know that
​
​1 × 20 = 20

2 × 10 = 20

4 × 5 = 20
​
From this, we have Divisors of 20 are 1,2,4,5,10,20

Factors of 20 are divisors of 20 are 1,2,4,5,10,20

Therefore, the Factors of 20 are 1,2,4,5,10,20.

Page 23  Exercise 1.8  Problem 2

Given: Integer 12

To find – The factors of 12

Find the factors of 12 from the  shown above.

Given: Integer 12

We know that

2 × 6 = 12

From this, we have Divisors of 12 are 2,6

Factors of 12 are divisors of 12 are 2,6

Therefore, the factors of 12 are 2,6.

Primary Mathematics Workbook 4A Chapter 1 Exercise 1.7 Breakdown Page 23  Exercise 1.8  Problem 3

Given: Integer 8

To find –  The factors of 8

Find the factors of 8 from the  shown above.

Given: Integer 8

We know that

1 × 8 = 8

From this, we have Divisors of 8 are 1,8

Factors of 8 are divisors of 8 are 1,8

Therefore the factors of 8 are 1,8.

Page 23  Exercise 1.8  Problem 4

Given: Integer 21

To find – The factors of 21

Find the factors of 21 from the shown above.

Given: Integer 21

We know that

3 × 7 = 21

From this, we have Divisors of 21 are 3,7

Factors of 21 are divisors of 21 are 3,7

Therefore, the factors of 21 are 3,7.

Exercise 1.7 Whole Numbers Primary Mathematics Workbook Step-By-Step Page 24  Exercise 1.8  Problem 5

Given: 2×__= 8

Question is to fill the blank

Find the value in blank using factors of 8

Given: 2×___= 8

Let the number be x, we have

2x = 8

Now, evaluating the value of x

​2x = 8

x = 4
​
The value in the blanks is 4, 2 × − 4 = 8

Therefore, the value of the missing factor in the blanks is 4, 2× − 4 = 8

Page 24  Exercise 1.8  Problem 6 

Given:  __×6 = 18

Question is to fill the blank

Find the value in blank using factors of 18

Given:  ___× 6 = 18

Let the number be x, we have

6x = 18

Now, evaluating the value of x

​6x = 18

x = 3
​
The value in the blanks is 3, −3 × 6 = 18

Therefore, the value of the missing factor in the blank is 3, −3 × 6 = 18.

Primary Mathematics Workbook 4A Common Core Edition 1.7 Practice Page 24  Exercise 1.8  Problem 7

Given: 5 ×___= 45

Question is to fill the blank

Find the value in blank using factors of 45

Given: 5×___ = 45

Let the number be x, we have

5x = 45

Now, evaluating the value of x

​5x = 45

x = 9
​
The value in the blanks is 9, 5×−9 = 45

Therefore, the value of the missing factor in the blanks is 9, 5×− 9 = 45.

Page 24  Exercise 1.8  Problem 8

Given: 6×___= 48

Question is to fill the blank

Find the value in blank using factors of 48

Given: 6 × ___= 48

Let the number be x, we have

6x = 48

Now, evaluating the value of x

​6x = 48

x = 8
​
The value in the blanks is 8, 6 × 8 = 48

Therefore, the value of the missing factor in the blanks is  8, 6 ×  8 = 48.

Page 24  Exercise 1.8  Problem 9

Given: 7×___ = 56

Question is to fill the blank

Find the value in blank using factors of 56

Given: 7 ×___= 56

Let the number be x, we have

7x = 56

Now, evaluating the value of x

​7x = 56

x = 8
​
The value in the blanks is  8, 7 × 8 = 56

Therefore, the value of the missing factor in the blanks is 8, 7 × 8 = 56

Common Core 4A Chapter 1 Whole Numbers 1.7 Solutions Page 24  Exercise 1.8  Problem 10

Given: 9×__= 72

Question is to fill the blank

Find the value in blank using factors of 72

Given: 9 × __= 72

Let the number be x, we have

9x = 72

Now, evaluating the value of x

​9x = 72

x = 9
​
The value in the blanks is 8, 9 ×  8 = 72

Therefore, the value of the missing factor in the blanks is 8, 9×8 = 72

Page 24  Exercise 1.8  Problem 11

Given: ___×4 = 72

Question is to find the missing factors and then fill the blank

Find the value in blank using factors of 72.

Given: ___×4 = 72

Let the number be x, we have

4x = 72

Now, evaluating the value of x

​4x = 72

x = 18

The value in the blanks is 18, 18 × 4 = 72.

Therefore, the value of the missing factor in the blanks is 18, 18 × 4 = 72.

Page 24  Exercise 1.8  Problem 12

Given:  ___× 6 = 54

Question is to fill the blank

Find the value in blank using factors of 54

Given:  ___ × 6 = 54

Let the number be x, we have

6x = 54

Now, evaluating the value of x

​6x = 54

x = 9

The value in the blanks is 9, 9 × 6 = 54

Therefore, the value of the missing factor in the blanks is 9, 9 × 6 = 54

Page 24  Exercise 1.8  Problem 13

Given: ___× 7 = 70

Question is to fill the blank

Find the value in blank using factors of 70

Given: ___ × 7 = 70

Let the number be x, we have

7x = 70

Now, evaluating the value of x

​​7x = 70

x = 10
​
The value in the blanks is 10, 10 × 7 = 70

Therefore, the value of the missing factor in the blanks is 10, 10 × 7 = 70

Page 24  Exercise 1.8  Problem 14

Given: ___× 8 = 64

Question is to fill the blank

Find the value in blank using factors of 64

Given: ___× 8 = 64

Let the number be x, we have 8x=64

Now, evaluating the value of x

​8x = 64

x =  8
​
The value in the blanks is 8, 8 × 8 = 64

Therefore, the value of the missing factor in the blanks is 8, 8 × 8 = 64

Detailed Solutions For Exercise 1.7 Primary Mathematics Workbook 4A Page 24  Exercise 8  Problem 15

Given:
​
​8=1 × ___

8=2 × ___
​
Question is to fill the blanks and find the factors of 8

Find the value in blank using factors of 8

Given:  8 = 1×___

Let the number be x,  we have

x = 8

8 = 1 × 8

Given: 8 = 2 × ___

Let the number be x,  we have

2x = 8

8 = 2 × 4

Factors of 8 are 1,2,4,8

Therefore, the blank values are 8,4,  8 = 1 × 8, and 8 = 2 × 4. Factors of 8 are 1,2,4 and 8.

Page 24  Exercise 8  Problem 16

Given:

​15 = 1×___

15 = 3×___
​
Question is to fill the blanks and find the factors of 15

Find the value in blank using factors of 15

Given: 15 = 1×___

Let the number be x, we have

x = 15

15 = 1 × 15

Given: 15 = 3 × ___

Let the number be x, we have

3x = 15

15 = 3 × 5

Factors of 15 are 1,3,5,15

Therefore, the blank values are 15,5 15 = 1 × 15 and 15 = 3 × 5. Factors of 15 are 1,3,5 and 15

Page 24  Exercise 8  Problem 17

Given: 16,27,13,19,21

To find –  The prime numbers out of these five numbers

Check the number according to the definition of prime number

Given: 16

As we know
​
​1 × 16 = 16

2× 8 = 16

4  × 4 = 16
​
It means the factor of 16 is 1,2,4,8,16. 16 is not a prime number.

Given: 27

As we know
​
​1 × 27 = 27

3 × 9 = 27
​
It means the factor of 27 is 1,3,9,27. 27 is not a prime number.

Given: 13

As we know

1 × 13 = 13

It means the factor of 13 is 1,13. 13 is a prime number.

Given: 19

As we know

1 × 19 = 19

It means the factor of 19 is 1,19. 19 is a prime number.

Given: 21

As we know

​1 × 21 = 21

3 × 7 = 21
​
It means factor of 21 is 1,3,7,21. 21

Therefore, the prime numbers out of 16,27,13,19,21 are 13 and 19.

Page 25  Exercise 1.9  Problem 1

Given: Is 2 a factor of 35

Question is to check the statement

Use the Divisor method to find the factors of 35 and check that 2 is a factor of 35

Given: Is 2 a factor of 35

Using Factors of 35 by divisor method

Dividing 35 by 1, we have

\(\frac{35}{1}\) = 35

1 is a factor of 35

Dividing 35 by 5, we have

\(\frac{35}{5}\) = 7

5 is a factor of 35

Dividing 35 by, we have

\(\frac{35}{7}\) = 5

7 is a factor of 35

Dividing 35 by 35, we have

\(\frac{35}{35}\) = 1

35 is a factor of 35

Factors of Number 35 are 1,5,7,35. If we divide the number 35 by any integer other than these the remainder will not be 0.

It means if we divide 35 by 2 the remainder will not be. Or we can say 2 is not a factor of 35.

Factors of Number 35 are 1,5,7,35. If we divide the number 35 by any integer other than these the remainder will not be 0 Or we can say 2 is not a factor of 35.

Page 25  Exercise 1.9  Problem 2

Given: Is 3 a factor of 45

Question id to check the statement

Use the Divisor method to find the factors of 45 and check that 3 is a factor of 45

Given: Is 3 a factor of 45

Using Factors of 45 by divisor method

Dividing 45 by 1, we have

\(\frac{45}{1}\) = 45

1 is a factor of 45

Dividing 45 by 3, we have

\(\frac{45}{3}\) = 15

3 is a factor of 45

Dividing 45 by 5, we have

\(\frac{45}{5}\)=9

9 is a factor of 5

Dividing 45 by 15, we have

\(\frac{45}{15}\)= 3

15 is a factor of 45

Dividing 45 by 45, we have

\(\frac{45}{45}\)=1

45 is a factor of 45

Factors of Number 45 are 1,3,5,9,15,45.

If we divide the number 45 by any integer other than these the remainder will not be 0.

It means if we divide 45 by 3 the remainder will be 0. Or we can say 3 is a factor of 45.

Factors of Number 45 are 1,3,5,9,15,45. If we divide the number 45 by any integer other than these the remainder will not be 0 Or we can say 3 is a factor of 45.

Page 25  Exercise  1.9  Problem 3

Given: 36,48,60,75,84 and digit 3,4,5

To check that integer from 36,48,60,75,84 has 3,4,5 as a factor of integer

Use condition for multiples of 3,4,5 and check it

Factors of 36

Sum of digits of 36 is 9 which is a multiple of 3 so 3 is a factor of 36

Integer 36 is an even number and its last two digits are divisible by 4 so 4 is a factor of 36.

Integer 36 has 6 at ones place so 5 is not a factor of 36.

Factors of 48

Sum of digits of integer 48 is 12 which is a multiple of 3 so 3 is a factor of 48

Integer 48 is an even number and its last two digits are divisible by 4 so 4 is a factor of 48.

Integer 48 has 8 at ones place so 5 is not a factor of 48.

Factors of 60

Sum of digits of integer 60 is 6 which is a multiple of 3 so 3 is a factor of 60

Integer 60 is an even number and its last two digits are divisible by 4 so 4 is a factor of 60.

Integer 60 has 0 at ones place so 5 is a factor of 60.

Factors of 75

Sum of digits of integer 75 is 12 which is a multiple of 3 so 3 is a factor of 75

Integer 75 is an odd number so 4 is not a factor of 75.

Integer 75 has 5 at ones place so 5 is a factor of 75.

Factors of 84

Sum of digits of integer 84 is 12 which is a multiple of 3 so 3 is a factor of 84

Integer 84 is an even number and its last two digits are divisible by 4 so 4 is a factor of 84.

Integer 84 has 4 at ones place so 5 is not a factor of 84.

Combining all the answers, we have

Therefore

Integer 36 : 3 is a factor of 36, 4 is a factor of 36, and 5 is not a factor of 36.

Integer 48 : 3 is a factor of 48,4 is a factor of 48, and 5 is not a factor of 48.

Integer 60 : 3 is a factor of 60,4 is a factor of 60, and 5 is a factor of 60.

Integer 75 : 3 is a factor of 75,4 is not a factor of 75, 5 is a factor of 75.

Integer 84 : 3 is a factor of 84, 4 is a factor of 84, and 5 is not a factor of 84.

The combined answers of questions above are:

Page 25  Exercise  1.9  Problem 4

Given: Answer from above Question

To find – Common factor of all the integer

Observe the result of the above Question and find the common factor

Result of  above Question

As we can see from the result of above Question, 3 is a common factor of all integers 30,36,48,60,75,84

As we can see from the result of above Question, 3 is a common factor of all integers 30,36,48,60,75,84.

Page 26  Exercise  1.9  Problem 5

Given: 64

To find all the factor of the given number.

We have to find all the numbers when multiplied is equal to 64

​1 × 64 = 64

2 × 32 = 64

4 × 16 = 64

8 × 8 = 64

​64 is a multiple of 1,2,4,8,16,32 and 64

Therefore, the factors of 64 are 1,2,4,8,16,32 and 64

The factors of 64 are 1,2,4,8,16,32 and 64.

Page 26  Exercise  1.9   Problem 6

Given: 72

To find all the factor of the given number.

We have to find all the numbers when multiplied is equal to 72

​1 × 72 = 72

2 × 36 = 72

4 × 18 = 72

8 × 9 = 72
​
72 is a multiple of 1,2,4,8,9,18,36 and 72

Therefore, the factors of 72 are 1,2,4,8,9,18,36 and 72

The factors of 72 are 1,2,4,8,9,18,36 and 72

Page 26  Exercise  1.9  Problem 7

Given: 84

To find all the factor of the given number.

We have to find all the numbers when multiplied is equal to 84

​1 × 84 = 84

2 × 42 = 84

4 × 21= 84

7 × 12 = 84
​
84 is a multiple of 1,2,4,7,12,21,42 and 84

Therefore, the factors of 84 are 1,2,4,7,12,21,42 and 84

The factors of 84 are 1,2,4,7,12,21,42 and 84

Page 26  Exercise  1.9  Problem 8

Given: 98

To find all the factor of the given number.

We have to find all the numbers when multiplied is equal to 98

​1 × 98 = 98

2 × 49 = 98

14 × 7 = 98
​
98 is a multiple of 1,2,7,14,49, and 98

Therefore, the factors of 98 are 1,2,7,14,49, and 98

The factors of 98 are 1,2,7,14,49, and 98

Page 26   Exercise  1.9  Problem 9

Given: 60

To find all the factor of the given number.

We have to find all the numbers when multiplied is equal to 60

​1 × 60 = 60

2 × 30 = 60

4 × 15 = 60

5 × 12 = 60

6 × 10 = 60
​
60 is a multiple of 1,2,4,5,6,10,12,15,30 and 60

Therefore, the factors of 60 are 1,2,4,5,6,10,12,15,30 and 60

The factors of 60 are 1,2,4,5,6,10,12,15,30 and 60

Page 27   Exercise  1.9  Problem 10

Given: 64 = 2 × 8 ×_____ × _____

To find – The missing factors.

We have to use prime numbers for the missing factors.

Solve for x.

Let the missing factor be x

​64 = 2 × 8 × x

⇒ x = \(\frac{64}{16}\)

⇒ x = 4
​
Here, the missing factor should be of the form of prime numbers.

We know that 4 can be written as 4=2×2 and we also know that is a prime number.

Therefore, the missing factors are 2 and 2

64 =  2 × 8 × 2 × 2

Page 27   Exercise  1.9  Problem 11

Given: 84 = 6 ×_____ × _____

To find-  The missing factors.

We have to use prime numbers for the missing factors.

Solve for x.

Let the missing factor be x

​84 = 6 × x

⇒ x =  \(\frac{84}{6}\)

⇒ x = 14

​Here, the missing factor should be of the form of prime numbers.

We know that 14 can be written as 14 = 7 × 2 and we also know that 2 and 7 are prime number.

Therefore, the missing factors are 2 and 7

Hence, the missing factors are 84=6 × 2 × 7

Page 27   Exercise  1.9   Problem 12

Given: 45 =_____×_____×5

To find – The missing factors.

We have to use prime numbers for the missing factors.

Solve for x.

Let the missing factors be x

​45 = x × 5

⇒ x = \(\frac{45}{5}\)

⇒ x = 9
​
Here, the missing factor should be of the form of prime numbers.

We know that 9 can be written as 9 = 3 × 3 and we also know that 3 and 3 are prime number.

Therefore, the missing factors are 3 and 3

Hence the factors are 45 = 3 × 3 × 5

Page 27   Exercise  1.9  Problem 13

Given: 72=_____×4×_____×_____

To find – The missing factors.

We have to use prime numbers for the missing factors.

Solve for x.

Let the missing factors be x

​72 = x × 4

⇒ x = \(\frac{72}{4}\)

⇒ x = 18
​

Here, the missing factor should be of the form of prime numbers.

We know that 18 can be written as 18 = 2 × 3 × 3 and we also know that 2 and 3 are prime number.

Therefore, the missing factors are 2 ,3 and 3

Hence, the missing factors are 72 = 2 × 4 × 3 × 3

Page 27   Exercise  1.9  Problem 14

Given: 24 = 3 × 2 × n

To find – The missing factors n.

Solve the equation for n.

Simplifying the equation
​
​24 = 3 × 2 × n

⇒ 24 = 6n

​Dividing
​
​⇒ n = \(\frac{24}{6}\)

⇒ n = 4
​
The missing factor is n = 4

Page 27   Exercise  1.9  Problem 15

Given: 18 = 3 × 2 × n

To find – The missing factors n.

Solve the equation for n.

Simplifying the equation
​
​18 = 3 × 2 × n

⇒ 18 = 6n
​
Dividing
​
​⇒ n = \(\frac{18}{6}\)

⇒ n = 3
​
Therefore the value of n in the expression 18=3×2×n will be n = 3

Page 27   Exercise  1.9  Problem 16

Given: 25 × 4 = 5 × n × 4

To find – The missing factors n.

Solve the equation for n.

Simplifying the equation

​25 × 4 = 5 × n × 4

⇒ 25 × 4 = 20n
​
Dividing

​​⇒ n = \(\frac{25×4}{20}\)

⇒ n = 5
​
The value of n in the equation 25 × 4 = 5 × n × 4 will be n=5

Page 27  Exercise  1.9  Problem 17

Given: 21 × 20 = 21 × n × 2

To find-  The missing factors n.

Solve the equation for n.

Simplifying the equation

​21 × 20 = 21 × n × 2

⇒ 21 × 20 = 21 × 2 × n
​
Dividing
​
​⇒ n = \(\frac{21×20}{21×2}\)

⇒ n = 10
​
The missing factors represented by n is 10.

Page 27  Exercise  1.9  Problem 18

Given: 3 × 32 = 6 × n

To find- The missing factors n.

Solve the equation for n.

Simplifying the equation

​3 × 32 = 6 × n

⇒ n=\(\frac{3×32}{6}\)

Dividing
​
⇒ n= \(\frac{1×32}{2}\)

⇒ n = 16
​
The value of n in the equation 3 × 32 = 6 × n will be n = 16

Page 27  Exercise  1.9  Problem 19

Given: 16 × 2 = 4 × n

To find-  The missing factors n.

Solve the equation for n.

​Simplifying the equation

​16 × 2 = 4 × n

⇒ n = \(\frac{16×1}{2}\)

n = 8

​The value of n in the equation 16×2=4×n will be n = 8

Page 27   Exercise  1.9  Problem 20

Given: To find if 4 is a common factor of 36 and 60

To solve this question, 36 and 60 by divide 4

If it leaves a remainder, then 4 is not a factor.

If it doesn’t leave a remainder, then 4 is a factor

Divide 36 by divide 4

​⇒  \(\frac{36}{4}\)

⇒ 9
​

When dividing 36 by 4, there is no reminder.

Therefore, 4 is a common factor of 36

Divide 60 by divide 4

​⇒ \(\frac{60}{4}\)

⇒ 15
​
When divided 60 by 4, there is no reminder.

Therefore, 4 is a common factor of 60

4 is a common factor of 36 and 60.

Page 27  Exercise  1.9  Problem 21

Given: To find if 4 is a common factor of 48 and 90

To solve this question, 48 and 90 by divide 4

If it leaves a remainder, then 4 is not a factor.

If it doesn’t leave a remainder, then 4 is a factor

Divide 48 by divide 4

⇒ 22.5
​
Since when we divide 90 by 4, the answer is of the decimal form. Therefore it has a reminder.

Therefore, 4 is not the common factor of 90

​⇒ 90

4 is a common factor of 48 but not the common factor of 90.

Page 27  Exercise  1.9  Problem 22

Given: To find if 6 is a common factor of 30 and 78

To solve this question, 30 and 78 by divide 6

If it leaves a remainder, then 6 is not a factor.

If it doesn’t leave a remainder, then 6 is a factor

Divide 30 by divide 6

​⇒ \(\frac{30}{6}\)

⇒ 5
​
When dividing 30 by 6, there is no reminder.

Therefore, 6 is a common factor of 30

Divide 78 by divide 6

​⇒ \(\frac{78}{6}\)

​⇒ 13

When dividing 78 by 6, there is no reminder.

Therefore, 6 is a common factor of 78

6 is a common factor of 30 and 78.

Page 28  Exercise 9  Problem 23

Given:

Multiple of 3: 3,6,9,12,15,18,…

Multiple of 2:​​​ 2,4,6,8,10,12,…

To find –The first two common multiples of 3 and 2

The numbers which are both the multiple of 3 and 2 are the common multiples of 3 and 2.

By observing the multiples of 3 and 2, 6 and 12 are both the multiple of 3 and 2.

Therefore, 6 and 12 are the first two common multiples of 3 and 2.

The first two common multiples of 3 and 2 are 6 and 12.

Page 27   Exercise  1.9   Problem 24

Given:

Multiple of 8: 8,16,24,32…….

Multiple of 4:​​​ 4,8,12,16,…

To find the first two common multiples of 8 and 4

The numbers which are both the multiple of 8 and 4 are the common multiples of 8 and 4.

By observing the multiples of 8 and 4, 8and 16are both the multiples of 8 and 4.

Therefore, 8 and 16 are the first two common multiples of 8 and 4.

The first two common multiples of 8 and 4 are 8 and 16.

Page 27   Exercise  1.9  Problem 25

To find – The first two common multiples of 9 and 6

The numbers which are both the multiple of 9 and 6 are the common multiples of 9 and 6.

First, find the multiples of 9 and 6

Then observe the multiples of 9 and 6 and find their first two common multiples.

Multiple of 9: 9,18,27,36,45…

Multiple of 6:6,12,18,24,30,36…

By observing the multiples of 9 and 6, 18 and 36 are both the multiples of 9 and 6.

Therefore, 9 and 6 are the first two common multiples of 18 and 36.

The first two common multiples of 9 and 6 are 18 and 36.

Page 27  Exercise  1.9  Problem 26

To find – The first two common multiples of 8 and 6

The numbers which are both the multiple of 8 and 6 are the common multiples of 8 and 6.

First, find the multiples of 8 and 6

Then observe the multiples of 8 and 6 and find their first two common multiples.

Multiple of 8: 8,16,24,32,40,48,56,…

Multiple of 6: 6,12,18,24,30,36,42,48,54,…

By observing the multiples of 8 and 6, 24 and 48 are both the multiple of 8 and 6.

Therefore, 8 and 6 are the first two common multiples of 24 and 48.

The first two common multiples of 8 and 6 are 24 and 48.

Page 29   Exercise 1.10  Problem 1

Given: 8 + 12 + 20

To find – The value of each of the given expressions.

Add the first two-term
​
​⇒ 8 + 12 + 20

⇒ 20 + 20
​
Now add the remaining terms

Therefore, the value of the expression, 8 + 12 + 20 = 40

Page 29   Exercise 1.10  Problem 2

Given: 40 − 14 −9

To find – The value of each of the given expressions.

Add the terms that are of the same signs.

​⇒ 40 − 14 − 9

⇒ 40 − 23
​
Now subtract the remaining terms (since the sign of the greatest number is positive, the answer also has a positive sign.)

⇒ 17

Therefore, the value of the expression, 40 − 14 − 9 = 17

Page 29   Exercise 1.10  Problem 3

Given: 26 + 8 − 9

To find –  The value of each of the given expressions.

Add the terms that are of the same signs.
​
​⇒ 26 + 8 − 9

⇒ 34 − 9
​
Now subtract the remaining terms (since the sign of the greatest number is positive, the answer also has a positive sign.)

⇒ 25

Therefore, the value of the expression, 26 + 8 − 9 = 25

Page 29   Exercise 1.10   Problem 4

Given: 21−5 + 8

To find –  The value of each of the given expressions.

Add the terms that are of the same signs.
​
​⇒ 21 − 5 + 8

⇒ 29 − 5

⇒ 24
​
Now subtract the remaining terms (since the sign of the greatest number is positive, the answer also has a positive sign.)

⇒ 24

Therefore, the value of the expression, 21−5 + 8 = 24

Page 29   Exercise 1.10  Problem 5

Given: 3 × 5 × 8

To find – The value of each of the given expressions.

First, multiply the first two terms.
​
​⇒ 3 × 5 × 8

⇒ 15 × 8
​
Now multiply the remaining terms.

⇒ 120

Therefore, the value of the expression,3 × 5 × 8 = 120

Page 29   Exercise 1.10  Problem 6

Given: 36 ÷ 3 ÷ 4

To find – The value of each of the given expressions.

First, divide the first two terms.
​
​⇒ 36 ÷ 3 ÷ 4

⇒ 12 ÷ 4
​
Now divide the remaining terms.

⇒ 3

Therefore, the value of the expression, 36 ÷ 3 ÷ 4 = 3

Page 29   Exercise 1.10  Problem 7

Given: 4 × 9 − 3

To find – The value of each of the given expressions.

Use BODMAS rule to find the value of the expression.

By BODMAS rule, first, multiply the first two terms.
​
​⇒ 4 × 9 − 3

⇒ 36 − 3
​
Now subtract the remaining terms. (Since the sign of the greatest number is positive, the answer also has a positive sign.)

⇒ 36 − 3 = 33

Therefore, the value of the expression,4 × 9 − 3 = 33

Page 29   Exercise 1.10   Problem 8

Given: 64 ÷ 8 × 5

To find – The value of each of the given expressions.

By BODMAS rule, we have to first divide the given expression and then multiply.(since in the order of operations division is followed by multiplication)

First, divide the first two terms.

​⇒ 64 ÷ 8 × 5

⇒ 8 × 5
​
Now multiply the remaining terms.

⇒ 40

Therefore, the value of the expression,64 ÷ 8 × 5 = 40

Page 29  Exercise 1.10  Problem  9

Given: 24 ÷ 6 × 8

To find – The value of each of the given expressions.

By BODMAS rule, we have to first divide the given expression and then multiply.(Since in the order of operations division is followed by multiplication)

First divide the first two terms.

​⇒ 24 ÷ 6 × 8

⇒ 4 × 8

Now multiply the remaining terms.

⇒ 32

Therefore, the value of the expression, 24 ÷ 6 × 8 = 32

Page 29  Exercise  1.10  Problem 10

Given: 140 − 40 × 3

To find-  The value of each of the given expressions.

By BODMAS rule, we have to first multiply the given expression and then subtract.(Since in the order of operations multiplication is followed by subtraction)

​First, multiply the last two terms.
​
​⇒ 140−40 × 3 = 140 − 120
​
Now subtract the remaining terms.

Here, since the greatest number is negative the answer holds a negative sign.

⇒ 140 − 120 = 20

Therefore, the value of the expression,140 − 40 × 3 = 20

Page 29   Exercise  1.10  Problem 11

Given: 46 + 32 ÷ 8

To find – The value of each of the given expression.

By BODMAS rule, we have to first divide the given expression and then add.(Since in the order of operations division is followed by addition)

First divide the last two terms.
​
​⇒ 46 + 32 ÷ 8

⇒ 46 + 4
​
Now add the remaining terms.

⇒ 50

Therefore, the value of the expression,46 + 32 ÷ 8 = 50

Page 29   Exercise  1.10  Problem 12

Given: 100−60÷4

To find – The value of each of the given expressions.

By BODMAS rule, we have to first divide the given expression and then subtract.(Since in the order of operations division is followed by subtraction)

First divide the last two terms.
​
​⇒ 100−60 ÷ 4

⇒ 100 −15
​
Now subtract the remaining terms. (since the sign of the greatest number is positive, the answer takes a positive sign.)

⇒ 85

Therefore, the value of the expression,100−60 ÷ 4 = 85

Page 29  Exercise  1.10  Problem 13

Given: 8 × 6 + 14

To find – The value of each of the given expressions.

By BODMAS rule, we have to first multiply the given expression and then add.(Since in the order of operations multiplication is followed by addition)

First multiply the first two terms.

​⇒ 8 × 6 + 14

⇒ 48 + 14
​
Now add the remaining terms. (since the sign of the greatest number is positive, the answer takes a positive sign.)

⇒ 62

Therefore, the value of the expression,8 × 6 + 14 = 62

Page 29   Exercise  1.10   Problem 14

Given: 12 + 18 ÷ 6

To find – The value of each of the given expressions.

By BODMAS rule, we have to first divide the given expression and then add.(Since in the order of operations multiplication is followed by addition)

First divide the last two terms.
​
​⇒ 12 + 18 ÷ 6

⇒12 + 3

​Now add the remaining terms.

⇒15

Therefore, the value of the expression,12 + 18 ÷ 6 = 15

Page 29   Exercise  1.10  Problem 15

Given: 6 × 10 − 5

To find-  The value of each of the given expressions.

By BODMAS rule, we have to first multiply the given expression and then subtract. (Since in the order of operations multiplication is followed by addition)

First multiply the first two terms.
​
​⇒ 6 × 10 − 5

⇒ 60 − 5
​
Now subtract the remaining terms. (Since the sign of the greatest number is positive, the answer takes a positive sign.)

⇒ 55

Therefore, the value of the expression,6 × 10 − 5 = 55

Page 29   Exercise  1.10  Problem 16

Given: 72 + 6 × 6

To find – The value of each of the given expressions.

By BODMAS rule, we have to first multiply the given expression and then add.(Since in the order of operations multiplication is followed by addition)

First, multiply the last two terms.
​
​⇒ 72 + 6 × 6

⇒ 72 + 36
​
Now add the remaining terms.

⇒ 108

Therefore, the value of the expression, 72 + 6 × 6 = 108

Page 30   Exercise 1.10  Problem 17

Given: 20 + 4 ÷ 4 − 4

To find the value of each of the given expressions.

By BODMAS rule, we have to first divide the given expression, then add and then subtract. (Since in the order of operations multiplication is followed by addition and then by subtraction)

First divide the middle two terms.
​
​⇒ 20 + (4 ÷ 4) − 4

⇒ 20 + 1 − 4
​

Now add the first two terms and then subtract.(Since the sign of the greatest number is positive, the answer takes a positive sign.)
​
​⇒ 21 − 4

⇒ 17

​Therefore, value of the expression,20 + 4 ÷ 4 − 4 = 17

Page 30   Exercise 1.10   Problem 18

Given: 6 × 2−10 ÷ 5

To find – The value of each of the given expression.

By BODMAS rule, we have to first divide the given expression, then multiply and then subtract.(Since in the order of operations division is followed by multiplication and then by subtraction)

First divide the last two terms.
​
​⇒ 6 × 2 − 10 ÷ 5

⇒ 6 × 2−2
​
Now multiply the first two terms and then subtract. (Since the sign of the greatest number is positive, the answer takes a positive sign.)
​
​⇒ 12 − 2

⇒ 10

​Therefore, the value of the expression,6 × 2−10 ÷ 5 = 10

Page 30   Exercise 1.10  Problem 19

Given: 80−36 ÷ 4 × 3

To find – The value of each of the given expressions.

By BODMAS rule, we have to first divide the given expression, then multiply and then subtract. (Since in the order of operations division is followed by multiplication and then by subtraction)

First divide the middle two terms.
​
​⇒ 80 − (36÷4) × 3

⇒ 80−9 × 3
​
Now multiply the last two terms and then subtract.(Since the sign of the greatest number is positive, the answer takes a positive sign.)
​
​⇒ 80 − 27

⇒ 53
​
Therefore, the value of the expression, 80−36 ÷ 4 × 3 = 53

Page 30  Exercise 1.10  Problem 20

Given: 32 + 8 + 10 × 2.

To find – The value of each of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be multiplication and then addition.

Referring to the question

32 + 8 + 10 × 2

Using BODMAS

32 + 8 + 20

=  60

Hence, the value of 32 + 8 + 10 × 2 is 60.

Page 30  Exercise 1.10  Problem 21

Given: 52−35 ÷ 7 − 7 × 2.

To find –  The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be division, then multiplication, and then addition and subtraction.

Referring to the question

52 − 35 ÷ 7 − 7 × 2

Using BODMAS

52−5−14

= 33

Hence, the value of 52−35÷7−7 × 2 is 33.

Page 30  Exercise 1.10  Problem 22

Given: 9 × 8 − 6 × 10.

To find – The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be multiplication and subtraction.

Referring to the question

9 × 8−6 × 10

Using BODMAS

72 − 60

Hence, the value of  9 × 8−6 × 10 is 12.

Page 30  Exercise 1.10  Problem 23

Given: 7 × 8 + 24 ÷ 8.

To find – The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be division, then multiplication and then addition.

Referring to the question

7 × 8 + 24 ÷ 8

Using BODMAS

56 + 3

= 59

Hence, the value of 7 × 8 + 24 ÷ 8 is 59.

Page 30  Exercise 1.10  Problem 24

Given: 63÷9 + 20 ÷ 10.

To find – The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be division and then addition.

Referring to the question

63 ÷ 9 + 20 ÷ 10

Using BODMAS

7 + 2

= 9

Hence, the value of 63 ÷ 9 + 20 ÷ 10 is 9.

Page 30  Exercise 1.10  Problem 25

Given:

To find – The value of 12 + 49 ÷ 7 × 3.

Use the strategy of BODMAS.

Thus, the first operation will be division, then multiplication, and then addition.

Referring to the question

12 + 49 ÷ 7 × 3

Using BODMAS

12 + 21

=  33

Hence, the value of 12 + 49 ÷ 7 × 3 is 33.

Page 30  Exercise 1.10  Problem 26

Given: 5×8−32÷4+18.

To find – The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be division, then multiplication, and then addition and subtraction.

Referring to the question

5 × 8 − 32 ÷ 4 + 18

Using BODMAS

40 − 8 + 18

= 50

Hence, the value of 5 × 8 − 32 ÷ 4 + 18 is 50.

Page 31  Exercise 1. 11  Problem 1

Given: 9 + (26−15).

To find –  The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be opening the brackets followed by addition and subtraction.

Referring to the question

⇒ 9 + (26 − 15)

Using BODMAS

⇒  9 + 26 − 15

= 20

Hence, the value of 9 + (26−15) is 20.

Page 31  Exercise 1. 11  Problem 2

Given: 90−(4 + 6).

To find –  The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be opening the brackets followed by addition and subtraction.

Referring to the question

⇒  90− (4 + 6)

Using BODMAS

⇒  90 − 4 − 6

= 80

Hence, the value of  90 − (4 + 6) is 80.

Page 31   Exercise 1. 11  Problem 3

Given: 12 − (10 − 8).

To find – The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be opening the brackets followed by addition and subtraction.

Referring to the question

⇒ 12 − (10 − 8)

Using BODMAS

⇒ 12 − 10 + 8

= 10

Hence, the value of 12−(10−8) is 10.

Page 31   Exercise 1. 11  Problem 4

Given: (31 − 20) − 8

To find –  The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be opening the brackets followed by addition and subtraction.

Referring to the question

⇒ (31−20)−8

Using BODMAS

⇒  31−20−8

= 3

Hence, the value of (31−20)−8 is 3.

Page 31   Exercise 1. 11  Problem 5

Given: 8 × (3 × 2).

To find – The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be opening the brackets followed by multiplication.

Referring to the question

⇒  8 × (3 × 2)

Using BODMAS

⇒  8 × 3 × 2

= 48

Hence, the value of 8 × (3 × 2) is 48.

Page 31   Exercise 1. 11  Problem 6

Given: 20 ÷ (4 ÷ 2).

To find – The value of the given expression.

Use the strategy of BODMAS. Thus, the first operation will be solving the operation in the bracket followed by division.

Referring to the question

⇒ 20 ÷ (4 ÷ 2)

Using BODMAS

⇒ 20 ÷ 2

= 10

Hence, the value of 20 ÷ (4 ÷ 2) is 10.

Page 31   Exercise 1. 11  Problem 7

Given: 9 × (15 ÷ 3)

To find – The value of the given expression.

Use the strategy of BODMAS. Thus, the first operation will be solving the operation in the bracket followed by multiplication.

Referring to the question

⇒ 9 × (15 ÷ 3)

Using BODMAS

⇒ 9 × 5

= 45

Hence, the value of  9 × (15 ÷ 3) is 45.

Page 31   Exercise 1. 11  Problem 8

Given: 15 ÷ (5 × 3).

To find –  The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by division.

Referring to the question

⇒ 15 ÷ (5 × 3)

Using BODMAS

⇒ 15 ÷ 15

= 1

Hence, the value of 15 ÷ (5 ×3 ) is 1.

Page 31   Exercise 1. 11  Problem  9

Given: (9+6)÷5

To find the value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by division.

Referring to the question

⇒ (9 + 6) ÷ 5

Using BODMAS

⇒ 15 ÷ 5

= 3

Hence, the value of (9 + 6) ÷ 5 is 3.

Page 31   Exercise 1. 11  Problem  10

Given: 2 × (9−4)

To find –  The value of

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by multiplication.

Referring to the question

⇒ 2 × (9−4)

Using BODMAS

⇒ 2 × 5

= 10

Hence, the value of 2 × (9−4) is 10.

Page 31   Exercise 1. 11  Problem  11

Given: 12 ÷ (8−6)

To find –  The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by division.

Referring to the question

⇒ 12 ÷ (8−6)

Using BODMAS

⇒ 12 ÷ 2

= 6

Hence, the value of 12 ÷ (8−6) is 6.

Page 31   Exercise 1. 11  Problem  12

Given: (4 + 6) × 5.

To find – The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by multiplication.

Referring to the question

⇒ (4 + 6) × 5

Using BODMAS

⇒ 10 × 5

= 50

Hence, the value of (4 + 6) × 5 is 50.

Page 31   Exercise 1. 11  Problem  13

Given: 10 × (15 ÷ 5)

To find –  The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by multiplication.

Referring to the question

⇒ 10 × (15 ÷ 5)

Using BODMAS

⇒ 10 × 3

= 30

Hence, the value of 10 × (15 ÷ 5) is 30.

Page 31   Exercise 1. 11  Problem  14

Given:  (51 − 44) ÷ 7

To find – The value of the given expression

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by division.

Referring to the question

⇒ (51 − 44) ÷ 7

Using BODMAS

⇒ 7 ÷ 7

= 1

Hence, the value of (51− 44) ÷ 7 is 1.

Page 31   Exercise 1. 11  Problem  15

Given: 72 ÷ (9 − 3)

To find – The value of the given expression 72÷(9−3).

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by division.

Referring to the question

⇒ 72 ÷ (9−3)

Using BODMAS

⇒ 72 ÷ 6

= 12

Hence, the value of 72 ÷ (9−3) is 12.

Page 31   Exercise 1. 11  Problem  16

Given: (28 − 18) × 10

To find – The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by multiplication.

Referring to the question

⇒ (28−18) ×10

Using BODMAS

⇒ 10 × 10

= 100

Hence, the value of (28−18)×10 is 100.

Page 32   Exercise 1. 11  Problem 17

Given: 20 + (8 + 4) ÷ 3 .

To find –  The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by division and addition.

Referring to the question

⇒ 20 + (8 + 4) ÷ 3

Using BODMAS

⇒ 20 + 12 ÷ 3

⇒ 20 + 4

= 24

Hence, the value of 20+(8+4)÷3 is 24.

Page 32   Exercise 1. 11  Problem 18

Given: 16 + (9 − 3)× 5

To find –  The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by multiplication and addition.

Referring to the question

⇒ 16 + (9 − 3) × 5

Using BODMAS

⇒ 16 + 6 × 5

⇒ 16 + 30

= 46

Hence, the value of  16 + (9−3) × 5 is 46.

Page 32   Exercise 1. 11  Problem 19

Given:  3 × (4 + 2) ÷ 2

To find – The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by division and then multiplication.

Referring to the question

⇒ 3 × (4 + 2) ÷ 2

Using BODMAS

⇒ 3 × 6 ÷ 2

⇒ 3 × 3

Hence, the value of 3 × (4 + 2) ÷ 2 is 9.

Page 32   Exercise 1. 11  Problem 20

Given: 7 × (13 − 6) −19

To find – The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by multiplication and subtraction.

Referring to the question

⇒ 7 × (13 − 6) − 19

Using BODMAS

⇒ 7 × 7−19

⇒ 49 − 19

= 30

Hence, the value of 7 × (13−6)−19 is 30.

Page 32  Exercise 1. 11 Problem 21

Given: 60 + (18 + 7) ÷ 5

To find –  The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by division and addition.

Referring to the question

⇒ 60 + (18 + 7) ÷ 5

Using BODMAS

⇒ 60 + 25 ÷ 5

⇒ 60 + 5

= 65

Hence, the value of 60 + (18 + 7) ÷ 5 is 65.

Page 32  Exercise 1. 11 Problem 22

Given: 8 × (11 − 8) ÷ 6

To find – The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by multiplication and division.

Referring to the question

⇒ 8 × (11− 8) ÷ 6

Using BODMAS

⇒ 8 × 3 ÷ 6

⇒ 24 ÷ 6

Hence, the value of 8 × (11− 8) ÷ 6 is 4.

Page 32  Exercise 1. 11 Problem 23

Given: 24 ÷ 6 + 3 × (6−4)

To find – The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by division and multiplication, and then addition.

Referring to the question

⇒ 24 ÷ 6 + 3 × (6−4)

Using BODMAS

⇒ 24 ÷ 6 + 3 × 2

⇒ 4 + 6

= 10

Hence, the value of 24 ÷ 6 + 3 × (6−4) is 10.

Page 32  Exercise 1. 11 Problem 24

Given: 10 + (28 − 8) ÷ 5 × 2

To find – The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by division and multiplication, and then addition.

Referring to the question

⇒ 10 + (28−8) ÷ 5 × 2

Using BODMAS

⇒ 10 + 20 ÷ 5 × 2

⇒ 10 + 4 × 2

⇒ 10 + 8

= 18

Hence, the value of  10 + (28−8) ÷ 5 × 2 is 18.

Page 32  Exercise 1. 11 Problem 25

Given: 15×(8+2)−25÷5

To find –  The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by division and multiplication, and then subtraction.

Referring to the question

⇒ 15 × (8 + 2)−25 ÷ 5

Using BODMAS

⇒ 15 × 10 − 25 ÷ 5

⇒ 150 − 5

= 145

Hence, the value of 15 × (8 + 2) − 25 ÷ 5 is 145.

Page 32  Exercise 1. 11 Problem 26

Given: 100−8 × (5 + 2) ÷ 4

To find – The value of the given expression.

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by multiplication and division, and then subtraction.

Referring to the question

⇒ 100 − 8 × (5 + 2) ÷ 4

Using BODMAS

⇒ 100 − 8 × 7 ÷ 4

⇒ 100 − 14

=86

Hence, the value of  100−8 × (5 + 2) ÷ 4 is 86.

Page 33  Exercise 1. 12 Problem 1 

Given: Total number of beads = 50

Number of beads used to make necklace = 32

Number of beads bought = 18

To Find: Number of beads left

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by addition.

Referring to the question, the following is the required expression

⇒ (50−32) + 18

Using BODMAS

⇒ 18 + 18

= 36

Hence, the number of beads left is 36.

Page 33  Exercise 1. 12 Problem 2

Given: Total number of muffins = 20

Number of muffins eaten = 5

Number of muffins given away = 10

To Find: Number of muffins left

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by subtraction.

Referring to the question, the following is the required expression

⇒ 20−(5 + 10)

Using BODMAS

⇒ 20 − 15

= 5

Hence, the number of muffins left with Patrick is 5.

Page 33  Exercise 1. 12 Problem 3

Given: Total number of baseball cards with Sean = 15

Number of baseball cards with Adam = twice the number of cards with Sean

Number of baseball cards Adam bought = 10

To Find: Number of baseball cards with Adam

Use the strategy of BODMAS.

Thus, the first operation will be solving the operation in the bracket followed by multiplication.

Referring to the question, the following is the required expression

⇒ (15 × 2) + 10

Using BODMAS

⇒ 30 + 10

= 40

Hence, the number of baseball cards that Adam has is 40

Page 34  Exercise 1. 12 Problem  4

To Check: 24 = 3 × 8

Use the strategy of BODMAS.

Compare the LHS and RHS.

Referring to the question

LHS = 24

Using BODMAS

RHS = 3 × 8

= 24

Therefore, LHS = RHS so the given equation is true.

Page 34  Exercise 1. 12 Problem  5

To Check: 9 × 11 = 88

Use the strategy of BODMAS.

Compare the LHS and RHS.

Referring to the question

RHS =88

Using BODMAS

LHS = 9 × 11

= 99

Therefore, LHS ≠ RHS so the given equation is false.

Page 34  Exercise 1. 12 Problem  6

To Check: 8 + 35 = (3 × 5) + 8

Use the strategy of BODMAS.

Compare the LHS and RHS.

Referring to the question and using BODMAS
​
​LHS = 8 + 35

⇒ 43
​
Referring to the question and using BODMAS
​
​RHS = (3 × 5) + 8

⇒ 15 + 8

⇒ 23
​
Therefore, LHS ≠ RHS so the given equation is false.

Page 34  Exercise 1. 12 Problem  7

To Check: 16−9 = (7 × 8) − 49

Use the strategy of BODMAS.

Compare the LHS and RHS.

Referring to the question and using BODMAS
​
​LHS = 16 − 9

⇒ 7
​
Referring to the question and using BODMAS
​
​RHS = (7 × 8) − 49

⇒ 56 − 49

⇒ 7
​
Therefore, LHS = RHS so the given equation is true.

Page 34  Exercise 1. 12 Problem  8

To find – The value of (1×5)×10=5×10

Use the strategy of BODMAS.

Thus, the first operation will be multiplication in the brackets.

Check LHS = RHS

Referring to the question and using BODMAS
​
​LHS = (1 × 5) × 10

= 5 × 10

= 50
​
Further Simplifying the equation
​
​RHS = 5 × 10

= 50
​
So, LHS = RHS

Therefore, the equation (1 × 5) × 10 = 5 × 10 is True as

LHS=RHS

Page 34  Exercise 1. 12 Problem  9

To find – The value of 8+6=(2×3)+(5×2)

Use the strategy of BODMAS.

Thus, the first operation will be multiplication in the brackets.

Check LHS = RHS

Referring to the question and using BODMAS
​
​LHS = 8 + 6

=14
​
Further Simplifying the equation

​RHS = (2 × 3) + (5 × 2)

= 6 + 10

= 16
​
So,  LHS ≠ RHS

Therefore, the equation 8+6=(2×3)+(5×2) is False as LHS ≠ RHS

Page 34  Exercise 1. 12 Problem  10

To find – The value of (20÷5)+2=(2×4)−(1×2)

Use the strategy of BODMAS.

Thus, the first operation will be multiplication in the brackets.

Check LHS = RHS

Referring to the question and using BODMAS
​
​LHS = (20 ÷ 5) + 2

= 4 + 2

= 6
​
Further Simplifying the equation
​
​RHS = (2 × 4) − (1 × 2)

= 8 − 2

= 6
​
So, LHS = RHS

Therefore, the equation (20 ÷ 5) + 2 = (2 × 4) − (1 × 2) is True as LHS  = RHS

Page 34  Exercise 1.12 Problem 11

To find –  The value of the blank in 36−(20−7)=……..−13

Use the strategy of BODMAS.

Thus, the first operation will be subtraction in the brackets.

Check LHS=RHS

Solve LHS to find the blank.

Referring to the question and using BODMAS
​
​LHS = 36 − (20 − 7)

= 36 −13
​
Further Simplifying and comparing the equation

RHS= ………−13

So, Comparing LHS and RHS the value of the blank is 36

Therefore, the value of the blank is 36 making the equation True.

Page 34  Exercise 1.12 Problem 12

To find – The value of the blank in (5+8)×(4+6)=……..×10

Use the strategy of BODMAS.

Thus, the first operation will be an addition in the brackets.

Check LHS = RHS

Solve LHS to find the blank.

Referring to the question and using BODMAS

​LHS = (5 + 8) × (4 + 6)

= 13 × 10
​
Further Simplifying and comparing the equation

RHS=………×10

So, Comparing LHS and RHS the value of the blank is 13

Therefore, the value of the blank is 13 making the equation True.

Page 34  Exercise 1.12 Problem 13

To find –  The value of the blank in 100×(9÷3)=……..×3

Use the strategy of BODMAS.

Thus, the first operation will be division in the brackets.

Check LHS=RHS

Solve LHS to find the blank.

Referring to the question and using BODMAS
​
​LHS = 100 × (9 ÷ 3)

= 100 × 3
​
Further Simplifying and comparing the equation

RHS =………×3

So, Comparing LHS and RHS the value of the blank is 100

Therefore, the value of the blank is 100 making the equation True.

Page 34  Exercise 1.12 Problem 14

To find –  The value of the blank in (26−11)÷5 × 4 =……..×4

Use the strategy of BODMAS.

Thus, the first operation will be division in the brackets.

Check LHS = RHS

Solve LHS to find the blank.

Referring to the question and using BODMAS
​
​LHS = (26−11) ÷ 5 × 4

= 15 ÷ 5 × 4

= 3 × 4
​
Further Simplifying and comparing the equation

RHS =………×4

So, Comparing LHS and RHS the value of the blank is 3

Therefore, the value of the blank is 3 making the equation True.

Page 34  Exercise 1.12 Problem  15

To insert the parentheses in the given equation 2+4÷2=3

Use the strategy of BODMAS to insert the brackets.

Check LHS = RHS

Solve LHS using parentheses to make it true for the equation.

Adding the parentheses at the addition rule to make the equation true
​
​LHS = 2 + 4 ÷ 2

= (2 + 4) ÷ 2
​

Further Simplifying and comparing the equation

​RHS = 3

LHS = (2 + 4) ÷ 2

= 6 ÷ 2

= 3
​
So, the parentheses will be inserted at addition making LHS as (2 + 4) ÷ 2

Therefore, the parentheses will be inserted at addition making LHS as (2+4)÷2 making the equation True.

Page 34  Exercise 1.12 Problem  16

To insert the parentheses in the given equation 6−2×3=0

Use the strategy of BODMAS to insert the brackets.

Check LHS = RHS

Solve LHS using parentheses to make it true for the equation.

Adding the parentheses at the multiplication rule to make the equation true

​LHS = 6 − 2 × 3

= 6 − (2 × 3)
​
Further Simplifying and comparing the equation

​RHS = 0

LHS = 6 − (2× 3)

= 6−6

= 0
​
So, the parentheses will be inserted at multiplication making LHS as  6−(2 × 3)

Therefore, the parentheses will be inserted at multiplication making LHS as 6−(2×3) making the equation True.

Page 34  Exercise 1.12 Problem  17

To insert the parentheses in the given equation 2 × 4− 3 + 2 = 7

Use the strategy of BODMAS to insert the brackets.

Check LHS = RHS

Solve LHS using parentheses to make it true for the equation.

Adding the parentheses at the multiplication rule to make the equation true

​LHS = 2 × 4 − 3 + 2

= (2 × 4) − 3 + 2

​Further Simplifying and comparing the equation
​
​RHS = 7

LHS = (2 × 4) − 3 + 2

=8 − 3 + 2

= 5 + 2

= 7

So, the parentheses will be inserted at multiplication making LHS as (2 × 4)−3 + 2

Therefore, the parentheses will be inserted at multiplication making LHS as (2 × 4)−3 + 2 making the equation True.

Page 34  Exercise 1.12 Problem  18

To insert the parentheses in the given equation 2 × 4− 3 + 2 = 4

Use the strategy of BODMAS to insert the brackets.

Check LHS = RHS

Solve LHS using parentheses to make it true for the equation.

Adding the parentheses at the addition rule to make the equation true

​LHS = 2 × 4 − 3 + 2

= 2 × (4−3) + 2
​
Further Simplifying and comparing the equation
​
​RHS = 4

LHS = 2 × (4 − 3) + 2

= 2 × 1 + 2

= 2 + 2

= 4
​
So, the parentheses will be inserted at subtraction making LHS as  2 × (4 − 3) + 2

Therefore, the parentheses will be inserted at subtraction making LHS as  2 × (4 − 3) + 2 making the equation True.

Page 34  Exercise 1.12 Problem  19

To insert the parentheses in the given equation 2 × 4 − 3 + 2 = 3

Use the strategy of BODMAS to insert the brackets.

Check LHS = RHS

Solve LHS using parentheses to make it true for the equation.

Adding the parentheses at the addition rule to make the equation true

​LHS = 2 × 4 − 3 + 2

= 2 × 4 − (3 + 2)
​
Further Simplifying and comparing the equation
​
​RHS = 3

LHS = 2 × 4−(3 + 2)

= 8 − 5

= 3
​
So, the parentheses will be inserted at addition making LHS as 2 × 4 − (3 + 2)

Therefore, the parentheses will be inserted at addition making LHS as 2 × 4 − (3 + 2) making the equation True.