Big Ideas Math Integrated Math Chapter 1 Maintaining Mathematical Proficiency
Page 1 Exercise 1 problem 1
Question:
Simplify the following expression step-by-step:
Solution
Given
In this question {−1 + (−3)} first, we have to multiply the sign appears before the number.
If any question don’t have any sign before the number then by default it is a positive sign (+).
After that we do the addition or subtraction.
Multiply the sign presented before the no.
−1 + (−3)
We know that
(+) × (−)=(−)
So here after the multiplication
− 1 − 3
Here we do that addition or subtraction operation.
− 1 − 3 = −4
The desired solution is −1 + (−3) = −4.
Page 1 Exercise 2 Problem 2
Question: Simplify the following expression step-by-step:
Answer:
Given expression is −4−7
If any question doesn’t have any sign before the number then by default it is positive sign.
After that, we do addition or subtraction.
We have to do subtraction operation
− 4 − 7 = −11
The desired solution is −4 − 7 = 11
Page 1 Exercise 3 Problem 3
Question: Find two pairs of integer numbers whose sum is
.
We have to let two integer numbers whose sum is −6
Let two numbers pairs (4,−10) and (−3,−3).
Addition of first pair = 4 + (−10)
We know that
(+) × (−) = (−)
After that
4 − 10 = − 6
Addition of second pair = −3 + (−3)
We know that
(+) × (−) = (−)
After that
−3 − 3 = −6
The required two pair are (4,−10) and (−3,−3) whose sum is −6
Question:
The record monthly high temperature for March is 56°F, and the record monthly low temperature for March is -4°F.
Using the formula for the range of a parameter, calculate the range of temperatures for the month of March.
Page 1 Exercise 4 Problem 4
Given
The record monthly high temperature for March is 56°F.
The record monthly low temperature for March is −4°F.
Now use the formula for range of a parameter.
Range of a parameter
= Highest value of the parameter − The lowest value of parameter
= 56°F − (−4°)F
= 56°F + 4°F
= 60°F
The range of temperatures for the month of March is 60°F.
Page 1 Exercise 5 Problem 5
Determine the algebraic sign of the product of the given numbers and find the final value.
Given:
Determine the algebraic sign of the given numbers.
Here 8 has a negative algebraic sign and 5 also has a negative algebraic sign.
Determine the algebraic sign of the final answer.
In this case it is a positive sign.
Simply multiply the given numbers and write the final answer with appropriate sign.
We have
⇒ − 8 × (−5)
= −8 × (−5)
= 40
The value of −8 × (−5) is 40.
Page 1 Exercise 6 Problem 6
Question:
Write
as
and determine the algebraic sign of the given numbers.
Write \(\frac{14}{2}\) as \(\frac{1}{2}\) × 14
Determine the algebraic sign of the given numbers.
Here \(\frac{1}{2}\) has a positive algebraic sign and 14 also has a positive algebraic sign.
Determine the algebraic sign of the final answer.
In this case it is a positive sign.
Simply multiply the given numbers and write the final answer with appropriate sign.
We have
⇒ \(\frac{14}{2}\)
= \(\frac{1}{2}\) × 14
= \(\frac{1}{2}\) × (2 × 7)
Cancel out of 2
= 7
The value of \(\frac{14}{2}\) is 7
Page 1 Exercise 7 Problem 7
Question: Simplify the following expression and determine the algebraic sign of the final answer:
Write −30/(−3) = \(\frac{−30}{−3}\)
Now \(\frac{−30}{−3}\)
= \(\frac{1}{−3}\) × (−30)
Determine the algebraic sign of the given numbers.
Here 1 has a negative algebraic sign and 30 also has a negative algebraic sign.
Determine the algebraic sign of the final answer.
In this case it is a positive sign.
Simply multiply the given numbers and write the final answer with appropriate sign.
We have
−30/(−3)
= \(\frac{−30}{−3}\)
= \(\frac{1}{−3}\) × (−30)
= \(\frac{1}{3}\) × 3 × 10
= 10
The value of −30/(−3) is 10.
Page 1 Exercise 8 Problem 8
Question:
Find two pairs of integers whose product is -20 by factorizing the number
Answer:
Given number
To find the integers whose product is -20 can be found by factorizing number −20
Factors of number -20 are given as
−20 = −(2 × 2 × 5)
Therefore two pairs of integers are
−(4 × 5) = −20
−(2 × 10) = −20
Two pair of integers are : −(4×5) and −(2×5)
Page 1 Exercise 9 Problem 9
Question:
A football team loses 3 yards in 3 consecutive games.
Calculate the total yardage gained by negating the magnitude of the total yardage loss.
Answer:
Given that a football team loses 3 yards in 3 consecutive game.
We have to find total yardage gained by negating the magnitude of total yardage loss.
Here a football team losses 3 yards in 3 consecutive game.
Total yardage loss therefore total yardage gained = − (Total yardage loss)
= −(9)
The total yardage gained is − 9.
Page 2 Exercise 10 Problem 10
Question:
Explain how simple linear equations can be used to solve real-life problems. Provide specific examples.
Uses of simple equations to solve real-life problems
There are various real-life situations where unknown quantity can be expressed as linear equation.
Some are given as below-
To compare ages of two persons and find their ages.
To find the runs scored by a batsman.
Number of trees planted by an organization.
Cost of travelling in a taxi from place A to place B.
Cost of buying mangoes from a market.
To find profit/loss of a shop.
The final answer is that some of the real-life problem that can be solved using simple equations are:
To compare ages of two persons and find their ages
To find the runs scored by a batsman.
Number of trees planted by an organization.
Cost of travelling in a taxi from place A to place B.
Cost of buying mangoes from a market.
To find profit/loss of a shop.
Page 2 Exercise 11 Problem 11
Question:
Measure all the four angles of a given quadrilateral using a protractor and check the precision of your measurements.
For a given quadrilateral have 4 sides and 4 angles denoted as ∠A, ∠B, ∠C, ∠D
We have to measure all the four angles using protractor and check how precise our measurement.
By using a protractor measuring the angle of the quadrilateral given below:
m∠A = 100 degrees
m ∠ B = 91 degrees
m∠C = 92 degrees
m∠D = 67 degrees
m∠A + m∠B + m∠C + m∠D = 100 + 91 + 92 + 67
= 360 degrees
Measurement of angles of given quadrilateral:
m∠A = 100 degree
m∠B = 91 degree
m∠C = 92 degree
m∠D = 67 degree
m∠A + m∠B + m∠C + m∠D = 360degrees
Page 2 Exercise 11 Problem 12
Question:
Measure all four angles of a given quadrilateral using a protractor and verify the precision of your measurements.
Answer:
For a given quadrilateral have 4 sides and 4 angles denoted as ∠A, ∠B, ∠C, ∠D
We have to measure all the four angle using protractor and check how precise our measurement.
By using protractor measure the angle of the quadrilateral given below:
m∠A = 67 degree
m∠B = 147 degree
m∠C = 56 degree
m∠D = 90 degree
m∠A + m∠B + m∠C + m∠D = 67 + 147 + 56 + 90 = 360 degree
Measurement of angles of given quadrilateral:
m∠A = 67 degree
m∠B = 147 degree
m∠C = 56 degree
m∠D = 90 degree
m∠A + m∠B + m∠C + m∠D = 67 + 147 + 56 + 90 = 360 degree
Page 2 Exercise 11 Problem 13
Question:
Measure all four angles of a given quadrilateral using a protractor and verify the precision of your measurements.
For a given quadrilateral have 4 sides and 4 angles denoted as ∠A, ∠B, ∠C, ∠D
We have to measure all the four angles using protractor and check how precise our measurement.
By using a protractor measuring the angle of quadrilateral given below:
m∠A = 94 degrees
m∠B = 79 degrees
m∠C = 72 degrees
m∠ D = 115 degrees
m∠A + m∠B + m∠C + m∠D = 94 + 79 + 72 + 115 = 360 degrees
Measurement of angles of given quadrilateral:
m∠A = 94 degrees
m∠B = 79 degrees
m∠C = 72 degrees
m∠ D = 115 degrees
m∠A + m∠B + m∠C + m∠D = 94 + 79 + 72 + 115 = 360 degrees
Page 2 Exercise 12 Problem 14
For a given quadrilateral have 4 sides and 4 angles denoted as ∠A,∠B,∠C,∠D
We have to measure all four angles using a protractor and check how precise our measurement.
By using a protractor measure of the angles of the quadrilaterals are given below:
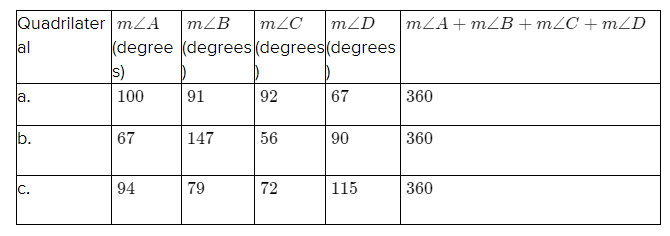
Making the three different quadrilaterals.
1)
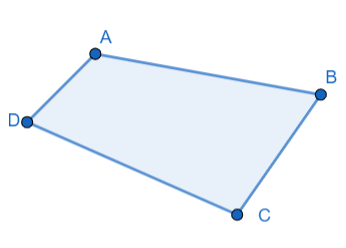
2)
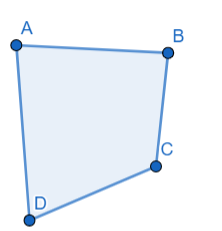
3)
Measuring the angles of the three different quadrilaterals using protractor and verifying the values
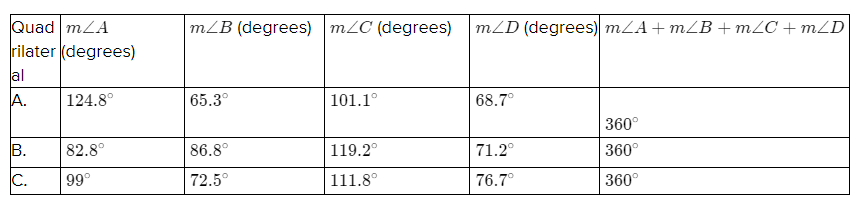
Hence, The measurements are accurate so, by using a protractor we can measure the angles of the quadrilateral.
And the sum of all four of any quadrilateral is 360°
Page 3 Exercise 13 Problem 15
A quadrilateral is given with its measurement of angle as:
m∠A = 85degrees
m∠B = 80 degrees
m∠C = 100 degrees
m∠D = x degrees
We can find the m∠D using conjecture of Page 2 Exercise 11 Problem 11
Sum of the angle measures of a quadrilateral are equals to 360 degrees.
Hence writing the simple equation :
85 + 80 + 100 + x = 360
⇒ x = 95
Hence m∠D = 95 degrees
Measure angle D of given quadrilateral is 95 degrees.
Page 3 Exercise 13 Problem 16
A quadrilateral is given with its measurement of angle as:
m∠A = 72degrees
m∠B = 60 degrees
m∠C = 78degrees
m∠D = x degrees
We can find the m∠D
Using conjecture of Page 2 Exercise 11 Problem 11
Sum of the angle measures of a quadrilateral are equals to 360 degrees.
Hence writing the simple equation :
72 + 60 + 78 + x = 360
⇒ x = 150
m∠D = 150 degrees
Measure angle D of given quadrilateral is 150 degrees.
Page 3 Exercise 13 Problem 17
A quadrilateral is given with its measurement of angle as:
m∠A = 90degrees
m∠B = 30 degrees
m∠C = 90degrees
m∠D = x degrees
We can find the m∠D = using conjecture of Page 2 Exercise 11 Problem 11
Sum of the angle measures of a quadrilateral are equals to 360 degrees.
Hence writing the simple equation :
90 + 30 + 90 + x = 360
⇒ x = 150
m∠D = 150 degrees
Measure angle D of given quadrilateral is 150 degrees.
Page 6 Exercise 14 Problem 18
We have a simple equation as −15 + w = 6
We can find solution of equation by using core concept of the addition property of equality.
We have
−15 + w = 6…….(1)
Applying addition property of equality.
−15 + w + 15 = 6 + 15
⇒ w = 21
Hence solution of equation is w = 21
To verify the solution, put w = 21 in equation (1)
We get, −15 + 21 = 6
6 = 6
Therefore the solution w = 21 satisfying the equality of given equation.
The solution of given equation −15 + w = 6 is w = 21
Page 6 Exercise 15 Problem 19
We have a simple equation as: z−5 = 8
We can find solution of equation by using core concept
We have
z−5 = 8……………(1)
Applying addition property of equality.
⇒ z −5 + 5 = 8 + 5
⇒ z = 13
Hence solution of equation is z = 13
To verify the solution, put z = 13 in equation (1)
We get, 13 − 5 = 8
⇒ 8 = 8
Therefore the solution z=13
Satisfying the equality of given equation.
The solution of given equation z−5 = 8 is z = 13
Page 6 Exercise 16 Problem 20
We have simple equation as: −2 = y − 9
We can find solution of equation by using core concept of addition property of equality.
We have
−2 = y − 9……………. (1)
Applying addition property of equality.
⇒ −2 + 9 = y − 9 + 9
⇒ 7 = y
Hence solution of equation is y = 7
To verify the solution put y = 7 in equation (1)
we get, −2 = 7−9
−2 = −2
Therefore the solution y = 7 satisfying the equality of given equation.
The solution of given equation −2 = y−9 is y = 7
Page 6 Exercise 17 Problem 21
We will first form the linear equation with variable p.
We will solve the linear equation to get the value of p.p will be the desired result.
Price of headphone = $ p
Price of headphone after applying coupon= $ (p − 17.95)
Price paid after applying coupon for headphone = $ 71.80
Price of headphone after applying coupon = Price paid for headphone
(p- 17.95) = 71.80
p = 71.80 + 17.95
p = $ 89.75
Original price of headphone = $ 89.75
Original price of headphone = $ 89.75
Page 6 Exercise 18 Problem 22
We will let the number of browines made for the party be x.
We will first form the linear equation with variable x.
We will solve the linear equation to get the value of x.
x will be the desired result.
Let, x brownies made for the party.
Number of brownies left = 16
Brownies left = 2/5 of total brownies
Then
\(\frac{2}{5}\) of x = 16
\(\frac{2}{5}\) of x = 16
x = 16
2x = 16 × 5
2x = 80
x = \(\frac{80}{2}\)
x= 40
I made 40 brownies for the party.
40 brownies were made for the party.
Page 7 Exercise 19 Problem 23
We will form the equation 30°+9x°+(30+x)°=180° and solve it to get the value of x.
Sum of angles of triangle = 180°
30° + 9x° + (30+x)° = 180°
60° + 10x° = 180°
10x° = 180°− 60°
10x° = 120°
x° = \(\frac{120°}{10}\)
x = 12°
First angle = 30°
Second angle = 9x°
= 108°
Third angle = (30+x)°
= 42°
We can check the answer by substituting value of x
30° + (9 × 12)° + (30 + 12)° = 180°
Angles of triangles are 30°,108°,42°
Page 7 Exercise 19 Problem 24
We will substitute the sum of angles = 180°
50°+ (x + 20)°+ (x + 10)°= 180°
By solving this, we will get the value of x.
Sum of angles of triangle = 180°
50° + (x + 20)° + (x + 10)° = 180°
80° + 2x = 180°
2x = 180° − 80°
2x = 100°
x = 50°
First angle = 50°
Second angle = 70°
Third angle = 60°
We can check the value of x by substituting
50° + (50 + 20)° + (50 + 10)° = 180°
Angles of triangle are 50°,70°,60°
Page 7 Exercise 19 Problem 25
We will take the sum the value of all angles of diagram.
Sum of all angles will be equal to 360°
We get 50° + (2x + 30)° + (2x + 20)° + x° = 360°
On solving we will get the value of x and angles.
Sum of all angles = 360°
50° + (2x + 30)°+(2x + 20)° + x° = 360°
100° + 5x° = 360°
5x° = 360° − 100°
5x° = 260°
x° = \(\frac{260°}{5}\)
x° = 52°
First angle = 50°
Second angle = 134°
Third angle = 124°
Fourth angle = 52°
We can check by substituting the value of x
50° + (2 × 52 + 30)° + (2 × 52 + 20)° + 52° = 360°
x° = 52°
Angles are 50°,52°,124°,134°
Page 7 Exercise 19 Problem 26
We will substitute the sum of all values of angles that is 360°
We will get the linear equation as (x+35)° + (x + 42)° + (x − 17)° + x° = 360°.
We will solve the linear equation to get the value of x and angles.
On solving we will get the value of x and angles.
Sum of all angles = 360°
(x + 35)° + (x + 42)° + (x−17)° + x° = 360°
60° + 4x° = 360°
4x° = 360° − 60°
4x°= 300°
x° = \(\frac{300°}{4}\)
x° = 75°
First angle = 75°
Second angle = 110°
Third angle = 117°
Fourth angle = 58°
We can check by substituting the value of x
(75 + 35)° + (75 + 42)° + (75 − 17)° + 75° = 360°
Angles are 75°,110°,117°,58°
Page 8 Exercise 20 Problem 27
We will draw an irregular polygon of 3 sides of different lengths and angles.
We draw a triangle
Page 8 Exercise 20 Problem 28
We will measure the angles of an irregular polygon drawn in a part.
Angles are 50°,70°,60°
Page 8 Exercise 20 Problem 29
We will find the different value of angles by letting variable x.
Let, the value of x be 50∘
Then , other two angles will be (x + 20)° ,(x + 60)°
Angles in variable are x°,(x + 20)°,(x + 10)°
Page 8 Exercise 20 Problem 30
We take any polygon drawn by our friend and measure the sides.
Polygon by my friend is
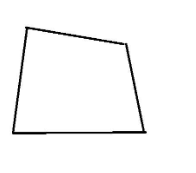
Angles are 75°,88°,110°,87°
Page 8 Exercise 20 Problem 31
We will measure the angle by a protractor and then by making equation and find out equation are helpful in finding angles.
Let, Angles are (x + 35)°,(x + 48),°(x + 70)°,(x + 47)°
(x+35)° + (x + 48)°+ (x + 70)°+ (x + 47)° = 360°
x = 40°
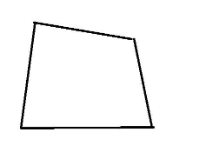
Angles are 75°,88°,110°,87°
Yes, Answer seems reasonable.
Both method that is protractor and equations gave the same answer.
Angles are 75°,88°,110°,87°
Page 8 Exercise 21 Problem 32
We have to tell a real life problem which can be solved by the use of the multistep solution.
So say you work part-time with your three friends to mow a lawn, you get total 40 dollars.
All of you incurred 10 dollars in total to get to the work site.
Now how much money each of you will get can simply be calculated by using the multi-step equation.
Let the money each of you get be x
Now the above situation can be written in the equation form as below
3x + 10 = 40
Here 10 is the cost you incurred to reach the work site.
Subtract 10 from both sides, and we get
⇒ 3x + 10 − 10 = 40 − 10
⇒ 3x = 30
In the next step we divide both sides by 3 we get
⇒ \(\frac{3x}{3}\)
= \(\frac{30}{3}\)
⇒ x = 10
Hence each of you gets $10
This is just one of the many ways we can use the multistep equations in our real life to solve day-to-day problem
The use of multistep equation in real life are multi-faceted one such example of their utility has been given above.
Page 8 Exercise 22 Problem 33
We have to prove that the formula for the sum of interior angles is
S = 180 (n−2)
The steps of the proof of the formula will be to first prove that the sum of all angles of the triangles the polygon is made of is equal to 180×n.
Then we will prove that sum of the angles other than the interior angle is 360∘
Then upon subtracting the 360 from the total angle 180×n we will get the sum of the interior angles as
S = 180(n−2)
ABCDE is an n sides polygon, Taking any point inside the polygon and joining we get n triangles.
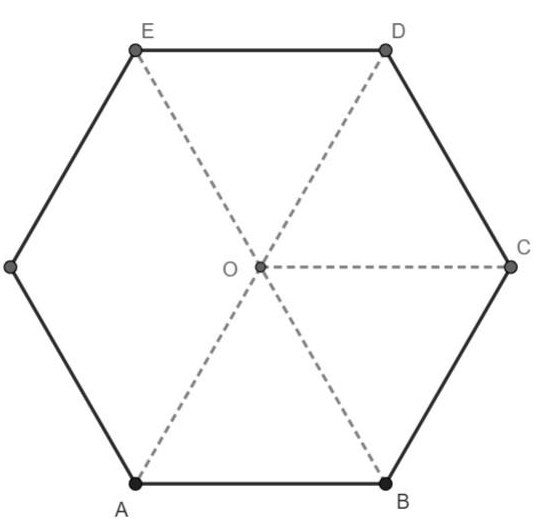
The sum of these triangles will be 180 × n
Thus we can write that sum of angles at O + sum of interior angles = 180 × n (1)
The sum of angles at O will be 360∘because total angle of a circle is always 360∘and the angles at O make a circle.
The equation 1can then be written as
⇒ 360+ sum of interior angles = 180 × (n)
⇒ Sum of interior angles = 180n − 360
⇒ Sum of interior angles = 180(n−2)
Hence the theorem is proved.
The formula for the calculation of interior angle of the polygon: S = 180 (n − 2) is correct and we have proved it above.
Page 10 Exercise 23 Problem 34
We have to solve the equation.
3x + 4 = 19 and find the value of x
We will solve it as below
First, subtract 4 on both sides, we get
⇒ 3x + 4 − 4 = 19 − 4
We get as
⇒ 3x = 15
Then we divide both sides by 3, we get
⇒ \(\frac{3x}{3}\) = \(\frac{15}{3}\)
⇒ x = 5
Thus the value of the variable x is
x = 5
The solution of the equation: 3x + 4 = 19 is x = 5
Page 10 Exercise 24 Problem 35
We have to solve the equation :
17 = z − (−9) and find the value of the variable z.
First, we will solve the brackets given on the left-hand side of the equation.
Then we will subtract 9 from both sides of the equation so that the right side is free of constants.
We have to solve the equation :
17 = z − (−9) and find the value of the variable z
First, we will solve the brackets given on the left-hand side of the equation.
Then we will subtract 9 from both sides of the equation so that the right side is free of constants.
The solution of the equation: 17 = z−(−9) is z = 8
Page 10 Exercise 25 Problem 36
We have to solve the equation:
15 = 2 + 4 − d
We have to find the value of the variable d
First, we will solve the right-hand side addition in the given equation.
We will then subtract 6 on both sides of the equation then multiply −1 to get the variable in the positive value.
15 = 2 + 4 − d
15 = 6 − d
Solving further we get
15 − 6 = 6 − d − 6
9 = −d
9 × −1 = − d × − 1
d = −9
Thus the value of the variable d is
The solution of the equation: 15 = 2 + 4 − d is d = −9
Page 10 Exercise 26 Problem 37
We have to solve the equation:
\(\frac{q+(−5)}{3}\) = 8 and find the value of the variable q
First multiply both the sides of the equation with the number 3 to remove the denominator present on the left side of the equation.
Now after opening the bracket we will add 5 to both the sides of the equation.
\(\frac{q+(−5)}{3}\) = 8
\(\frac{q+(−5)}{3}\) × 3 = 8 × 3
q+ (−5) = 24
q−5 + 5 = 24 + 5
q = 29
Thus the value of the variable q is ⇒ q = 29
The solution of the equation\(\frac{q+(−5)}{3}\) = 8 is q = 29
Page 10 Exercise 27 Problem 38
We have to solve the equation :
5z−2z−4=−7 and find the value of the variable,z.
First, we will add the terms of the variable z
5z − 2z − 4 = −7
3z − 4 = − 7
Add 4 on both the sides of the equation.
3x − 4 + 4 = − 7 + 4
Divide both the sides of the equation by 3
3x = −3
\(\frac{3x}{3}\) = \(\frac{−3}{3}\)
x = −1
Thus the value of the variable x is
x = −1
The solution of the equation: 5z − 2z − 4 = −7 is z = −1
Page 11 Exercise 28 Problem 39
We have to solve the equation:
3(z + 7) = 21 and find the value of the variable z
First, solve the bracket on the left-hand side of the equation:
Subtract 21 from both sides of the equation:
Since the right-hand side will be 0, after dividing both sides of the equation with 3
3(z + 7) = 21
⇒ 3(z + 7) = 21
⇒ 3z + 21 = 21
Solving further we get
3z + 21 − 21 = 21 − 21
3z = 0
\(\frac{3z}{3}\)= \(\frac{0}{3}\)
z = 0
Thus the value of the variable z is ⇒ z = 0
The solution of the equation : 3(z+7) = 21 is z = 0
Page 11 Exercise 29 Problem 40
To find the value of z for given equation
⇒ −4(z − 12) = 42
First applying the distributive property to the given equations, then simplifying using the mathematical operations, and then the value of z can be obtained.
Applying distributive property on left-hand side of the given equation.
−4(z−12) = 42
−4 × z−{(−4) × 12} = 42
As (−) × (−) = (+)
(−) × (+) = (−)
Therefore equation obtained is
− 4z − (−48) = 42
− 4z + 48 = 42
Subtracting 48 on both sides of the equation, we get
− 4z = 42 − 48
− 4z = −6
Multiplying −1 on both sides of the equation, we get
⇒ 4z=6
Dividing both sides of the equation by 4 and simplifying
\(\frac{4z}{4}\) = \(\frac{6}{4}\)
z = \(\frac{3}{2}\) or z = 1.5
The value of z is 1.5 for equation − 4(z−12) = 42
Page 11 Exercise 30 Problem 41
For the given equation is 33 = 12r−3(9−r), we have to calculate the value of r.
Value of r can be obtained by using distributive property in the given equation and mathematical properties like
(−) × (−) = (+)
(−) × (+) = (−)
Given equation is
33 = 12r − 3 (9 − r)
Using distributive property on right-hand side of the equation and simplifying using mathematical operations
33 = 12r + {(−3) × 9 + (−3) × (−r)}
33 = 12r + (−27 + 3r)
On simplification, we get
33 = 12r − 27 + 3r
Adding the terms containing unknown r, we get
33 = 15r − 27
Adding 27 on both side of the above-obtained equation and simplifying
33 + 27 = 15r − 27 + 27
60 = 15r
Dividing both sides of the above equation by 15, then simplifying
\(\frac{60}{15}\)=\(\frac{15r}{15}\)
4 = r or r = 4
The desired value of ris 4for the given equation, 33 = 12r − 3(9 − r).
Page 11 Exercise 31 Problem 42
Value of g is to be calculated for given equation 7 + 3 (2g − 6) = −29
The first distributive property is applied in the equation and then the mathematical operations are used to obtain the desired value of unknown g.
The given equation is
7 + 3(2g−6) = −29
Using distributive property on the left-hand side of the equation and simplifying
7 + {3 × 2g − 6 × 3} = −29
7 + 6g − 18 = −29
6g − 11 = −29
Adding 11 on both sides of the equation and then simplifying
6g − 11 + 11 = − 29 + 11
6g = −18
Dividing both sides of the equation by 6 and we get
\(\frac{6g}{6}\)= −\(\frac{−18}{6}\)
g = −3
Hence, the value of g is −3 for the equation 7 + 3(2g−6) =−29
Page 11 Exercise 32 Problem 43
Odd integer is given with an expression 2n+1where n is any integer, then three consecutive integers are
2n + 1,2n + 1 + 2, 2n + 1 + 4
Therefore 2n + 1,2n + 3,2n + 5
It is given that sum of these consecutive odd integers is 63.
On solving the value for n, consecutive odd integers are calculated.
Consecutive odd integers for an odd integer having the expression 2n + 1 are
2n + 1,2n + 3,2n + 5
As sum of consecutive odd integers is 63, therefore
(2n + 1) + (2n + 3) + (2n + 5) = 63
Simplifying above equation 6n + 9 = 63
Subtracting 9 from both sides of the equation
6n + 9 − 9 = 63 − 9
On simplifying we get 6n = 54
Dividing both sides of the equation by 6 and we get
\(\frac{6n}{6}\)= \(\){54}{6}[\latex]
n = 9
Hence, the odd integers are
First odd integer = 2n + 1
= 2 × 9 + 1
= 19
2n + 1 = 19
Second odd integer = 2n+3
= 2 × 9 + 3
= 21
2n+3 = 21
Third odd integer = 2n + 5
= 2 × 9 + 5
= 23
2n + 5 = 23
Hence, three consecutive odd integers having sum 63are 19,21and 23 having odd integer with expression 2n + 1.
Page 11 Exercise 33 Problem 44
Given: Cousin is 8 years older than your brother.
Three years ago, cousin was twice as old as brother.
To find- Present age of brother and cousin.
First of all we will define the present ages of cousin and brother.
Then we will define their ages three years ago.
Using given condition to find the value of x and then ages of cousin and brother.
Let the present age of brother be x years.
⇒ Present age of cousin will be (x+8)years.
Three years ago
Age of brother = (x−3) years and
Age of cousin = (x + 8 − 3)years
= (x + 5)years.
According to given condition, we get
x + 5 = 2(x − 3)
⇒ x + 5 = 2x − 6
⇒ 5 + 6 = 2x − x
⇒ 11 = x
⇒ Present age of brother = 11years and
Present age of cousin = 11 + 8
= 19 years.
The final answer is that the present age of brother and his cousin are 11 and 19 years respectively.