Big Ideas Math Integrated Math Chapter 8 Maintaining Mathematical Proficiency
Big Ideas Math Integrated Math 1 Student Journal Chapter 8 Solutions Page 215 Exercise 1 Problem 1
Question 1.
Evaluate the expression |−3 + (−1)|.
Answer:
Given Expression
|−3 + (−1)|.
We have to find the value of
∣−3 + (−1)∣
we will first solve the number inside the modulus then get its positive value.
Then use the conditions of modulus function to evaluate it further.
⇒ ∣−3+(−1)∣
⇒ ∣−3−1∣
⇒ ∣−4∣
Since for the modulus function when x<0
f(x) = −x
We can write
∣−4∣ = −(−4)
∣−4∣ = 4
Read and Learn More Big Ideas Math Integrated Math 1 Student Journal Solutions
The value of the expression: ∣−3+(−1)∣ is 4
Page 215 Exercise 2 Problem 2
Question 2.
Evaluate the expression |10 – 11|.
Answer:
Given Expression
|10 – 11|.
We have to find the value of the expression
∣10 − 11∣
We will first solve the expression inside the bracket
⇒ ∣10 − 11∣ = ∣−1∣
Now since x<0 the value of
f(x) = −x
⇒ ∣−1∣ = −(−1)
⇒ 1
Hence the value of the given expression is 1
The solution of the expression: ∣10 − 11∣ is 1
Page 215 Exercise 3 Problem 3
Question 3.
Evaluate the expression |9 – (-1)|.
Answer:

The value of the expression : ∣9−(−1)∣ upon solving is 10
Page 215 Exercise 4 Problem 4
Question 4.
Evaluate the expression |-15 – 7|.
Answer:
Given Expression
|-15 – 7|.
We have to find the value of the expression
∣−15−7∣
We will first solve the expression inside the modulus sign and then evaluate it further using the definition of modulus function
⇒ ∣−15−7∣ = ∣−22∣
We know from the definition of modulus functions that when x<0 like in this case the f(x) is given by
f(x) = −(−x)
Since −22<0
⇒ ∣−22∣ = −(−22)
⇒ ∣−22∣ = 22
Thus the required value is 22
The value of the expression: ∣−15−7∣ upon solving is given by 22
Page 215 Exercise 5 Problem 5
Question 5.
Evaluate the expression |-12 + 3|.
Answer:
Given Expression
|-12 + 3|.
We have to find the value of the expression
∣−12 + 3∣
We will first solve the expression inside the modulus sign and then evaluate it further using the definition of modulus function
⇒∣ −12 + 3∣ = ∣−9∣
Since we know from the definition of modulus function that when x<0 the value of the f(x) is given by
f(x) = −x
As we know that −9<0 , the expression will be written as
⇒ ∣−9∣ = −(−9)
⇒ ∣−9∣ = 9
Hence the value of the expression is 9
The value of the expression: ∣−12 + 3∣ upon solving is given by 9
Page 215 Exercise 6 Problem 6
Question 6.
Evaluate the expression |5 + (-15)|.
Answer:
Given Expression
|5 + (-15)|.
We have to find the value of the expression
∣5+(−15)∣
We will first solve the expression inside the modulus sign and then evaluate it further using the definition of modulus function
⇒ ∣5+(−15)∣ = ∣5 − 15∣
⇒ ∣5+(−15)∣ = ∣−10∣
Since we know from the definition of modulus function, when x<0 , the function f(x) is given by, f(x) = −(−x) since −10<0 , we will write
⇒ ∣−10∣ = −(−10)
⇒ ∣−10∣ = 10
Hence 10 is the value of the expression.
The value of the expression: ∣5+(−15)∣ upon solving is given by 10
Chapter 8 Maintaining Mathematical Proficiency Solutions Big Ideas Math Integrated Math 1 Page 215 Exercise 7 Problem 7
Question 7.
Evaluate the expression |1 – 12|.
Answer:
Given Expression
|1 – 12|.
We have to find the value of the expression
∣1−12∣
We will first solve the expression inside the modulus sign and then evaluate it further using the definition of modulus function
⇒ ∣1 − 12∣ = ∣−11∣
Since we know from the definition of modulus function that when x<0 the value of the f(x) is given by
f(x) = −x
As −11<0 , we can write the expression ∣−11∣ as
⇒ ∣−11∣ = −(−11)
⇒ ∣−11∣ = 11
Hence 11 is the value of the expression.
The value of the expression: ∣1 − 12∣ upon solving is given by 11
Page 216 Exercise 8 Problem 8
Question 8.
How can Dynamic Geometry Software (DGS) be used to visualize geometric concepts effectively?
Answer:
We need to explain that how can we use DGS to visualize geometric concepts.
We will do this by discussing how to create and manipulate the geometrical models in DGS.
We will also discuss the different uses of DGS to visualize geometrical concepts and also how DGS makes geometrical concepts more interesting and understandable.
We should use dynamic geometric software to show the real-time effects of changes on the geometric models and, it provides the visual of.
What’s happening and what should be the result of any change, which is really helpful to visualize geometric concepts.
Page 216 Exercise 9 Problem 9
Question 9.
Given the lines formed by the walls, floor, and ceiling in a classroom, identify which lines intersect, which are parallel, and which are perpendicular. Provide examples of each type of line relationship using the classroom setting.
Answer:
Given two lines can intersect or not intersect.
We want to see examples using the lines formed by the walls, floor, and ceiling in classroom.
Identfy the lines in your classroom and check they intersect or not.
Intersecting lines are two or more lines that are coplanar to each other and meet at a common point.
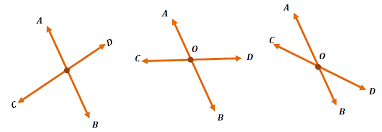
An example of this would be the lines in the floor of classroom the lines of floors intersect each other as well and share points of intersection.

Two lines that intersect and form right angles are called perpendicular lines.
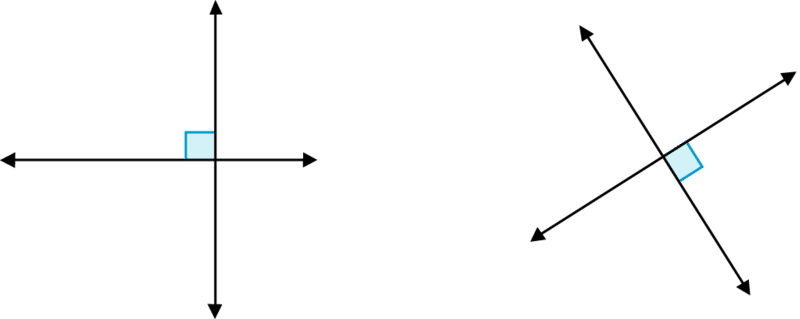
An example of this would be the lines in brick walls of classrooms.

Parallel lines are the lines that do not intersect or meet each other at any point in a plane. They are always parallel and are at equidistant from each other.
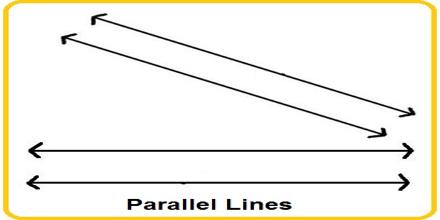
An example of this would be the lines in wooden ceiling of classrooms.

The lines of floors intersect each other as well and share points of intersection.

The lines in brick walls of classrooms intersect each other perpendicularly.

The lines in wooden ceiling of classrooms are parallel to each other

Page 216 Exercise 9 Problem 10
Question 10.
Given a line and a plane, determine whether they intersect or not. Use examples from the lines formed by the walls, floor, and ceiling in a classroom to illustrate each scenario.
Answer:
Given one line and one plane can intersect or not intersect.
We want to see examples using the lines formed by the walls, floor, and ceiling in classroom.
Identfy the lines in your classroom and check they intersect or not.
A line can lie entirely in a plane. An example of this would be the intersection of two walls in your classrom.
The two walls both represent planes and the intersection is the line that lies in both walls.
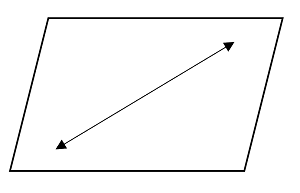
A line can pass through a plane at only one point as shown below.
An example of this would be the intersection of two walls and the floor since the intersection of the two walls represent a line, the floor represents a plane and the intersection of the walls only intersect the floor at one point.
A line could also nver intersect a plane.
An example of this would be the intersection of two walls and the wall on the opposite side of the room since the intersection of the two walls is a line that will never intersect a wall on the opposite side of the room.
The two walls both represent planes and the intersection is the line that lies in both walls.
The intersection of the two walls represent a line, the floor represents a plane and the intersection of the walls only intersect the floor at one point
The intersection of the two walls is a line that will never intersect a wall on the opposite side of the room.
Page 216 Exercise 9 Problem 11
Question 11.
Given two planes can intersect or not intersect.
We want to see examples using the planes formed by the walls, floor, and ceiling in a classroom.
Identify the planes in your classroom and check if they intersect or not.
Answer:
Given one line and one plane can intersect or not intersect.
We want to see examples using the lines formed by the walls, floor, and ceiling in classroom.
Identfy the lines in your classroom and check they intersect or not.
Two planes can intersect each other.
An example of this would be the intersection of two walls would be like the walls going through each other in the center to make a kind of cross like shape.

If two planes intersect each other, the intersection will always be a line.An example of this would be the intersection of two walls of a classroom.

Two non-intersecting planes are parallel to each other an example of this would be the stairs of a classroom.

The intersection of two walls would be like the walls going through each other.

The two walls of a classroom intersect at a line.

The stairs of a classroom are examples of planes that never intersecting

Big Ideas Math Integrated Math 1 Chapter 8 Step-By-Step Solutions Page 217 Exercise 10 Problem 12
Question 12.
Using dynamic geometry software, explore the properties of different types of triangles. Describe how the software helps you understand the following concepts:
- Definition of a triangle.
- The sum of internal angles in a triangle.
- Different types of triangles (equilateral, isosceles, scalene).
- Verification of the Pythagorean theorem using a right triangle.
Explain how the interactive nature of the software enhances your understanding of these geometric concepts.
Answer:
We want to explore geometry using dynamic geometry software.
Search for a familiar concept as for example triangle.
Now search for the keyword “Triangle”.
The screen will show the definition of triangle along with a “Triangle” as follows.
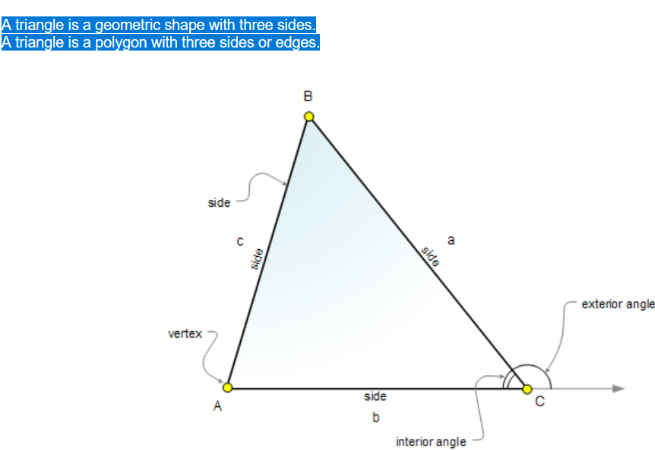
The software explained the term “Triangle” as follows
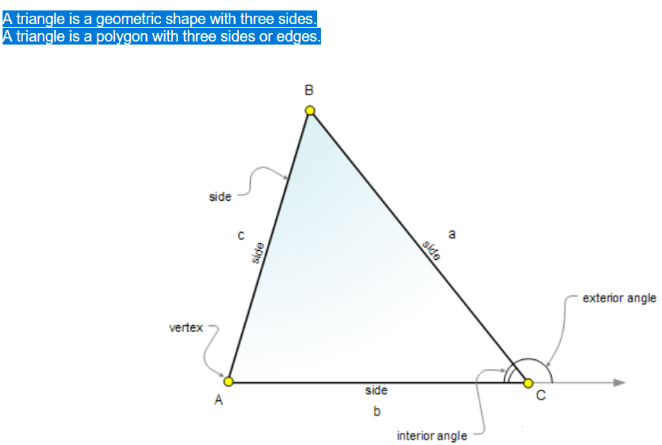
Page 220 Exercise 11 Problem 13
Question 13.
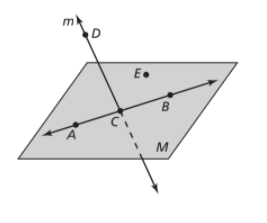
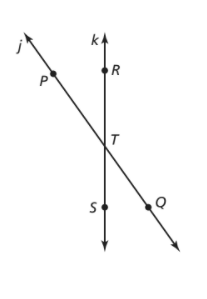
In the given diagram, identify two other sets of non-collinear points that can be used to name plane M. Explain why these sets of points are considered non-collinear and provide the alternative names for plane M.
Answer:
We are given a diagram:
Here, A, B, C, D, and E are different points and M is a
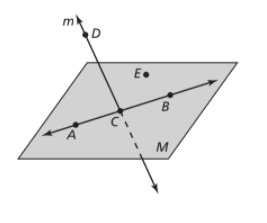
We need to give another name for plane M.
Here, A, C, and E are non-collinear points, so another name for plane M is plane ACE.
A, B, and E are also non-collinear points, so there is one more name possible for plane M that is plane ABE.
In the given diagram: The other name for plane M is plane ACE.
Page 220 Exercise 12 Problem 14
Question 14.
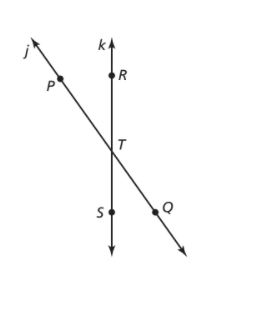
Identify all possible names for the line \(\overleftrightarrow{R S}\) using the points R, S, and T. Explain why each name is valid and provide an additional way to denote the line.
Answer:
We are given a diagram: Here, P, Q, R, S, and T are different points.
We need to find another name for \(\begin{aligned}
& \leftrightarrow \\
& \text { RS }
\end{aligned}\)
As R, S, and T are different points lying on the line \(\begin{aligned}
& \leftrightarrow \\
& \text { RS }
\end{aligned}\) , so it can also be named as \(\begin{aligned}
& \leftrightarrow \\
& \text { RS }
\end{aligned}\)
\(\begin{aligned}
& \leftrightarrow \text { or } \leftrightarrow \text { or } \leftrightarrow \text { or } \leftrightarrow \text { or } \leftrightarrow \\
& \begin{array}{lllll}
\text { SR } & \text { ST } & \text { TS } & \text { RT } & \text { TR }
\end{array} \\
&
\end{aligned}\)
It can also be denoted as line k.
In diagram:
Another name for \(\begin{aligned}
& \leftrightarrow \\
& \text { RS }
\end{aligned}\) is \(\begin{aligned}
& \leftrightarrow \\
& \text { SR }
\end{aligned}\).
Solutions For Big Ideas Math Integrated Math 1 Chapter 8 Maintaining Mathematical Proficiency Exercises Page 220 Exercise 13 Problem 15
Question 15.
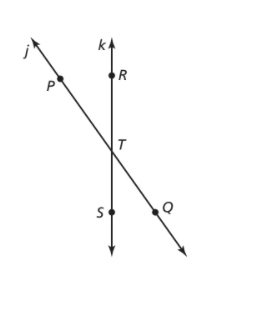
Given points P, Q, R, S, and T in the diagram, identify all rays that have T as the endpoint. Also, identify pairs of opposite rays from these rays. Explain why each identified pair is considered opposite rays.
Answer:
We are given a diagram: Here, P, Q, R, S, and T are different points.
We need to find all the rays with endpoint T and also opposite rays among these rays.
We know that a ray can be named by any letter or by any two points lying on it.
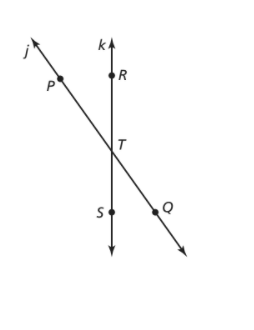
All the rays with endpoint T are and → TS, → TR,→ TP, → TQ.
In the given diagram, there are two pairs of opposite rays
1. → TS and → TR
2. → TP and → TQ
In the diagram:
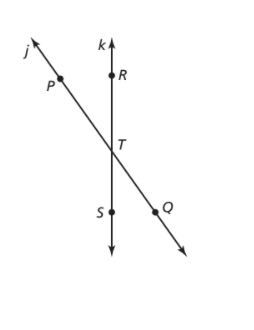
All the rays with endpoint T are → TS, → TR,→ TP, and → TQ
In the given diagram, there are two pairs of opposite rays
1. → TS and → TR
2. → TP and → TQ
Page 220 Exercise 14 Problem 16
Question 16.
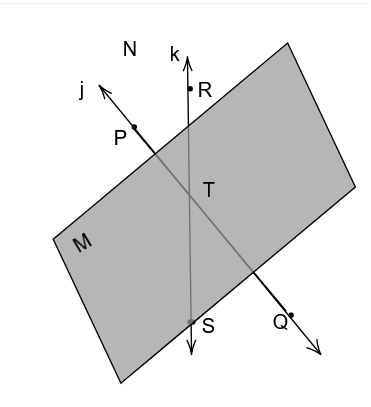
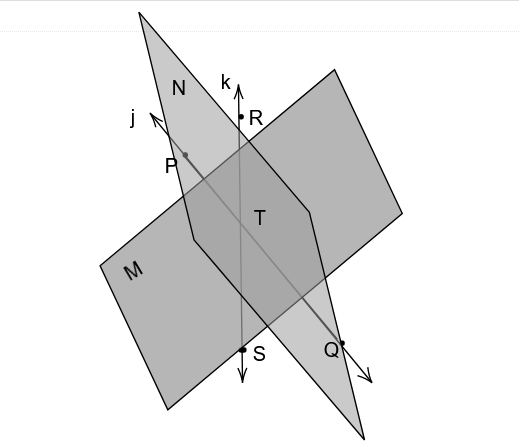
Using dynamic geometry software, we need to draw two planes, M and N, that intersect at line k.
Answer:
We are given a diagram:
We are going to draw two planes M and N that will intersect at line k using dynamic geometry software.
Draw plane M passing through line j.
Draw plane N passing through line k.
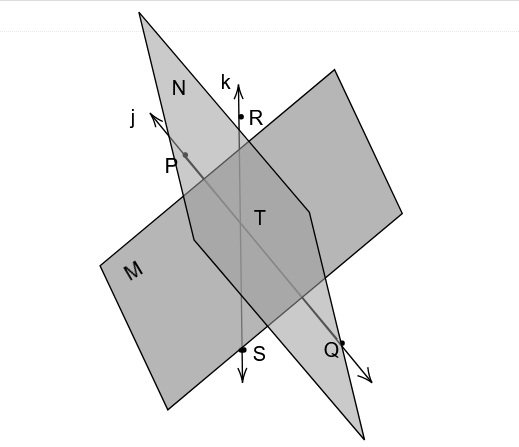
The diagram that shows planes M and N intersecting at line k:
Big Ideas Math Integrated Math 1 Student Journal Chapter 8 Guide Page 220 Exercise 15 Problem 17
Question 17.
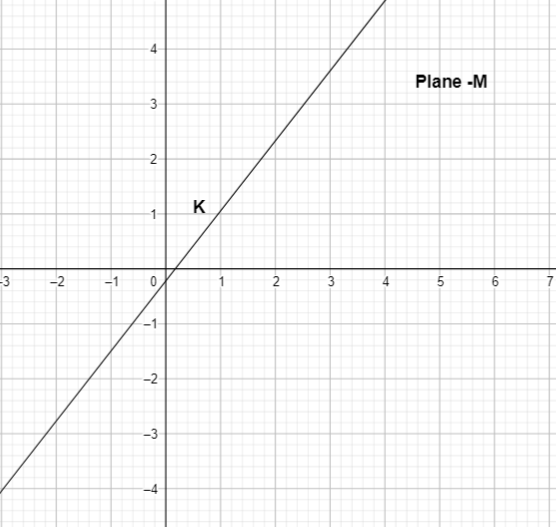
Given a plane M, we need to sketch the graph of line k on plane M.
Steps to sketch the graph:
- Identify and Plot Two Points:
- Choose and plot two points on plane M that will lie on line k.
- Draw Line K:
- Draw a straight line passing through these two points.
- Extend the line on both sides to represent the infinite length of the line.
Answer:
Given a plane M.
And we have to sketch the graph of line k on plane M.
To sketch the graph of line k plot two-point of the line and draw line between them and extend their both side.
So the graph of line k is
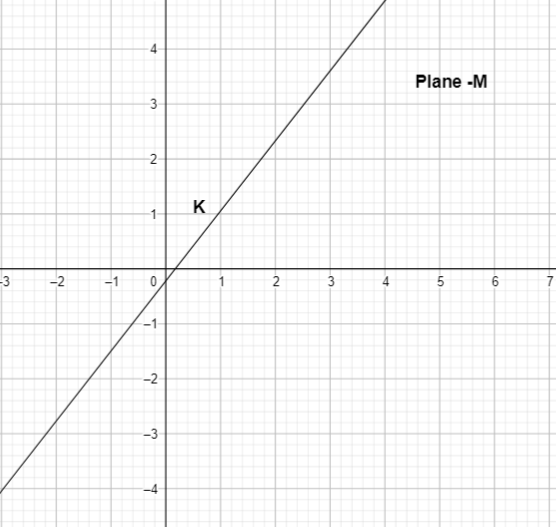
The graph of line k is
Chapter 8 Maintaining Mathematical Proficiency Explained Big Ideas Math Integrated Math Page 221 Exercise 16 Problem 18
Question 18.
Explain how to measure and construct a line segment using a ruler. Provide a step-by-step guide for both processes, including diagrams.
Answer:
In this question, we have to tell how can we measure and construct a line segment.
So for construct, a line segment mark the starting point and put the ruler at zero mark at starting point mark endpoint.
Corresponding distance and then put a pencil at starting point and move along the edge of ruler till you reach the endpoint.
And for the measure, a line segment keep zero ruler at starting point and read the number on the scale where the line segment end.
Like this
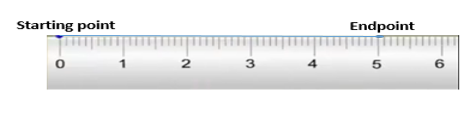
For construct, a line segment mark the starting point and put the ruler at zero mark at starting point mark endpoint.
Corresponding distance and then put a pencil at starting point and move along the edge of ruler till you reach the endpoint and for the measure.
A line segment keep zero ruler at starting point and read the number on the scale where the line segment end.
Like this
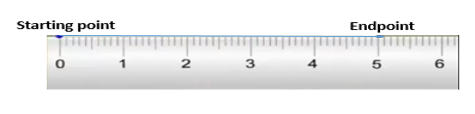
Worked examples For Big Ideas Math Integrated Math 1 Chapter 8 Maintaining Mathematical Proficiency Page 222 Exercise 17 Problem 19
Question 19.
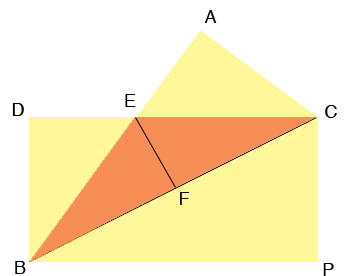
Given a 3-inch index card, fold it along of its diagonals. Describe the steps and illustrate the process using diagrams.
Answer:
Given an index card 3-inch by 5-inch
And we have to fold an index card on one of its diagonals.
Let index card CDBP and is CB its diagonals
To fold the index card on one of its diagonals try to match one corner of the index card with the opposite side of an index card.
So P moved to A.
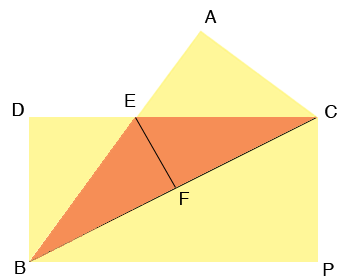
For fold a 3-inch by 5-inch index card on one of its diagonals do like this
Page 222 Exercise 18 Problem 20
Question 20.
Given a 3-inch by 5-inch index card, fold it along one of its diagonals. Use the Pythagorean Theorem to algebraically determine the length of the diagonal in inches. Then, use a ruler to check your answer.
Answer:
Given a fold 3-inch by 5-inch index card fold on one of its diagonals.
And we have to use the Pythagorean Theorem to algebraically determine the length of the diagonal in inches.
Use a ruler to check our answer.
To find the diagonal of index card use the pythagorean Theorem a2 + b2 = c2
Where use a = 3 inch , b = 5 inch and c = length of the diagonal therefore
32 + 52 = c2
⇒ c2 = 9+25
⇒ c2 = 34
⇒ c = \(\sqrt{34}\) ≈ 5.83 inch
Also by measuring the with ruler its same so our answer is correct.
Measuring the diagonal in inches. the with ruler its same therfore our answer is correct.
Page 225 Exercise 19 Problem 21
Question 21.
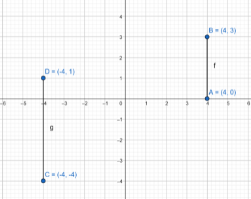
Given the points A(4,0), B(4,3), C(−4,4), and D(−4,1), plot these points on a coordinate plane and determine whether the line segments AB and CD are congruent. Use the distance formula to calculate the lengths of AB and CD.
Answer:
Given A(4,0), B((4,3) and C(−4,4), D(−4,1).
And we have to plot the points in the coordinate plane. Then determine whether AB and CD are congruent
Plot the points in the coordinate plane.
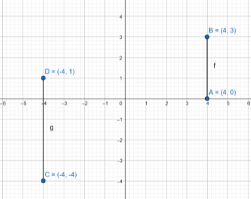
The distance between A and B is AB
Then AB =\(\sqrt{(4-4)^2+(3-0)^2}\)
= \(\sqrt{0+3^2}\)
= 3
The distance between C and D is CD
Then CD = \(\sqrt{(-4+4)^2+(1+4)^2}\)
= \(\sqrt{0+5^2}\)
= 5
Plot the points A(4,0), B((4,3) and C(−4,4), D(−4,1) in the coordinate plane is AB and CD lines are not congruent because there not lengths are equal
Page 225 Exercise 20 Problem 22
Question 22.
Given the line segment UW with a length of 18 units, and a point V between U and W such that UV = 6 units, find the length of the segment VW.
Answer:
Given line segment is UW and V is any point between U and W.
UW = 18 and
UV = 6 then find VW.
UW = UV + VW
18 = 6 + VW
VW = 18−6
VW = 12
The value of VW is 12 .
Page 225 Exercise 21 Problem 23
Question 23.
Given the line segment WV with U as a point between W and V. The lengths of WU and UV are 45 units and 30 units respectively. Find the length of the segment VW.
Answer:
Given line segment is WV and U is any point between W and V.
WU = 45 and UV = 30 then find VW .
VW = VU + UW
VW = 30 + 45
VW = 75
The value of VW is 75 .
Big Ideas Math Integrated Math 1 Chapter 8 Detailed Answers Page 225 Exercise 21 Problem 24
Question 24.
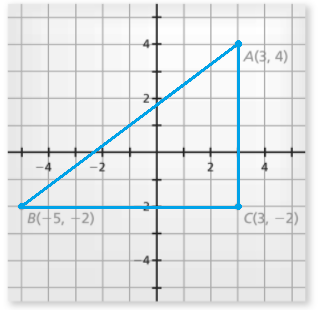
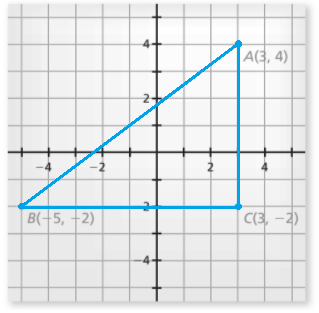
Given a line segment with endpoints A(3,4) and B(−5,−2). Add point C(3,−2) in such a way that it makes a right-angle triangle with AB as the hypotenuse. Use the Pythagorean theorem to find the length of AB.
Answer:
Given a line segment with endpoints A(3,4) and B(−5,−2).
Add point C (3,−2) in such a way that it makes a right angle triangle with AB as hypotenuse.
Now use Pythagoras theorem to find the length of AB.
From graph it is clear that BC = 8 and AC = 6 .
AB2 = BC2+AC2
⇒ AB2 = 64 + 36
⇒ AB2 = 100
⇒ AB = 10
Length of the line segment AB is 10 units.
Big Ideas Math Integrated Math 1 Student Journal Chapter 8 Maintaining Proficiency Answers Page 227 Exercise 22 Problem 25
Question 25.
Solve the endpoints of the line segment are D(−10,−4) and E(14,6).
To find: The coordinates of the midpoint and the length of the line segment. Find the length of the given line segment.
Answer:
Given: The endpoints of the line segment are D(−10,−4),E(14,6)
To find: The coordinates of the midpoint and the length of the line segment.
Here, we will use the mid-point formula of a line segment.
And, distance formula to find the length of the given line segment.
The mid-point formula of the line segment.
(x,y) = \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)
Since the coordinates of the endpoints are D(−10,−4),E(14,6)
x1 = −10, x2 = 14, y1 = −4, y2 = 6
So, (x,y) = \(\left(\frac{-10+14}{2}, \frac{-4+6}{2}\right)\)
(x,y) = (\(\frac{4}{2}\), \(\frac{2}{2}\)
(x,y) = (2,1)
Hence, the coordinates of the midpoint of the given line segment is M(2,1)
Distance of the given line segment
Distance formula, D = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)
Since the coordinates are D(−10,−4), E (14,6) x1= −10, x2 = 14, y1 = −4, y2 = 6
DE = \(\sqrt{(14-(-10))^2+(6-(-4))^2}\)
DE = \(\sqrt{(14+10)^2+(6+4)^2}\)
DE = \(\sqrt{(24)^2+(10)^2}\)
DE = \(\sqrt{576+100}\)
DE = \(\sqrt{676}\)
Hence, the coordinates of the midpoint of the line segments whose coordinates of the endpoint are given as D(−10,−4) ,E(14,6)is M(2,1)and the length of the line segment is 24 unit.
