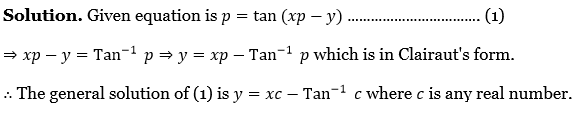Differential Equations

An Equation Of The Form \(\frac{d y}{d x}=f(x, y)\) is called a differential equation of the first order and of the first degree.

We study the following four methods for solving \(\frac{d y}{d x}=f(x, y)\)

1. Variables separable.
2. Homogeneous equations and equations reducible to homogeneous form.
3. Exact equations can be made exact by the use of integrating factors.
4. Linear equations and Bemouli’s form.

Before discussing the methods for solving \(\frac{d y}{d x}=f(x, y)\) without proof concerning the existence and uniqueness of solutions.

Differential Equations Introduction Existence And Uniqueness Theorem

Let S denote the rectangular region defined by \(\left|x-x_0\right| \leq a\) and \(\left|y-y_0\right| \leq b\) a region with the point \(\left(x_0, y_0\right)\) at its centre. If f(x,y) and \(\frac{\partial f}{\partial y}\) are continuous functions of x and y in a region S of the xy – plane and if \(\mathrm{P}\left(x_0, y_0\right) \in\) S, then there exists one and only one function say Φ(x), which in some neighbourhood of P, is a solution of the differential equation \(\frac{d y}{d x}=f(x, y)\) and is such that \(\phi\left(x_0\right)=y_0\)

In other words, the theorem states that if f(x,y) and \(\frac{\partial f}{\partial y}\) are continuous functions of x and y in a region S., then the differential equation \(\frac{d y}{d x}=f(x, y)\) has infinitely many solutions say Φ (x,y,c)=0,c being an arbitrary constant such that through each point of S, one and only one member of the family Φ (x,y, c) = 0 passes.

Differential Equations Introduction Variables Separable

If the differential equation \(\frac{d y}{d x}=f(x, y)\) can be expressed in the form \(\frac{d y}{d x}=\frac{f(x)}{g(y)}\) or \(\frac{d y}{d x}=f(x) \cdot g(y)\) where f and g are continuous functions of a single variable, it is said to be of the form variables separable.

Differential Equations Introduction Working rule to find the General Solution (G. S.)

1. The given equation \(\frac{d y}{d x}=\frac{f(x)}{g(y)}\) can be written by separating variables as f(x) d x=g(y) d y.

2. Integrate both sides of (1) and add an arbitrary constant of integration to any one of the two sides.

3. General solution of (1) is \(\int f(x) d x=\int g(y) d y+c\) or \(\phi(x, y, c)=0\).

Note 1. The constant of integration c can be selected in any suitable form as \(c / 2, \log c, \sin c, e^c\) or \(\text{Tan}^{-1} c\) etc.

4. Some differential equations can be brought to variables’ separable form by some substitution

Consider \(\frac{d y}{d x}=f(a x+b y+c)\) ………………….(1)

Put \(a x+b y+c=u \Rightarrow \frac{d u}{d x}=a+b \frac{d y}{d x} \Rightarrow \frac{d y}{d x}=\frac{1}{b}\left(\frac{d u}{d x}-a\right)\) …………………….(2)

From (1) and (2), we have : \(\frac{1}{b}\left(\frac{d u}{d x}-a\right)=f(u) \Rightarrow d u=[a+b f(u)] d x\)

Separating the variables, we get: \(\frac{d u}{a+b f(u)}=d x\)

⇒ \(\int \frac{d u}{a+b f(u)}=\int d x+c_1\)

∴ The general solution of (1) is \(\int \frac{d u}{a+b f(u)}=\int d x+c_1\) where \(\mathbf{c}_1\) is an arbitrary constant or \(\phi\left(u, x, \mathrm{c}_1\right)=0 \text { or } \phi\left(a x+b y+c, x, \mathrm{c}_1\right)=0\)

Differential Equations of First Order and First Degree Solved Example Problems Exercise 2.6

Example. 1. Solve \(\left(y^2+2 x^2 y\right) d x+\left(2 x^3-x y\right) d y=0\)

Solution.

Given equation is \(\left(y^2+2 x^2 y\right) d x+\left(2 x^3-x y\right) d y=0\)

⇒ \(y\left(y+2 x^2\right) d x+x\left(2 x^2-y\right) d y=0\) . Let \(x^h y^k\) be the integrating factor.

Multiplying the given equation by \(x^h y^k\).

⇒ \(\left(x^h y^{k+2}+2 x^{h+2} y^{k+1}\right) d x+\left(2 x^{h+3} y^k-x^{h+1} y^{k+1}\right) d y=0\) …………………..(1)

where \(\mathrm{M}=x^h y^{k+2}+2 x^{h+2} y^{k+1}, \mathrm{~N}=2 x^{h+3} y^k-x^{h+1} y^{k+1}\)

If (1) exact , then \(\frac{\partial \mathrm{M}}{\partial y}=\frac{\partial \mathrm{N}}{\partial x}\)

⇒ \((k+2) x^h y^{k+1}+2(k+1) x^{h+2} y^k=-(h+1) x^h y^{k+1}+2(h+3) x^{h+2} y^k\)

Equating the coefficients of \(x^h y^{k+1} \text { and } x^{h+2} y^k\)

we get \(k+2=-(h+1), k+1=h+3 \Rightarrow h+k+3=0 ; h-k+2=0\)

Solving these equations: h = -5/2,k = -1/2.

∴ Integrating factor is [latexx^{-5 / 2} y^{-1 / 2}][/latex].

Multiplying the given equation with this I. F. we get \(\left(x^{-5 / 2} y^{3 / 2}+2 x^{-1 / 2} y^{1 / 2}\right) d x+\left(2 x^{1 / 2} y^{-1 / 2}-x^{-3 / 2} y^{1 / 2}\right) d y=0\) …………………….(2)

(2) is an exact equation where \(\mathrm{M}_1=x^{-5 / 2} y^{3 / 2}+2 x^{-1 / 2} y^{1 / 2}, \mathrm{~N}_1=2 x^{1 / 2} y^{-1 / 2}-x^{-3 / 2} y^{1 / 2}\) and \(\frac{\partial \mathrm{M}_1}{\partial y}=\frac{\partial \mathrm{N}_1}{\partial x}\) now solving (2).

⇒ \(\int \mathrm{M}_1 d x=\int\left(x^{-5 / 2} y^{3 / 2}+2 x^{-1 / 2} y^{1 / 2}\right) d x\) treating y as constant.

= \(y^{3 / 2} x^{-3 / 2}(-2 / 3)+4 x^{1 / 2} y^{1 / 2} \text { and } \int \mathrm{N}_1 d y\) = integrating the terms not having x = 0.

The required solution is \(\int \mathrm{M}_1 d x+\int \mathrm{N}_1 d y=c \Rightarrow-(2 / 3) x^{-3 / 2} y^{3 / 2}+4 x^{1 / 2} y^{1 / 2}=c\)

Differential Equations Of First Order And First Degree Exercise 2.6

Example. 2. Solve \((2 y d x+3 x d y)+2 x y(3 y d x+4 x d y)=0\)

Solution.

The given equation can be written as \(\left(2 y+6 x y^2\right) d x+\left(3 x+8 x^2 y\right) d y=0\) …………………(1)

Let \(x^h y^k\) be the integrating factor. Multiplying (1) by \(x^h y^k\) :

⇒ \(\left(2 x^h y^{k+1}+6 x^{h+1} y^{2+k}\right) d x+\left(3 x^{h+1} y^k+8 x^{h+2} y^{k+1}\right) d y=0\) ………………….(2)

(2) is an exact equation if \(\frac{\partial \mathrm{M}}{\partial y}=\frac{\partial \mathrm{N}}{\partial x}\) where

M\(=2 x^h y^{k+1}+6 x^{h+1} y^{2+k}, \mathrm{~N}=3 x^{h+1} y^k+8 x^{h+2} y^{k+1}\)

⇒ \(2(k+1) y^k x^h+6(k+2) y^{k+1} x^{h+1}=3(h+1) x^h y^k+8(h+2) x^{h+1} y^{k+1}\)

⇒ \(2 k+2=3 h+3,6 k+12=8 h+16 \Rightarrow 3 h-2 k+1=0,8 h-6 k+4=0\)

Solving these equations we get h=1,k=2.

∴ I.F. = xy²

Multiplying (1) with \(x y^2 \Rightarrow\left(2 x y^3+6 x^2 y^4\right) d x+\left(3 x^2 y^2+8 x^3 y^3\right) d y=0\)

where \(\dot{\mathrm{M}}_1=2 x y^3+6 x^2 y^4 \text { and } \mathrm{N}_1=3 x^2 y^2+8 x^3 y^3\)

⇒ \(\int \mathrm{M}_1 d x=\int\left(2 x y^3+6 x^2 y^4\right) d x=2\left(x^2 / 2\right) y^3+6\left(x^3 / 3\right) y^4\) treating y constant.

⇒ \(\int \mathrm{N}_1 d y\) = integrating the terms of N, not having x = 0.

∴ Solution of(1) is \(x^2 y^3+2 x^3 y^4+c=0 \Rightarrow x^2 y^3+2 x^3 y^4=c\)

Homogeneous Equations Solved Problems Exercise 2.6

3. Solve: \(\left(2 x^2 y-3 y^4\right) d x+\left(3 x^3+2 x y^3\right) d y=0\) ………………….(1)

Solution:

Given

\(\left(2 x^2 y-3 y^4\right) d x+\left(3 x^3+2 x y^3\right) d y=0\) ………………….(1)

Let \(x^a y^b\) be the integrating factor. multiplying (1) with this factor, we get :

⇒ \(\left(2 x^{a+2}+y^{b+1}-3 x^a y^{b+4}\right) d x+\left(3 x^{a+3} y^b+2 x^{a+1} y^{b+3}\right) d y=0\)

where  \(\mathrm{M}=2 x^{a+2} y^{b+1}-3 x^a y^{b+4}, \quad \mathrm{~N}=3 x^{a+3} y^b+2 x^{a+1} y^{b+3}\) …………………..(2)

For (2) to be exact: \(\frac{\partial \mathrm{M}}{\partial y}=\frac{\partial \mathrm{N}}{\partial x}\)

⇒ \(2(b+1) x^{a+2} y^b-3(b+4) x^a y^{b+3}=3(a+3) x^{a+2} y^b+2(a+1) x^a y^{b+3}\)

⇒ \(2(b+1)=3(a+3), 2(a+1)=-3(b+4) \Rightarrow 3 a-2 b+7=0, \quad 2 a+3 b+14=0\)

Solving for a and b: a=-49/13,b=-28/13

∴ I. F = \(x^{-49 / 13} y^{-28 / 13}\)

Multiplying (1) by \(x^{-49 / 13} y^{-28 / 13}\) we get: \(\left(2 x^2 y \cdot x^{-49 / 13} y^{-28 / 13}-3 y^4 x^{-49 / 13} y^{-28 / 13}\right) d x\)

+\(\left(3 x^3 \cdot x^{-49 / 13} y^{-28 / 13}-2 x y^3 x^{-49 / 13} y^{-28 / 15}\right) d y=0\)

⇒ \(\left(2 x^{-23 / 13} \cdot y^{-15 / 13}-3 x^{-49 / 13} \cdot y^{24 / 13}\right) d x+\left(3 x^{-10 / 13} y^{-28 / 13}+2 x^{-36 / 13} y^{11 / 13}\right) d y=0\)

where \(\mathrm{M}_1=2 x^{-23 / 13} y^{-15 / 13}-3 x^{-49 / 13} y^{24 / 13}\) and \(\mathrm{N}_1=3 x^{-10 / 13} y^{-28 / 13}+2 x^{-36 / 13} y^{11 / 13}\)

⇒ \(\int \mathrm{M}_1 d x=2 y^{-15 / 13} \frac{x^{-10 / 13}}{-10 / 13}-3 y^{24 / 13} \frac{x^{-36 / 13}}{-36 / 13}=5 x^{-36 / 13} y^{24 / 13}-12 x^{-10 / 13} y^{-15 / 13}, \mathrm{~N}_1 d y=0\)

G S. is \(5 x^{-36 / 13} y^{24 / 13}-12 x^{-10 / 13} y^{-15 / 13}=c\)

Methods To Find Integrating Factors For Exercise 2.6

Example.4. Solve \(x(4 y d x+2 x d y)+y^3(3 y d x+5 x d y)=0\)

Solution.

Given equation is \(\left(4 x y+3 y^4\right) d x+\left(2 x^2+5 x y^3\right) d y=0\) …………….(1)

verify \(\frac{\partial \mathrm{M}}{\partial y} \neq \frac{\partial \mathrm{N}}{\partial x}\) => (1) is not an exact equation.

Let \(x^a y^b\) be an integrating factor. Multiplying (1) with I.F.

⇒ \(\left(4 x^{a+1} y^{b+1}+3 x^a y^{b+4}\right) d x+\left(2 x^{a+2} y^b+5 x^{a+1} y^{b+3}\right) d y=0\) …………………(2)

where \(\mathrm{M}=4 x^{a+1} y^{b+1}+3 x^a y^{b+4}, \mathrm{~N}=2 x^{a+2} y^b+5 x^{a+1} y^{b+3}\)

⇒ \(\frac{\partial \mathrm{M}}{\partial y}=4 x^{a+1}(b+1) y^b+3(b+4) x^a y^{b+3}, \frac{\partial \mathrm{N}}{\partial x}=2(a+2) x^{a+1} \cdot y^b+5(a+1) x^a y^{b+3}\)

for(2) to be an exact, \(\frac{\partial \mathrm{M}}{\partial y}=\frac{\partial \mathrm{N}}{\partial x}\)

⇒ \(4(b+1) x^{a+1} y^b+3(b+4) x^a y^{b+3}=2(a+2) x^{a+1} y^b+5(a+1) x^a y^{b+3}\)

⇒ \(4(b+1)=2(a+2), 3(b+4)=5(a+1) \Rightarrow a-2 b=0,5 a-3 b-7=0\)

Solving these equation: 10b – 36 = 7 ⇒ b =1  ∴ a= 2

Multiplying (1) by \(x^2 \cdot y\); we get: \(\left(4 x^3 y^2+3 x^2 y^5\right) d x+\left(2 x^4 y+5 x^3 y^4\right) d y=0\)

Here \(\mathrm{M}_1=4 x^3 y^2+3 x^2 y^5, \mathrm{~N}_1=2 x^4 \dot{y}+5 x^3 y^4\)

⇒ \(\int M_1 d x=\int\left(4 x^3 y^2+3 x^2 y^5\right) d x=\frac{4 x^4}{4} y^2+\frac{3 x^3}{3} y^5 . \int N_1 d y=0\)

∴ GS. is \(x^4 y^2+x^3 y^5=c\)

Differential Equations Introduction Solved Problems

Existence And Uniqueness Theorem Solved Problems

Example. 1: Solve : \(\frac{d y}{d x}+\sqrt{\frac{1-y^2}{1-x^2}}=0\)

Solution.

Given equation is \(\frac{d y}{d x}+\sqrt{\frac{1-y^2}{1-x^2}}=0\)…..(1)

Separating the variables: \(\frac{d y}{\sqrt{1-y^2}}+\frac{d x}{\sqrt{1-x^2}}=0\)

⇒ \(\int \frac{d y}{\sqrt{1-y^2}}+\int \frac{d x}{\sqrt{1-x^2}}=c\) (c being arbitrary constant)

∴ The general solution of (1) is: \(\text{Sin}^{-1} y+\text{Sin}^{-1} x=c\)

Examples Of Solved Problems On Existence And Uniqueness Theorem 

Example. 2: Solve : \(y \frac{d y}{d x}=x e^{x^2+y^2}\)

Solution.

Given equation is \(y \frac{d y}{d x}=x e^{x^2} \cdot e^{y^2}\) …………………(1)

Separating the variables we have : \(x e^{x^2} d x=y e^{-y^2} d y \Rightarrow \int x e^{x^2} d x=\int y e^{-y^2} d y\)

Put \(x^2=u, y^2=t \Rightarrow 2 x d x=d u, 2 y d y=d t\)

∴ \(\frac{1}{2} \int e^u d u=\frac{1}{2} \int e^{-t} d t+\frac{c}{2} \Rightarrow e^u=-e^{-t}+c\)

∴ The general solution of (1) is \(e^{x^2}+e^{-y^2}=c\)

Application Of Existence And Uniqueness Theorem In Differential Equations

Example. 3: Solve : \(\left(\frac{d y}{d x}\right) \tan y=\sin (x+y)+\sin (x-y)\)

Solution.

Given \(\left(\frac{d y}{d x}\right) \tan y=2 \sin x \cos y\) ………………..(1)

Separating the variables : \(\frac{\tan y}{\cos y} d y=2 \sin x d x\)

=> \(\int\) sec y tan y dy = \(\int\) 2 sin x dx => \(\sec y=-2 \cos x+c\)

∴ The general solution of (1) is sec y + 2 cos x = c

Solved Examples Of Initial Value Problems Using The Existence And Uniqueness Theorem

Example. 4: Solve: \(\log \left(\frac{d y}{d x}\right)=a x+b y\)

Solution:

Given equation is \(\log \left(\frac{d y}{d x}\right)=a x+b y\) ………………………(1)

⇒ \(\frac{d y}{d x}=e^{a x+b y}=e^{a x} \cdot e^{b y} \Rightarrow e^{a x} d x=e^{-b y} d y\)

Separating the variables => \(\int e^{a x} d x=\int e^{-b y} d y+\mathrm{c} \Rightarrow \frac{e^{a x}}{a}=\frac{e^{-b y}}{-b}+\mathrm{c}\)

∴ The given solution of (1) is \(b e^{a x}+a e^{-b y}=c\)

Problems On Existence And Uniqueness Theorem With Solutions 

Example. 5: Solve : \(\frac{d y}{d x}=\frac{x(2 \log x+1)}{\sin y+y \cos y}\)

Solution:

Given equation is \(\frac{d y}{d x}=\frac{x(2 \log x+1)}{\sin y+y \cos y}\) ……………………..(1)

Separating the variables : x(2 log x +1) dx = (sin y + y cos y) dy

Integrating: \(2 \int x \log x d x+\int x d x=\int \sin y d y+\int y \cos y d y\)

⇒ \(2\left(\frac{x^2}{2} \log x-\int \frac{x^2}{2} \cdot \frac{1}{x} d x\right)+\frac{x^2}{2}=-\cos y+y \sin y-\int \sin y d y\)

⇒ \(x^2 \log x-\frac{x^2}{2}+\frac{x^2}{2}=-\cos y+y \sin y+\cos y+c \Rightarrow x^2 \log x=y \sin y+c\)

The general solution of (1) is \(x^2 \log x=y \sin y+c\)

Lipschitz Condition In Existence And Uniqueness Theorem Problems

Example. 6: Solve \(y-x \frac{d y}{d x}=a\left(y^2+\frac{d y}{d x}\right)\)

Solution:

Given equation is \(y-x \frac{d y}{d x}=a\left(y^2+\frac{d y}{d x}\right)\) ………………….(1)

⇒ \((a+x) \frac{d y}{d x}=y-a y^2\)

Separating the variables : \(\frac{1}{y-a y^2} d y=\frac{1}{a+x} d x \Rightarrow \int \frac{1}{y(1-a y)} d y=\int \frac{1}{a+x} d x+c_1\)

⇒ \(\int\left(\frac{1}{y}+\frac{a}{1-a y}\right) d y=\int \frac{1}{a+x} d x+c_1 \Rightarrow \log |y|-\log |1-a y|=\log \mid a+x \mid+\log c\)

⇒ \(\log \left|\frac{y}{1-a y}\right|=\log |c(a+x)| \Rightarrow \frac{y}{1-a y}=c(a+x)\)

∴ The general solution of (1) is y = c (a + x) (1 – ay)

Existence And Uniqueness Theorem Numerical Examples

Example. 7: Solve : \(3 e^x \tan y d x+\left(1-e^x\right) \sec ^2 y d y=0\)

Solution.

Given equation is \(3 e^x \tan y d x+\left(1-e^x\right) \sec ^2 y d y=0\) …………………..(1)

Separating the variables: \(\frac{3 e^x}{1-e^x} d x+\frac{\sec ^2 y}{\tan y} d y=0\)

⇒ \(3 \int \frac{e^x}{1-e^x} d x+\int \frac{\sec ^2 y}{\tan y} d y=\log c \quad \Rightarrow-3 \log \left|\left(1-e^x\right)\right|+\log |\tan y|=\log c\)

⇒ \(\log \left|\left(1-e^x\right)^{-3}\right|+\log |\tan y|=\log c \Rightarrow \log \left|\frac{\tan y}{\left(1-e^x\right)^3}\right|=\log c \Rightarrow \frac{\tan y}{\left(1-e^x\right)^3}=c\)

∴ The general solution of (1) is \(\tan y=c\left(1-e^x\right)^3\)

Differential Equations Problems Explained Using Existence And Uniqueness Theorem

Example. 8: Solve : \(\frac{d y}{d x}=(4 x+y+1)^2\)

Solution:

Given equation is \(\frac{d y}{d x}=(4 x+y+1)^2\)……..(1)

Let \(4 x+y+1=u \Rightarrow 4+\frac{d y}{d x}=\frac{d u}{d x} \Rightarrow \frac{d y}{d x}=\frac{d u}{d x}-4\)…..(2)

From (1) and (2): \(\frac{d u}{d x}-4=u^2 \Rightarrow \frac{d u}{d x}=u^2+4\).

Separating the variables: \(\frac{d u}{u^2+4}=d x\)

⇒ \(\int \frac{d u}{u^2+2^2}=\int d x+\frac{c}{2} \Rightarrow \frac{1}{2} \text{Tan}^{-1}\left(\frac{u}{2}\right)\)

= \(x+\frac{c}{2} \Rightarrow \text{Tan}^{-1}\left(\frac{u}{2}\right)=2 x+c\)

u = \(2 \tan (2 x+c)\)

∴ The General solution is \(4 x+y+1=2 \tan (2 x+c)\)

(because \(u=4 \dot{x}+y+1)\)

Worked Examples On Existence And Uniqueness Theorem In Differential Equations

Example 9: Solve : \(\frac{d y}{d x}=\cos (x+y)+\sin (x+y)\)

Solution:

Given equation is \(\frac{d y}{d x}=\cos (x+y)+\sin (x+y)\) …………………..(1)

Let \(x+y=u \Rightarrow 1+\frac{d y}{d x}=\frac{d u}{d x} \Rightarrow \frac{d y}{d x}=\frac{d u}{d x}-1\) ……………………..(2)

(1)and (2) => \(\frac{d u}{d x}-1=\cos u+\sin u \Rightarrow \frac{d u}{d x}=(1+\cos u)+\sin u\)

⇒ \(\frac{d u}{d x}=2 \cos ^2 \frac{u}{2}+2 \sin \frac{u}{2} \cos \frac{u}{2}=2 \cos ^2 \frac{u}{2}\left(1+\tan \frac{u}{2}\right)\)

Separating the variables : \(\frac{d u}{2 \cos ^2(u / 2)[1+\tan (u / 2)]}=d x\)

⇒ \(\int \frac{\sec ^2(u / 2)}{2[1+\tan (u / 2)]} d u=\int d x+c \Rightarrow \log \left(1+\tan \frac{u}{2}\right)=x+c\)

∴ The General Solution is \(\log \left[1+\tan \left(\frac{x+y}{2}\right)\right]=x+c\)

Example. 10: solve : \(\frac{d y}{d x}-x \tan (y-x)=1\)

Solution:

Given equation is \(\frac{d y}{d x}-x \tan (\cdot y-x)=1\) …………………..(1)

Put \(y-x=z \Rightarrow \frac{d y}{d x}-1=\frac{d z}{d x} \Rightarrow \frac{d y}{d x}=\frac{d z}{d x}+1\) ……………………(2)

(1)and(2) => \(\frac{d z}{d x}+1-x \tan z=1 \Rightarrow \frac{d z}{d x}=x \tan z\)

Separating the variables: \(\frac{d z}{\tan z}=x d x \Rightarrow \int \cot z d z=\int x d x+c \Rightarrow \log |\sin z|=\frac{x^2}{2}+\frac{c}{2}\)

∴ The general solution of (1) is \(2 \log |\sin (y-x)|=x^2+c\)

Example. 11: Solve : \(\left(\frac{x+y+a}{x+y-b}\right) \frac{d y}{d x}=\frac{x+y-a}{x+y+b}\)

Solution:

Given equation is

Put x + y = z in the given equation => \(1+\frac{d y}{d x}=\frac{d z}{d x}\)

∴ Given differential equation becomes \(\left(\frac{z+a}{z-b}\right)\left(\frac{d z}{d x}-1\right)=\frac{z-a}{z+b}\)

⇒ \(\frac{d z}{d x}=1+\frac{(z-a)(z-b)}{(z+a)(z+b)}=\frac{z^2+z(a+b)+a b+z^2-z(a+b)+a b}{(z+a)(z+b)}\)

⇒ \(\frac{d z}{d x}=\frac{2\left(z^2+a b\right)}{z^2+z(a+b)+a b}\)

Separating the variables: \(\Rightarrow \frac{z^2+z(a+b)+a b}{z^2+a b} d z=2 d x\)

⇒ \(\int\left[\frac{z^2+a b}{z^2+a b}+\frac{z(a+b)}{z^2+a b}\right] d z=\int 2 d x+c\)

⇒ \(\int d z+\frac{a+b}{2} \int \frac{2 z}{z^2+a b} d z=2 x+c \Rightarrow z+\frac{a+b}{2} \log \left|z^2+a b\right|=2 x+c\)

∴ The general solution is \(x+y+\frac{a+b}{2} \log \left|(x+y)^2+a b\right|=2 x+c\)

Example. 12: Find the equation of the curve passing through the point (1,1) whose differential equation is (y- yx) dx + (x+xy) dy = 0.

Solution :

Given equation is (y- yx) dx + (x+xy) dy = 0 => y (1 – x) dx + x (1+ y) dy =0

Separating the variables: \(\frac{1-x}{x} d x+\frac{1+y}{y} d y=0 \Rightarrow\left(\frac{1}{x}-1\right) d x+\left(\frac{1}{y}+1\right) d y=0\)

⇒ \(\int\left(\frac{1}{x}-1\right) d x+\int\left(\frac{1}{y}+1\right) d y=c \Rightarrow \log |x|-x+\log |y|+y=c\)

Given the curve passes through the point (1,1): = log 1 -1+ log 1 +1 = c => c = 0

∴ The equation of the curve passing through the point (1,1) is \(\log |x y|+y-x=0 \Rightarrow x y=e^{x-y}\)

Differential Equations of First Order But Not of First Degree Differential Equations Solvable For X

Let f(x,y,p) = 0 be the given differential equation ……………………(1)

If equation (1) cannot be split up into rational and linear factors and (1) is of first degree in x, then (1) can be solved for x.

(1) can be expressed in the form x = F(y,p) ……………………….(2)

Differentiating (2) w.r.t. y gives an equation of the form \(\frac{1}{p}=g\left(y, p, \frac{d p}{d y}\right)\) …………………(3)

Since (3) is an equation in two variables p and y , it can be solved.

∴ The solution of (3) is \(\phi(y, p, c)=0\) …………………(4).

Eliminating p from (1) and (4), general solution of (1) is \(\psi(x, y, c)=0\).

Note 1. If it is not possible to eliminate p, then the values of x and y in terms of p in the form \(x=f_1(p, c)\) and \(y=f_2(p, c)\) together give the general solution.

2. This method is especially useful for equations y being absent.

Differential Equations of First Order But Not of First Degree Solved Problems

Example. 1. Solve \(y^2 \log y=x p y+p^2\)
Solution.

Given equation is \(y^2 \log y=x p y+p^2\) …………………………(1)

Since x is the first degree in (1), it can be solved for x. \(x=\frac{y \log y}{p}-\frac{p}{y}\) ………………………(2)

Differentiating (2) w.r.t. y: \(\frac{1}{p}=(1+\log y) \frac{1}{p}-\frac{y \log y}{p^2} \frac{d p}{d y}-\frac{1}{y} \frac{d p}{d y}+\frac{p}{y^2}\)

⇒ \(\frac{1}{p}=\frac{1}{p}+\frac{1}{\mathrm{p}} \log y+\frac{p}{y^2}-\left(\frac{y \log y}{p^2}+\frac{1}{y}\right) \frac{d p}{d y}\)

⇒ \(\frac{p}{y}\left(\frac{y \log y}{p^2}+\frac{1}{y}\right)-\left(\frac{y \log y}{p^2}+\frac{1}{y}\right) \frac{d p}{d y}=0\)

⇒ \(\left(\frac{y \log y}{p^2}+\frac{1}{y}\right)\left(\frac{p}{\mathrm{y}}-\frac{d p}{d y}\right)=0 \Rightarrow \frac{y \log y}{p^2}+\frac{1}{y}=0\) ………………………(3)

∴ \(\frac{p}{y}-\frac{d p}{d y}=0\) ……………………….(4)

(3) is discarded as it gives a singular solution

Solving(4) : \(\frac{d p}{d y}=\frac{p}{y} \Rightarrow \frac{d p}{p}=\frac{d y}{y} \Rightarrow \int \frac{d p}{p}=\int \frac{d y}{y}+\log c\)

⇒ \(\log p=\log y+\log c \Rightarrow \log p=\log c y \Rightarrow p=c y\) …………………………(5)

Eliminating p from (1) and (5): \(y^2 \log y=c x y^2+c^2 y^2 \Rightarrow \log y=c x+c^2\)

∴ The general solution of (1) is \(\log y=c x+c^2\)

Differential Equations Of First Order But Not First Degree

Example. 2. Solve \(x=y+p^2\)
Solution.

Given equation is \(x=y+p^2\) ………………………….(1)

Differentiating (1) w.r.t. \(y \Rightarrow \frac{d x}{d y}=1+2 p \frac{d p}{d y} \Rightarrow \frac{d p}{d y}=\frac{1-p}{2 p^2}\)

Separating the variables : \(d y=\frac{-2 p^2}{p-1} d p \Rightarrow \int d y=\int \frac{-2 p^2}{p-1} d p+c\)

⇒ \(y=-2 \int\left(p+1+\frac{1}{p-1}\right) d p+c \Rightarrow-2\left[\frac{1}{2} p^2+p+\log (p-1)\right]+c\) ………………………..(2)

Substituting the value of y from (2) in (1), we get: \(x=c-2[p+\log (p-1)]\) ………………………(3)

which shows that it is not possible to eliminate p from (1) and (2).

∴ The general solution of(1) is \(x=c-2[p+\log (p-1)], y=-p^2-2 p-2 \log (p-1)+c\)

Differential Equations Solvable For x Explained

Example. 3. Solve \(a y p^2+(2 x-b) p-y=0\) where p = dy / dx, a and h are real numbers.

Solution.

Given equation is \(a y p^2+(2 x-b) p-y=0\)

Since x is of first degree in (1), it can be solved for x. \(\Rightarrow 2 x=\frac{y}{p}-a y p+b\)

Differentiating w.r.t.y: \(\frac{2}{p}=\frac{1}{p} \cdot 1-\frac{y}{p^2} \frac{d p}{d y}-a\left(p+y \frac{d p}{d y}\right)\)

⇒ \(\frac{1}{p}+\frac{y}{p^2} \frac{d p}{d y}+a\left(p+y \frac{d p}{d y}\right)=0\)

⇒ \(\frac{1}{p^2}\left(p+y \frac{d p}{d y}\right)+a\left(p+y \frac{d p}{d y}\right)=0 \Rightarrow\left(p+y \frac{d p}{d y}\right)\left(\frac{1}{p^2}+a\right)=0\)

∴ \(p+y \frac{d p}{d y}=0\) ……………………..(2)

∴ \(\frac{1}{p^2}+a=0\) …………………….(3)

(3) is discarded as it gives a singular solution.

Solving (2): \(p+y \frac{d p}{d y}=0 \Rightarrow \frac{d p}{p}+\frac{d y}{y}=0\)    (separating variables)

Integrating : \(\int \frac{d p}{p}+\int \frac{d y}{y}=\log c \Rightarrow \log p+\log y=\log c\)

⇒ \(\log p y=\log c \Rightarrow p y=c \Rightarrow p=c / y\)………………….(4)

By eliminating p from (1) and (4) => \(\text { ay }\left(\frac{c^2}{y^2}\right)+(2 x-b) \frac{c}{y}-y=0\)

∴ The general solution of (1) is \(a c^2+(2 x-b) c-y^2=0\)

Examples Of Differential Equations Solvable For x 

Example. 4. Solve \(a p^2+p y-x=0\)
Solution.

Given equation is \(x=y p+a p^2\) ……………………..(1)

Differentiating (1) w.r.t.y \(\Rightarrow \frac{d x}{d y}=p+y \frac{d p}{d y}+2 a p \frac{d p}{d y}\)

⇒ \(\frac{1}{p}-p=(y+2 a p) \frac{d p}{d y} \Rightarrow \frac{d y}{d p}=\frac{p y+2 a p^2}{1-p^2}\)

⇒ \(\frac{d y}{d p}-\frac{p}{1-p^2} y=\frac{2 a p^2}{1-p^2}\) which is linear in y and p ……………………….(2)

∴ \(\text { I.F. }=\exp \left(\int \frac{-p}{1-p^2} d p\right)=\exp \left[\frac{1}{2} \log \left(1-p^2\right)\right]=\sqrt{1-p^2}\)

The general solution of (2) is \(y \sqrt{1-p^2}=2 a \int \frac{p^2}{1-p^2}, \sqrt{1-p^2} d p+c\)

⇒ \(y \sqrt{1-p^2}=2 a \int \frac{1-\left(1-p^2\right)}{\sqrt{1-p^2}} d p+c=2 a \int \frac{d p}{\sqrt{1-p^2}}-2 a \int \sqrt{1-p^2} d p+c\)

⇒ \(y \sqrt{1-p^2}=2 a \sin ^{-1} p-2 a\left[\frac{p}{2} \sqrt{1-p^2}+\frac{1}{2} \sin ^{-1} p\right]+c\)

= \(a \sin ^{-1} p-a p \sqrt{1-p^2}+c \Rightarrow y=\frac{a \sin ^{-1} p+c}{\sqrt{1-p^2}}-a p\) ……………………….(3)

By eliminating y from (1) and (3) \(\Rightarrow x=\frac{p}{\sqrt{1-p^2}}\left(a \sin ^{-1} p+c\right)\) …………………….(4)

∴ (3) and (4) together form the general solution of (1).

First-Order Equations Not Of First Degree With Solutions 

Example. 5. Solve \(\)
Solution.

Given \(p^3-4 x y p+8 y^2=0 \Rightarrow 4 x=\frac{p^2}{y}+\frac{8 y}{p}\) …………………………(1)

Differentiating (1) w.r.t.y \(\Rightarrow \frac{4}{p}=\frac{2 p}{y} \frac{d p}{d y}-\frac{p^2}{y^2}+\frac{8}{p}-\frac{8 y}{p^2} \frac{d p}{d y}\)

⇒ \(\frac{p^2}{y^2}-\frac{4}{p}=\left(\frac{2 p}{y}-\frac{8 y}{p^2}\right) \frac{d p}{d y} \Rightarrow \frac{p^3-4 y^2}{p y^2}=\frac{2\left(p^3-4 y^2\right)}{p^2 y} \frac{d p}{d y}\)

⇒ \(\left(p^3-4 y^2\right)\left(\frac{1}{y}-\frac{2}{p} \frac{d p}{d y}\right)=0 \Rightarrow p^3-4 y^2=0\) …………………….(2)

\(\frac{1}{y}-\frac{2}{p} \frac{d p}{d y}=0\) …………………….(3)

(2) is discarded as it gives a singular solution.

Solving (3): \(\frac{d y}{y}-\frac{2}{p} d p=0 \Rightarrow \int \frac{d y}{y}-2 \int \frac{d p}{p}=-\log c\)

⇒ \(\log y-2 \log p=-\log c \Rightarrow \log y+\log c=\log p^2\)

⇒ \(\log (c y)=\log p^2 \Rightarrow p^2=y c\) ………………………(4)

Eliminating p from (1) and (4): general solution of (1) is

8 \(y^2=p\left(4 x y-p^2\right)=p(4 x y-c y) \Rightarrow 64 y^4=p^2 y^2(4 x-c)^2\)

⇒ \(64 y^4=c y^3(4 x-c)^2 \Rightarrow 64 y=c(4 x-c)^2\)

Problems On First-Order Non-First-Degree Differential Equations

Example. 6. Solve \(2 p x=2 \tan y+p^3 \cos ^2 y\)

Solution.

Given equation is \(2 p x=2 \tan y+p^3 \cos ^2 y\) ……………………..(1)

Since x is of first degree in (1), it can be solved for x:

∴ \(x=\frac{\tan y}{p}+\frac{p^2 \cos ^2 y}{2}\) ……………………..(2)

Differentiating (2) w.r.t.y:

⇒ \(\frac{1}{p}=\frac{1}{p} \sec ^2 y-\frac{1}{p^2} \tan y \frac{d p}{d y}+p \cos ^2 y \frac{d p}{d y}-p^2 \sin y \cos y\)

⇒ \(\left[\frac{1}{p} \tan ^2 y-p^2 \sin y \cos y\right]+\left(p \cos ^2 y-\frac{\tan y}{p^2}\right) \frac{d p}{d y}=0\)

⇒ \(-p \tan y\left(p \cos ^2 y-\frac{\tan y}{\dot{p}^2}\right)+\left(p \cos ^2 y-\frac{\tan y}{p^2}\right) \frac{d p}{d y}=0\)

⇒ \(\left(p \cos ^2 y-\frac{\tan y}{p^2}\right)\left(\frac{d p}{d y}-p \tan y\right)=0\)

∴ \(p \cos ^2 y-\frac{\tan y}{p^2}=0\) ………………………(3)

∴ \(\frac{d p}{d y}-p \tan y=0\) ……………………..(4)

(3) is rejected as it gives a singular solution.

Solving (4): \(\frac{d p}{d y}=p \tan y \Rightarrow \frac{d p}{p}=\tan y d y\)

⇒ \(\int \frac{d p}{p}=\int \tan y d y+\log c \Rightarrow \log p=\log \sec y+\log c\)

⇒ \(\log p=\log (c \sec y) \Rightarrow p=c \sec y\) ………………………(5)

Eliminating p from (1) and (5) \(\Rightarrow 2 c x y=2 \tan y+c^3 \sec ^3 y \cos ^2 y \Rightarrow 2 c x=2 \sin y+c^3\)

∴ The general solution of (1) is \(2 c x=2 \sin y+c^3\).

Differential Equations of First Order But Not of First Degree Differential Equations Solvable For Y:

Let f(x, y, p) = 0 be the giiven differential equation ………………..(1)

If (1) cannot be resolved into two rational and linear factors and (1) is of first degree in y , then it can be solved for y .

(1) can be expressed in the form y = F(x,p) …………………….(2)

Differentiation of (2) w.r.t.x. gives an equation of the form \(p=g\left(x, p, \frac{d p}{d x}\right)\) ……………………(3)

Since (3) is an equation in two variables p and x, it can be solved.
The solution of (1) is ψ(x,y,c) = 0 ……………….(4)

Note 1. If it is not possible to eliminate P from (1) and (4), the general solution of (1) is given in the form (1) Φ(x, p, c) = 0, f(x,y,p) = 0 or \(x=f_1(p, c), y=f_2(p, c)\)

This is regarded as a parametric form of the required solution where p is regarded as a parameter.

2. This method is especially useful for equations in which x is absent.

Differential Equations of First Order But Not of First Degree Solved Problems

Example. 1. Solve \(y=2 p x-p^2\)
Solution.

Given equation is \(y=2 p x-p^2\) ……………………(1)

Differentiating (1) w.r.t.x => \(p=2 p+2 x \frac{d p}{d x}-2 p \frac{d p}{d x}\)

⇒ \(2(p-x) \frac{d p}{d x}=p \Rightarrow p \frac{d x}{d p}+2 x=2 p \Rightarrow \frac{d x}{d p}+\frac{2 x}{p}=2\) …………………….(2)

(2) is a linear equation in x.

Then \(\text { I.F. }=\exp \left[\int \frac{2}{p} d p\right]=\exp (2 \log p)=\exp \left(\log p^2\right)=p^2\)

∴ The general solution of (2) is x \((\mathrm{I} . \mathrm{F})=\int \mathrm{Q}(\mathrm{I} . \mathrm{F}) d p+\mathrm{c}\)     where Q = 2.

⇒ \(x p^2=\int 2 p^2 d p+c=\frac{2 p^3}{3}+c \Rightarrow x=\frac{2}{3} p+\frac{c}{p^2}\) ………………………(3)

It is not possible to eliminate p from (1) and (3)

∴ The general solution of (1) is given by two equations:

x = \((2 p / 3)+\left(c / p^2\right) \text { and } y=2 p\left(\frac{2 p}{3}+\frac{c}{p^2}\right)-p^2=\frac{p^2}{3}+\frac{2 c}{p}\)

Differential Equations Of First Order But Not First Degree Solvable For y 

Example. 2. Solve \(y=x p^2+p\)
Solution.

Given equation is \(y=x p^2+p\) …………………….(1)

Differentiating w.r.t. x => \(p=p^2+2 x p \frac{d p}{d x}+\frac{d p}{d x}\)

⇒ \(\left(p^2-p\right) \frac{d x}{d p}+2 x p+1=0 \Rightarrow \frac{d x}{d p}+\frac{2}{p-1} x=-\frac{1}{p(p-1)}\) ………………………..(2)

(2) is a linear equation in x where \(\mathrm{P}=\frac{2}{p-1}, \quad \mathrm{Q}=\frac{-1}{p(p-1)}\)

⇒ \(\int \mathrm{P} d p=\int \frac{2}{p-1} d p=2 \log (p-1)=\log (p-1)^2\)

∴ \(\text { I.F. }=e^{\log (p-1)^2}\)

∴ The general solution of (2) is \(x(\mathrm{I} . \mathrm{F})=\int \mathrm{Q}(\mathrm{I} . \mathrm{F}) d p+c \Rightarrow x(p-1)^2=\int \frac{-1}{p(p-1)}(p-1)^2 d p+c\)

⇒ \(x(p-1)^2=c-\int \frac{p-1}{p} d p=c-p+\log p\) ……………………..(3)

It is not possible to eliminate 7 from (1) and (3).

∴ The G.S. of (1) is given by \(x=(c-p+\log p)(p-1)^{-2} \text { and } y=x p^2+p\).

Examples Of Differential Equations Solvable For y

Example. 3. Solve \(y+p x=p^2 x^4\)
Solution.

Given equation is \(y+p x=p^2 x^4\) ………………………(1)

But (1) is of first degree in y and hence (1) can be solved for y.

Differentiating (1) w.r.t. x, we get \(p+p+x \frac{d p}{d x}=2 p x^4 \frac{d p}{d x}+4 p^2 x^3 \Rightarrow 2 p+\left(x-2 p x^4\right) \frac{d p}{d x}-4 p^2 x^3=0\)

⇒ \(x\left(1-2 x^3 p\right) \frac{d p}{d x}+2 p\left(1-2 x^3 p\right)=0 \Rightarrow\left(1-2 x^3 p\right)\left(x \frac{d p}{d x}+2 p\right)=0\)

⇒ \(1-2 x^3 p=0\) ………………………..(2)

x\(\frac{d p}{d x}+2 p=0\) ………………………..(3)

(2) is discarded as it gives a singular solution

Solving(3): \(x \frac{d p}{d x}+2 p=0 \Rightarrow \frac{d p}{p}+\frac{2 d x}{x}=0\)

Integrating: \(\int \frac{d p}{p}+2 \int \frac{d x}{x}=\log c \Rightarrow \log p+2 \log x=\log c\)

⇒ \(\log p+\log x^2=\log c \Rightarrow \log p x^2=\log c \Rightarrow p x^2=c \Rightarrow p=c / x^2\)

Eliminating p from (1) and (4), the general solution of (1) is \(y+(c / x)=\left(c^2 / x^4\right) x^4 \Rightarrow y+(c / x)=c^2\)

Note 1. From (2) : \(p=1 /\left(2 x^3\right)\) ………………….(5)

Eliminating p from (1) and (5)

⇒ \(y+\left(1 / 2 x^2\right)=1 /\left(4 / x^2\right) \Rightarrow y+1 /\left(4 x^2\right)=0 \Rightarrow 4 x^2 y+1=0\). which is called a singular solution since it does not contain an arbitrary constant.

2. While finding the G.S. the factor not involving \(\frac{d p}{d x}\) is discarded.

First-Order Equations Not Of First Degree Solvable For y Examples 

Example. 4. Solve \(y=2 x p+x^2 p^4\)
Solution.

Given equation is \(y=2 x p+x^2 p^4\) ………………………..(1)

Differentiating (1) w.r.t. x, we get: \(\frac{d y}{d x}=2 p+2 x \frac{d p}{d x}+2 x p^4+4 x^2 p^3 \frac{d p}{d x}\)

⇒ \(p=2 p+2 x p^4+2 x\left(1+2 x p^3\right) \frac{d p}{d x}\)

⇒ \(p\left(1+2 x p^3\right)+2 x\left(1+2 x p^3\right) \frac{d p}{d x}=0 \Rightarrow\left(1+2 x p^3\right)\left(p+2 x \frac{d p}{d x}\right)=0\)

⇒ \(1+2 x p^3=0\) …………………….(2)

p\(+2 x \frac{d p}{d x}=0\) ……………………(3)

(2) is discarded as it gives a singular solution.

Solving(3): \(p+2 x \frac{d p}{d x}=0 \Rightarrow \frac{2 d p}{p}+\frac{d x}{x}=0\)

Integrating: \(\Rightarrow 2 \int \frac{d p}{p}+\int \frac{d x}{x}=\log c \Rightarrow 2 \log p+\log x=\log c\)

⇒ \(\log p^2 x=\log c \Rightarrow p^2 x=c \Rightarrow p^2=c / x\) …………………….(4)

Eliminating p from (1) and (4) \(\Rightarrow\left(y-x^2 p^4\right)^2=4 x^2 p^2\)

∴ The general solution of (1) is \(\left[y-\left(x^2 c^2 / x^2\right)\right]^2=4 x^2(c / x) \Rightarrow\left(y-c^2\right)^2=4 c x\).

Examples Of Solvable For y Differential Equations 

Example. 5. Solve \(x p^2-2 y p+x=0\)
Solution.

Given equation is \(x p^2-2 y p+x=0\) ………………………..(1)

Differentiating (1) w.r.t. \(x \Rightarrow p^2+2 p x \frac{d p}{d x}-2 p \frac{d y}{d x}-2 y \frac{d p}{d x}+1=0\)

⇒ \(p^2+2(p x-y) \frac{d p}{d x}-2 p^2+1=0 \Rightarrow\left(1-p^2\right)+2(p x-y) \frac{d p}{d x}=0\) ………………………..(2)

Eliminating y from (1) and (2) : \(\left(1-p^2\right)+2\left(p x-\frac{x p^2+x}{2 p}\right) \frac{d p}{d x}=0\)

⇒ \(\left(1-p^2\right)+\frac{2\left(2 p^2 x-x p^2-x\right)}{2 p} \frac{d p}{d x}=0 \Rightarrow p\left(1-p^2\right)+\left(p^2-1\right) x \frac{d p}{d x}=0\)

⇒ \(\left(1-p^2\right)\left(p-x \frac{d p}{d x}\right)=0 \Rightarrow 1-p^2=0\) …………………….(3)

p\(-x \frac{d p}{d x}=0\) ………………………(4)

(3) is discarded as it does not contain \(\) and it gives the singular solution.

Solving (4) : \(p=x \frac{d p}{d x} \Rightarrow \frac{d x}{x}=\frac{d p}{p}\)

Integrating: \(\int \frac{d p}{p}=\int \frac{d x}{x}+\log c \Rightarrow \log p=\log x+\log c \Rightarrow \log p=\log c x \Rightarrow p=c x\) ……………………(5)

Eliminating p from (1) and (5): G.S.. of(1) is \(c^2 x^3-2 c x y+x=0 \Rightarrow c^2 x^2-2 c y+1=0\).

Solved Examples Of Differential Equations Solvable For y 

Example. 6. Solve \(y+x p \log p=(2+3 \log p) p^3\)
Solution.

Given equation is \(y=-x p \log p+(2+3 \log p) p^3\) ………………………..(1)

Solving for y: Differentiating (1) w.r.t. x

⇒ \(p=-p \log p-x(\log p+1) \frac{d p}{d x}+\frac{3}{p} \cdot p^3 \frac{d p}{d x}+(2+3 \log p) 3 p^2 \frac{d p}{d x}\)

⇒ \(p(1+\log p)=-x(\log p+1) \frac{d p}{d x}+9 p^2(1+\log p) \frac{d p}{d x}\)

⇒ \((1+\log p)\left[\left(-x+9 p^2\right) \frac{d p}{d x}-p\right]=0\) ……………………(2)

⇒ \(1+\log p=0\) …………………..(3)

p = \(\left(-x+9 p^2\right) \frac{d p}{d x}\) …………………..(4)

(3) is discarded as it gives the singular solution.

Solving (4): \(p \frac{d x}{d p}+x=9 p^2 \Rightarrow \frac{d x}{d p}+\frac{1}{p} x=9 p\) ……………………(5)

(5) is a linear equation in x.

∴ I.F = \(\exp \left(\int \frac{1}{p} d p\right)=e^{\log p}=p\)

The general solution of(5) is \(x_p=\int 9 p \cdot p d p+c=3 p^2+c\) ……………………..(6)

Eliminating x from (1) and (6): \(y=-\left(3 p^2+\frac{c}{p}\right) p \log p+(2+3 \log p) p^3\)

⇒ \(y=-3 p^3 \log p-c \log p+2 p^3+3 p^3 \log p=2 p^3-c \log p\) …………………….(7)

It is not possible to eliminate p from (6) and (7).

∴ The general solution of (1) is \(x=3 p^2+c p^{-1} \text { and } y=2 p^3-c \log p\)

Example. 7. Solve \(x-y p=a p^2\)
Solution.

Given equation is \(x-y p=a p^2 \Rightarrow y=\frac{x}{p}-a p\) ………………………..(1)

Differentiating (1) w.r.t x => \(\frac{d y}{d x}=p=\frac{1}{p}-\frac{x}{p^2} \frac{d p}{d x}-a \frac{d p}{d x}\)

⇒ \(\left(a p^2+x\right) \frac{d p}{d x}=p\left(1-p^2\right) \Rightarrow p\left(1-p^2\right) \frac{d x}{d p}-x=a p^2\)

⇒ \(\frac{d x}{d p}-\frac{1}{p\left(1-p^2\right)} x=\frac{a p}{1-p^2}\) is a linear equation in x ………………………….(2)

where P = \(-\frac{1}{p\left(1-p^2\right)}\) and \(\mathrm{Q}=\frac{a p}{1-p^2}\)

⇒ \(\int \mathrm{P} d p=\int \frac{1}{p\left(1-p^2\right)} d p=\int\left[\frac{1}{p}+\frac{1}{2(1-p)}-\frac{1}{2(1+p)}\right] d p\)

= \(\log p-\frac{1}{2} \log (1-p)-\frac{1}{2} \log (1+p)=\log \left(\frac{p}{\sqrt{1-p^2}}\right)\)

∴ \(\text { I.F. }=\exp \left[\int \mathrm{P} d p\right]=\exp \left[-\log \frac{p}{\sqrt{1-p^2}}\right]=\exp \left[\log \frac{\sqrt{1-p^2}}{p}\right]=\frac{\sqrt{1-p^2}}{p}\)

The general solution of (2) is \(\frac{x \sqrt{1-p^2}}{p}=\int \frac{a p}{1-p^2} \cdot \frac{\sqrt{1-p^2}}{p} d p+c\)

⇒ \(\frac{x \sqrt{1-p^2}}{p}=a \int \frac{d p}{\sqrt{1-p^2}}+c=a \sin ^{-1} p+c \Rightarrow x=\frac{p}{\sqrt{1-p^2}}\left(a \sin ^{-1} p+c\right)\) …………………….(3)

It is not possible to eliminate p from (1) and (3)

∴ The general solution of (1) is given by the two equations

y = \(x p^2+p \text { and } x=\frac{p}{\sqrt{1-p^2}}\left(a \sin ^{-1} p+c\right)\)

Example 8. Solve : \(x^2+p^2 x=y p\)
Solution.

Given equation is \(x^2+p^2 x=y p\) ……………………….(1)

Solving for y: \(y=p x+\left(x^2 / p\right)\)

Differentiating w.r.t.x : \(\frac{d y}{d x}=p=p+x \frac{d p}{d x}+\frac{p(2 x)-x^2(d p / d x)}{p^2}\)

⇒ \(x \frac{d p}{d x}+\frac{2 p x-x^2(d p / d x)}{p^2}=0 \Rightarrow p^2 x \frac{d p}{d x}+2 p x-x^2 \frac{d p}{d x}=0\)

⇒ \(x\left(p^2-x\right) \frac{d p}{d x}=-2 p x \Rightarrow\left(p^2-x\right) \frac{d p}{d x}=-2 p \Rightarrow\left(x-p^2\right) \frac{d p}{d x}=2 p \Rightarrow 2 p \frac{d x}{d p}-x=-p^2\)

⇒ \(\frac{d x}{d p}-\frac{1}{2 p} x=-\frac{p}{2}\). This is a linear equation in x. ………………………..(2)

Now I.F. = \(e^{\int-(1 / 2 p) d p}=e^{-(1 / 2) \log p}=e^{\log p^{-1 / 2}}=p^{-1 / 2}\)

∴ The general solution of (2) is \(x \cdot p^{-1 / 2}=\int-\frac{p}{2} \cdot p^{-1 / 2} d p+c\)

⇒ \(\frac{x}{\sqrt{p}}=-\frac{1}{2} \int p^{1 / 2} d p+c \Rightarrow \frac{x}{\sqrt{p}}=-\frac{1}{2} \frac{p^{3 / 2}}{3 / 2}+c=-\frac{1}{3} p^{3 / 2}+c\)

⇒ \(x=c \sqrt{p}-(1 / 3) p^2\) …………………………(3)

Substituting x from (3) in (1):

y = \(p\left(c \sqrt{p}-(1 / 3) p^2\right)+\frac{\left[c \sqrt{p}-(1 / 3) p^2\right]^2}{p}\) …………………………(4)

(3) and (4) together is the solution of (1)

Differential Equations of First Order But Not of First Degree Equations Homogeneous In X and Y

When the given equation is homogeneous in x and y it can be written as \(\mathrm{F}\left(\frac{d y}{d x}, \frac{y}{x}\right)=0\).

It is then possible to solve it for \(p=\frac{d y}{d x}\).

Differentiating with respect to x, we get \(p=f(p)+x f^{\prime}(p) \frac{d p}{d x}\) from which we can separate the variables and write \(\frac{d x}{x}=\frac{f^{\prime}(p) d p}{p-f(p)}\) and solve

Differential Equations of First Order But Not of First Degree Solved Problems

Example. 1. Solve the D.E. \(y^2+x y p-x^2 p^2=0\) which is homogeneous in x and y.
Solution.

Given equation is \(y^2+x y p-x^2 p^2=0\) …………………… (1)

Dividing(1)by \(x^2\), we have \(\frac{y^2}{x^2}+\frac{y}{x} p-p^2=0\)

⇒ \(\frac{y}{x}=\frac{-p \pm \sqrt{p^2+4 p^2}}{2}=\frac{1 \pm \sqrt{5}}{2} p \Rightarrow \frac{y}{x}=c \cdot \frac{d y}{d x}\) where c = \(\frac{-1 \pm \sqrt{5}}{2}\)

⇒ \(\frac{d x}{x}=c \cdot \frac{d y}{y}\)

∴ Integrating \(\log x=c \log y+\log c_1\) (where \(c_1\) is a constant)

⇒ \( \log x=\log \left(c_1 y^c\right) \Rightarrow x=c_1 y^c \Rightarrow x-c_1 y^c=0\)

∴ The required general solution of equation (1) is

⇒ \(\left[x-c_1 y^{\left(\frac{-1+\sqrt{5}}{2}\right)}\right]\left[x-c_1 y^{\left(\frac{-1-\sqrt{5}}{2}\right)}\right]=0\)

∴ \(c=\frac{-1 \pm \sqrt{5}}{2}\)

Differential Equations Of First Order But Not Of First Degree Examples

Example. 2. Solve \(8 y^2-4 x y p-x^2 p^2=0\)
Solution.

Given equation is \(8 y^2-4 x y p-x^2 p^2=0\)

Dividing with \(x^2, 8(y / x)^2-4(y / x) p-p^2=0\)

Solving for (y / x), we get \(\frac{y}{x}=\frac{4 p \pm \sqrt{16 p^2+32 p^2}}{2}=(2 \pm 2 \sqrt{3}) p \Rightarrow \frac{y}{x}=(2 \pm 2 \sqrt{3}) \frac{d y}{d x}\)

Separating the variables, \(\frac{d y}{y}=\frac{1}{2 \pm 2 \sqrt{3}} \cdot \frac{d x}{x}\)

Integrating on both sides,

log y \(=\frac{1}{2(1+\sqrt{3})} \log x+\log c \text { and } \log y=\frac{1}{2(1-\sqrt{3})} \log x+\log c\)

⇒ \(y=c x^{1 / 2(1+\sqrt{3})} \text { and } y=c x^{1 / 2(1-\sqrt{3})}\)

C.S. is \(\left[y-c x^{1 / 2(1+\sqrt{3})}\right]\left[y-c x^{1 / 2(1-\sqrt{3})}\right]=0\)

Solved Problems On Homogeneous Equations In x And y

Example. 3. Solve \(y=y p^2+2 p x\)
Solution.

Given equation is \(y=y p^2+2 p x \text { i.e. } y\left(1-p^2\right)=2 p x . \quad y=\frac{2 p x}{1-p^2}\) ………………………(1)

Differentiating w.r.t. x, \(\frac{2 d p}{p\left(1-p^2\right)}+\frac{d x}{x}=0\)

=> Using partial fractions, \(\left(\frac{2}{p}+\frac{1}{1-p}-\frac{1}{1+p}\right) d p+\frac{d x}{x}=0\)

Integrating, \(x=\frac{c\left(1-p^2\right)}{p^2}\) …………………………..(2)

Eliminating p between (1) and (2) we get, \(y^2=4 x c+4 c^2\) which is the required solution.

Differential Equations of First Order But Not of First Degree Clairaut’s Equation

The differential equation of the form y = xp + f (p) is called Clairaut’s equation.

This equation is solved by considering it as y = f(x,p), solvable for the y type.

Solution of Clairaut’s Equation :

Let the given equation be y = xp + f (p) ……………………..(1)

Differentiating (1) w.r.t. x: \(\Rightarrow \frac{d y}{d x}=x \frac{d p}{d x}+p+f^{\prime}(p) \frac{d p}{d x}\)

⇒ \(p=\left[x+f^{\prime}(p)\right] \frac{d p}{d x}+p \Rightarrow\left[x+f^{\prime}(p)\right] \frac{d p}{d x}=0\)

⇒ \(\frac{d p}{d x}=0\) ……………………(2)

x\(+f^{\prime}(p)=0\) …………………….(3)

Solving (2): \(\frac{d p}{d x}=0 \Rightarrow p=c\) where c is a real number. ………………………..(4)

Eliminating p from (1) and (4) y = cx + f(c).

∴ The general solution of Clairaut’s equation (1) is y = cx + f(c).

Note. Solving the equation (3): \(x+f^{\prime}(p)=0\) ……………………….(5)

By eliminating p from (1) and (5) we get the solution Φ (x,y) = 0.

As this solution does not contain any arbitrary constant this is not the general solution. This solution is called the singular solution of (1).

Differential Equations of First Order But Not of First Degree Working Rule for Solving Clairaut’s Equation :

1. The given equation can be written in the form y = xp + f(p) ………………..(a)

2. In order to find the solution of (a), replace p by c where c is any real number.

3. Putting p = c in (a), we get y = xc + f(c).

∴ The general solution of (a) is y = xc + f{c).

Differential Equations of First Order But Not of First Degree Solved Problems

Example. 1. Solve \((y-x p)(p-1)=p\)
Solution.

Given equation is \((y-x p)(p-1)=p\) …………………….(1)

⇒ \(y(p-1)-x p(p-1)=p \Rightarrow y(p-1)=x p(p-1)+p\)

⇒ \(y=x p+\frac{p}{p-1}\) which is in Clairaut’s form.

The genera] solution of (1) is \(y=x c+\frac{c}{c-1}\) where c is any real number

Example. 2. Solve \(p=\tan (x p-y)\)
Solution:

Given equation is \(p=\tan (x p-y)\)

⇒ x p-y=\text{Tan}^{-1} p \Rightarrow y=x p-\text{Tan}^{-1} p[/latex] which is in Clairaut’s form.

∴ The general solution of (1) is \(y=x c-\text{Tan}^{-1} c\) where c is any real number.

Problems On First-Order But Not First-Degree Equations Homogeneous In x And y

Example. 3. Solve \(y^2-2 p x y+p^2\left(x^2-1\right)=m^2\)
Solution.

Given equation is \(y^2-2 p x y+p^2\left(x^2-1\right)=m^2\) ……………………….(1)

⇒ \(y^2-2 p x y+p^2 x^2=p^2+m^2 \Rightarrow(y-p x)^2=p^2+m^2\)

⇒ \(y-p x=\sqrt{p^2+m^2} \Rightarrow y=x p+\sqrt{p^2+m^2}\) which is in Clairaut s form.

∴ The general solution of (1) is \(y=x c+\sqrt{c^2+m^2}\)

Applications Of Clairaut’s Equation In Differential Equations.

Example. 4. Solve \(\sin p x \cos y=\cos p x \sin y+p\)
Solution.

Given equation is \(\sin p x \cos y-\cos p x \sin y=p\) …………………..(1)

⇒ \(\sin (p x-y)=p \Rightarrow p x-y=\sin ^{-1} p \Rightarrow y=p x-\sin ^{-1} p\) which is in Clairaut’s form.

∴ The general solution of (1) is \(y=c x-\sin ^{-1} c\), c being an arbitrary real number.

Solved Problems On Homogeneous Equations Of First Order Not First Degree

Example. 5. Solve \(p=\log (p x-y)\)
Solution.

Given equation is \(p=\log (p x-y)\) ……………….. (1)

⇒ \(p x-y=e^p \Rightarrow y=p x-e^p\) which is in Clairaut’s form.

∴ The general solution of (1) is \(y=c x-e^c\) where c is any real number.

Differential Equations Introduction Solved Problems

Reducible To Homogeneous Differential Equation Examples With Solutions

Example. 1: Solve : \((x+y-1) \frac{d y}{d x}=x-y+2\)

Solution.

Given equation is \(\frac{d y}{d x}=\frac{x-y+2}{x+y-1}\) ………………..(1)

where \(a_1=1, b_1=1, a_2=1, b_2=-1 \Rightarrow a_1 b_2-a_2 b_1=2 \neq 0\)

Put \(x=\mathrm{X}+h \text { and } y=\mathrm{Y}+k \text { in (1) } \Rightarrow \frac{d y}{d x}=\frac{d \mathrm{Y}}{d \mathrm{X}}\) ……………………….(2)

(1) and (2) => \(\frac{d \mathrm{Y}}{d \mathrm{X}}=\frac{\mathrm{X}-\mathrm{Y}+(h-k+2)}{\mathrm{X}+\mathrm{Y}+(h+k-1)}\)

Choose h and k such that h-k + 2 = 0 ……………….(4)
and h + k – 1 = 0 …………………..(5)

Solving (4) and (5): \(h=-\frac{1}{2}, k=\frac{3}{2}\)

Now (3), (4), (5) => \(\frac{d \mathrm{Y}}{d \mathrm{X}}=\frac{\mathrm{X}-\mathrm{Y}}{\mathrm{X}+\mathrm{Y}}\) ………………….(6)

∵ f(kX, kY) = f(X, Y), (6) is homogeneous equation.

Putting \(\mathrm{Y}=v \mathrm{X} \Rightarrow \frac{d \mathrm{Y}}{d \mathrm{X}}=v+\mathrm{X} \frac{d v}{d \mathrm{X}}\) in (6), we get \(v+\mathrm{X} \frac{d v}{d \mathrm{X}}=\frac{1-v}{1+v}\)

⇒ \(\mathrm{X} \frac{d v}{d \mathrm{X}}=\frac{1-v}{1+v}-v=\frac{-v^2-2 v+1}{1+v}\)

Separating the variable: \(\frac{1+v}{v^2+2 v-1} d v=-\frac{d \mathrm{X}}{\mathrm{X}} \Rightarrow \frac{1}{2} \int \frac{2 v+2}{v^2+2 v-1} d v=-\int \frac{d \mathrm{X}}{\mathrm{X}}+\frac{1}{2} \log c\)

⇒ \(\frac{1}{2} \log \left(v^2+2 v-1\right)=-\log \mathrm{X}+\frac{1}{2} \log c \Rightarrow \log \left(\frac{\mathrm{Y}^2}{\mathrm{X}^2}+\frac{2 \mathrm{Y}}{\mathrm{X}}-1\right)+2 \log \mathrm{X}=\log c\)

(∵ \(v=\frac{\mathrm{Y}}{\mathrm{X}}\))

⇒ \(\log \frac{\mathrm{Y}^2+2 \mathrm{XY}-\mathrm{X}^2}{\mathrm{X}^2}+\log \mathrm{X}^2=\log c \Rightarrow \log \left(\frac{\left(\mathrm{Y}^2+2 \mathrm{XY}-\mathrm{X}^2\right)}{\mathrm{X}^2} \cdot \mathrm{X}^2\right)=\log c\)

⇒ \(\mathrm{Y}^2+2 \mathrm{XY}-\mathrm{X}^2=c\)

Now substitute: \(X=x+\frac{1}{2}, Y=y-\frac{3}{2}\)

∴ The general solution of (1)[ is \(\left(y-\frac{3}{2}\right)^2+2\left(x+\frac{1}{2}\right)\left(y-\frac{3}{2}\right)-\left(x+\frac{1}{2}\right)^2=c\)

Aliter: The given equation can be written as

(x+2) d x-y d x=(y-1) d y+x d y

(x+2) d x=(y d x+x d y)+(y-1) d y[/latex]

⇒ \(\int(x+2) d x=\int d(x y)+\int(y-1) d y \Rightarrow\left(x^2 / 2\right)+2 x=x y+\left(y^2 / 2\right)-y+(c / 2)\)

∴ The solution is \(x^2-y^2-2 x y+4 x+2 y=c\)

Step-By-Step Examples Of Reducible To Homogeneous Differential Equations

Example. 2: Solve : \((4 x+3 y+1) d x+(3 x+2 y+1) d y=0\)

Solution.

Given equation is \(\frac{d y}{d x}=\frac{-(4 x+3 y+1)}{(3 x+2 y+1)}\) ……………(1)

where \(a_1=-4, b_1=-3, c_1=-1, a_2=3, b_2=2, c_2=1 \Rightarrow a_1 b_2-a_2 b_1 \neq 0\)

to solve (1): put \(x=\mathrm{X}+h, y=\mathrm{Y}+k \Rightarrow \frac{d y}{d x}=\frac{d \mathrm{Y}}{d \mathrm{X}}\) …………………(2)

(1) and (2) => \(\frac{d \mathrm{Y}}{d \mathrm{X}}=-\frac{4(\mathrm{X}+h)+3(\mathrm{Y}+k)+1}{3(\mathrm{X}+h)+2(\mathrm{Y}+k)+1}=\frac{-(4 \mathrm{X}+3 \mathrm{Y})-(4 h+3 k+1)}{(3 \mathrm{X}+2 \mathrm{Y})+3(h+2 k+1)}\) ……………………..(3)

Choose h and 4 such that 4h + 3k + 1 = 0 ………………………..(4)

and 3h + 2k + 1 = 0 …………………(5)

Solving (4) and (5) h = -1, k = 1.

Then (3), (4), (5) \(\Rightarrow \frac{d Y}{d X}=-\frac{4 X+3 Y}{3 X+2 Y}\) …………………..(6)

∵ f(hx, ky) = f(X, Y),, (6) is homogeneous equation.

Putting \(\mathrm{Y}=v \mathrm{X} \Rightarrow \frac{d \mathrm{Y}}{d \mathrm{X}}=v+\mathrm{X} \frac{d v}{d \mathrm{X}}\) in (6), we get

v\(+\mathrm{X} \frac{d v}{d \mathrm{X}}=-\frac{4+3 v}{3+2 v} \Rightarrow \mathrm{X} \frac{d v}{d \mathrm{X}}=\frac{-4-3 v}{3+2 v}-v=\frac{-2\left(v^2+3 v+2\right)}{3+2 v}\)

Separating the variables : \(\frac{2 v+3}{v^2+3 v+2} d v=-2 \frac{d \mathrm{X}}{\mathrm{X}}\)

Integrating: \(\int \frac{2 v+3}{v^2+3 v+2} d v=-2 \int \frac{d \mathrm{X}}{\mathrm{X}}+\log c \Rightarrow \log \left(v^2+3 v+2\right)=-2 \log \mathrm{X}+\log c\)

⇒ \(\log \left(v^2+3 v+2\right)+\log \mathrm{X}^2=\log c \Rightarrow \log \left(v^2+3 v+2\right) \mathrm{X}^2=\log c\)

(∵ \(V=\frac{\mathrm{Y}}{\mathrm{X}}\))

⇒ \(\left(v^2+3 v+2\right) \mathrm{X}^2=c \Rightarrow\left(\frac{\mathrm{Y}^2}{\mathrm{X}^2}+3 \frac{\mathrm{Y}}{\mathrm{X}}+2\right) \mathrm{X}^2=c\)

⇒ \(\mathrm{Y}^2+3 \mathrm{XY}+2 \mathrm{X}^2=c\)

Substituting X = x+1, Y = y -1, in this

The general solution of (1) is \((y-1)^2+3(x+1)(y-1)+2(x+1)^2=c\)

Aliter: Given equation can be written as –\((4 x+1) d x=3(y d x+x d y)+(2 y+1) d y \Rightarrow(-4 x-1)^{\prime} d x=3 d(x y)+(2 y+1) d y\)

Integrating : \(-2 x^2-x=3 x y+y^2+y\)

∴ G. S. is \(2 x^2+3 x y+y^2+x+y=c\)

Reducible To Homogeneous Differential Equation Solved Examples Tutorial

Example. 3 : Solve : \(\frac{d y}{d x}=\frac{(x+y-1)^2}{4(x-2)^2}\)

Solution.

Given equation is \(\frac{d y}{d x}=\left(\frac{x+y-1}{2 x-4}\right)^2\) …………………….(1)

where \(a_1=1, b_1=1, a_2=2, b_2=0 \Rightarrow a_1 b_2-a_2 b_1=0-2=-2 \neq 0\)

to solve (1): put \(x =\mathrm{X}+h, y=\mathrm{Y}+k \Rightarrow \frac{d y}{d x}=\frac{d \mathrm{Y}}{d \mathrm{X}}\) ……………………(2)

(1) and (2) => \(\frac{d \mathrm{Y}}{d \mathrm{X}}=\frac{(\mathrm{X}+h+\mathrm{Y}+k-1)^2}{4(\mathrm{X}+h-2)^2}=\frac{[(\mathrm{X}+\mathrm{Y})+(h+k-1)]^2}{4[\mathrm{X}+(h-2)]^2}\) …………………….(3)

Choose, h and k such that h + k – 1 = 0 ……………………….(4)

and h – 2 = 0 ………………………..(5)

Solving (4) and (5): h = 2, k = -1

∴ \(\mathrm{X}=x-2, \mathrm{Y}=y-(-1)=y+1\)

(3), (4), (p) => \(\) …………………(6)

∵ f(kX, kY) = f(X, Y), (6) is homogeneous equation

Putting \(\mathrm{Y}=v \mathrm{X} \Rightarrow \frac{d \mathrm{Y}}{d \mathrm{X}}=v+\mathrm{X} \frac{d v}{d \mathrm{X}}\) in (6), we get

v\(+x \frac{d v}{d \mathrm{X}}=\frac{(\mathrm{X}+v \mathrm{X})^2}{4 \mathrm{X}^2}=\frac{(1+v)^2}{4} \Rightarrow \mathrm{X} \frac{d v}{d \mathrm{X}}=\frac{(1+v)^2}{4}-v=\frac{(1+v)^2-4 v}{4}=\frac{(1-v)^2}{4}\)

Separating the variables : \(\frac{4}{(1-v)^2} d v=\frac{d \mathrm{X}}{\mathrm{X}} \Rightarrow 4 \int \frac{d v}{(1-v)^2}=\int \frac{d \mathrm{X}}{\mathrm{X}}+c\)

⇒ \(4 \cdot \frac{-1}{1-v} \cdot \frac{1}{-1}=\log \mathrm{X}+c \Rightarrow \frac{4}{1-(\mathrm{Y} / \mathrm{X})}=\log \mathrm{X}+c\)

(∵ \(v=\frac{\mathrm{Y}}{\mathrm{X}}\))

⇒ \(\frac{4 X}{X-Y}=\log X+c\) ……………………(7)

Substituting X = x-2, Y = y +1, in (7)

∴ The general solution of (1) is \(\frac{4(x-2)}{x-y-3}=\log (x-2)+c\)

Reducible To Homogeneous Differential Equations Examples Explained

Example 4: Solve \((4 x+6 y+5) \frac{d y}{d x}=3 y+2 x+4\)

Solution: 

Given Equation is \(\frac{d y}{d x}=\frac{2 x+3 y+4}{4 x+6 y+5}\) ………………………(1)

Here \(a_1=2, b_1=3, a_2=4, b_2=6 \Rightarrow a_1 b_2-a_2 b_1=12-12=0\)

Also \(a_2=2 a_1, b_2=2 b_1 \text { and } c_2 \neq 2 c_1\)

Hence Put \(2 x+3 y=u \Rightarrow 2+3 \frac{d y}{d x}=\frac{d u}{d x} \Rightarrow \frac{d y}{d x}=\frac{1}{3}\left(\frac{d u}{d x}-2\right)\) ………………………(2)

(1) and (2) => \(\frac{1}{3}\left(\frac{d u}{d x}-2\right)=\frac{u+4}{2 u+5} \Rightarrow \frac{d u}{d x}=\frac{3 u+12}{2 u+5}+2 \Rightarrow \frac{d u}{d x}=\frac{7 u+22}{2 u+5}\) ………………………..(3)

Separating the variables : \(\frac{2 u+5}{7 u+22} d u=d x \Rightarrow \int \frac{2 u+5}{7 u+22} d u=\int d x+c\)

⇒ \(\int\left(\frac{2}{7}-\frac{9}{7} \cdot \frac{1}{7 u+22}\right) d u=x+c \Rightarrow \frac{2}{7} u-\frac{9}{7} \cdot \frac{1}{7} \log (7 u+22)=x+c\)

∴ General solution of (3) is \(14 u-9 \log (7 u+22)=49 x+49 c\)

Hence the G. S. of (1) is \(14(2 x+3 y)-9 \log |(14 x+21 y+22)|=49 x+c_1\) [from (2)]

Common Mistakes In Solving Reducible To Homogeneous Differential Equations

Example.5 : Solve \((2 x+2 y+1) \frac{d y}{d x}=x+y+3\)

Solution.

Given equation is \(\frac{d y}{d x}=\frac{x+y+3}{2 x+2 y+1}\) …………………………..(1)

where \(a_1=1, b_1=1, c_1=3, a_2=2, b_2=2, c_2=1 \text { and } a_1 b_2-a_2 b_1=2-2=0\)

Also \(a_2=2 a_1, b_2=2 b_1 \text { and } c_2 \neq 2 c_1\)

Let \(x+y=u \Rightarrow 1+\frac{d y}{d x}=\frac{d u}{d x} \Rightarrow \frac{d y}{d x}=\frac{d u}{d x}-1\) ………………………….(2)

(1) and (2) \(\Rightarrow \frac{d u}{d x}-1=\frac{u+3}{2 u+1} \Rightarrow \frac{d u}{d x}=\frac{u+3}{2 u+1}+1=\frac{3 u+4}{2 u+1}\) ……………………………(3)

Separating the variables : \(\frac{2 u+1}{3 u+4} d u=d x\)

⇒ \(\int\left[\frac{2}{3}-\frac{5}{3(3 u+4)}\right] d u=\int d x+c \Rightarrow \frac{2 u}{3}-\frac{5}{9} \log (3 u+4)=x+c\)

G.S. of (3) is \(6 u-5 \log (3 u+4)=9 x+9 c\)

∴ The general solution of (1) is \(6(x+y)-5 \log (3 x+3 y+4)=9 x+c_1\)

Differential Equations Introduction Solved Problems

Example. 1: Solve : \(x^2 y d x-\left(x^3+y^3\right) d y=0\)

Solution:

Given: \(x^2 y d x=\left(x^3+y^3\right) d y \Rightarrow \frac{d y}{d x}=\frac{x^2 y}{x^3+y^3}\) …………………..(1)

Since \(f(k x, k y)=f(x, y)\), (1) is homogeneous equation.

Put \(y / x=v \text { in (1) } \Rightarrow y=v x \Rightarrow \frac{d y}{d x}=v+x \frac{d v}{d x}\) ……………………(2)

(1) and (2) => \(v+x \frac{d v}{d x}=\frac{v}{1+v^3} \Rightarrow x \frac{d v}{d x}=\frac{v}{1+\dot{v}^3}-v=\frac{-v^4}{1+v^3}\)

Separating the variables: \(\frac{1+v^3}{v^4} d v=-\frac{d x}{x}\)

Integrating: \(\int \frac{1+v^3}{v^4} d v=-\int \frac{d x}{x}+c \Rightarrow \int\left(v^{-4}+\frac{1}{v}\right) d v=-\int \frac{d x}{x}+c\)

⇒ \(\frac{v^{-3}}{-3}+\log v=-\log x+c \Rightarrow \log v-\frac{1}{3 v^3}+\log x=c\) …………………….(3)

Putting v = y/x in (3), the general solution is \(\log (y / x)-\left(x^3 / 3 y^3\right)+\log x=c\)

Solved Problems On First Order And First-Degree Homogeneous Differential Equations

Example. 2: Solve : \((x-y \log y+y \log x) d x+x(\log y-\log x) d y=0\)

Solution:

The given equation is

x\(\log \left(\frac{y}{x}\right) d y+\left[x-y \log \left(\frac{y}{x}\right)\right] d x=0 \Rightarrow \frac{d y}{d x}=\frac{y \log (y / x)-x}{x \log (y / x)}=\frac{(y / x) \log (y / x)-1}{\log (y / x)}\) ………………(1)

Clearly \(\frac{d y}{d x}=f\left(\frac{y}{x}\right)\) => Given equation.is homogeneous.

Put y/x = v in (1) \(y=v x \Rightarrow \frac{d y}{d x}=v+x \frac{d v}{d x}\) …………………..(2)

(1) and (2) \(\Rightarrow v+x \frac{d v}{d x}=\frac{v \log v-1}{\log v} \Rightarrow x \frac{d v}{d x}=-\frac{1}{\log v}\)

Separating the variables: \((\log v) d v=-\frac{d x}{x}\)

⇒ \(\int \log v \cdot d v=\int-\frac{d x}{x}+c \Rightarrow v \log v-\int v \cdot \frac{1}{v} d v=-\log x+c\)

⇒ \(v \log v-v=-\log x+c\) …………………….(3)

Put v = y/x in (3)

∴ The general solution of (1) is (y/x) log(y/x)-(y/x) = -log x + c

=> y (log y – log x) – y = -x log x + cx => y log y + (x – y) log x = y + cx

Example. 3. Solve : \(x \frac{d y}{d x}=y+x e^{y / x}\)

Solution.

Given equation is \(x \frac{d y}{d x}=y+x e^{y / x} \Rightarrow \frac{d y}{d x}=\frac{y}{x}+e^{y / x}\) …………………(1)

∵ \(f(k x, k y)=f(x, y)\), (1) is a homogeneous equation.

Put \(y=v x \text { in }(1) \Rightarrow \frac{d y}{d x}=v+x \frac{d v}{d x}\) ……………………..(2)

Then (1) and (2) \(\Rightarrow v+x \frac{d v}{d x}=v+e^v \Rightarrow x \frac{d v}{d x}=e^v\)

Separating the variables: \(\frac{d v}{e^v}=\frac{d x}{x} \Rightarrow e^{-v} d v=\frac{d x}{x}\)

Integrating : \(\int e^{-v} d v=\int \frac{d x}{x}+c \Rightarrow-e^{-v}=\log |x|+c\) …………………..(3)

Putting v = y / x in (3), the general solution of (1) is \(e^{-(y / x)}+\log |x|+c=0\)

Step-By-Step Guide To Homogeneous Differential Equations First Order

Example. 4. Solve : \(x d y-y d x=\left(\sqrt{x^2+y^2}\right) d x\)

Solution.

Given equation is \(x d y-y d x=\left(\sqrt{x^2+y^2}\right) d x\)

⇒ \(x \frac{d y}{d x}=y+\sqrt{x^2+y^2} \Rightarrow \frac{d y}{d x}=\frac{y+\sqrt{x^2+y^2}}{x}\) …………………(1)

∵ \(f(k x, k y)=f(x, y)\), (1) is a homogeneous equation.

Put y/x = v in (1) y = vx in (1) \(\Rightarrow \frac{d y}{d x}=v+x \frac{d v}{d x}\) …………………….(2)

(1) and (2) ⇒ \(v+x \frac{d v}{d x}=v+\sqrt{1+v^2} \Rightarrow \frac{x d v}{d x}=\sqrt{1+v^2}\)

Separating the variables: \(\frac{d v}{\sqrt{1+v^2}}=\frac{d x}{x}\)

Integrating: \(\int \frac{d v}{\sqrt{1+v^2}}=\int \frac{d x}{x}+\log c \Rightarrow \log \left|v+\sqrt{1+v^2}\right|=\log x+\log c\)

⇒ \(\log \left|v+\sqrt{1+v^2}\right|=\log c x \Rightarrow v+\sqrt{1+v^2}=c x\)

Putting v = y/x in (3), the general solution of (1) is \(y+\sqrt{x^2+y^2}=c x^2\)

Example. 5: Solve : [x – y arctan(y / x)] Jx + [x arctan(y / x)] dy = 0

Solution.

Given equation

[x – y arctan(y / x)] Jx + [x arctan(y / x)] dy = 0

The given equation is rearranged as follows: \(\frac{d y}{d x}=\frac{y \text{Tan}^{-1}(y / x)-x}{x \text{Tan}^{-1}(y / x)}\)

= \(\frac{(y / x) \text{Tan}^{-1}(y / x)-1}{\text{Tan}^{-1}(y / x)}\)…….(1)

because f(k x, k y)=f(x, y),(1) is homogeneous equation.

Put y=v x in (1) ⇒ \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)……(2)

(1) and (2) ⇒ \(v+x \frac{d v}{d x}=\frac{v \text{Tan}^{-1} v-1}{\text{Tan}^{-1} \cdot v} \Rightarrow x \frac{d v}{d x}\)

= \(\frac{v \text{Tan}^{-1} v-1}{\text{Tan}^{-1} v}-v \Rightarrow x \frac{d v}{d x}=\frac{-1}{\text{Tan}^{-1} v}\)

Separating the variables: \(\text{Tan}^{-1} v d v=-\frac{d x}{x}\).

Integrating: \(\int \text{Tan}^{-1} v d v=-\int \frac{d x}{x}+c\).

⇒ \(v \text{Tan}^{-1} v-\int \frac{v}{1+v^2} d v=-\log |x|+c\)

⇒ \(v \text{Tan}^{-1} v-\frac{1}{2} \log \left(1+v^2\right)=-\log |x|+c \ldots\)……(3)

Putting \(v=y / x\) in (3), the general solution of (1) is \(\frac{y}{x} \text{Tan}^{-1}\left(\frac{y}{x}\right)-\frac{1}{2} \log \left(1+\frac{y^2}{x^2}\right)=-\log |x|+c\)

Working Rules Of First Order Homogeneous Differential Equations With Examples

Example. 6. Solve \((y d x+x d y) x \cos (y / x)=(x d y-y d x) y \sin (y / x)\)

Solution.

Given : \(\left[x y \cos (y / x)+y^2 \sin (y / x)\right] d x=\left[x y \sin (y / x)-x^2 \cos (y / x)\right] d y\)

⇒ \(\frac{d y}{d x}=\frac{x y \cos (y / x)+y^2 \sin (y / x)}{x y \sin (y / x)-x^2 \cos (y / x)}\) ………………..(1)

f(k x, k y)=f(x, y), (1) is a homogeneous equation.

Put \(y / x=v \Rightarrow y=v x \text { in }(1) \Rightarrow \frac{d y}{d x}=v+x \frac{d v}{d x}\) ……………………..(2)

(1) and (2) \(\Rightarrow v+x \frac{d v}{d x}=\frac{v \cos v+v^2 \sin v}{v \sin v-\cos v} \Rightarrow x \frac{d v}{d x}=\frac{v \cos v+v^2 \sin v}{v \sin v-\cos v}-v=\frac{2 v \cdot \cos v}{v \sin v-\cos v}\)

Separating the variables : \(2 \frac{d x}{x}=\frac{v \sin v-\cos v}{v \cos v} d v\)

Integrating : \(2 \int \frac{d x}{x}=\int \frac{v \sin v-\cos v}{v \cos v} d v+\log c\)

⇒ \(2 \log |x|=\int \tan v d v-\int \frac{1}{v} d v+\log c \Rightarrow 2 \log |x|=-\log |\cos v|-\log |v|+\log c\)

⇒ \(\log x^2=\log \left|\frac{c}{v \cos v}\right| \Rightarrow x^2 v \cos v=c \Rightarrow x^2 \cdot \frac{y}{x} \cos \frac{y}{x}=c\)

∴ The general solution of (1) is xy cos(y/x) = c

Example. 7 : Solve: \(\left(1+e^{x / y}\right) d x+e^{x / y}[1-(x / y)] d y=0\)

Solution.

Given equation is \(\left(1+e^{x / y}\right) d x+e^{x / y}[1-(x / y)] d y=0\)

Here we shall not be able to write the given equation in the form \(\frac{d y}{d x}=f\left(\frac{y}{x}\right)\).

But we can express it in the form \(\frac{d x}{d y}=f\left(\frac{x}{y}\right)\)

∴ Given equation is \(\frac{d x}{d y}=\frac{e^{x / y}[(x / y)-1]}{1+e^{x / y}}=f\left(\frac{x}{y}\right)\) ……………………(1)

f(kx, ky) = f(x, y), (1) is a homogeneous equation.

Put x/y = v where v is a function of y => x = vy => \(\frac{d x}{d y}=v+y \frac{d v}{d y}\) …………………..(2)

(1) and (2) => \(v+y \frac{d v}{d y}=\frac{e^v(v-1)}{1+e^v} \Rightarrow y \frac{d v}{d y}=\frac{e^v(v-1)}{1+e^v}-v=-\frac{e^v+v}{1+e^v}\)

Separating the variables: \(\frac{d y}{y}=-\frac{1+e^v}{v+e^v} d v\)

Integrating: \(\int \frac{d y}{y}=-\int \frac{1+e^v}{v+e^v} d v+\log c \Rightarrow \log |y|=-\log \left|v+e^v\right|+\log c\)

⇒ \(\log y+\log \left(v+e^v\right)=\log c \Rightarrow \log y\left(v+e^v\right)=\log c \Rightarrow y\left(v+e^v\right)=c\) …………………….(3)

Putting v = x/y in (3), the general solution of (1) is \(x+y e^{x / y}=c\)

Introduction To First Degree Homogeneous Differential Equations Tutorial

Example. 8: Solve \(x^2 \frac{d y}{d x}=\frac{y(x+y)}{2}\)

Solution:

Given equation is \(\frac{d y}{d x}=\frac{x y+y^2}{2 x^2}\) ……………………..(1)

∴ f(kx>ty) = f(x,y), (1) is a homogeneous equation.

Put y = vx in(1) \(\Rightarrow \frac{d y}{d x}=v+x \frac{d v}{d x}\) ……………………(2)

(1),(2) ⇒ \(v+x \frac{d v}{d x}=\frac{v x^2+v^2 x^2}{2 x^2}=\frac{v^2+v}{2}\)

⇒ \(x \frac{d v}{d x}=\frac{v^2+v}{2}-v=\frac{v^2+v-2 v}{2}=\frac{v^2-v}{2}\)

Separating variables: \(2 \frac{d v}{v(v-1)}=\frac{d x}{x}\)

⇒ \(2 \int \frac{d v}{v(v-1)}=\int \frac{d x}{x}+\log c\)

2\( \int\left(\frac{1}{v-1}-\frac{1}{v}\right) d v=\log x+\log c \Rightarrow 2[\log (v-1)-\log v]=\log c x\)

⇒ \(\log \left(\frac{v-1}{v}\right)^2=\log (c x) \Rightarrow\left(\frac{v-1}{v}\right)^2=c x\)

Putting \(v=\frac{y}{x}\), the general solution of (1) is \(\left[\frac{(y / x)-1}{y / x}\right]^2=c x \Rightarrow(y-x)^2=c x y^2\)

Homogeneous Differential Equations Working Rules Step By Step

Example. 9: Find the equation of the curve, which passes through the point (1, π/4) whose differential equation is \(\left[x \cos ^2(y / x)-y\right] d x+x d y=0(x>0, y>0)\)

Solution.

Given \(\left[x \cos ^2(y / x)-y\right] d x+x d y=0\)

⇒ \(\frac{d y}{d x}=\frac{y-x \cos ^2(y / x)}{x}=\frac{y}{x}-\cos ^2\left(\frac{y}{x}\right)\) ……………………..(1)

Clearly, \(\frac{d y}{d x}=\mathrm{F}\left(\frac{y}{x}\right)\) => Given equation is homogeneous.

Put v = y/x in (1) => \(y=v x \Rightarrow \frac{d y}{d x}=v+x \frac{d v}{d x}\) …………………..(2)

(1) and (2) \(\Rightarrow v+x \frac{d v}{d x}=v-\cos ^2 v \Rightarrow x \frac{d v}{d x}=-\cos ^2 v\).

Separating the variables: \(\sec ^2 v d v=-\frac{d x}{x}\)

⇒ \(\int \sec ^2 v d v=-\int \frac{d x}{x}+c \Rightarrow \tan v=-\log |x|+c\) ………………..(3)

Putting v = y/x in (3), the G. S. is tan (y/x) = —log 1 x | +c …………………………..(4)

Putting x = 1 and y = π/4 in (4):

tan (π / 4) = – log 1 + c tan (π / 4) = – log 1 + c => c = 1

The equation of the curve is tan(y/x) + log | x | = 1

Differential Equations of First Order But Not of First Degree Equations Reducible To Clairaut’s Form

Some differential equations can be transformed to Clairaut’s form by suitable substitution.

For example : \(y^2=p x y+f\left(\frac{p y}{x}\right)\) ………………….(1)

Put \(x^2=X\) and \(y^2=\mathrm{Y} \Rightarrow 2 x d x=d \mathrm{X}\) and \(2 y d y=d \mathbf{Y}\)

Let \(\mathrm{P}=\frac{d \mathrm{Y}}{d \mathrm{X}}=\frac{y}{x} \frac{d y}{d x}=\frac{y}{x} p\) …………………….(2)

(1) and (2) \(\Rightarrow \mathrm{Y}=x y\left(\frac{x \mathrm{P}}{y}\right)+f(\mathrm{P})=x^2 \mathrm{P}+f(\mathrm{P})\) …………………..(3)

=> Y = PX+f(P) which is Clairaut’s differential equation.

∴ The general solution of (3) is Y = cX+f(c) where c is any real number.

⇒ \(y^2=c x^2+f(c)\) is the general solution of (1).

Differential Equations of First Order But Not of First Degree Solved Problems

Example. 1. Solve \(x^2(y-p x)=p^2 y\)

Solution.

Given equation is \(x^2(y-p x)=y p^2\) ……………………..(1)

Put \(x^2=\mathrm{X} \text { and } y^2=\mathrm{Y} \Rightarrow 2 x d x=d \mathrm{X} \text { and } 2 y d y=d \mathrm{Y}\)

⇒ \(\mathrm{P}=\frac{d \mathrm{y}}{d \mathrm{x}}=\frac{2 y d y}{2 x d x}=\frac{y}{x} \frac{d y}{d x}=\frac{y}{x} p \Rightarrow p=\frac{\mathrm{P} x}{y}\) ……………………….(2)

(1) and (2) \(\Rightarrow \mathrm{X}\left(y-x \cdot \frac{\mathrm{P} x}{y}\right)=y \cdot \frac{\mathrm{P}^2 x^2}{y^2} \Rightarrow \mathrm{X}\left(y^2-x^2 \mathrm{P}\right)=x^2 \mathrm{P}^2\)

⇒ \(X(Y-X P)=X P^2 \Rightarrow Y-X P=P^2 \Rightarrow Y=X P+P^2\) ……………………(3)

(3) is Clairaut’s equation.

∴ General solution of (3) is \(Y=C X+C^2\)

∴ The general solution of (1) is \(y^2=C x^2+C^2\)

Differential Equations Of First Order But Not First Degree Reducible To Clairaut’s Form

Example. 2. Solve \((p y+x)(p x-y)=2 p\)

Solution.

Given equation is \((p y+x)(p x-y)=2 p\) ………………………..(1)

Put \(x^2=\mathrm{X} \text { and } y^2=\mathrm{Y} \Rightarrow 2 x d x=d \mathrm{X}, 2 y d y=d \mathrm{Y}\)

⇒ \(\mathrm{P}=\frac{d \mathrm{Y}}{d \mathrm{X}}=\frac{y}{x} \frac{d y}{d x}=\frac{y}{x} \cdot p \Rightarrow p=\frac{x}{y} \mathrm{P}\) …………………………..(2)

(1) and (2) \(\Rightarrow\left(\frac{x}{y} \mathrm{P} \cdot y+x\right)\left(\frac{x}{y} \mathrm{P}, x-y\right)=2\left(\frac{x}{y}\right) \mathrm{P}\)

⇒ \(x(\mathrm{P}+1)\left(x^2 \mathrm{P}-y^2\right)=2 x \mathrm{P} \Rightarrow(\mathrm{P}+1)\left(x^2 \mathrm{P}-y^2\right)=2 \mathrm{P}\)

⇒ \((\mathrm{P}+1)(\mathrm{XP}-\mathrm{Y})=2 \mathrm{P} \Rightarrow \mathrm{PX}-\mathrm{Y}=\frac{2 \mathrm{P}}{\mathrm{P}+1}\)

⇒ \(\mathrm{Y}=\mathrm{PX}-\frac{2 \mathrm{P}}{\mathrm{P}+1}\) is Clairaut’s equation. ………………………….(3)

The general solution of (3) is \(Y=c X-\frac{2 c}{c+1}\)

∴ The general solution of (1) is \(y^2=c x^2-\frac{2 c}{c+1}\)

Solved Problems On First-Order Non-First-Degree Reducible To Clairaut’s Form

Example. 3. Use the transformation \(u=x^2\) and \(v=y^2\) to solve \(a x y p^2+\left(x^2-a y^2-b\right) p-x y=0\).

Solution.

Given: \(a x y p^2+\left(x^2-a y^2-b\right) p-x y=0\).

Put \(x^2=u\) and \(y^2=v \Rightarrow 2 x dx=du, 2y dy=d v\)

⇒ \(\mathrm{P}=\frac{d v}{d x}=\frac{y}{x} \frac{d y}{d x}=\frac{y}{x} p \Rightarrow p=\frac{x}{y} \mathrm{P}\)

(1) and (2) ⇒ \(a x y\left(\frac{x^2}{y^2}\right) \mathrm{P}^2+\left(x^2-a y^2-b\right) \frac{x}{y} \mathrm{P}-x y=0\)

⇒ \(a x^2 \mathrm{P}^2+\left(x^2-a y^2-b\right) \mathrm{P}-y^2=0 \Rightarrow a u \mathrm{P}^2+(u-a v-b) \mathrm{P}-v=0\)

⇒ \(a u \mathrm{P}^2+u \mathrm{P}-a v \mathrm{P}-b \mathrm{P}-v=0 \Rightarrow u \mathrm{P}(a \mathrm{P}+1)-v(a \mathrm{P}+1)-b \mathrm{P}=0\)

⇒ \(v(a \mathrm{P}+1)=u \mathrm{P}(a \mathrm{P}+1)-b \mathrm{P} \Rightarrow v=u \mathrm{P}-\frac{b \mathrm{P}}{a \mathrm{P}+1} \ldots \ldots\) (3) is in Clairaut’s form.

The general solution of (3) is \(v=u \mathrm{C}-\frac{b \mathrm{C}}{a \mathrm{C}+1}\)

∴ The general solution of (1) is \(y^2=x^2 \mathrm{C}-\frac{b \mathrm{C}}{a \mathrm{C}+1}\)

Problems On Equations Reducible To Clairaut’s Form

Example. 4. Reduce the equation \(y^2(y-x p)=x^4 p^2\) to Clairaut’s form by the substitution \(x=1 / u, y=1 / v\) and hence solve the equation.
Solution.

Given equation is \(y^2(y-x p)=x^4 p^2\) ………………………(1)

Also given \(x=1 / u \text { and } y=1 / v \Rightarrow d x=-\frac{1}{u^2} d u, d y=-\frac{1}{v^2} d v\)

⇒ \(\frac{d y}{d x}=\frac{u^2}{v^2} \frac{d v}{d u} \Rightarrow p=\frac{u^2}{v^2} \mathrm{P}\) where \(\mathrm{P}=\frac{d v}{d u}, p=\frac{d y}{d x}\) ……………………..(2)

(1) and (2) \(\Rightarrow \frac{1}{v^2} \cdot\left(\frac{1}{v}-\frac{1}{u} \cdot \frac{u^2}{v^2} \mathrm{P}\right)=\frac{1}{u^4} \cdot \frac{u^4}{v^4} \mathrm{P}^2\)

⇒ \(\frac{1}{v^4}(v-u p)=\frac{\mathrm{P}^2}{v^4} \Rightarrow v-u \mathrm{P}=\mathrm{P}^2 \Rightarrow v=u \mathrm{P}+\mathrm{P}^2\) ……………………..(3)

The general solution of (3) is \(v=u c+c^2\)

Hence the general solution of (1) is \(\frac{1}{y}=\frac{1}{x} c+c^2 \Rightarrow x=c y+c^2 y x\)

Differential Equations Introduction Homogeneous Functions

Definition. A function f(x,y) is said to be a homogeneous function of degree n in x and y if \(f(k x, k y)=k^n f(x, y)\) for all values of k where n is a real number.

Introduction To Homogeneous Differential Equations

Example 1.

Given

A function f(x,y) is said to be a homogeneous function of degree n in x and y if \(f(k x, k y)=k^n f(x, y)\) for all values of k where n is a real number.

Let \(f(x, y)=\left(x^2+y^2\right) /\left(x^3+y^3\right)\)

Now \(f(k x, k y)=\left(k^2 x^2+k^2 y^2\right) /\left(k^3 x^3+k^3 y^3\right)=\frac{1}{k}\left(\frac{x^2+y^2}{x^3+y^3}\right)=k^{-1} f(x, y)\)

∴ f(x,y) is a homogeneous function of degree -1.

Illustrations Of Homogeneous Differential Equations

Example. 2. Let \(f(x, y)=(\sqrt[3]{x}+\sqrt[3]{y}) /(x+y)\)

Now \(f(k x, k y)=\frac{\sqrt[3]{(k x)}+\sqrt[3]{(k y)}}{k x+k y}=\frac{k^{1 / 3}(\sqrt[3]{x}+\sqrt[3]{y})}{k(x+y)}=k^{-2 / 3}\left(\frac{\sqrt[3]{x}+\sqrt[3]{y}}{x+y}\right)=k^{-2 / 3} f(x, y)\)

∴ f(x,y) is a homogeneous function of degree  -2/3.

Example 3. Let \(f(x, y)=\frac{y^2+x^2 e^{-x / y}}{x+y}\)

Now \(f(k x, k y)=\frac{k^2 y^2+k^2 x^2 e^{-k x / k y}}{k x+k y}=k \frac{y^2+x^2 e^{-x / y}}{x+y}=k f(x, y)\)

∴ f(x,y) is a homogeneous function of degree 1.

Example 4. Let f(x,y) = cos x + tan y

Now \(f(k x, k y)=\cos k x+\tan k y \neq k^n f(x, y)\) for any value of n

∴ f(x,y) is not a homogeneous function.

Further a homogeneous function of degree n in x and y can be expressed as , \(x^n f(x / y) \text { or } y^n f(x / y)\)

Example 5. Let \(f(x, y)=a x^3+3 b x^2 y+c y^3\)

Now \(f(x ; y)=x^3\left[a+3 b(y / x)+c(y / x)^3\right]=x^3 f(y / x)\)

Also \(f(x, y)=y^3\left[c+3 b(x / y)^2+a(x / y)^3\right]=y^3 f(x / y)\)

∴ f(x,y) is a homogeneous function of degree 3.

Methods To Convert Differential Equations To Homogeneous Form 

Example 6. Let \(f(x, y)=(\sqrt{x}+\sqrt{y}) /(\sqrt{x}-\sqrt{y}) .\)

Now \(f(x, y)=\frac{x^{1 / 2}\left[1+(y+x)^{1 / 2}\right]}{x^{1 / 2}\left[1-(y / x)^{1 / 2}\right]}=x^0 f(y / x)\)

∴ f(x, y) is a homogeneous function of degree 0.

Note. If f(x,y) is a homogeneous function of degree zero, then f(x,y) is a function of y/x or x/y alone.

Differential Equations Introduction Homogeneous Differential Equation

Definition. A differential equation \(\frac{d y}{d x}=f(x, y)\) of first order and first degree is called homogeneous in x and y if the function f(x,y) is a homogeneous function of degree zero in x and y.

Differential Equations Introduction Working rule to solve a Homogeneous Differential Equation

1. Let \(\frac{d y}{d x}=f(x, y)\) be the homogeneous equation.

Then express it in the form \(\frac{d y}{d x}=\phi\left(\frac{y}{x}\right)\) ……………………….(1)

2. To solve (z), put \(y / x=v \Rightarrow y=v x\) …………………….(2)

3. Differentiating (2) w.r.t. x: \(x: \frac{d y}{d x}=v+x \frac{d v}{d x}\) ……………………….(3)

4. Now (1), (2), (3) => \(v+x \frac{d v}{d x}=\phi(v) \Rightarrow x \frac{d v}{d x}=\phi(v)-v\)

Separating the variables : \(\frac{d x}{x}=\frac{d v}{\phi(v)-v}\)

Integrating: \(\int \frac{d x}{x}=\int \frac{d v}{\phi(v)-v}+c\) where c is an arbitrary constant.

5. After integration replaced by (y / x) to get the general solution of the given homogeneous equation.

Note: If the given homogeneous equation is reduced to the form \(\frac{d x}{d y}=\mathrm{F}\left(\frac{x}{y}\right)\) then put \(x=v y \Rightarrow \frac{d x}{d y}=v+y \frac{d v}{d y}\). This gives a differential equation in v and y where the variables are separable. After integration replace v by (x/y) to obtain the required general solution.

Differential Equations Introduction Equations Reduced to Homogeneous Form

Non-homogeneous equations of the first degree in x and y:

If the equation \(\frac{d y}{d x}=f(x, y)\) is of the form \(\left(a_2 x+b_2 y+c_2\right) \frac{d y}{d x}=a_1 x+b_1 y+c_1\) where \(a_1, b_1, c_1, a_2, b_2, c_2\) are real numbers and \(c_1 \neq 0 \text { or } c_2 \neq 0\), then it is called a non-homogeneous differential equation of the first degree in x and y.

2. General solution of non-homogeneous equation \(\left(a_2 x+b_2 y+c_2\right) \frac{d y}{d x}=a_1 x+b_1 y+c_1\)…… (1)

Equation (1) can be reduced to a homogeneous form or variables separable form by some transformation.

Differential Equations Introduction Working rule to solve the equation \(\left(a_2 x+b_2 y+c_2\right) \frac{d y}{d x}=a_1 x+b_1 y+c_1\)

Case 1.

(1) Let \(a_1 b_2-a_2 b_1=0\)

Let \(\frac{a_2}{a_1}=\frac{b_2}{b_1}=t\) (non-zero real number) \(\Rightarrow a_2=t a_1, b_2=t b_1\)

(2) Substitute the value \(a_2=t a_1, b_2=t b_1\) in (1)

(1) \(\Rightarrow\left[t\left(a_1 x+b_1 y\right)+c_2\right] \frac{d y}{d x}=a_1 x+b_1 y+c_1\) …………………….(2)

(3) If \(c_2=t c_1\), then (2) reduces to \(\frac{d y}{d x}=\frac{1}{t}\)

∴ G. S. of (1) is ty = x + c

(4) If \(\) then put \(a_1 x+b_1 y=u \Rightarrow \frac{d u}{d x}=a_1+b_1 \frac{d y}{d x}\) ……………………….(3)

(2) and (3) => \(\left(t u+c_2\right)\left[\frac{1}{b_1}\left(\frac{d u}{d x}-a_1\right)\right]=u+c_1 \Rightarrow \frac{d u}{d x}=\frac{\left(b_1+t a_1\right) u+\left(c_2+c_1 b_1\right)}{t u+c_2}\) ……………………..(4)

(4) is in variables separable form hence it can be solved by separating the variables.

∴ The G. S. of (4) is \(\phi(u, x, c)=0\)

Hence the G. S. of (1) is \(\phi\left(a_1 x+b_1 y, x, c\right)=0\)

Case 2. : Let \(a_1 b_2-a_2 b_1 \neq 0 \Rightarrow \frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)

1. (1) \(\Rightarrow \frac{d y}{d x}=\frac{a_1 x+b_1 y+c_1}{a_2 x+b_2 y+c_2}\) ………………………..(2)

2. Put x = X + h and y = Y + k in (1) => \(\frac{d x}{d \mathrm{X}}=1, \frac{d y}{d \mathrm{Y}}=1 \Rightarrow \frac{d y}{d x}=\frac{d \mathrm{Y}}{d \mathrm{X}}\) ………………………….(3)

3. (2) and (3) \(\frac{d Y}{d X}=\frac{\left(a_1 X+b_1 Y\right)+\left(a_1 h+b_1 k+c_1\right)}{\left(a_2 X+b_2 Y\right)+\left(a_2 h+b_2 k+c_2\right)}\) …………………..(4)

4. Choose h and k such that \(a_1 h+b_1 k+c_1=0\) and \(a_2 h+b_2 k+c_2=0\)
Solve these equations to get h and k. ………………………..(5)

5. (4) and (5) \(\frac{d \mathrm{Y}}{d \mathrm{X}}=\frac{a_1 \mathrm{X}+b_1 \mathrm{Y}}{a_2 \mathrm{X}+b_2 \mathrm{Y}}\)

This is clearly a homogeneous equation which can be solved by putting Y = VX ……………………….(6)

6. The G. S. of (6) is F (X,Y,c) = 0 …………….(7)

7. The G.S. of (1) is obtained by replacing X and Y with x – h and y – k in (7)

∴ General solution of (1) is f(x-h,y-k,c) = 0

Note: In case 2 of the above method geometrically (A, k) is the point of intersection of two lines \(a_1 x+b_1 y+c_1=0, a_2 x+b_2 y+c_2=0\)