McGraw Hill

Pre-Calculus 11 Student Edition Chapter 1 Sequences and Series

Page 66 Problem 1 Answer

First determine 36,40,44,48,……. sequence is in arithmetic or not. If in arithmetic, find the common difference.

The given sequence is

36,40,44,48,……..

Here,

First term(t1)=36

Second term(t2)=40

Third term (t3)=44

fourth term(t4)=48

Now,

t2−t1=40−36=4

t3−t2=44−40=4

t4−t3=48−44=4

​Sequence has the constant common difference. So, the given sequence is in arithmetic progression. The common difference is 4.

The sequence 36,40,44,48 is in arithmetic and common difference is 4.

Precalculus Textbook Mcgraw Hill Answers

Page 66 Problem 2 Answer

Given: −35,−40,−45,−50,…..

To find: To check whether the given sequence is arithmetic or not

Consider the sequence −35,−40,−45,−50

The above sequence will be arithmetic sequence if the difference between the consecutive terms is equal hence we have

−40+35=−5

−45+40=−5

−50+45=−5

​The common difference of consecutive terms is equal

Hence the given sequence is arithmetic sequence

The given sequence is an arithmetic sequence.

Read and Learn More Precalculus Textbook Mcgraw Hill Answers

Page 66 Problem 3 Answer

Given: −35,−40,−45,−50,…..

To find: To check whether the given sequence is arithmetic or not

Consider the sequence −35,−40,−45,−50,….

The above sequence will be arithmetic sequence if the difference between the consecutive terms is equal

hence we have

−40+35=−5

−45+40=−5

−50+45=−5

​The common difference of consecutive terms is equal

Hence the given sequence is arithmetic sequence

The sequence is an arithmetic sequence.

Page 66 Problem 4 Answer

Given: 8.3,4.3,0.3,−3.7

To find: To check whether the given sequence is arithmetic or not

Consider the sequence 8.3,4.3,0.3,−3.7

The above sequence will be arithmetic sequence if the difference between the consecutive terms is equal

hence we have

4.3−8.3=−4

0.3−4.3=−4

−3.7−0.3=4

The common difference of consecutive terms is equal

Hence the given sequence is arithmetic sequence

Hence the given sequence is a arithmetic sequence

Precalculus Textbook Mcgraw Hill Answers

Page 66 Problem 5 Answer

Given: ​a)18,30,42,54,66,…

b)7,12,17,22,….

c)2,4,6,8,…

d)−8,−12,−16,−20,…

e)4,7,10,13,….

​A)tn=3n+1

B)tn=−4(n+1)

C)tn=12n+6

D)tn=5n+2

E)tn=2n​

To find: match the sequence to its nth terms.

Consider the sequence 18,30,42,54,66

These are arithmetic sequence

Hence they have equal common difference

Hence the common difference-30−18=12

And the first term(a)=18

The nth terms of sequence is- a+(n−1)d

=18+(n−1)12

=18+12n−12

=12n+6​

Consider the sequence 7,12,17,22,…

These are arithmetic sequence

Hence they have equal common difference

Hence the common difference-12−7=5

The first term of the sequence (a)=7

The nth of the sequence is=a+(n−1)d

=7+(n−1)5

=7+5n−5

=5n+2

​Consider the sequence 2,4,6,8,…

These are arithmetic sequence

Hence they have equal common difference

Hence the common difference-4−2=2

The first term of the sequence is (a)=2

The nth term of the sequence is​=a+(n−1)d

=2+(n−1)2

=2+2n−2​

=2n

Precalculus Textbook Mcgraw Hill Answers

​Consider the sequence −8,−12,−16,−20,….

These are arithmetic sequence

Hence they have equal common difference

Hence the common difference-=−12+8=−4

The first term of the sequence (a)=−8

The nth term of the sequence is​=a+(n−1)d

=−8+(n−1)(−4)

=−8−4n+4

=−4n−4

​Consider the sequence 4,7,10,13,….

These are arithmetic sequence

Hence they have equal common difference

Hence the common difference-7−4=3

The first term of the sequence is (a)=7

The nth term of the sequence is=a+(n−1)d

=7+(n−1)3

=7+3n−3

=3n+4

​Hence the correct match of sequence and their nth term is

a)18,30,42,54,66,…

b)7,12,17,22,….

c)2,4,6,8,…

d)−8,−12,−16,−20,…

e)4,7,10,13,….

​C)tn=12n+6

D)tn=5n+2

E)tn=2n

B)tn=−4(n+1)

A)tn=3n+1

Precalculus Textbook Mcgraw Hill Answers

​Page 66 Problem 6 Answer

Given: 98 and a sequence 7,14,21,28,…

To find: Whether the given number belongs to the given sequence and if it does find the corresponding value of n.

Consider the sequence 7,14,21,28

This is an arithmetic sequence hence it has equal common difference

Hence the common difference is 14−7=7

The first term of the sequence is (a)=7

Hence the nth term of the sequence is =a+(n−1)d

=7+(n−1)7

=7+7n−7

=7n

​Consider tn=98

Hence 98=7n

∴n=14​

Hence 98 does belong to the given sequence and the value of n=14.

Page 66 Problem 7 Answer

Given: 110 and a  sequence 7,14,21,…

To find : whether the given number belongs to the sequence and if it does find the corresponding value of n

Given: Consider the sequence 7,14,21,…

t1=7

t2=14

Common difference:t2−t1

=14−7

=7

The general term of the arithmetic sequence is tn=t1+(n−1)d…(1)

Substitute the values t1=7,d=7 in equation (1)

tn=7+(n−1)7…(2)

Substitute tn=110 in equation(2)

110=7+7n−7

110=7n

n=110/7

n=15.71

Therefore, 110 does not belong to the given sequence.

Therefore, 110 does not belong to the given sequence.

Mcgraw Hill Precalculus Textbook Answers

Page 66 Problem 8 Answer

Given: tn=378 and the sequence 7,14,21,…

To find: whether the given number belongs to the sequence and if it does find the corresponding value of n

Given: Consider the sequence 7,14,21,…

The given sequence is arithmetic sequence.

t1=7 , t2=14

Common difference: t2−t1

=t2−t1

=14−7

The general term of an arithmetic sequence is tn=t1+(n−1)d…(1)

Putting these values d=7,t1=7,tn=378 in equation (1)

378=7+(n−1)7

378=7+7n−7

378=7n

n=378/7

n=54

Therefore, 378 does belong to the given sequence and the value of n is 54

Therefore, 378 does belong to the given sequence and the value of n is 54

Page 66 Problem 9 Answer

Given: tn=575 and the sequence is 7,14,21,…

To find: whether the given number belongs to the sequence and if it does find the corresponding value of n

Given: Consider the sequence 7,14,21,…

The given sequence is arithmetic sequence.

t1=7,t2=14

Common difference:t2−t1

=14−7

=7

The general term of an arithmetic sequence is

tn=t1+(n−1)d…(1)

Putting these values d=7,t1=7,tn=575 in equation (1)

Mcgraw Hill Precalculus Textbook Answers

575=7+(n−1)7

575=7+7n−7

575=7n

n=575/7

n=82.14

Therefore, 575 does not belong to the given sequence.

Therefore, 575 does not belong to the given sequence.

Page 66 Problem 10 Answer

Given: Sequence 1: 2,9,16,23

t1=2,t2=9

Common difference: d=t2−t1

=9−2

=7

General term of an arithmetic sequence is tn=t1+(n−1)d…(1)

Putting these values  d=7,t1=2,n=17 in equation (1)

t17=2+(17−1)7

t17=2+16×7

t17=2+112

t17=114

Sequence2: 4,10,16,22

t1=4,t2=10

Common difference:d=t2−t1

=10−4

=6​

General term of an arithmetic sequence is tn=t1+(n−1)d….(2)

Putting the values n=17,d=6,t1=4 in equation(2)

t17=4+(17−1)6

=4+16×6

=4+96

=100

​Since, 114>110

t17 is greater in sequence 1

Mcgraw Hill Precalculus Textbook Answers

So, the option A is correct.

114>100

t17 is greater in sequence 2

So, the option B is not correct .

114>100

t17 is equal in sequences.

So, the option C is not correct.

The option A  is correct.

t17 is greater in sequence 1.

Page 66 Problem 11 Answer

In the graph , sequence 1 has a larger positive slope than sequence 2.

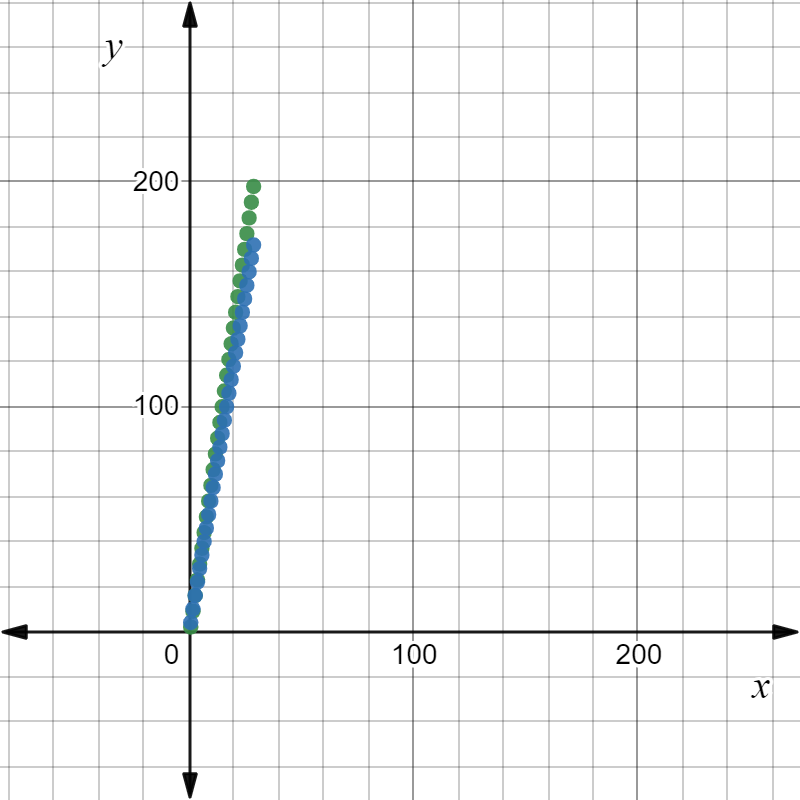
The value of term 17 is greater in sequence 1 than in sequence 2.

So, the option A is correct.

The value of term 17 is  greater in sequence 1 than not in sequence 2

So, the option B is not correct.

The value of term 17  is not equal to both the sequences1 and sequence2.

So, the option C is not correct.

In the graph, sequence 1 has a larger positive slope than the sequence 2.

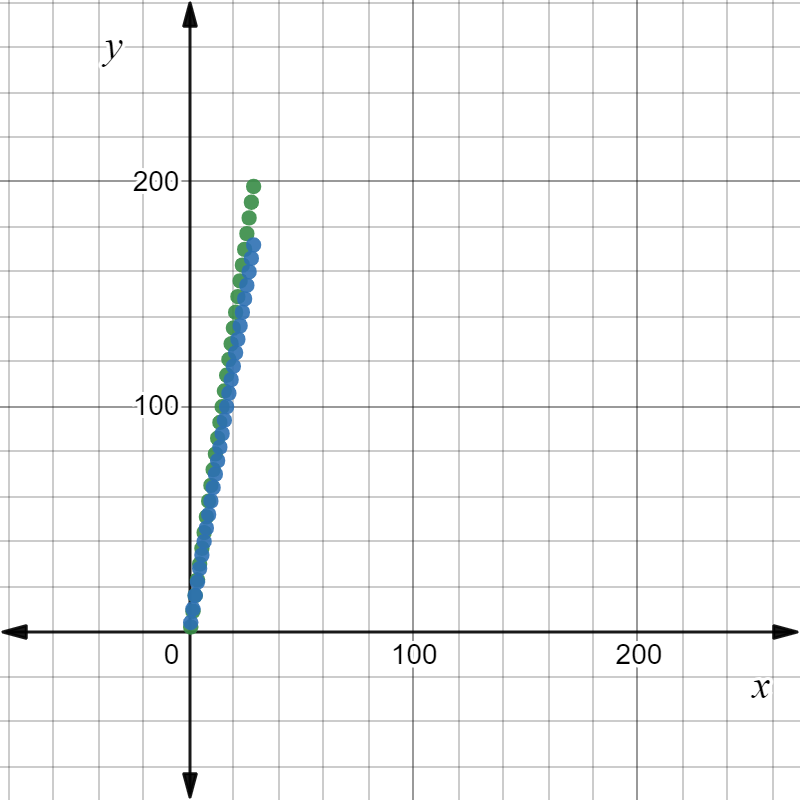
The value of term 17 is greater in sequence 1 than in sequence 2.

So, the option A is correct.

Page 66 Problem 12 Answer

Given : The first term of the A.P. is 5.

The fourth term of the A.P. is 17.

At first , we have to assume the common difference of the A.P. be d.

Then we have to find the fourth term in terms of the first term and d and after that we have to equate this fourth term to the given fourth term to find d.

Lastly , after finding the value of d, we will be able to find the tenth term.

First term of the A.P. = 5

Let the common difference of the A.P. be d.

Then the fourth term of the A.P. is

5+(4−1)d=17

=>5+3d=17

=>3d=17−5

=>3d=12

=>d=12/3

=>d=4

Then , the tenth term is 5+(10−1)4=5+36=41

​Hence, the tenth term of the Arithmetic sequence is 41.

Mcgraw Hill Precalculus Textbook Answers

Page 66 Problem 13 Answer

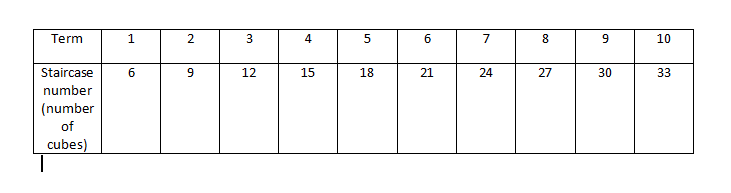
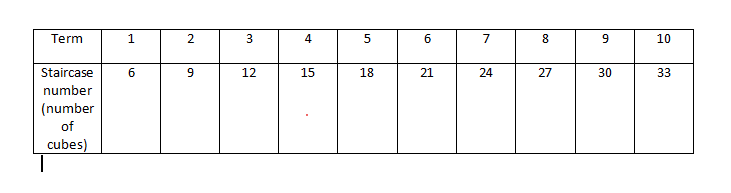
The given arithmetic series is 6+9+12+⋯(S10).

We have to find out the sum of the series for 10th term.

Here t1=6

n=10

d=3​

Using the above formula we will calculate the sum of the series.

Sn =n/2 [2t1 + (n − 1)d]

⇒ S10 =10/2 [2(6) + (10 − 1)3] [∵ t1 = 6, n = 10, d = 3]

⇒ S10 = 5[12 + 27]

⇒ S10 = 195

The indicated sum 6+9+12+⋯(S10) is 195.

Page 66 Problem 14 Answer

The given arithmetic series is 4.5+8+11.5+⋯(S12).

We have to find out the sum of the series for 12th term.

Here  t1=4.5

n=12

d=3.5

Using the above formula we will calculate the sum of the series.

Sn =n/2[2t1 + (n − 1)d]

⇒ S12 =12/2 [2(4.5) + (12 − 1)3.5] [∵ t1 = 4.5, n = 12, d = 3.5]

⇒ S12 = 6[9 + 38.5]

⇒ S12 = 285

The indicated sum of 4.5+8+11.5+⋯(S12) is 285.

Page 66 Problem 15 Answer

The given arithmetic series is 6+3+0+⋯(S10 ).

We have to find out the sum of the series for 10th term.

Here t1=6

n=10

d=−3

Using the above formula we will calculate the sum of the series.

Sn =n/2[2t1 + (n − 1)d]

⇒ S10 =10/2[2(6) + (10 − 1)(−3)] [∵ t1 = 6, n = 10, d = −3]

⇒ S10 = 5[12 − 27]

⇒ S10 = −75

The indicated sum 6+3+0+⋯(S10 ). is −75.

Mcgraw Hill Precalculus Textbook Answers

Page 66 Problem 16 Answer

The given arithmetic series is 60+70+80+⋯(S20).

We have to find out the sum of the series for 20th term.

Here t1=60

n=20

d=10

Using the above formula we will calculate the sum of the series.

Sn =n/2 [2t1 + (n − 1)d]

⇒ S20 =20/2 [2(60) + (20 − 1)10] [∵ t1 = 60, n = 20, d = 10]

⇒ S20 = 10[120 + 190]

⇒ S20 = 3100

The sum of the given series for 20^th term is 3100.

Page 66 Problem 17 Answer

Given : The sum of first 12 terms of an arithmetic series is 186.

The 20^th term is 83.

To find the sum of first 40 terms , at first we have to find the first term a1 and the common differenced with the given information.

Lastly , by putting the values of n,a1,d in the given formula, we will get the required answer.

Since the 20^th term is 83,we have :

a1+(20−1)d=83=>a1+19d=83

∴a1=83−19d

Sum of 1st 12 terms is 186, so :186=(12/2)[2(83−19d)+(12−1)d]

=>186=6[2(83−19d)+11d]

=>186/6

=166−38d+11d

=>31=166−27d

=>27d=166−31

=>27d=135

=>d=135/27

=>d=5

a1 = 83 − 19(5) = 83 − 95 = −12

a40 = −12 + (40 − 1)(5)

=> a40 = −12 + 39(5)

=> a40 = −12 + 195

∴ a40 = 183

S40 = (40/2)[2(−12) + (40 − 1)(5)]

= 20[−24 + 195]

= 20(171)

= 3420

Hence, the indicated sum is 3420.

Page 66 Problem 18 Answer

Here on the first day, I am able to contact only one person.

So a1=1

As each day progresses, I am able to contact two more people than the previous day.

So, the common difference d=2

To find the number of people I would contact on the 15th day, we have to find a15

We know

a15=a1+(15−1)d

as a1=1 and d=2,

a15=1+(15−1)2

⇒a15=1+14.2

⇒a15=1+28

⇒a15=29

If You have taken a job that requires being in contact with all the people in your neighbourhood.

On the first day, you are able to contact only one person.

On the second day, you contact two more people than you did on the first day.

On day three, you contact two more people than you did on the previous day.

Assume that the pattern continues then you would contact 29 people on 15 th day.

Page 66 Problem 19 Answer

Here on the first day, I am able to contact only one person. So a1=1

As each day progresses, I am able to contact two more people than the previous day. So, the common difference d=2

To find the total number of people I would have been in contact with by the end of the 15th day, we have to find S15.

Here n=15

We know,

S15=(15/2)(2a1+(15−1)d) as a1=1,d=2,

S15=(15/2)(2.1+(15−1)2)⇒S15

=(15/2)(2+14.2)⇒S15

=(15/2)(2+28)⇒S15

=(15/2).30⇒S15

=15.15⇒S15

=225

You have taken a job that requires being in contact with all the people in you neighbourhood.

On the first day, you are able to contact only one person.

On the second day, you contact two more people than you did on the first day.

On day three, you contact two more people than you did on the previous day.

Assume that the pattern continues then the total number of people you would be in contact with by the end of the 15^th day is 225

Page 66 Problem 20 Answer

We consider the number of people I am able to meet every day as the individual term of the series.

Given that, on the first day the man is able to contact with one person, so the first term of the series, i.e. a=1.

We observe that as days pass, the number of people I am able to interact increases constantly by 2. Hence d=2

At the end, I am supposed to meet with a sum of 625 people. Hence Sn=625.

We need to find the number of days required to meet the sum of 625 people, i.e. n.

We know that,

Sn=n/2{2a+(n−1)d}⇒625=n/2

{2.1+(n−1).2}

(Given)

⇒625=n/2.2(1+n−1)

⇒625=n.n

⇒625=n2

⇒n=25

Hence it will take 25days to know 625 people.

It will take 25 days to know 625 people in the neighbourhood.

Page 67 Problem 21 Answer

The objective of the problem is to find the number of seats in the entire concert hall.

Given: The first row has 10 seats

The second row has 12 seats

Total 30 rows of seats.

Here, the first row has 10 seats and the second row has 12 seats.

Also, each row has 2 seats more than the previous row.

Therefore,

a=10

d=2

n=30

By using the formula of the sum of the first n terms of A.P.:

S30=30/2[2(10)+(30−1)2]

S30=15[20+(29)2]

S30=15[78]

S30=1170

So, a total 1170 seats are there in concert hall.

Hence, a total 1170 seats are there in a concert hall.

Page 67 Problem 22 Answer

The objective of the problem is to check whether the given series is geometric or not.

If yes, then find the first term, common ratio, and general term of a sequence.

Given:3,6,10,15,…

Taking common ratio between terms,

6/3=2

10/6

=1.67

​As the ratio between the consecutive terms is not constant, the given series is not geometric.

Hence, given series is not geometric as consecutive term ratio is not constant.

Page 67 Problem 23 Answer

Given:

1,−2,4,−8,…

The objective of the problem is to check whether the given series is geometric or not.

If yes, then find the first term, common ratio, and general term of a sequence

Taking the common ratio of consecutive terms,−2/1=−2/4

−2=−2/−8

4=−2

As this ratio is the same, the given sequence is geometric series.

As seen common ratio is −2, i.e., r=2.

By analyzing the given sequence, the first term is t1=1

Nth term of a geometric sequence is:tn=t1/rn−1

Therefore, the general term of a sequence,

tn=1⋅(−2)n−1

tn=(−2)n−1

Hence, the given sequence is a geometric sequence.

The first term is t1=1

Common ratio is r=−2

General term is tn=(−2)n−1

Page 67 Problem 24 Answer

Given sequence: 1,1/2,1/4,1/8,………..

Determine whether each of the following sequences is geometric.

If it is geometric, determine the common ratio, r, the first term, t1, and the general term of the sequence.

Determine ratio between consecutive terms

t2/t1=1/2

1→r=1/2

t3/t2=1/4

1/2→r=1/2

t4/t3=1/8

1/4→r=1/2

Ratio is same between consecutive terms

So, sequence is geometric.

common ratio: r=1/2

The first term: t1=1

General term of the sequence: tn=t1/rn−1

tn=1(1/2)n−1

tn=1/2n−1

common ratio: r=1/2

The first term: t1=1

General term of the sequence: tn=1/2n−1

Page 67 Problem 25 Answer

Given sequence: 16/9,−3/4,1,………..

Determine whether each of the following sequences is geometric.

If it is geometric, determine the common ratio, r, the first term, t1, and the general term of the sequence.

Determine ratio between consecutive terms

t2/t1=−3/4

16/9→r=−27/4

t3/t2=1−3/4

→r=−4/3

Ratio is not same between consecutive terms

So, the sequence is not geometric.

The sequence 16/9,−3/4,1,……….. is not geometric.

Page 67 Problem 26 Answer

Given: Initial number of bacteria:

P0=5000

Growth rate r=8%

r=0.08​

To find number of bacteria at end of n=5 hours.

P = P0(1 + r)n

P = 5000(1 + 0.08)5

P = 5000(1.08)5

P = 5000(1.4693280768)

P = 7346

Number of bacteria present at end of 5 hours is 7346

Page 67 Problem 27 Answer

Given: Initial number of bacteria: P0=5000

Growth rate r=8%

r=0.08​

Determine a formula for the number of bacteria present after n hours.

P=P0/(1+r)n

P=5000(1+0.08)n

P=5000(1.08)n

Formula for the number of bacteria present after n hours:

P=5000(1.08)n

Page 67 Problem 28 Answer

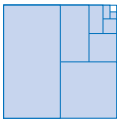
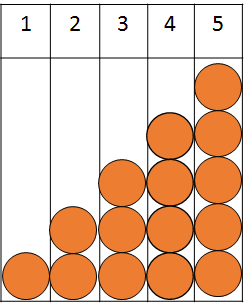
Given: Radius of circle in original diagram 81cm

To find circumference of the smallest circle in the 4th stage.

Original radius: 81

Smallest circle radius in stage1:1/3

(81)=27

Smallest circle radius in stage 2:1/3

(27)=9

Smallest circle radius in stage 3:1/3

(9)=3

Smallest circle radius in stage 4:1/3

(3)=1

Circumference of the smallest circle in the 4th

stage is: =2πr

=2π(1)

=2π​

Circumference of the smallest circle in the 4th stage is: 2πcm

Page 67 Problem 29 Answer

Arithmetic Sequence

Definition: The difference between two consecutive terms in an arithmetic sequence is constant.

This difference is known as a common difference.

Formula: The formula to find the general term of an arithmetic sequence is:

tn=t1/+(n−1)d

Here, n is the number of terms, d is a common difference, tn is the general term and t1 is the first term.

Example: Consider the sequence: 4,8,12,16,20,…

We can observe that the difference between two consecutive terms in the above sequence is constant, 4.

Geometric Sequence

Definition: The ratio of consecutive terms in a geometric sequence is constant.

Formula: The formula to find the general term of a geometric sequence is:

tn=t1/rn−1

Here, n is the number of terms, r is the common ratio, t1 is the first term and tn is the general term.

Example: Consider the sequence: 3,9,27,81,…

We can observe that the ratio of consecutive terms in the above sequence is constant, 3.

Therefore, the definition, formula and example of arithmetic and geometric sequence are explained as;

Arithmetic Sequence

Definition: The difference between two consecutive terms in an arithmetic sequence is constant. This difference is known as a common difference.

Geometric Sequence

Definition: The ratio of consecutive terms in a geometric sequence is constant.

Pre-Calculus 11 Student Edition Chapter 1 Sequences and Series

Page 58 Problem 1 Answer

Given that a big square is given (as shown in the following figure) it is divided into two equal parts and one of the portions is shaded.

Then the unshaded portion is again divided in half and one of the halves is shaded.

This process is continued.

To find: A sequence that represents the area of the newly shaded region as a fraction of the entire region.

Let the total area be A square units.

The area of first shaded region = A/2

A=1/2.

Now, this half region is again divided into two halves, and one half is shaded, therefore area of 2nd shaded region is:

A/4

A=1/4

Similarly area of the third shaded region = 1/8

Area of fourth shaded region = 1/16

Area of fifth shaded region = 1/32

Therefore, the sequence is 1/2,1/4,1/8,1/16,1/32.

The answer is 1/2,1/4,1/8,1/16,1/32.

Read and Learn More Precalculus Textbook Mcgraw Hill Answers

Page 58 Problem 2 Answer

As we find in the previous question the sequence that is given here is:-

A geometric series as 1/2,1/4,1/8,1/16,1/32., with

First term, t₁=1/2 and

Common ratio,r=1/2.

We have to  find: The 6th and 7th term.

Let us use the formula for a general term to find the answer.

Applying the formula and putting the values, we have:

Precalculus Textbook Mcgraw Hill Answers

Sixth term:

t₆=1/2⋅(1/2)6−1⇒t6

=1/2⋅(1/2)5⇒t6

=1/64

Seventh term:

t₇=1/2⋅(1/2)7−1

⇒t₇ =1/2⋅(1/2) 6

⇒ t₇ =1/128

The answer is 1/64,1/128.

Page 59 Problem 3 Answer

Given that, start with a square piece of paper draw a line dividing it in half, and shade one of the halves.

In the unshaded half of the square, draw a line to divide it in half, and shade one of the halves. Repeat this process.

We need to verify whether the sequence of these shaded regions is arithmetic, geometric, or neither.

For this, check whether a constant is added or multiplied to get the successive terms of the sequence.

Since we draw a line that divides the square as two equal parts, therefore each shaded region is half of its previous shaded region.

So 1/2 is multiplied by each term of the sequence to get the successive terms of the sequence.

Hence the sequence is geometric.

The sequence is geometric.

Page 59 Problem 4 Answer

Given that, start with a square piece of paper draw a line dividing it in half, and shade one of the halves. In the unshaded half of the square, draw a line to divide it in half, and shade one of the halves. Repeat this process.

We need to verify whether it is an infinite sequence.

By ignoring physical conditions, we can continuously divide the square into two equal parts indefinitely.

As we repeat the process continuously again and again, the area of the resulting square approaches zero.

Hence the given sequence can be an infinite sequence.

The given sequence can be an infinite sequence.

Precalculus Textbook Mcgraw Hill Answers

Page 59 Problem 5 Answer

Given that, start with a square piece of paper draw a line dividing it in half, and shade one of the halves. In the unshaded half of the square, draw a line to divide it in half, shade one of the halves. Repeat this process.

We need to write the conclusion that can be made about the area of the square that would remain unshaded as the number of terms in the sequence approaches infinity.

As we repeat the process of dividing the square into two equal parts by drawing a line continuously again and again, the resulting squares will get smaller and smaller and the area of the square that would remain unshaded approaches zero.

The area of the square that would remain unshaded approaches to zero.

Page 59 Problem 6 Answer

Given function is y=(1/2)x.

We need to draw the graph of a given function using a graphing calculator and make a conclusion about the value of y=(1/2)x as x gets larger and larger.

For this, use the graphing calculator and input the given function.

The graph and the table of values is,

From the above table of values and graph, we can conclude that the value of y=(1/2)x

approaches to zero as x gets larger and larger.

The value of y=(1/2)x approaches to zero as x gets larger and larger.

Page 59 Problem 7 Answer

 We need to find if the value of (1/2)x can become equal to zero.

Assume that there exists some value at which the value (1/2)x equals zero and then show that the consequences of this are not possible.

This would imply that there exists no x where(1/2)x equals zero.

Precalculus Textbook Mcgraw Hill Answers

The graph of the functiony=(1/2)x is:

From the graph, we observe that the value (1/2)x approaches zero for greater values of x.

Suppose there exists a point say x₁ at which the value of the function y=(1/2)x equals zero.

Then, x₁ ≠ 0.

For if, x₁=0, then,(1/2) 0=1, which is not equal to 0.

Therefore, x₁>0 or x₁<0.

Now,(1/2)x​₁=0, where x₁≠0

Raising both sides to the power of 1/x₁, we get,

((1/2)x₁)​1/​x​₁=0​1/​x₁

1/2=0, which is not possible.

Therefore, there exists no x where the value of (1/2)x equals zero.

Therefore, it is not possible for the value of (1/2)x to equal zero.

Page 59 Problem 8 Answer

Given infinite geometric series is 1/2+1/4+1/8+1/16+….. and the formula to determine the sum of this series is given to be S_x=1−(1/2)x.

We need to observe the behavior of the function S_x=1−(1)x as x gets larger.

Precalculus Textbook Mcgraw Hill Answers

\(\begin{array}{|l|l|}
\hline x & S_x=1-\left(\frac{1}{2}\right)^x \\
\hline 2 & 0.75 \\
\hline 5 & 0.96875 \\
\hline 10 & 0.999023 \\
\hline 15 & 0.999969 \\
\hline 20 & 0.999999046 \\
\hline 30 & 0.999999999068 \\
\hline
\end{array}\)

 

Enter the function into the calculator and use the table feature to find the sum S_x =1−(1/2)x for increasing values of x.

The value of the function S_x = 1−(1/2)x for increasing values of x is shown in the table below:

We observe that as x gets larger, the value of Sx approaches 1.

Therefore, as x gets larger, the sum S_x = 1−(1/2)x goes closer and closer to 1.

Page 59 Problem 9 Answer

Given geometric series is 1/2+1/4+1/8+1/16+.… and the formula to determine the sum of this series is S_x =1−(1/2)x.

We need to find if the sum increases without limit.

The formula to find the sum of the geometric series

2+1/4+1/8+1/16+.…is S₁ =1−(1/2)x.

The sum S_x=1+(−(1/2)x) increases without limit provided the amount being added to 1 which is−(1/2)x increases without limit.

Now, −(1/2)x increases without limit, provided (1/2)x decreases without limit.

Now, as x increases, the denominator of (1/2)x increases, as a result, the value of(1/2)x decreases below 1 but never becomes negative.

Therefore,(1/2)x does not decrease without limit.

Therefore, it is not possible for the sum to increase without limit.

Therefore, it is not possible for the sum S_x

=1−(1/2)x  to increase without limit.

Page 59 Problem 10 Answer

Given an expression rx

\(\begin{array}{|l|ll|}
\hline x & r^x \\
\hline 1 & \frac{1}{2} \\
\hline 2 & \frac{1}{4} & \\
\hline 5 & \frac{1}{64}=0.015625 & \\
\hline 10 & \frac{1}{1024}=0.000976 & \\
\hline
\end{array}\)

 

To find as the value of x gets very large, what value does r_x come close to.

When−1<r<1, say when r=1/2.

We observe that as x increases, the value of(1/2)x approaches 0.

Therefore, based on this, we assume that when −1<r<1, the value of r_x Approaches 0.

Mcgraw Hill Precalculus Textbook Answers

If, r>1,say when r=10

We observe that as the value of x increases, the value of (10)x approaches infinity.

Therefore, based on this we conclude that when r >1, the value of rx approaches∞.

As the value of x gets very large, the value of r^x

for −1<r<1 becomes close to 0 and for r>1 the value of rx comes close to ∞

\(\begin{array}{|l|l|}
\hline x & r^x \\
\hline 1 & 10 \\
\hline 2 & 100 \\
\hline 5 & 100000 \\
\hline 10 & 10000000000 \\
\hline
\end{array}\)

 

Page 59 Problem 11 Answer

We need to find the formula for the sum of an infinite geometric series, using the answer from parta.

The formula to determine the sum of a geometric series is S_x=a(1−r^x)/1−r

Where a is the first term and r is the common ratio.

In an infinite geometric series,−1<r<1.

Now from part a, we have,rx approaches 0 as x becomes large when−1<r<1.

Therefore, as x gets large, the partial sum S_x

Approaches a/1−r.

Therefore, the sum of an infinite geometric series is S_∞=a/1−r, where−1<r<1.

The sum of an infinite geometric series is,S_∞=a/1−r, where−1<r<1.

Page 59 Problem 12 Answer

The sum of an infinite geometric series is S=a/1−r,where−1<r<1

We need to find the sum of the given infinite series.

Given geometric series;1/2+(1/2)2+(1/2)3+(1/2)4….

Now,r=(1/2)2

1/2=1/2 and a=1/2

Therefore,

S=a/1−r=1/2

1−1/2

S=1/2

2−1/2=1/2⋅2/1=1

Therefore, the sum of the infinite geometric series is 1.

Page 61 Problem 13 Answer

The objective of the problem is to determine whether the given geometric series converges or diverges and calculate the sum if it exists.

Given: 1+1/5+1/25+…

Given series is 1+1/5+1/25+…

Here,

t₁=1

r=1/5

As −1<r<1, the series is convergent.

Mcgraw Hill Precalculus Textbook Answers

Using the formula for the sum of an infinite geometric series,

S_∞=t₁/1−r

S_∞=1/1−1/5

S_∞ = 5/5−1

S_∞ = 5/4

Hence, the given series is convergent and a sum of the given infinite geometric series is 5/4.

Page 61 Problem 14 Answer

The objective of the problem is to determine whether the given geometric series converges or diverges and calculate the sum if it exists.

Given: 4+8+16+…

Given: 4+8+16+…

Here, t₁=4 and r=2

As r>1, the series is divergent and has no sum.

Hence, the given series is divergent and there is no sum exists.

Page 63 Problem 15 Answer

The given values are:

t₁ = 8

r=−1/4

First, we need to find whether the infinite geometric series is convergent or divergent.

If it is convergent, then we will use the formula of the sum of an infinite geometric series.

We know that, −1/4=−0.25 and −1<−0.25<1.

Since −1<r<1, therefore the series is convergent and the sum of infinite geometric series exists.

Using the formula of the sum of an infinite geometric series, we get

S_∞=8/1−(−1/4)

S_∞=8/1+1/4

S_∞=8/4+1/4

S_∞ =8×4/5

S∞=32/5

The sum of infinite geometric series is 32/5.

Mcgraw Hill Precalculus Textbook Answers

Page 63 Problem 16 Answer

Given: t₁=3 and r=4/3

To find: The sum of an infinite geometric series.

First, we need to check whether an infinite geometric series is convergent or divergent.

If it is convergent, then we will use the formula of the sum of an infinite geometric series.

We have t₁=3 and r=4/3

First, we will check that the value of ris lies between −1/ to 1 or not :

Since r=4/3=1.3333

Thus,1.3333>1

So the value of r doesn’t lie between −1 to 1.

Therefore, the series is divergent and it has no sum.

Sincer>1, the series is divergent and it has no sum.

Page 63 Problem 17 Answer

Given: t₁=5 and r=1

To find: The sum of an infinite geometric series.

First, we need to check whether an infinite geometric series is convergent or divergent.

If it is convergent, then we will use the formula of the sum of an infinite geometric series.

We have t₁=5 and r=1.

First, we will check that the value of r is lies between −1 to 1 or not :

Since r=1

Then all of the terms of the series are the same and the series is infinite.

Thus, if r=1 then the series does not converge.

Since r=1, the series is divergent and it has no sum.

Mcgraw Hill Precalculus Textbook Answers

Page 63 Problem 18 Answer

Given: The series 1+0.5+0.25+⋯

To find: The sum of an infinite geometric series.

First, we need to find the value of rand and then check whether an infinite geometric series is convergent or divergent.

If it is convergent, then we will use the formula of the sum of an infinite geometric series.

We have the series1+0.5+0.25+⋯

First, find r:

r=0.5

1 =0.5

Now we have t1=1 andr=0.5and we know that−1<0.5<1

Since −1<r<1, the series is convergent and the sum of an infinite geometric series exists.

Using the formula for the sum of an infinite geometric series, we get

S_∞ = t₁/1−r

=1/1−0.5

=1/0.5

=2

∴S∞=2

Thus, the sum of an infinite geometric series is 2.

Page 63 Problem 19 Answer

Given: The series 4−12/5+36/25−108/125+⋯

To find: The sum of an infinite geometric series.

First we need to find the value of r and then check whether an infinite geometric series is convergent or divergent.

If it is convergent, then we will use the formula of the sum of an infinite geometric series.

We have the series 4−12/5+36/25−108/125+⋯

First, find r:

r=−12/5

4  =−12/5×1

4  =−3/5

=−0.6

Now we have t₁ = 4 and r=−0.6 and we know that −1<−0.6<1.

Since −1<r<1, the series is convergent and the sum of an infinite geometric series exists.

Using the formula for the sum of an infinite geometric series, we get

S_∞=t₁/1−r

=4/1−(−0.6)

=4/1+0.6

=4/1.6

=2.5

∴ S_∞=2.5

Thus, the sum of an infinite geometric series is 2.5.

Page 63 Problem 20 Answer

Given: 0.87

0.87 can be expressed as an infinite geometric series.

i.e.,0.87 =0.87878787…

=0.87+0.0087+0.000087+0.00000087+⋯

To find: The sum of an infinite geometric series.

First, we need to find the value of r and then check whether an infinite geometric series is convergent or divergent.

If it is convergent, then we will use the formula of the sum of an infinite geometric series.

We have the series0.87+0.0087+0.000087+0.00000087+⋯

By rewriting each term as a fraction,

87/100+87/10000+87/1000000+87/100000000+⋯

=87/100+87/100(1/100)+87/100(1/10000)+87/100(1/1000000)+…

=87/100+87/100(1/100)+87/100(1/100)2+87/100(1/100)3+⋯

So herer=1/100

=0.01

Now we have t₁=87/100 and r=0.01 and w know that −1<0.01<1.

Since −1<r<1, the series is convergent and the sum of an infinite geometric series exists.

Using the formula for the sum of an infinite geometric series, we get

S_∞=t₁/1−r

=87/100/1−1/100

=87/100/99/100

=87/99

∴ S_∞=87/99

Thus, the sum of an infinite geometric series is 87/99.

Mcgraw Hill Precalculus Textbook Answers

Page 63 Problem 21 Answer

0.437 can be written as a geometric progression of an infinite series

0.437 =0.437+0.000437+0.000000437+−−−−−−

t₁=0.437

r=1/103

find the sum of this given series

0.437 =0.437+0.000437+0.000000437+−−−−−−

437 =0.437/1 − 0.001

0.437 =0.437/0.999

0.437 = 437/999

hence,the sum of the infinite geometric series is 437/999

Page 63 Problem 22 Answer

Given statement: 0.9999=1 this is absolutely wrong because when we extend this number to infinite then also 0.9999 will tend to 1 that doesn’t mean that it is equal to 1.

hence we can say clearly that0.999≠1

Page 63 Problem 23 Answer

Given:S∞=5+5(2/3)+5(2/3)2+5(2/3)3−−−−∞

t₁ = 5

r=2/3​

find the sum of this given series.

S_∞ = 5 + 5(2/3 ) + 5(2/3 )2  + 5(2/3 )3 −−−− ∞

S_∞ =5/1 −2/3

S_∞ = 15

hence the sum of an infinite given geometric series is 15.

Page 63 Problem 24 Answer

Given:

S_∞ = 1+(−1/4)+(−1/4)2+5(−1/4)3−−−−∞

t₁=1

r = −1/4

find the sum of the given series.

S_∞ = 1 + (−1/4 ) + (−1/4 )2 + 5(−1/4 )3 −−−− ∞

S_∞ =1/1 − (−1/4 )

S_∞ =4/5

hence the sum of infinite geometric series is 4/5

Page 63 Problem 25 Answer

Given: S_∞=7+7(1/2)+7(1/2)2+7(1/2)3−−−−∞

Where t1=7 r=1/2 find S_∞

S_∞ = 7 + 7(1/2 ) + 7(1/2 )2 + 7(1/2 )3 −−−− ∞

S_∞ =7/1 − 1/2

S_∞ = 14

hence the sum of this infinite geometric series is 14.

Pre-Calculus 11 Student Edition Chapter 1 Sequences and Series

Page 46 Problem 1 Answer

Given:

To do: Complete the table.

In a fractal tree, every branch in each stage has two new branches.

In a fractal tree, every branch in each stage has two new branches.

Stage1 has one branch.Draw two line segments at the top of the segment in such a way that they are splitting away from each other.

Thus Stage 2 has two branches.

Read and Learn More Precalculus Textbook Mcgraw Hill Answers

Draw two line segments at the top of each segment of Stage 2 in such a way that they are splitting away from each other.

Since there are 2 branches in Stage 2, hence there will be 4 branches in Stage 3.

Similarly, Stage 4 has 8 branches and Stage 5 has 16 branches.

Now complete the table.

Hence the complete table is

Page 47 Problem 2 Answer

Definition: A geometric sequence is generated at each stage, after the first stage, is found by multiplying with the previous stage by a non-zero constant r, called the common ratio.

The general geometric sequence is t1,t1/r,t1/r2,t1/r3,………..

Mcgraw Hill Precalculus Textbook Answers

The first term in the geometric sequence is t1

The common ratio is the ratio of successive terms of a geometric sequence.

The common ratio is calculated by dividing any two consecutive terms r=tn/tn−1

The general term of the geometric sequence is tn=t1/rn−1

Where tn is the general term r is the common ratio t1 is the first term n is number of terms

​The first term in the geometric sequence is t1

The common ratio of the geometric sequence is r=tn/tn−1

The general term of the geometric sequence is tn=t1/rn−1

Page 47 Problem 3 Answer

To find: Determine whether the geometric sequence is used to find the total number of branches formed at the end of stage 5.

Given: The number of stages the branches formed is 5 (i.e)n=5.

The general term of the geometric sequences is tn=t1/rn−1

Yes, A geometric sequence can be generated.

By given t 5 be the total number of branches formed at the end of stage 5.

Let a be the initial number of branches (i.e) t1=a.

Let r be the common ratio.

Substituting in the  geometric sequences we get,

​t5=ar5−1

t5=ar4

Thus, The total number of branches formed at the end of stage 5 is t5=ar4.

Page 47 Problem 4 Answer

To find: Determine whether the geometric sequence is used to find the total number of branches formed at the end of stage 100.

Given: The number of stages the branches formed is 100 (i.e)n=100.

The general term of the geometric sequences is tn=t1/rn−1

Yes, A geometric sequence can be generated.

By given t100 be the total number of branches formed at the end of stage 100.

Let a be the initial number of branches (i.e) t1=a

Let r be the common ratio.

Substituting in the  geometric sequences we get,

t100 =ar100−1

t100 =ar99

Thus, The total number of branches formed at the end of stage 100 is t100=ar99.

Mcgraw Hill Precalculus Textbook Answers

Page 50 Problem 5 Answer

Sequence given in the question is,5+15+45+⋯

We will use the expression for the sum of 8 terms of the given geometric sequence.

Sn=a(rn−1)/r−1

For the given sequence,a=5

r=15/5=3

n=5

By substituting the values of a=5,r=3 and n=8 in the given expression,

Sn=a(rn−1)/r−1

S8=5(38−1)/3−1

=5(6561−1)/3−1

=5(6560)/2

=16400

Sum of 8 terms of the given geometric sequence (5+15+45+⋯) will be 16400.

Page 50 Problem 6 Answer

Expression for the sum of n terms of a geometric series → Sn=a(1−rn/)1−r

By substituting the values,

a=64,n=8,r=1/4

S8=64[1−(1/4)8]/1−1/4

=64[1−1/65536]/1−1/4

=64(65535/65536)/3/4

=64(65535)/65536×4/3

=5592320/65536

=21845/256

Sum of the 8 terms of the series with the first term 64,common ratio 1/4 will be 21845/256.

Mcgraw Hill Precalculus Textbook Answers

Page 51 Problem 7 Answer

Series given in the question is, 1/64+1/16+1/4,…+1024

We will find the number of terms in the series with the expression,

Tn=arn−1 Where, Tn= nth term

a= First term

r= Common ratio

n= Number of term

Then we will use the expression for the sum of n terms of the series,

Sn=a(rn−1)/r−1

Where r>1

Given geometric series,

1/64+1/16+1/4+….+1024

Here, nth term of the series=1024

First terma=1/64

r=1/16

1/64  =64/16

=4

Substitute the values in the expression for nth term,

Tn=arn−1

1024=1/64(4n−1)/4n−1

=65536/4n−1

=48

n−1=8

n=9

Therefore, we have to find the sum of 9 terms of the given series.

Substitute the values in the expression for the sum of 9 terms of the given series,

Mcgraw Hill Precalculus Textbook Answers

Sn=a(rn−1)/r−1

=1/64(49−1)/4−1

=(262144−1)/64×3

=262143/192

=87381/64

Sum of the given series (1/64+1/16+1/4+⋯+1024) will be 87381/64.

Page 51 Problem 8 Answer

Geometric series given in the question is,−2+4−8+….−8192

We will find the number of terms in the given series first.

Expression to get the number of terms in the series,

Tn=arn−1

Then we will find the sum of n terms by substituting the values of a,r and n in the expression,

Sn=a(1−rn)/1−r

where r<1

Given series in the question,−2+4−8+.…−8192

First terma=−2

r=4/−2

=−2 nth term of the series =−8192

Expression for the nth term of the given series,

Tn=arn−1

Substitute the values in the expression,−8192=(−2)(−2)n−1

4096=(−2)n−1/(−2)12

=(−2)n−1

12=n−1

n=13

We have to find the sum of 13 terms of the given series.

By using the expression,

Sn=a(1−rn)/1−r

Bu substituting the values a=(−2),r=−2,n=13,

S13=(−2)[1−(−2)13]/1−(−2)

=−2(1+8192)/1+2

=(−2)(8193)/3

=−5462

Sum of given series in the question in the question(−2+4−8+.…−8192) will be−5462.

Page 52 Problem 9 Answer

Number of participants in a tournament = 512

Therefore, in first round number of matches playedt1

=512/2

=256

In each round half the payers are eliminated, so the common ratio r=1/2

And the last term of the series will be final match, tn=1

By substituting these values in the expression, we can get the total matches played.

Expression for the sum of n terms of the geometric series,

Sn =rtn−t1/r−1

Here, tn=nth term of the series=1

t1=Matches played in first round=256

r=Common ratio=1/2

Substitute these values in the expression,

Sn=1/2(1)−256/1/2−1

=−511/2−1/2

=511

Total matches to be played with 512  participants will be 511.

Precalculus Textbook Mcgraw Hill Answers

Page 53 Problem 10 Answer

The given series is 4+24+144+864+.………

We have to check whether the series is geometric or not.

Find the ratio of all terms to their preceding terms and check if the ratios are equal or not, if the ratio is equal then the given series will be a geometric series.

The given series is 4+24+144+864+.……….

The ratios are calculated as:

24/4=6/144

24=6/864

144=6​

Since, the ratio  of the term and their preceding term is constant  throughout the series

Hence the given series is a geometric series.

The common ratio of the given series is 6, thus the given series is a geometric series.

Page 53 Problem 11 Answer

The given series is −40+20−10+5−.…

We have to check whether the series is geometric or not.

Find the ratio of all terms to their preceding terms and check if the ratios are equal or not, if the ratio is equal then the given series will be a geometric series.

The given series is −40+20−10+5−.……….

The ratios are calculated as:

20/(−40)=−1/2

(−10)/20=−1/2

5/(−10)=−1/2​

Since, the ratio  of the term and their preceding term is constant  throughout the series.

Hence the given series is a geometric series.

The common ratio of the given series is −1/2, thus the given series is a geometric series.

Page 53 Problem 12 Answer

The given series is 3+9+18+54+.…..

We have to check whether the series is geometric or not.

Find the ratio of all terms to their preceding terms and check if the ratios are equal or not, if the ratio is equal then the given series will be a geometric series.

The given series is 3+9+18+54+.…

The ratios:​9/3=3

18/9=2

54/18=3​

Since the ratio of the term and their preceding term is not constant throughout the series.

Hence the given series is not a geometric series.

The ratio of the terms and their preceding terms are not constant in the given series, thus the given series is not a geometric series.

Page 53 Problem 13 Answer

The given series is 10+11+12.1+13.31+.…

We have to check whether the series is geometric or not.

Find the ratio of all terms to their preceding terms and check if the ratios are equal or not, if the ratio is equal then the given series will be a geometric series.

The given series is 10+11+12.1+13.31+⋯

Now the ratios are calculated as,

11/10=1.1

12.1/11=1.1

13.31/12.1=1.1​

Since the ratio of the term and its preceding term is constant throughout the series.

Hence the given series is a geometric series.

The common ratio of the series is 1.1  so the given series is a geometric series.

Precalculus Textbook Mcgraw Hill Answers

Page 53 Problem 14 Answer

We need to find sum of 10 terms if t1=12,r=2,n=10

Substitute these values in formula of sum of geometric series and solve.

S10 = 12(210 − 1)/2 − 1

=12(1024 − 1)/1

= 12(1023)

= 12276

The sum Sn for given geometric series is 12276

Page 53 Problem 15 Answer

We need to find sum Sn If t1=27,r=1/3,n=8

Substitute these values in formula of sum of geometric series and solve.

Sn =27[(1/3 )8 − 1]/1/3− 1

=27(1/6561 − 1)/−2/3

= −81(−6560)/2(6561)

=3280/81

The sum Sn for given geometric series is 3280/81.

Page 53 Problem 16 Answer

We are given

t1=1/256,r=−4,n=10

It is asked to find the Sn as exact values in fraction form.

The sum of the geometric series can be found by applying nth term sum formula.

We have

t1=1/256,r=−4,n=10

Apply the sum formula: Sn=t1(rn−1)/r−1

Plug values into the sum formula

S10=1/256((−4)10−1)/−4−1

S10=−209715/256

Hence, the sum in exact values is in fraction form S10=−209715/256

Precalculus Textbook Mcgraw Hill Answers

Page 53 Problem 17 Answer

We are given t1=72,r=1/2,n=12

It is asked to find the Sn as exact values in fraction form.

The sum of the geometric series can be found by applying nth term sum formula.

We have t1=72,r=1/2,n=12

Apply the sum formula: Sn=t1(rn−1)/r−1

Plug values into the sum formula

S12=72((1/2)12−1)/1/2−1

S12=36855/256

Hence, the sum in exact values is in fraction form S12=36855/256

Page 53 Problem 18 Answer

We are given a geometric series 27+9+3+…..+1/243

It is asked to find the Sn in  nearest hundredth

It can be found by finding the first term, common ratio, and the number of terms into the sum formula.

The series is 27+9+3+…..+1/243

Firstly, find the first term t1=27

Now, we can find the common ratio

The common ratio is the ratio of the second term and first term

r=9/27

r=1/3

Now, we can find the n

Apply general terms formula: tn

=t1(r)n−1

Plug these values into the formula

1/243=27(1/3)n−1

Solve for n(1/3)n−1=1/27×243(1/3)n−1

=1/33×35/(1/3)n−1

=1/38/(1/3)n−1

=(1/3)8

Compare exponent on both sides because bases are the same.

n−1=8

n=9

We have got

t1=27,r=1/3,n=9

Apply the sum formula: Sn=t1(rn−1)/r−1

Plug these values into the formula

S9=27((1/3)9−1)1/3−1

S9=9841/243

S9=40.50

Hence, the sum of geometric series is S9=40.50

Page 53 Problem 19 Answer

We are given a geometric series 1/3+2/9+4/27+……+128/6561

It is asked to find the Sn in  nearest hundredth

It can be found by finding the first term, common ratio, and the number of terms into the sum formula.

The series is

1/3+2/9+4/27+……+128/6561

Firstly, find the first term

t1=1/3

Now, we can find the common ratio

The common ratio is the ratio of the second term and first term

r=2/9

1/3

r=2/3

Now, we can find the n

Apply general terms formula: tn

=t1(r){n−1}

Plug these values into the formula

128/6561=1/3(2/3)n−1

Solve for n(2/3)n−1

=3×128/6561(2/3)n−1

=128/2187(2/3)n−1

=27/37(2/3)n−1=(2/3)7

Compare exponent on both sides

n−1=7

n=8

We have got

t1=1/3,r=2/3,n=8

Apply the sum formula: Sn=t1(rn−1)/r−1

Plug these values into the formula

S8=1/3((2/3)8−1)/2/3−1

S8=6305/6561

S8=0.96

Hence, the sum is S8=0.96

Precalculus Textbook Mcgraw Hill Answers

Page 53 Problem 20 Answer

We are given t1=5,tn=81920,r=4

It is asked to find the value of Sn

to the nearest hundred th The sum of the geometric series can be found by applying nth term sum formula.

We have

t1=5,tn=81920,r=4

Firstly, find the value of n

Apply general terms formula: tn=t1/(r){n−1}

Plug these values

81920=5(4){n−1}

5⋅​4{n−1}=81920

5⋅​4{n−1}

5=81920/5

4{n−1}=16384

4{n−1}=47Compare

exponent on both sides n−1=7

n=8

We have t1=5,tn

=81920,r=4,n=8

Apply the sum formula:  Sn=t1(rn−1)/r−1

Plug these values into the formula

S8=5((4)8−1)/4−1

S8=109225

Hence, the sum of geometric series is S8=109225

Page 53 Problem 21 Answer

Given :-t1=3,tn=46875,r=−5

To find :- The sum of the series i.e.Sn.

To find the sum we have to first find number of terms in the series then put it in in formula of sum.

Put the given values in formula tn=t1/rn−1

46875=3(−5)n−1

⇒15625=(−5)n−1

⇒(−5)6

=(−5)n−1

having the same base so the power must be same

⇒n−1=6

n=7

​So the number of term in the series are 7 put this value in second formula to obtain the sum.

Sn = t1(rn − 1)/r − 1

⇒ Sn = 3[(−5)7 − 1]/−5 − 1

⇒ Sn = 3[−78126]/−6

⇒ Sn = 39063

The sum of the given series is 39063

The sum of the given series is 39063.

Page 54 Problem 22 Answer

Given :-Sn=33,tn=48,r=−2

To find :- The first term of the given geometric series.

By using both formulas we will calculate the first term and number of terms in series.

First we will find out number of terms by dividing both the given formula.

Sn/an=a(rn−1)/r−1

a(rn−1)⇒sn

tn=(rn−1)

(r−1)(rn−1)⇒33

48=(−2)n−1−3(−2)n−1⇒33/16

=−(−2−1/(−2)n−1)⇒33/16

=2+1/(−2)n−1⇒33/16

−2=1/(−2)n−1⇒1/(−2)4

=1/(−2)n−1

⇒n−1=4

⇒n=5

​Put this value of n in the formula we will get first term of the series.

tn=t1(rn−1)⇒48=t1/(−2)n−1

⇒48=t1(−2)5−1

⇒48=16t1

⇒t1=3​

Hence we get the first term of the series is 3

The first term of the series is 3

Page 54 Problem 23 Answer

Given :-Sn=443,n=6,r=1/3

To find :- The first term of the series.

As the common ratio of the series is less than 1 and greater than -1 so we will use the given formula as in tip.

443 = t1(1 − (1/3 )6 )/1 − 1/3

⇒ 443 = t1(1 −1/729 )/2/3

⇒ 443 = t1x728 × 3/2 × 729

⇒ t1 =443 × 243/364

⇒ t1 = 295.73

⇒ t1 ≈ 296

The first term  of the geometric series is 296

Page 54 Problem 24 Answer

Given :- The first term of the series is 4 and the common ratio of the series is 3 and also we have the sum of the series is 4372.

To find :- The number of the term of the series.

Put all the value in the formula 4372=4(3n−1)/3−1

⇒2186=3n−1

⇒3n

=2187

⇒3n

=37

We will compare the power since same base⇒n=7​

The number of term in the geometric series are 7.

The number of term in the geometric series are 7.

Pre-Calculus 11 Student Edition Chapter 1 Sequences and Series

Page 33 Problem 1 Answer

When three coins are tossed, total outcomes is 8 ,expanded form is (2)(2)(2) and exponents is 2³.

When four coins are tossed, total outcomes is 16, expanded form is (2)(2)(2)(2) and exponents is 2⁴.

\(\begin{array}{c|c|c|c}
\hline \begin{array}{c}
\text { Number of } \\
\text { Coins, } \boldsymbol{n}
\end{array} & \begin{array}{c}
\text { Number of } \\
\text { Outcomes, } \boldsymbol{n}_{\boldsymbol{n}}
\end{array} & \begin{array}{c}
\text { Expanded } \\
\text { Form }
\end{array} & \begin{array}{c}
\text { Using } \\
\text { Exponents }
\end{array} \\
\hline 1 & 2 & (2) & 2^1 \\
\hline 2 & 4 & (2)(2) & 2^2 \\
\hline 3 & & & \\
\hline 4 & & & \\
\hline \vdots & \vdots & \vdots & \\
\hline n & & & \\
\hline
\end{array}\)

 

Hence, the three , four coins are tossed the total outcomes will become 8 and 16.

Page 33 Problem 2 Answer

Given,

As the number of coins increases, a sequence is formed by the number of outcomes.

To find =  What are the first four terms of this sequence?

If 1 coins is tossed, the total outcomes will become 2.

If 2 coins is tossed, the total outcomes will become 4.

If 3 coins is tossed, the total outcomes will become 8.

If 4 coins is tossed, the total outcomes will become 16.

So, the first four terms of this sequence is 2,4,8,16

Hence, the first four terms of this sequence is 2,4,8,16.

Read and Learn More Precalculus Textbook Mcgraw Hill Answers

Page 33 Problem 3 Answer

To find = Describe how the terms of the sequence are related. Is this relationship different from an arithmetic sequence? Explain.

An arithmetic sequence is a sequence where the difference d between successive terms is constant. …

An arithmetic series is the sum of the terms of an arithmetic sequence.

The nth partial sum of an arithmetic sequence can be calculated using the first and last terms.

An arithmetic sequence can be defined by an explicit formula in which an=a+(n−1)d, where d is the common difference between consecutive terms.

So, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. An arithmetic sequence is a list of numbers with a definite pattern.

Precalculus Textbook Mcgraw Hill Answers

Page 33 Problem 4 Answer

Given, As the number of coins increases, a sequence is formed by the number of outcomes.

To find=  Predict the next two terms of the sequence. Describe the method you used to make your prediction.

If 5 coins is tossed, the total outcomes will become 32.

If 6 coins is tossed, the total outcomes will become 64.

So, the next two terms of the sequence is 32 and 64.

The method is to first, find the common difference for the sequence.

Subtract the first term from the second term.

Subtract the second term from the third term.

To find the next value, add to the last given number.

Hence,  the next two terms of the sequence is 32 and 64.

Page 33 Problem 5 Answer

Given:  n coins are tossed.

To find: The method you could use to generate one term from the previous term.

For 2 coins, the outcomes are 2²=4 and for 3 coins the total number of outcomes is 2³=8.

Just need to multiply 2 with the total number of outcomes of the previous outcomes.

Need to multiply 2 to the previous term to get the term.

Precalculus Textbook Mcgraw Hill Answers

Page 33 Problem 6 Answer

Given: n coins are tossed

To find: divide the second term by the preceding term.

N coins are tossed, and the total number of outcomes is 2ⁿ

n−1 coins are tossed, the total number of outcomes are 2^n-1

Divide the terms:

2ⁿ/2ⁿ⁻¹=2

Dividing the term with the previous term, we get 2.

Page 33 Problem 7 Answer

Given: n coins are tossed

To discuss: The prediction of the terms.

All we need to do is to multiply 2 by the previous term to get the term.

All we need to do is to multiply 2 by the previous term to get the term.

Page 35 Problem 8 Answer

Given: n coins are tossed

To find: divide the second term by the preceding term.

N coins are tossed, and the total number of outcomes is 2ⁿ

n−1 coins are tossed, the total number of outcomes are 2ⁿ⁻¹

Divide the terms: 2ⁿ/2^n-1=2

Dividing the term with the previous term, we get 2.

Page 33 Problem 9 Answer

Given: n coins are tossed

To discuss: About the prediction of the terms.

All we need to do is to multiply 2 to the previous term to get the trem.

All we need to do is to multiply 2 to the previous term to get the term.

Precalculus Textbook Mcgraw Hill Answers

Page 35 Problem 10 Answer

Given, t₁ = 10

t₂ = 20

t₃ = 40

To find = General term of the sequence.

Common ratio= 20/10=2

40/20=2

The common ratios is 2.

Use the geometric sequence

t_n=t₁/rn−1

t_n =10(2)n−1

The general term of the sequence is tn

=10(2)n−1.

Page 35 Problem 11 Answer

Given,

First term= 42

Common ratio= 0.60

Number of terms= 9

Because you need to find the eighth term of the sequence.

t_n =t₁/rn−1

t₉=42(0.60)9−1

t₉=42(0.60)8

t₉=0.705

Hence, after 8 reductions, the shortest possible length of a photograph is approximately 0.7cm.

Precalculus Textbook Mcgraw Hill Answers

Page 37 Problem 12 Answer

Given, In a geometric sequence, the second term is 28 and the fifth term is 1792.

To find= t, r, and the first three terms of the sequence.

t₂=28

t₅=1792

t₅=t2/r³

1792=28r³

1792/28=r³

r=4

t₁=28/4= 7

t_n =7(4)n−1

t_n =28n−1

7,28,112….. is the first three terms of sequence.

Hence, the common ratio is 4 , the first number is 7 and the first three terms of sequence are 7, 28,112.

Page 39 Problem 13 Answer

Given, 1, 2, 4, 8, …

To find=.Determine if the sequence is geometric. If it is, state the common ratio and the general term in the form tn

=t₁/rn−1

Common ratio: 2/1=2

4/2=2

8/4=2

Here, 2 is a common ratio.

Use the general term of a geometric sequence.

t_n=t₁/rn−1

t_n=1(2)n−1

t_n = 2n−1

Hence, the common ratio is 2 and general term of the sequence is tn =2n−1.

Mcgraw Hill Precalculus Textbook Answers

Page 39 Problem 14 Answer

Given, 2,4,6,8

To find=.Determine if the sequence is geometric. If it is, state the common ratio and the general term in the form tn=t1/rn−1

The sequence is not geometric or arithmetic because there is no common difference or common ratio between each term.

Common ratios are = 4/2=2

6/4=3/2

8/6=4/3

Here, common ratios are different.

So this sequence is not geometric.

Hence, the sequence is not geometric or arithmetic.

Page 39 Problem 15 Answer

Given, 3, -9, 27, -81, …

To find= Determine if the sequence is geometric.

If it is, state the common ratio and the general term in the form

t_n=t₁/rn−1

Common ratio= −9/3=−3

= 27/−9=−3

=−81/27=−3

Here, common ratios is -3.

So, this sequence is geometric.

Use the general form

t_n=t₁/rn−1

t_n=3(−3)n−1

t_n =−9n−1

Hence, the common ratio is -3 and the general term is tn=−9n−1.

Page 39 Problem 16 Answer

Given, 1, 1, 2, 4, 8, …

To find =  Determine if the sequence is geometric.

If it is, state the common ratio and the general term in the form

t_n = t₁/rn−1

Common ratio= 1/1=1

=2/1=2

4/2=2

8/4=2

Here, the common ratios are different.

The sequence is not geometric or arithmetic because there is no common difference or common ratio between each term.

Hence, the sequence is not a geometric sequence.

Mcgraw Hill Precalculus Textbook Answers

Page 39 Problem 17 Answer

Given,

10, 15, 22.5, 33.75, …

To find =  Determine if the sequence is geometric.

If it is, state the common ratio and the general

Look at the ratios between successive terms. If the ratios are all the same, the sequence is geometric. If not, it isn’t.

Common ratio = 15/10=1.5

22.5/15=1.5

33.75/22.5=1.5

Here, common ratios are 1.5.

The ratios are all the same, so this is a geometric sequence.

Use the general term,

t_n =t₁/rn−1

t_n=10(1.5)n−1

t_n =15n−1

Hence, the common ratios is 1.5 and the general term is tn=15n−1.

Page 39 Problem 18 Answer

Given, -1, -5, -25, -125, …

To find =  Determine if the sequence is geometric. If it is, state the common ratio and the general form

Common ratio= −5/−1=5

−25/−5=5

−125/−25=5

Here, common ratio is 5.

So, this sequence is geometric.

Use the general form

t_n =t₁/rn−1

t_n=−1(5)n−1

Hence, the common ratios is 5 and the general term is tn=−5n−1

Mcgraw Hill Precalculus Textbook Answers

Page 39 Problem 19 Answer

Given; The table showing the first term.

\(\begin{array}{|c|c|c|c|}
\hline \begin{array}{c}
\text { Geometric } \\
\text { Sequence }
\end{array} & \begin{array}{c}
\text { Common } \\
\text { Ratio }
\end{array} & \begin{array}{c}
\text { 6th } \\
\text { Term }
\end{array} & \begin{array}{c}
10 \text { th } \\
\text { Term }
\end{array} \\
\hline 6,18,54, \ldots & & & \\
\hline 1.28,0.64,0.32,- & & & \\
\hline \frac{1}{5}, \frac{3}{5}, \frac{9}{5},- & & & \\
\hline
\end{array}\)

 

We have to find the common ratio,6th term and 10 term.

Therefore the following table for the given geometric sequences.

\(\begin{array}{|c|c|c|c|}
\hline \begin{array}{l}
\text { Ceometric } \\
\text { Sequence }
\end{array} & \begin{array}{l}
\text { Common } \\
\text { Ratio }
\end{array} & \begin{array}{l}
\text { 6th } \\
\text { Term }
\end{array} & \begin{array}{l}
\text { 10th } \\
\text { Term }
\end{array} \\
\hline 6,18,54, \ldots & 2 & 192 & 3,072 \\
\hline 1.28,0.64,0.32 \ldots & 0.5 & 0.04 & 0.0025 \\
\hline \begin{array}{l}
\frac{1}{5}, \frac{3}{5} \frac{9}{5},
\end{array} & 0.4 & 0.0020 & 5.2428 \\
\hline
\end{array}\)

 

Hence,Therefore the  following table for the given geometric sequences.

Page 39 Problem 20 Answer

Given ; t1=2,r=3

To find the first four terms of each geometric sequence.

To find first four terms take n = 1,2,3 and 4 respectively.

​⇒first term =2⋅31−1

=2⋅30

=2

⇒Second term =2⋅32−1

=2⋅31

=6

⇒Third term =2⋅33−1

=2⋅32

=2⋅9

=18

⇒ Fourth term =2⋅34−1

=2⋅27

=54​

Hence , the first four terms of each geometric sequence are 2,6,18 and 54.

Page 39 Problem 21 Answer

Given ; t₁=−3,r=−4

Determine the first four terms of each geometric sequence.

To find first four terms take n = 1,2,3 and 4 respectively.

⇒ First term =−3(−4)1−1

=−3(−4)⁰

=−3

⇒Second term =−3(−4)^2-1

=−3(−4)

=12

⇒Third term =−3(−4)3−1

=−3(−4)²

=−3(16)

=−48

⇒Fourth term =−3(−4)4−1

=−3(−4)³

=−3(−64)

=192

​Hence, the first four terms of each geometric sequence are −3,12,−48 and 192.

Mcgraw Hill Precalculus Textbook Answers

Page 39 Problem 22 Answer

Given ; t₁=4,r=−3

To Determine the first four terms of each geometric sequence.

To find the first four terms take n = 1,2,3 and 4 respectively.

⇒First term =4⋅(−3)^1-1

=4⋅(−3)⁰

=4

⇒Second term =4⋅(−3)^2-1

=4⋅(−3)

=−12

⇒Third term =4⋅(−3)^3-1

=4⋅(−3)²

=36

⇒Fourth term =4⋅(−3)^4-1

=4(−3)³

=4⋅(−27)

=−108

​Hence, the first four terms of each geometric sequence are 4,−12,36 and −108.

Page 39 Problem 23 Answer

Given ; t₁ =2, r=0.5

To find the first four terms of each geometric sequence.

To find the first four terms take n = 1,2,3 and 4 respectively.

⇒First term = 2⋅(0.5)^1-1

=2⋅(0.5)⁰

=2

⇒Second term =2.(0.5)^2-1

=2⋅(0.5)

=1

⇒Third term =2⋅(0.5)^3-1

=2⋅(0.5)²

=2⋅0.25

=0.5

⇒Fourth term =2⋅(0.5)^4-1

=2⋅(0.5)³

=2⋅(0.125)

=0.25

​Hence, the first four terms of each geometric sequence are 2,1,0.5 and 0.25.

Page 39 Problem 24 Answer

Given; t₁,t₂,t₃,t₄,t₅ in the geometric sequence.

⇒t₁=8.1,t₅

=240.1

To find the missing term: t_n,t₃,t₄.

⇒ t₄ = 240.1

⇒ 240.1 = 8.1(r)^5-1

⇒ 240.1 = 8.1(r)⁴

⇒ 240.1/8.1= r⁴

⇒ 29.64 = r⁴

⇒ 2.3 = r

⇒ t₂ = 8.1(2.3)^2-1

= 8.1(2.3)

= 18.63

⇒ t₃ = 8.1(2.3)^3-1

= 8.1(2.3)²

= 8.1(5.29)

= 42.849

⇒ t₄ = 8.1(2.3)4−1

= 8.1(2.3)³

= 8.1(12.16)

= 98.55

Hence, the missing terms are:t₂

=18.63,t₃

=42.849,t₄

=98.55.

Page 39 Problem 25 Answer

Given ; r=2,t₁=3

To Determine a formula for the nth term of each geometric sequence.

For the given sequence,t₁=3, r=2

Use the general term of a geometric sequence.

⇒ t_n =t₁/rn−1

⇒ t_n =(3)(2)n−1

=3(2)n−1

The general term of the sequence is t_n=3(2)n−1.

Hence, formula for the nth term of each geometric sequence:tn

=3(2)n−1.

Page 39 Problem 26 Answer

Given ; 192, -48, 12, -3, …

Determine a formula for the nth term of each geometric sequence.

Common difference of the geometric progression is −48/192=−1/ 4

Use the general term of a geometric sequence.

⇒t_n =t₁/rn−1

⇒t_n=192(−1/4)n−1

Hence, the general term of a geometric sequence is 192(−1/ 4)n−1.

Mcgraw Hill Precalculus Textbook Answers

Page 39 Problem 27 Answer

Given :t₃=5,t₆=135

To Determine a formula for the nth term of each geometric sequence.

The third term of the sequence is 5 and sixth term is 135.

Since the sequence is geometric .

⇒ t₄ =t₃

r ⇒ t₅

=t₃/r⋅r

⇒ t₆⋅r⋅r⋅r=t₃

⇒ 135=5⋅r³

⇒ 135/5=r3

⇒ 27=r³

​We have to find first term

⇒t₃=t₁/(3)3−1

⇒ 5=t₁⋅9

⇒ t₁ =5/9​

The general formula for nth term is 5/9(3)n−1

Hence, the general formula for nth term is 5/9(3)n−1.

Page 39 Problem 28 Answer

For the given sequence, t₁= 4, t₁₃₁ = 16384

Determine a formula for the nth term of each geometric sequence.

⇒ t₁₃ = t ⋅ r n−1

⇒ 16384 = 4 ⋅ r13−1

⇒16384/4= r12

⇒ 2.2 = r

Use general term for geometric sequence

⇒ t_n = t₁rn−1

⇒ t_n = 4(2.2)n−1

Hence, the general formula  for the nth term of each geometric sequence is :tn

=4(2.2)n−1.

Page 39 Problem 29 Answer

Given the following geometric sequences, determine the number of terms, n.

\(\begin{array}{c|c|c|c|}
\hline \begin{array}{c}
\text { First } \\
\text { Term, } \\
\boldsymbol{t}_1
\end{array} & \begin{array}{c}
\text { Common } \\
\text { Ratio, } \boldsymbol{r}
\end{array} & \begin{array}{c}
\text { Term, } \\
\boldsymbol{t}_{\boldsymbol{n}}
\end{array} & \begin{array}{c}
\text { Number } \\
\text { of } \\
\text { Terms, } \boldsymbol{n}
\end{array} \\
\hline 5 & 3 & 135 & \\
\hline-2 & -3 & -1458 & \\
\hline \frac{1}{3} & \frac{1}{2} & \frac{1}{48} & \\
\hline 4 & 4 & 4096 & \\
\hline-\frac{1}{6} & 2 & -\frac{128}{3} & \\
\hline \frac{p^2}{2} & \frac{p}{2} & \frac{p^2}{256} & \\
\hline
\end{array}\)

 

Therefore the complete value of n;

\(\begin{array}{|c|c|c|c|}
\hline \begin{array}{c}
\text { First } \\
\text { Term, } \\
\boldsymbol{t}_1
\end{array} & \begin{array}{c}
\text { Common } \\
\text { Ratio, } \boldsymbol{r}
\end{array} & \begin{array}{c}
\text { Term, } \\
\boldsymbol{t}_{\boldsymbol{n}}
\end{array} & \begin{array}{c}
\text { Number } \\
\text { of } \\
\text { Terms, } \boldsymbol{n}
\end{array} \\
\hline 5 & 3 & 135\\
\hline-2 & -3 & -1458\\
\hline \frac{1}{3} & \frac{1}{2} & \frac{1}{48}\\
\hline 4 & 4 & 4096\\
\hline-\frac{1}{6} & 2 & -\frac{128}{3}\\
\hline \frac{p^2}{2} & \frac{p}{2} & \frac{p^2}{256}\\
\hline
\end{array}\)

 

 

 

Mcgraw-Hill Textbook Answers Pre-Calculus 11 Student Edition Chapter 1 Sequences and Series

Page 22 Problem 1 Answer

Here, we are given 30 disks.

The sequence to be considered is 1, 2, 3, 4, 5.

We are asked to represent each number by small counting disk which are to be arranged in a triangular table.

The series may be represented as:

The answer is:

Page 22 Problem 2 Answer

As per the answer of part (a) is:

To find: The sum of numbers in the sequence.

Here, we can sum the numbers to find the answer.

The sum of numbers in the sequence is:

Read and Learn More Precalculus Textbook Mcgraw Hill Answers

1 + 2 + 3 + 4 + 5 = 15.

The answer is 15.

Page 22 Problem 3 Answer

As per the answer of part (a), we have:

As per answer of part (b), we have the sum of numbers of sequence as 15.

To find: The relation between the number of disks used with the sum of sequence.

We can find the number of disks used by counting the number of disks.

The number of disks used here are 15 and sum of numbers of sequence is also 15.

Therefore, we can conclude that the number of disks used is equal to the sum of numbers of sequence.

The number of disks used is equal to the sum of numbers of the sequence.

Mcgraw-Hill Textbook Answers

Page 23 Problem 4 Answer

We have to draw a triangle with the help of disks to represent the sequence 1, 2, 3, 4, 5.

We are required to copy the triangle of disks.

The answer can be:

The answer is:

Page 23 Problem 5 Answer

As per the answer of part(a), we have the following triangle:

We are required to rotate the triangle by180°.

On rotating the triangle, we get:

Now, when both the triangles are joined, the rectangle formed is:

The rotated triangle is:

The triangle formed by joining the triangles is:

Page 23 Problem 6 Answer

As per the answer of part (b), we have the following rectangle:

To find: The number of disks in the length and width of the rectangle.

Let us count the number of disks in vertical and horizontal direction.

The number of disks in the vertical direction is 6 so length is 6.

The number of disks in the horizontal direction is 5 so width is 5.

The length is 6 and width is 5.

Mcgraw-Hill Textbook Answers

Page 23 Problem 7 Answer

As per the answer of part (b), the rectangle obtained is:

As per answer of part (c), the length is 6 and width is 5.

To find: The number of disks in the area of rectangle.

The area can be found by multiplying the length with the width of rectangle.

The area of rectangle or the number of disks in the area of rectangle can be found as: 6⋅5=30.

Or simply, we can also count the number of disks as 30.

The answer is 30.

Page 23 Problem 8 Answer

As per the answer of part (d), the area of rectangle is equal to 30 sq units.

To find: The relation between the sum of sequence 1, 2, 3, 4, 5 and area of the rectangle.

First, let us find the sum of numbers of sequence.

The sum of sequence is1+2+3+4+5=15.

And area of rectangle is30=15∗2.

Therefore, the area of rectangle is twice the sum of sequence.

Area of rectangle is equal to twice of sum of sequence.

Page 23 Problem 9 Answer

Earlier, we found the area of rectangle that was made by first arranging the number of disks in sequence 1, 2, 3, 4, 5.

And then this triangular arrangement was rotated180°

and joined with original triangle to form a rectangle as shown below:

Then area of this rectangle was found by multiplying 5 with 6 which comes out to be equal to the number of disks used i.e. 30.

Now, we are asked to develop a formula to find the sum of n consecutive integers.

Here, we can see that the sum of first 5 consecutive integers is 15.

The rectangle thus formed contains the width as 5 which is equal to the number of integers and length is 6 which is 1 more than the number of integers.

The area thus found is 30 which is the double of product of the number and number plus 1.

And the sum of 5 consecutive integers is half the area of rectangle.

Therefore we can write the formula as:

Mcgraw-Hill Textbook Answers

Sum of n consecutive integers=n(n+1)/2.

The formula is: Sum of n consecutive integers=n(n+1)/2.

Page 23 Problem 10 Answer

Earlier, we found the area of rectangle that was made by first arranging the number of disks in sequence 1, 2, 3, 4, 5.

And then this triangular arrangement was rotated180°

and joined with original triangle to form a rectangle as shown below:

Then area of this rectangle was found by multiplying 5 with 6 which comes out to be equal to the number of disks used i.e. 30.

Then the sum of five consecutive integer is half of 30 which is 15.

We are asked to find how this method is related to Gauss method.

In Gauss method, we add the original series to its reverse and then we divide by 2.

If we closely observe, both the methods of finding the sum of n consecutive integers are working in similar manner.

Both the methods are working in similar manner.

Mcgraw-Hill Textbook Answers

Page 23 Problem 11 Answer

We are given that we have to start from the center of the grid and we have to draw a segment of one unit vertically upwards.

The segment can be drawn as follows:

The answer is:

Page 23 Problem 12 Answer

As per the answer of part(a), we have the following graph:

We are asked to draw another line to right of previous segment and is one unit longer than previous segment.

The line segments can be represented as follows:

The answer is:

Page 23 Problem 13 Answer

As per the answer of part (b), we have:

Now, we have to draw another segment vertically downwards which is one unit more than the previous segment.

The diagram can be draw

The answer is:

Page 23 Problem 14 Answer

As per the answer of part (c), we have the following diagram:

To find: The graph after continuing to 14 segments.

The graph can be drawn as follows:

The answer is:

Page 23 Problem 15 Answer

We are given that we have to follow the following steps:

1. Draw a line segment 1 unit up.
2. Draw a line segment to the right 2 units.
3. Draw a line segment downwards 3 units.

This pattern is repeated 14 times.

We are asked to record the lengths of segments as an arithmetic sequence.

The arithmetic sequence may be written as: 1, 2, 3, 4, …., 14.

Where first term is 1 and common difference is also 1.

The answer is: 1, 2, 3, 4, …., 14.

Where first term is 1 and common difference is also 1.

Mcgraw Hill Precalculus Textbook Answers

Page 23 Problem 16 Answer

As per the answer of part (a), the arithmetic sequence to represent the spiral is:

1, 2, 3, …. , 14.

To find: The total length of the spiral.

We are required to find the sum of these 14 terms here for calculating the total length of the spiral.

The sum to be found is:

1 + 2 + 3 + 4 + … + 14

We can take seven terms each to make the sum easier.

The sum of first seven terms is 1+2+3+4+5+6+7=28.

The sum of next seven terms is8+9+10+11+12+13+14=77.

Now, the total sum is 28+77=105.

The answer is 105.

Page 23 Problem 17 Answer

As per the answer of part (a), the sum of sequence to be found is 1, 2, 3, 4, … , 14.

As per answer of part (b), the sum is 105.

Here, we are asked to explain the method by which we have found the sum.

The method used to find the sum is:

1. Write the sequence in two smaller haves.
2. Add them separately.
3. Add both the results.

Page 23 Problem 18 Answer

Given 14 terms as:

1, 2, 3, 4, …. , 14.

To find: The sum of numbers using Gauss method.

Let us rewrite the series in reverse order first and add them.

Here, first the sequence can be written again in reverse order and then added to original sequence.

1+2+3+⋯+14

14+13+12+⋯+1

−−−−−−−−−−−−−−−−−−−−−−−−−−−

15+15+15+⋯+15(14 times)

⇒14⋅15

⇒210​

Now, the series has been added twice, therefore the sum is:

210/2=105.

This sum is same as already calculated by adding the terms simply.

The answer is 105 which is same as already calculated by adding the numbers algebraically.

Mcgraw Hill Precalculus Textbook Answers

Page 23 Problem 19 Answer

The series to be added using Gauss’s method is:

1+2+3+⋯+14.

As per part (a), number of terms were equal to 14.

Sum of each pair was 15.

To find: The sum of each pair and total number of terms.

Let us observe the part (a).

As per part(a), the number of terms are 14 which is equal to the number of segments itself.

And the sum of each pair was 15 which is 1 more than the number of terms.

The sum of each pair was 15 and number of terms were 14.

Sum of each pair was 1 more than the number of terms.

Page 23 Problem 20 Answer

Given 20 segments in a spiral where length of each segment is one more than the previous segment.

To find: The formula to find the sum of 20 such segments in the spiral.

First, let us derive the formula if n segments were there in the spiral.

Deriving the formula:

Let the series be 1, 2, 3, …. , n.

Adding the term and its reverse:

1+2+3+⋯+n

n+(n−1)+⋯1

−−−−−−−−−−−−−−−−−−

(n+1)+(n+1)+…+(n+1) [n times]

⇒n(n+1)/2

Finding the sum for 20 terms:

Now, putting n=20:

The sum of 20 segments in the spiral is:

20(20+1)/2

⇒10⋅21

⇒210

​The answer is 210.

Mcgraw Hill Precalculus Textbook Answers

Page 26 Problem 21 Answer

Given that sum of first two terms of an arithmetic series is 19 and sum of first four terms is 50.

To find: The first six terms and sum to 20 terms.

We can apply the formula and make equations to solve it.

Finding the first 6 terms:

The sum of first two terms may be written as:

S2=19=2

2(2⋅t1+(2−1)d)

⇒19=2t1+d…(1)

​The sum of first four terms may be written as:

50=4/2(2t1+(4−1)d)

⇒50=2(2t1+3d)

⇒50=4t1+6d…(2)

​Solving the equations, we have t1 =8,d=3.

Therefore, the first six terms are:

8,8+3,8+6,8+9,8+12,8+15

⇒8,11,14,17,20,23

​Finding the sum of 20 terms:

Using the formula, we have the following sum:

S20=20/2(2⋅8+(20−1)⋅3)

⇒S20

=10(16+19⋅3)

⇒S20

=10(71)

⇒S20

=710

​The series is 8, 11, 14, 17, 20, 23.

The sum of 20 terms is 710.

Mcgraw Hill Precalculus Textbook Answers

Page 27 Problem 22 Answer

Given: t1=5

d=3

tn=53​

We will find the sum of the given arithmetic series using the formula mentioned in the tip section.

For that, first we need to find the value of n which we will find using the formula of nth term of AP.

Then we will substitute the values and find the sum.

Calculation for finding the value of n

Formula for nth term is as follows:

⇒tn=t1+(n−1)d

Substitute the known values, we get

⇒53=5+(n−1)3

Simplify, we get

⇒48/3

=n−1

⇒n=17

Calculation to find the sum of each arithmetic series with given values

Formula for the sum is as follows:

⇒Sn

=n/2(t1+tn)

Substitute the known values, we get

⇒S17

=17/2(5+53)

Simplify, we get

⇒S17

=17/2×58

⇒S17=17⋅29

⇒S17

=493

Hence, the sum of the given arithmetic series is 493.

Mcgraw Hill Precalculus Textbook Answers

Page 27 Problem 23 Answer

Given:t1=7

d=7

tn=98

We will find the sum of the given arithmetic series using the formula mentioned in the tip section.

For that, first we need to find the value of n which we will find using the formula of nth term of AP.

Then we will substitute the values and find the sum.

Calculation for finding the value of n

Formula for nth term is as follows:

⇒tn

=t1+(n−1)d

Substitute the known values, we get

⇒98=7+(n−1)7

Simplify, we get

⇒91/7

=n−1

⇒n=14

Calculation to find the sum of each arithmetic series with given values

Formula for the sum is as follows:

⇒Sn=n/2(t1+tn)

Substitute the known values, we get

⇒S14

=14/2(7+98)

Simplify, we get

⇒S14

=7⋅105

⇒S14

=735

Hence, the sum of the given arithmetic series is 735.

Mcgraw Hill Precalculus Textbook Answers

Page 27 Problem 24 Answer

Given: t1=8

d=−5

tn=−102​

We will find the sum of the given arithmetic series using the formula mentioned in the tip section.

For that, first we need to find the value of n which we will find using the formula of nth term of AP.

Then we will substitute the values and find the sum.

Calculation for finding the value of n

Formula for nth term is as follows:

⇒tn=t1+(n−1)d

Substitute the known values, we get

⇒−102=8+(n−1)(−5)

Simplify, we get

⇒−110

−5=n−1

⇒n=23

Calculation to find the sum of each arithmetic series with given values

Formula for the sum is as follows:

⇒Sn

=n/2(t1+tn)

Substitute the known values, we get

⇒S23

=23/2(8+(−102))

Simplify, we get

⇒S23

=23/2(−94)

⇒S23

=23⋅(−47)

⇒S23

=−1081

Hence, the sum of the given arithmetic series is -1081.

Page 27 Problem 25 Answer

Given:t1=2/3

d=1/tn=41/3​

We will find the sum of the given arithmetic series using the formula mentioned in the tip section.

For that, first we need to find the value of n which we will find using the formula of nth term of AP.

Then we will substitute the values and find the sum.

Calculation for finding the value of n

Formula for nth term is as follows:

⇒tn

=t1+(n−1)d

Substitute the known values, we get

⇒41/3=2/3+(n−1)1

Simplify, we get

⇒13=n−1

⇒n=14

Calculation to find the sum of each arithmetic series with given values

Formula for the sum is as follows:

Precalculus Textbook Mcgraw Hill Answers

⇒Sn

=n/2(t1+tn)

Substitute the known values, we get

⇒S14

=14/2(2/3+41/3)

Simplify, we get

⇒S14

=7⋅43/3

⇒S14

=301/3

Hence, the sum of the given arithmetic series is 301/3.

Page 27 Problem 26 Answer

Given:1+3+5+⋯(S8)

We will find the sum of the given arithmetic series using the formula mentioned in the tip section.

⇒1+3+5+⋯(S8)

Here,  t1=1 and d = 2 i.e., 3 – 1

Formula for the sum of an arithmetic series is as follows:

⇒Sn

=n/2[2t1+(n−1)d]

Substitute the known values, we get

⇒S8

=8/2[2⋅1+(8−1)2]

Simplify, we get

⇒S8

=4(2+14)

⇒S8

=64

Hence, t1=1 , d = 2 and the indicated sum of the given arithmetic series is 64.

Precalculus Textbook Mcgraw Hill Answers

Page 27 Problem 27 Answer

Given:40+35+30+⋯(S11)

We will find the sum of the given arithmetic series using the formula mentioned in the tip section.

⇒40+35+30+⋯(S11)

Here, t1=40 and d = -5 i.e., 35 – 40

Formula for the sum of an arithmetic series is as follows:

⇒Sn

=n/2[2t1+(n−1)d]

Substitute the known values, we get

⇒S11

=11/2[2⋅40+(11−1)−5]

Simplify, we get

⇒S11

=11/2[80−50]

⇒S11

=11/2⋅30

⇒S11

=165

Hence, t1=40 , d = -5 and the indicated sum of the given arithmetic series is 165.

Page 27 Problem 28 Answer

Given:1/2+3/2+5/2+⋯(S7)

We will find the sum of the given arithmetic series using the formula mentioned in the tip section.

⇒1/2+3/2+5/2+⋯(S7)

Here, t1=1/2 and d = 1 i.e., 3/2−1/2

Formula for the sum of an arithmetic series is as follows:

⇒Sn

=n/2[2t1+(n−1)d]

Substitute the known values, we get

⇒S7

=7/2[2⋅1/2+(7−1)1]

Simplify, we get

⇒S7

=7/2[1+6]

⇒S7

=49/2

Hence, t1=1/2 , d = 1 and the indicated sum of the given arithmetic series is 49/2.

Precalculus Textbook Mcgraw Hill Answers

Page 27 Problem 29 Answer

Given:(−3.5)+(−1.25)+1+⋯(S6)

We will find the sum of the given arithmetic series using the formula mentioned in the tip section.

⇒(−3.5)+(−1.25)+1+⋯(S6)

Here, t1=−3.5 and d = 2.25 i.e., – 1.25 – ( – 3.5)

Formula for the sum of an arithmetic series is as follows:

⇒Sn

=n/2[2t1+(n−1)d]

Substitute the known values, we get

⇒S6

=6/2[2⋅−3.5+(6−1)2.25]

Simplify, we get

⇒S6

=3(−7+11.25)

⇒S6

=3(4.25)

⇒S6

=12.75

Hence, t1=−3.5, d = 2.25 and the indicated sum of the given arithmetic series is 12.75.

Pre-Calculus 11 Student Edition Chapter 1 Sequences and Series

Page 7 Problem 1 Answer

Follow the process of obtaining the staircase numbers mentioned above for each blank.

Complete the given box by the obtained values in the appropriate places.

For the third staircase number, add the number of cubes present in the third and fourth column.

Therefore, the third staircase number is 3+4=7.

Repeat the same process upto the tenth staircase number.

The fourth staircase number is4+5=9

The fifth staircase number is5+6=11

The sixth staircase number is6+7=13

The seventh staircase number is7+8=15

The eighth staircase number is8+9=17

The ninth staircase number is9+10=19

The tenth staircase number is10+11=21

Therefore the complete table is,

Read and Learn More Precalculus Textbook Mcgraw Hill Answers

The complete table is,

Page 7 Problem 2 Answer

Follow the process of obtaining the staircase numbers mentioned above for each blank.

Complete the given box by the obtained values in the appropriate places.

For the third staircase number, add the number of cubes present in the third, fourth and fifth column.

Therefore, the third staircase number is 3+4+5=12

Repeat the same process upto the tenth staircase number.

Precalculus Textbook Mcgraw Hill Answers

The fourth staircase number is4+5+6=15

The fifth staircase number is5+6+7=18

The  sixth staircase number is6+7+8=21

The seventh staircase number is7+8+9=24

The eighth staircase number is8+9+10=27

The ninth staircase number is9+10+11=30

The tenth staircase number is10+11+12=33

Therefore the complete table is,

The complete table is,

Page 8 Problem 3 Answer

The previously obtained numbers of cubes for a two step staircase are 3,5,7,9,11,…

If we observe  we can see that each number is two more than the previous number.

Hence the pattern of the numbers is, ” Number of cubes in n+1th column = Number of cubes in nth column +2″

For a two step staircase, each number is two more than the previous number.

Hence the pattern of the numbers is, ” Number of cubes in n+1th column = Number of cubes in nth column +2″

Page 8 Problem 4 Answer

Following the mentioned rule, obtain the required data.

the number of cubes in the 11th term =11+12=23

And the number of cubes in the 12th term =12+13=25

the number of cubes in the 11th term =23

And the number of cubes in the 12th term =25

Page 8 Problem 5 Answer

Use the mentioned rule as the strategy to obtain the number of cubes required for staircases with three, four, five, or six steps.

Therefore, to obtain a particular three step staircase number, obtain the sum of the number of cubes present in that particular staircase and in it’s next 3−1=2columns.

to obtain a particular four step staircase number, obtain the sum of the number of cubes present in that particular staircase and in it’s next 4−1=3 columns.

to obtain a particular five step staircase number, obtain the sum of the number of cubes present in that particular staircase and in it’s next 5−1=4 columns.

to obtain a particular six step staircase number, obtain the sum of the number of cubes present in that particular staircase and in it’s next6−1=5 columns.

to obtain a particular three step staircase number, obtain the sum of the number of cubes present in that particular staircase and in it’s next 3−1=2 columns.

to obtain a particular four step staircase number, obtain the sum of the number of cubes present in that particular staircase and in it’s next 4−1=3 columns.

Precalculus Textbook Mcgraw Hill Answers

to obtain a particular five step staircase number, obtain the sum of the number of cubes present in that particular staircase and in it’s next 5−1=4 columns.

to obtain a particular six step staircase number, obtain the sum of the number of cubes present in that particular staircase and in it’s next 6−1=5 columns.

Page 8 Problem 6 Answer

We know that, To obtain a particular n step staircase number, add the number of cubes present in that particular staircase and in it’s next n−1 columns.

and following the previous results we can conclude that, the difference between two consecutive numbers of the number of cubes is n in each case.

Which means the numbers follow a particular pattern of order, following which they can be considered a sequence with difference nbetween each consecutive terms.

Yes, the term of the number of cubes are considered as a sequence as, each consecutive terms has a difference of n.

Page 8 Problem 7 Answer

Following the previous results we can conclude that, the difference between two consecutive numbers of the number of cubes is n in each case.

Which means the numbers follow a particular pattern of order, following which they can be considered a sequence with difference n between each consecutive terms.

We observed a pattern of difference n between each consecutive terms. Specifically, each term is n more than it’s previous term.

Page 8 Problem 8 Answer

We know that, To obtain a particular n step staircase number, add the number of cubes present in that particular staircase and in it’s next n−1 columns and following the previous results we can conclude that, the difference between two consecutive numbers of the number of cubes is n  in each case.

Therefore, for staircases of n steps (more than two steps), each term is generated by adding n more to the previous term.

For staircases of n steps (more than two steps), each term is generated by addingn

more to the previous term.

Page 8 Problem 9 Answer

To obtain a particular n step staircase number, add the number of cubes present in that particular staircase and in it’s next n−1 columns and each term can be generated by adding n to the previous terms.

Hence, the difference between two consecutive numbers of the number of cubes is n in each case.

Yes, the difference is same through out the whole sequence which is n for n staircase number.

Page 8 Problem 10 Answer

Follow the mentioned rule to obtain the 100th term of a two step staircase.

That is add the cubes present in the 100th and 101th column which results the addition of the numbers 100 and 101.

Total number of cubes

=100+101=201

To obtain the 100th term in a two-step staircase, we can find the sum of the 100th and 101th column which results the addition of the numbers 100 and 101, that is 201

Precalculus Textbook Mcgraw Hill Answers

Page 8 Problem 11 Answer

Let, pn be the number of cubes in nth term.

If we convert the mentioned pattern in a formula, it becomes,

Then.  pn=n+n+1=2n+1.

Substitute 100 for n in the above formula to obtain the 100th term.

So, for 100th term, the formula becomes, p100

=2⋅100+1

The formula by which the 100th term can be derived is p100

=2⋅100+1 where p100 is the 100th term.

Page 8 Problem 12 Answer

Let, the number of cubes in nth term be pn.

If we convert the mentioned pattern in a formula, it becomes,

pn=n+n+1=2n+1

The general formula to obtain the nth term is pn

=2n+1, where pn is the number of cubes in the nth term.

Mcgraw Hill Precalculus Textbook Answers

Page 11 Problem 13 Answer

Given, the child was 70 cm tall at the age of 3 and we have to obtain the child’s height at any age starting from age 3, therefore, 70 can be considered as the first term. So, a=7.

The child increases 5 cm per year. Therefore the common difference is 5. So, d=5.

Now, the height at any age p, is the p−2 th term of the sequence, as the first term of the sequence occurs at age 3=1+2.

Substitute the above values in the formula mentioned to obtain the required formula.

At any age p, height of the child is tp−2=70+(p−2−1)5

tp−2=70+(p−3)5

tp−2=70+5p−15

tp−2=55+5p

​At any age p, height of the child is, t_p−2=55+5p.

Page 11 Problem 14 Answer

To obtain the height of the child at age 10, Substitute 10 for p in the mentioned formula and simplify it.

The child’s height at age 10 is ,

t10−2=55+5⋅10

t8=55+50=105

​The child is expected to be of height 105 cm at age 10.

Page 14 Problem 15 Answer

Given that the 8th row contains 14 cans and the 12th row contains 10 cans. which implies, t8=14 and t12=10

Use the mentioned formula to substitute the values of t8 and t12 and simplify them to obtain the value of a in terms of d.

Next compare them to obtain the value of d.

Substitute the value of d in any of the values of d.

t8=14 implies, ​a+(8−1)⋅d=14

a+7d=14

a=14−7d​

And t12=10

implies a+(12−1)d=10

a+11d=10

a=10−11d​

Mcgraw Hill Precalculus Textbook Answers

Comparing, 14−7d=10−11d

11d−7d=10−14

4d=−4

d=−1

Therefore substituting this value in the equation a=10−11d

we obtain,a=10−11⋅(−1)

a=10+11=21​

Hence, tn=21+(n−1)(−1)

tn=21−n+1

tn=22−n

t1 is the first element which is already obtained as 21.

The final answers are,t1=21

d=−1

tn=22−n

​Page 15 Problem 16 Answer

Given:  Furnace technician charges $45, $46 per hour, for 10 hours

To find: The charge

For 10 hours the charge:

$460×10

=$460

Technician charge: $45

Total charge: $460+45=505

The total charge is $505.

Page 16 Problem 17 Answer

Given: t1=5 and  d=3

We have to find the first four terms of the sequence.

Consider the first term of the sequence is t1=5 and d=3

Then, add the common difference to the previous term for the next term.

Therefore,

t2⇒5+3=8

t3⇒8+3=11

t4⇒11+3=14

Thus, the terms are 5,8,11,14.

Hence, the first four terms are 5,8,11,14.

Mcgraw Hill Precalculus Textbook Answers

Page 16 Problem 18 Answer

Given:t1=−1 and d=−4

We have to find the first four terms of the sequence.

Consider the first term of the sequence is t1=−1 and d=−4

Then, add the common difference to the previous term for the next term.

Therefore,

t2⇒−1+(−4)=−5

t3⇒−5+(−4)=−9

t4⇒−9+(−4)=−13

Thus, the terms are−1,−5,−9,−13.

Hence, the first four terms are−1,−5,−9,−13.

Page 16 Problem 19 Answer

Given:t1=4 and d=1/5

We have to find the first four terms of the sequence.

Consider the first term of the sequence is t1=4 and d=1/5

Then, add the common difference to the previous term for the next term.

Therefore,

t2=4+1/5

t2=20+1/5

t2=21/5

t3=21/5+1/5

t3=22/5

t4=22/5+1/5

t4=23/5

Thus, the terms are 4,21/5,22/5,23/5.

Mcgraw-Hill Textbook Answers

Hence, the first four terms are 4,21/5,22/5,23/5.

Page 16 Problem 20 Answer

Given : t1=1.25 and d=−0.25

We have to find the first four terms of the sequence.

Consider the first term of the sequence is t1=1.25 and d=−0.25

Then, add the common difference to the previous term for the next term.

Therefore,

t2⇒1.25+(−0.25)=1

t3⇒1+(−0.25)=0.75

t4⇒0.75+(−0.25)=0.5

Thus, the terms are1.25,1,0.75,0.5.

Hence, the first four terms are1.25,1,0.75,0.5.

Page 16 Problem 21 Answer

Given:tn=3n+8

We have to find t1​

To find the indicated term, substitute the term number (n) in the given formula.

Consider tn=3n+8

Substitute n=1

Therefore,

t1=3(1)+8

t1=3+8

t1=11

Thus, t1=11.

Hence, the first term is t1=11.

Mcgraw-Hill Textbook Answers

Page 16 Problem 22 Answer

Given:tn=3n+8

We have to find t7

To find the indicated term, substitute the term number (n) in the given formula.

Consider tn=3n+8

Substitute n=7

Therefore,

t7=3(7)+8

t7=21+8

t7=29

Thus, t7=29.

Hence, the seventh term is t7=29.

Page 16 Problem 23 Answer

Given:tn=3n+8

We have to find t14

To find the indicated term, substitute the term number (n) in the given formula.

Consider tn =3n+8

Substitute n=14

Therefore,

t14=3(14)+8

t14=42+8

t14=50

Thus, t14=50.

Hence, the 14^th term is t14=50.

Precalculus Glencoe Answers

Page 16 Problem 24 Answer

Given: The first term is 6 and the fourth term is 33.

We have to find the second and third term of the sequence.

Consider t1 =6 and t4 =33

Use formula tn=t1+(n−1)d

Substitute for t4.

t4=6+(4−1)d

33=6+3d

3d=33−6

3d=27

d=9

Now, Second term

t2=t1+d

t2=6+9

t2=15

t3=t2+9

t3=15+9

t3=24

Thus, the second term is 15 and the third term is 24.

Hence, the second term is 15 and the third term is 24.

Page 16 Problem 25 Answer

Given: The first term is 8 and the fourth term is 41.

We have to find the second and third term of the sequence.

Consider t1=8 and t4=41

Use formula tn

=t1+(n−1)d

Substitute for t4.

Precalculus Glencoe Answers

t4=8+(4−1)d

41=8+3d

3d=41−8

3d=33

d=11

Now,  t2=t1+d

t2⇒8+11=19

t3⇒19+11=30

Thus, the second term is 19 and the third term is 30.

Hence, the second term is 19 and the third term is 30.

Page 16 Problem 26 Answer

Given: The first term is 42  and the fourth term is 27

We have to find the second and third term of the sequence.

Consider t1=42 and t4=27

Use formula tn =t1+(n−1)d

Substitute for t4.

t4=t1+(4−1)d

27=42+3d

3d=27−42

3d=−15

d=−5

Now, t2⇒t1+d

t2⇒42+(−5)=37

t3⇒t2+d

t3⇒37+(−5)=32

Thus, the second term is 37 and the third term is 32.

Hence, the second term is 37 and the third term is 32.