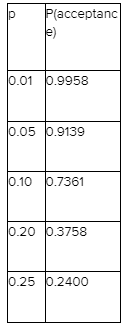
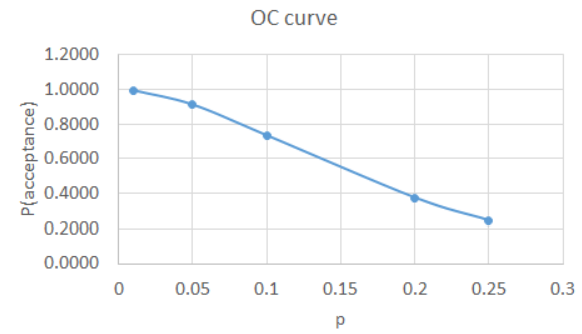
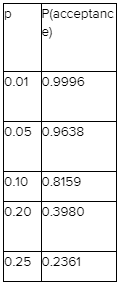
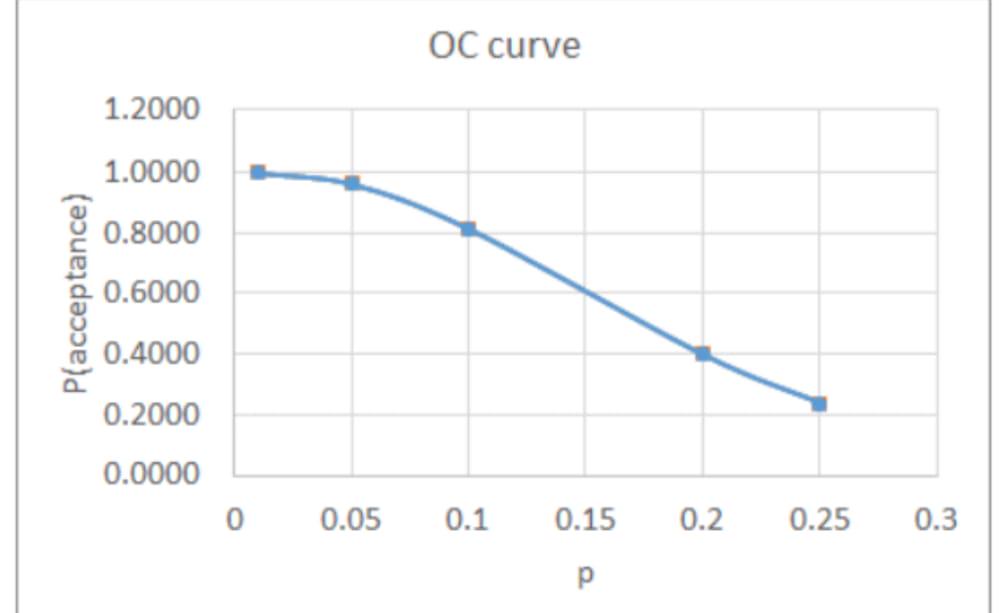
Probability And Statistics Solutions

Probability and Statistics for Engineering and the Sciences 8th Edition Chapter 2 Probability

Page 86 Problem 1 Answer

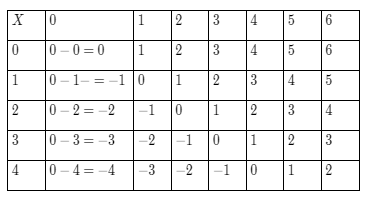
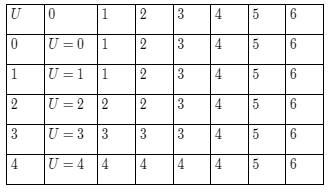
Given: Random student is selected from a university.

Given: A={ Visa } .

B={ MasterCard }

​Given: P(A)=0.5

P(B)=0.4

P(A∩B)=0.25

​To show that A and B are dependent by using the definition of independence.

To verify that the multiplication property does not hold.We will have to show that: P(A∣B)≠P(A) and P(A∩B)≠P(A)⋅P(B)

​Firstly, we will find P(A∣B) with the definition of conditional probability.

P(A∣B)=P(A∩B)/P(B)

=0.3/0.4

=0.75​

Also, we are given P(A)=0.6.

We clearly see that 0.75=P(A∣B)≠P(A)=0.6

Hence, events A and B are dependent.

We will verify this by using multiplication rule.

We know that if the two events are independent then they will satisfy P(A∩B)=P(A)⋅P(B)

From the given data, we see, P(A∩B)=0.3;P(A)⋅P(B)=0.6⋅0.4

=0.24

​Thus, we get P(A∩B)≠P(A)⋅P(B)

∴It is verified that these two events are independent.

We have shown that the events A and B are dependent and that the multiplication property does not hold.

Page 86 Problem 2 Answer

Given: An oil exploration company currently has two active projects, one in Asia and the other in Europe.

Let A be the event that the Asian project is successful and B be the event that the European project is successful.

Given: A and B are independent events with P(A)=0.4 and P(B)=0.7

To find the probability that the European project is not successful given that the Asian project is not successful.

We will use the above stated propositions to find the probability.

A and B are given to be independent.

Now, using above preposition we know that A​′ and B​′ are also independent.

We will now find the conditional probability of B​′ and given that the event A​′ has occurred and is denoted by P(B′∣A′).

Here, event B​′ is European project is successful and event A​′ is the Asian project is not successful.

if P(A∣B)=P(A)  ,where A and B are the two events then this implies that they are independent.

Now, ​P(B′∣A′)=P(B′)

=1−P(B)

=1−0.7

=0.3

​The probability that the European project is also not successful given that the Asian project is not successful is : P(B′∣A′)=0.3

Page 86 Problem 3 Answer

Given: An oil exploration company currently has two active projects, one in Asia and the other in Europe.

Let A be the event that the Asian project is successful and B be the event that the European project is successful.

Given: A and B are independent events with P(A)=0.4 andP(B)=0.7

To find the probability that at least one of the two projects will be successful.

We will use the property P(A∪B)=P(A)+P(B)−P(A∩B)

The probability that at least one of the two projects will be successful is :

P(A∪B)=P(A)+P(B)−P(A∩B)

=0.4+0.7−0.4⋅0.7

=0.82​

From the above preposition when two sets A and B are independent then :

P(A∩B)=P(A)⋅P(B)

=0.4⋅0.7

=0.28​

The probability that at least one of the two projects will be successful is :P(A∪B)=0.82.

Page 86 Problem 4 Answer

Given: An oil exploration company currently has two active projects, one in Asia and the other in Europe.

Let A be the event that the Asian project is successful and B be the event that the European project is successful.

Given: A and B are independent events with P(A)=0.4 and P(B)=0.7

To find the probability only the Asian project is successful given that at least one of the two is successful.

We will use conditional probability P(A∣B)=P(A∩B)

P(B) where P(B)>0

We have A and B are independent which implies that A and B​′ are independent.

A∩B′  is the event only the Asian project is successful.

Now, we will find the conditional probability of A∪B given that the event  A∩B′ has occurred is denoted by P(A∩B′∣A∪B).

P(A∩B′∣A∪B)=P[(A∩B​′)∩(A∪B)]/P(A∪B)

=P(A∩B​′)/P(A∪B)

=P(A)⋅P(B​′)/P(A∪B)

=0.4⋅(1−0.7)/0.82

=0.146

​The probability that only the Asian project is successful is :P(A∩B′∣A∪B)=0.146

Page 86 Problem 5 Answer

Given: A and B events are independent.To show that events A​′ and B are independent.

We will show that: P(A′∣B)=P(A′)

To prove that event A​′ and B are independent.

Using conditional probability we have,

P(A′∣B)=P(A′∩B)/P(B) [Now using, P(B)=P[(A′∩B)∪(A∩B)]=P(A′∩B)+P(A∩B)

That is P(A′∩B)=P(B)−P(A∩B)]

=P(B)−P(A∩B)/P(B) [Now using multiplication property where events A and B are independent.]

=P(B)−P(A)P(B)/P(B)

=P(B)(1−P(A))/P(B)​ [Now, for any event C we know that P(C)+P(C′)=1 .]

=1−P(A)

=P(A′)​

Hence we get: P(A′∣B)=P(A′)

Therefore events A​′ and B are independent.

We have shown that the events A′ and B are independent if A and B are independent.

Page 87 Problem 6 Answer

Given: One of the assumptions underlying the theory of control charting is that successive plotted points are independent of one another.

Each plotted point can signal either that a manufacturing process is operating correctly or that there is some sort of malfunction.

Given: The probability that a particular point will signal a problem with the process is 0.5.

To find the probability that at least one of 10 successive points indicates a problem when in fact the process is operating correctly.

To find the probability for 25 successive points.

We will use multiplication property for independent events and the fact that if A and B are independent then A′ and B′are also independent events.

Let us denote the event as :Ai={ point i error was signaled incorrectly }

where i=1,2,…,25

The probability of each of the event is given 0.05 is same for all events.

Now, the probability that at least one of 10 successive points indicates a problem when in fact the process is operating correctly is denoted as the union of the events A1,A2,…,A10.

Now, using De Morgan’s Law we have :

P(A1∪A2∪…∪A10)=P[(A1′∩A2′∩…∩A10′)′]

[Now, using the property when A be an event P(A′)+P(A)=1 ]

=1−P(A1′∩A2′∩…∩A10′) [Now using multiplication property]

=1−P(A1′)⋅P(A2′)⋯…P(A10′)∣ [Again using P(A′)+P(A)=1]

=1−(1−0.05)⋅(1−0.05)⋅…⋅(1−0.05)

=1−0.9510

=0.401

​Similarly for 25 successive points we get :

P(A1∪A2∪…∪A25)=P[(A1′∩A2′∩…∩A25′)′]

=1−P(A1′∩A2′∩…∩A25′)

=1−P(A1′)⋅P(A2′)⋯…P(A25′)

=1−(1−0.05)⋅(1−0.05)⋅…(1−0.05)

=1−0.9525

=0.723.​

The probability that at least one of 10 successive points indicates a problem when in fact the process is operating correctly is 0.401.

The probability for 25 successive points is 0.723.

Page 87 Problem 7 Answer

Given:  In October, 1994, a flaw in a certain Pentium chip installed in computers was discovered that could result in a wrong answer when performing a division.

The manufacturer initially claimed that the chance of any particular division being incorrect was only 1 in 9 billion, so that it would take thousands of years before a typical user encountered a mistake.

However, statisticians are not typical users; some modern statistical techniques are so computationally intensive that a billion divisions over a short time period is not outside the realm of possibility.

Given that the 1 in 9 billion figure is correct and that results of different divisions are independent of one another.

To find the probability that at  least one error occurs in one billion divisions with the chip.

We will use multiplication of independent events and the fact that if A and B are independent then A′ and B′ are also independent.

We will denote the event as :

Denote event A={ the division is incorrect }.

And the probability of event A is given as P(A)=0.0000000009

And the probability of the same of one in nine billion is :

P(A)=1/9,000,000,000

=a

Now, we have assume that we have one billion divisions with the same chip.

Let us denote this event as Ai={ the ith division is incorrect } , from i=1 to billion,  where (i=1,2,…,109) .

​Now, the probability that at least one error occurs in one billion divisions with this chip is the union of the billion Ai events is :

Using De Morgan’s Law,

P(A1∪A2∪…∪A10​9)=P[(A1′∩A2′∩…∩A10​9′)′

=1−P(A1′∩A2′∩…∩A10​9′)

=1−P(A1′)⋅P(A2′)⋯⋅⋅P(A10​9′)

=1−(1−a)⋅(1−a)⋅…⋅(1−a)

=1−0.895

=0.105

​The probability that at least one error occurs in one billion divisions with the chip is 0.105

Page 87 Problem 8 Answer

Given: An aircraft seam requires 25 rivets.

The seam will have to be reworked if any of these rivets is defective.

Suppose rivets are defective independently of one another, each with the same probability.

To find the probability that a rivet is defective if 20% of all seams need reworking.

We will use the multiplicative property of independent events.

Given that an aircraft seam requires 25 rivets.

Let us consider the probability that a rivet is defected is p.

Now, let us consider the probability that a rivet is not defected is 1−p

And it is given that the rivets are defective independently of one another, each with the same probability.

The probability that the seam is to be reworked is :

P( reworked )=1−P( not reworked )

=1−P( all 25 rivets are non−defective )

=1−[P( rivet is non−defective )]25

(​ Since defective  probabilities are independent ​)

P( reworked )=1−[(1−p)25]

P( reworked )=0.2 is given then:

​0.2(1−p)25/1−p

p=1−(1−p)25

=0.8

=25/√0.8

=0.0088.

​⇒p≈0.009

​The probability that a rivet is defective if 20%  of all seams need reworking is 0.009

Page 87 Problem 9 Answer

Given: An aircraft seam requires 25 rivets.

The seam will have to be reworked if any of these rivets is defective.

Suppose rivets are defective independently of one another, each with the same probability.

To find how small the probability of a defective rivet should be to ensure that only 10% of all seams need reworking.

We will use the multiplicative property of independent events

Given that an aircraft seam requires 25 rivets…

Let us consider the probability that a rivet is defected is p.

Now, let us consider the probability that a rivet is not defected is 1−p.

And it is given that the rivets are defective independently of one another, each with the same probability.

The probability of a defective rivet be to ensure that only 10% of all seams need reworking is :

​P( reworked )=1−∣(1−p)25∣

⇒0.10=1−[(1−p)]{25}

⇒[1−p]25

=1−0.10

⇒(1−p)=0.901/25

⇒p=1−0.90{1/25}

⇒p=1−0.99579

p=0.00421

​The probability of a defective rivet should be 0.00421 to ensure that only 10% of all seams need reworking.

Page 87 Problem 10 Answer

Given: A boiler has five identical relief valves.

Given: The probability that any particular valve will open on demand is 0.96.

To assume independent operation of the valves and find P(at least one valve opens) and P(at least one valve fails to open).

We will multiplication rule on independent events and the fact that if two events are independent then their complements are also independent events.

Lets us consider the event A be that at least one valve open and event B be that at least one valve fails to open.

And let Vi be the events that i th valve open.

We have P(A)=1−P(A′) Where event A​′  be that has no valve opens. Now, the probability of A​′is :

P(A′)=P(V1′∩V2′∩V3′∩V4′∩V5′)

Now, using the multiplication rule we have :

P(A′)=P(V1′∩V2′∩V3′∩V4′∩V5′)=P(V1′)⋅P(V2′)⋅P(V3′)⋅P(V4′)⋅P(V5′)

=[P(Vi′)]5

=[1−P(Vi)]5

=[1−0.95]{5}

=[0.05]{5}

=0.0000003125

Now, the probability that at least one valve open is :

P(A)=1−P(A′)

=1−(0.0000003125)

=0.99999969

≈0.9999

​Now, we have P(B)=1−P(B′) where event B​′ is that all valves open.

Now, the probability of B​′is :

P(B′)=P(V1∩V2∩V3∩V4∩V5)

The probability that at least one valve fails to open is P(B)=1−P(B′)

By using multiplication rule,

P(B′)=P(V1∩V2∩V3∩V4∩V5)

=P(V1)⋅P(V2)⋅P(V3)⋅P(V4)⋅P(V5)

=[P(Vi)]5

=0.95{5}

=0.7737

Now, P(B)=1−P(B′)

=1−(0.774)

=0.2262

​The probability that at least one valve opens is 0.9999. The probability that at least one valve fails to open is0.2262

Page 87 Problem 11 Answer

Given: Two pumps connected in parallel fail independently of one another on any given day.

Given: The probability that only the older pump will fail is 0.10, and the probability that only the newer pump will fail is 0.05.

To find the probability that the pumping system will fail on any given day (which happens if both pumps fail).

Let us denote the events as :

A={ older pump fails }

B={ newer pump fails }​

Now, the probabilities are given :

P(A∩B′)=P(A)−P(A∩B)

=0.1/P(B∩A′)=P(B)−P(A∩B)

=0.05

Now, lets consider x=P(A∩B) , then

P(A)=0.1+x and

P(B)=0.05+x

Now, using the multiplication property we have :

P(A∩B)=P(A)⋅P(B)

=(0.1+x)⋅(0.05+x)

The quadratic equations will be :

x=0.005+0.1⋅x+0.05⋅x+x2/x2−0.85⋅x+0.005=0

​Now, the roots of this quadratic equation is :

x12=−b±√b²−4ac/2a

=0.85±√0.85²−4⋅1⋅0.005/2⋅1

x1=0.85+√0.85²−4⋅0.005/2

x{1}=0.8441

x2=0.85−√0.85²−4⋅0.005/2

x{2}=0.0059.

​We have P(A∪B)=P(A)+P(B)−P(A∩B).

Lets assume x1 is true then :

P(A∪B)=0.1+0.8441+0.05+0.8441−0.8441

P(A∪B)=0.9941

​Now, lets assume x²is true then :

P(A∪B)=0.1+0.0059+0.05+0.0059−0.0059

P(A∪B)=0.1559

Both are the possible solutions.

If x1 is true then we have P(A∪B)>1 which is not possible.x² is only possible solution.

The probability that the pumping system will fail on any given day (which happens if both pumps fail) is 0.0059.

Page 87 Problem 12 Answer

Given: Consider the system of components connected as in the accompanying picture.

Components 1 and 2 are connected in parallel, so that subsystem works iff either 1 or 2 works; since 3 and 4 are connected in series, that subsystem works iff both 3 and 4 work.

Given figure:

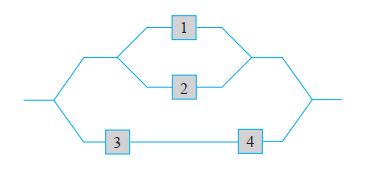
To find probability that the system works given that components work independently of one another.

We will use the multiplication property for independent events.

The given components are independent.

Their probability is :​P( component 1 works )=0.9

P( component 2 works )=0.9

P( component 3 works )=0.8

P( component 4 works )=0.8

​Now, using the multiplication rule :

P( component 1 and 2 work )=P( component 1 works )×P( component 2 works )

=0.9⋅0.9

=0.81​

Now, using the general addition rule for any two events –

If component 1 or component 2 works then the top subsystem works that is :

P( top subsystem works )=P( component 1 works )+P( component 2 works )−P( component 1 and 2 work )

=0.9+0.9−0.81

=0.99​

Similarly, if both components 3 and component 4 works then the bottom subsystem works that is :

P( bottom subsystem works )=P( component 3 works )×P( component 4 works )

=0.8⋅0.8

=0.64

​Each component is given independent which implies that the two subsystems are independent.

Using the multiplication rule for independent events we get :

P (both subsystems work) =P (top subsystem works) ×P (bottom subsystem works)

=0.99×0.64

=0.6336​

When the top subsystem works or the bottom subsystem works then the system will work.

P( system works )=P( top subsystem works )+P( bottom subsystem works )−P( both subsystems work )

=0.99+0.64−0.6336

=0.9964

=99.64%

​The probability that system works : P(system works) is 0.9964.

Page 87 Problem 13 Answer

Given: Components arriving at a distributor are checked for defects by two different inspectors (each component is checked by both inspectors).

The first inspector detects 90% of all defectives that are present, and the second inspector does likewise.

Given: At least one inspector does not detect a defect on  20% of all defective components.

To find the probability that a defective component will be detected only by the first inspector.

To find the probability that a defective component will be detected only by exactly one of the two inspectors.We will use the property P(A′)+P(A)=1

Let us denoted the events as :

A1={ first inspector detects }

A2={ second inspector detects}

​And the probabilities of the above events are given as :

P(A1)=0.9

P(A2)=0.9

​The probability that at least one inspector does not detect a defect is the union of the events A1′ and A2′ is given to be :

P(A1′∪A2′)=0.2

From the above given probability we can obtain :

P(A1∩A2)=1−P[(A1∩A2)′]

Now, using the property P(A′)+P(A)=1

we get :=1−P(A1′∪A2′)

=1−0.2

=0.8

​Now, the probability of event A1 intersection event A2 is :

P(A1∩A2′)=P(A1)−P(A1∩A2)

=0.9−0.8

=0.1

​Now, the probability that one of the two inspectors detect is the sum of the probability we just calculate above and the probability that a  defective component will be detected only by the second inspector  is :

P(A1′∩A2)=P(A2′)−P(A1∩A2)

=0.9−0.8

=0.1​

Now, we will define an event C as:C={ exactly one inspector detects }

And the probability of the event C is:

P(C)=P(A1∩A2′)+P(A1′∩A2)

=0.1+0.1

=0.2

​The probability that  a defective component will be detected only by the first inspector isP(A1

∩A2′)=0.1 .The probability that  a defective component will be detected by exactly one of the two inspectors is P(C)=0.2.

Page 87 Problem 14 Answer

Given: Components arriving at a distributor are checked for defects by two different inspectors (each component is checked by both inspectors).

The first inspector detects 90% of all defectives that are present, and the second inspector does likewise.

Given: At least one inspector does not detect a defect on  20%of all defective components.

To find the probability that all three defective components in a batch escape detection by both inspectors.

We will use the multiplication of independent events.

Let us denoted the events as :

A1={ first inspector detects }

A2={ second inspector detects }

​And the probabilities of the above events are given as :

P(A1)=0.9

P(A2)=0.9​

The probability that at least one inspector does not detect a defect is the union of the events A1′and A2′  is given to be :

P(A1′∪A2′)=0.2

From the above given probability we can obtain :

P(A1∩A2)=1−P∣∣(A1∩A2)′∣∣

Now using the property P(A′)+P(A)=1

we get :

=1−P(A1′∪A2′)

=1−0.2

=0.8

​The probability that neither of inspectors detect a defect is the complement of union of events A1 and A2 is : ( from part )

Using identity P(A)+P(A′)=1 we have,

P[(A1∪A2)′]=1−P(A1∪A2)

The union of two events can always be represented as the sum of these three events. So, we have

=1−[P(A1∩A2)+P(C)](P(C) from part (a) )

=1−0.8−0.2

=0

​Now we consider an event A3  which is denoted as :

A3={ all three defective components escape detection }

Now, the probability of event A3 is :

Using multiplication property we have,

P(A3)=P[(A1∪A2)′]⋅P[(A1∪A2)′∣⋅P[(A1∪A2)′]

=0⋅0⋅0

=0​

The probability that all three defective components in a batch escape detection by both inspectors is : P(A3)=0

Page 87 Problem 15 Answer

Given: Seventy percent of all vehicles examined at a certain emissions inspection station pass the inspection.

Given: Successive vehicles pass or fail independently of one another.

To calculate the probability: P(all of the next three vehicles inspected pass)We will use the multiplication rule for independent events.

We have: P( Pass )=0.7

Now we are given that the successive events are independent, hence we can apply multiplicative rule of multiplication for independent evets.

Therefore we get:

P( All three pass )

=P( Pass )×P( Pass )×P( Pass )

=0.7×0.7×0.7

=0.343

=34.3%

​We obtain: P(all of the next three vehicles inspected pass)=0.343

Page 87 Problem 16 Answer

Given: Seventy percent of all vehicles examined at a certain emissions inspection station pass the inspection.

Given: Successive vehicles pass or fail independently of one another.

To calculate the probability : P(at least one of the next three inspected fails)We will use the complement rule to calculate.

We have obtained in part a)

P (all of the next three vehicles inspected pass) =0.343

Hence by using complement rule we get:

P( At least one fail )

=1−P( All three pass )

=1−0.343

=0.657

=65.7%

​We obtain: P(at least one of the next three inspected fails)=0.657

Page 87 Problem 17 Answer

Given: Seventy percent of all vehicles examined at a certain emissions inspection station pass the inspection.

Given: Successive vehicles pass or fail independently of one another.

To calculate: P(exactly one of the next three inspected passes)We will use complement rule to calculate.

We have: P( Pass )=0.7 by using complement rule we get: P( Fail )

=1−P( Pass )

=1−0.7

=0.3

​We are given that the events are independent.

Hence by using the multiplicative rule for independent events we get:

P( Exactly one pass )

=3×P( Pass )×P( Fail )×P( Fail )

=3×0.7×0.3×0.3

=0.189

​We obtain: P(exactly one of the next three inspected passes)=0.189

Page 87 Problem 18 Answer

Given: Seventy percent of all vehicles examined at a certain emissions inspection station pass the inspection.

Given: Successive vehicles pass or fail independently of one another.

To calculate: P(at most one of the next three vehicles inspected passes)We will use addition rule for mutually exclusive events.

We have obtained in part c) that: P( Fail )=0.3

The events are independent.

Hence by using the multiplication rule:

P( None pass )

=P( Fail )×P( Fail )×P( Fail )

=0.3×0.3×0.3

=0.027​

We know from c that: P (exactly one of the next three inspected passes) =0.189

At most one vehicle passes when none of the vehicle passes OR exactly one vehicle passes.

These events are mutually exclusive hence we have: P( At most one pass )

=P( None pass )+P( Exactly one pass )

=0.027+0.189

=0.216​

We obtain: P(at most one of the next three vehicles inspected passes)=0.216.

Page 87 Problem 19 Answer

Given: Seventy percent of all vehicles examined at a certain emissions inspection station pass the inspection.

Given: Successive vehicles pass or fail independently of one another.

To find the probability all three vehicles pass given that at least one of the next three vehicles passes inspection.

We will use conditional probability formula: P(B∣A)=P(A∩B)

P(A),P(A)>0

From d) we have that: P( None pass )=0.027

Hence using complement rule we get:

P( At least one pass )

=1−P( None pass )

=1−0.027

=0.973

Now using conditional probability we get:

​​P( All three pass ∣ At least one pass )

=P( All three pass and At least one pass /P( At least one pass )

=P( All three pass )/P( At least one pass )

=0.343/0.973

​⇒P ( All three pass ∣ At least one pass )=0.3525

​The probability all three vehicles pass given that at least one of the next three vehicles passes inspection is 0.3525.

Page 88 Problem 20 Answer

Given: Professor Stan der Deviation can take one of two routes on his way home from work.

On the first route, there are four railroad crossings.

The probability that he will be stopped by a train at any particular one of the crossings is 0.1, and trains operate independently at the four crossings.

The other route is longer but there are only two crossings, independent of one another, with the same stoppage probability for each as on the first route.

On a particular day, Professor Deviation has a meeting scheduled at home for a certain time.

Whichever route he takes, he calculates that he will be late if he is stopped by trains at at least half the crossings encountered.

To determine which route to take so that he can minimize the probability of being late to the meeting.

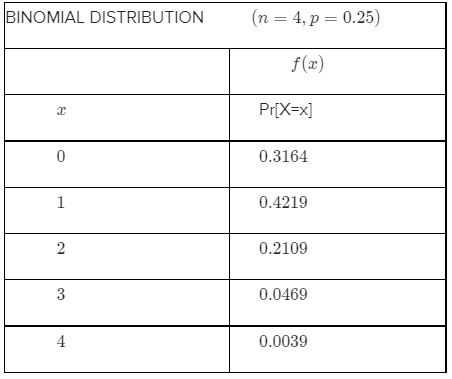
We will use the probability mass function of binomial random variable.

Let R1 and R2 be the events that the professor is late when taking the first route and the second route respectively.

Hence we have:

P(R1)=P(2 crossings )+P(3 crossings )+P(4 crossing )

=P(X=2)+P(X=3)+P(X=4)

=(​4/2​)p2/(1−p)4−2+(​4/3​)p3/(1−p)4−3+(​4/4​)p4/(1−p)4−4

=6⋅0.12⋅0.92+4⋅0.13⋅0.9+0.14

=0.05.

​For the second rule we will have :P(R2)

=P(1 crossings )+P(2 crossings )

=P(X=1)+P(X=2)

=(​2/1​)p1(1−p)2−1+(​2/2​)p2/(1−p)2−2

=0.1⋅0.9+0.9⋅0.1+0.1⋅0.1

=0.19.

We can see that the probability to get late of route one is lesser than that of route 2 the professor must choose the first route.

The professor should take the first route to minimize the probability of being late to the meeting.

Page 88 Problem 21 Answer

Given: Professor Stan der Deviation can take one of two routes on his way home from work. On the first route, there are four railroad crossings.

The probability that he will be stopped by a train at any particular one of the crossings is 0.1, and trains operate independently at the four crossings.

The other route is longer but there are only two crossings, independent of one another, with the same stoppage probability for each as on the first route.

On a particular day, Professor Deviation has a meeting scheduled at home for a certain time.

Whichever route he takes, he calculates that he will be late if he is stopped by trains at at least half the crossings encountered.

Given: The professor tosses a fair coin to decide on a route and he is late.

To find the probability that he took the four crossing route.We will use the law of total probability.

Let L denote the event that the professor is late home.

R1 and R2 are  the events that the professor is late when taking the first route and the second route respectively

Hence we need to find the probability of event R1∣L

Now we have:

P(R1∣L)=P(L∩R1)/P(L)

By using the multiplicative rule P(A∩B)=P(A∣B)⋅P(B)

we get: P(L∩R1)

P(L)=P(L∣R1)P(R1)/P(L)

By Law of total probability we get:

​P(L∣R1)P(R1)/P(L)

=P(L∣R1)P(R1)/P(L∣R1)P(R1)+P(L∣R2)P(R2)

=0.5⋅0.05/0.5⋅0.05+0.5⋅0.19

=0.22.

Hence P(R1∣L)=0.22

The probability that the professor took the four crossing route is 0.22.

 

Probability and Statistics for Engineering and the Sciences 8th Edition Chapter 2 Probability

Page 88 Problem 1 Answer

Given: A small manufacturing company will start operating a night shift.

There are 20 machinists employed by the company.

To find how many different crews are possible if a night crew consists of 3 machinists.

We will use combination formula: ​

C_k,n=(​n/k​)=n!/k!(n−k)!

We have n=20 individuals

We have to get a subset of k=3

Hence:

C_3,20=(​20/3​)

=20!/3!(20−3)!

=1140.

​1140 different crews are possible if a night crew consists of 3 machinists.

Page 88 Problem 2 Answer

Given: A small manufacturing company will start operating a night shift.

There are 20 machinists employed by the company.

To find the number of crews not having the best machinist given that the machinist are ranked 1,2,…,20 in order of competence.

We will use combination formula: ​

C_k,n=(​n/k​)

=n!/k!(n−k)!

We have to take out the best machinists .

Hence: n=19

We need to crew crew of 3

Hence k=3

Therefore we have:

​C3,19=(​19/3​)

=19!/3!(19−3)!

=969

​The number of crews not having the best machinist given that the machinist are ranked1,2,…,20 in order of competence is 969.

Page 88 Problem 3 Answer

Given: A small manufacturing company will start operating a night shift.

There are 20 machinists employed by the company.

To find the number of crews that will have at least 1 of the 10 best machinists.

We will use combination formula: ​

C_k,n=(​n/k​)

=n!/k!(n−k)!

There are a total of 1140

Hence if we subtract 1140 from the number of to select 3 machinists from of group of 10 bottom machinists we will get the required answer.

Hence we have:

C3,20−C3,10

=1140−(​10/3​)

=1140−120

=1020​

The number of crews that will have at least 1 of the 10 best machinists is 1020.

Page 88 Problem 4 Answer

Given: A small manufacturing company will start operating a night shift.

There are 20 machinists employed by the company.

To find the probability that the best machinist will not work that night given that one of these crews is selected at random to work on a particular night.

We will use combination formula: ​

C_k,n=(​n/k​)

=n!/k!(n−k)!

We know that for an event A we have

P(A)= number of favorable outcomes in A number of outcomes in the sample space

Now here A is the event  that the best machinist will not work that night

We have found the favorable outcomes in part b) 969 and the total number of outcomes in part a) 1140

Hence P(A)=C3,19/C3,20

=969/1140

=0.85

​The probability that the best machinist will not work that night is 0.85.

Page 89 Problem 5 Answer

Given: One satellite is scheduled to be launched from Cape Canaveral in Florida, and another launching is scheduled for Vandenberg Air Force Base in California.

Given: A denotes the event that the Vandenberg launch goes off on schedule, and B represent the event that the Cape Canaveral launch goes off on schedule.

Given that A and B are independent events.Given:​P(A)>P(B),P(A∪B)=.626, and P(A∩B)=.144

​To determine: P(A) and P(B)

We will use the properties:  P(A∪B)=P(A)+p(B)-P(A∩B) and

P(A∩B)=P(A).P(B)

Since there are two questions and two unknowns,

Substitute the values in one of the equation,

P(A∩B)=P(A)⋅P(B)

0.144=P(A)⋅P(B)

P(A)=0.144

P(B)

Substitute the values in the other equation,

P(A∪B)=P(A)+P(B)−P(A∩B)

0.626=P(A)+P(B)−0.144

Now replace the value of P(A),

0.626=0.144

P(B)+P(B)−0.144/0.626⋅P(B)=0.144+P(B)2−0.144⋅P(B)

0=0.144+P(B)2−0.77⋅P(B)

After solving the quadratic equation, the solutions are,

P(A) or P(B)=0.45 or 0.32

Since P(A)>P(B),

P(A)=0.45.

P(B)=0.32.

The values of P(A) and P(B), calculated using the given values was found to be 0.45 and 0.32 respectively.

Page 89 Problem 6 Answer

Given: There are six friends namely, A,B,C,D,E,and F.A has heard a rumor and wants to share it with all the friends.

A selects one of the five at random and tells the rumor to the chosen individual.

Given: individual then selects at random one of the four remaining individuals and repeats the rumor. Continuing, a new individual is selected from those not already having heard the rumor by  the individual who has just heard it, until everyone has been told.

To find the probability that the rumor is repeated in the order B,C,D,E and F.

We will use permutation to find the favorable outcomes and then find the probability.

The number of ways to arrange all the friends is,P5,5

=5!/(5−5)!

P=5!.

P=120.

But the required condition is a very specific order (B,C,D,E,and ,F),

T=1/120

T=0.0083.

The probability that the rumor is repeated in the order (B,C,D,E,and ,F) is 0.0083.

Page 89 Problem 7 Answer

There are six friends namely,A,B,C,D,E,and F A has heard a rumor and wants to share it with all the friends.

A selects one of the five at random and tells the rumor to the chosen individual.

Given:  individual then selects at random one of the four remaining individuals and repeats the rumor.

Continuing, a new individual is selected from those not already having heard the rumor by the individual who has just heard it, until everyone has been told.

To find the probability that F is the third person at the party to be told the rumor.

We will use permutation to find the favorable outcomes and then find the probability.

The probability of F being the third person,

P4,4=4!/(4−4)!

P=4⋅3⋅1⋅2⋅1

P=24.

The probability of the above situation to occur is,

T=24/120

T=0.2.

The probability that F is the third person at the party to be told the rumor is 0.2.

Page 89 Problem 8 Answer

There are six friends namely, A,B,C,D,E,and F.A has heard a rumor and wants to share it with all the friends.

A selects one of the five at random and tells the rumor to the chosen individual.

Given:  individual then selects at random one of the four remaining individuals and repeats the rumor.

Continuing, a new individual is selected from those not already having heard the rumor by the individual who has just heard it, until everyone has been told.

To find the probability that F is the last person to hear the rumor.

We will use permutation to find the favorable outcomes and then find the probability.

The probability of F being the last person,

P4,4=4!/(4−4)!

P=4⋅3⋅2⋅1⋅1

P=24.

The probability of the situation to occur is,

T=24/120

T=0.2.

The probability that F  is the last person to hear the rumor is 0.2.

Page 89 Problem 9 Answer

There are six friends namely, A,B,C,D,E,and F.A has heard a rumor and wants to share it with all the friends,  A selects one of the five at random and tells the rumor to the chosen individual.

Given:  individual then selects at random one of the four remaining individuals and repeats the rumor.

Continuing, a new individual is selected from those not already having heard the rumor by the individual who has just heard it, until everyone has been told.

Given: at each stage the person who currently “has” the rumor does not know who has already heard it and selects the next recipient at random from all five possible individuals, To find the probability that F has still not heard the rumor after it has been told ten times at the party.

We will use the definition of probability.

The probability of F to have not heard after 10 times,

F=410

F=1048576.

The total probability of everyone hearing the rumor,T=510

T=9565625.

Now the probability of the event happening is,

P=F/T

P=1058576/9565625

P=0.1074.

The probability that F has still not heard the rumor after it has been told for 10 times is 0.1074.

Page 89 Problem 10 Answer

Given: Each contestant on a quiz show is asked to specify one of six possible categories from which questions will be asked Given: P( contestant requests category i)=1/6

Given: successive contestants choose their categories independently of one another.

To find the probability that exactly one contestant has selected category 1 given that there are three contestants on each show and all three contestants on a particular show select different categories.We will use combination formula n

Cr=(​nr​)n!/r!(n−r)! in order to find the favorable and total number of outcomes and then find the probability.

We have:

​P( contestant requests category i)

i=1/6

=1,2,3,4,5,6

​We need 3 of the 6 categories which can be done in C6,3

=(​6/3​) ways

Hence the number of possible outcomes are:

(​6/3​)=6!/3!(6−3)!

=20

There are C5,2=(​5/2​) ways to select the remaining two categories of the five excluding 1

Hence the number of favorable outcomes is:

(​5/2​)=5!/2!(5−2)!

=10

​Therefore the probability that category 1 is selected is:

P( Category 1 is selected )= number of favorable outcomes/ number of possible outcomes

=10/20

=1/2

=0.5

​The probability that exactly one contestant has selected category 1 is 0.5.

Page 90 Problem 11 Answer

Given: One percent of all individuals in a certain population are carriers of a particular disease.

A diagnostic test for this disease has a 90% detection rate for carriers and a 5% detection rate for noncarriers

Given: The test is applied independently to two different blood samples from the same randomly selected individual.

To find the probability that both the tests yield the same result.

We will use the complement rule and general multiplication rule: P(A∩B)=P(A)×P(B∣A)

Let: A=Event that the person has the disease

B=Event that the test is positive.

Hence:

P(A)=0.01

P(B∣A)=0.9

P(B∣A′)=0.05​

Therefore by using complement rule we have:

P(A′)=1−P(A)

=1−0.01

=0.99

P(B′∣A)=1−P(B∣A)

=1−0.9

=0.1 and

P(B′∣A′)=1−P(B∣A′)

=1−0.05

=0.95

​Using the multiplication rule we have:

P(A∩B)=P(A)×P(B∣A)

=0.01×0.9

=0.009

P(A∩B′)=P(A)×P(B′∣A)

=0.01×0.1

0.001

P(A′∩B)=P(A′)×P(B∣A′)

=0.99×0.05

=0.0495

P(A′∩B′)=P(A′)×P(B′∣A′)

=0.99×0.95

=0.9405

​Hence we have:

P(B)=P(A∩B)+P(A′∩B)

=0.009+0.0495

=0.0585

P(B′)=P(A∩B′)+P(A′∩B′)

=0.001+0.9405

=0.9415

​The tests are independent and therefore we get:

P( Both B)=0.0585×0.0585

≈0.0034

P( Both B′)

=0.9415×0.9415

≈0.8864

​Hence P( Same result )

=P( Both B)+P( Both B′)

=0.0034+0.8864

=0.8898​

The probability that both the tests yield the same result is 0.8898.

Page 90 Problem 12 Answer

Given: One percent of all individuals in a certain population are carriers of a particular disease.

A diagnostic test for this disease has a 90% detection rate for carriers and a 5% detection rate for noncarriers.

Given: The test is applied independently to two different blood samples from the same randomly selected individual.

To find the probability that the selected individual is a carrier given that both tests are positive.

We will use conditional probability.

We have:

A=Event that the person has the disease

B=Event that the test is positive.

From part a we have: P( Both B)≈0.0034

Hence P( Both (A∩B))

=P(A∩B)×P(A∩B)

=0.009×0.009

=0.000081

​Using the definition of conditional probability we have:P(A∣ Both B)

=P(A∩ Both B)/P( Both B)

=P( Both (A∩B))/P( Both B)

=0.000081/0.0585×0.0585

≈0.02367

=2.367%

​The probability that the selected individual is a carrier given that both tests are positive is 0.02367.

Page 90 Problem 13 Answer

Given: System consists of two components.

Given: The probability that the second component functions in a satisfactory manner during its design life=0.9.

The probability that at least one of the two components does so=0.96.

The probability that both components do so=0.75. the first component functions in a satisfactory manner throughout its design life.

To find the probability that the second one also functions in a satisfactory manner throughout its design life.We will use conditional probability P(B∣A)=P(A∩B)/P(A)

Let us consider following events,

A={ the event of the first component functioning}

B={ the event of the second component functioning}

We are given that,

P(B)=0.9

P(A∪B)=0.96

P(A∩B)=0.75

Using Addition Rule,

P(A∪B)=P(A)+P(B)−P(A∩B)

This implies, P(A)=−P(B)+P(A∩B)+P(A∪B)

Thus,P(A)=−0.9+0.75+0.96

P(A)=0.81

Using definition of conditional probability,

P(B∣A)=P(A∩B)/P(A)

P(B∣A)=0.75/0.81

P(B∣A)≈0.9259

The probability that the second component functions in a satisfactory manner throughout its design life given that the first one does is 0.9259.

Page 90 Problem 14 Answer

Given: A certain company sends 40% of its overnight mail parcels via express mail service E1.

of which 2% arrive after the guaranteed delivery time .

Given: a record of an overnight mailing is randomly selected from the company’s file.

To find the probability that the parcel went via E1and was late.

We will use the multiplication property: P(A∩B)=P(A∣B)⋅P(B)

We have: P(E1)=0.4

Now if L denotes the event :late arrived” then:

P(L∣E1)=0.02

Hence by using multiplication rule we have:

P(L∩E1)=P(L∣E1)⋅P(E1)

=(0.02)⋅(0.4)

=0.008

​The probability that the parcel went via E1 and was late is 0.008.

Page 90 Problem 15 Answer

Given percentages of the assembly lines that they need rework:

A1=5%

A2=8%

A3=10%

Given percentages of components produced:

A1=50%

A2=30%

A3=20%

Given: a randomly selected component needs rework

To find: the probability that it came from lineA1.

To find: the probability that it came from line A2.

To find: the probability that it came from lineA3.

We will use Bayes’ theorem in order to find the required probability.

Let us consider the following event,

R={Component needs rework}

It is given that,

P(A1)=0.5

P(A2)=0.3

P(A3)=0.2

P(R∣A1)=0.05;

P(R∣A2)=0.08

P(R∣A3)=0.1

​Now, we need to find the probability such that if a random selected component needs rework, it is from the lineA1

i.e.,P(A1∣R)

Using Bayes’ theorem, we get,

P(A1∣R)=P(A1∩R)/P(R)=P(A1)⋅P(R∣A1)

P(A1)⋅P(R∣A1)+P(A2)⋅P(R∣A2)+P(A2)⋅P(R∣A2)

=0.5⋅0.05/0.5⋅0.05+0.3⋅0.08+0.2⋅0.1

=0.025/0.025+0.024+0.02

=0.025/0.069

P(A1∣R)=0.377

Now, we need to find the probability such that if a random selected component needs rework, it is from the lineA2

i.e.,P(A2∣R).

Using Bayes’ Theorem, we get

P(A2∣R)=P(A2∩R)/P(R)

=P(A2)⋅P(R∣A2)

P(A1)⋅P(R∣A1)+P(A2)⋅P(R∣A2)+P(A2)⋅P(R∣A2)

=0.3⋅0.08/0.5⋅0.05+0.3⋅0.08+0.2⋅0.1

=0.024/0.025+0.024+0.02

=0.024/0.069

P(A2∣R)=0.348

Now, we need to find the probability such that if a random selected component needs rework, it is from the line A3

i.e.,P(A3∣R).

Using Bayes’ Theorem, we get

P(A3∣R)=P(A3∩R)/P(R)

=P(A3)⋅P(R∣A3)

P(A1)⋅P(R∣A1)+P(A2)⋅P(R∣A2)+P(A2)⋅P(R∣A2)

=0.2⋅0.1/0.5⋅0.05+0.3⋅0.08+0.2⋅0.1

=0.02/0.025+0.024+0.02

=0.02/0.069

P(A3∣R)=0.29 the probability that the component  came from lineA1 is 0.377 the probability that the component  came from line A2 is 0.348 the probability that the component  came from line A3 is 0.29

Page 90 Problem 16 Answer

Given: A subject is allowed a sequence of glimpses to detect a target where Gi={ the target is detected on the ith glimpse } with  h pi=P(Gi)

Given: Gi′s are independent events.

To write an expression for the probability that the target has been detected by the end of the nth glimpse.

We will use the multiplication property of mutually independent events.

An event Gi is defined as follows,

Gi= the target is detected on theith glimpse

Also, the probability of the event Gi is denoted by pi, then the probability that the target is not observed on ithglimpse is denoted by(1−pi).

The objective is to find the probability that the target has been detected by the end of thenth glimpse.

As it is given thatGi′s are independent, therefore their complementary events are also independent.

Now, the probability that the target has been detected by the end of then th glimpse is equal to the combined probability that the target is not detected by first′n−1′ trials.

Therefore,

P(Gn) = P(target that is not detected in previous ′n′ trials)

P(Gn) = 1 − P(G1∪G2∪……∪Gn)

P(Gn) = 1 − P(G1​′∪G2​′∪……∪Gn′)

P(Gn) = 1 − [P(G1​′)×P(G2​′)×……P(Gn​′)]

P(Gn) = 1 − [(1−p1)×(1−p2)×….…×(1−pn)]

​The expression for the probability that the target has been detected by the end of then th glimpse is P(Gn)=1−[(1−p1)×(1−p2)×….…×(1−pn)]=1−i=1∏n(1−pi)

​Page 91 Problem 17 Answer

Given : A particular airline has 10 A.M. flights from Chicago to New York, Atlanta, and Los Angeles and the events are describes as:

A= New York flight is full

B =The Atlanta flight is full

C =The Los Angeles flight is full

Given: All the three events are independent events.

Given probabilities: ​P(A)=0.9

P(B)=0.7

P(C)=0.8​

To find the probability that all three flights are full.To find the probability that at least one flight is not full.

We will use the complement rule and multiplication property for independent events in order to find the required probabilities.

Now, we will find the probability that all three flights are full.

This means that all the events are occurring together, since all the events are independent, so by using the multiplication rule of probability

Let probability that all the fights are full be P(A∩B∩C)

As P(A1∩A2∩A3∩………An)=P(A1)⋅P(A2)⋅P(A3)⋅…………P(An)

Therefore, P(A∩B∩C)=P(A)⋅P(B)⋅P(C)

P(A∩B∩C)=0.9⋅0.7⋅0.8

P(A∩B∩C)=0.504

​Now, we will calculate the probability if at least one flight is not full.

We will calculate it using the definition of the complement of an event as the event that at least one flight is not full is a complement to that event that all the three flights are full (let the probability that all the flights are full be P(A) )

​ P(Z) = 1 − P(A)

P(Z) = 1 − 0.504

P(Z) = 0.496

​The probability that all three flights are full is 0.0504 .

The probability that at least one flight is not full is0.496.

Page 91 Problem 18 Answer

Given : A particular airline has 10 A.M. flights from Chicago to New York, Atlanta, and Los Angeles and the events are describes as:

A= New York flight is full

B = The Atlanta flight is full

C =The Los Angeles flight is full

Given: All three events are independent events.Given probabilities:

P(A)=0.9

P(C)=0.8

P(B)=0.7

To find the probability that only the New York flight is full.To find the probability that exactly one of the three flights is full.

We will use the complement rule and multiplication property for independent events in order to find the required probabilities.

First, we will find the probability that only the New York flight is full. It means that event A will occur but at the same time events, A and B will not occur.

The probability that only the New York flight is full-

By using the multiplication rule of probability –

P(A∩Bˉ∩Cˉ)=P(A)⋅P(Bˉ)⋅P(Cˉ)

we have ,P(Aˉ) = 1−P(A)

P(A∩Bˉ∩Cˉ)=0.9⋅ (1 − 0.7)⋅(1−0.8)

P(A∩Bˉ∩Cˉ)=0.9⋅0.3⋅0.2

P(A∩Bˉ∩Cˉ)=0.054​

Now, we need to find the probability that exactly one of the three flights is full.

There are three possible ways either the New York flight is full, or The Atlanta flight is full or The Los Angeles flight is full.

The probability that exactly one of the three flights is full –

P(exactly one of the three flights is full) = P(A∩Bˉ∩Cˉ)+ P(Aˉ∩B∩Cˉ)+ P(Aˉ∩Bˉ∩C)

P(exactly one of the three flights is full) = P(A)P(Bˉ)P(Cˉ)+ P(Aˉ)P(B)P(Cˉ) + P(A)ˉP(B)ˉP(C)

Now, we will use the multiplication rule of probability,

P(exactly one of the three flights is full)= ​(0.9)⋅(1−0.7)⋅(1−0.8?) + (1−0.9)⋅(0.7)⋅(1−0.8) + (1−0.9)⋅(1−0.7)⋅(0.8)

​P(exactly one of the three flights is full)= 0.9⋅0.3⋅0.2 + 0.1⋅0.7⋅0.2 + 0.1⋅0.3⋅0.8

P(exactly one of the three flights is full)= 0.092

The probability that only the New York flight is full is0.054 .

The probability that exactly one of the three flights is full is0.092 .

Page 91 Problem 19 Answer

Given: a box is containing four slips and each having same dimension

Given events:A1 = {win prize 1}

A2 = {win prize 2}

A3 = {win prize 3}

​To show that A1 and A2 are independent,A2  and A3 are independent and A1 and A3 are also independent.

To showP(A1∩A2∩A3) ≠ P(A1)⋅P(A2)⋅P(A3), so the three are not mutually independent.

We will use the multiplication property is not hold to prove that they are not mutually independent.

P(A1)=win prize 1(A1)+win prize 1,2,3(A4)

Therefore,P(A1) = 1/2,  P(A2) = 1/2   ,   P(A3) = 1/2

P(A1∩A2) = A4

A1+A2+A3+A4

P(A1∩A2) = 1/4

As, P(A1)⋅P(A2) = 1/2⋅1/2

P(A1)⋅P(A2)= 1/4 which is equal to P(A1∩A2)

This shows that A1 and A2 are independent events.

​Similarly, we will solve

P(A1∩A3) = P(A1)⋅P(A3)

P(A1∩A3) = 1/2 ⋅ 1/2

P(A1∩A3) = 1/4 which is equal to P(A1 ∩A3)

This shows that A1 and A3 are independent events

​Now, for P(A2∩A3) = P(A2)⋅P(A3)

P(A2∩A3) = 1/2 ⋅ 1/2

P(A2∩A3) = 1/4 which is equal to P(A2∩A3)

This shows that A2 and A3 are independent events

​P(A1∩A2∩A3) = A4

A1+A2 +A3+A4

P(A1∩A2∩A3) = 1/4

And P(A1)⋅P(A2)⋅P(A3) = 1/2 ⋅ 1/2 ⋅ 1/2

P(A1)⋅P(A2)⋅P(A3) = 1/8

Therefore, it shows that P(A1∩A2∩A3)≠ P(A1)⋅P(A2)⋅P(A3)

Hence Proved.​

We have proved that P(A1∩A2∩A3) ≠ P(A1)⋅P(A2)⋅P(A3) and also we have shown that the three events are pairwise independent.

Page 91 Problem 20 Answer

Given: A1,A2, and A3are independent events.To show that: P(A1∣A2∩A3)=P(A1)

We will use Bayes’ Theorem in order to show the required.

We have to consider that A1,A2 and A3 are independent events

By using Bayes Theorem, we will simplify  for P(A1∣A2∩A3).

P(A1∣A2∩A3) = P(A1∩A2∩A3)

P(A2∩A3)

As all the events are independent, then it follows the multiplication rule,

P(A1∩A2∩A3) = P(A1)P(A2)P(A3)

P(A2∩A3) = P(A2)P(A3)

Therefore, P(A1∣A2∩A3) = P(A1∩A2∩A3)

P(A2∩A3)

P(A1∣A2∩A3) = P(A1)P(A2)P(A3)

P(A2)P(A3)

P(A1∣A2∩A3) = P(A1)

Hence proved.

​We have shown that if A1,A2 , and A3 are independent events then P(A1∣A2∩A3)=P(A1).

Page 91 Problem 21 Answer

Given: a box is containing four slips and each having same dimension

Given events:A1 = {win prize 1}

A2 = {win prize 2}

A3 = {win prize 3}

​To show that A1 and A2 are independent,A2  and A3 are independent and A1 and A3 are also independent.To show P(A1∩A2∩A3) ≠ P(A1)⋅P(A2)⋅P(A3), so the three are not mutually independent.

We will use the multiplication property is not hold to prove that they are not mutually independent.

P(A1)=win prize 1(A1)+win prize 1,2,3(A4)

Therefore,P(A1) = 1/2,  P(A2) = 1/2   ,  P(A3) = 1/2

P(A1∩A2) = A4

A1+A2+A3+A4

P(A1∩A2) = 1/4

As, P(A1)⋅P(A2) = 1/2⋅1/2

P(A1)⋅P(A2)= 1/4 which is equal to P(A1∩A2)

This shows that A1 and A2 are independent events.

Similarly, we will solve

P(A1∩A3) = P(A1)⋅P(A3)

P(A1∩A3) = 1/2 ⋅ 1/2

P(A1∩A3) = 1/4 which is equal to P(A1 ∩A3)

This shows that A1 and A3 are independent events

​Now, for P(A2∩A3) = P(A2)⋅P(A3)

P(A2∩A3) = 1/2 ⋅ 1/2

P(A2∩A3) = 1/4 which is equal to P(A2∩A3)

This shows that A2 and A3 are independent events

​P(A1∩A2∩A3) = A4

A1+A2 +A3+A4

P(A1∩A2∩A3) = 1/4 And P(A1)⋅P(A2)⋅P(A3) = 1/2 ⋅ 1/2 ⋅ 1/2

P(A1)⋅P(A2)⋅P(A3) = 1/8

Therefore, it shows that P(A1∩A2∩A3)≠ P(A1)⋅P(A2)⋅P(A3)

Hence Proved.

​We have proved that P(A1∩A2∩A3) ≠ P(A1)⋅P(A2)⋅P(A3) and also we have shown that the three events are pairwise independent.

Page 91 Problem 22 Answer

Given: A1,A2, and A3 are independent events.To show that: P(A1∣A2∩A3)=P(A1)

We will use Bayes’ Theorem in order to show the required.

We have to consider that A1,A2and A3 are independent events

By using Bayes Theorem, we will simplify  for P(A1∣A2∩A3).

P(A1∣A2∩A3) = P(A1∩A2∩A3)

P(A2∩A3)

As all the events are independent, then it follows the multiplication rule ,

P(A1∩A2∩A3) = P(A1)P(A2)P(A3)

P(A2∩A3) = P(A2)P(A3)

Therefore, P(A1∣A2∩A3) = P(A1∩A2∩A3)

P(A2∩A3)

P(A1∣A2∩A3) = P(A1)P(A2)P(A3)

P(A2)P(A3)

P(A1∣A2∩A3) = P(A1)

Hence proved.

​We have shown that if A1,A2, and A3 are independent events then P(A1∣A2∩A3)=P(A1).

Probability and Statistics for Engineering and the Sciences 8th Edition Chapter 3 Discrete Random Variables and Probability Distributions

Page 104 Problem 1 Answer

Given -An automobile service facility specializing in engine tune-ups knows that 45% of all tune-ups are done on four-cylinder automobiles,40% on six-cylinder automobiles, and 15% on eight cylinder automobiles.

We assume number of cylinders on the next car to betuned.

We will find the pmf of X.

We note that the probabilities are given in question as percentages.

We will convert it in integers to obtain the pmf.

Hence, the probability mass function is given by

​P(X=4)=0.45

P(X=6)=0.4

P(X=8)=0.15 and

P(X=x)=0

for every other x.

We obtain:

​P(X=4)=0.45

P(X=6)=0.4

P(X=8)=0.15

For other numbers, the probability is zero.

Page 104 Problem 2 Answer

Given -An automobile service facility specializing in engine tune-ups knows that 45% of all tune-ups are done on four-cylinder automobiles, 40% on six-cylinder automobiles, and 15% on eight cylinder automobiles.

We suppose number of cylinders on the next car to be tuned.

We will draw both a line graph and a probability histogram for the pmf of parta).

From part a), we know the probability values.

We will plot the graph as follows:

We will plot the histogram as follows :

The required graph is:

The required Histogram is:

Page 104 Problem 3 Answer

Given -An automobile service facility specializing in engine tune-ups knows that 45% of all tune-ups are done on four-cylinder automobiles,40% on six-cylinder automobiles, and 15% on eight cylinder automobiles.

We suppose number of cylinders on the next car to be tuned.

We will find the probability that the next car tuned has at least six cylinders and more than six cylinders.

We will obtain the probability that the next car tuned has at least six cylinders as shown below:

P( at least 6)

=P6+P8

=0.4+0.15

=0.55

The probability that the next car tuned has more than six cylinders is given as:

P8=15/100

P8=0.15

We obtain:

P(X≥6)=0.55

P(X>6)=0.15

​Page 105 Problem 4 Answer

Given – In some parts of California are particularly earthquake-prone.

We suppose that in one metropolitan area, 25% of all homeowners are insured against earthquake damage.

Four homeowners are to be selected at random; let X denote the number among the four who have earthquake insurance.

We will find the Probability Distribution of X.

We suppose that S denote a homeowner who has insurance and F one who does not.

Now, one possible outcome is SFSS , with probability (.25)(.75)(.25)(.25) and associated X value 3.

There are 15 other outcomes.

We have:

n=4

p=25%

=0.25

​The possible outcomes are {SSSS, SSSF, SSFS, SSFF, SFSS, SFSF, SFFS, SFFF, FSSS, FSSF, FSFS,FSFF, FFSS, FFSF, FFFS, FFFF}

The event SSSS corresponds to X=4.

Also, the events SSSF, SSFS, SFSS, FSSS  corresponds toX=3.

The events SSFF , SFSF, SFFS, FSSF, FSFS, FFSS  correspond toX=3.

Events  FFFS, FFSF,FSFF,SFFF corresponds to X=1 .

Event FFFF corresponds to X=0.

Using “Binomial Probability”, we get:

P(X=k)=4!/k!(4−k)!×0.25k×(1−0.2)4−k

We obtain:

We obtain probability distribution of X as follows:

Page 105 Problem 5 Answer

Given – In some parts of California are particularly earthquake-prone.

We suppose that in one metropolitan area,25% of all homeowners are insured against earthquake damage.

Four homeowners are to be selected at random;X will denote the number among the four who have earthquake insurance.

We need to draw the corresponding probability distribution.

We suppose that S denote a homeowner who has insurance and F one who does not.

Then one possible outcome is SFSS , with probability (.25)(.75)(.25)(.25) and associated X value 3.

There are 15 other outcomes.

We note that the width of bars should be same and the length of bars is equal to probability.

We can draw the bars sa follows:

We obtain probability distribution histogram as follows:

Page 105 Problem 6 Answer

Given – In some parts of California are particularly earthquake-prone.

We assume that in one metropolitan area,25% of all homeowners are insured against earthquake damage.

Four homeowners are to be selected at random.

We suppose that X denotes the number among the four who have earthquake insurance.

We will find the most likely value for X.

We note that the most likely value for X is 1.

This is due to the fact that the probability for X=1 is highest.

We can check this by constructing the probability distribution table that X=1:

We conclude that the most likely value for X is 1.

Page 105 Problem 7 Answer

Given that in some parts of California are particularly earthquake-prone.

We assume that in one metropolitan area,25% of all homeowners are insured against earthquake damage.

Four homeowners are to be selected at random; let X denote the number among the four who have earthquake insurance.

We will find the probability that at least two of the four selected have earthquake insurance.

We will use the addition rule.

With the help of the the addition rule for disjoint events, we havet :

P(A or B)=P(A)+P(B) .

Now, adding the possibilities of the corresponding events, we get:

P(X≥2)=P(X=2)+P(X=3)+P(X=4)

=0.2109+0.0469+0.0039

=0.2617.​

We obtained that the probability that at least two of the four selected have earthquake insurance is 0.2617.

Page 105 Problem 8 Answer

We note that probability mass function= probability distribution.

We are given in the question thatY= the number of days beyond Wednesday that it takes for both magazines to arrive.

Hence,

P(Wed.) = .3

P(Thurs.) = .4

P(Fri.) = .2

P(Sat.) = .1

In order to get the probability mass function (pmf) of Y

we note that the possible values of Y are0,1,2,3.

We note that the possible outcomes are:

(W,W),(W,T),(W,F),(W,S)

(T,W),(T,T),(T,F),(T,S)

(F,W),(F,T),(F,F),(F,S)

(S,W),(S,T),(S,F),(S,S)

​For y=0, we get:

P(Y=0)

=P(W,W)

=P(W)×P(W)

=0.3×0.3

=0.09

Fory=1, we get:

P(Y=1)=P[(W,T),(T,W),(T,T)]

=[P(W)×P(T)]+[P(T)×P(W)]+[P(T)×P(T)]

=[0.3×0.4]×[0.4×0.3]+[0.4×0.4]

=0.12+0.12+0.16

=0.4

​Fory=2, we get:

P(Y=2)=P[(W,F),(T,F),(F,W),(F,T),(F,F)]

=[P(W)×P(F)]+[P(T)×P(F)]+[P(F)×P(W)]+[P(F)×P(T)]+[P(F)×P(F)]

=[0.3×0.2]+[0.4×0.2]+[0.2×0.3]+[0.2×0.4]+[0.2×0.2]

=0.06+0.08+0.06+0.08+0.04

=0.32

​Fory=3, we get:

​P(Y=3)=P[(W,S),(T,S),(F,S),(S,W),(S,T),(S,F),(S,S)]

[P(W)×P(S)]+[P(T)×P(S)]+[P(F)×P(S)]+[P(S)×P(W)]+[P(S)×P(T)]+[P(S)×P(F)]+[P(S)×P(S)]

=[0.3×0.1]+[0.4×0.1]+[0.2×0.1]+[0.1×0.3]+[0.1×0.4]+[0.1×0.2]+[0.1×0.1]

=0.03+0.04+0.02+0.03+0.04+0.02+0.01

=0.19

​The probability mass function (pmf) of Y are given below:

P(Y=0)=0.09​

P(Y=1)=0.4

P(Y=2)=0.32

P(Y=3)=0.19

​Page 105 Problem 9 Answer

We have three couples and two single individuals.We will denote events as:

Ci={ couple i arrives late }

Aj={ individual j arrives late }

​Here i:1,2,3 and j:4,5, we are given the probabilities Ci,Aj=0.4​.

We assumeX= the number of people who arrive late for the seminar.

We note that the probability mass function (pmf) of a discrete random variable X Is p(x)=P(X:x)

​=P(ω∈S:X(ω):x)

​It is true for every number x .

When none are late, x=0  , we have

p(0)=P(X=0)

​=P(C1′C2′C3′A4′A5′)

​=P(C1′)⋅P(C2′)⋅P(C3′)⋅P(A4′)⋅P(A5′)

=(1−0.4)⋅(1−0.4)⋅(1−0.4)⋅(1−0.4)⋅(1−0.4)

=0.07776

​When one individual arrives late, we have x=1.

So we get

p(1)=P(X=1)

=P[(C1′C2′C3′A4A5′)∪(C1′C2′C3′A4′A5)

=P(C1′C2′C3′A4A5′)+(C1C2C3′A4′A5)

=[(1−0.4)⋅(1−0.4)⋅(1−0.4)⋅(0.4)⋅(1−0.4)]+[(1−0.4)⋅(1−0.4)⋅(1−0.4)⋅(1−0.4)⋅(0.4)]

=0.10368

When x=2, we obtain:

p(2)=P(X:2)

=P(C1′C2′C3′A4A5)+P(C1C2′C3′A4′A5)+P(C1′C2C3′A4A5′)+P(C1′C2′C3A4′A5)

=[(1−0.4)⋅(1−0.4)⋅(1−0.4)⋅(0.4)⋅(0.4)]+[(1−0.4)⋅(1−0.4)⋅(1−0.4)⋅(0.4)⋅(0.4)]+[(1−0.4)⋅(1−0.4)⋅(1−0.4)⋅(0.4)⋅(0.4)]+[(1−0.4)⋅(1−0.4)⋅(1−0.4)⋅(0.4)⋅(0.4)]

​=0.19008​​

When x=3 , we obtain

p(3)=P(X=3)

=P(C1C2′C3′A4A5′)+P(C1C2′C3′A4′A5)+P(C1′C2C3′A4A5′)+P(C1′C2C3′A4′A5)+P(C1′C2C3A4A5′)+P(C1′C2′C3A4′A5)

=6⋅(1−0.4)3⋅(0.4)2

=0.20736

​In the same way, we get:

p(4)=P(X=4)​=3⋅(1−0.4)3⋅(0.4)2+3⋅(1−0.4)2⋅(0.4)3

=0.1728

​Also, we obtain:

p(5)=P(X=5)=6.(1−0.4)2⋅(0.4)3

=0.13824

​In the same way, we get:

p(6)=P(X=6)=(1−0.4)2⋅(0.4)3+3.(1−0.4)⋅(0.4)4

=0.06912

p(7)=2.(1−0.4)⋅(0.4)4

=0.03072

p(8)=(0.4)5

=0.01024

​Summing up, we get rhe probability mass function (pmf) of X as follows:

Page 105 Problem 10 Answer

Using the part a) , we get the pmf of x as :

We need to calculate P(2≤X≤6).

Using definition, we get the cumulative distribution function (cdf) of Xas follows:

In order to get P(2≤x≤6)

​we will use the definition of cdf as follows:

here,P(a≤x≤b)=F(b)−F(a−1)

​SoP(2≤x≤6)=F(6)−F(2−1)

=F(6)−F(1)

=0.95904−0.18144

=0.7776

​We obtain: P(2≤x≤6)=0.7776.

Page 105 Problem 11 Answer

We have:

P(x)=log10(x+1/x)

​Here,x:1,2,3,…,9 is termed as Benford’s law.

We are given that:

P(x)=log10

(x+1/x)

x=1,2,3,…,9

​Now, summing up both sides, we get:

∑P(x)=1

⇒∑x=1/9log10(x+1/x)=1

Hence, using the logarithmic property, we get:

⇒x=1∑9log10(x+1/x)=log10

(1+1/1)+log10(2+1/2)+….+log10(9+1/9)

​=log10(2)+log10(3/2)+log10(4/3)+log10(5/4)+log10(6/5)+log10(7/6)+log10(8/7)+log10(9/8)+log10(10/9)

​=log10[2×3/2×43×5/4×6/5×7/6×87×9/8×10/9]

=log10[10]

=1

​We proved the legitimate probability mass function.

It is,

∑P(x)=1

⇒∑x=1/9log10(x+1/x)=1

​Page 105 Problem 12 Answer

For the given data, we need to find the probability of corresponding to X values.

We need to compare with actual solution.

We will use the pdf of uniform distribution.

We will obtain the individual probabilities using the probability distribution function as follows:

The probability distribution value decreases as the corresponding X values increases and the discrete uniform distribution value is constant the corresponding X values are increasing.

Page 105 Problem 13 Answer

The Benford’s law is given as :

p(x)=log10((x+1)/x)

​Here, we note that the leading digits of each number from the given possibilities x=1,2,3…….9.

We need to find the Cumulative Distribution Function (CDF).

We will calculate the probability for each leading digit and by summing up all the probabilities we can arrive at the desired output.

Firstly, we will take the leading number asx=1:

Hence p(1)=log10((1+1)/1)

p(1)=log10(2/1)

​Now, taking the leading number x=2 :

p(2)=log10((2+1)/2)

p(2)=log10(3/2)

Taking the leading numbers of3,4,5… up to 9, we can obtain the required values in the similar way.

We get:

p(3)=log10(4/3)

p(4)=log10(5/4)

p(5)=log10(6/5)

Similarly,

p(6)=log10(7/6)

p(7)=log10(8/7)

p(8)=log10(9/8)

p(9)=log10(10/9)

​Now, we will determine the CDF of the given leading numbers.

We will sum up the individual probabilities from 0 to 9

to get:cdf(1≤x≤9)=p(1)+p(2)+p(3)+p(4)+p(5)+p(6)+p(7)+p(8)+p(9)

Hence, putting the values, we get:

log10(2/1)+log10(3/2)+log10(4/3)+log10(5/4)+log1(6/5)+log1(7/6)+log10(8/7)+log10(9/8)+log10(10/9)cdf(1≤x≤9)=log10(10)=1

​We obtain the Cumulative Distribution Function (CDF) for the given leading numbers as1.

Page 105 Problem 14 Answer

The Benford’s law probability function is given by:p(x)=log10((x+1)/x)

​The leading digits of every number from the given possibilities is x=1,2,3….8,9.

​We will find the probability that the leading digit will be at most3 or P(x≤3) ​and at least 5 or P(x≥5).We will use Benford’s law.

The probability that the leading digit will be at most 3 can be calculated as follows:

P(x≤3): p(x≤3)=p(1)+p(2)+p(3)

=log10(2/1)+log10(3/2)+log10(4/3)

=log10(4)

=0.6020

​The probability that the leading digit is at least 5 is calculated by P(x≥5) :

We get: p(x≥5)=p(5)+p(6)+p(7)+p(8)+p(9)

=cdf(9)−cdf(5)

=1−log10(5)

=0.3010

The probability that the leading digit is at most 3 is0.6020

The probability that the leading digit is at least 5 will be 0.3010.

Page 106 Problem 15 Answer

Given – In the New York city there are six ATM machines for a certain bank.

We suppose X represents number of ATM’s in use at some of point time in a day.

We have: F(x)=0;x<0

=0.06;0≤x<1

=0.19;1≤x<2

=0.39;2≤x<3

=0.67;3≤x<4

=0.92;4≤x<5

=0.97;5≤x<6

=1.00;6≤x

​We will find the respective probability.

We will use the cdf values given above based on the conditions laid.

We will find p(2) as follows:

We will calculate this as follows:

p(2) , that is p(X=2)

p(2)=F(2)−F(1)

=0.39−0.19

=0.20

​The cdf forp(2) is 0.20.

Page 106 Problem 16 Answer

Given – In the New York city there are six ATM machines for a certain bank.

We suppose X represents number of ATM’s in use at some of point time during a day.

So, F(x)=0;x<0

=0.06;0≤x<1

=0.19;1≤x<2

=0.39;2≤x<3

=0.67;3≤x<4

=0.92;4≤x<5

=0.97;5≤x<6

=1.00;6≤x

​We will find the respective probability .We will use the cdf values given above based on the conditions laid.

Using the definition of cdf, we obtain:

p(X>3)=p(X=4,5,6)

=F(6)−F(3)

=1.00−0.67

=0.33

​The probability using the cdf for p(X>3) is 0.33,

Page 106 Problem 17 Answer

Given – In the New York city there are six ATM machines for a certain bank.

We suppose X represents number of ATMs in use at some of point time in a day.

We have F(x)=0;x<0

=0.06;0≤x<1

=0.19;1≤x<2

=0.39;2≤x<3

=0.67;3≤x<4

=0.92;4≤x<5

=0.97;5≤x<6

=1.00;6≤x

​We will find the probability from the cdf values given above based on the conditions required.

We will use the definition of cumulative density function.

We know that p(a≤X≤b)=F(b)−F(a).

Using this, we get:

p(2≤X≤5)=p(X=2,3,4,5)

=F(5)−F(2)

=0.97−0.19

=0.78​

We obtain the probability​p(2≤X≤5) as 0.78.

Page 106 Problem 18 Answer

Given – In a New York city a bank consists of six ATM machines.

We suppose X represents number of ATM’s in use at any instant in a day.

We have F(x)=0;x<0

=0.06;0≤x<1

=0.19;1≤x<2

=0.39;2≤x<3

=0.67;3≤x<4

=0.92;4≤x<5

=0.97;5≤x<6

=1.00;6≤x

​We will calculate the respective probability from the cdf values.

We will use the definition of the cumulative density function.

Using the definition of cumulative density function, we get:

p(2<X<5)=p(X=3,4)

=F(4)−F(2)

=0.92−0.39

=0.53​

For the given data, the probability​p(2<X<5) is equal to 0.53.

Page 106 Problem 19 Answer

Given -X

represents the number of months between successive payments.

We have :F(x)=0;x<1

=0.30;1≤x<3

=0.40;3≤x<4

=0.45;4≤x<6

=0.60;6≤x<12

=1.00;12≤x

​​We will find the pmf of X.

We will use the definition of Probability Mass Function to get the pmf of X.

We need to find Probability Mass Function of X:

Here, we know that X= number of months between successive payments can be taken from the data.

X will be 1,3,4,6 and 12.

Using the definition, we get:

p(1)=F(1)−F(0)

=0.30−0

=0.30

p(3)=F(3)−F(1)

=0.40−0.30

p(4)=F(4)−F(3)

=0.45−0.40

=0.05

​Similarly, we can get the following values:

p(6)=F(6)−F(4)

=0.60−0.45

=0.15

p(12)=F(12)−F(6)

=1.00−0.60

=0.40

Now, we will sum up the data obtained in the tabular form:

The desired Probability mass function of X is given below:

Page 106 Problem 20 Answer

Given -X represents the number of months between successive payments.

We have: F(x)=0;x<1

=0.30;1≤x<3

=0.40;3≤x<4

=0.45;4≤x<6

=0.60;6≤x<12

=1.00;12≤x​

​We will find the values of P(3≤X≤6)

We will also find P(4≤X)

We know that:X= number of months between successive payments can be taken from the data.

Now, we note that X∈{1,3,4,6,12}

Using the definitions, we get:

p(3≤x≤6)

=p(x=3,4,6)

=F(6)−F(1)

=0.60−0.30

=0.30

​We will now find P(4≤X) as follows:

P(4≤X)=1−P(X<4)

=1−(0.40)

=0.60

​The probability for p(3≤x≤6) is 0.30.

The probability for p(4≤x) is 0.60.

Probability and Statistics for Engineering and the Sciences 8th Edition Chapter 3 Discrete Random Variables and Probability Distributions

Page 95 Problem 1 Answer

Given – A concrete beam may fail either by shear(S) or flexure(F). We also have that randomly3

failed beams are selected and the type of failure is determined for each one.

Here,X =the number of beams among the three selected that failed by shear.

We will obtain each outcome in the sample space along with the associated value of X.

We will construct a table to summarize the values obtained.

We have:

X= the number of beams among the three selected that failed by shear

S= shear

F= flexure

We will construct the table as follows :

OUTCOME	BEAM 1	BEAM 2	BEAM 3	X
Outcome 1	S	S	S	3
Outcome 2	S	S	F	2
Outcome 3	S	F	S	2
Outcome 4	F	S	S	2
Outcome 5	S	F	F	1
Outcome 6	F	S	F	1
Outcome 7	F	F	S	1
Outcome 8	F	F	F	0

 

Hence, we obtained each outcome in the sample space along with the associated value of X.

We get total 8 outcomes in the sample space.

The values of X associated with the outcomes are listed below:

OUTCOME	BEAM 1	BEAM 2	BEAM 3	X
Outcome 1	S	S	S	3
Outcome 2	S	S	F	2
Outcome 3	S	F	S	2
Outcome 4	F	S	S	2
Outcome 5	S	F	F	1
Outcome 6	F	S	F	1
Outcome 7	F	F	S	1
Outcome 8	F	F	F	0

 

Page 95 Problem 2 Answer

Given -X=the number of nonzero digits in a randomly selected 4-digit PIN that has no restriction on the digits.

We will find the possible values of X.We will also give three possible outcomes and their associated X values.

We note that U.S. zip codes can have 4 digit PIN.

The values of X can be: X = 0,1,2,3,4

This is because the pin can have at most 4 nonzero digits.

We have X= the number of nonzero digits in a PIN.

We are given that there is no restriction on the digits of a pin, the three possible outcomes will be-

9022,when  X=3

2356, when X=4

1000, when X=1

Possible values of X are:

X = 0,1,2,3,4

Possible outcomes are :

​9022, when X= 3

2356, when X=4

1000, when X= 1

​Page 95 Problem 3 Answer

Given – The sample space S is an infinite set We have to find that if we have any random variable,X defined from S will have an infinite set of possible values or not.

We will assume any infinite set for the following case.

Here we will suppose that S is a sample space which is an infinite set, where a randomly a number has been selected from N which includes digits 1,3 or 5.

X={1 if a randomly selected number from N includes digits 1 or 3 or 5; 0 otherwise

We see that X has only two values, but the sample space is infinite.

So, it means that it is not necessary that if sample space is an infinite set, then any random variable X defined from that sample spaceS will have an infinite number of possible values.

If the sample spaceS is an infinite set, it is not necessarily imply that any random variable X defined from S will have an infinite set of possible values.

Page 95 Problem 4 Answer

Given – The variable X is the number of unbroken eggs in a randomly chosen standard egg carton.

We will find the set of possible values for the variable .

We will also need to check whether they are discrete or not.

Generally, a standard egg carton contains a dozen of eggs(dozen means12).

It means that standard egg carton has 12 eggs.

Hence, the number of unbroken eggs can be:

{0,1,2,3,4,5,6,7,8,9,10,11,12}

(at most12)(This is because we cannot take any negative or decimals values as it is not possible to have number of eggs in negative or decimal values).

Hence, we get the set of possible values as:

{0,1,2,3,4,5,6,7,8,9,10,11,12}.

We will now check whether the set is discrete or not.

We note that a variable is said to be discrete if it has a specific values and are restricted to separate values like integers or we can say if the variable has counts.

A variable is said to be continuous if it can have any value over a continuous range like decimals, real numbers, etc.

We know the unbroken eggs are restricted to separate values and cannot be a decimal(any value over continuous range).

Hence, we can say that X is discrete or countable.

ForX= number of unbroken eggs in a randomly chosen standard egg carton, the set of possible values are:{0,1,2,3,4,5,6,7,8,9,10,11,12}

The given variable is discrete as it has counts.

Page 95 Problem 5 Answer

Given -Y = the number of students on a class list for a particular course who are absent on the first day of classes.

We will find the set of possible values of students who were absent on the first day of classes and also check if the set is discrete or not.

We will check if the set is countable or not.

Clearly, the number of students will not be negative integer because the count of students cannot be a negative or decimal value.

Hence, the set of possible values will be: {0,1,2,3,4,5,6,7,8,9,……….}

We would have been able to reduce the set to that particular number if we had known the exact number of students.

We know that a variable is said to be discrete if it has a specific values and are restricted to separate values like integers or we can say if the variable has counts.

Also, a variable is continuous if it can have any value over a continuous range like decimals, real numbers, etc.

Hence, the variable is discrete because it has specific values .

It means it has countable number of possible values.

ForY = the number of students on a class list for a particular course who are absent on the first day of class, the set of possible values are:

{0,1,2,3,4,5,6,7,8,9,…………}

The variable is discrete because it has counts.

Page 95 Problem 6 Answer

Given -U =the number of times a duffer has to swing at a golf ball before hitting it.

We will find the set of possible values of the number of times a duffer has to swing at a golf ball before hitting it and also determine if the set is discrete or not.

We will use the definition of discrete random variables.

We note that the number of swings have to be positive integer.

This is due to the fact that a negative or decimal number of swings will not make sense and also 0 is not possible.

The set of possible values is:N={1,2,3,4,5,6,7,…..}

We note that a variable is said to be discrete if it has a specific values and are restricted to separate values like integers or we can say if the variable has counts.

However, a variable is continuous if it can have any value over a continuous range like decimals, real numbers, etc.

Thus, the variable is discrete as it has counts.

ForU= the number of times a duffer has to swing at a golf ball before hitting it, the set of possible values is: N={1,2,3,4,5,6,7,…..}

The variable is discrete because it has counts.

Page 95 Problem 7 Answer

Given that X=the length of a randomly selected rattle snake We will find the set of possible values for the variable.

We will also need to check if it is discrete or not.

Clearly, the length will be positive because negative length is meaningless.

Also the length of a snake is always non zero.

The length will be any integral value and it may take on decimal values .

Hence any non negative integer real number can be the length of a snake.

Therefore, the set of possible values is:{x is a real number∣x>0}.

Now, we will check for discrete.

Using the definition, we have:

Discrete random variable are restricted to defined separated values for example integers or count.

Continuous random variable are not restricted to defined separated values but can occupy any value over a continuous range for example decimal, real or rational numbers.

Hence,X is continuous but not discrete .

This is due to the fact that the length of a snake can take decimal values as well.

ForX =  the length of a randomly selected rattle snake, the set of possible values is:

{x is a real number∣x>0}

Here,x is continuous but not discrete as the length of a snake can take decimal values as well.

Page 95 Problem 8 Answer

Given that Z= the sales tax percentage for a randomly selected amazon.com purchase.

We will find the set of possible values for the variable and also need to check whether it is discrete or not.

We will use the definition of discrete random variables.

Clearly, the sales tax percentage has to be positive, because a negative sales tax percentage is pointless.

A sales tax= 0 can be possible when we do not have to pay any sales tax.

The sales tax percentage can be at most100%, hence the sales tax is between0−100 %.

The sales tax percentage can take on integer values ans decimal values .

Hence any real number between 0 and100 % is possible.

Therefore, the set of possible values are :

{x %∣ x is a real number and 0≤x≤100}

We will now check whether the set is discrete or not.

We know that a variable is said to be discrete if it has a specific values and are restricted to separate values like integers or we can say if the variable has counts.

However, a variable is continuous if it can have any value over a continuous range like decimals, real numbers, etc.

Thus,x is continuous and not discrete.

This is due to the fact that sales tax percentage can take on decimal values as well.

ForZ= the sales tax percentage for a randomly selected amazon.com purchase , the set of possible values is : {x %∣ x is a real number and 0≤x≤100}

Here,x is continuous as sales tax percentage can take on decimal values as well.

Page 95 Problem 9 Answer

Given – Y= pH of a randomly chosen soil sample.

We will find the set of possible values for the variable and whether it is discrete or not.

We will use the definition of discrete random variables.

We know that the pH can only take on values between 0 and 14  including both the numbers.

Hence, the pH can take on integer values and can also take decimal values as well like pH of 2.5,etc.

Thus, any real number as pH can take number between 0 and 14 is possible.

We obtain the set of possible values as : {x∣x is a real number and 0≤x<14}

To determine it is discrete or not :

Now, we have to check if the set is discrete or not.

As we know, a variable is said to be discrete if it has a specific values and are restricted to separate values like integers or we can say if the variable has counts.

But a variable is continuous if it can have any value over a continuous range like decimals, real numbers, etc.

Hence,x is continuous but not discrete as pH can take on decimal values as well.

ForY = the pH of a randomly chosen soil sample, the set of possible values are : {x∣x is a real number and 0≤x<14}

Here,x is continuous but not discrete as pH can take on decimal values as well.

Page 95 Problem 10 Answer

Given that X is the tension (psi) at which a randomly selected tennis racket has been strung.

We need to find the set of possible values for the variable and check whether it  is discrete or not.

We will use the definition of discrete random variables.

This will take values between the minimum possible tension, denoted as M1, and the maximum possible tension, denoted as M2.

Hence, all the possible values are: {x|M1≤x≤M2 , x ϵ R}

The tension can not be negative as a string cannot support negative tension which means, M1, M2 ≥ 0.

Now, we will check whether it is discrete or not.

We note that a variable is said to be discrete if it has a specific values and are restricted to separate values like integers or we can say if the variable has counts.

However, a variable is continuous if it can have any value over a continuous range like decimals, real numbers, etc.

We know that a random variable X that has a countable number of possible values either finite or countable infinite will be termed as discrete random variable.

As the given random variable has uncountable number of possible values,  so we can say that it is not discrete.

For x to be the tension (psi) at which a randomly selected tennis racket has been strung, the set of possible values is: {M1≤x≤M2 , x ϵ R}

As the given random variable has uncountable number of possible values, we can conclude that it is not discrete.

Page 95 Problem 11 Answer

Given – X=the total number of coin tosses required for three individuals to obtain a match (HHH or TTT).

We will describe the set of possible values for the variable, and state whether the variable is discrete.

We haveX= number of coin tosses required until three individuals obtain a match.

Here, don’t know how many coin tosses are required at most, the number of coin tosses required can be any positive integer .

Possible values ={1,2,3,….}=Z+

As the possible values are all integers, we can say that the variable is discrete.

We obtain : Possible values ={1,2,3,….}=Z+

The given variable is discrete.

Page 96 Problem 12 Answer

Given -T= the number of pumps at two pumps in use.

We need to give the possible values for given random variables.

We note that the possible values for T will begin from 0 up to the maximum number of pumps.

We know that the number of pumps at one station =6.

Also, the number of pumps at another station=4.

Hence, the total number of pumps=10.

Using the number of pumps, we can say that the possible values for Random variableT∈[0,10].

Total number of pumps in use or possible values for T are give as: 0,1,2,3,4,5,6,7,8,9,10

Page 96 Problem 13 Answer

Given – X denote the difference between pumps at each station.

We will give the possible values for the given random variable.

For station,  1. Number of pumps ∈{1,2,3,4,5,6}

We will construct a table for differences when the number of pumps are6

for the first stations and 4 for second station.

By taking differences of every pump at every station, we obtain table which is given below:

Looking at the above table we can conclude that the possible values of X will be: {−4,−3,−2,−1,0,1,2,3,4,5,6}

The possible values of X are :{−4,−3,−2,−1,0,1,2,3,4,5,6}

Page 96 Problem 14 Answer

Given – U denote the maximum between pumps at each station.

For1 st station, Numbe of pumps ∈{1,2,3,4,5,6}

For 2^nd station,  Number of pumps ∈{1,2,3,4}

We need to give the possible values for the given random variables.We will ta

We will construct a table for maximum pumps when the number of pumps are 6 for the first stations and 4 for the second station.

We obtain : The possible values for the maximum number of pumps at either station is U∈[0,6].

The possible values of U are given below: 0,1,2,3,4,5,6.

Page 96 Problem 15 Answer

Given – The number of pumps at two pump stations are 6 And 4.

Also,Z=number of stations having exactly two pumps in use.

We will find the possible values of Z.

We will assign the values for the two stations.

The number of stations which have exactly two pumps in use :=2

Hence, the possible values for Random Variable Z∈[0,2].

The possible values for stations having exactly two pumps in use are: 0,1,2.

Probability and Statistics for Engineering and the Sciences 8th Edition Chapter 3 Discrete Random Variables and Probability Distributions

Page 120 Problem 1 Answer

Given -n=25, so X∼Bin(25,.05).We will determineP(X≤2).We will use binomial distribution.

Using the definition, we obtain:

=B(2;25,0.05)

2
=∑ b(y;25,0.05)
y=0

(​25/0​)p/0

P(X≤2) =(1−p)25−0+(​25/1​)p1

=(1−p)25−1+(​25/2​)p2

=(1−p)25−2

0.28+0.36+0.23/0.87.

​We obtain: P(X≤2)=0.87

Page 120 Problem 2 Answer

Given -n=25,X∼Bin(25,.05).We will determine P(X≥5).We will use Binomial distribution.

Using the definition, we get :

P(X≥5) =1−P(X<5)

1−B(4;25,0.05)=

4
∑  b(y;25,0.05)
y=0

1−[(​25/0​)p0

=(1−p)25−0+(​25/1​)p1

= (1−p)25−1+(​25/2​)p2

=(1−p)25−2+(​25/3​)p3

=(1−p)25−3+(​25/4​)p4

(1−p)25−4]

1−0.28−0.36−0.23−0.09−0.03

0.007.

​We obtain: P(X>5)=0.007

Page 120 Problem 3 Answer

Given -n=25, so X∼Bin(25,.05).We will find P(1≤X≤4).We will use the binomial distribution.

Using the data, we obtain:

P(1≤X≤4)=P(X=1,X=2,X=3,X=4)

=B(4;25,0.05)−P(X=0)

4
∑   b(y;25,0.05)−P(X=0)
y=0

=0.28+0.36+0.23+0.09+0.03−0.28

=0.72.

​We obtain: P(1≤X≤4)=0.72

Page 120 Problem 4 Answer

Given -n=25, so X∼Bin(25,.05).

We will find the probability that none of the 25 boards is defective.

We will use the binomial distribution.

Using the binomial probability table, we obtain:

P(X=0)=b(0;25,0.05)​

=0.28

​The required probability is 0.28.

Page 120 Problem 5 Answer

Given -n=25, X∼Bin(25,..05).

We will calculate the expected value and standard deviation of X.

We will use the binomial distribution.

We will calculate the expected value and standard deviation of the random variableX

as follows:

E(X)=np​

=25⋅0.05

=1.25

σX=√np(1−p)

=√25⋅0.05⋅(1−0.05)

=1.09

We obtain: E(X)=1.25

σX=1.09

​Page 120 Problem 6 Answer

Given – A particular telephone number is used to receive both voice calls and fax messages.

We suppose that 25% of the incoming calls involve fax messages, and consider a sample of 25  incoming calls.

We will find the probability that at most 6 of the calls involve a fax message.

We will use​b(x;n,p)=​(​n/x​),x=0,1,2,…,n 0px(1−p)n−x, otherwise

​We suppose X= number of incoming calls that involve fax messages.

Here,​X∼Bin(25,0,25)

​So, according to the question, we calculate:

B(6;25,0.25)=P(X≤6)

=0.5611

​The probability that at most 6 of the calls involve a fax message is 0.5611

Page 120 Problem 7 Answer

We supposeX= number of incoming calls that involve fax messages.

As 25% of the incoming calls involve fax messages, so p=0.25.

Also, there are n=25 incoming calls. Hence,X∼Bin(25,0,25)

(Binomial Distribution).We will find the probability that exactly 6 of the calls involve a fax message.

We will use the formula:​b(x;n,p)={​(​n/x​)px(1−p)n−x/0,x=0,1,2,…,n, otherwise

​Using the definition, we calculate:

P(X=6)=b(6;25,0.25)

=(​25/6​)0.256

(1−0.25)25−6

=0.1828

​We obtain the probability of the event that exactly 6 of the calls involve a fax message as:

P(X=6)= 0.1828

Page 120 Problem 8 Answer

Given – A particular telephone number is used to receive both voice calls and fax messages.

Suppose that​25% of the incoming calls involve fax messages, and consider a sample of 25 incoming calls.

We suppose X= number of incoming calls that involve fax message.

We will find the probability that least 6 of the calls involve a fax message is given.

Using the formula:

b(x;n,p)={​(​n/x​)px

(1−p)n−x/0,x=0,1,2,…,n, otherwise

​We get:

P(X≥6)=1−P(X<6)

=1−P(X≤5)

=1−B(5;25,0.25)

=1−0.3783

=0.6217

​Now, the complement of event {X≥6} is event {X<6} ;

So,X takes only non negative values.

We will get the value using Appendix Table A.1.(column 0.25 and row 5).

We obtain the probability that at least 6 of the calls involve a fax message as: 0.6217

Page 120 Problem 9 Answer

We assumeX= number of incoming calls that involve fax messages.

Now, given that 25% of the incoming calls involve fax messages, and consider a sample of 25 incoming calls.

We find more than 6 of the calls involve a fax message by,

B(x;n,p)=P(X≤x)

y=0
∑ b(y;n,p),
x

= ​x:0,1,…,n

​Applying the formula for binomial property:

b(x;n,p)={​(​n/x​)px(1−p)n−x/0,x=0,1,2,…,n, otherwise

​We get:

P(X>6)=1−P(X≤6)

=1−0.5611

=0.4389

​Its complement{X>6} is event {X≤6}

We obtain the probability of more than 6 of the calls involve a fax message :0.4389

Page 121 Problem 10 Answer

Given -90% of all batteries from a certain supplier have acceptable voltages.

A certain type of flashlight requires two type-D batteries, and the flashlight will work only if both its batteries have acceptable voltages.

We will find the probability that at least nine will work? What assumptions did you make in the course of answering the question posed.

We suppose X=the number of working flashlights.

There is 0.9 probability that a battery have acceptable voltage, which indicates that probability of event A={battery with acceptable voltage} is 0.9.

We have:

n=10

p=P(A)∩P(A)

=0.9⋅0.9

=0.81

X≈Bin(25,0.81)​

Using the formula:

b(x;n,p)={​(​n/x​)px

(1−p)n−x/0,x=0,1,2,…,n, otherwise

​We get:

P(X≥9)=0.407

​=P(X=9)+P(X=10)

=b(9;10,0.81)+b(9;10,0.81)

=(​10/9​)0.819

(1−0.81)10−9+(​10/10​)0.8110

(1−0.81)10−10

=0.285+0.122​

We assume that batteries voltages are independent.

We obtain the probability of the event that at least nine will work is: P(X≥9)=0.407

Page 121 Problem 11 Answer

We suppose p= proportion of defective components.

Also X=number of defective components in the sample. Here, n=10 and p is the actual proportion, which implies that X can binomial distribution.

X∼Bin(10,p).Now, we assume A= {the batch is accepted} .

We will find the probability that the batch will be accepted when the actual proportion of defectives is 0.01,0.05,0.10,0.20,0.25.

We know that the batch will be accepted if at most 2 out of 10 are defective.

Hence, the general formula for p is:

P(A)=P(X≤2)

=B(2;10,p)

y=0
∑ b(y;10,p)
2

= When p=0.01

we get: P(X≤2)=B(x;n,p)

=B(2,10,0.01)

=[= BINOM.DIST (2,10,0.01, TRUE )]

≈0.9999

​Whenp=0.05, we get:

P(X≤2)=B(x;n,p)

=B(2,10,0.05)

=[=BINOM⋅DIST(2,10,0.05,TRUE)]

=0.9885

​Whenp=0.1, we get:

P(X≤2)=B(x;n,p)

=B(2,10,0.10)

=[= BINOM.DIST (2,10,0.1, TRUE )]

=0.9298

​Whenp=0.2, we get:

P(X≤2)=B(x;n,p)

=B(2,10,0.20)

=[=BINOM⋅DIST(2,10,0.2,TRUE)]

=0.6778

​Whenp=0.25, we get:

P(X≤2)=B(x;n,p)

=B(2,10,0.25)

=[= BINOM.DIST (2,10,0.25, TRUE )]

=0.5256

​We obtain:

P(A)=

{0.99988,p=0.01

{0.9885,p=0.05

{0.92981,p=0.1

{0.6778,p=0.2

{0.52559,p=0.25​

Page 121 Problem 12 Answer

Given – A graph of P(batch is accepted) as a function of p, with p on the horizontal axis and P(batch is accepted) on the vertical axis, is called the operating characteristic curve for the acceptance sampling plan.

We will use the results of part a) to sketch this curve f.

We will use the graphical utility.

We know that P(A) is a function of p

P(A)=B(2;10,p)

2
∑ b(y;10,p)
y=0

Hence, the exact operating characteristic curve i

The graph of the dat when 0≤p≤1 is:

Page 121 Problem 13 Answer

We need to calculate the probability at the different proportion of defective components such asp=0.01,0.05,0.10,0.20,0.25.

We will put different values of p to obtain the probability.

Now, for p=0.01, we get:

P(X≤1)=B(x;n,p)

=B(1,10,0.01)

=[=BINOM.DIST(1,10,0.01,TRUE)]

=0.9957

​Now, for p=0.05

we get:

P(X≤1)=B(x;n,p)

=B(1,10,0.05)

=[=BINOM⋅DIST(1,10,0.05,TRUE)]

=0.9139

​Now,p=0.10

we get:

P(X≤1)=B(x;n,p)

=B(1,10,0.10)

=[=BINOM⋅DIST(1,10,0.10,TRUE)]

=0.7361​

Now, for p=0.20, we get

P(X≤1)=B(x;n,p)

=B(1,10,0.20)

=[=BINOM⋅DIST(1,10,0.20,TRUE)]

=0.3758

​Now, ifp=0.25

we get:

P(X≤1)=B(x;n,p)

=B(1,10,0.25)

=[=BINOM.DIST(1,10,0.25,TRUE)]

=0.2440

​The probability in tabular form is given below :

The required operating characteristic curve obtained is

Thus, the given probabilities form a linear curve.

Page 121 Problem 14 Answer

We suppose X= the number of defective components.

We will use binomial distribution to calculate the probability at different proportion of defective components whenp=0.01,0.05,0.10,0.20,0.25.

We will put different values of p to obtain the probability.

Here,n=15.

Whenp=0.01, we get:

P(X≤2)=B(x;n,p)

=B(2,15,0.01)

=[=BINOM⋅DIST(2,15,0.01,TRUE)]

=0.9996

​Whenp=0.05, we get:

P(X≤2)=B(x;n,p)

=B(2,15,0.05)

=[=BINOM⋅DIST(2,15,0.05,TRUE)]

=0.9638

​Whenp=0.10, we get

P(X≤2)=B(x;n,p)

=B(2,15,0.10)

=[=BINOM⋅DIST(2,15,0.10,TRUE)]

=0.8159

​Whenp=0.20, we get

P(X≤2)=B(x;n,p)

=B(2,15,0.20)

=[=BNOM⋅DIST(2,15,0.20,TRUE)]

=0.3980

​Whenp=0.25, we get:

P(X≤2)=B(x;n,p)

=B(2,15,0.25)

=[=BINOM⋅DIST(2,15,0.25,TRUE)]

=0.2361

​The probability in tabular form is given below :

We obtain the operating characteristic curve as follows:

Therefore, the given probability form a polynomial curve.

Page 121 Problem 15 Answer

We need to calculate the probability at different proportion of defective component such asp=0.01,0.05,0.10,0.20,0.25

We will substitute different values of p to obtain the probability and obtain the curve.

We will construct the tables to summarize the data.

We obtain the probability in tabular form of part d as given below:

Using the graphical utility, we get:

Now, for part c) we have:

Using the graphical utility, we obtain:

We observe that the sampling plan of part c is more satisfactory as it has a linear relationship between p and P(acceptance).

Page 121 Problem 16 Answer

We assumeX= number of homes with detectors among 25 samples.

We will find the probability that the claim is rejected when the actual value of p=0.8.It follows binomial distribution X∼Bin(25,p)

.Here we considered the decision rule.We reject the claim that p≥0.8 if x≤15.

We calculate the probability of rejecting claim when the actual valuep=0.8 as follows:

P(X≤15 when p=0.8)

P(X≤15 when p=0.8)

x=0
∑ b(x;25,0.8)
15

x=0
∑(​25/x​)(0.8)x(0.2)25−x
15

Use Excel formula= BINOMDIST (15,25,0.8,1)​

0.017 We obtain the probability that the claim is rejected when the actual value of p Is 0.8 =0.017.

Page 121 Problem 17 Answer

We define X= number of houses with a fire detector.

Here,n=25.

Here, we suppose N={ not rejecting claim when p=0.7} .

We will reject the claim p≥0.8 if x≤15.

We will find the probability of not rejecting the claim when p=0.7.

We will denote N={ not rejecting claim whenp:0.7}.

We will reject the claim when x≤15, so we actually need to calculate probability thatX>15

whenp=0.7.

Hence,P(N)

p=0.7)

=1−B(15;25,0.7)

=P(X>15

=1−0.189

=0.811

​In the same way, whenp=0.6, we have:

P(N) =1−B(15;25,0.6)

=P(X>15 and p:0.6)

=1−0.575

=0.425

​When p is 0.7,

we get P(N)=0.811.

Whenp=0.6, we getP(N)=0.425.

Page 121 Problem 18 Answer

If the value 15 in the decision rule is replaced by 14, the probability that the claim is not rejecting when X:14 and p:0.8 then F(14):0.006.

We will determine how the “error probabilities” of parts (a) and (b) will change if the value 15 in the decision rule is replaced by 14.

We will calculate the following:

P(X>14)=1−P(X≤14 when p=0.7)

=1−x=0

∑  b(x;25,0.7)

15

=1−0.098

=0.902

​We obtain the probability as 0.902.

Page 122 Problem 19 Answer

Given – A toll bridge charges $1.00 for passenger cars and $2.50 for other vehicles.

Suppose that during daytime hours 60% of all vehicles are passenger cars.

We also know 25 vehicles  cross the bridge during a particular daytime period.

We will find the resulting expected toll revenue.

We suppose X= the number of passenger cars; then the toll revenue h(X) is a linear function of X.

We suppose h(X) denote the total revenue.

We get:

h(X)= Revenue from Passenger Vehicles + Revenue from Other Vehicles  =(\) Number of Passenger Vehicles })+(\.50) { Number of Other Vehicles }

=(1)(X)+(2.5)(25−X)

=62.5−1.5⋅X

​By the properties of expected value, we will simplify the formula for the expected value of h(X).

So, E[h(X)]

=E(62.5−1.5⋅X)

=E(62.5)−E(1.5⋅X)

=62.5−1.5⋅E(X)

​Finally, we will use the general formula for the expected value of a binomial random variable to compute the desired expected value.

We get:

E[h(X)]=62.5−1.5⋅E(X)

=62.5−1.5⋅n⋅p

=62.5−1.5⋅(25)⋅(0.6)

=40

​We obtain resulting expected toll revenue as $40.

Page 122 Problem 20 Answer

Given – We have a fixed value of n.

We will determine the values of p for which the variance is zero.

We will use the fact that the variance of constant is zero.

We note that the variance is a quadratic equation in terms of p.

Hence, we determine the roots by factoring.

V(x)np(1−p)=0

=0

⇒p=0 or 1−p=0

⇒p=0 or p=1

​Hence, these values of p gives zero variance.

Reason : if p=0,1 then the outcome of the of every trial is the same.

Basically, a binomial random variable is supposed to have a positive number of trials, that is n>0.

But, when n is fixed as n=0, the variance will be zero for any value of p.

This makes sense because if n=0 there are no trials to measure the variance of, and hence no variance.

We conclude that the variance of a binomial random variable will be zero whenp=0,1

for fixed values of n>0.If n=0, then the variance is zero for all values of probability p.

Page 122 Problem 21 Answer

To find-value of p is V(X) maximized

The critical values of a function i.e. maximized or minimized values occur where the first derivative is equal to zero.

Firstly, we assume that nis fixed and positive.

Now, we note that variance as a function of p, is:V(p)=np(1−p)​(0≤p≤1)

Now, we calculate V′(p):V′(p)

=d/dp[np(1−p)]

=d/dp[np−np²]

=n−2np

​We will substitute V′(X)=0 to get p as follows:

V′(p)n−2np

2np/p=0

=0

=n

=0.5

​We need to verify that p=0.5 is point of maximum.

We need to find the second derivative V′′(X)-V′′(p)

=d/dp[V′(p)]

=d/dp[n−2np]

=−2n

​We will now substitute p=0.5 in  V′′(0.5)-V′′(0.5)=−2n<0( since n>0)

​Hence, by the second derivative test, p=0.5 is a maximum as the second derivative is negative at the critical point.

The value of V(X) is maximum when p=0.5.

Probability and Statistics for Engineering and the Sciences 8th Edition Chapter 3 Discrete Random Variables and Probability Distributions

Page 113 Problem 1 Answer

Given –

​y	​0	​1	​2	​3
P(y)	0.6	0.25	0.1	0.05

We will find E(Y).

We will use the formula E(Y)=∑yp(y).

Applying the formula of expectation for the given data, we get:

E(Y)=∑yp(y)

=(0×0.6)+(1×0.25)+(2×0.1)+(3×0.05)

=0+0.25+0.2+0.15

=0.6

​We obtain: E(Y)=0.6

Page 113 Problem 2 Answer

Given –

​y	​0	​1	​2	x
P(y)	0.6	0.25	0.1	0.05

​We will calculate E(100Y²)

We note from previous part that E(Y²)=57.25.

We have:

E(Y²)=57.25

E(100Y²)=100E(Y²)

=100⋅57.25

=5725

We obtain : E(100Y²)=5725

Page 113 Problem 3 Answer

We are given that P(X=0)=1−p

P(X=1)=p

​We will find E(X²).We will useE(X²)=∑x²p(x).

Applying the formula, we get:

E(X²)=∑x²p(x)=[02×p(0)]+[12×p(1)]=[02×(1−p)]+[12×p]=p

​We obtain: E(X²)=p

Page 113 Problem 4 Answer

Given -P(X:0)=1−p

P(X:1)=p

​We will show that V(X)=p(1−p).

We know the formula V(X)=E(X²)−[E(x)]².

We know that V (X)

E(X)= E(X − [E(x)]2)²

= ∑xp(x)

Now, = [0 × p(0)] + [1 × p(1)]

= [0 × (1 − p)] + [1 × p]

= p

Putting these values in the above formula, we get:

V (X) = E(X − [E(x)]²)²

= p − [p]²

= p − p²

= p(1 − p)

We showed that V(X)=p(1−p).

Page 113 Problem 5 Answer

Given: If X be the Bernoulli random variable with P(X:0)=1−p

P(X:1)=p

​We will find E(X79)

Using the definition, we obtain:

E(X79)=[079×p(0)]+[179×p(1)]=[079×(1−p)]+[179×p]=p

​We obtain the value:

E(X79)=p

Page 113 Problem 6 Answer

Given – The data:

x           1          2            3            4           5           6

 

p(x)      1/15    2/15     3/15       4/15     5/15    6/15

We also know that owner bought copy for $2.00 and sells it for$4.00.

We will justify whether to buy 3 or 4 copies per week. We will find E(X),

If n=3, we note that owner bought 3copies.

E(x) is the expected value it is given by sum of the products ofx

value with p(x).

Hence, after x=3 multiply p(x) with 3.

Using E(x)=x=1

∑     x⋅p(x)    ∞, we get L E(x)=1(1/15)+2(1/15)+3(1/15)+3(4/15)+3(3/15)+3(2/15)

=41/15

=2.733

​The cost of 3 copies is given as 3(2)=6

We conclude that the owner sells those 3 copies at 4 each.

We suppose the net revenue, R=4(x)−6.

IT is in the form of W=a(x)+b.

Using the formula for expectation, we get:

​E(aX+b)=a(E(x))+b

Here E(x)=E[4(x)−6] here a=4 ,b=6

Hence E(W)=4

E(x)−6

​Using its value from the previous step , we get:

E(x)=41/15

=2.733

Thus,E(W)=4(41/15)−6

≈4.933

​Now, we will suppose n=4.

let us assume that owner bought 4 copies .

We note the formula:

E(x)=n=0

∑ x⋅p(x)

∞ So , the expectation is:

E(x)=n=0

∑     x⋅p(x) ∞

E(x)=1(1/15)+2⋅(1/15)+3(1/15)+4(4/15)+4(3/15)+4(2/15)

=50/15

≈3.33

The cost of 4 copies is given as 4(2.00)=8.00.

Hence, the owner sells those 4 copies at 8 each.

We know that the net revenue is R=4(x)−8.

It is in the form of W=a(x)+b.

Therefore, the expected value of this can be calculated as:

​E(x)=E[4(x)−8]

Here a=4 b=8

Hence E(W)=4

E(x)−8

​Using the previous step, we get:

​E(x)=10/3=3.733 approx

Hence E(W)=4(10/3)−8=5.33 3approx.

​If owner buys 3 copies he will get net revenue of 4.933.

If he if owner buys 4 copies he will get net revenue of 5.333

Clearly, it is better to buy 4 copies.

Page 114 Problem 7 Answer

Given – A random variable x  and x is the random variable for both the batches. so we need to calculate both mean and variance of x .

After computing mean and variance we also need to compute  expected number of pounds after the next customer product is shipped and variance of pound left

We also have that a company has 100 lb of certain chemical in stock The customer orders in 5 lb batches do we are left with100−5X lb’s in total

We will find mean and variance for this.

Using the definition, we get:

E(x)=x=1

∑   xp(x) ∞

=1(0.2)+2(0.4)+3(0.3)+4(0.1)

=2.3

Also, the variance is:

V(x)E(x²)=[E(x²)−E(x)²]

=1(0.2)+2(0.4)+3(0.3)+4(0.1)

=6.1​

Putting the obtained values, we get:

V(x)=[E(x²)−[E(x)]²]

=6.1−(2.3)²

=0.81

​We observe that  100−5X  is in the form of a(x)+b

So, applying the rule:

E(aX+b)=a(E(x))+b=(−5)E(x)+100

Here a=−5

​​b=100

So −5(E(x))+100=−5(2.3)+100

=88.5.

​We also have the rule V(ax)=a²

v(x) for constant v(x)  is zero.

Hence,

V(100−5x)=(−5)²

V(x)=20.25

​We obtain:

E(x)=2.3

V(x)=0.81

E(100−5X)=88.5

V(100−5X)=20.25

​Page 113 Problem 8 Answer

We will plot a graph for pm f(x), We are given x and p(x) values.

For the data given , we obtain the graph as:

We note that for the given x values and p(x) values, in order to plot graph for negative values of x  we will multiply x with−1.

Clearly, the spread of both these graphs is same.

Therefore, we can say that V(X)=V(−X).

Using the spread in graphs, we showed that V (X) = V (−X).

Page 114 Problem 9 Answer

Using the formula we can prove that V(X)=V(−X)

We note that the variance is given as V(aX+b)=a{2}

(v(x)) for constant V(x) is zero

According to the formula V(aX+b)=a{2}

V(x) for constant V(x) is zero

Here, inV(−X)

we have: a=−1

b=0

Now, using the formula we can prove that V(x)=V(−x) , It is in the form of V(aX+b) here a=−1 and b=0

ThusV(−x)=(−1){2} V(x).

It is equal to V(x).

Hence,V(x)=V(−x)

With the help of proposition involving V(aX+b), we showed that V(x)=V(−x).

Page 114 Problem 10 Answer

We will prove that V(aX+b)=a²⋅σX²

​We note that:

h(X)=aX+bV(aX+b)

=a²⋅σy²

​We also note that

h(X)=aX+bE[h(X)]

=aμ+b

Here μ=E(X).

The variance of a X+b is given by:V(aX+b)=[E(aX+b)²−(E(aX+b))²]

Using the given data, we obtain:
∞
V (aX + b) = ∑ (x − μ)2 p(x)V (aX + b)
∀

∞
=∑    [E ( (aX + b)2) − (E(aX + b))2]
∀

V (aX + b) = [aX − aμ] ⋅ p(x)

We see that a is constant so taking a out of the summation it becomes a²

Thus, V(aX+b)=a²

∀
∑          (x−(E(x))²)⋅p(x)
∞

V(aX+b)=a{2}

V(x) We showed that V(aX+b)=a² V(X).

Page 114 Problem 11 Answer

Given -a≤X≤b

We need to show that a≤E(X)≤b.

We will use: E(X)=μx

μx=∑x∈S x⋅p(x)

​Multiplying p(x) in the given inequality, we get:

a≤x≤b

So, a⋅p(x)≤x⋅p(x)≤b⋅p(x)

For all x∈S. This now implies that for the sum over all x∈S, the given inequality is satisfied.

x∈S

∑ a⋅p(x)≤x∈S

∑ x⋅p(x)≤x∈S

∑ b⋅p(x)

We obtain:

x∈S

∑ a⋅p(x) x∈S

∑ b⋅p(x) =a⋅x∈S

∑ p(x) =a⋅1=a;

=b⋅x∈S

∑ p(x) =b⋅1=b;

So, the sum over all x∈S of pmf p(x) is 1

We have that E(X)=x∈S

∑ x⋅p(x)

Hence, using the data obtained, we get: a≤E(X)≤b

Fora≤X≤b we showed that a≤E(X)≤b.