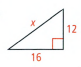
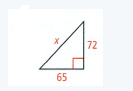
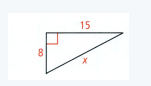
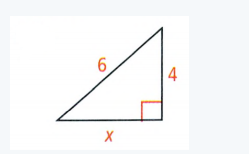
Savvas Learning Co Geometry Student Edition Chapter 9 Transformations Exercise 9.1 Translations
Savvas Learning Co Geometry Student Edition Chapter 9 Exercise 9.1 Translations Solutions Page 548 Exercise 1 Problem 1
Given: △JPT→ΔJ′P′T′
To find – The image of P
To find the image of \(\overline{T J}\).
In geometry, a translation is the shifting of a figure from one place to another without rotating, reflecting or changing its size.
Given that , △JPT → △J′P′T′
In translation, it is valid to list the points of the preimage and image in the same order, where we use the notation prime to mark the preimage.
Therefore, we see that in △JPT mark of the point P is in the second place, and in the △J′P′T′
in the second place is the mark of the point P′ , so we have that the image of P is point P′.
Considering what we said in the previous step, we see that the image of is \(\overline{T J}\) line \(\overline{T′ J′}\) .
The image of P is point P′, The image of \(\overline{T J}\) is line \(\overline{T′ J′}\).
Read and Learn More Savvas Learning Co Geometry Student Edition Solutions
Exercise 9.1 Translations Savvas Geometry answers Page 548 Exercise 2 Problem 2
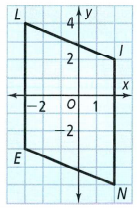
Given: (x ,y) → (x − 3, y − 4)
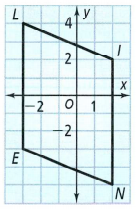
Identify the coordinates for each vertex:
N(2,−5) , I(2,2), L(−3,4), E(−3,−4)
Use the translation rule that is given to us to find the coordinates of each vertex of the image.
Our translation rule is , (x ,y) → (x − 3,y − 4)
For point N the image is, (2,−5 ) → (2 − 3, −5 − 4)
When we simplify, the image is point N′ (−1,−9).
Identify the coordinates for each vertex:
N(2,−5), I(2,2), L(−3,4), E(−3,−4)
Use the translation rule that is given to us to find the coordinates of each vertex of the image.
Our translation rule is
(x ,y) → (x − 3,y − 4)
For point N the image is: (2,−5) → (2 − 3,−5 − 4)
When we simplify, the image is point N′ (−1,−9).
For point I the image is: (2,2) → (2 − 3, 2 − 4)
When we simplify, the image is point I′ (−1,−2).
For point L the image is: (−3,4) → (−3 − 3, 4 − 4)
When we simplify, the image is point L′ (−6,0).
For point E the image is: (−3,−4)→(−3−3,−4−4)
When we simplify, the image is point E′(−6,−8).
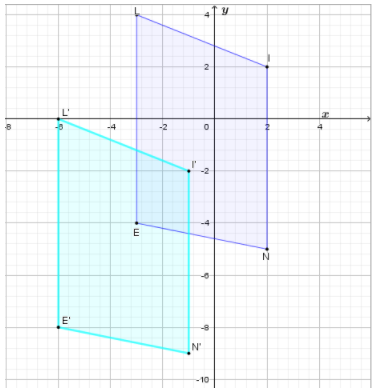
To graph the image, first we graph points: N′,I′,L′ and E′.
Then draw \(\overline{N’ I’}\), \(\overline{I’ L’}\), \(\overline{L’ E’}\), \(\overline{E’ N’}\).
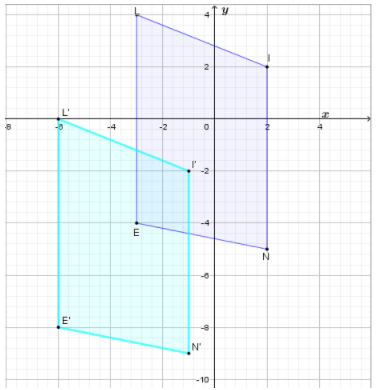
The image of NILE for the given translation is
Translations Solutions Chapter 9 Exercise 9.1 Savvas Geometry Page 548 Exercise 3 Problem 3
Given: Point H(x ,y) moves 12 units left and4 units up
The given graph is
To find – The rule that describes this given translation.
In geometry, a translation is the shifting of a figure from one place to another without rotating, reflecting or changing its size.
Given point H(x ,y).
This point moves 12 units to the left and 4 units up.
Move it 12 units to the left
It is like we subtract 12 from x coordinate, and when we move it4 units up it is like we add 4 to y coordinate.
Based on the previous step, the translation rule is (x ,y)→(x − 12,y + 4).
The translation rule is (x ,y) → (x − 12,y + 4).
Savvas Learning Co Geometry Student Edition Chapter 9 Page 548 Exercise 4 Problem 4
Given:
To explain and correct her error.
A translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction.
Given a sketch
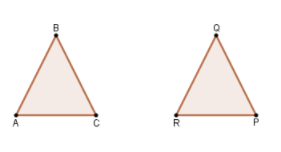
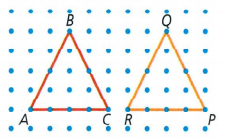
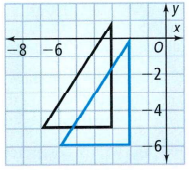
Friend says that transformation △ABC → △PQR is a translation.
The image of A is R, image of B is Q , image of C is P.
Based on that, the transformation that is translation is , △ABC → △RQP
A friend’s mistake is that for a transformation that is rotation, he said it is translation.
Friend’s mistake is that for a transformation that is rotation, he said it is translation.
Translations Solutions Chapter 9 Exercise 9.1 Savvas Geometry Page 548 Exercise 5 Problem 5
A translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction.
To write translation (x ,y) → (x + 1,y − 3) as a composition of a horizontal and vertical translation.
First, the(x ,y) translates to (x + 1,y)
This represents a horizontal translation.
Then, (x + 1, y) translates to (x + 1,y − 3)
This represents a vertical translation.
The(x ,y) translates to (x + 1, y).
This represents horizontal translation. (x + 1, y) translates to (x + 1,y − 3). This represents vertical translation.
Chapter 9 Exercise 9.1 Translations Savvas Learning Co Geometry Explanation Page 549 Exercise 6 Problem 6
Given:
A sequence of transformations is a set of translations, rotations, reflections, and dilations on a figure.
Based on the sketch, we see that preimage and image are congruent.
Therefore, this transformation is isometry.
The given preimage and image are congruent, so this transformation is isometry.
Solutions For Translations Exercise 9.1 In Savvas Geometry Chapter 9 Student Edition Page 549 Exercise 7 Problem 7
Given:
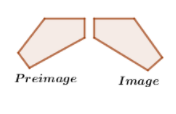
A translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction.
Based on the sketch.
The preimage and image are congruent, so this transformation is isometry.
The preimage and image are congruent, so this transformation is isometry.
Solutions For Translations Exercise 9.1 In Savvas Geometry Chapter 9 Student Edition Page 549 Exercise 8 Problem 8
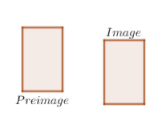
Given:
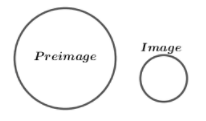
A translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction.
Based on the sketch.
The preimage and image are not congruent, because we have a change in size.
Therefore, this transformation is not isometry.
The preimage and image are not congruent, because we have a change in size so the transformation is not isometry.
Exercise 9.1 Translations Savvas Learning Co Geometry Detailed Answers Page 549 Exercise 9 Problem 9
Given:
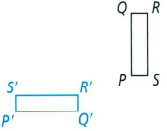
To choose an angle or point from the preimage and name its image.
A translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction.
The image of the point p from the preimage is p′
The image of the point Q from the preimage is Q′
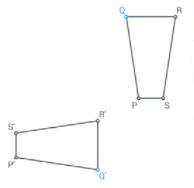
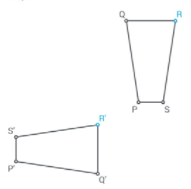
The image of the point R from the preimage is R′
The image of the point S from the preimage is S′
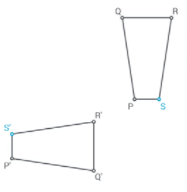
The image of the point p from the preimage is p′, The image of the point Q from the preimage is Q′, The image of the point R from the preimage is R′, The image of the point S from the preimage is S′.
Savvas Learning Co Geometry Student Edition Chapter 9 Page 549 Exercise 9 Problem 10
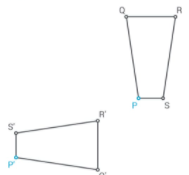
Given:
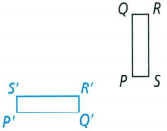
To list all pairs of corresponding sides.
Using the method of geometrical transformation.
The matching side to \(\overline{P Q}\) is \(\overline{P’ Q’}\)
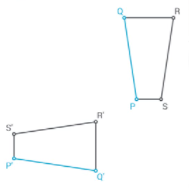
The matching side to \(\overline{Q R}\) is \(\overline{Q’ R’}\)
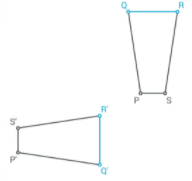
The matching side to \(\overline{R S}\) is \(\overline{R’ S’}\)
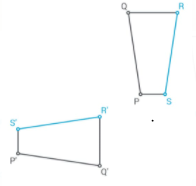
The matching side to \(\overline{S P}\) is \(\overline{S’ P’}\)
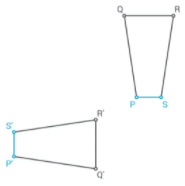
The matching sides are
\(\overline{P Q}\) and \(\overline{P’ Q’}\)
\(\overline{Q R}\) and \(\overline{Q’ R’}\)
\(\overline{R S}\) and \(\overline{R’ S’}\)
\(\overline{S P}\) and \(\overline{S’ P’}\).
Geometry Chapter 9 Translations Savvas Learning Co Explanation Guide Page 549 Exercise 10 Problem 11
Given: (x ,y) → (x − 2,y + 5)
To graph the image of each figure under the given translation.
A translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction.
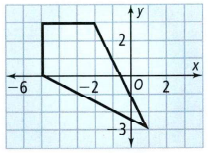
The given a preimage, a rectangle, whose vertices we will mark with A,B,C and D
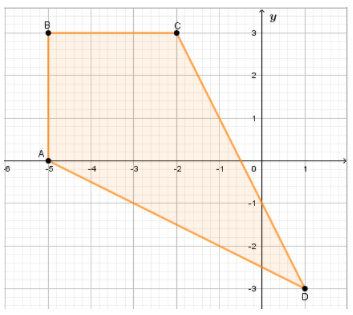
To identify the coordinate of each vertex
A(−5,0), B(−5,3), C(−2,3), D(1,−3)
Use the translation rule that is given to us to find the coordinates of each vertex of the image.
Our translation rule is (x ,y) → (x − 2, y + 5)
For point A the image is: (−5,0) → (−5 − 2, 0 + 5)
When we simplify, the image is point A′(−7,5).
For point B the image is: (−5,3) → (−5 − 2,3 + 5)
When we simplify, the image is point B′(−7,8).
For point C the image is: (−2,3) → (−2 − 2,3 + 5)
When we simplify, the image is point B′ (−4,8).
For point D the image is: (1,−3) → (1 − 2,−3 + 5)
When we simplify, the image is point D′ (−1,2).
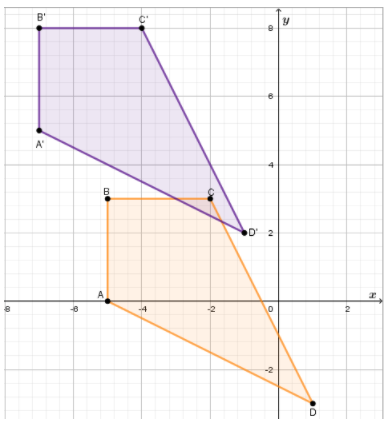
To graph the image, first we graph points: A′ , B’, C’, and D’
The draw \(\overline{A^{\prime} B^{\prime}}, \overline{B^{\prime} C^{\prime}}, \overline{C^{\prime} D^{\prime}} \text { and } \overline{D^{\prime} A^{\prime}}\)
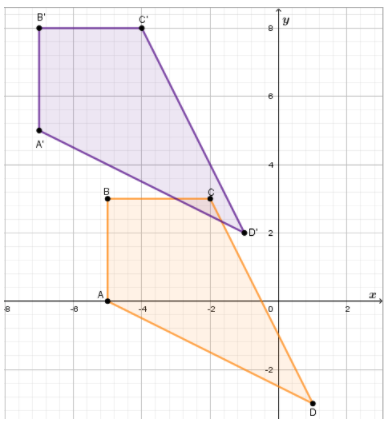
The graph of the image of each figure under the given translation is
Exercise 9.1 Translations Savvas Geometry Answers Page 549 Exercise 11 Problem 12
Given:
To write a rule to describe each translation.
A translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction.
The vertices of the preimage are A(−7,−5) ,B(−3,−5) and C(−3,1).
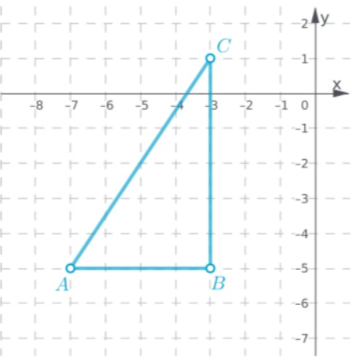
Compare the r = \(\sqrt{(x-4)^2+(y-0)^2+(z-z)^2}\) and y coordinates of the points A(−7,−5) and its image A′ (−6,−6).
The r = \(\sqrt{(x-4)^2+(y-0)^2+(z-z)^2}\) coordinate of the image A′ is 1 unit right from the point A’−6−(−7) = 1
It follows that the horizontal change is: x ⟶ x + 1
The y coordinate of the image A′ is 1 unit down from the point A ,−6 − (−5) = −1
It follows that the vertical change is: y ⟶ y − 1
The rule for the translation of a point (x ,y) 1 unit right and 1 unit down is
T<1,−1> (x ,y) = (x + 1,y − 1)
The rule should be valid for every vertex.
T<1,−1>(x ,y) = (x + 1, y − 1)
Check if the rule is valid for B(−3,−5) and its image B′ by inserting x = −3 and y = −5
T<1,−1> (−3,−5) = (−3 + 1, −5 − 1)
Calculate the coordinates
T<1,−1> (−3,−5) = (−2,−6)
Since the image B′ has coordinates (−2,−6) , it follows that the rule is valid for this vertex.
T<1,−1>(x ,y) = (x + 1,y − 1)
Check if the rule is valid for C(−3,1) and its image B′ by inserting x = −3 and y = 1
T<1,−1>(−3,1) = (−3 + 1,1 − 1)
Calculate the coordinates
T<1,−1>(−3,1) = (−2,0)
Since the image C′ has coordinates (−2,0), it follows that the rule is valid for this vertex.
The translation rule is T<1,−1>(x ,y).
The translation rule is T<1,−1>(x ,y).
Translations Solutions Chapter 9 Exercise 9.1 Savvas Geometry Page 549 Exercise 12 Problem 13
Given: Walk 4 blocks east and 4 blocks north to the Wells Fargo History Museum.
Walk 5 blocks west and 3 blocks north to the Cable Car Barn Museum.
To find where is the Cable Car Barn Museum in relation to your hotel.
A translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction.
Based on the given data, Point A(0,0) represents the position of the hotel
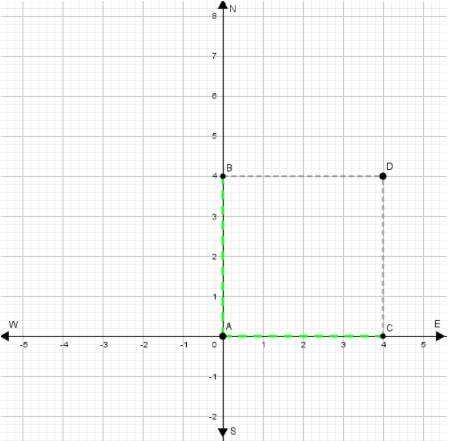
When you go 4 blocks east (which is represented by AC ) and 4 blocks north (which is represented by AB) we see that we get to the point D(4,4)which represents the position of Wells Fargo History Museum.(0,0) → (0 + 4,0 + 4)
When we simplify, we get D(4,4), as we said.
Then we from point D move 5blocks west (which is represented by DF) and 3 blocks west (which is represented by DG) and we see that we get to the point H(−1,7) which represents the position of Cable Car Barn Museum.(4,4) → (4 − 5 ,4 + 3)
When we simplify, we get H(−1,7), as we said.
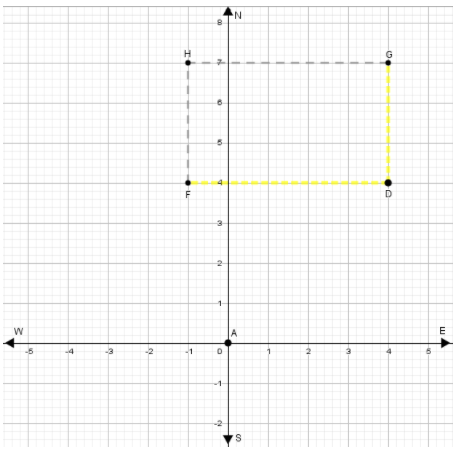
To find the Cable Car Barn Museum in relation to hotel, that is, we need to see where point H is in relation to point A.
When we go east 1 block (which is represented by HI ) and 7 blocks south (which is represented by HJ ), we get to point A.
⇒ (−1,7)→(−1 + 1,7 − 7)
When we simplify, we get A(0,0), as we said.
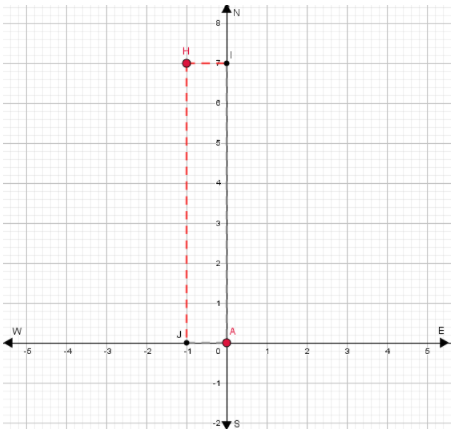
Based on the previous step, we see that the Cable Car Barn Museum is 1 block west and 7 blocks north in relation to hotel.
The Cable Car Barn Museum is 1 block west and 7 blocks north.
Chapter 9 Exercise 9.1 Translations Savvas Learning Co Geometry Explanation Page 550 Exercise 13 Problem 14
Given: hey leave their home in Enid, Oklahoma, and drive to Tulsa, which is 107 mi east and 18 mi south of Enid.
From Tulsa, they go to Norman,83 mi west and 63 mi south of Tulsa.
To find – Where is Norman in relation to Enid.
A translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction.
Based on the given data, Point O(0,0) represent the position of home, Enid.
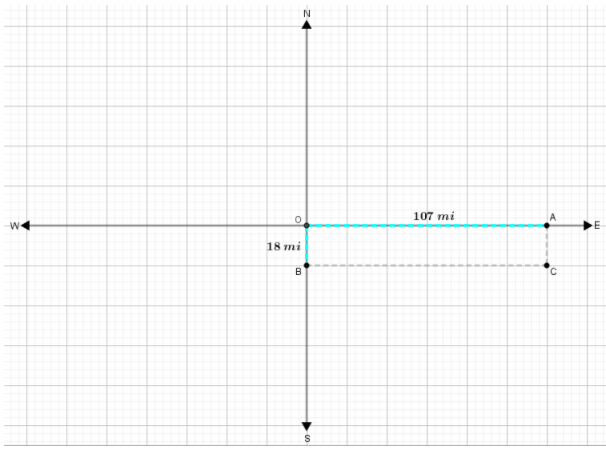
When you go 107mi east (which is represented by OA ) and 18 mi south (which is represented by OB) we see that we get to the point C(107,−18) which represents the position of Tulsa.
(0,0)→(0 + 107,0 − 18) When we simplify, we get C(107, − 18)
Then we from point C move 83 mi west (which is represented by CD ) and 63 mi south (which is represented by CF) and we see that we get to the point G(24,−81)which represents the position of Norman. (107,−18) → (107 − 83,− 18 − 63)
When we simplify, we get G (24, − 81)
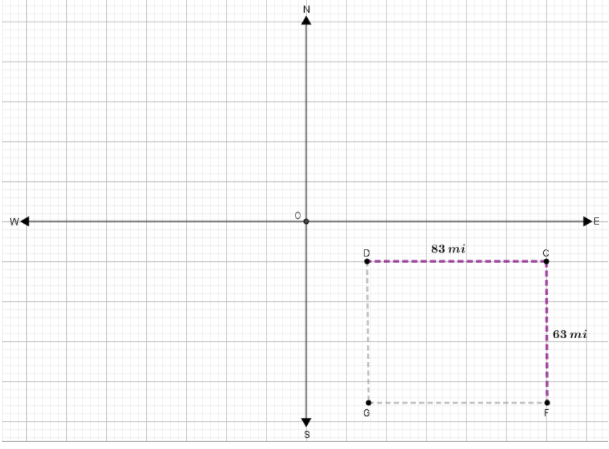
To find where is the Norman in relation to Enid, that is, we need to see where point G is in relation to point O.
When we go west 24mi (which is represented by GH ) and 81 mi north (which is represented by GI), we get to point O.
⇒ (24 ,− 81) → (24 − 24, −81 + 81)
When we simplify, we get O(0,0)
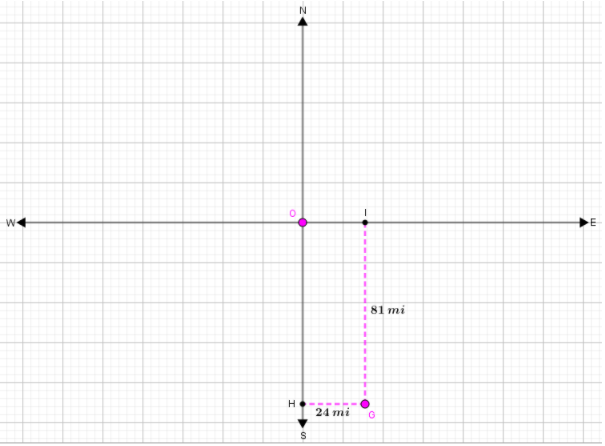
Based on the previous step, the Norman is 24 mi east and 81 mi south in relation to Enid.
The Norman is 24 mi east and 81 mi south in relation to Enid.
Solutions For Translations Exercise 9.1 In Savvas Geometry Chapter 9 Student Edition Page 550 Exercise 14 Problem 15
Given :
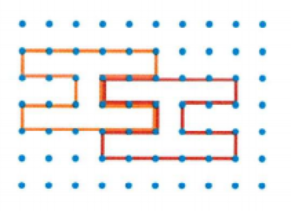
Write a rule that describes the translation.
The given translation is
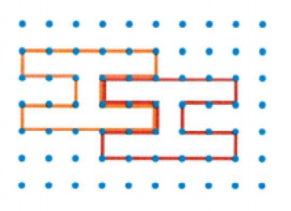
Here the orange figure is the translation image of the red figure
Hence the translation rule is (x ,y) → (x − 3,y + 1)
Therefore the required rule for the translation is (x ,y) n→ (x − 3,y + 1).
Exercise 9.1 Translations Savvas Learning Co Geometry Detailed Answers Page 550 Exercise 15 Problem 16
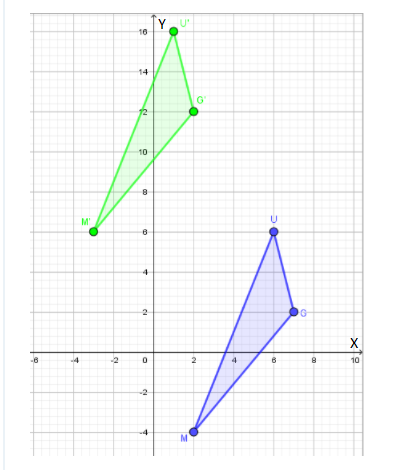
Given: △MUG has coordinates M(2,−4), U(6,6) , and G(7,2).
A translation maps point M to M′ (−3,6).
To find the coordinates of U′ and G′ for this translation.
To find how can you use a graph to help you visualize the problem.
To find how can you find a rule that describes the translation.
Based on the given data, the graph is
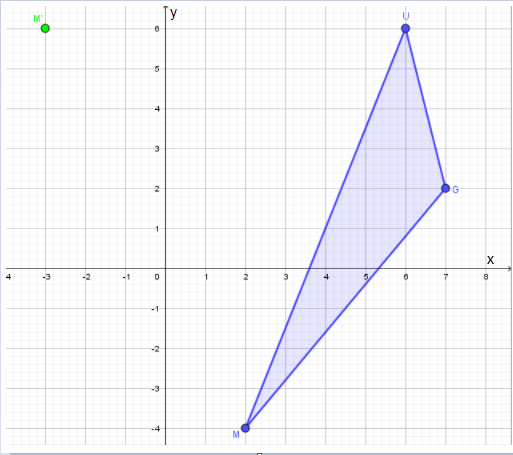
Given △MUG and that translation maps point M(2,−4) to point M′ (−3,6).
Our assignment is to find the coordinates of U′ and G′ , that is, the coordinates of the points that are images of points U and G.
In order to find this coordinates, we will use points M and M′ to find the translation rule.
Then we will use the rule to find required coordinates.
Let’s look at the sketch.
If we move 5 units left from point M (Which is represented by MA ) and 10 units up from point M ( Which is represented by MB ) we see that we would reach to the point M′.
So, the x coordinate is reduced by 5 (Because we are going left) and the y coordinate is increased by 10
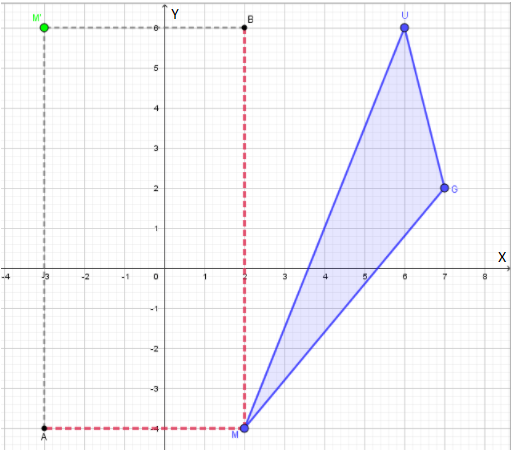
Based on the previous step, our translation rule is
(x ,y)→ (x − 5, y+ 10)
For point U(6,6) the image is: (6,6) → (6 − 5,6 + 10)
When we simplify, the image is point U′ (1,16).
For point G(7,2) the image is: (7,2) → (7 − 5, 2 + 10)
When we simplify, the image is point G′ (2,12).
So, we have, U′ (1,16) G′(2,12)
Sketch a graph and enter the data given we can see how a point is translated (whether it goes left or right, up or down) or if we have a translation rule we can use it to find preimages.
When we have an image and a preimage, sketch a graph and observe the movement of the point that is the image to the point of the image that is the preimage.
Depending on whether the point moves left or right, up or down and how much, we conclude how much the coordinates of the point that represents the image decrease or increase, and that is how we find the translation rule.
The coordinates of U′ (1,16) and G′(2,12)
Sketch a graph and enter the data given we can see how a point is translated (whether it goes left or right, up or down) or if we have a translation rule we can use it to find preimages.
When we have an image and a preimage, sketch a graph and observe the movement of the point that is the image to the point of the image that is the preimage.
Depending on whether the point moves left or right, up or down and how much.
We conclude how much the coordinates of the point that represents the image decrease or increase, and that is how we find the translation rule.
Savvas Learning Co Geometry Student Edition Chapter 9 Page 550 Exercise 16 Problem 17
Given: (x ,y) → (x − 3,y − 5)
To use the rectangle and (x ,y)→ (x + 3,y + 1) to draw a box.
A translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction.
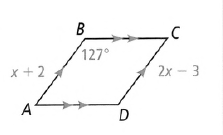
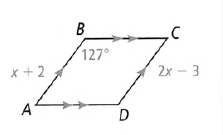
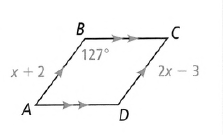
Given a trapeze, whose vertices we will mark with A,B,C and D
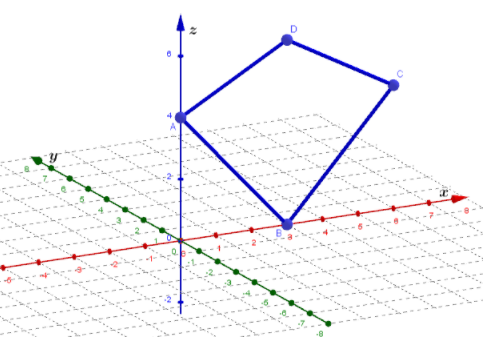
The coordinates of the points A,B,C and D with respect to the two-dimensional coordinate system x Or y are
A(0,0), B(3,0), C(6,0), D(3,0)
The translation rule is
⇒ (x ,y) → (x − 3,y − 5)
To find the images of A,B,C and D.
For point A(0,0) the preimage is: (0,0) → (0 − 3,0 − 5)
When we simplify, the preimage is point A′(−3,−5).
For point B(3,0) the preimage is: (3,0) → (3 − 3,0 − 5)
When we simplify, the preimage is point B′ (0,−5).
For point C(6,0) the preimage is: (6,0) → (6 − 3,0 − 5)
When we simplify, the preimage is point C′(3,−5).
For point D(3,0) the preimage is: (3,0) → (3 − 3, 0 − 5)
When we simplify, the preimage is point D′(0,−5).
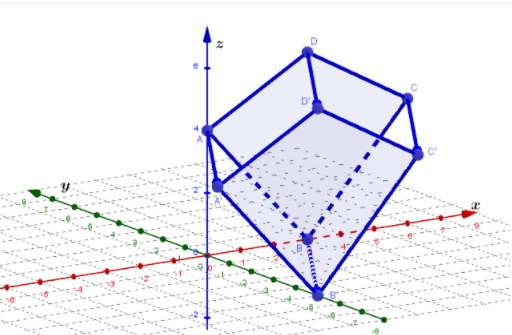
Points A and Care in the plane z = 4,point Bis in the plane z = 0, point Dis in the plane z = 6, and that is why we switch to three-dimensional space.
So we find the points: A′(−3,−5,4) , B′(0,−5,0), C′(3,−5,4), D′(0,−5,6)
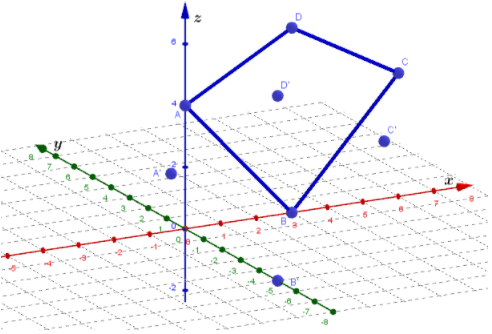
To draw \(\overline{A A^{\prime}}, \overline{B B^{\prime}}, \overline{C C^{\prime}} \text { and } \overline{D D^{\prime}} \text {. }\)
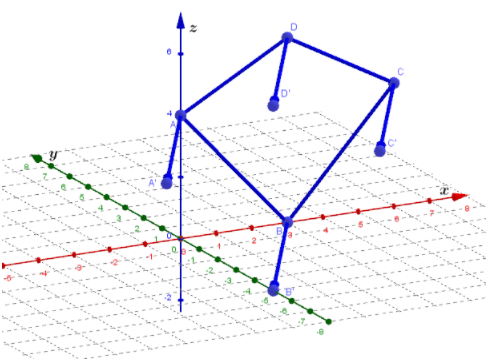
To connect points and we have our three-dimensional figure
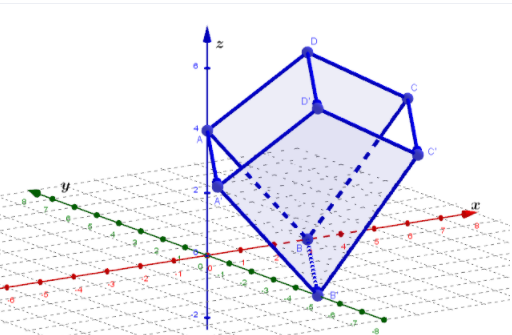
Using the rectangle and (x ,y) → (x + 3,y + 1) the box is
Savvas Learning Co Geometry Student Edition Chapter 9 Page 550 Exercise 17 Problem 18
Draw a parallelogram ABCD
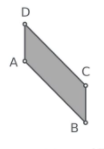
Draw a reflection line on the right of the parallelogram that is parallel to one of the sides.
Reflect points A,B,C, and D.
Draw a parallelogram A′B′C′D′.
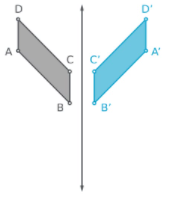
Translate parallelograms ABCD and A′B′C′D′ downwards for a little bit more than BC.
Draw another two parallelograms and Repeat transformations to make a pattern.

The translations are

Savvas Learning Co Geometry Student Edition Chapter 9 Page 550 Exercise 18 Problem 19
Given: Translation (x ,y) → (x + 5, y + 7) maps △MNO onto △M′ N′O′
To determine translation rule maps △M′N′O′ onto △MNO.
A translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction.
In the assignment we are given translation, (x ,y) → (x + 5, y + 7)
This translation maps △MNO onto △M′N′O′.
For example, take some random triangle, like one on the sketch below.
We then used the given translation and we sketched the image, △M′N′O′.
For example, at point O, we see that we have moved7units up ( which is represented by OA) and 5 units to the left ( which is represented by OB ) and we reached to the point O′.
If we want to get back from the point O′ to the point O we need to move 7 units down ( which is represented by O′B) and 5units to the right ( which is represented by O′A) and we reached to the point O.
If we checked for the remaining two points, we would get the same.
The graph is
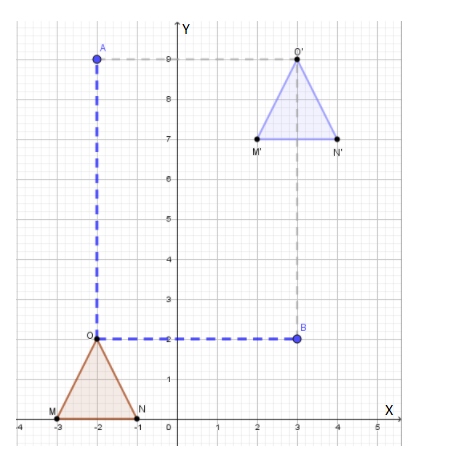
The translation that maps △M′N′O′ onto △MNO is (x ,y) → (x − 5,y − 7).
The translation that maps △M′N′O′ onto △MNO is (x ,y) → (x − 5,y − 7).
Savvas Learning Co Geometry Student Edition Chapter 9 Page 550 Exercise 19 Problem 20
Given:
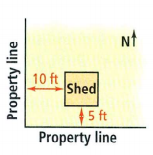
To describe how to move the shed to comply with the law.
A translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction.
Given
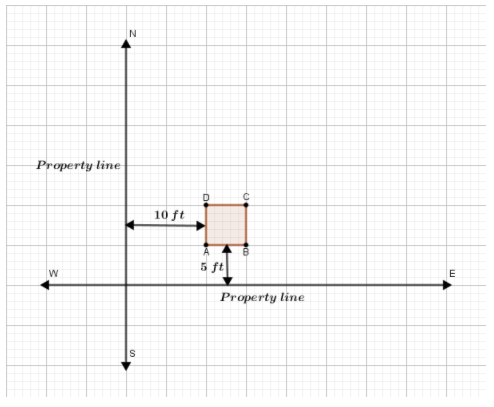
If we move points A,B,C and D5 ft east ( to the right) and 10ft north (upwards), we would get to the points
To mark with A′,B′,C′ and D′
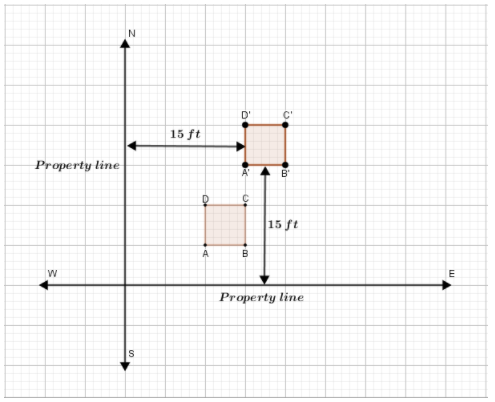
We see that □ A′B′C′D′ satisfies the law.
Used to satisfy the law is the translation of the shed.
The rule of the mentioned translation is (x ,y) → (x + 5, y + 10).
The rule of the mentioned translation is( x ,y)→(x + 5,y + 10).
Savvas Learning Co Geometry Student Edition Chapter 9 Page 550 Exercise 20 Problem 21
Given: (x ,y) → (x + 5, y + 7) followed by (x ,y) → (x − 9, y − 2).
The program makes the letter W by connecting the points 1, 2, (2,0), 3, 2, (4,0) and (5,2)
To find the points does the program connect to make the last W.
A translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction.
Given that when program connects to points (1,2),(2,0)(3,2)(4,0) and (5,2) a letter W appears.
Our assignment is to find the point that program connects to, to make the last appearance of the letter W.
The given translations are, (x ,y) → (x + 5,y + 7), (x ,y) → (x − 9 ,y − 2)
The problem can solve in two ways.
The first way is to use the first translation and find the point where the letter W is repeated for the first time, and then use the second translation to that point that we found and find the point where W appears for the last time.
The second way is to present these two translations as one translation in the following way.
Use this translation: (x ,y) → (x + 5, y + 7).
Have (x + 5,y + 7) and we use the second translation on this point so we have, (x + 5,y + 7) → (x + 5 − 9,y + 7 − 2)
When we simplify, we have (x − 4, y + 5).
The new translation that leads us directly to the point that connected with our program shows the last W is, (x ,y) → (x − 4, y + 5)
We will mark point (1,2) with A.
For this point find the required point in both ways.
If we move 5 unit to the right ( which is presented with AF ) and 7 ,units up ( which is presented with AG ) we would reach point A1 , where letter W appears the first time.
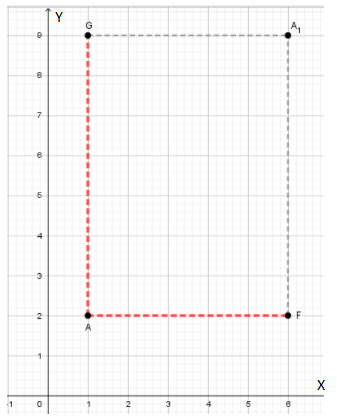
(1,2) → (1 + 5,2 + 7), When we simplify, we get A1 (6,9).
At point A1 . move 9 unit to the left ( which is presented with A1H ) and 2 units down ( which is presented with A1 I) we would reach point A′, where letter W appears the second time.
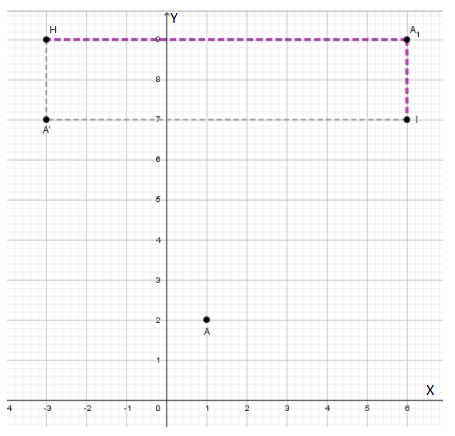
(6,9) → (6 − 9,9 − 2) , When we simplify, we get, A′(−3,7).
At point A1 . move 9 unit to the left ( which is presented with A1 H) and 2 units down ( which is presented with A1I) we would reach point A, where letter W appears the second time .(6,9) → (6 − 9, 9 − 2)
When we simplify, we get: A′ (−3,7).
If we use the new translation that leads us directly from point A(1,2) to required point, we would have, (1,2) → (1 − 4, 2 + 5)
Letter W shows the second time when point A′ (−3,7) is connected to the program.
We see that it is easier for us to use the second way to find the desired point, so we will use only the second way for the other points.
We will mark point (2,0) with B.
We use the new translation, that is, we move 4 unit to the left ( which is presented with BF1 ) and 5 units up ( which is presented with BG1 ) and we reach to the point B′ , where letter W appears the second time.
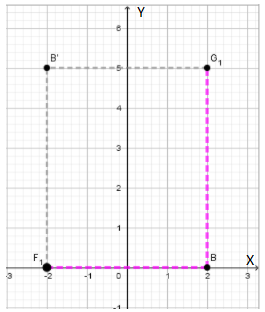
(2,0) → (2 − 4,0 + 5)
When we simplify, we get: B′(−2,5).
Letter W shows the second time when point B′ (−2,5) is connected to the program
We will mark point (3,2) with C.
We use the new translation, that is, we move 4 unit to the left ( which is presented with CG2 ) and 5 units up (which is presented with CF2 m) and we reach point C′ , where letter w appears the second time.
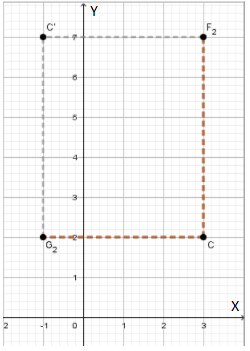
(3,2) → (3 − 4,2 + 5)
When we simplify, we get: C′ (−1,7).
Letter W shows the second time when point C′ (−1,7) is connected to the program.
We will Mark point(4,0) with D .
We use the new translation, that is, we move 4 unit to the left ( which is presented with DF3 ) and 5 units up (which is presented with DG3) and we reach point D′ , where letter W appears the second time.
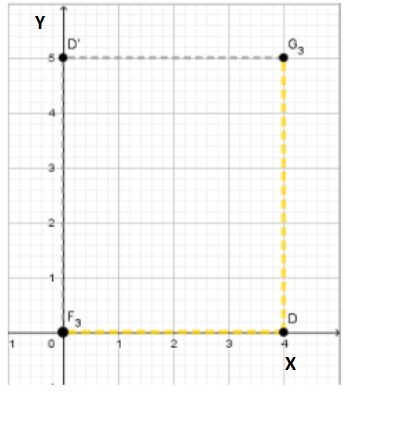
(4,0) → (4 − 4,0 + 5)
When we simplify, we get: D′ (0,5).
Letter W shows the second time when point D′ (0,5) is connected to the program.
We will mark point (5,2) with E.
We use the new translation, that is, we move 4 unit to the left ( which is presented with EG4) and 5 units up (which is presented with EF4) and we reach point E′, where letter W appears the second time.
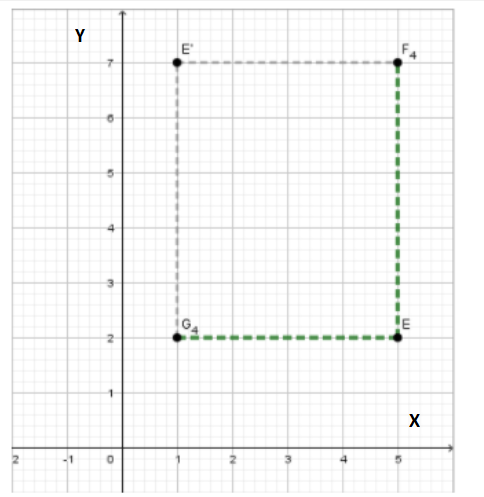
(5,2) → (5 − 4, 2 + 5)
When we simplify, we get: E′ (1,7).
Letter W shows the second time when point E′ (1,7) is connected to the program.
The required points are
A′(−3,7), B′(−2,5), C′(−1,7), D′(0,5), E′(1,7)
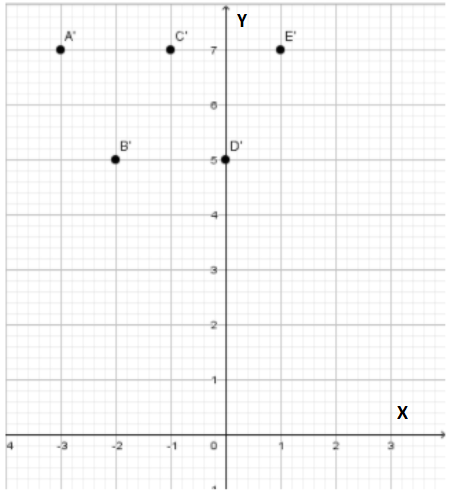
The points does the program connect to make the last W,(−3,7),(−2,5),(−1,7),(0,5)
Savvas Learning Co Geometry Student Edition Chapter 9 Page 551 Exercise 21 Problem 22
Given:
To write three different translation rules for which the image of △JKL has a vertex at the origin.
A transformation is a general term for four specific ways to manipulate the shape and/or position of a point, a line, or geometric figure.
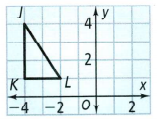
The coordinates of the vertices of △KLM are, K(−4,1) , L(−2,1) , M(−4,4)
The image of a triangle to have one vertex at the origin, we observe which translation would satisfy the condition that, for example, the image of vertex L, which we will mark with L′ has coordinates (0,0) (which would mean that this point represents the origin).
Consider the point K.
If move 4 units to the right (which is presented with KA) and 1 unit down (which is presented with KB) we would reach to the point K′.
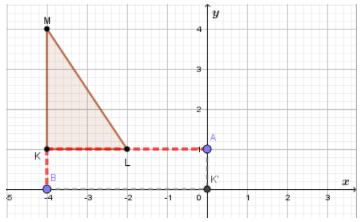
(−4,1)→(−4 + 4,1 − 1)
When we simplify, we have: K′ (0,0).
So, we have translation, (x ,y) → (x + 4,y − 1)
If we use translation (x ,y) → (x + 4, y− 1) to find image of △KLM we would get

Use this translation, the image △K′L′M′ has one vertex at the origin, vertex K′.
Consider the point L.
If we move 2 units to the right (which is presented with LA1) and 1 unit down (which is presented with LB1) we would reach to the point L1′.
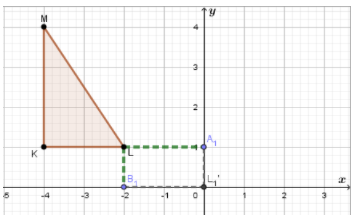
(−2,1) → (−2 + 2,1 − 1)
When we simplify, we have: L1′(0,0).
So, we have translation, (x ,y) → (x + 2, y − 1)
If we use translation (x ,y) → (x + 2, y − 1) to find image of △KLM we would get
Use this translation, the image△K1′L1′M1′has one vertex at the origin, vertex L1′.
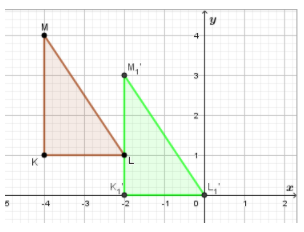
Consider the point M.
If we move 4 units to the right (which is presented with MA2) and 4 unit down (which is presented with MB2) we would reach to the point M2′.
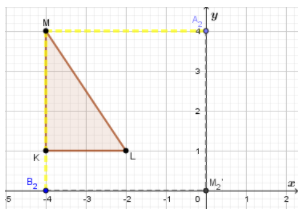
(−4,4) → (−4 + 4,4 − 4)
When we simplify, we have: M’2(0,0)
So, the translation,(x ,y) → (x + 4,y − 4).
If we use translation (x ,y) → (x + 4, y − 4)to find image of △KLM
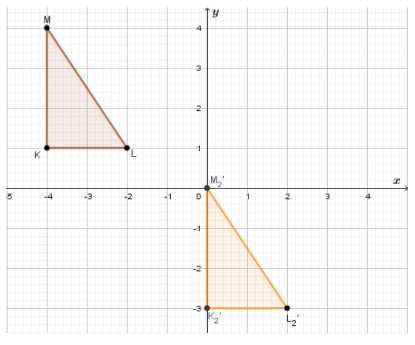
Use this translation, the image △K′2L′2M‘2 has one vertex at the origin, vertex M′2.
The required translations are, (x ,y) → (x + 4, y − 1)
⇒ (x ,y) → (x + 2, y − 1)
⇒ (x ,y) → (x + 4, y − 4)
The translations are
⇒ (x, y) → (x + 4, y − 1)
⇒ (x,y) → (x + 2, y − 1)
⇒ (x, y) → (x + 4, y − 4)
Savvas Learning Co Geometry Student Edition Chapter 9 Page 551 Exercise 22 Problem 23
Given: (x ,y) → (x + 2, y + 5) followed by (x ,y) → (x − 4, y + 9).
To find a translation that has the same effect as each composition of translations.
A translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction.
We have translations
⇒ (x ,y) → (x + 2,y + 5)
⇒ (x ,y) → (x − 4, y + 9)
Our assignment is to find a translation that would bring us to the same point that the composition of these translations would bring us to.
Suppose we have a point A(x ,y).
If we use translation (x , y) → (x + 2, y + 5) for point A, we would get
A(x , y) → (x + 2, y + 5)
When we simplify, we have: A1 (x + 2, y + 5).
Now apply translation (x ,y) → (x − 4, y + 9) to point A1, we have
⇒ (x + 2,y + 5) → (x + 2 − 4, y + 5 + 9)
When we simplify, we have: A′ (x − 2, y + 14)
Based on the previous step, the required translation is
⇒ (x ,y) → (x − 2, y + 14).
The translation is (x,y) → (x−2, y + 14).
Page 551 Exercise 23 Problem 24
Given: (x ,y) → (x + 12, y + 0.5) followed by (x, y) → (x + 1, y − 3).
To find a translation that has the same effect as each composition of translations.
A translation is a geometric transformation that moves every point of a figure, shape or space by the same distance in a given direction.
We have translations
⇒ (x ,y) → (x + 12, y + 0.5)
⇒ (x ,y) → (x + 1,y − 3)
Our assignment is to find a translation that would bring us to the same point that the composition of these translations would bring us to.
Suppose we have a point A(x ,y).
If we use translation (x ,y) → (x + 12, y + 0.5) for point A we would get
⇒ A(x ,y) → (x + 12, y + 0.5)
When we simplify, we have: A1 (x + 12, y + 0.5).
When we now apply translation (x ,y) → (x + 1, y − 3)to point A1, we have
⇒ (x + 12, y + 0.5) → (x + 12 + 1, y + 0.5 − 3)
When we simplify, we have: A′(x + 13, y − 2.5)
Based on the previous step, we see that required translation is,(x ,y) → (x + 13, y − 2.5).
The translation is( x ,y)→ (x + 13, y − 2.5).
Savvas Learning Co Geometry Student Edition Chapter 9 Page 551 Exercise 24 Problem 25
Given : △ABC has vertices A(−2,5), B(−4,−1), and C(2,−3).
To Find – The images of the midpoints of the sides of △ABC are the midpoints of the sides of △A′B′C′ for the translation (x ,y) → (x + 4, y + 2).
Translation means the displacement of a figure or a shape from one place to another.
In translation, a figure can move upward, downward, right, left or anywhere in the coordinate system.
In translation, only the position of the object changes, its size remains the same.
Based on the data from the assignment we have △ABC
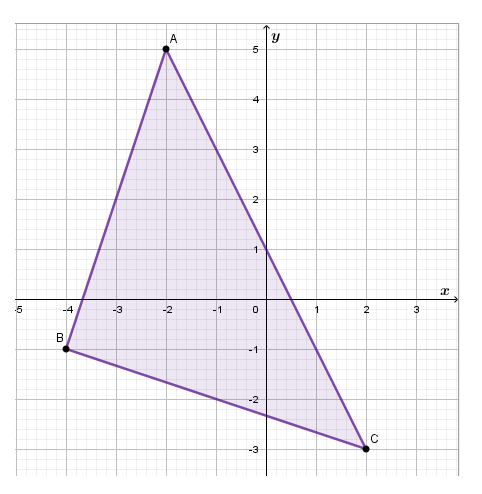
Our assignment is to prove that midpoints of sides \(\overline{A B}\) ,\(\overline{B C}\) and \(\overline{C A}\) are preimages of the sides of triangle △A′B′C′ , which represents the image of △ABC.
First we will use translation (x ,y)→(x + 4, y + 2) to find the image of △ABC.
For point A(−2,5) the image is: (−2,5) → (−2 + 4, 5 + 2)
When we simplify, the image is point A′ (2,7).
For point B(−4,−1) the image is: (−4,−1) → (−4 + 4,−1 + 2)
When we simplify, the image is point B′(0,1).
For point C(2,−3) the image is: (2,−3) → (2 + 4,−3 + 2)
When we simplify, the image is point C′(6,−1).
The image of △ABC is △A’B’C’.
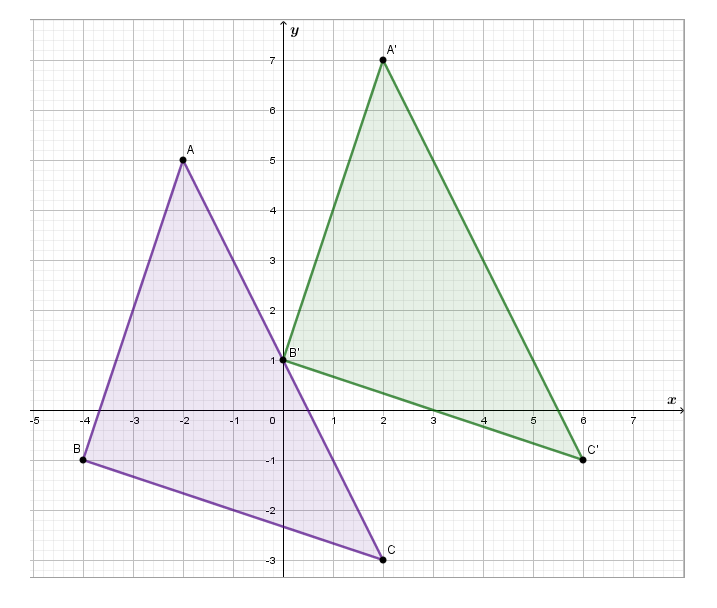
To find the midpoints of the sides of a triangle we use:
In order to find the midpoint M of the line segment from point K(x1,y1) to point L(x2 ,y2 ) we use
⇒ M \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)
We find midpoint D of , \(\overline{A B}\) where A(−2,5),B(−4,−1)in the following way
⇒ \(D\left(\frac{-2+(-4)}{2}, \frac{5+(-1)}{2}\right)\)
Simplify
⇒ D \(\left(\frac{-6}{2}, \frac{4}{2}\right)\)
Simplify , D(-3,2)
We find midpoint E of BC \(\overline{B C}\) where B(−4,−1),C(2,−3)in the following way
⇒ E \(\left(\frac{-4+2}{2}, \frac{-1+(-3)}{2}\right)\)
Simplify
⇒ E\(\left(\frac{-2}{2}, \frac{-4}{2}\right)\)
Simplify , E(-1,2)
We find midpoint F of \(\overline{C A}\) where C(2,−3),A(−2,5)in the following way
⇒ F\(\left(\frac{2+(-2)}{2}, \frac{-3+5}{2}\right)\)
Simplify
⇒ F \(\left(\frac{0}{2}, \frac{2}{2}\right)\)
Simplify , F (0,1)
We find midpoint D′ of \(\overline{A’ B’}\)where A′(2,7),B′(0,1)in the following way
D’\(\left(\frac{2+0}{2}, \frac{7+1}{2}\right)\)
Simplify
⇒ D’\(\left(\frac{2}{2}, \frac{8}{2}\right)\)
Simplify, D’ (1,4)
We find midpoint E′ of \(\overline{B’ C’}\) where B′ (0,1),C′(6,−1)in the following way
E′\(\left(\frac{0+6}{2}, \frac{1+(-1)}{2}\right)\)
Simplify
⇒ E’ \(\left(\frac{6}{2}, \frac{0}{2}\right)\)
Simplify , E'(3,0)
We find midpoint F′ of \(\overline{C’ A’}\), where C′ (6,−1),A′(2,7) in the following way
⇒ F′\(\left(\frac{6+2}{2}, \frac{-1+7}{2}\right)\)
Simplify
⇒ F′\(\left(\frac{8}{2}, \frac{6}{2}\right)\)
Simplify , F′(4,3)
Now we sketch all mid point that found and draw triangles △DEF is △D’E’F’
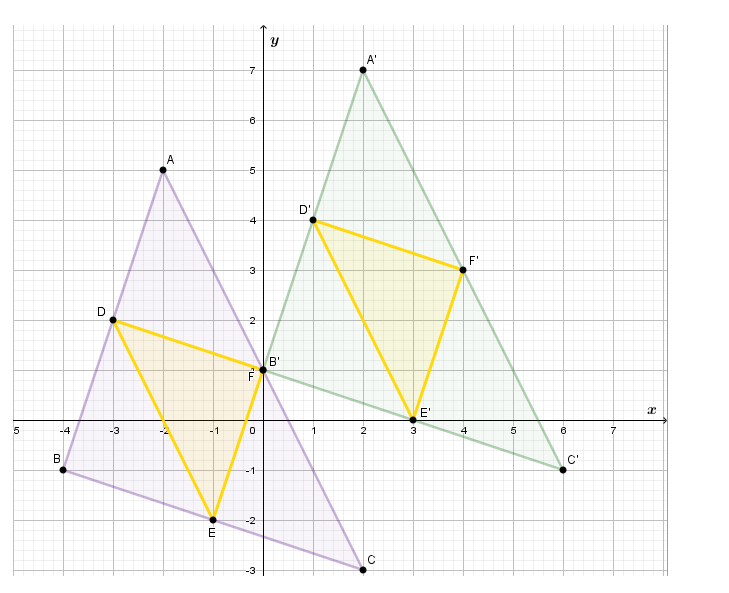
To prove what we are required to, we will show that .
When we apply a given translation to points D, E and F, we obtain points D′,E′ and F′.
For point D(−3,2), which presents the midpoint of\(\overline{A B}\)
The image is (−3,2) → (−3 + 4,2 + 2)
When we simplify, the image is point D′(1,4), which we have shown to be the midpoint of \(\overline{A’ B’}\)
For point E (−1,−2), which presents the midpoint of \(\overline{B C}\) ,
The image is (−1,−2) → (−1 + 4,−2 + 2)
When we simplify, the image is point E′(3,0), which we have shown to be the midpoint of \(\overline{B’ C’}\) .
For point F(0,−1), which presents the midpoint of \(\overline{C A}\)
The image is (0,1) → (0 + 4,1 + 2)
When we simplify, the image is point F′(4,3), which we have shown to be the midpoint of \(\overline{C’ A’}\).
It is shown that the images of the midpoints of the sides of △ABC are the midpoints of the sides of △A′B′C′ for the translation (x ,y) → (x + 4, y + 2).
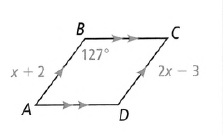
Savvas Learning Co Geometry Student Edition Chapter 9 Page 551 Exercise 25 Problem 26
Given:
To Find – How to use translations to draw a parallelogram.
Method used : Translation method.
A translation moves a shape up, down or from side to side but it does not change its appearance in any other way.
Translation is an example of a transformation.
Our assignment is to explain how to use translation to draw parallelogram.
We know that parallelogram is a quadrilateral with parallel and congruent opposite sides.
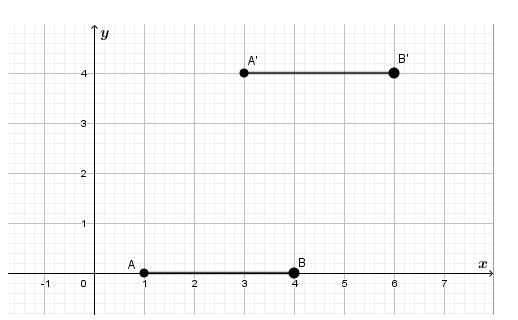
Suppose we have segment \(\overline{A B}\)
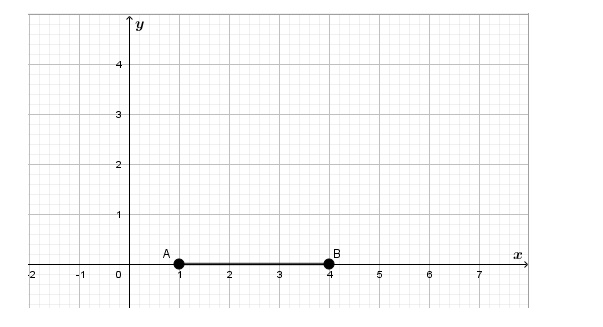
Now we want to use the translation to get the opposite parallel line \(\overline{A, B’}\).
The translation that satisfies this conditions is.
For example: (x ,y) → (x + 2, y + 4)
First let’s observe point A.
If we move 2 units to the right (which is presented with AC) and 4 units up (which is
presented with AC) we would reach to the point A’.
Now we observe point B.
If we move 2 units to the right (which is presented with BE) and 4 units up(which is Presented with BF) we would reach to the point B’.
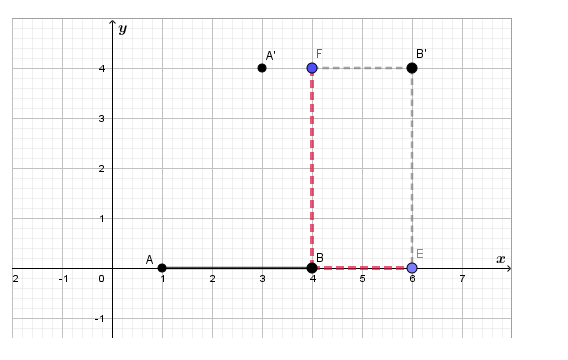
We now have \(\overline{A B}\) and \(\overline{A’ B’}\) which are parallel and congruent.
To sketch a parallelogram, it is enough to connect the sides AA’ and BB’.
When we connect AA’ and BB’ , we have parallelogram ABB’ A’
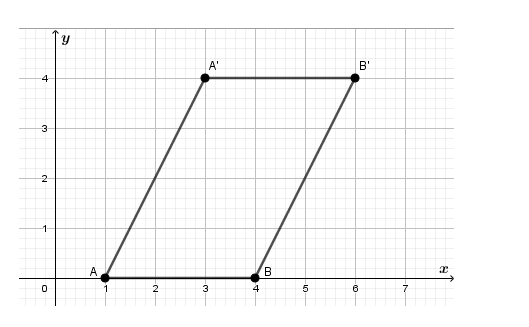
The above steps we have explained how to draw a parallelogram using translation.