Susan Colley

• Susan Colley Vector Calculus 4th Edition Chapter 1 Exercise 1.1 Vectors
• Susan Colley Vector Calculus 4th Edition Chapter 1 Exercise 1.2 Vectors
• Susan Colley Vector Calculus 4th Edition Chapter 1 Exercise 1.3 Vectors
• Susan Colley Vector Calculus 4th Edition Chapter 1 Exercise 1.4 Vectors
• Susan Colley Vector Calculus 4th Edition Chapter 1 Exercise 1.5 Vectors
• Susan Colley Vector Calculus 4th Edition Chapter 1 Exercise 1.6 Vectors
• Susan Colley Vector Calculus 4th Edition Chapter 1 Exercise 1.7 Vectors
• Susan Colley Vector Calculus 4th Edition Chapter 2 Exercise 2.1 Differentiation in Several Variables
• Susan Colley Vector Calculus 4th Edition Chapter 2 Exercise 2.2 Differentiation in Several Variables
• Susan Colley Vector Calculus 4th Edition Chapter 3 Exercise 3.1 Vector-Valued Functions
• Susan Colley Vector Calculus 4th Edition Chapter 4 Exercise 4.1 Maxima and Minima in Several Variables
• Susan Colley Vector Calculus 4th Edition Chapter 5 Exercise 5.1 Multiple Integration
• Susan Colley Vector Calculus 4th Edition Chapter 6 Exercise 6.1 Line Integrals
• Susan Colley Vector Calculus 4th Edition Chapter 7 exercise 7.1 Surface Integrals and Vector Analysis
• Susan Colley Vector Calculus 4th Edition Chapter 8 Exercise 8.1 Vector Analysis in Higher Dimensions

Vector Calculus 4th Edition Chapter 2 Differentiation in Several Variables

Page 114 Problem 1 Answer

Given: {(x,y)∈R²∣1≤x²+y²≤4}

To determine whether the given set is open or closed.

Evaluate to find the answer.

Let us consider the given set and simplify,

X={(x,y)∈R²∣1≤x²+y²≤4}

This set is closed in R², since, it contains all of its boundary points.

The boundary of X consist the circumference of circles of radius 1, and 2

Finally, it can be seen from the image

Hence, the given set is closed.

Page 114 Problem 2 Answer

Given: {(x,y)∈R²∣1≤x²+y²<4}

To determine the given set is open or closed.

Evaluate to find the answer.

Let us consider the given set and simplify.

This set contains the points on the circle described with an equation.

Read and Learn More Susan Colley Vector Calculus Solutions

x²+y²=1

but does not contain the points described with an equation,

x²+y²=4

So this set is neither open nor closed because it does not contain all of its boundaries.

Hence, the given set is neither open nor closed.

Page 114 Problem 3 Answer

Given: {(x,y,z)∈Rs

∣1≤x²+y²+z²≤4}

To determine whether the given set is open or closed.

Evaluate to find the solution.

Let us consider the given set and simplify

X={(x,y,z)∈R3∣1≤x²+y²+z²≤4}

This set is closed in R2,

As it can be seen it contains all of its boundary points.

The boundary of X consist of surfaces of spheres of radius 1 and 2

Similarly, we have the image here.

Hence, the given set is closed.

Page 114 Problem 4 Answer

Given: {(x,y,z)∈R3

∣1<x²+y²<4}

To determine whether the given set is open or closed.

Evaluate to find the solution.

Let us consider the given set and state.

First, the given set does not contain any restriction on z.

Also, the given set does not include its boundaries. So it should be the open set.

Hence, the given set is open.

Page 114 Problem 5 Answer

Given: [x​y]→[0,0]_I’m∣y∣√x²+y²

To find: Whether the limit exists or not.

Evaluate to find the solution.

Let us consider the given expression and simplify

Let us approach the value of y from the side where x=0 we get: (0,p)→(0,0)_lim f(x,y)=1

Nevertheless, let us see what happens when we set x=t and y=2t. If we approach the limit from this side we get: (x=t,p=2t)→(0,0)_lim f(x,y)=2∣t∣√5∣t∣

By cancelling out the terms t in the fraction above we can clearly see that the limit along these paths is not zero.

Hence, the limit does not exist.

Page 114 Problem 6 Answer

Given: A limit, (x,y)→(0,0)_lim ex ey x+y+2

To Find: The value of the limit or why does the given limit not exist.

Evaluate the given limit by plugging in the approaching values of x and y.

⇒ (x,y)→(0,0) _limex ey x+y+2

= (x,y)→(0,0)_lim e0 e0

0+0+2

⇒ (x,y)→(0,0)_limex ey x+y+2

=1/2

Hence, the value of the given limit is 1/2.

Page 114 Problem 7 Answer

Given: A limit, (x,y)→(−1,2)_lim 2x²+y²

x²+y²

To Find: The value of the limit or why does the given limit not exist.

In the given case, just plug in the values for x andy.

Since the given expression is well defined for (x,y)= (−1,2) the limit’s value can be calculated.

x,y)→(−1,2)_lim

2x²+y²

x²+y²

⇒ 2(−1)²+2(−1)²+2

= 6/5

Hence, the value of the given limit is 6/5.

Page 114 Problem 8 Answer

Given: A limit, (x,y)→(0,0)_lim x²+2xy+y²x+y

To Find: The value of the limit or why does the given limit not exist.

Solve the given limit using the standard formula:

(x+y)²=x²+2xy+y²

Apply the formula on the numerator:

(x,y)→(0,0)_lim (x+y)²

x+y⇒x+y=0

Hence, the value of the given limit is 0.

Page 114 Problem 9 Answer

Given: A limit, (x,y)→(0,0)_lim xy/x²+y²

To Find: The value of the limit or why does the given limit not exist.

It is known that the limit exists if the limit is the same when approached to it along all paths.

Consider the limit along the pathx=y :(x,y)→(0,0)_lim xy/x²+y²

⇒ y²2y²

= 1/2

Now take limit along the path x=0:

(x,y)→(0,0)_lim

xyx²+y²⇒0

y²=0

As the limits are not the same. Hence the limit does not exist

Hence, the given limit does not exist.

Page 114 Problem 10 Answer

Given: A limit, (x,y)→(0,0)_lim

x⁴−y⁴

x²+y²

To Find: The value of the limit or why does the given limit not exist.

The given limit can be easily solved by factoring and canceling out one factor with denominator we get:

(x,y)→(0,0) _lim

x⁴−y⁴

x²+y² ⇒ (x²−y²)(x²+y²)

x²+y²=0

Hence, the value of the given limit is 0.

Page 114 Problem 11 Answer

Given: A limit, (x,y)→(0.0)_limx²

x²+y²

To Find: The value of the limit or why does the given limit not exist.

It is known that the limit exists if the limit is the same when approached it from every path. Consider the pathx=y

(x,y) → (0,0)_limx²

x²+y² ⇒ y²

2y² = 1/2

On the other hand, along the path x=0, the result is:

(x,y) → (0,0) _limx²

x² + y² ⇒ 0

y² = 0

Since the results are different when we approach from the different parts, the limit does not exist.

Hence, the given limit does not exist.

Page 114 Problem 12 Answer

Given: A limit, (x,y)→(0,0),x≠y

_limx²−xy√x−√y

To Find: The value of the limit or why does the given limit not exist.

Here, firstly factor out the x

term in numerator. Then rewrite the other term as factors:

(x,y)→(0,0)_lim

x²−xy√x−√y

⇒x(x−y)/√x−√y

=x(√x−√y)(√x+√y)√x−√y

Now cancel out the terms and calculate limit effortlessly:

(x,y)→(0,0)_lim x(√x+√y)=0

The value of the given limit is 0.

Page 114 Problem 13 Answer

Given: A limit, (x,y)→(2,0)_lim

x²−y²−4x+4

x²+y²−4x+4

To Find: The value of the limit or why does the given limit not exist.

It is known that the limit exists if the limit of the expression is the same when approached it from any path.

Examine the case then we approach to the limit along the pathx=2

xy)→(2,0)_lim x²−y²−4x+4

x²+y²−4x+4 ⇒ −y²/y²

=−1

However, if it is approached along the path y=0 the expressions in the numerator and denominator become the same and they cancel out.

In that case, the limit is equal to 1.

Hence, the limit does not exist.

Hence, the given limit does not exist.

Page 114 Problem 14 Answer

Given: (x,y,z)→(0,√​π,1)_lim exz cosy²−x

To find: The limit and explain why the limit fails to exist.

Evaluate to get the answer.

The expression given in this task is well-defined for all triplets of real numbers.

Therefore we obtain the limit by simply plugging in the values in the expression:

(x,y,z)→(0,√​π,1)_lim e xz cos y²−x=e0⋅(−1)−0

=−1

Therefore, the required limit is −1.

Page 114 Problem 15 Answer

Given: (x,y,z)→(0,0,0)_lim2x²+3y²+z²

x²+y²+z²

To find: The limit or explain why the limit fails to exist.

Evaluate to get the answer.

This case is the same as the previous cases in two variables.

We again try to find two different paths that will give the different limit as a result.

If we manage to do this, the limit does not exist.

First, we take the path (x,y,z)=(t,t,t)

(x,y,z)→(0,0,0)_lim 2x²+3y²+z²

x²+y²+z²=6t²/3t²

=2

If we inspect the path (x,y,z)=(t,0,t)

We get the result:

(x,y,z)→(0,0,0)_lim 2x²+3y²+z²

x²+y²+z²= 3t²/2t²

=3/2

So, we found that the limits are different for the paths that lead to the same point and thus the limit does not exist.

Vector Calculus 4th Edition Chapter 1 Vectors

Page 73 Problem 1 Answer

Given: Points whose polar coordinates  are (√3,5π/6)

To find: The Cartesian coordinates of the point.

Use the relation between polar and Cartesian coordinatesEvaluate to obtain the final answer

To convert from polar to Cartesian coordinates, use the following formula:

x = r cos θ

y = r sin θ

x = √3⋅cos 5 π/6

= √3⋅(−√3/2)

= −3/2

y = √3⋅sin 5 π/6

= √3⋅1/2

= √3/2

Hence the evaluated value is, (x,y)=(−3/2,√3/2)

Page 73 Problem 2 Answer

Given: Points whose polar coordinates  is (3,0)

To find: The Cartesian coordinates of the point Use the relation between polar and Cartesian coordinates Evaluate to obtain the final answer

To convert from Polar to Cartesian coordinates, use the following formula:

x = r cosθ

y = r sinθ

So, ​x=3⋅cos0=3

​y=3⋅sin0

=3⋅0

=0​

Hence, the evaluated value is (x,y)=(3,0)

Read and Learn More Susan Colley Vector Calculus Solutions

Page 73 Problem 3 Answer

Given: Points whose Cartesian  coordinates  are (−2,2)

To find: The polar coordinates of the point Use the relation between polar and Cartesian coordinates Evaluate to obtain the final answer

To convert from Cartesian to Polar coordinates, use the following formula:

r² = x² + y²

tanθ = y/x

So, r² = (−2)² + 2²

= 8

r = √8

= 2√2​

tanθ = 2/−2

​= −1

θ = 3π/4

Hence, the evaluated value is (r,θ)=(2√2,3π/4)

Page 73 Problem 4 Answer

Given: Points whose cylindrical  coordinates  are (2,2,2)

To find: The polar cartesian  of the point the relation between cylindrical  and Cartesian coordinatesEvaluate to obtain the final answer

The  relation to converting from Cylindrical to Cartesian coordinates:

x = r cosθ

y = r sinθ

z = z

So, x = 2 cos²

y = 2 sin²

z = 2​

Hence, the evaluated value is (x,y,z)=(2cos²,2sin²,2)

Page 73 Problem 5 Answer

Given: Points whose cylindrical  coordinates  are (π,π/2,1)

To find: The polar cartesian  of the pointUse the relation between cylindrical  and Cartesian coordinatesEvaluate to obtain the final answer

Use the following relation to converting from Cylindrical to Cartesian coordinates:

x = r cosθ

y = r sinθ

z = z

So,

x=π cos π/2=0

​y = π sinπ/2

​= π⋅1

= π

z = 1

​Hence the evaluated value is, (x,y,z) = (0,π,1)

Page 73 Problem 6 Answer

Given: Cylindrical coordinates  (1,2π/3,−2)

To find: The Cartesian coordinatesEvaluate to get the result.

Use following relation to convert from Cylindrical to Cartesian coordinates:

x = r cosθ

y = r sinθ

z = z

x = 1cos 2π/3

= 1⋅(−1/2)

=−1/2

y = 1sin 2 π/3

= 1⋅√3/2

= √3/2

​​z =−2

​Therefore, these are the cartesian coordinates for the cylindrical coordinates:

(x,y,z)=(−1/2,√3/2,−2)

Page 73 Problem 7 Answer

Given: Spherical coordinates (4,π/2,π/3)

To find: The Rectangular coordinates Evaluate to get the result.

Use following relation to convert from spherical to rectangular (Cartesian) coordinates:

x = ρ sin φ cosθ

y = ρ sin φ sinθ

z = ρ cosφ

​x = 4 sin π/2c osπ/3

= 4⋅1⋅1/2

= 2

y = 4 sin π/2 sinπ/3

= 4⋅1⋅√3/2

= 2√3

z=4cosπ/2

= 4⋅0

= 0

Therefore, these are the rectangular coordinates:

(x,y,z) = (2,2√3,0)

Page 73 Problem 8 Answer

Given: Spherical Coordinates (3,π/3,π/2)

To find: The Rectangular coordinates Evaluate to get the final result

Use following relation to convert from spherical to rectangular (Cartesian) coordinates:

x = ρ sin φ cosθ

y = ρ sin φ sinθ

z = ρ cos φ

x=3sinπ/3cosπ/2

=3⋅√3/2⋅0    =0

y = 3 si nπ/3 sinπ/2

= 3⋅√3/2⋅1

= 3√3/2

z = 3cosπ/3

=3⋅1/2

=3/2

Therefore,following are the rectangular coordinates of the above data:

(x,y,z) = (0,3√3/2,3/2)

Page 73 Problem 9 Answer

Given: Spherical coordinates  (1,3π/4,2π/3)

To find: The Rectangular coordinates.

Evaluate to get the final answer

Use following relation to convert from spherical to rectangular (Cartesian) coordinates:

x=  ρ sin φ cosθ

y = ρ sin φ sinθ

z = ρ cosφ

​x = 1 sin3π/4cos2π/3

= √2/2⋅(−1/2)

= −√2/4

y = 1 sin 3π/4 sin2π/3

= √2/2⋅√3/2

= √6/4

z = 1cos3π/4

= −√2/2

Therefore,following are the rectangular coordinates of the above data:

(x,y,z) = (−√2/4,√6/4,−√2/2)

Page 73 Problem 10 Answer

Given: Spherical coordinates (2,π,π/4)

To find: The Rectangular coordinates.

Evaluate to get the final answer.

Use following relation to convert from spherical to rectangular (Cartesian) coordinates:

x = ρ sinφ cosθ

y =ρ  sinφ sinθ

z =ρ cosφ

x = 2 sin π cosπ/4

= 2⋅0⋅√2/2

= 0

y = 2sinπsinπ/4

=2⋅0⋅√2/2

=0

z=2cosπ

=2⋅(−1)

=−2

Therefore,following are the rectangular coordinates of the above data:

(x,y,z)=(0,0,−2)

Page 73 Problem 11 Answer

Given : Cartesian Coordinates (−1,0,2)

To find: A set of cylindrical coordinates.

Evaluate to get the final result

Use the following relation to convert from Cartesian to cylindrical coordinates:

r² = x² + y²

tanθ = y/x

z=z

r²=(−1)²+0²

= 1+0

= 1

r=1

tanθ = 0−1

=0

θ=π, because x coordinate is negative z=2

Therefore these are a set of cylindrical coordinates of the given data:

(r,θ,z)=(1,π,2)

Page 73 Problem 12 Answer

Given : Cartesian Coordinates  (−1,√3,13)

To find:  A set of cylindrical coordinates.

Evaluate to get the final result

Use following relation to convert from Cartesian to cylindrical coordinates:

r² = x² + y²

tanθ = y/x

z = z

r² = (−1)² + √3/2

=1+3

= 4

r = 2

tanθ = √3 −1

= − √3

θ= 2π/3, because x coordinate is negative

z =13

Therefore these are a set of cylindrical coordinates of the given data:

(r,θ,z) = (4,2π/3,13)

Vector Calculus 4th Edition Chapter 1 Vectors

Page 59 Problem 1 Answer

Given: (1,2,3,…n)

To find the terms in standard basis.

Use the vector method and find the answer.

Therefore,

(1,2,3…,n)=1(1,0,0…,0)+2(0,1,0,0,…,0)+…+n(0,0,0,…0,1)

=e¹+2e²+3e³+…+neⁿ

Hence, e¹+2e²+3e³+…+nen is the standard form of vector.

Page 59 Problem 2 Answer

Given: (1,0,−1,1,0,−1,…,1,0,−1)

To find the terms in standard basis.

Use vector method and find the answer.

Therefore,

(1,0,−1,1,0,−1,…,1,0,−1)=1(1,0,0…,0)+0(0,1,0,0,…,0)−1(0,0,1,0,..,0)…−n(0,0,0,….0,1)

=e¹−e³+e⁴−e⁶+…+eⁿ⁻²−eⁿ

Hence, e¹−e³+e⁴−e⁶+…+eⁿ⁻²−eⁿ is the standard form of vector.

Page 59 Problem 3 Answer

Given:e¹−2e²+3e³−4e⁴+⋯+(−1)ⁿ⁺¹ neⁿ

To find the terms in standard basis.

Use the vector method and find the answer.

Read and Learn More Susan Colley Vector Calculus Solutions

Therefore,

e¹−2e²+3e³−4e⁴+…+(−1)ⁿ⁺¹neⁿ

=(1,0,0,…,0)+(0,−2,0,0,…,0)+(0,0,3,0,…0)+(0,0,0,1,−4,0,…,0)+…+(0,0,0,…0,(−1)n+1n)

=(1,−2,3,−4…,(−1)n+1n)

Hence,(1,−2,3,−4…,(−1)n+1n) is the given vectors without recourse to standard basis notation.

Page 59 Problem 4 Answer

To find the given vectors without recourse to standard basis notation,

e¹+eⁿ=(1,0,0,…,0)+(0,0,0,…0,1)

=(1,0,0,…,0,1)..

(1,0,0,…,0,1) is the given vectors without recourse to standard basis notation.

Page 59 Problem 5 Answer

Given: a=(1,3,5,…2n−1) and b=(2,−4,6,…,(−1)n+12n).To find: a+b.Evaluate and find the answer.

Calculating by using the given information, we get,

a+b=(1,3,5,7,…,2n−1)+(2,−4,6,−8,…,(−1)n+12n)

=(3,−1,11,−1,…,2n(1+(−1)n+1)−1)​

Hence, the required solution is (3,−1,11,−1,…,2n(1+(−1)n+1)−1).

Page 59 Problem 6 Answer

Given: a=(1,3,5,…2n−1) and b=(2,−4,6,…,(−1)n+12n).To find: a−b.Evaluate and find the answer.

Calculating by using the given information, we get,

a−b=(1,3,5,7,…,2n−1)−(2,−4,6,−8,…,(−1)n+12n)

=(−1,7,−1,15,…,2n(1+(−1)n)−1)

​Hence, the required solution is (−1,7,−1,15,…,2n(1+(−1)n)−1).

Page 59 Problem 7 Answer

Given: a=(1,3,5,…2n−1) and b=(2,−4,6,…,(−1)n+12n).To find: −3a.Evaluate and find the answer.

Calculating by using the given information, we get,

−3a=−3(1,3,5,7,…,2n−1)

=(−3,−9,−15,−21,…,−6n+3)

​Hence, the required solution is (−3,−9,−15,−21,…,−6n+3).

Page 59 Problem 8 Answer

Given: a=(1,3,5,…2n−1) and b=(2,−4,6,…,(−1)n+12n).

To find: ∥a∥.

Evaluate and find the answer.

Calculating by using the given information, we get,

∥a∥=∥(1,3,5,7,…,2n−1)∥

=√12+32+52+⋯+(2n−1)2

Hence, the required solution is √12+32+52+⋯+(2n−1)2.

Page 59 Problem 9 Answer

Given:  a=(1,3,5,….2n−1)

And b=(2,−4,6,…,(−1)n+12n)

To Find: Calculate a.b

Evaluate the given question to get the answer.

Since

a=(1,3,5,…2n−1)

And b=(2,−4,6,…,(−1)n+1/2n)

Therefore,

a⋅b=(1,3,5,7,…,2n−1)⋅(2,−4,6,−8,…,(−1)n+1/2n)

=2−12+30−56+⋯+(−1)n+1/2(2n−1)n

Hence, the required answer is a.b=2−12+30−56+⋯+(−1)n+1/2(2n−1)n.

Page 59 Problem 10 Answer

To Prove: The triangle inequality in Rn

for a=(1,0,1,0,…,0)

And b=(0,1,0,1,…,1).

Evaluate the given question to get the answer.

Let, ∥a+b∥≤∥a∥+∥b∥ where a=(1,0,1,0…,0)

And b=(0,1,0,1,…,0,1)

Now, a+b=(1,1,1….1,1)

Since,  there are exactly n/2I′

s in the a vector

Therefore, ∥a∥=√12+12+…+12=√n/2

Similarly for b we have:

∥b∥=√n/2

Thus, ∥a∥+∥b∥=2√n/2

Now, ∥a+b∥=√12+12+…+12

=√n

=√(2)√n/2≤2√n/2

=∥a∥+∥b∥

Hence, the required answer is ∣∣a+b∣∣≤∥a∣∣+∥b∣

Page 59 Problem 11 Answer

Given: The vectors are: a=(1,2,…,n)

And b=(1,1,…,1)

To Prove: The Cauchy–Schwarz inequality holds for the given vectorsEvaluate the given question to get the answer.

Let,∣a⋅b∣=1+2+⋯+n=n(n+1)/2

∥a∥=√12+22+⋯+n2

=√n(n+1)(2n+1)/6

 

∥b∥=√12+12+⋯+12=√n

And, 2n+1/6≥n+1/4.

Now, ∥a∥2∥b∥2=n2(n+1)(2n+1)/6

=n2(n+1)2n+1/6≥n2(n+1)n+1/4

=n2(n+1)2/4

=∣a⋅b∣2

Now, taking square root on both sides we h get,

∥a∥∥b∥=∣a⋅b∣

Hence, the Cauchy–Schwarz inequality holds for the given vectors is verified.

Page 59 Problem 12 Answer

Given: a=(1,−1,7,3,2)

And b=(2,5,0,9,−1).

To Find: The projection proj a/b.

Evaluate the given question to get the answer.

Let, a=(1,−1,7,3,2), And b=(2,5,0,9,−1)

Now, projb=2−5+27−2

1+1+49+9+4aˉ

=11/32aˉ

=11/32(1,−1,7,3,2)

=(11/32,−11/32,77/32,33/32,11/16)

Hence the projection is given by: proja

b=(11/32,−11/32,77/32,33/32,11/16)

Page 59 Problem 13 Answer

Given:  The vectors, a,b,c∈Rn,

To Prove: ∣∣a−b∥≤∥a−c∣+∣c−b∣

Evaluate the given question to get the answer.

Let, the triangle inequality be

∥a+b∥≤∥a∥+∥b∣

Now ∥a−b∥=∥(a−c)+(c−b)∥

Thus, from the triangle inequality we get,

∣(a−c)+(c−b)∥≤∥(a−c)∥+∥(c−b)∥

Hence the requited answer is proved ∣∣a−b∥≤∥a−c∥+∥c−b∥.

Page 59 Problem 14 Answer

Given:  The Pythagorean theorem where,a,b,and c are vectors in Rn

such that a+b=c

And a⋅b=0, To Prove: ∣a∥2+∥b∣2=∥c∣2 and why is this called the Pythagorean theorem Evaluate the given question to get the answer.

Here, a+b=c

Since, If the vectors are equal then there magnitude must also be equal

Therefore,

∥c∥²=∥a+b∥²

∥c∥²=(a+b)⋅(a+b)

∥c∥²=a⋅a+a⋅b+b⋅a+b⋅b

Now, since a⋅b=0

Therefore, ∥c∥²=a⋅a+b⋅b

∥c∣²=∥a∥²+∥b∥²

Since, a and b are like the pair of orthogonal sides of a right angled triangle also called the base and height and the third side of the triangle is a+b=c.

According to theorem, the sum of the squares of the lengths of the ⊥r sides is the square of the length of the “hypotenuse”, which is c in our case.

Thus this is called the Pythagorean theorem.

Hence, ∥c∣²=∥a∥²+∥b∥² is proved and it is also found why it is called the Pythagorean theorem.

Page 59 Problem 15 Answer

Given: a and b be vectors in Rn .To Prove: If ∣a+b∥=∥a−b∣, then a and b are orthogonal Evaluate the given question to get the answer.

Here, ∥a+b∥=∥a−b∣

Since, equal vectors have the same magnitude

Therefore,

∥a+b∥²=∥a−b∥²

(a+b)⋅(a+b)=(a−b)⋅(a−b)

a⋅a+a⋅b+b⋅a+b⋅b=a⋅a−a⋅b−b⋅a+b⋅b

Since a⋅b=b⋅a

Thus, 4a⋅b=0

Since a⋅b=0,

Hence, the final answer is a and b are orthogonal vectors.

Page 59 Problem 16 Answer

Given: a and b be vectors in Rn.

To Prove: If ∣a−bˉ∣>∣a+b∣  then the angle between a and b is obtuse Evaluate the given question to get the answer.

Here, ∥a−b∣>∣∣a+b∣∣

Now, squaring both sides we get,

∣∣a−b∥² >∥∥a+b∥²

(a−b)⋅(a−b)>(a+b)⋅(a+b)

a⋅a−a⋅b−b⋅a+b⋅b>a⋅a+a⋅b+b⋅a+b⋅b

Since, a⋅b=b⋅a

Therefore,4a⋅b<0

Now, since a⋅b<0 we get:cosθ=a⋅

∥a∣∥b∥<0

Since, cosine is negative for angles between (π/2,π)

Hence, the angle between a and b, that is θ is obtuse.

Page 59 Problem 17 Answer

Given:  The points in R5 satisfying the equation 2(x1−1)+3(x2+2)−7×3+x4−4−5(x5+1)=0.

To Find: Describe geometrically the set of the given points.

Evaluate the given question to get the answer.

Since it passes through the point (1,−2,0,4,−1) and is parallel to every vector which is perpendicular to (2,3,−7,1,−5).

It is a 4-dimensional affine space

Thus this is a hyperplane in R5.

Hence, the set of the given points is a hyperplane in R5.

Page 59 Problem 18 Answer

Given: An inventory of 20 shirts that can sell for$8 each, 30 shirts that sell for $10 each, 24 shirts that sell for $12 each and20 shirts that you sell for $15each and in friend’s inventory it has 30 caps that can be sold for$10 each, 16 caps that can be sold for $10 each, 20 caps that can be sold for $12 each, and 28 caps that can be sold for $15 each.

To Find: If suggested swapping half the inventory of each type of T-shirt for half his inventory of each type of baseball cap. Is our friend likely to accept your offer? Why or why not? Evaluate the given question to get the answer.

Let  the number of each t-shirt in my inventory be

n₁=(20,30,24,20)

And their respective costs (per unit) be,

c₁=(8,10,12,15)

Also, n₂=(30,16,20,28)

And c₂=(10,10,12,15) be the friend’s inventory.

Now, the value of half of my inventory is

1/2 n₁⋅c₁=1/2(160+300+288+300)=$524

And the value of half of friend’s inventory is

1/2 n₁⋅c₁=1/2(300+160+240+420)

=$560

Hence, the friend may not be so happy with the deal as he’d be losing $36 worth of assets.

Page 59 Problem 19 Answer

Given:  Prices of the six type of grains are $200,$250,$300,$375,$450,$500

per ton and the  commodity bundle vector is x=(x₁,…,x₆)

To Find: Express the total cost of the commodity bundle as a dot product of two vectors in R6

Evaluate the given question to get the answer.

Now,

Total cost = cost per unit × number of units.

Since, while buying more than one product, it needs to sum each subtotal.

Therefore,

Total cost=(200,250,300,375,450,500)⋅(x1,x2,x3,x4,x5,x6)

=200×1+250×2+300×3+375×4+450×5+500×6

Hence, the  total cost of the commodity bundle as a dot product of two vectors in R6 is 200×1+250×2+300×3+375×4+450×5+500×6.

Page 59 Problem 20 Answer

Given:  The prices of six type of grains are $(200,250,300,375,450,500)

per ton and a customer has $100,000

to be to purchase the grain.

To Find: The set of possible commodity bundle vectors that the customer can afford.

Also describe the relevant budget hyperplane in R6

Evaluate the given question to get the answer.

Let,100000≥(200,250,300,375,450,500)⋅x

According to set-builder notation, the set is,

{x∈R6∣(200,250,300,375,450,500)⋅x≤100000}.

Geometrically, this describes the region in R6 between the hyperplanes

Now,

(200,250,300,375,450,500)⋅x=100000

And,(200,250,300,375,450,500)⋅x=−100000

Hence, the set of possible commodity bundle vectors that the customer can afford.

Also describe the relevant budget hyperplane in R6 is found.

Vector Calculus 4th Edition Chapter 1 Vectors

 

Page 38 Problem 1 Answer

Given :

|​2       1|
​|  4    3 |

​Evaluate to get the final answer.

Definition  4.2, gives a formula for evaluating determinants.

|2        1|
|4        3|

=(2)(3)−(1)(4)

=6−4

=2.​

Hence, the required solution is 2.

Page 38 Problem 2 Answer

Given :

|0        −1|
|5          6|.

Evaluate to get the final answer.

Definition 4.2,

gives a formula for evaluating determinants.

=|0    −1|
|5      6|

=(0)(6)−(5)(−1)

=0+5

=5​

Hence, the required solution is 5.

Read and Learn More Susan Colley Vector Calculus Solutions

Page 38 Problem 3 Answer

Given :

|1   0   −1|
|3    2    0|
|5     7   3|

​Evaluate to get the final answer.

Definition 4.2, gives a formula for evaluating determinants.

∴ \(\left|\begin{array}{ccc}
1 & 3 & 5 \\
0 & 2 & 7 \\
-1 & 0 & 3
\end{array}\right|=1\left|\begin{array}{ll}
2 & 7 \\
0 & 3
\end{array}\right|-3\left|\begin{array}{cc}
0 & 7 \\
-1 & 3
\end{array}\right|+5\left|\begin{array}{cc}
0 & 2 \\
-1 & 0
\end{array}\right|\)

= 1(6-0) -3(0+7)+5(0+2)

= 6-21+10

= -5

Hence, the required solution is −5.

Page 38 Problem 4 Answer

Given :

|−2       3       4|
|0         6     −8|
|1/2   −1       2|

Evaluate to get the final answer.

Definition 4.2, gives a formula for evaluating determinants.

∴ \(\left|\begin{array}{ccc}
-2 & 0 & 1 / 2 \\
3 & 6 & -1 \\
4 & -8 & 2
\end{array}\right|=-2\left|\begin{array}{cc}
6 & -1 \\
-8 & 2
\end{array}\right|-0\left|\begin{array}{cc}
3 & -1 \\
4 & 2
\end{array}\right|+\frac{1}{2}\left|\begin{array}{cc}
3 & 6 \\
4 & -8
\end{array}\right|\)

= -2(12-8) – 0 + 1/2(-24-24)

= -8-24

= -32

Hence, the required solution is  −32.

Page 38 Problem 5 Answer

Given : (3i−2j+k)×(i+j+k).

Evaluate to get the final answer.

Let us consider and simplify,

Apply Formula 2:

a×b=(a₂b₃−a₃b₂)i+(a₃b₁−a₁b₃)j+(a₁b₂−a₂b₁)k

Evaluate cross product using formula (2):

=(3,−2,1)×(1,1,1)

=(−2−1)i+(1−3)j+(3+2)k

=−3i−2j+5k

Formula 3:

∴ \(a \times b=\left|\begin{array}{ccc}
i & j & k \\
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3
\end{array}\right|\)

Evaluate cross-product using formula (3):

= (3, -2, 1) x (1, 1, 1)

= \(\left|\begin{array}{ccc}
i & j & k \\
3 & -2 & 1 \\
1 & 1 & 1
\end{array}\right|\)

= -3i – 2j + 5k

​Hence, the required answer is −3i−2j+5k.

Page 38 Problem 6 Answer

Given : (i+j)×(−3i+2j).

Evaluate to get the final answer.

Let us consider and simplify,

Formula (2):

a×b=(a₂b₃−a₃b₂)i+(a₃b₁−a₁b₃)j+(a₁b₂−a₂b₁)k

Evaluate cross product using formula (2):

=(1,1,0)×(−3,2,0)

=(0−0)i+(0−0)j+(2+3)k

=5k

Apply Formula (3):

∴ \(a \times b=\left|\begin{array}{ccc}
i & j & k \\
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3
\end{array}\right|\)

Evaluate cross-product using formula (3):

= (1, 1, 0) x (-3, 2, 0)

= \(\begin{gathered}
\left|\begin{array}{ccc}
i & j & k \\
1 & 1 & 0 \\
-3 & 2 & 0
\end{array}\right| \\
\end{gathered}\)

= 5k

Hence, the required solution is 5k.

Page 38 Problem 7 Answer

To Prove property 3 of cross products.

Using properties 1 and 2

Evaluate to get the final answer.

We have to prove that (a+b)×c=a×c+b×c using properties 1 and 2.

Proof:

(a+b)×c=(1)−c×(a+b)=(2)−c×a−c×b=(1)a×c+b×c

​Hence using property (1) and (2) we have proved.

Page 38 Problem 8 Answer

Given: If vector a×b=3i−7j−2k.

To find: Value of(a+b)×(a−b).

Evaluate to get the final answer.

For solve this problem, first we find the Cross Product of (a+b)(a−b), and then we put the value of ab=3i−7j−2k into this Cross Product.

First we use the property of Cross Product

(a+b)c=ac+bc(distributivity)…(1)

Hence,(a+b)(a−b)=a(a−b)+b(a−b)

=a(a+(−b))+b(a+(−b))…(1)

Now we use the property of Cross Product

a(b+c)=ab+ac(distributivity) into (1),

we get,(a+b)(a−b)=a(a+(−b))+b(a+(−b))

=aa+a(−b)+ba+b(−b)

=aa−ab+ba+bb…(2)

Now we use the property of Cross Product

aa=0 into (1), we get (a+b)(a−b)=0−ab+ba+0

=−ab+ba…(3)

Now we use the property of Cross Product

ab=−b a (anticommutativity), into (3),

we get,(a+b)(a−b)=−ab−ab

=−2(ab)…(4)

Now, put the value ofab=3i−7j−2k into (iv), we get (a+b)(a−b)=−2(3i−7j−2k)

=−6i+14j+4k

(a+b)(a−b)=−6i+14j+4k

Hence, the required solution is (a+b)(a−b)=−6i+14j+4k.

Page 38 Problem 9 Answer

Given : The parallelogram have vertices(1,1),(3,2),(1,3),(−1,2).

To calculate: The area of the parallelogram of given vertices.

Evaluate to get the final answer.

We need to form vectors from two adjacent sides.

Drawing a picture, we see that the side with vertices (1,1) and(3,2) and the side with vertices (1,1)and(−1,2) are adjacent.

The vectors corresponding to these sides area=(3,2)−(1,1)=(2,1) and b=(−1,2)−(1,1)=(−2,1).

Now we just need to find the length of the cross product of these.

Except these vectors are in R², not R³.

No worries, just embed these vectors in R³ by setting their z-components equal to 0 (i.e. a=2i+j+0k=2i+j and similarly for b)Then,

Area of Parallelogram

=∥a×b∥

=∥(2i+j)×(−2i+j)∥

=∥−4i×i+2i×j−2j×i+j×j∥

=∥4i×j∥

=∥4k∥

=4​

The area of the given parallelogram is 4.

Page 38 Problem 10 Answer

Given : The parallelogram have vertices(1,2,3),(4,−2,1),(−3,1,0),(0,−3,−2).

To calculate: The area of parallelogram having above vertices.

Evaluate to get the final answer.

We need two adjacent sides to form vectors.

A bit of thought shows that the side with vertices(1,2,3) and(4,−2,1) and the side with vertices(1,2,3) and(−3,1,0) are adjacent.

The vectors corresponding to these sides area=(4,−2,1)−(1,2,3)=(3,−4,−2) and b=(−3,1,0)−(1,2,3)=(−4,−1,−3).

Now we use the fact that the length of the cross product is equal to the area of the parallelogram determined by the vectors:

Area of Parallelogram

=∥a×b∥

=∥(3i−4j−2k)×(−4i−j−3k)∥

=∥−3i×j−9i×k+16j×i+12j×k+8k×i+2k×j∥

=∥−3k+9j−16k+12i+8j−2i∥

=∥10i+17j−19k∥

=√10²+17²+(−19)²

=5√30

The area of given parallelogram is 5√30.

Page 38 Problem 11 Answer

Given: Vector is perpendicular to indices 2i+j−3k and i+k.

To find: The unit of vector having both indices.

Evaluate to get the final answer.

The cross product will give us the right direction; if we then divide this result by its length we will get a unit vector.

Let, the desired vector,

=(2,1,−3)×(1,0,1)

∥(2,1,−3)×(1,0,1)∥=(1,−5,−1)

∥(1,−5,−1)∥=1/√27(1,−5,−1)

Hence, The desired vector is 1/√27(1,−5,−1).

Page 38 Problem 12 Answer

Given :(a×b)⋅c=0

To determine: The geometric relation between a,b, and c.

Evaluate to get the final answer.

For (a×b)⋅c to be zero either of the following conditions are true:

One or more of the three vectors is 0

a×b=0 which would happen if a=kb for some real k, or c is in the plane determined by a and b.

Hence, For (a×b)⋅c to be zero either of the following conditions are true:

One or more of the three vectors is 0a×b=0 which would happen ifa=kb for some real k, orc is in the plane determined by a and b.

Page 38 Problem 13 Answer

Given: The triangle is determined by vectors a=i+j andb=2i−j.

To Compute: The area of triangle determined by above vectors.

Evaluate to get the final answer.

We know that the magnitude of the cross product of these two vectors will give the area of a parallelogram spanned by them as shown in the adjacent figure.

It follows that area of the triangle is half of the magnitude of the cross product.

The area is half of the magnitude of the cross product of the two vectors−(1,1,0) and(2,−1,0)

Area of triangle :

=(1/2)∗∥(1,1,0)×(2,−10)∥

=(1/2)∗∥(0,0,−3)∥

=3/2

Hence, we get that the area of triangle is 3/2.

Page 38 Problem 14 Answer

Given: The triangle is determined by vectors a=i−2j+6k and b=4i+3j−k.

To compute: The area of triangle determined by above vectors.

Evaluate to get the final answer.

We know that the magnitude of the cross product of these two vectors will give the area of a parallelogram spanned by them as shown in the adjacent figure.

It follows that area of the triangle is half of the magnitude of the cross product.

The area is half of the magnitude of the cross product of the two vectors−(1,−2,6) and (2,−1,0)(4, 3, −1)

The area of triangle is :

=(1/2)∗∥(1,−2,6)×(4,3,−1)∥

=(1/2)∥(−16,25,11)∥

=√1002/2

Hence, we get that the area of triangle is =√1002/2.

Vector Calculus 4th Edition Chapter 1 Vectors

Page 47 Problem 1 Answer

Given: The plane containing the point (3,−1,2) and perpendicular to i−j+2k.

To find: An equation for the plane.E

valuate to get the final answer.

The equation of a plane containing a point P(x₀,y₀,z₀) and a vector perpendicular to the plane given by n=Ai+Bj+Ck is given by the following equation A(x−x₀)+B(y−y₀)+C(z−z₀)=0.

Here point is (3,−1,2) and vector perpendicular is i−j+2k.

Hence using the above equation we get the equation of plane as:

1(x−3)−1(y+1)+2(z−2)=0.

Hence, the required solution is  x−y+2z=8.

Page 47 Problem 2 Answer

Given : The point (9,5,−1) and perpendicular to i−2k.

To find: Equation for the plane.

Evaluate to get the final answer.

The equation of a plane containing a point P(x₀,y₀,z₀) and a vector perpendicular to the plane given by n=Ai+Bj+Ck is given by the following equation A(x−x₀)+B(y−y₀)+C(z−z₀)=0.

Here point is (9,5,−1) and vector perpendicular is i−2k.

Hence using the above equation we get the equation of plane as:

1(x−9)−2(z+1)=0

Hence, the required solution is  x−2z=11.

Read and Learn More Susan Colley Vector Calculus Solutions

Page 47 Problem 3 Answer

Given: Plane containing the points (A,0,0),(0,B,0), and (0,0,C)

at least two of A, B, and C are nonzero.

To find: An equation for the plane containing the given points.

Evaluate the expression to obtain the final answer.

Let’s apply cross product of two vectors on the plane.

(A−0,0−B,0−0)×(0−0,0−B,C−0)=(−BC,−AC,−AB)

Hence, above vector is perpendicular to the plane containing the three points.

Here, equation of a plane containing a point P(x₀,y₀, z₀)

Vector perpendicular to the given plan is n=Ji+Kj+Lk

A(x−x₀)+B(y−y₀)+C(z−z₀)=0

By taking points(A,0,0) and vector perpendicular is −BCi−ACj−ABk

Therefore , the equation is BC(x−A)−AC(y−0)−AB(z−0)=0

Hence, equation for the plane containing the given points is BCx+ACy+ABz=ABC

Page 47 Problem 4 Answer

Given:  A plane 5x−4y+z=1 passes through a point (2,−1,−2)

To find:  An equation for the plane that is parallel to the given plan.

Evaluate the expression to obtain the final answer

If two planes are parallel, then the vector perpendicular to the plane is also perpendicular to the desired plan

Therefore,

For a plan 5x−4y+z=1,  perpendicular vector is (5,−4,1)

The above vector is perpendicular to the plane containing the point (2,−1,−2).

Here, the equation of a plane containing a point P(x₀,y₀, z₀)

Vector perpendicular to the given plan is n=Ai+Bj+Ck

A(x−x₀)+B(y−y₀)+C(z−z₀)=0

By taking points (2,−1,−2) and vector perpendicular is 5i−4j+k

Therefore, the equation is

5(x−2)−4(y+1)+(z+2)=0

Hence, 5x−4y+z=12 is an equation for the plane that is parallel to the given plan.

Page 47 Problem 5 Answer

 Given:  A plane 2x−3y+z=5 and  that passes through the point (−1,1,2)

To find: An equation for the plane that is parallel to the given plan.

Evaluate the expression to obtain the final answer.

If two planes are parallel, then the vector perpendicular to the plane is also perpendicular to the desired plan

Therefore,

For a plan 2x−3y+z=5, perpendicular vector is (2,−3,1)

The above vector is perpendicular to the plane containing the point (−1,1,2)

Here, the equation of a plane containing a point P(x₀,y₀, z₀)

Vector perpendicular to the given plan is n=Ai+Bj+Ck

A(x−x₀)+B(y−y₀)+C(z−z₀)=0

By taking points (−1,1,2) and vector perpendicular is  2i−3j+k

Therefore, The equation is 2(x+1)−3(y−1)+(z−2)=0

Hence, 2x−3y+z=−3 is an equation for the plane that is parallel to the given plan.

Page 47 Problem 6 Answer

Given: A plane x−y+7z=10 and hat passes through the point(−2,0,1)

To Find: An equation for the plane that is parallel to the given plan.

Evaluate the expression to obtain the final answer.

If two planes are parallel, then the vector perpendicular to the plane is also perpendicular to the desired plan.

Therefore, For a plan x−y+7z=10, perpendicular vector is (1,−1,7)

The above vector is perpendicular to the plane containing the point (−2,0.1)

Here, equation of a plane containing a point P(x₀,y₀, z₀)

Vector perpendicular to the given plan is n=Ai+Bj+Ck

A(x−x₀)+B(y−y₀)+C(z−z₀)=0

By taking points (−2,0.1) and vector perpendicular is i−j+7k

Therefore, The equation is 1(x+2)−1(y−0)+7(z−1)=0

Hence, from the above steps x−y+7z=5 is an equation for the plane that is parallel to the given plan.

Page 47 Problem 7 Answer

Given: A plane 2x+2y+z=5 that contains the line with parametric equations​ x=2−t

y=2t+1

z=3−2t

T​o Find: An equation for the plane that is parallel to the given plan.

Evaluate the expression to obtain the final answer.

If two planes are parallel, then the vector perpendicular to the plane is also perpendicular to the desired plan.

Therefore, For a plan 2x+2y+z=5, perpendicular vector is (2,2,1)

The above vector is perpendicular to the plane containing the point is given in an equation format

that is, 2x+2y+z=D……….(1)

Here D is unknown.

From the given, x=2−t

y=2t+1

z=3−2t

​substitute in equation 1 to find D i,e 2(2−t)+2(2t+1)+1(3−2t)=D

4−2t+4t+2+3−2t=D

D=9

Hence,  2x+2y+z=9 is an equation for the plane that is parallel to the given plan.

Page 47 Problem 8 Answer

Given: The plan 5x−3y+2z=10 that contains the line with parametric equations​ x=t+4

y=3t−2

z=5−2t

​To find: Why there is no plane parallel to the given plane.

Evaluate the expression to obtain the final answer.

If two planes are parallel, then the vector perpendicular to the plane is also perpendicular to the desired plan.

Therefore, For a plan 5x−3y+2z=10, perpendicular vector is (5,−3,2)

The above vector is perpendicular to the plane containing the point given by in an equation format

that is,

5x−3y+2z=D

Here D is unknown.

From the given, x=t+4

y=3t−2

z=5−2t substitute in equation  1 to find D value.

Hence,

D=5(t+4)−3(3t−2)+2(5−2t)

D=5t+20−9t+6+10−4t

D=36−8t

But the value of D  is not constant which suggests that the line will surely intersect the planes parallel to 5x−3y+2z=10

Hence, it concludes that there is no plane parallel to the given plane which can completely contain the line.

Page 47 Problem 9 Answer

Given: The line ​x=3t−5

y=7−2t

z=8−t

​and that passes through the point(1,−1,2).

To find: Find an equation for the plane that is perpendicular to the line.

Evaluate the expression to obtain the final answer.

Assume that,

The vector 3i−2j−k is parallel to the line

Hence, perpendicular to the plan which passes through  (1,−1,2)

Therefore, the perpendicular to that vector is 3(x−1)−2(y+1)−(z−2)=0

Hence, 3(x−1)−2(y+1)−(z−2)=0 is an equation for the plane that is perpendicular to the line.

Page 47 Problem 10 Answer

Given: Equation of two lines l1:x=t+2,y=3t−5,z=5t+1,l2=x=5−t,y=3t−10,z=9−2t.

To Find: Equation of the plane that contains the given lines.

The vector i+3j+5k is parallel to the first line and the vector −i+3j−2k is parallel to the second line.

So the cross product of these two is perpendicular to the plane containing these two lines:

n=(i+3j+5k)×(−i+3j−2k)

=−21i−3j+6j

Now, find a single point on either line and it is known that point will also be in the plane.

Notice that (2,−5,1) is a point in the first line. So the equation of the plane is then

−21(x−2)−3(y+5)+6(z−1)=0

⇒7(x−2)+(y+5)−2(z−1)=0

Hence, the required equation of the plane is 7(x−2)+(y+5)−2(z−1)=0.

Page 47 Problem 11 Answer

Given: Equation of two planes x+2y−3z=5,5x+5y−z=1.

To Find: Line of equation of the planes.

A normal vector for the first plane is i+2j−3k and a normal vector for the second plane is 5i+5j−k.

A nonzero vector perpendicular to these will be parallel to the line of intersection.

So, find the cross product as follows:

(i+2j−3k)×(5i+5j−k)=13i−14j−5k

Now, find a point on the line of intersection.

Let x=0 and then solve the resulting system of equations:

{​2y−3z=5

5y−z=1

⇒ y =−2/13 and z=−23/13.

Following will be the scalar equations

{x=13t

y=−2/13−14t

z=−23/13−5t​

Hence, the required set of parametric equations:⎧

{x=13t

y=−2/13−14t

z=−23/13−5t

​Page 47 Problem 12 Answer

Given: Equation of plane 2x−3y+5z=−1.

To Find: Set of parametric equation for the line perpendicular to the plane.

The fact that the line is perpendicular to the plane 2x−3y+5z=−1

⇒it is parallel to the vector 2i−3j+5k.

So, using the point(5,0,6) on the line, it is obtained:

{​x=5+2t

y=−3t

z=6+5t

​Hence, the required set of parametric equation of lines:{​x=5+2t

y=−3t

z=6+5t​

Page 47 Problem 13 Answer

Given: Equations of parallel planes 8x−6y+9Az=6, Ax+y+2z=3

To Find: The value of A.

For the planes to be parallel, they must be perpendicular to the same vectors.

Now, the first plane is perpendicular to every scalar multiple of 8i−6j+9Ak and the second plane is perpendicular to every scalar multiple of Ai+j+2k

It is required to find a solution to 8i−6j+9Ak=K(Ai+j+2k)

The one we obtained should be equal to:

{8=AK

−6=K

9A=2K

The unique solution to this is A=−4/3, K=−6.

⇒A=−4/3

The value of A=−4/3

Vector Calculus 4th Edition Chapter 1 Vectors

Page 26 Problem 1 Answer

Given: Two vectors with their coordinates.

To Find: The dot product of both vectors and magnitude of each of the given vectors

a=(1,5),and b=(−2,3)

The Dot Product of two vectors a and b is given by

a⋅b=a₁b₁+a₂b₂

The Magnitude of a vector is given by

∥a∥=√a⋅a

First, find out the dot product i.e., a⋅b

of the two vectors by substituting the respective coordinates in the formula.

a⋅b=(1)(−2)+(5)(3)

a⋅b=−2+15

∴a⋅b=13

Magnitude of vector a is,∥a∥=√12+52

∥a∥=√26

Magnitude of vector b is,∥b∥=√(−2)2+32

∥b∥=√13

Therefore, the required dot product i.e., a⋅b is 13 and the magnitude of the vectors are:

∥a∥=√26

∥b∥=√13

Read and Learn More Susan Colley Vector Calculus Solutions

Page 26 Problem 2 Answer

Given: Two vectors a and b with coordinates (4,−1) and (1/2,2) respectively.To Find: The dot product and magnitude of each vectors,

a=(4,−1),

b=(1/2,2)

The Dot Product of two vectors is given by,

a⋅b=a₁b₁+a₂b₂

The magnitude of a vector is given by,

∥a∥=√a⋅a

First, find out the dot product i.e., a⋅b of the two vectors by substituting the respective coordinates in the formula.

a⋅b=(4)(1/2)+(−1)(2)

a⋅b=2−2

∴a⋅b=0

Magnitude of vector a,

∥a∥=√42+(−1)2

∥a∥=√17

Magnitude of vector b,

∥b∥=√(1/2)2+22

∥b∥=√17/4

∥b∥=√17/2

Therefore, the required dot product i.e., a⋅b is 0 and the magnitude of the vectors are:

∥a∥=√17

∥b∥=√17/2

Page 26 Problem 3 Answer

Given: Two vectors a and b having coordinates (−1,0,7) and (2,4,−6) respectively.

To Find: We have to compute the dot product i.e., a⋅b of the vectors and magnitude of each vectors i.e.,

∥a∥ and ∥b∥.Substitute the coordinates in the respective formula and compute the result.

The dot product of two vectors is,

a⋅b=a₁b₁+a₂b₂

∴a⋅b=(−1)(2)+(0)(4)+(7)(−6)

a⋅b=−2+0−42

a⋅b=−44

The magnitude of a vector,

∥a∥=√a⋅a

∴∥a∥=√(−1)2+02+72

∥a∥=√50

∥a∥=5√2

And ∥b∥=√22+42+(−6)2

∥b∥=√4+16+36

∥b∥=√56

∥b∥=2√14

Therefore, the required dot product i.e., a⋅b is −44 and the magnitude of the vectors are:

∥a∥=5√2

∥b=2√14

Page 26 Problem 4 Answer

Given: Two vectors are given as follows:

a=(2,1,0)

b=(1,−2,3).To Find: The dot product and magnitude of each of the vectors a and b with coordinates (2,1,0) and (1,−2,3).

Substitute the coordinates in the respective formula for the dot product and magnitude of the vectors and compute the answer.

The dot product of the vectors a and b,

a⋅b=a₁b₁+a₂b₂

Substitute the coordinates of the respective vectors in the above formula.

a⋅b=(2)(1)+(1)(−2)+(0)(3)

a⋅b=2−2+0

∴a⋅b=0

The magnitude of a vector is,∥a∥=√a⋅a

Substitute the coordinates of vector a in the above formula.

∥a∥=√2²+1²+0²

∴∥a∥=√5

Substitute the coordinates of vector b in the formula.

∥b∥=√1²+(−2)²+3²

∥b∥=√1+4+9

∴∥b∥=√14

Therefore, the required dot product of the given vectors is 0. The magnitude of the vectors are:

∥a∥=√5

∥b∥=√14

Page 26 Problem 5 Answer

Given: Two vectors,

a=4i−3j+k

b=i+j+k

To Find: To find the dot product i.e., a⋅b and the magnitude i.e., ∥a∥ of the vectors a and b.

The vectors are represented by unit vector notation and we can get their coordinates from it.

After that, substitute the coordinates in the respective formulas to compute the dot product and their magnitudes.

The vectors are given in unit vector notation i.e.,

a=4i​−3j+k

b=i+j+k

Converting it into their coordinate form we get,

a=(4,−3,1)

b=(1,1,1)

Now, the dot product of the vectors are,

a⋅b=a1b1+a2b2

Substitute the respective coordinates to compute it.

Dot Product:

a⋅b=(4)(1)+(−3)(1)+(1)(1)

a⋅b=4−3+1

∴a⋅b=2

Magnitude of a vector is given by:

∥a∥=√a⋅a

Magnitude of vector a,

∥a∥=√4²+(−3)²+1²

∥a∥=√16+9+1

∥a∥=√26

Magnitude of vector b,

∥b∥=√1²+1²+1²

∥b∥=√3

Therefore, the required dot product i.e., a⋅b is 2 and the magnitude of the vectors are:

∥a∥=√26

∥b∥=√3

Page 26 Problem 6 Answer

Given: Two vectors a and b in their unit vector notation.To Find The dot product and magnitude of the vectors,

a=i+2j−k

b=−3j+2k.

We can find the coordinates from the unit vector representation easily.

After that, substitute the values in the formulas to find their dot product and the magnitude.

From the unit vector representation of the vectors, we found,

a=(1,2,−1)

b=(0,−3,2)

Now, the dot product of the vectors:

a⋅b=a₁b₁+a₂b₁₂

∴a⋅b=(1)(0)+(2)(−3)+(−1)(2)

a⋅b=0−6−2

a⋅b=−8

The magnitude of a vector is,

∥a∥=√a⋅a

∴∥a∥=√1²+2²+(−1)²

∥a∥=√1+4+1

∥a∥=√6

And ∥b∥=√0²+(−3)²+2²

Therefore, the required dot product i.e., a⋅b is −8 and the magnitude of the vectors are:

∥a∥=√6

∥b∥=√13

Page 26 Problem 7 Answer

Given: Two vectors a and b in their unit vector notation. To Find The angle between the vectors,

a=√3i+j, b=−√3i+j

First, find the dot product and the magnitude of the given vectors, then plug them into the formula,

θ=cos−1a⋅b

∥a∥∥b∥  and calculate the angle.

From the given vectors, we know can find out the coordinates. C

alculate the dot product and the magnitudes of the given vectors.

a⋅b=(√3)(−√3)+(1)(1)

a⋅b=−3+1

a⋅b=−2

And ∥a∥=√√3/2+12

∥a∥=√4

∥a∥=2,

∥b∥=√(−√3)²+1²

∥b∥=√4

∥b∥=2

Plug them into the formula and find the angles between the vectors.

θ=cos−1−2/(2)(2)

θ=cos−1(−1/2)

θ=120∘

Therefore, the required angle between the given vectors is 120∘.

Page 26 Problem 8 Answer

Given: Two vectors a and b along with coordinates (−1,2) and (3,1) respectively.

To Find:  The angle between the vectors,

a=(−1,2)

b=(3,1)

The angle between two vectors can be calculated as:

θ=cos−1a⋅b

∥a∥∥b∥

Calculate the dot product and the magnitude of the given vectors and plug them into the above formula to get the angle.

First, compute the dot product and magnitude of the vectors.

a⋅b=(−1)(3)+(2)(1)

a⋅b=−3+2

a⋅b=−1

And ∥a∥=√(−1)²+2²

∥a∥=√5

∥b∥=√3²+1²

∥b∥=√10

Now, plug these values into the formula to calculate the angle between the two vectors.

θ=cos−1−1(√5)(√10)

θ=cos−1(−1/√50)

θ=98.13∘

Thus, the required angle between the given two vectors is 98.13∘.

Page 26 Problem 9 Answer

Given:a=i+j,

b=i+j+k

To find: Find the angle between each of the pairs of vectors. Evaluate to get the final answer.

By using this formula:θ=cos−1/a⋅b∥a∣∣∣b∣∣

First we finda⋅b,∥a∥,∥b∥:

a⋅b=(1)(1)+(1)(1)+(0)(1)

=1+1+0

=2∥a∥=√(1)2+1²+0²

=√2

∣∣b∥=√1²+1²+1²

=√3

Now find angle between vectors:

​θ=cos−1/2(√2)(√3)

⇒cos−1(2√6)

θ=33.26∘

Hence, the angle between the given the pair of vectors isθ=33.26∘

Page 26 Problem 10 Answer

Given:a=i+j−k,

b=−i+2j+2k

To find: Find the angle between each of the pairs of vectors. Evaluate to get the solution.

By using this formula:θ=cos−1/a⋅b

∥a∥∣∣b∣∣

First we find a⋅b,∥a∥,∥b∥:

a⋅b=(1)(−1)+(1)(2)+(−1)(2)

⇒−1+2−2=−1

∣a∥=√1²+1²+(−1)²=√3

∥b∥=√(−1)²+2²+2²

⇒√9

=3

Now angle between vectors are:

θ=cos−1−1(√3)(3)

θ=101.10∘

Hence, the angle between the given pair of vectors isθ=101.10∘

Page 26 Problem 11 Answer

Given:a=1,−2,3,

b=3,−6,−5

To find: Find the angle between each of the pairs of vectors. Evaluate to get the final angle.

By using this formula:θ=cos−1/a⋅b

∥a∥∣∣b∥

First we find a⋅b,∥a∥,∥b∥:

a⋅b=(1)(3)+(−2)(−6)+(3)(−5)

=3+12−15

=0

∥a∥=√1²+(−2)²+3²

=√14

∥b∥=√3²+(−6)²+(−5)²

=√70

Now find angle between vectors are:

θ=cos−10(√14)(√70)

​=cos−10

θ=90∘

Hence, the angle between the given pair of vectors isθ=90∘

Page 26 Problem 12 Answer

Given:a=i+j,

b=2i+3j−k

To find: Calculate the projection ab.

Evaluate to get the final answer.

By using this formula:proj ab=(a⋅b/a⋅a)a

First we find a⋅b,a⋅a:

a⋅b=(1)(2)+(1)(3)+(0)(−1)

⇒2+3=5

a⋅a=1²+1²+0²

=2

Now, we find projection:

projb=(5/2)(1,1,0)

=(5/2,5/2,0)

Hence, the required projection is:(5/2,5/2,0)

Page 26 Problem 13 Answer

Given:a=(i+j)/√2,´

b=2i+3j−k

To find: Calculate the projection a b

Evaluate to get the projection.

By using this formula we get:proj ab=(a⋅b/a⋅a)a

Then first we find a⋅b,a⋅a:

a⋅b=(1/√2)(2)+(1/√2)(3)+(0)(−1)

=5/√2a⋅a=(1/√2)2+(1/√2)2+02

=1/2+1/2 =1

Now find projection:

projb=(5/√21)(1/√2,1/√2,0)

=5/√2(1/√2,1/√2,0)=(5/2,5/2,0)

Hence, the projection a b are(5/2,5/2,0)

Page 26 Problem 14 Answer

Given:a=5k,

b=i−j+2k

To find: Calculate projection of ab.

Evaluate to get the final answer.

By using this formula:proj ab=(a⋅b/a⋅a)a

Then first find a⋅b,a⋅a:

a⋅b=(0)(1)+(0)(−1)+(5)(2)

=0+0+10

=10

a⋅a =0²+0²+5²=25

Now find projection:

Proj b=(10/25)(0,0,5)

=(0,0,2)

Hence, the projection are:(0,0,2)

Page 26 Problem 15 Answer

Given:a=−3k,

b=i−j+2k

To find: Calculate the projection ab.

Evaluate to get the final answer.

By using this formula:proj ab=(a⋅b/a⋅a)a

Then first we find a⋅b,a⋅a:

a⋅b=(0)(1)+(0)(−1)+(−3)(2)

=0+0−6

=−6

a⋅a=0²+0²+(−3)²

=9

Now find projection:

Proj b=(−6/9)(0,0,−3)

=(0,0,2)

Hence, the projection are :(0,0,2)

Vector Calculus 4th Edition Chapter 1 Vectors

Page 16 Problem 1 Answer

Given: The vector(2,4)

To write:  The given vector by using the standard basis vectors for R² and R³.

Evaluate to get the required solution.

Firstly, the standard notation in R²:

a=(a₁,a₂)=a₁i+₁₂j

In R3:a=(a₁,a₂,a₃)=a₁i+a₂j+a₃k

Given vector in standard notation is: (2,4)=2i+4j

Therefore, we can write the given vector as (2,4)=2i+4j.

Page 16 Problem 2 Answer

Given: The vector (9,−6)

To find:The given vector by using the standard basis vectors for R² and R³.

Evaluate to get the final result.

The Standard notation in R²:

a=(a₁,a₂)=a₁i+a₂j

In R³: a=(a₁,a₂,a₃)=a₁i+a₂j+a₃k

Given vector in standard notation is:

(9,−6)=9i−6j

Read and Learn More Susan Colley Vector Calculus Solutions

​Therefore, rewriting the given vector we get 9i−6j.

Page 16 Problem 3 Answer

Given : The vector(3,π,−7)

To find :The given vector by using the standard basis vectors for R² and R³ .

Evaluate to get the final result.

Standard notation in R2:a=(a₁,a₂)=a₁i+a₂j

In R³:

a=(a₁,a₂,a₃)=a₁i+a₂j+a₃k

Given vector in standard notation is:

(3,π,−7)=3i+πj−7k

​Therefore, rewriting the given vector we get 3i+πj−7k.

Page 16 Problem 4 Answer

Given : The vector(−1,2,5)

To write: The given vector by using the standard basis vectors for R² and R³.

Evaluate to get the final result.

Standard notation in R²:

a=(a₁,a₂)=a1i+a2j

In R² :a=(a₁,a₂,a₃)=a₁i+a₂j+a₃k

Given vector in standard notation is: (−1,2,5)=−i+2j+5k

Therefore, we can write the given vector as −i+2j+5k.

Page 16 Problem 5 Answer

Given: The vector (2,4,0)

To write: The given vector by using the standard basis vectors for R² and R³.

Evaluate to get the required solution.

Standard notation in R²

a=(a₁,a₂)=a₁i+a₂j

In R³: a=(a₁,a₂,a₃)=a₁i+a₂j+a₃k

Given vector in standard notation is: (2,4,0)

=2i+4j+0k

=2i+4j​

Therefore, we can write the given vector by using the standard basis vectors as 2i+4j.

Page 16 Problem 6 Answer

Given: The vector i+j−3k

To write: The given vector without using the standard basis notation.

Evaluate to get the required answer.

Standard notation in R²:

a=(a₁,a₂)=a₁i+a₂j

In R³ : a=(a₁,a₂,a₃)=a₁i+a₂j+a₃k

Given the vector without standard notation is:

i+j−3k=(1,1,−3)

Therefore, we can write the given vector without using the standard basis notation as(1,1,−3).

Page 16 Problem 7 Answer

Given: The vector 9i−2j+√2k

To write: The given vector without using the standard basis notation.

Evaluate to get the final solution.

Standard notation in R²:

a=(a₁,a₂)=a₁i+a₂j

In R³: a=(a₁,a₂,a₃)=a₁i+a₂j+a₃k

Given vector without standard notation is:

9i−2j+√2k=(9,−2,√2)​

Therefore, we can write the given vector without using the standard basis notation as(9,−2,√2).

Page 16 Problem 8 Answer

Given : The vector−3(2i−7k)

To find: The given vector without using the standard basis notation. Evaluate to get the final answer.

The Standard notation in R²:

a=(a₁,a₂)=a₁i+a₂j

In R³ :a=(a₁,a₂,a₃)=a₁i+a₂j+a₃k

Given vector without standard notation is:

−3(2i−7k)

=−6i+0j+21k

=(−6,0,21)​

Therefore, we can write the given vector without using the standard basis notation as (−6,0,21).

Page 16 Problem 9 Answer

Given: The vector π i−j

To write: The given vector without using the standard basis notation.

Evaluate to get the final answer.

Standard notation in R²:

a=(a₁,a₂)=a₁i+a₂j

​In R³ : a=(a₁,a₂,a₃)=a₁i+a₂j+a₃k

Given vector without standard notation is:

πi−j=(π,−1)

Therefore, we can write the given vector without using the standard basis notation as(π,−1).

Page 16 Problem 10 Answer

Given: πi−j in R³

To write: Without using the standard basis notation.

Evaluate to get the answer.

The standard notation in R² is a=(a₁,a₂)

= a₁i+a₂j In R³:

a = (a₁,a₂,a₃)=a₁i+a₂j+a₃k

Given vector without standard notation is:

πi−j=πi−j+0k

=(π,−1,0)

Therefore, the given vector without standard notation is (π,−1,0)

Page 16 Problem 11 Answer

Given: a1=(1,1)  and  a2=(1,−1).

To write : c₁a₁+c₂a₂=b for b=(3,1).

Evaluate to get the solution.

First solve system c₁a₁+c₂a₂=b.

Substitute the values for a₁ and a₂.

c₁(1,1)+c₂(1,−1)=(3,1)

We obtain system:

c₁+cv₂=3

c₁−c₂=1

On solving these equations we get the value of c1 and c₂: c₁=2c₂=1

Thus, b=2a₁+a₂.

Therefore, we can write b as b=2a₁+a₁₂.

Page 16 Problem 12 Answer

Given: a₁=(1,1) and a₂=(1,−1)

To write: Vector b=(3,−5) using part a of the question.

Evaluate to get the answer.

Solve system c{1}a{1}+c{2}a{2}=b.

c₁(1,1)+c₂(1,−1)=(3,−5)

We obtain system:

c₁+c₂=3

c₁−c₂=−5

Solution:

c₁=−1 and c₂=4

Thus, b=−a₁+4a₂

Therefore, we rewrite vector b as b=−a₁+4a₂.

Page 16 Problem 13 Answer

Given: a₁=(1,1) and a₂=(1,−1)

To show: Vector b=(b₁,b₂) in R₂ in the form c₁a₁+c₂a₂

Evaluate to get the answer.

Solving the system c₁a₁+c₂a₂=b for an arbitrary vector b=(x,y).

c₁(1,1)+c₂(1,−1)=(x,y)

We obtain the system:

c₁+c₂=xc₁−c₂=y

Solution is

c₁=x+y/2

c₂=x−y/2

Thus, b can be written as a linear combination of a1 and a2.

Therefore, we have shown that b can be written as a linear combination of a1 and a2.

Page 16 Problem 14 Answer

Given: Vector i+3j+6k is parallel to the point (2,−1,5) and the line in R3 passes through the point.

To find:  Give a set of parametric equations for the lines.

Evaluate to get the answer.

By using proposition, we can write:

r(y)=b+ta

=(2,−1,5)+t(1,3,−6)

The parametric equation is

x(t)=2+t

y(t)=−1+3t

z(t)=5−6t​

Hence, the parametric equations for the given line are

x(t)=2+t

y(t)=−1+3t

z(t)=5−6t

​Page 16 Problem 15 Answer

Given: Vector 5i−12j+k and point (12,−2,0)

To find: Give a set of parametric equations for the described lines.

Evaluate to get the answer.

Let us use a Proposition to write:

r(y)=b+ta=(12,−2,0)+t(5,−12,1)

The parametric equation is:

x(t)=12+5t

y(t)=−2−12t

z(t)=t

Hence, the set of parametric equations for the lines so described are ​x(t)=12+5t

y(t)=−2−12t

z(t)=t​

Page 16 Problem 16 Answer

Given: Vector i−7j and points (2,−1)

To find: Give a set of parametric equations

Evaluate to get the answer.

Using Proposition, we can write:

r(y)=b+ta

=(2,−1)+t(1,−7)

Parametric equation is:

x(t)=2+t

y(t)=−1−7t​

Therefore, the required set of parametric equations for the lines so described is x(t)=2+t

y(t)=−1−7t

Vector Calculus 4th Edition Chapter 8 Vector Analysis in Higher Dimensions

Page 535 Problem 1 Answer

Given: 2dx+6dy−5dz;a=(1,−1,−2)

​To determine the values of the following differential forms on the ordered sets of vectors.Using the determination method.

Once again, recall that the 1−form acting on a3 dimensional vector is simply a projection of the i−th coordinate.

Once again use the linearity of the form to obtain:

(2dx+6dy−5dz)(1,−1,−2)=2dx(1,−1,2)+6dy(1,−1,−2)−5dz(1,−1,−2)⇒2−6+10=6

The values of the following differential forms on the ordered set of vectors are 6.

Page 535 Problem 2 Answer

Given:​4dx∧dy−7dy∧dz;a=(0,1,−1),b=(1,3,2)

​To determine the values of the following differential forms on the ordered sets of vectors.Using the determination method.

Here, given a 2−form acting on3 dimensional object. First, use the linearity of the differential forms to split the form into two parts.

(4dx∧dy−7dy∧dz)((0,1,−1),(1,3,2))=4dx∧dy((0,1,−1),(1,3,2))−7dy∧dz((0,1,−1),(1,3,2))

​Next, place the vectors into the columns of the matrix but cross out the terms that are not shown in the differential form operator.

For example, we cross out the last row in the matrix in the first case since there is no dx in the form and we cross out the first row in the second matrix since there is no dx.

=4[0 1 1 3]−7[1−1​3 2]

⇒−4−35=−39

The values of the following differential forms on the ordered sets of vectors indicated are −39.

Read and Learn More Susan Colley Vector Calculus Solutions

Page 535 Problem 3 Answer

Given:​7dx∧dy∧dz;a=(1,0,3),b=(2,−1,0),c=(5,2,1)

​To determine the values of the following differential forms on the ordered sets of vectors.Using the determination method.

A 3−the form has to act on 3 vectors. Additionally, since we are in 3 dimensions, the 3 form acting on 3

vectors are equal to the determinant of the matrix formed by given vectors placed into columns:

7dx∧dy∧dz((1,0,3),(2,−1,0),(5,2,1))

​=[103​2−10​521]

⇒182

The values of the following differential forms on the ordered sets of vectors are 182.

Page 535 Problem 4 Answer

Given: The differential form dx1

∧dx2+2dx2∧dx3+3dx3∧dx4;​a=(1,2,3,4),b=(4,3,2,1).To determine the values of the differential forms on the ordered sets of vectors.Using the concepts of vectors.

The2 -form acting on 4 dimensional vectors. Just like in task, use linearity and cross out the rows in the matrix corresponding to the missing coordinates.

​(dx1∧dx2+2dx2∧dx3+3dx3∧dx4)((1,2,3,4),(4,3,2,1))​

=∣12​43∣+2∣∣23​32∣+3∣∣34​21∣

=−5−10−15

=−30

Therefore the value of the differential form is −30.

The value of the differential form is −30.

Page 535 Problem 5 Answer

Given:The differential form 2dx1∧dx3∧dx4+dx2∧dx3∧dx5;​a=(1,0,−1,4,2),b=(0,0,9,1,−1),c=(5,0,0,0,−2).

To determine the values of the differential forms on the ordered sets of vectors indicated.

Using the concepts of vectors.

This is a 3 -form acting on 5 dimensional vector. Once again use the linearity and we place the 3 vectors into the matrices as their columns.

Then cross out the rows that are not present in the form.

For the first part of the form, cross out the second and the fifth row, for the second part cross out first and the fourth row.

Therefore the expression can be obtained as:  2∣1−14​091​500∣∣+∣∣0−12​09−1​00−2∣=−370

The value of the differential form is −370.

Page 535 Problem 6 Answer

Given:  Let ω be the 1 -form on R3 defined by ω=x2ydx+y2zdy+z3xdz.To find ω(3,−1.4)(a), where a=(a1,a2,a3).

Using the concepts of vector.

If the form contains some functional expression (as in this task), to specify additional vector that will be plugged into the functional expression part of the form.

In this case, replace every x

in front of (dx,dy,dz)with3 , everyy with −1 and every z with4. Therefore,ω3,−1,4(a)=(32(−1)dx+(−1)2⋅4dy+43⋅3dz)(a1,a2,a3)

Now simply calculate the expression: −9a1+4a2+192a3

The value of ω(3,−1,4)(a) is −9a1+4a2+192a3.

Page 535 Problem 7 Answer

Given:  Let ω be the 2 -form on R4 given by ω=x1x3dx1∧dx3−x2x4dx2∧dx4.

To findω12,−1,−3,1)(a,b).Using the concepts of vector.

The function is xi where i∈{1,2,3,4}plug in the appropriate coordinates of the vector (2,−1,−3,1).

We have 2 -form acting on 4 dimensional vectors, therefore cross out even rows in first matrix and odd rows in second one before calculating the determinant:

(−6dx1∧dx3+dx2∧dx4)((a1,a2,a3,a4),(b1,b2,b3,b4))

=6∣a1a3​b1b3∣+∣a2a4​b2b4∣

=−6a1b3+6a3b1+a2b4−a4b2

Therefore ω12,−1,−3,1)(a,b) is −6a1b3+6a3b1+a2b4−a4b2.

The solution of ω12,−1,−3,1)(a,b)is −6a1b3+6a3b1+a2b4−a4b2.

Page 535 Problem 8 Answer

Given: Let ω be the 2 -form on R3 given by ω=cosxdx∧dy−sinzdy∧dz+(y2+3)dx∧dz.To findω(0,−1,π/2)

(a,b), wherea=(a1,a2,a3) and b=(b1,b2,b3).Using the concepts of vector.

Instead of x,y and z the values of (0,−1,π2) are plugged in inside the differential form.

This is a2 -form so cross the missing coordinate row inside the matrix  (dx∧dy−dy∧dz+4dx∧dz)/((a1,a2,a3),(b1,b2,b3))

=∣a1a2​b1b2∣−∣​a2a3​b2b3∣+4∣a1a3​b1b3∣==a1b2−a2b1−a2b3+a3b2+4a1b3−4a3b1

Therefore ω(0,−1,π/2)(a,b)= a1b2−a2b1−a2b3+a3b2+4a1b3−4a3b1.

The solution of the ω(0,−1,π/2)(a,b)= a1b2−a2b1−a2b3+a3b2+4a1b3−4a3b1.

Page 535 Problem 9 Answer

Given function ω

To findω(x,y,z) ((2,0,−1),(1,7,5)

Method used with determinants.

Given a function ω

Now to find out ω(x,y,z) ((2,0,−1),(1,7,5)

Find out the values using determinants

Also Here, Repeat the same process as in previous task.

But this time there is no vector to plug in.

So functions in front of the forms remain.

We have ω(x,y,z) ((2,0,−1),(1,7,5)=cosx​20​17​−sinz​0−1​75​+(y2+3)​2−1​15

​=14cosx−7sinz+11y2+33

The solution of ω(x,y,z) ((2,0,−1),(1,7,5) is14cosx−7sinz+11y2+33

Page 535 Problem 10 Answer

Given function ω the 3 form R3

To findω(0,0,0) (a,b,c)

where a=(a1,a2,a3),b=(b1,b2,b3),c=(c1,c2,c3) Method used is determinant.

Given that, Function ω the three form R3

ω=(excos y+(y2+2)e2z)dx∧dy∧dz

To find out ω(0,0,0) (a,b,c)

Where,a=(a1,a2,a3)

b=(b1,b2,b3)

c=(c1,c2,c3)

Notice that

We are dealing with the three form on three dimensional space.

Hence the resulting form is just a determinant of vectors placed in the matrix as its columns.

We only need to deal with the functional expression in front of the matrix.

But this is easy due to the fact that we plug in x=y=z=0 to obtain 3

Hence the resulting form is three times the determinant of the matrix.

ω(0,0,0)(a,b,c)=3∣a1a3​b1b3​c1c3∣

Or expressed as the total result equal to 3(a1b2c3+b1c2a3+c1a2b3−c1b2a3−b1a2c3−a1c2b3)

The solution of ω(0,0,0) (a,b,c) is 3(a1b2c3+b1c2a3+c1 a2b3−c1b2a3−b1a2c3−a1c2b3)

Page 535 Problem 11 Answer

Given The given expression is ω=(excosy+(y2+2)e2z)dx∧dy∧dz.

To find The value of the expression ω(x,y,z)((1,0,0),(0,2,0),(0,0,3)).

Method used The method used for this is the concept of determinant.

Given ω=(excosy+(y2+2)e2z)dx∧dy∧dz.

ω(x,y,z)((1,0,0),(0,2,0),(0,0,3)) can be written as (excosy+(y2+2)e2z)∣100​020​003∣

ω(x,y,z)((1,0,0),(0,2,0),(0,0,3))= (excosy+(y2+2)e2z)∣​100​020​003∣

Now, solve the determinant.

det[​adg​beh​cfi​]=a⋅det[​eh​fi​]−b⋅det[​dg​fi​]+c⋅det[​dg​eh​]

On solving.

ω(x,y,z)((1,0,0),(0,2,0),(0,0,3))= 6(excosy+(y2+2)e2z).

The value of ω(x,y,z) ((1,0,0),(0,2,0),(0,0,3)) is equal to 6(excosy+(y2+2)e2z).

Page 535 Problem 12 Answer

Given The given expressions are ω=3dx+2dy−xdz;​η=x2 dx−cosydy+7dz.To find The value of the expression ω∧η.

Method used The method used in this is vector product.

The given expressions are ω=3dx+2dy−xdz

η=x2 dx−cosydy+7dz

ω∧η= (3dx+2dy−xdz)∧(x2dx−cosydy+7dz)

Now, do the product

= 3x2dx∧dx+2x2dy∧dx−x3dz∧dx−3cosydx∧dy−2cosydy∧dy+xcosydz∧dy+21dx∧dz+14dy∧dz−7xdz∧dz                [dx∧dx =dy∧dy=dz∧dz= 0]

Simplifying the terms.

= (−2×2−3cosy)dx∧dy+(x3+21)dx∧dz+(14−xcosy)dy∧dz.

The value of the expression ω∧ηis equal to (−2×2−3cosy)dx∧dy+(x3+21)dx∧dz+(14−xcosy)dy∧dz.

Page 535 Problem 13 Answer

Given The given functions are On R3:ω=ydx−xdy;η=zdx∧dy+ydx∧dz+xdy∧dz.To find The value of the expressionω∧η.

Method used Do the wedge product for simplifying.

Given functions are ω=ydx−xdy

η=zdx∧dy+ydx∧dz+xdy∧dz

Thus,ω∧η= (ydx−xdy)∧(zdx∧dy+ydx∧dz+xdy∧dz)

Multiply the terms.

= yxdx∧dy∧dz−xydy∧dx∧dz+yzdx∧dx∧dy+yydx∧dx∧dz−xzdy∧dx∧dy−xxdy∧dy∧dz

[dx∧dx=dy∧dy=dz∧dz=0]

Simplifying the terms.

= 2xydx∧dy∧dz.

By using property of alternation the terms of the second term are swapped and sign is flipped.

The value of the expression ω∧η is equal to 2xydx∧dy∧dz.

Page 536 Problem 14 Answer

Given The given functions are On R4:ω=2dx1∧dx2−x3dx2∧dx4;η=2x4dx1∧dx3+(x3−x2)dx3∧dx4.

To find The value of the expression ω∧η.

Method used The method used to simplify the given expression is wedge product.

Given ω=2dx1∧dx2−x3dx2∧dx4

η=2x4dx1∧dx3+(x3−x2)dx3∧dx4

Thus, ω∧η= (2dx1∧dx2−x3dx2∧dx4)∧(2x4dx1∧dx3+(x3−x2)dx3∧dx4)

There are 4 coordinates so the term obtained in result are those which have all the four coordinates only.

Thus,ω∧η= 2x3x4dx2∧dx4∧d1∧dx3+2(x3−x2)dx1∧dx2∧dx3∧dx4

Using alternating property reorder the terms of the product.

= (2x3x4+2×3−2×2)dx1∧dx2∧dx3∧dx4.

The value of the expression ω∧η is equal to (2x3x4+2×3−2×2)dx1∧dx2∧dx3∧dx4 .

Vector Calculus 4th Edition Chapter 7 Surface Integrals and Vector Analysis

Page 467 Problem 1 Answer

Given the X(s,t)=(s²−t²,s+t,s²+3t)

To find the a normal vector to this surface at the point(3,1,1)=X(2,−1)

Using the method of cross product of vector.

We have givenX(s,t)=(s²−t²,s+t,s²+3t)

First we calculate

dX/ds=(2s,1,2s)

dX/dt=(−2t,1,3)

Now, we have to find the value of these factor for(s,t)=(2,−1)

Two vector we obtain are(4,1,4) and(2,1,3)

Now, normal vector is given as cross product of these two vector:

(4,1,4)×(2,1,3)=(−1,−4,2)

The normal vector to this surface at the point(3,1,1)=X(2,−1) is given by(−1,−4,2).

Page 467 Problem 2 Answer

Given the parametrized surface X(s,t)=(s²−t²,s+t,s²+3t)

To find the an equation for the plane tangent to this surface at the point(3,1,1)

Using the formula for equation of tangent.

The formula for equation of tangent line is given point(a,b,c) is n(x−a,y−b,z−c)=0

Where n denote normal vector.

Hence our equation become

Read and Learn More Susan Colley Vector Calculus Solutions

(−1,−4,2)×(x−3,y−1,z−1)=0 where is(3,1,1)

Expand everything to expand the equation x+4y−2z−5=0

An equation for the plane tangent to this surface at the point (3,1,1) is x+4y−2z−5=0

Page 467 Problem 3 Answer

Given:X(s,t)=(5+2cost)coss,(5+2cost)sins

To find  an equation for the plane tangent to the torus at point

(5−√3/√2,5−√3/√2,1)

Using the method of equation of tangent.

The given parameterization of surface is(5+2cost)coss,(5+2cost)sins,2sint

To find the value of s,t

we have to find the partial derivatives of the given parameterization.

Dϕ/ds=(−(5+2cost)sins,(5+2cost)coss,0)

dϕ/dt=(−2sintcoss,−2sintsins,2cost)

Take the cross product of derivatives above to obtain the formula for the normals,t

(−(5+2cost)sins,(5+2cost)coss,0).(−2sintcos,−2sintsins,2cost)

Plugging the value of s,t we get,

n=√3−5/√2(√3,√3,−√2)

Now we get equation of tangent as

√3x+√3y−√2z−5√6+4√2=0

The equation of tangent is given by √3x+√3y−√2z−5√6+4√2=0

Page 468 Problem 4 Answer

Given: The parametrized surface X(s,t)=(s,s²+t,t²)

To find the graph for this surface−2≤s≤2,−2≤t≤2

Using the method of graph.

The graph is given by

The graph is given by

Page 468 Problem 5 Answer

Given: The parametrized surface isX(s,t)=(s,s²+t,t²).To find the is the surface smooth.

Using the method of vector.

We haveX(s,t)=si^+s2+tj^+t2k^

The surface is smooth if and only if N≠0⃗

Ts=∂x/∂si^+∂y/∂sj^+∂z/∂sk^ And

Tt=∂x/∂ti^+∂y/∂tj^+∂z/∂tz^ Now,

⃗Ts=0i^+1j^+2tk^And

Tt=1i^+2sj^+0k^

Hence,N=Ts×Tt

N=4sti^+2tj^−1k^

Since,k component of normal vector never be zero so the surface is smooth.

Yes,the surface is smooth.

Page 468 Problem 6 Answer

Given: The parametrized surface isX(s,t)=(s,s2+t,t2)

To find an equation for the tangent plane at the point(1,0,1) using the method of tangent plane equation.

We have N=4sti^+2tj^−1k^

Put value of s=1andt=−1

We get,N=−4i^−2j^−1k^

Hence the tangent plane equation is given by

(−4,−2,−1).(x−1,y−0,z−1)=0

−4(x−1)−2y−1(z−1)=0

The tangent plane equation equation is given by−4(x−1)−2y−1(z−1)=0

Page 468 Problem 7 Answer

Given: Equation of formz=f(x,y)

To find the parametrized surface of Exercise1

Using the method of vector.

We look at the parameterization given to us in exercise 1.

Since,x=s2−t2 andy=s+t

We want to express x overy then and we do this with:

x=y(s−t)

With this, now the goal is to isolatet and s in term of x,y

We can reform above equation as

X/y=s−t

From this and second coordinate in parametrized we have

2s=y+x/y and 2t=y−x/y

Now, write down z in term of newly expressed s,t

We have,

z=1/4(y+x/y)2+3/2(y−x/y)

The parametrized surface of Exercise1 is given by 1/4(y+x/y)2+3/2(y−x/y)

Page 468 Problem 8 Answer

Given: S be the surface parametrized bex=scost,y=ssint,z=s2

To find an equation for the tangent plane at the point(1,√3,4)’Using the method of cross product of vector.

The parametrized surface is given as ϕ(s,t)=(scost,ssint,s2)

Partial derivative of the parametrization

dϕ/ds=(cost,sint,2s)

dϕ/dt=(−ssint,−scost,0)

Normal is given with cross product

dϕ/ds×dϕ/dt=(−2s2cost,−2s2sint,s)

Now, recall that surface surface is smooth at every point except origin.

Hence, equation of tangent plane is given as

(x−1,y−√3,z−4).(−4,−4√3,2)=02x+2√3y−z−4=0

​Yes, the point S is smooth and the equation of tangent plane is given as2x+2√3

y−z−4=0

Page 468 Problem 9 Answer

Given: S be the surface parametrizedx=scost,y=ssint,z=s2 wheres≥0,0≤t≤2π

To find the sketch the graph of S and recognize S as a familiar surface.Using the method of graph.

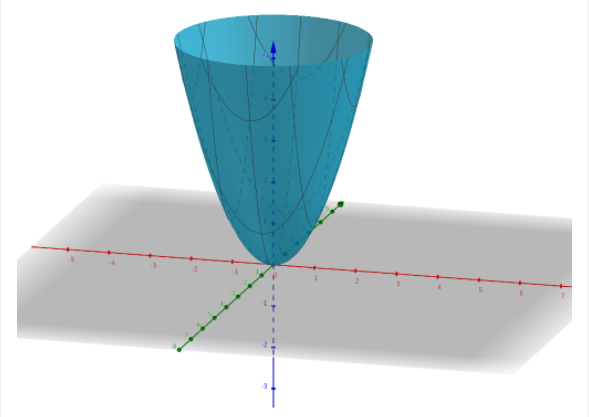
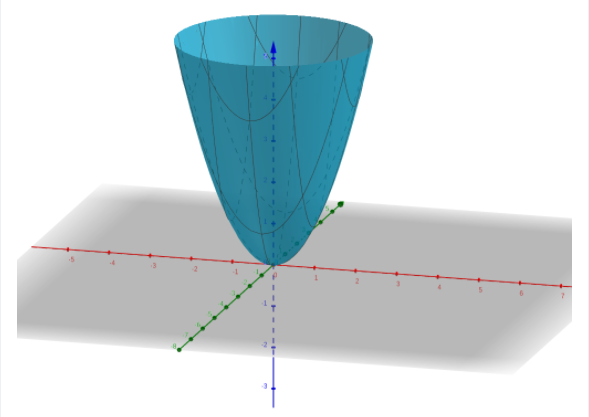
Using the geogebra and we plot the surface as paraboloid.

The surface is paraboloid.

Page 468 Problem 10 Answer

Given S be the surface parametrized byx=scost,y=ssint,z=s2 wheres≥0,0≤t≤2π

To find equation of formz=f(x,y)

Using the method of normal vector.

From parametrization we conclude that

z=x2+y2

This due the fact that we easily cancel out the term with sine and cosine once we square them.

The equation of formz=f(x,y) is z=x2+y2

Page 468 Problem 11 Answer

Given: S be the surface of parameterized byx=scost,y=ssint,z=s2

To find the Using answer in part(c), discuss whether S has a tangent plane at every point.

Using the method of vector and surface integral.

It does. For any point on surface expect the origin we can use the same process as in part(a).

At the origin the tangent plane is the planez=0.

Yes,S has a tangent plane at every point.

Page 468 Problem 12 Answer

Given: The parametrized surface is given asX(s,t)=(2sinscost,3sinssint,coss) where0≤s≤π,0≤t≤2π

To find the parametrized surface is ellipsoid.

Using the method of surface integral.

Simply try fitting the parametrized of the given surface into the ellipsoid equation.

The general ellipsoid equation is given by, ax2+by2+cz2=1

Now we simplify to find the value of a,b,c for which the parametrized satisfy.

a(2sinscost)2+b(3sinssint)2+c(coss)2=1

From this we have,a=1/4,b=1/9,c=1

The equation of ellipsoid is given by x²/4+y²/9+z²=1

Page 468 Problem 13 Answer

Given: The coordinate curve, when t=t0, is a circle of radiusa+bcost0

To find the torus of example 5 is a circle.Using the method of surface integral.

When we fixt=t0 the parametrization only depend on s.

Hence the new parametrization is a single variable function.

γ(s)=((a+bcost0)coss,(a+bcost0)sins,bsint0)

You can write this as

γ(s)=((a+bcost0)coss,(a+bcost0)sins,(0,0,bsint0))

This is circle with radiusa+bcost0

displayed from the origin on point(0,0,bsint0)

The parametrized as a function of a single variable to confirm the result.

Page 468 Problem 14 Answer

Given The surface in R3 parametrized byX(r,θ)=(rcosθ,rsinθ,θ),​r≥0,−∞<θ<∞

To find the r-coordinate curve Method used for  vector calculus

(a) When θ=π/3, the r-coordinate curve is given by(r/2,r√3/2,π/3) where r≥0.

This is the ray y=√3/x where x≥0 and z=π/3.

In general, the r-coordinate curve when θ=θ0

0 is a ray in the z=θ0 plane.

The solution is simpler than the following four cases make it seem.

If cosθ0≠0then y=(tanθ0)x

where x≥0

if cosθ0>0and x≤0.

If cosθ0=0,

Then the ray is x=0 with y≥0 if sinθ0>0 and y≤0 if sinθ0<0.

If cosθ0=0 then the ray is x=0

with y≥0 if sinθ0 >0 and y≤0 if sinθ0<0.

Page 468 Problem 15 Answer

Given The surface in R3

parametrized by X(r,θ)=(rcosθ,rsinθ,θ),​r≥0,−∞<θ<∞

To find the θ-coordinate curve Method used for vector calculus

When r=1 the θ-coordinate curve is the helix (cosθ,sinθ,θ).

In general, when r=r0 the θ-coordinate  curve is the helix (r0cosθ,r0sinθ,θ)

The θcoordinate curve in the helix is: (r0cosθ,r0sinθ,θ)

Page 468 Problem 16 Answer

Given The surface in R3

parametrized by X(r,θ)=(rcosθ,rsinθ,θ),​r≥0,−∞<θ<∞

To find  the graph of the helicoidMethod used for vector calculus

(c) You can see that the helicoids are made up of the helices that are the θ-coordinate curves

The graph of the helicoid

Page 468 Problem 17 Answer

Given the equation form of f(x,y)=√4−(x−2)2−(y+1)2

To find an equation for the plane tangent to it at the pointMethod used for vector calculus

(a) First we consider the sphere as the graph of the function f(x,y)=√4−(x−2)2−(y+1)2.

The partial derivatives are fx=−(x−2)√4−(x−2)2−(y+1)2,fy=−(y+1)√4−(x−2)2−(y+1)2.

So, fx(1,0,√2)=1/√2 and fy(1,0,√2)=−1/√2.

By Theorem 3.3 of Chapter 2, z=f(a,b)+fx(a,b)(x−a)+fy(a,b)(y−b).

In this case, this is z=√2+(1/√2)(x−1)−(1/√2) y, or equivalently −x+y±√2 z=1

An equation for the plane tangent to it at the point (1,0,√2) by considering the sphere as the graph of the function f(x,y)=√4−(x−2)2−(y+1)2 is: z=√2+(1/√2)(x−1)−(1/√2)y, or equivalently −x+y±√2 z=1

Page 468 Problem 18 Answer

Given the equation form of F(x,y,z)=(x−2)2+(y+1)2+z2

To find an equation for the plane tangent to it at the pointMethod used for vector calculus

(b) Now we look at the sphere as a level surface of F(x,y,z)=(x−2)²+(y+1)²+(z)².

The gradient ∇F(x,y,z)=2(x−2,y+1,z) and,Therefore, ∇F(1,0,√2)=(−2,2,2,√2).

By formula (5) of Section 2.6, the tangent plane is given by 0=∇F(1,0,√2).(x−(1,0,√2))=(−2,2,2,√2)⋅(x−(1,0,√2).

This too is equivalent to −x+y+√2z=1.

an equation for the plane tangent to it at the point (1,0,√2) by considering the sphere as a level surface of the function ∇F(x,y,z)=2(x−2,y+1,z) is: −x+y+√2 z=1.

Page 468 Problem 19 Answer

Given  the sphere as the surface parametrized by X(s,t)=(2sinscost+2,2sinssint−1,2coss)

To find an equation for the plane tangent to it at the pointMethod used for vector calculus

(c) Now we’ll use the results of this section.

Considering the z-component, We see 2coss=√2

so cos s=√2/2.

Considering the y- and x-components, 2sinssint=1 and sinscost=−1.

Thus we have that s=π/4 and t=3π/4.

Also Ts(s,t)=(2cosscost,2cosssint,−2sins) and

Tt(s,t)=(−2sinssint,2sinscost,0).

A normal vector to the sphere at the specified point is

N(π/4,3π/4)=Ts (π/4,3π/4)×Tt(π/4,3π4)

N(π/4,3π/4)=(−1,1,−√2)×(−1,−1,0)

N(π/4,3π/4)=(−√2,√2,2)

The tangent plane is given by(−√2,√2,2).(x−(1,0,√2))=0

Which is also equivalent to−x+y+√2z=1.

An equation for the plane tangent to it at the point (1,0,√2) by considering the sphere as the surface parametrized by X(s,t)=(2sinscost+2,2sinsint−1,2coss) is: −x+y+√2z=1.

Page 468 Problem 20 Answer

Given the cylinder x2+z2=4 lying between y=−1 and y=3

To find represent the given surface as a piecewise smooth parametrized surface.

Method used for vector calculus.

Imagine the cylinder as a trace of the circle which has its origin slid between (0,−1,0) and (0,3,0).

From here, this gives us the idea how to parametrize such object.

If y=0 our cylinder is just a circle in x,z plane.

The radius of the circle is 2 hence the parametrization becomes:

Υ(t)=(2cost,0,2sint),t∈[0,2Π]

We want to allow the circle to slide, so we vary the y coordinate.

Final parametrization of the cylinder is:ϕ(t,s)=(2cost,s,2sint),t∈[0,2Π],s∈[−1,3]

Parametrization of the cylinder is: ϕ(t,s)=(2cost,s,2sint),t∈[0,2Π],s∈[−1,3]

Page 468 Problem 21 Answer

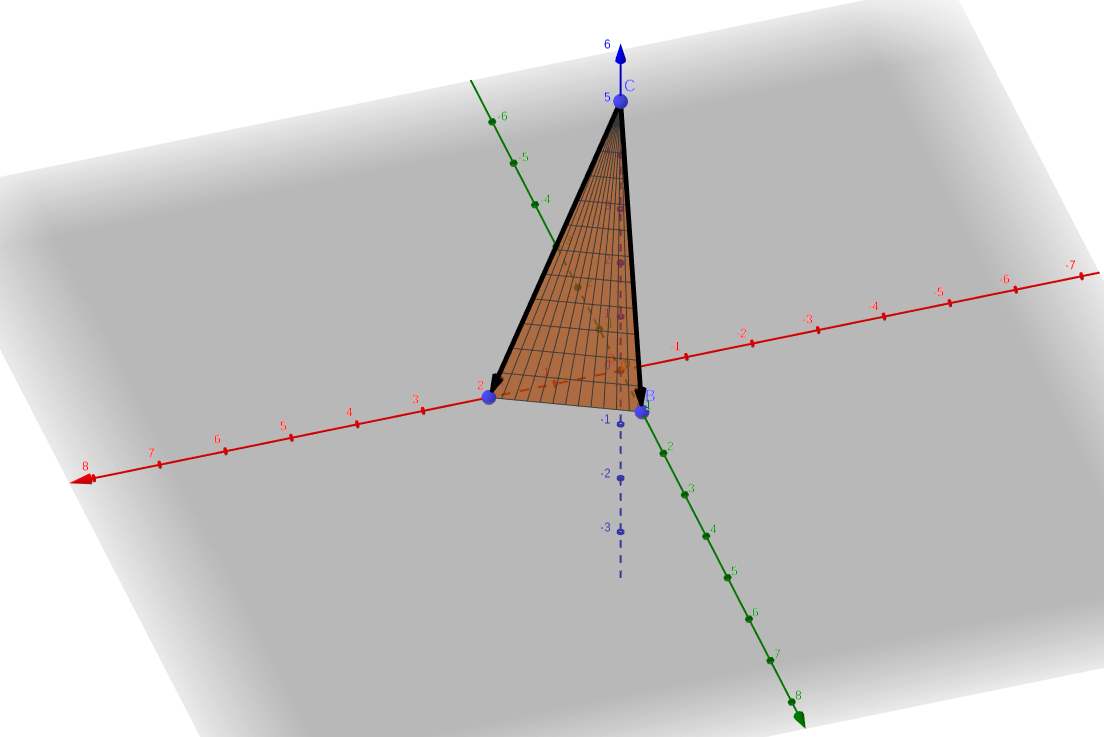
Given The closed triangular region in R3 with vertices (2,0,0),(0,1,0) and (0,0,5)

To find represent the given surface as a piecewise smooth parametrized surface.

Method used for vector calculus.

Easiest way to parametrize the triangle is to consider it as a convex combination of its sides.

To do it, first draw two segments from the point (0,0,5) to the points (2,0,0) and (0,1,0).

Next, we parametrize these segments on such way that they both start at (0,0,5)

and end at their respective end points.

We obtain two curves:

Υ1(t)=(2t,0,5−5t),t∈[0,1]

Υ2 (t)=(0,t,5−5t),t∈[0,1]

The triangle can be viewed  as a convex combination of these two curves, hence define the surface parametrization as:

ϕ(t,s)=(1−s)Υ1(t)+Υ2(t),t,s∈[0,1]

The final parametrization is:

ϕ(t,s)=(2t−2ts,ts,5−5t−5s+5ts+5s−5ts)

ϕ(t,s)=(2t−2ts,ts,5−5t)

The image of the area is below.

From there one can see where the idea from the solution comes in.

Every line in the interior of the tringle is a linear combination of its two sides.

Parametrization of triangle is: (2t−2ts,ts,5−5t)

Page 467 Problem 22 Answer

Given the point (1,−1,−1) and the parametrized surface X(s,t)=(s3,t3,st).To find the equation for the parametric surface on the point (1,−1,−1)

Using the partial derivation.

Partial derivative of X=(s3,t3,st) with respect to s

dX/ds=(3s2,0,t)

Partial derivative of X=(s3,t3,st) with respect to t

dX/dt=(0,3t2.s)

Cross multiplication of dX

Ds and dX/dt

(3s2,0,t)×(0,3t2,s)=(3,−3,9)

Now, the required equation of the plane

3(x−1)+(−3)(y+1)+9(z+1))=0

⇒3x−3y+9z+3=0

⇒x−y+3z=−1

The required equation is x−y+3x=−1

Page 467 Problem 23 Answer

Given the parametric plane X(s,t) on (1,−1,−1)

To find whether the curve was plane or not.Using the normal of the plane

The surface is smooth , if its normal vector is non-zero at origin.

Normal vector

(3s3,−3t3,9st) at t=0 and s=0

⇒(0,0,0)

So the surface is not plane.

The surface is not smooth as its normal vector is zero at origin.

Page 467 Problem 24 Answer

Given the parametric plane X(s,t) and condition −1≤t≤1 and −1≤s≤1.

To find the surface along the given condition.Using plotting of parametric curves.

The surface made under given conditions is

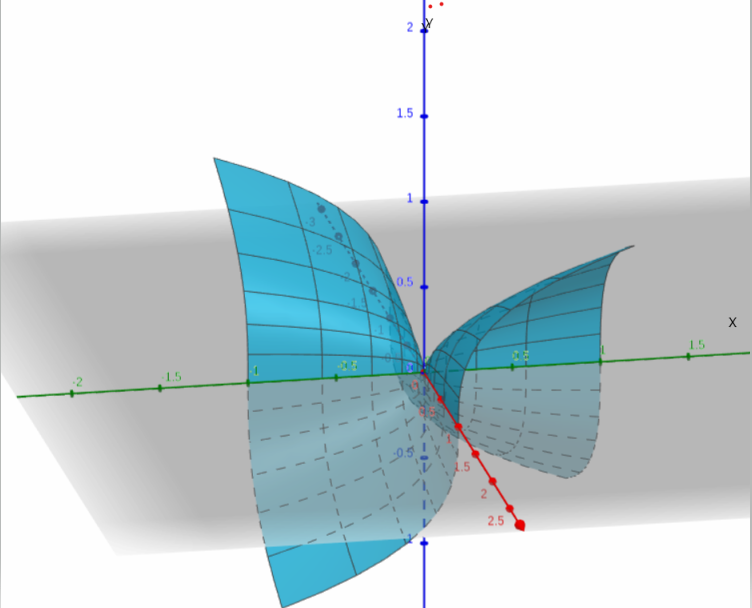
The required graph is

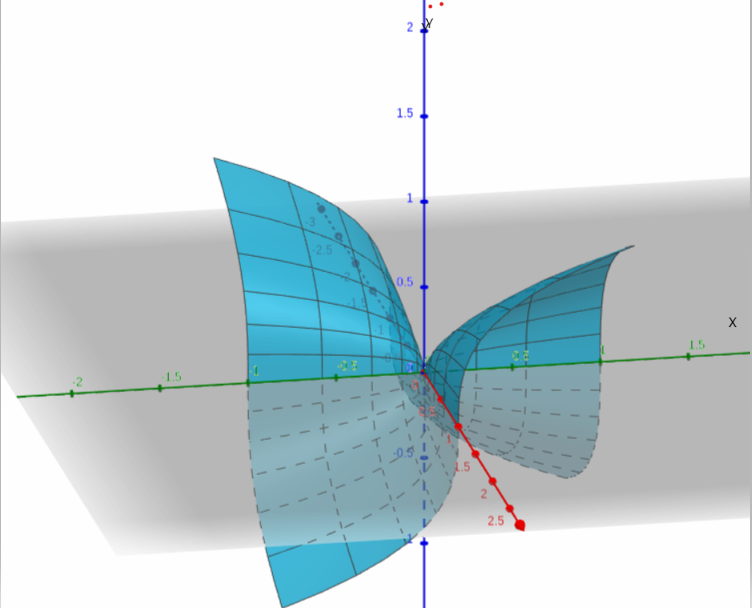
Page 467 Problem 25 Answer

Given the parametrized surface X(s,t) and the equation z=(xy)​1/3

To find that X(s,t) at t,s∈[−1,1] ,also shows z=(xy)​1/3

Method used for plotting the surfaces on same graph.

The graph plotted for X(s,t)=(s3,t3,st) at s,t∈[−1,1] and the equationz=(xy)​1/3

Here, numerically if x=s3 and y=t3,

Then z=(s3⋅t3)​1/3z=st

Which satisfies X(s,t)=(s3,t3,st)

The graph of z=(xy)1/3 also include the graph of X(s,t)