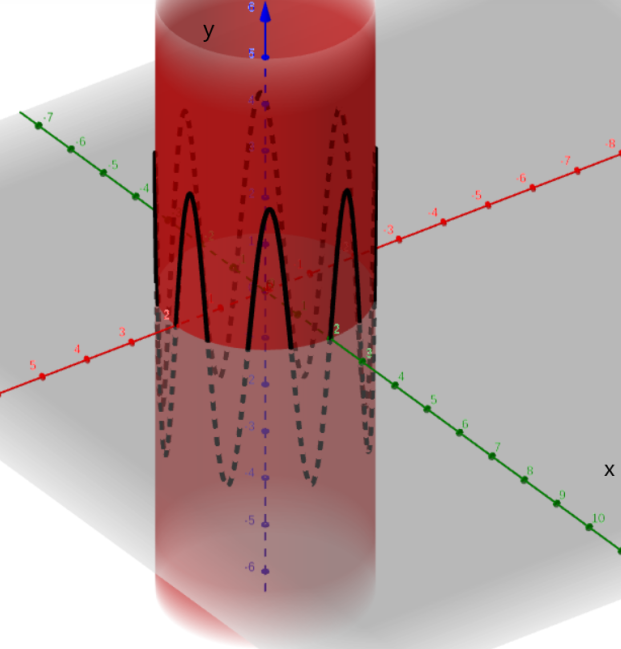
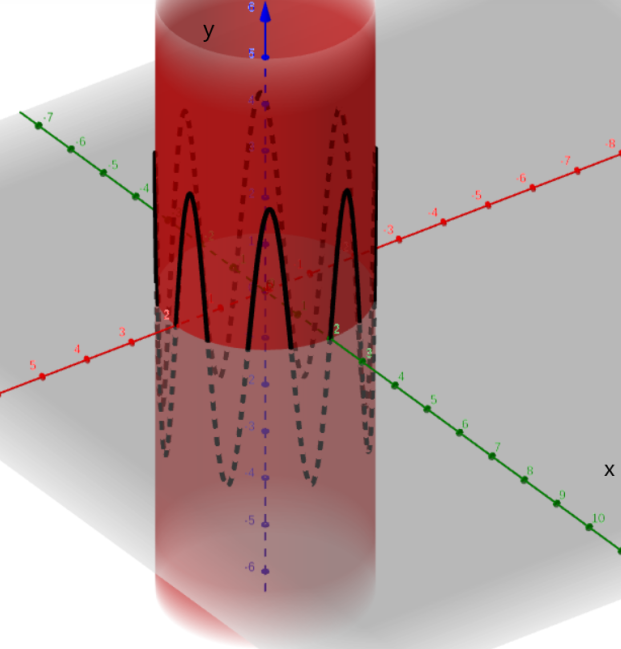
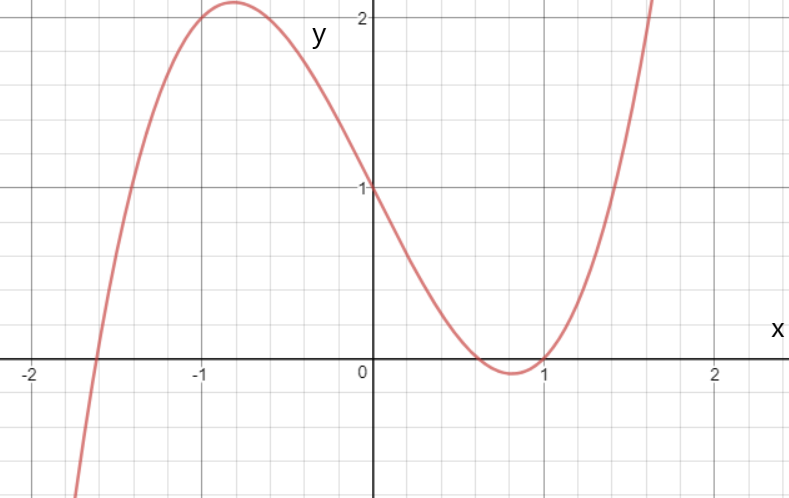
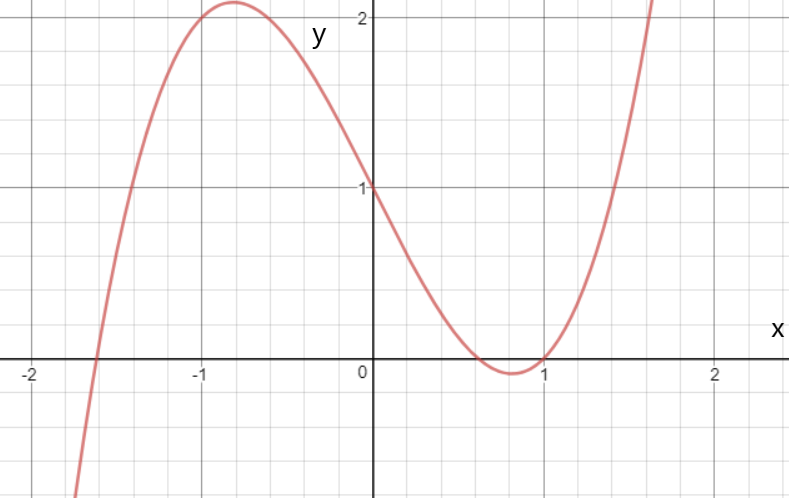
Susan Colley

Susan Colley Vector Calculus 4th Edition Chapter 6 Line Integrals

Page 426 Problem 1 Answer

Given: The function f(x,y)=x+2y

To Find: Evaluate scalar line integral of x(t)=2−3t,4t−1,0≤t≤2

Evaluate to get the final result.

Let (x,y) = x + 2y.

Let x(t) = (2-3t, 4t – 1), 0 ≤ t ≤ 2

We have that f(x) = f(2 – 3t, 4t – 1) = (2 – 3t) + 2(4t – 1) = 2 – 3t + 8t – 2 = 5t

for all 0 ≤ t ≤ 2 and

x'(t) = (-3,4) for all 0 ≤ t ≤ 2

Which gives us that

⇒ \(\left\|\mathbf{x}^{\prime}(t)\right\|=\sqrt{(-3)^2+4^2}=\sqrt{9+16}=\sqrt{25}=5\)

for all. 0 ≤ t ≤ 2

Thus,

⇒ \(\int_{\mathbf{X}} f d s=\int_0^2 f(\mathbf{x}(t))\left\|\mathbf{x}^{\prime}(t)\right\| d t\)

= \(\int_0^2(5 t) \cdot 5 d t=\int_0^2 25 t d t\)

= \(\left.\frac{25 t^2}{2}\right|_0 ^2\)

= \(\frac{25 \cdot 2^2}{2}-\frac{25 \cdot 0^2}{2}\)

= 50 – 0 = 50.

The required solution is 50.

Page 426 Problem 2 Answer

Given: The functionf(x,y)=x+2y.

To Find: Evaluate scalar line integral of x(t)=(cost,sint),0≤t≤π.

Evaluate to get the final result.

Let f(x,y) =x + 2y.

Let x(t) = (cos t, sin t), 0 ≤ t ≤ π.

We have that f(x(t)) = f (cost, sin t) = cos t + 2 sin t for all 0 ≤ t ≤ π and

x'(t) = (-sint, cos t) for all 0 ≤ t ≤ π which gives us that

⇒ \(\left\|\mathbf{x}^{\prime}(t)\right\|=\sqrt{(-\sin t)^2+(\cos t)^2}=\sqrt{\sin ^2 t+\cos ^2 t}=\sqrt{1}=1 \text { for all } 0 ≤ t ≤ \pi\)

Thus,

⇒ \(\int_{\mathbf{x}} f d s=\int_0^\pi f(\mathbf{x}(t))\left\|\mathbf{x}^{\prime}(t)\right\| d t\)

= \(\int_0^\pi(\cos t+2 \sin t) \cdot 1 d t=\int_0^\pi(\cos t+2 \sin t) d t\)

= \((\sin t-2 \cos t)_0^\pi=(\sin \pi-2 \cos \pi)-(\sin 0-2 \cos 0)\)

= (0-2.(1)) – (0-2.1) = 2 – (-2)

= 4.

The required solution is 4.

Read and Learn More Susan Colley Vector Calculus Solutions

Page 426 Problem 3 Answer

Given: The expressionf(x,y,z)=xyz,x(t)=(t,2t,3t),0≤t≤2

To Find: ∫x fds, where f and x are as indicated.

Evaluate to get the final result.

Recal the way that we evaluate the line integral of a scalar field. First, for the given curve:

x = (t, 2t, 3t), t ∈ [0,2]

we find its derivative x’ = (1,2,3) ⇒ ||x|| = √14

Next, recall that the integral is evaluated by the formula:

⇒ \(\int_{\mathbf{x}} f d s=\int_a^b f(\mathbf{x})\|\mathbf{x}\| d t\)

where [a,b] is the segment on which we are considering the curve.

That is this is the segment on which the curve is, given.

Finally, we evaluate the integral

⇒ \(\int_0^2 \sqrt{14} f(t, 2 t, 3 t) d t=\sqrt{14} \int_0^2 6 t^3 d t\)

= 24√14

The required solution is 24√14

Page 426 Problem 4 Answer

Given : The expression is f(x,y,z)=x+z/y+z,

x(t)=(t,t,t3/2),1≤t≤3

To Find: Calculate the expression .

Evaluate the question to get the answer.

Let us evaluate the line integral of a scalar field.

First, for the given curve: x=(t,t,t​3/​2),t∈[1,3]

We find its derivative x′=(1,1,3/2√t)

⇒∥x∥=1/2√9t+8

Next, recall that the integral is evaluated by the formula:

⇒ \(\int_{\mathbf{x}} f d s=\int_a^b f(\mathbf{x})\|\mathbf{x}\| d t\)

Where [a,b] is the segment on which we are considering the curve, that is the segment on which the curve is given.

Finally, we evaluate the integral:

⇒ \(\int_1^3 f(\mathbf{x}) \frac{1}{2} \sqrt{9 t+8} d t=\frac{1}{2} \int_1^3 \sqrt{9 t+8} d t\)

= \(\frac{35 \sqrt{35}-17 \sqrt{17}}{27}\)

Calculating fx/fds we get 35√35 −17√17/27.

Page 426 Problem 5 Answer

Given : The function is f(x,y,z)=3x+xy+z3,

x(t)=(cos4t,sin4t,3t),​0≤t≤2π

To Find: Calculate the function.

Evaluate the question to get the answer .

Recall the way that we evaluate the line integral of a scalar field.

First, for the given curve:

x(t)=(cos4t,sin4t,3t),t∈[0,2π]

We find its derivative x′(t)=(−4sin4t,4cos4t,3)

⇒∥x(t)∥=5

Next, recall that the integral is evaluated by the formula:

⇒ \(\int_{\mathbf{x}} f d s=\int_a^b f(\mathbf{x})\|\mathbf{x}\| d t\)

where [a,b] is the segment on which we are considering the curve, that is the segment on which the curve is given.

Finally, we evaluate the integral:

⇒ \(\int_{\mathbf{x}} f d s=\int_0^{2 \mathrm{~T}} f(\mathbf{x}(t))\|\mathbf{x}\| d t\)

= \(5 \int_0^{2 \pi}\left(3 \cos 4 t+\frac{\sin 8 t}{2}+27 t^3\right) d t\)

= \(\left.5\left(\frac{3 \sin 4 t}{4}-\frac{\cos 8 t}{16}+\frac{27 t^4}{4}\right)\right|_0 ^{2 \pi}\)

= 540 π⁴

Calculating the function f{x}fds we get, 540π⁴.

Page 426 Problem 6 Answer

Given : The function is f(x,y,z)=z x²+y²,

x(t)=(e2tcos3t,e2tsin3t,e2t),​0≤t≤5.

To Find: Calculate the integral.

Evaluate he function to get the answer.

Recall the way that we evaluate the line integral of a scalar field.

First, for the given curve:

x(t)=(e2tcos3t,e2tsin3t,e2t),t∈[0,5]

We find its derivative x′(t)=(2e2tcos3t−3e2tsin3t,2e2tsin3t+3e2tcos3t,2e2t)

From here we find∥x∥:∥x∥=√17e^2t

Next, recall that the integral is evaluated by the formula:

⇒ \(\int_{\mathbf{x}} f d s=\int_a^b f(\mathbf{x})\|\mathbf{x}\| d t\)

where [a,b] is the segment on which we are considering the curve, that is the segment on which the curve is given.

Finally, we evaluate the integral:

⇒ \(\int_0^5 \frac{e^{2 t}}{e^{4 t} \cos ^2 3 t+e^{4 t} \sin ^2 3 t} \cdot \sqrt{17} e^{2 t} d t=\int_0^5 \frac{1}{e^{2 t}} \sqrt{17} e^{2 t} d t\)

= 5√17

Calculating the integral∫xfds we get,5√17.

Page 426 Problem 7 Answer

Given : The function is ​​f(x,y,z)=x+y+z,

x(t)={(2t,0,0)if0≤t≤1

(2,3t−3,0)if1≤t≤2

(2,3,2t−4)if2≤t≤3}

To Find: Calculate the function fx fds

Evaluate the question to get the answer .

Let us denote each of the 3 pieces of the curve with γ1,γ2and γ3respectively to ease the calculations.

The integral over the piecewise curve is the sum of integrals over every piece.

The function we are integrating is f(x,y,z)=x+y+z

Now,​γ1′(t)=(2,0,0)

⇒ ||γ₁|| = 2

⇒ \(\int_0^1 2 f\left(\gamma_1(t)\right) d t=\int_0^1 2 \cdot(2 t+0+0) d t\)

Next, we move on to the second piece:

||γ₂|| = 2

⇒ \(\int_1^2 3 f\left(\gamma_2(t)\right) d t=\int_1^2 3 \cdot(2+3 t-3+0) d t\)

= \(\frac{21}{2}\)

The third piece is:

||γ₃|| = 2

⇒ \(\int_2^3 2 f\left(\gamma_3(t)\right) d t=\int_2^3 2 \cdot(2+3+2 t-4) d t\)

= 12

Now, adding everything together we get \(\frac{49}{2}\).

​Calculating fxfds we get 49/2.

Page 426 Problem 8 Answer

Given : The function is \text { 7. }f(x,y,z)=2x−y1/2+2z2

​ x(t)={(t,t2,0)if0≤t≤1(1,1,t−1)if1≤t≤3

To Find: Calculate the function.

Evaluate the question to get the answer.

Once again we split the curve into two pieces and evaluate their norm to calculate 2 piecewise integrals.

The sum of the two integrals we will obtain will be the final result,

The first piece of the curve can be parametrized with:

γ1(t)=(t,t2,0),t∈[0,1]⇒γ1′(t)=(1,2t,0)

From the derivative above we find the norm:

∥γ1∥=√1+4t2

Finally, we calculate the integral over the first piece:

⇒ \(\int_0^1 f\left(\gamma_1(t)\right) d t=\int_0^1 t \sqrt{1+4 t^2} d t\)

= \(\left.\frac{\left(1+4 t^2\right)^{3/2}}{12}\right|_0 ^1\)

= \(\frac{5 \sqrt{5}-1}{12}\)

The second piece is given with:

γ₂(t) = (1,1, t-1)

⇒ γ₂(t) = (0,0,1)

The norm of the derivative is:

||γ₂|| = 1

Finally, we calculate:

⇒ \(\int_1^3 2-1+2 t^2-4 t+2 d t=9-\frac{5}{3}\)

Therefore, the final result is 5√5−1/12+9−5/3 =5√5+87/12.

Page 426 Problem 9 Answer

Given: The function isF=xi+yj+zk,

x(t)=(2t+1,t,3t−1),​0≤t≤1.

To Find: Calculate the function.

Evaluate the question to get the answer.

LetF(x,y,z)=xi+yj+zk and  letx(t)=(2t+1,t,3t−1),0≤t≤1

We have that F(x(t))=(2t+1)i+tj+(3t−1)k and x′(t)=(2,1,3)for all 0≤t≤1

which gives us that F(x(t))⋅x′(t)=(2t+1)⋅2+t⋅1+(3t−1)⋅3

=4t+2+t+9t−3

=14t−1 for all 0≤t≤1

Thus, \(\int_{\mathbf{x}} \mathbf{F} \cdot \mathrm{d} \mathbf{s}=\int_0^1 \mathbf{F}(\mathbf{x}(t)) \cdot \mathbf{x}^{\prime}(t) d t\)

= \(\int_0^1(14 t-1) d t\)

= \(\left.\left(7 t^2-t\right)\right|_0 ^1\)

= (7. 1² – 1) – (7. 0² – 0)

= (7-1) – (0 – 0)

= 6

Calculating the function we get,  ∫xF⋅ds=6.

Page 426 Problem 10 Answer

Given : The function isF=(y+2)i+xj,x(t) =(sint,− cost t),0≤t≤π/2

To Find: Calculate the function.

Evaluate the question to get the answer.

Recall the way we calculate the path integral of the given vector field.

For the sake of easier notation, if we are given the field.

F=a(x,y,z)i+b(x,y,z)j+c(x,y,z)k

where a,b,c are some scalar functions, we will write it down asF=(a(x,y,z),b(x,y,z),c(x,y,z)).

The path we are integrating over is: x(t)=(sint,−cost),t∈[0,π²]

Its derivate is:

x'(t) = (cos t, sin t)

Finally we use the formula for evaluating the path integral of the second kind:

⇒ \(\int_{\mathbf{x}} \mathbf{F} \cdot d s=\int_a^b \mathbf{F}(\mathbf{x}(t)) \cdot \mathbf{x}^{\prime}(t) d t\)

The field F is given in the task, so plugging everything into the formula we get:

⇒ \(\int_0^{\frac{\pi}{2}}(-\cos t+2) \cos t+\sin t \sin t=\int_0^{\frac{\pi}{2}} 2 \cos t-\cos 2 t d t\)

= 2.

Calculating the function we get ∫0​π²(−cost+2)cost+sintsint=2.

Page 426 Problem 11 Answer

Given : The function isF=xi+yj,x(t)

=(2t+1,t+2),0≤t≤1

To Find: Calculate the function.

Evaluate the question to get the answer.

Recall the way we calculate the path integral of the given vector field.

For the sake of easier notation, if we are given the field

F=a(x,y,z)i+b(x,y,z)j+c(x,y,z)k

where a,b,c are some scalar functions, we will write it down asF=(a(x,y,z),b(x,y,z),c(x,y,z)).

This time the field we are integrating is F(x,y)=(x,y)

The path we are integrating over is: x(t)=(2t+1,t+2),t∈[0,1]

Its derivative is:

x'(t) = (2,1)

Finally we use the formula for evaluating the path integral of the second kind:

⇒ \(\int_{\mathbf{x}} \mathbf{F} \cdot d s=\int_a^b \mathbf{F}(\mathbf{x}(t)) \cdot \mathbf{x}^{\prime}(t) d t\)

The field F is given above, so plugging everything into the formula we get:

⇒ \(\int_0^1((2 t+1) \cdot 2+(t+2) \cdot 1) d t=\int_0^1 5 t+4 d t\)

= \(\frac{13}{2}\)

Calculating the function we get ∫⁰((2t+1)⋅2+(t+2)⋅1)dt=13/2.
                                                             ¹

Page 426 Problem 12 Answer

Given : The function is F=(y−x)i+x4y3j,

x(t)=(t2,t3),−1≤t≤1

To Find: Calculate the function.

Evaluate the question to get the answer.

Recall the way we calculate the path integral of the given vector field.

For the sake of easier notation, if we are given the field

F=a(x,y,z)i+b(x,y,z)j+c(x,y,z)k

where a,b,c are some scalar functions, we will write it down as F=(a(x,y,z),b(x,y,z),c(x,y,z)).

This time, the vector field is:F(x,y)=(y−x,x4y3)

The path we are integrating over is:

x(t) = (t², t³), t ∈ [-1,1]

Its derivative is:

x'(t) = (2t, 3t²)

Finally we use formula for evaluating the path integral of the second kind:

⇒ \(\int_{\mathbf{x}} \mathbf{F} \cdot d s=\int_a^b \mathbf{F}(\mathbf{x}(t)) \cdot \mathbf{x}^{\prime}(t) d t\)

The field F is given in the task, so plugging everything into the formula we get:

⇒ \(\int_{-1}^1\left(\left(t^3-t^2\right) \cdot 2 t+\left(t^2\right)^4\left(t^3\right)^3 \cdot 3 t^2\right) d t=\int_{-1}^1 2 t^4-2 t^3+3 t^{19} d t\)

= \(\frac{4}{5}\)

Calculating the function we get ∫⁻¹ ((t³−t²)⋅2t+(t²)4(t³)3⋅3t²)dt=4/5.

Page 426 Problem 13 Answer

Given: The function is F=xi+xyj+xyzk,

x(t)=(3cost,2sint,5t),0≤t≤2π

To Find: Calculate the function. Evaluate the question to get the answer.

Recall the way we calculate the path integral of the given vector field.

For the sake of easier notation, if we are given the field

F=a(x,y,z)i+b(x,y,z)j+c(x,y,z)k

where a,b,c are some scalar functions, we will write it down as F=(a(x,y,z),b(x,y,z),c(x,y,z)).

The field we are given is:F(x,y,z)=(x,xy,xyz).

The path we are integrating over is: x(t)=(3cost,2sint,5t),t∈[0,2π]

Its derivative is: x′(t)=(−3sint,2cost,5)

Finally we use the formula for evaluating the path integral of the second kind:

⇒ \(\int_x \mathbf{F} \cdot d s=\int_a^b \mathbf{F}(\mathbf{x}(t)) \cdot \mathbf{x}^{\prime}(t) d t\)

⇒ \(\int_0^2-9 \cos t \sin t+12 \cos t \sin t \cos t+150 t \cos t \sin t d t\)

You can split this integral into 3 integrals, every integral containing a term of the original integral.

In the second term recognize that (-2 cos³ t)’ = 6 sin t cos² t. and for the first and third one use the double angle formula.

Calculating the function we get∫⁰2π−9

sin²t+12cos²tsint+75tsin2tdt=−75π.

Page 426 Problem 14 Answer

Given : The function is F=−3yi+xj+3z²k,

​x(t)=(2t+1,t²+t,et),​0≤t≤1

To Find : Calculate the function.

Evaluate the question to get the answer.

Recall the way we calculate the path integral of the given vector field.

For the sake of easier notation, if we are given the field

F=a(x,y,z)i+b(x,y,z)j+c(x,y,z)k

where a,b,c are some scalar functions, we will write it down as F=(a(x,y,z),b(x,y,z),c(x,y,z)).

The field we are given is F(x,y,z)=(−3y,x,3z²)

Its derivative is:

x'(t) = (2, 2t + 1, e^t)

Finally we use the formula for evaluating the path integral of the second kind:

⇒ \(\int_{\mathbf{x}} \mathbf{F} \cdot d s=\int_a^b \mathbf{F}(\mathbf{x}(t)) \cdot \mathbf{x}^{\prime}(t) d t\)

The field F is given in the task, so plugging everying into the formula we get:

⇒ \(\int_0^1\left(-3\left(t^2+t\right), 2 t+1,3 e^{2 t}\right) \cdot\left(2,2 t+1, e^t\right) d t=\int_0^1-2 t^2-2 t+1+3 e^{3 t} d t\)

= \(\frac{3 e^3-5}{3}\)

Calculating the function we get \(\)

The path we are integrating over is; x(t)=(2t+1,t²+t,et),t∈[0,1]

Page 426 Problem 15 Answer

Given : The function isF=xi+yj−zk,

x(t)=(t,3t²,2t³),−1≤t≤1

To Find: Calculate the function.

Evaluate the question to get the answer.

Recall the way we calculate the path integral of the given vector field.

For the sake of easier notation, if we are given the field

F=a(x,y,z)i+b(x,y,z)j+c(x,y,z)k

wherea,b,c are some scalar functions, we will write it down as F=(a(x,y,z),b(x,y,z),c(x,y,z)).

The field we are given in the task is F(x,y,z)=(x,y,−z).

Its derivate is:

x'(t) = (1,6t, 6t2)

Finally we use the formula for evaluating the path integral of the second kind:

⇒ \(\int_{\mathbf{x}} \mathbf{F} \cdot d s=\int_a^b \mathbf{F}(\mathbf{x}(t)) \cdot \mathbf{x}^{\prime}(t) d t\)

The field F is given in the task, so plugging everything into the formula we get:

⇒ \(\int_{-1}^1\left(t, 3 t^2,-2 t^3\right) \cdot\left(1,6 t, 6 t^2\right)=\int_{-1}^1 t+18 t^3-12 t^5 d t\)

= 0.

The path we are integrating over is: x(t)=(t,3t²,2t³),t∈[−1,1]

Calculating he function we get ,∫xF⋅ds=0.

Page 426 Problem 16 Answer

Given: The function isF=3zi+y²j+6zk,

x(t)=(cost,sint,t/3),0≤t≤4π

To Find: Calculate the function.

Evaluate the question to get the answe .

Recall the way we calculate the path integral of the given vector field.

For the sake of easier notation, if we are given the field

F=a(x,y,z)i+b(x,y,z)j+c(x,y,z)k

where a,b,c are some scalar functions, we will write it down as F=(a(x,y,z),b(x,y,z),c(x,y,z)).

The field we are integrating is: F(x,y,z)=(3z,y²,6z)

The path we are integrating over is:

x(t) = (3 cos t, 2 sin t, 5t), t ∈ [0,2π]

Its derivate is:

x'(t) = (-3 sin t, 2 cos t, 5)

Finally we use the formula for evaluating the path integral of the second kind:

⇒ \(\int_{\mathbf{x}} \mathbf{F} \cdot d s=\int_a^b \mathbf{F}(\mathbf{x}(t)) \cdot \mathbf{x}^{\prime}(t) d t\)

The field F is given in the task, so plugging everying into the formula we get:

⇒ \(\int_0^{4 \pi}\left(t, \sin ^2 t, 2 t\right) \cdot\left(-\sin t, \cos t, \frac{1}{3}\right)=\int_0^{4 \pi}-t \sin t+\sin ^2 t \cos t+\frac{2 t}{3} d t\)

Recognize the second term as the derivative of \(\frac{\sin ^3 t}{3}\)

The rest of the terms are easily integrated via table.

After the calculations the resulting number should be:

∴ \(\frac{12 \pi+16 \pi^2}{3}\)

Calculating the function we get, 12π+16π²3.

Page 426 Problem 17 Answer

Given : The function isF=ycoszi+xsinzj+xysinz²k,x(t)

=(t,t²,t³),0≤t≤1

To Find: Calculate the function.

Evaluate the question to get the answer.

Recall the way we calculate the path integral of the given vector field.

For the sake of easier notation, if we are given the field

F=a(x,y,z)i+b(x,y,z)j+c(x,y,z)k

where a,b,c  are some scalar functions, we will write it down as F=(a(x,y,z),b(x,y,z),c(x,y,z)).

The field we are integrating is: F(x,y,z)=(ycosz,xsinz,xysinz²)

The path we are integrating over is: x(t)=(t,t²,t³),t∈[0,1]

Finally we use the formula for evaluating the path integral of the second kind:

⇒ \(\int_{\mathbf{x}} \mathbf{F} \cdot d s=\int_a^b \mathbf{F}(\mathbf{x}(t)) \cdot \mathbf{x}^{\prime}(t) d t\)

The field F is given in the task, so plugging into the formula we get

⇒ \(\int_0^1 t^2 \cos \left(t^3\right)+2 t^2 \sin \left(t^3\right)+3 t^5 \sin \left(t^6\right) d t=\left.\left(\frac{\sin \left(t^3\right)}{3}-2 \frac{\cos \left(t^3\right)}{3}-\frac{\cos \left(t^6\right)}{2}\right)\right|_0 ^1\)

The final result should be:

∴ \(\frac{7-7 \cos 1+2 \sin 1}{6}\)

Calculating the function we get \(\int_{\boldsymbol{x}} \mathbf{F} \cdot d s=\frac{7-7 \cos 1+2 \sin 1}{6}\)

Its derivative is: x′(t)=(1,2t,3t²).

Vector Calculus 4th Edition Chapter 5 Multiple Integration

Page 313 Problem 1 Answer

Given: The expression is

∫⁰  ∫¹   y sin x dy dx.
^Π  2

 To find: The iterated integrals of the given expression.Apply the properties of integrals∫sinx=−cosx.

Let us consider the given expression:

⇒ \(\int_0^\pi \int_1^2 y \sin x d y d x\)

Integrate with respect to y,

⇒ \(\int_0^\pi\left[\frac{y^2}{2} \sin x\right]_1^2 d x\)

Evaluate, apply The Fundamental theorem of Calculus,

⇒ \(\int_0^\pi\left[\frac{(2)^2}{2} \sin x-\frac{(1)^2}{2} \sin x\right] d x\)

= \(\int_0^\pi\left(\frac{3}{2} \sin x\right) dx\)

= \(\frac{3}{2}\int_0^\pi sin x dx\)

Integrate and evaluate.

⇒ \(\frac{3}{2} \int_0^\pi \sin x d x=-\frac{3}{2}[\cos x]_0^\pi\)

= \(-\frac{3}{2}\left[\cos x\right]_0^\pi=-\frac{3}{2}[\cos \pi-\cos 0]\)

= \(-\frac{3}{2}[\cos x]_0^\pi=-\frac{3}{2}[-1-1]\)

= \(-\frac{3}{2}[\cos x]_0^\pi=3\)

Evaluate to obtain the final answer.

​The answer of given expression after evaluating is 3.

Page 313 Problem 2 Answer

Given: The expression is

∫⁻²∫⁰     x^ey/dydx.
 ^4     1

To find: The iterated integrals of the given expression.

Apply the properties of integrals∫ex/dx=ex.

Evaluate to obtain the final answer.

Let us consider the given expression;

⇒ \(\int_{-2}^4 \int_0^1 x e^y d y d x\)

Integrate with respect to y,

= \(\int_{-2}^4\left[x e^y\right]_0^1 d x\)

= \(\int_{-2}^4 x\left[e^y\right]_0^1 d x\)

Evaluate.

=\(\int_{-2}^4 x\left[e-e^0\right] d x\)

= \(\int_{-2}^4 x(e-1) d x\)

= \(\int_{-2}^{4^2}(e-1) x d x\)

Integrate and evaluate.

⇒ \(\int_{-2}^4(e-1) x d x=(e-1)\left[\frac{x^2}{2}\right]_{-2}^4\)

= \((e-1)\left[\frac{x^2}{2}\right]_{-2}^4=(e-1)\left[\frac{(4)^2}{2}-\frac{(-2)^2}{2}\right]\)

= \((e-1)\left[\frac{x^2}{2}\right]_{-2}^4=(e-1)(6)\)

= \((e-1)\left[\frac{x^2}{2}\right]_{-2}^4=6 e-6\)

The required result is 6e-6.

Read and Learn More Susan Colley Vector Calculus Solutions

Page 313 Problem 3 Answer

Given: The expression is

∫¹∫⁰(ex+y+x²+lny) dx.
^2     1

To find: The iterated integrals of the given expression. Apply the properties of integrals∫ex/dx=ex.

Evaluate to obtain the final answer.

Let us consider the given expression;

⇒ \(\int_1^2 \int_0^1\left(e^{z+y}+x^2+\ln y\right) d x d y\)

Integrate with respect to x,

⇒ \(\int_1^2\left[e^{x+y}+\frac{x^3}{3}+x \ln y\right]_0^1 d y\)

Estimate,

= \(\int_1^2\left[\left(e^{1+y}+\frac{(1)^3}{3}+(1) \ln y\right)-\left(e^{0+y}+\frac{(0)^3}{3}+(0) \ln y\right)\right] d y\)

= \(\int_1^2\left(e^{1+y}+\frac{1}{3}+\ln y-e^y\right) d y\)

Integrate and evaluate,

= \(\left[e^{1+y}+\frac{1}{3} y+y \ln y-y-e^y\right]^{2}\)

= \(\left[e^{1+y}-\frac{1}{3} y+y \ln y-e^y\right]^\frac{1}{2}\)

= \(\left[e^{1+2}-\frac{1}{3}(2)+2 \ln (2)-e^2\right]-\left[e^{1+1}-\frac{1}{3}(1)+2 \ln (1)-e^1\right]^1\)

= \(e^3-\frac{2}{3}+2 \ln (2)-e^2-e^2+\frac{1}{3}+e\)

= \(e^3-2 e^2+e+2 \ln 2-\frac{1}{3}\)

The required result is e3−2e2+e+2ln2−1/3.

Page 313 Problem 4 Answer

Given: The expression is

∫¹ ∫¹ln√​x/xydxdy.
^9   e​

To find: The iterated integrals of the given expression.

Apply the properties of integrals ∫2lnx/xdx=(lnx)2.

Evaluate to obtain the final answer.

Let us consider the given expression;

∴ \(\int_1^9 \int_1^e \frac{\ln \sqrt{x}}{x y} d x d y=\int_1^9\left(\int_1^e \frac{\ln x^2}{x y} d x\right) d y\)

= \(\int_1^9\left(\int_1^e \frac{\ln x}{2 x y} d x\right) d y\)

= \(\int_1^9\left(\left.\frac{(\ln x)^2}{4 y}\right|_1 ^e\right) d y\)

= \(\int_1^9\left(\frac{(\ln e)^2}{4 y}-\frac{(\ln 1)^2}{4 y}\right) d y\)

= \(\int_1^9\left(\frac{1^2}{4 y}-\frac{0^2}{4 y}\right) d y\)

Integrate and evaluate.

= \(\int_1^9 \frac{1}{4 y} d y\)

= \(\left.\frac{\ln y}{4}\right|_1 ^9\)

= \(\frac{\ln 9}{4}-\frac{\ln 1}{4}\)

= \(\frac{\ln 9}{4}-\frac{0}{4}\)

= \(\frac{1}{4} \ln 9\)

= In \(9^\frac{1}{4}\)

= In √3.

The required result is ln√3.

Page 313 Problem 5 Answer

Given: The paraboloid z=x²+y²+2 and over the rectangle R={(x,y)∣−1≤x≤2,0≤y≤2}.

To find: The volume of the given region.

Apply Cavalieri’s principle.Evaluate to obtain the final answer.

Let us consider the given expression;

V = \(\int_a^b A(x) d x\)

A (x) = \(\int^d f(x, y) d y\)

V = \(\int_{a}^{b} \int_c^d f(x, y) d y d x\)

V = \(\int_{-1}^2 \int_0^2 x^2+y^2+2 d y d x\)

V = \(\int_{-1}^2 x^2 y+\frac{y^3}{3}+\left.2 y\right|_0 ^2 d x\)

V = \(\frac{x^3}{3}+\left.\frac{20}{3} x\right|_{-1} ^2\)

= \(\frac{2}{3} \cdot 2^3+\frac{20}{3} \cdot 2+\frac{2}{3} \cdot 1+\frac{20}{3} \cdot 1\)

= 26

The volume of the given region is 26.

Page 313 Problem 6 Answer

Given: The paraboloid z=x²+y²+2 and over the rectangle R={(x,y)∣−1≤x≤2,0≤y≤2}.

To find: The volume of the given region.Apply Cavalieri’s principle.Evaluate to obtain the final answer.

Let us consider the given expression;

V = \(\int_a^b A(y) d y\)

A (y) = \(\int_c^d f(x, y) d x\)

V = \(\int_c^d \int_a^b f(x, y) d x d y\)

V = \(\int_0^2 \int_{-1}^2 x^2+y^2+2 d x d y\)

V = \(\int_0^2 \frac{x^3}{3}+y^2 x+\left.2 x\right|_{-1} ^2 d y\)

V = \(9 y+\left.y^3\right|_0 ^2\)

= 26.

The volume of the given region is 26.

Page 313 Problem 7 Answer

Given: The plane is z=x+3y+1.

To find: The volume of the given region.

Apply the formula of volume V=∫^a∫^cf(x,y) dxdy.
                                                              ^B  d

Evaluate to obtain the final answer.

Let us consider the given expression

V = \(\int_a^b \int_c^d f(x, y) d x d y\)

V = \(\int_1^2 \int_0^3 x+3 y+1 d x d y\)

V = \(\int_1^2 \frac{x^2}{2}+3 y x+\left.x\right|_0 ^3 d y\)

Integrate and evaluate.

V = \(\int_1^2 \frac{9}{2}+9 y+3 d y\)

V = \(\int_1^2 \frac{15}{2}+9 y d y\)

V = \(\frac{15}{2} y+\left.\frac{9 y^2}{2}\right|_1 ^2\)

= \(\frac{15}{2} \cdot 2+\frac{9}{2} \cdot 2^2-\frac{15}{2} \cdot 1-\frac{9}{2} \cdot 1^2\)

= 21

The volume of the given region is 21.

Page 313 Problem 8 Answer

Given: The function is f(x,y)=2x²+y⁴sinπx.

To find: The volume of the given region.

Apply the formula of volume V=∫^a∫^c f(x,y) dxdy.
                                                              ^B  d

Evaluate to obtain the final answer.

Let us consider the given expression;

f(x,y) = 2x² + y⁴ sin πx,

V = \(\int_a^b \int_c^d f(x, y) d x d y\)

V = \(\int_{-1}^2 \int_0^1 2 x^2+y^4 \sin \pi x d x d y\)

V = \(\int_{-1}^2 \frac{2}{3} x^3-\left.\frac{1}{\pi} y^4 \cos \pi x\right|_0 ^1 d y\)

Integrate and evaluate.

V = \(\int_{-1}^2 \frac{2}{3}(1)^3-\frac{1}{\pi} y^4 \cos \pi(1)-\frac{1}{\pi} y^4 \cos (1) \pi d y\)

V = \(\int_{-1}^2 \frac{2}{3}-\frac{2}{\pi} y^4 d y\)

V = \(\frac{2}{3} y-\left.\frac{2}{5 \pi} y^5\right|_{-1} ^2\)

= \(\frac{2}{3} \cdot 2+\frac{3}{5 \pi} \cdot 2^5+\frac{2}{3} \cdot 1+\frac{2}{5 \pi} \cdot 2^5\)

≈ 6.2.​

The volume of the given region is 6.2.

Page 314 Problem 9 Answer

Given: The expression is

∫⁰∫¹2dxdy.
^2    3

To find: The volume of the given region.

Evaluate to get the final answer.

This is the area of the region whose points are determined by (x,y,z) ∈ [1,3] x [0,2] x [0,2]

⇒ \(\int_0^2 \int_1^3 2 d x d y=2 \int_0^2(3-1) d y\)

= 4(2-0)

= 8.

The volume of the given region is 8.

Page 314 Problem 10 Answer

Given: The expression is

∫¹∫⁻²(16−x²−y²) dydx.
^3    2

To find: The volume of the given region.

Evaluate to obtain the final answer.

Let us consider the given expression;

⇒ \(\int_1^3 \int_{-2}^2\left(16-x^2-y^2\right) d y d x\)

This is the volume of the region whose bounded by 1 ≤ x ≤ 3 and -2 ≤ y ≤ 2.

⇒ \(\int_1^3 \int_{-2}^2\left(16-x^2-y^2\right) d y d x=\int_1^3\left[\left(16-x^2\right) y-\frac{y^3}{3}\right]_{y=-2}^{y=2} d x\)

= \(\int_1^3 4\left(16-x^2\right)-\frac{16}{3} d x\)

= \(\left[64 x-\frac{4 x^3}{3}-\frac{16}{3} x\right]_1^3\)

= \(\frac{248}{3}\).

The volume of the given region is 248/3.

Page 314 Problem 11 Answer

Given: The expression is ∫y=−π/2

y=π/2

∫x=0

x=π

sin(x)cos(y)dxdy.

To find: The volume of the given region.

Evaluate to obtain the final answer.

Let us consider the given expression;

⇒ \(\int_{y=-\pi / 2}^{y=\pi / 2} \int_{z=0}^{x=\pi} \sin (x) \cos (y) d x d y .\)

This is the volume of the region whose bounded by z = sin (x) cos (y), 0 ≤ x ≤ π, and -π/2 ≤ y ≤ π/2.

⇒ \(\int_{y=-\pi / 2}^{y=\pi / 2} \int_{x=0}^{x=\pi} \sin (x) \cos (y) d x d y=\int_{y=-\pi / 2}^{y=\pi / 2} \cos (y)\left[\int_{x=0}^{x=\pi} \sin (x) d x\right] d y\)

= \(2 \int_{y=-\pi / 2}^{y=\pi / 2} \cos (y) d y\)

= 4.

The volume of the given region is V=4.

Page 314 Problem 12 Answer

Given: The expression is∫y=0

y=5

∫x=−2

x=2

(4−x²) dxdy.

To find: The volume of the given region.

Evaluate to obtain the final answer.

Let us consider the given expression;

⇒ \(\int_{y=0}^{y=5} \int_{x=-2}^{x=2}\left(4-x^2\right) d x d y,\)

This is the volume of the region whose bounded by z = 4-x², -2 ≤ x ≤ 2,0 ≤ y ≤ 5.

⇒ \(\int_{y=0}^{y=5} \int_{x=-2}^{x=2}\left(4-x^2\right) d x d y=\int_{y=0}^{y=5}\left[\int_{x=-2}^{x-2}\left(4-x^2\right) d x\right] d y\)

= \(\frac{32}{3} \int_{y=0}^{y=5} d y\)

= \(\frac{160}{3}\)

The volume of the given region is 160/3.

Page 314 Problem 13 Answer

Given: The expression is∫x=−2 x=3

∫y=0y=1∣x∣sin(πy)dydx.

To find: The volume of the given region.

Evaluate to obtain the final answer.

Let us consider the given expression;

⇒ \(\int_{x=-2}^{x=3} \int_{y=0}^{y=1}|x| \sin (\pi y) d y d x\)

This is the volume of the region whose bounded by \(z=|x| \sin (\pi y),-2 \leq x \leq 3,0 \leq y \leq 1\)

⇒ \(\int_{x=-2}^{x-3} \int_{y=0}^{y=1}|x| \sin (\pi y) d y d x=\int_{x=-2}^{x=3}|x|\left[\int_{y=0}^{y=1} \sin (\pi y) d y\right] d x\)

= \(\frac{2}{\pi} \int_{x=-2}^{x-3}|x| d x\)

= \(\frac{13}{\pi}\)

The volume of the given region is 13/π.

Page 314 Problem 14 Answer

Given: The expression is ∫y=−5 y=5

∫x=−1x=2 (5−∣y∣) dxdy.

To find: The volume of the given region.

Evaluate to obtain the final answer.

Let us consider the given expression;

⇒ \(\int_{y=-5}^{y=5} \int_{x=-1}^{x=2}(5-|y|) d x d y\)

This is the volume of the region whose bounded by \(z=5-|y|,-1 \leq x \leq 2,-5 \leq y \leq 5\)

⇒ \(\int_{y=-5}^{y=5} \int_{x=-1}^{z=2}(5-|y|) d x d y=\int_{y=-5}^{y=5}(5-|y|)\left[\int_{x=-1}^{z-2} d x\right] d y\)

= \(3 \int_{y=-5}^{y=5}(5-|y|) d y\)

= 75.

The volume of the given region is 75.

Page 314 Problem 15 Answer

Given: The f(x,y) is a non negative-valued, continuous function defined on R={(x,y)∣a≤x≤b,c≤y≤d}.

To find: The Volume under the given region.

Apply the formula of volumeV=∬R f(x,y)dxdy.

Evaluate to obtain the final answer.

The volume under the surface is given by;

V = \(\iint_R f(x, y) d x d y\)

Yet f(x,y) ⩾ M,

Where M is some constant,

V = \(\int_a^b \int_c^d f(x, y) d y d x\)

= \(\int_a^b \int_c^d M d y d x\)

Integrate and evaluate.

= \(\left.M \int_a^b y\right|_c ^d d x\)

= \(\int_a^b(d-c) d x\)

= \(\left.M(d-c) x\right|_a ^b\)

= M (d-c)(b-a)

= \(V ⩾ M(d-c)(b-a)\)

The volume under the given region is V⩾M(d−c)(b−a).

Vector Calculus 4th Edition Chapter 4 Maxima and Minima in Several Variables

Page 262 Problem 1 Answer

Given f(x) = e^2x

To find the Taylor polynomials.Using the method of polynomial.

To find the Taylor polynomials.

Recall that the Taylor polynomial of the function f at the given point a of the kth order is calculated with:

Tk(x) = f(a)+f′(a)(x−y)+f′′(a)/2!(x−a)²+…+f(k)(a)/k!(x−a)k

So in this task we have f(x) = e^2x,k=4 and  a=0.

From there we calculate:

​f(a) = f(0) ⇒ 1

f′(0) = 2

f′′(0) = 4

f′′′(0) = 8

f(iv) = 16

Finally the polynomial is given with:

T4(x) = 1+2x+2x²+4/3x³+2/3x⁴

The Taylor polynomials is T4 (x) = 1+2x+2x²+4/3x³+2/3x⁴

Page 262 Problem 2 Answer

Given f(x)= ln(1+x)

To find the Taylor polynomials.Using the method of polynomial.

To find the Taylor polynomials.

Recall that the Taylor polynomial of the function f at the given point a of the k th order is calculated with:

Tk(x) = f(a)+f′(a)(x−y)+f′′(a)/2!(x−a)²+…+f(k)(a)/k!(x−a)k

Read and Learn More Susan Colley Vector Calculus Solutions

So in this task we have f(x)=ln(1+x), k=3 and a=0.

From there we calculate:

f(a) = f(0) = 0​

f′(x) = 1/1+x

f′(0) = 1

f′′(x) = −1/(1+x)²

f′′(0) = −1

f′′′(x) = 2/(1+x)³

f′′′(0) = 2

Finally the polynomial is given with:

T3(x) = x−x²/2+x³/3

The Taylor polynomials is T3 (x) = x−x²/2+x³/3

Page 262 Problem 3 Answer

Given f(x) = 1/x²

To find the Taylor polynomials.Using the method of polynomial.

To find the Taylor polynomials.

Recall that the Taylor polynomial of the function f at the given point a of the kth order is calculated with:

Tk(x) = f(a)+f′(a)(x−y)+f′′(a)/2!(x−a)²+…+f(k)(a)/k!(x−a)k

So in this task, we have f(x) = 1/x², k = 4 and a=1.

From there we calculate:

f(a) = f(1) = 1

​f′(x) = −2/x³

f′(1) = −2

f′′(x) = 6/x⁴

f′′(1) = 6

f′′′(x) = −24/x⁵

f′′′(1) = −24

f(iv)(x) = 120/x⁶

f{(iv)}(1) = 120

Finally the polynomial is given with:

T4(x) = 1 − 2(x−1) + 3(x−1)² − 4(x−1)³ + 5(x−1)4

The Taylor polynomials is T4 (x) = 1 − 2(x−1) + 3(x−1)² − 4 (x−1)³ + 5(x−1)⁴

Page 262 Problem 4 Answer

Given f(x)=√x

To find the Taylor polynomials.Using the method of polynomial.

To find the Taylor polynomials.

Recall that the Taylor polynomial of the function f at the given point a of the k th order is calculated with:

Tk (x)=f(a)+f′(a)(x−y)+f′′(a)/2!(x−a)²+…+f(k)(a)/k!(x−a)k

So in this task we have f(x)=√x, k=3 and a=1.

From there we calculate:

f(a) = 1

f′(x) = 1/2√x

f′(1) =1 /2

f′′(x) = −1/4×3/2

f′′(1) = −1/4

f′′′(x) = 3/8×5/2

f′′′(1) = 3/8

Finally the polynomial is given with:

T3(x) = 1 + 1/2(x−1 )−1/8 (x−1)² + 1/16(x−1)³

The Taylor polynomials is T3

(x) = 1+ 1/2(x−1) − 1/8(x−1)² + 1/16(x−1)³

Page 262 Problem 5 Answer

Given f(x)=√x

To find the Taylor polynomials.Using the method of polynomial.

To find the Taylor polynomials.

Recall that the Taylor polynomial of the function f at the given point a of the kth order is calculated with:

Tk(x) = f(a)+f′(a)(x−y)+f′′(a)/2!(x−a)²+…+f(k)(a)/k!(x−a)k

So in this task we have f(x)=√x, k=3 and a=9.

From there we calculate:

f(a)=f(9)=3​

f′(x)=1/2√x

f′(1)=1/6

f′′(x)=−1/4x​3/2

f′′(1)=−1/108

f′′′(x)=3/8x​5/2

f′′′(1)=1/648

Finally the polynomial is given with:

T3 (x)=3+1/6(x−9)−1/216(x−9)²+1/3888(x−9)³

The Taylor polynomials is T3 (x)=3+1/6(x−9)−1/216(x−9)²+1/3888(x−9)³

Page 262 Problem 6 Answer

Given f(x)=sinx

To find the Taylor polynomials.Using the method of polynomial.

To find the Taylor polynomials.

Recall that the Taylor polynomial of the function f at the given point a  of the kth  order is calculated with:

Tk(x)=f(a)+f′(a)(x−y)+f′′(a)/2!(x−a)²+…+f(k)(a)/k!(x−a)k

So in this task we have f(x)=sin(x),k=5 and a=0.

From there we calculate:

f(a)=f(0)=0​

f′(x)=cos(x)

f′(0)=1

f′′(x)=−sin(x)

f′′(0)=0

f′′′(x)=−cos(x)

f′′′(0)=−1

Forf(iv) (x)=sin(x)

f{(iv)} (0)=0

f(5) (x)=cos(x)

f{(5)}(0)=1

Finally the polynomial is given with:

T5(x)=x−x³/6+x⁵/120

The Taylor polynomials  is T5 (x)=x−x³/6+x⁵/120

Page 262 Problem 7 Answer

Given: f(x)=sinx

To find the Taylor polynomials pk of given order k at the indicated point a.

Using the method of maxima function method.

Critical points of a function of couple variables denote the points at which both partial derivatives of the function remain zero.

To find the Taylor polynomials pk of given order k at the indicated point a,

Tk (x)=f(a)+f′(a)(x−a)+f′′ (a)/2!(x−a)²+…+f(k)(a)/k!(x−a)k

f′(x)⇒cos(x)⇒f′(π²)=0

f′′(x)⇒−sin(x)⇒f′′(π²)=−1

f′′′(x)⇒−cos(x)⇒f′′′(π²)=0

f4(x)⇒sin(x)⇒f4(π²)=1

f(5)(x)⇒cos(x)⇒f(5)(π²)=0

T5(x)=1−(x−π²)²/2+(x−π²)⁴/24

The Taylor polynomial is T5

(x)=1−(x−π/2)²/2+(x−π/2)⁴/24.

Page 262 Problem 8 Answer

Given: f(x,y)=1/(x²+y²+1)

To find the first- and second-order Taylor polynomials.

Using the method of maxima function method.

Critical points of a function of couple variables denote the points at which both partial derivatives of the function remain zero.

To find the first- and second-order Taylor polynomials,

f(0,0)=1

∂f/∂x⇒−2x(x²+y²+1)²

⇒∂f/∂x(0,0)=0

∂f/∂y⇒−2y

(x²+y²+1)²⇒∂f/∂y(0,0)=0

∂²f/∂x²⇒6x²−2y²−2/(x²+y²+1)³⇒∂²f/∂x²

(0,0)=−2/∂²f/∂x∂y⇒8xy

(x²+y²+1)³⇒∂²f/∂x∂y(0,0)=0

T1(x)=1

T2(x)=1−x²−y²

The polynomial is given as T2(x)=1−x²−y².

Page 262 Problem 9 Answer

Given: f(x,y)=1/(x²+y²+1)

To find the first- and second-order Taylor polynomials.

Using the method of maxima function method.The first-order Taylor Polynomial at a point (a,b)

is given by L(x)=f(a,b)+fx(a,b)⋅(x−a)+fy(a,b)⋅(y−b)

where fx,fy are the partial derivatives with respect to x and y, respectively.

The second-order Taylor Polynomial, given that the first-order polynomial has been calculated, is given by Q(x)=L(x)+fxx(a,b)²(x−a)²+fxy(a,b)²(x−a)(y−b)+fyy(a,b)²(y−b)²

Critical points of a function of couple variables denote the points at which both partial derivatives of the function remain zero.

To find the first- and second-order Taylor polynomials,

f(1,−1)=1/3

∂f/∂x⇒−2x(x²+y²+1)²

⇒∂f/∂x(1,−1)=−2/9

∂f/∂y⇒−2y(x²+y²+1)²

 ⇒∂f/∂y(1,−1)=2/9

∂²f/∂y²⇒6y²−2x²−2(x²+y²+1)³

⇒∂²f∂y²(1,−1)=2/27

∂²f/∂x²⇒6x²−2y²−2/(x²+y²+1)³

⇒∂²f/∂x²(1,−1)=2/27

∂²f/∂x∂y⇒8xy(x²+y²+1)³

⇒∂²f/∂x∂y(1,−1)=−8/27

T1(x)=1/3−2(x−1)/9+2(y+1)/9

T2(x)=1/3−2(x−1)/9+2(y+1)/9+(x−1)²/27−8(x−1)(y+1)/27+(y+1)²/27

The polynomials are given as T1 (x)=1/3−2(x−1)/9+2(y+1) 9

and  T2(x)=1/3−2(x−1)/9+2(y+1)/9+(x−1)^2/27−8(x−1)(y+1)/27+(y+1)²/27.

Page 262 Problem 10 Answer

Given: f(x,y)=e2x+y

To find the first- and second-order Taylor polynomials.

Using the method of maxima function method.

Critical points of a function of couple variables denote the points at which both partial derivatives of the function remain zero.

To find the first- and second-order Taylor polynomials,

f(0,0)=1

∂f/∂x⇒2^e2x+y⇒∂f/∂x(0,0)=2

∂f/∂y⇒e^2x+y⇒∂f/∂y(0,0)=1

∂²f/∂x²⇒4e2x+y⇒∂²f/∂x²(0,0)=4

∂²f/∂x∂y⇒2e2x+y ⇒∂²f/∂x∂y(0,0)=2

T1(x)=1+2x+y

T2(x)=1+2x+y+2x²+2xy+y²/2

The polynomial is given as T2(x)=1+2x+y+2x²+2xy+y²/2.

Page 262 Problem 11 Answer

Given: f(x,y)=e2xcos3y

To find the first- and second-order Taylor polynomials.

Using the method of maxima function method.

Critical points of a function of couple variables denote the points at which both partial derivatives of the function remain zero.

To find the first- and second-order Taylor polynomials,

f(0,π)=−1

∂f/∂x⇒2e2xcos3y

⇒∂f/∂x(0,π)=−2

∂f/∂y⇒−3e2x sin3y⇒∂f/∂y(0,π)=0

∂²f/∂y²⇒−9e2x cos3y⇒∂²f/∂y²(0,π)=9

∂²f/∂x∂y⇒−6e2xsin3y⇒∂²f/∂x∂y(0,π)=0

T1(x)=−1−2x

T2(x)=−1−2x−2x²+9/2(y−π)²

The polynomial is given as T2(x)=−1−2x−2x²+9/2(y−π)².

Page 262 Problem 12 Answer

Given: f(x,y,z)=ye3x+ze2y

To find the first- and second-order Taylor polynomials.

Using the method of maxima function method.

Critical points of a function of couple variables denote the points at which both partial derivatives of the function remain zero.

To find the first- and second-order Taylor polynomials,

f(0,0,2)=2

∂f/∂x⇒3ye3x ⇒∂f/∂x(0,0,2)=0

∂f/∂z⇒e2y ⇒∂f/∂z(0,0,2)=1

∂²f/∂x∂y⇒3e3x ⇒∂²f/∂x∂y(0,0,6i)=3

Simplify,

∂²f/∂y∂z⇒2e2y⇒∂²f/∂y∂z(0,0,6)=2

∂²f/∂x∂z⇒0⇒∂²f/∂x∂z(0,0,6)=0

T1(x)=5y+z

T2 (x)=y+z+3xy+4y²+2yz

The polynomial is T2(x)=y+z+3xy+4y²+2yz.

Page 262 Problem 13 Answer

Given: f(x,y,z)=xy−3y²+2xz,a=(2,−1,1)

To find the first- and second-order Taylor polynomials.

Using the method of maxima function method.

Critical points of a function of couple variables denote the points at which both partial derivatives of the function remain zero.

To find the first- and second-order Taylor polynomials,

f(2,−1,1)=−1

∂f/∂x⇒y+2z⇒∂f/∂x(2,−1,1)=1

∂f/∂z⇒2x⇒∂f/∂z(2,−1,1)=4

T1(x)=1+x+8y+4z

T2=f

The polynomial is T2=f

Page 262 Problem 14 Answer

Given: f(x,y,z)=1/(x²+y²+z²+1)

To find the first- and second-order Taylor polynomials.

Using the method of maxima function method.

Critical points of a function of couple variables denote the points at which both partial derivatives of the function remain zero.

To find the first- and second-order Taylor polynomials,

f(0,0,0)=1

∂f/∂x⇒−2x

(x²+y²+z²+1)²

⇒∂f/∂x(0,0,0)=0

∂²f/∂x²⇒6x²−2y²−2z²−2(x²+y²+z²+1)³

⇒∂²f/∂x²(0,0,0)=−2

∂²f/∂z²⇒6z²−2x²−2y²−2(x²+y²+z²+1)³

⇒∂²f/∂z²(0,0,0)=−2

∂²f/∂x∂z⇒8xz(x²+y²+z²+1)³

⇒∂²f/∂x∂z(0,0,0)=0

T1(x)=1

T2(x)=1−x²−y²−z²

The polynomial is given as T1(x)=1

T2(x)=1−x²−y²−z².

Page 262 Problem 15 Answer

Given: f(x,y,z)=sinxyz,a=(0,0,0)

To find the first- and second-order Taylor polynomials.

Using the method of maxima function method.

Critical points of a function of couple variables denote the points at which both partial derivatives of the function remain zero.

To find the first- and second-order Taylor polynomials,

f(0,0,0)=0

∂f/∂x⇒yzcosxyz

⇒∂f/∂x(0,0,0)=0

∂²f/∂x²⇒−y²z²sinxyz

⇒∂²f/∂x²(0,0,0)=0

∂²f/∂x∂y⇒zcosxyz−xyz2/sinxyz

⇒∂²f/∂x∂y(0,0,0)=0

∂²f/∂x∂z=cosxyz−xy²/zsinxyz

⇒∂²f/∂x∂z(0,0,0)=0

T1(x)=0

T2(x)=0

The polynomial is given as T1(x)=0.

Vector Calculus 4th Edition Chapter 3 Vector-Valued Functions

Page 200 Problem 1 Answer

Given: {​x=tcost  y=tsint,−6π≤t≤6π }

To sketch the images of the following paths.

Using the method of graphing method.

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign.

To sketch the images of the following paths,

The path is parametrized to start at the left end and then follows that spiral-ish curve around to the rightmost end point.

The graph of the function,

Page 200 Problem 2 Answer

Given: {​x=3cost y=2sin2t}​0≤t≤2π

To sketch the images of the following paths.

Using the method of graphing method.

Read and Learn More Susan Colley Vector Calculus Solutions

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign.

To sketch the images of the following paths,

The path is parametrized to start at (3,0) and head upward from there – – coming back to its starting point after 1 lap.

The graph of the function,

Page 200 Problem 3 Answer

Given: x(t) = (t,3t²+1,0)

To sketch the images of the following paths.

Using the method of graphing method.

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign.

To sketch the images of the following paths,

This is a parabola in the xy-plane parametrizes to go in the direction of increasing x.

The graph of the function,

Page 200 Problem 4 Answer

Given: x(t) = (3t−5)i+(2t+7)j

To find the velocity, speed, and acceleration of the paths.

Using the method of speed method.

The speed of an article is the pace of progress of its situation regarding an edge of reference, and is a component of time.

To find the velocity, speed, and acceleration of the paths,

v(t) = x′(t) = 3i+2j

∥v(t)∥ = √32+22

=√13

a(t) ⇒ v′(t)=0

The velocity, speed, and acceleration of the paths is 0.

Page 200 Problem 5 Answer

Given: x(t) = 5costi+3sintj

To find the velocity, speed, and acceleration of the paths.

Using the method of speed method.

The speed of an article is the pace of progress of its situation regarding an edge of reference, and is a component of time.

To find the velocity, speed, and acceleration of the paths,

v(t) ⇒ x′(t) = −5sinti+3costj

∥v(t)∥ ⇒ √(5sint)² + (3cost)² = √25sin²t + 9cos²t

a(t) ⇒ v′(t)= −5costi−3sintj= −x(t)

The velocity, speed, and acceleration of the paths is −x(t).

Page 200 Problem 6 Answer

Given: x(t) = (tsint,tcost,t²)

To find the velocity, speed, and acceleration of the paths.

Using the method of speed method.

The speed of an article is the pace of progress of its situation regarding an edge of reference, and is a component of time.

To find the velocity, speed, and acceleration of the paths,

v(t) ⇒ x′(t) = (sint+tcost,cost−tsint,2t)

∥v(t)∥ ⇒ √(sint+tcost)² + (cost−tsint)² + (2t)²

= √5t²+1

a(t) = (cost+cost−tsint,−sint−sint−tcost,2)

= 2(cost,−sint,1)−t(sint,cost,0)

2(cost,−sint,1)−t(sint,cost,0) is the velocity, speed, and acceleration of the paths.

Page 200 Problem 7 Answer

Given: x(t)=(et,e2r,2et)

To find the velocity, speed, and acceleration of the paths.

Using the method of speed method.

The speed of an article is the pace of progress of its situation regarding an edge of reference, and is a component of time.

To find the velocity, speed, and acceleration of the paths,

v(t) = x′(t) ⇒ (et,2e2t,2et)

= x(t) + (0,e2t,0)

∥v(t)∥ ⇒ √(et)2+(2e²t)²+(2et)²=et

√5+4e²t

a(t) ⇒ v′(t)=x′(t)+(0,2e2t,0)

= x(t) + (0,3e2t,0)

x(t) + (0,3e2t,0) is the velocity, speed, and acceleration of the paths.

Page 200 Problem 8 Answer

Given: x(t) = (3cosπt,4sinπt,2t),−4≤t≤4

To find the direction in which t increases.

Using the method of speed method.

The speed of an article is the pace of progress of its situation regarding an edge of reference, and is a component of time.

To find the direction in which t increases,

The plotted point is,

The graph of the function,

Page 200 Problem 9 Answer

Given: x(t) = (3cosπt,4sinπt,2t),−4≤t≤4

To find the path lies on the given surface S.

Using the method of equation method.

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign.

To find the path lies on the given surface,

x(t)²

9 + y(t)²

16 =1,for x(t)=3cosπt, y(t)

= 4sinπt

The points lie on the surface4sinπt.

Page 200 Problem 10 Answer

Given: x(t) = (tcost,tsint,t),−20≤t≤20

To find the direction in which t increases.

Using the method of graphing method.

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign.

To find the direction in which t increases,

The graph of the function,

Page 200 Problem 11 Answer

Given: x(t) = (tcost,tsint,t),−20≤ t ≤20

To find the path lies on the given surface S.

Using the method of equation method.

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign.

To find the path lies on the given surface,

z² = x² + y²

⇒ t²cos²t + t²sin²t

The path lies on the given surface is t².

Page 200 Problem 12 Answer

Given: x(t)= (tsin2t,tcos2t,t²),−6≤t≤6

To find the graph of function.

Using the method of graphing method.

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign.

To find the graph of function,

The graph of the function,

Page 200 Problem 13 Answer

Given: x(t) = (tsin2t, tcos2t,t²), −6≤t≤6

To find the path lies on the given surface.

Using the method of equation method.

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign

To find the path lies on the given surface,

z = x²+y² ⇒ t²

= t²sin²2t + t²cos²2t

t²sin²2t + t²cos²2t is the path lies on the given surface.

Page 201 Problem 14 Answer

Given: x(t)=(2cost, 2sint, 3sin8t), 0≤t≤2π

To find the plotted points.

Using the method of graphing method.

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign.

To find the plotted points,

The graph of the function,

Page 200 Problem 15 Answer

Given: x(t) = (2cost, 2sint, 3sin8t), 0≤t≤2π

To find the path lies on the given surface S.

Using the method of equation method.

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign.

To find the path lies on the given surface,

To check if the curve lies on the given surface, we once again plug in the coordinate equations of the curve into the equation for the surface:

x² + y²= 4 ⇒ 4cos2t + 4sin2t = 4

The path lies on the given surface is 4.

Page 201 Problem 16 Answer

Given: x(t) = 4costi − 3sintj + 5tk, t=π/3

To find the equation for the line tangent to the given path at the indicated value for the parameter.

Using the method of equation method.

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign.

To find the equation for the line tangent to the given path at the indicated value for the parameter,

l(t) = x(π/3) + (t−π/3)x′(π/3)

l(t) = 2i−3√3/2j + 5π/3k + (t−π/3)(−2√3/i−3²j+5k)

l(t) = 2i−3√3/2j + 5π/3k + (t−π/3)(−2√3/i−3²j+5k)

is the equation for the line tangent to the given path at the indicated value for the parameter.

Page 201 Problem 17 Answer

Given: x(t) = (cos(et),3−t²,t)

To find the equation for the line tangent to the given path at the indicated value for the parameter.

Using the method of equation method.

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign.

To find the equation for the line tangent to the given path at the indicated value for the parameter,

l(t) = x(1) + (t−1) x ′(1)

= (cos(e), 3−1,1) + (t−1) (−sin(e) e,3−2,1)

= (cos(e)+sin(e)−tsin(e),1+t,t)

(cos(e)+sin(e)−tsin(e),1+ t,t) is the equation for the line tangent to the given path at the indicated value for the parameter.

Page 201 Problem 18 Answer

Given: x(t)=(t,t3−2t+1)

To find the sketch of the path.

Using the method of graphing method.

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign.

To find the sketch of the path,

The graph of the function,

Page 201 Problem 19 Answer

Given: t=2

To find the line tangent.

Using the method of vector method.

A vector field in the plane can be visualized as a gathering of indicators with a distributed importance each attached to a point in the plane.

To find the line tangent,

Xo ⇒ X(2)=2i^+[3⋅(2)3−2⋅(2)+1]j^

Xo = 2i^+5j^

⇒1

V ⇒ X′(t)=1i^+(6t−2)j^

Vo ⇒ X′(2)=1i^+(6⋅2−2)j^

I(t) = 2i^+5j^+(t−2)(1i^+10j^)

I(t) = ti^+10t−15j^

I(t) = ti^+10t−15j^ is the tangent line.

Page 201 Problem 20 Answer

Given: y=f(x)

To find the image of x by an equation of the form.

Using the method of equation method.

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign.

To find the image of x by an equation of the form,

Elimination of  text (converting vector valued function to scalar function)

text t=x, y=3t3−2t+1,

y = 3×3−2x+1

y = 3×3−2x+1 is the image form for value.

Page 201 Problem 21 Answer

Given: Tangent line.

To find the recalculating the tangent line, using your result in part (c).

Using the method of equation method.

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign.

To find the recalculating the tangent line, using your result in part (c),

Dy/dx=y−yo/x−xo

10=y−5/x−2​′′′′′

⇒ 10x−15 which is compatible with I(t) obtained.

y=10x−15 which is compatible.

Page 201 Problem 22 Answer

Given: Roger Ramjet.

To find the Roger Ramjet’s path in Example 6 is indeed a parabola.

Using the method of equation method.

A condition is an explanation that attests the uniformity of two articulations, which are associated by the equivalents sign.

To find the Roger Ramjet’s path in Example 6 is indeed a parabola,

x ⇒ tv0 cosθ ⇒ t=x

v0 cosθ y=−1/2gx²

v0²cos²θ+sinθ/cosθ

x=−1/2gx²

v0²cos²θ+xtanθ

The trajectory is indeed a parabola.

Vector Calculus 4th Edition Chapter 2 Differentiation in Several Variables

Page 95 Problem 1 Answer

Given : f: R→R be given by f(x)=2x²+1.

To find : The domain and range of function.Evaluate the function to get solution.

Consider given function,

f:R→R be given by f(x)=2x²+1 .

The domain and codomain of f are explicitly R.

Since 0≤x² for all x∈R we have that 0≤2x² for all x∈R.

Thus,1≤2x²+1=f(x) for all x∈R and therefore the range of f is {y∈R:y≥1}.

Hence, the domain of function f is R  and range of function is  {y∈R:y≥1}.

Page 95 Problem 2 Answer

Given : f:R→R be given by f(x)=2x²+1

To find : Whether the function is one-one or not .Evaluate the given function to find solution.

Consider above function,

f:R→R be given by f(x)=2x²+1

Observe that f(−1)=3=f(1) which gives us that f  is not one-to-one.

Therefore, the given function f is not one-to-one.

Read and Learn More Susan Colley Vector Calculus Solutions

Page 95 Problem 3 Answer

Given : f:R→R be given by f(x)=2x²+1 .

To find : If the function is onto.Evaluate above function to find solution.

Consider the above function ,

Let f:R→R be given by f(x)=2x²+1 .

By the item (a) we have that the range of f is not R.

Therefore f is not onto.

Therefore, f is not onto.

Page 95 Problem 4 Answer

Given:f(x,y)=ln(x+y)

To find: Domain and Range of the given function.

Evaluate to get the final answer.

From the given function f(x,y)=ln(x+y).

Observe that the expression,

ln(x+y)  is well defined if and only ifx+y>0.

Thus, the domain of  f is   {(x,y)∈R2:x+y>0}

given x∈R we have that 0<ex=ex+0.

Hence, we get f(ex,0)=ln(ex+0)

=ln(ex)

=x.

Therefore,  range off isR.

Therefore, domain of fis{(x,y)∈R2:x+y>0}.and  range of  f  is R

Page 95 Problem 5 Answer

Given: g(x,y,z)=√x²+(y−2)²+(z+1)²

To find: Domain and range of the function Evaluate to get the final answer.

We Consider the function,

g(x,y,z)=√x²+(y−2)²+(z+1)².

From the function we can observe that 0≤x²+(y−2)²+(z+1)² for all (x,y,z)∈R and therefore the expression,

√x²+(y−2)²+(z+1)² is well defined for all(x,y,z)∈R3

Thus, the domain of g is R3.

We now observe that 0≤√x²+(y−2)²+(z+1)² }  for all (x,y,z)∈R3

Given x∈R we have,

g(x,2,−1)=√x²+(2−2)²+(−1+1)²

=√x²

=∣x∣.

Thus, the range of g is [0,∞).

Hence, domain of g is R3 and  range of g is [0,∞).

Page 96 Problem 6 Answer

Given: g(x,y,z)=1

√4−x²−y²−z²

To find: Domain and range of the given function.

Evaluate to get the final result.

From the given function, we observe  that the function is always positive i.e.

√4−x²−y²−z²>0⇒x²+y²+z²<4 as long as the inequality above holds, the function will be well defined.

Hence, the domain of the function is a subset of R3 with the following properties:{(x,y,z)=x²+y²+z²<4}

As for the range of the function, we determine it by assigning y and z on 0.

The smaller the denominator the larger the expression will be, hence the biggest denominator is achieved if we set  x=0.

Therefore, the lowest value we can get in this case is 1/2

Since we can make denominator arbitrary small, we can consider any other real number larger than 1/2 by adjusting x and keeping the other two values intact.

Hence the range of the function is [1/2,∞⟩

Therefore, the given function has following,

Domain:{(x,y,z)=x²+y²+z²<4} and range: [1/2,∞⟩

Page 96 Problem 7 Answer

Given:f(x,y)=(x+y,1/y−1,x²+y²)

To Find:  Domain and Range of the given functionEvaluate to get the final answer.

Let us denote the components like below and discuss each of it separately.​​

f₁(x,y)=x+y

f₂(x,y)=1/y−1

f{3}(x,y)=x{2}+y{2}

The functions f1 and f3 are well defined for every pair  (x,y).

except the entire domain of  f  is the function f2 which is not well defined if  y=1 since we can not divide by zero.

Therefore the range of  f is the following set:

{(x,y)∈R2:y≠1}

We now write the range of f in terms of it’s components.

The first component of range, x, can be any real number.

This is due to the property of the function f1, you can find two real numbers that, when added, yield a fixed real number.

The second component is a typical one variable rational function. It will yield all real number except 0 .

The third component, z, will yield a positive real number or zero if both  x and  y  are zero.

Hence the range of f   is:{(x,y,z):x∈R,y∈R,y≠1,z∈[0,∞⟩}  which is not well defined if y=1  since we can not divide by zero.

Therefore the range of  f  is the following set: {(x,y)∈R2:y≠1}

Therefore, the range of f is :  {(x,y,z):x∈R,y∈R,y≠1,z∈[0,∞⟩}

Page 96 Problem 8 Answer

Given: f:R2→R3  and f(x,y)=(x+y,yex,x2y+7)

To find: Component function of f Evaluate to get the final answer.

Since f is the vector function, it’s components are separated by comma.

We can further simplify the given functions as,

f₁(x,y)=x+y

​f₂(x,y)=yex

f₃ (x,y)=x²y+7

Hence, component functions of f are:

f₁(x,y)=x+y

​f₂(x,y)=yex

f₃(x,y)=x²y+7

Page 96 Problem 9 Answer

Given: v(x,y,z,t) = (xy zt ,x²−y²,3z+t)

To find the component function for the given function.Evaluate to get the final answer.

The function in the given example is derived from the following  formula:

v(x,y,z,t) = (xyzt,x²−y²,3z+t)

Rewriting the components we get:

v₁(x,y,z,t)=xyzt

​v₂(x,y,z,t)=x²−y²

v₃(x,y,z,t)=(3z+t)

Hence, component functions of the given expression are:

v₁(x,y,z,t)=xyzt

​v₂(x,y,z,t)=x²−y²

v₃(x,y,z,t)=(3z+t)

Page 96 Problem 10 Answer

Given:- f(x)=x+3j

To find:-  The component functions off in terms of the components of the vector x

Evaluate to get the final answer.

Let us evaluate the vectors

Pay attention to two things.

First, f takes values from R3 and outputs the values in the same set.

This means that a vectorx∈R3 can be written as x=(x¹,x²,x³)

Second recall that  j=(0,1,0)

We can rewrite the components of f now like this:​

f₁ (x¹,x2,x3)=x¹

f₂ (x¹,x²,x³)=x²+3

f₃ (x¹,x²,x³)=x³

Note that this is in fact equal to the expression given to us in task,

But the only difference is that the f is rewritten in terms of its components.

Hence, the component functions of f in terms of the components of the vector x is f1

(x¹,x²,x³)=x¹ ,f₂(x¹,x²,x³)=x²+3 and f₃(x¹,x²,x³)= x³

Page 96 Problem 11 Answer

Given:-  A nonzero vector x in R3 the vector of length 2 that points in the direction opposite to x.

To find:-  An analytic (symbolic) description of  mapping Evaluate to get the final answer.

Let us evaluate the vectors

Analytically, take a vector and then return the vector of the exact same direction with an opposite orientation and the length of two.

Therefore, To turn x into a unit vector and then multiply the unit vector with−2.

The symbolic description of this operation is given below:−2x

∥x∥

Hence, the analytic (symbolic) description of  mapping is −2x

∥x∥.

Page 96 Problem 12 Answer

Given:- a nonzero vector x in R3 the vector of length 2 that points in the  direction opposite to x.

To find:-  the component functions of x=(x,y,z) mapping.

Let us evaluate the vectors

Apply the analytic explanation given above.

Recall that for vector (x,y,z) a norm function (∥⋅∥) representing it’s length is usually defined like this:

(x,y,z)∥=√x²+y²+z²

Scale every component by the factor of−2

√x²+y²+z²

therefore :

f₁(x,y,z)=−2x

√x²+y²+z²

f₂(x,y,z)=−2y

√x²+y²+z²

f₃(x,y,z)=−2z

√x²+y²+z²

Hence, the component function of x is f1

(x,y,z)=−2x

√x²+y²+z², f₂(x,y,z)=−2y

√x²+y²+z² and f₃(x,y,z)=−2z

√x²+y²+z²

Page 96 Problem 13 Answer

Given:- f(x)=Ax

Where, A=[​2/5 −6​−1 0/3​] and ​x=[​x¹/x²​]

To find:-  the component functions of f in terms of the components x1, x2 of the vector x.

Let us evaluate the vectors,

Consider the given function f(x¹,x²)=A(x¹,x²)

Where A=[​2/5−6​−1 0/3​]

Substitute A in the above function, to get;

f(x¹,x²)&=[​2/5−6​−1/0 3​][​x¹/x²​]

=[​2x¹−x²/5×1−6×1+3×2​]

Thus, f(x¹,x²)=(2×1−x²,5×1,−6×1+3×2)

Hence, the component functions of f in terms of x¹,x² are (2x¹−x²,5×1,−6×1+3×2).

Page 96 Problem 14 Answer

Given:- f(x)=Ax

Where, A=[​2/5−6​−1 0/3​] & ​x=[​x¹/x²​]

To find:- Range of f

Let us evaluate the vectors

The range of f is ;{(2×1−x²,5×1,−6×1+3×2):x1,x²∈R}

As linear combination of first and third component gives;

3(2x−y)+(−6x+3y)=0.

The range of f  is the plane 3u+w=0.

Hence, the range of f is the plane 3u+w=0.

Page 96 Problem 15 Answer

Given: A=[​2/0 2/0 3/0 −1/0−1/0 1​]

x=⎣x¹ x² x³ x⁴ ⎤

To find: Component functions of f in terms of x¹, x², x³, and x⁴.Multiply A with x to determine  f1, f2, f3.

Let us simplify the given exercise.

f₁(x¹,x²,x³,x⁴)=2x¹−x³+ x⁴

f₂(x¹,x²⁼²,x³,x⁴)=3×2

f₃(x¹,x²,x³,x⁴)=f1(x¹,x²,x³,x⁴)

​Hence, the obtained expression is

f₁=2×1−x³+x⁴,

f₂=3 x 2 and f3=f1(x¹,x²,x³,x⁴)

Page 96 Problem 16 Answer

Given:  A=[​2 /0 2/0 3/0​−1/0 −1/1  0/1]

X =⎣​x¹ x² x³ x⁴⎤

To describe: The range of f. Evaluate to get the final answer.

Let us solve the given exercise,

The range is the plane in R3

which contains the origin that is said to be parallel to both (1,0,1) (and thus (2,0,2) and (−1,0,−1)

which are both parallel to this vector) and they-axis (hence the vector (0,3,0)).

The range of f is plane in R3

Page 96 Problem 17 Answer

Given: Function f(x,y)=3

To find: Several level curves of the function f

Evaluate to get the final answer.

Let us solve the given exercise.

The entire graph is in the contour curve (on the actual contour surface).

This is the plane parallel to xy plane at z=3

Therefore, we can conclude that the entire graph for Function f(x,y)=3  is in the contour curve.

Page 96 Problem 18 Answer

Given: Function f(x,y)=3

To obtain: Sketch of the graph off

Evaluate to get the final answer.

Following is the graph,

Therefore, we conclude that the entire graph for function f(x,y)=3 is in the contour curve.

Page 96 Problem 19 Answer

Given: Function f(x,y)=x²+y²

To find: Several level curves of the given function f

Evaluate to get the final answer.

Let us solve the exercise.

For a fixed z we can observe that the curve is defined by x and y

The function given in the task is zero if and only if both x and y are zero.

Hence, let us pick a height (level) in such a way that the value of the level is positive.

For example,c By rewriting the curve equation, we can see that a level surface in question is in fact a circle of a radius√c.

x²+y²=c

Hence, the obtained expression is x²+y²=c

Page 96 Problem 20 Answer

Given: f(x,y)=x²+y²

To Find: sketch the graph of f.Evaluate to get the result.

For a fixed z we observe the curve defined by x and y.

Obviously, the function given in the task is zero if and only if both x and y are zero.

Therefore, let us pick a height (level) such that the value of level is positive, for example c.

By rewriting the curve equation, we can see that a level surface in question is in fact a circle of a radius √c.x²+y²=c

You can imagine a level curve in this case an intersection between the graph of a given surface and the plane z=c.

The example is given on the picture for c=1andc=2. The sketches of the level curves are then circles of radius 1 and√2  in the xy plane.

Let us plot a graph :

Hence, the required graph of f is :

Page 96 Problem 21 Answer

Given : f(x,y)=x²+y²−9

To find :  Determine several level curves of the given function f (make sure to indicate the height c of each curve).

Evaluate to get the result.

To find the type of the level curve, in this case it is enough to check the condition for the given function to be zero.

In fact one can easily observe that x²+y²−9=0 ⇒ x²+y²=9

The second equation is in fact the equation describing a circle with radius 3 and it’s center at origin.

All of the other level curves will in fact be circles, as shown on the image in step two.

If  set the surface height on z=2,

Let us plot a graph :

View from the top will in fact show all three circles :

Note that there are infinitely many level curves that can be obtained like this and all of them are circles.

The bottom one is, however the smallest circle.

Hence, through the following images we determined several levels of curves of the given function.

Page 96 Problem 22 Answer

Given :f(x,y)=x²+y²−9

To find : Use the information obtained in part (a) to sketch the graph of f.

Evaluate to get the result.

Finding the type of the level curve, in this case it is enough to check the condition for the given function to be zero.

In fact one can easily observe that

x²+y²−9=0 ⇒ x²+y²=9

The second equation is in fact the equation describing a circle with radius 3 and it’s center at origin.

All of the other level curves will in fact be circles, as shown on the image in step two.

If  set the surface height on z=2, we get another circle with a larger radius,

Hence, the graph of f is:

Page 96 Problem 23 Answer

Given : f(x,y)=√x²+y²

To find : (a) Determine several level curves of the given function f (make sure to indicate  the height c of each curve).

Evaluate to get the result.

This time, the given surface is a cone.

Intersecting the surface at any level other than zero will again yield the circle.

Let c be a level of a curve.

Then the equation of the curve is given by the following relation:

√x²+y²

=c ⇒ x²+y²

=c²

As you can see, a level curve on any height c is in fact a circle.

Below are sketches of circles on height 1 and 2.

Let us plot a graph:

Now

Technically, the correct sketches of the level curves are on picture number two.

Imagine that we fix the height c on a plane z=c. For z=1 in a smaller circle.

For height z=2 is the larger one. This is exactly the situation depicted on a picture one.

So level curves are in fact drawn as a projections on xy plane with assumption that z is fixed.

Hence, Determined several levels of curves of the given function of f

Page 96 Problem 24 Answer

Given :f(x,y)=√x²+y²

To find : (b) use the information obtained in part (a) to sketch the graph off.

Evaluate to get the result

This time, the given surface is a cone.

Intersecting the surface at any level other than zero will again yield the circle Let be a level of a curve.

Then the equation of the curve is given by the following relation:

As you can see, a level curve on any height  is in fact a circle. Below are sketches of circles on height 1 and 2.

Let us plot a graph :

Next,

Hence, the graph of f is,

Susan Colley Vector Calculus 4th Edition Chapter 1 Vectors

Page 7 Problem 1 Answer

Given : The vector(2,1)

To sketch : Vectors in R²

Evaluate to get the final answer

Indicated vectors are shown on the graph below :

Therefore, the graph is plotted with the given value.

Page 7 Problem 2 Answer

Given : (3,3)

To find : Vectors in R²

Evaluate to get the final answer

Indicated vectors are shown on the graph below :

Read and Learn More Susan Colley Vector Calculus Solutions

Hence, the graph is plotted with given value.

Page 7 Problem 3 Answer

Given : (−2,1)

To find : Vectors in R²

Evaluate to get the final answer

Indicated vectors are shown on the graph below :

Hence, the graph is plotted with given value.

Page 7 Problem 4 Answer

Given : (1,2,3)

To find : Vectors in R³

Evaluate to get the final answer

Indicated vectors are shown on the below graph :

Hence, the graph is plotted with given values.

Page 7 Problem 5 Answer

Given : (−2,0,2)

To find: Vectors in R³

Evaluate to get the final answer

Given : (−2,0,2)

To find: Vectors in R³

Evaluate to get the final answer

Hence, the graph is plotted with given values.

Page 7 Problem 6 Answer

Given : (2,−3,1)

To find : Vectors in R³

Evaluate to get the final answer

Indicated vectors are shown on the below graph :

Therefore, the graph is plotted with given values.

Page 7 Problem 7 Answer

Given : (3,1)+(−1,7)

To express: The given expression in single vector a=(a₁,a₂) in R²

Evaluate to get the required solution

Let us simplify in this way,

(3,1)+(−1,7)=(3−1,1+7)

=(2,8)

Hence, the required solution is (2,8)

Page 7 Problem 8 Answer

Given : −2(8,12)

To express: in the form of a single vector a=(a₁,a₂) in R²

Evaluate to get the final answer

Let us simplify in this way,

−2(8,12)=(−16,−24)

Therefore, the required solution is (−16,−24)

Page 7 Problem 9 Answer

Given : (8,9)+3(−1,2)

To express: In the form of a single vector a=(a₁,a₂) in R²

Evaluate to get the final answer

Let us simplify in this way,

(8,9)+3(−1,2)=(8,9)+(−3,6)

=(8−3,9+6)

=(5,15)

Therefore, the required solution is (5,15)

Page 7 Problem 10 Answer

Given : (1,1)+5(2,6)−3(10,2)

To find : Single vector a=(a₁,a₂) in R²

Evaluate to get the final answer

Let us simplify the equation in this way,

(1,1)+5(2,6)−3(10,2)=(1,1)+(10,30)−(30,6)

=(1+10−30,1+30−6)

=(−19,25)

Hence, the required solution is (−19,25)

Page 7 Problem 11 Answer

Given : (8,10)+3((8,−2)−2(4,5))

To find : Single vector a=(a₁,a₂) in R²

Evaluate to get the final answer

Let us simplify the equation in this way,

(8,10)+3((8,−2)−2(4,5))=(8,10)+3((8,−2)−(8,10))

​=(8,10)+3(0,−12)

=(8,10)+(0,−36)

=(8+0,10−36)

=(8,−26)

Hence, the required solution is (8,−26)

Page 7 Problem 12 Answer

Given : (2,1,2)+(−3,9,7)

To find : Single vector a=(a₁,a₂,a₃) in R³

Evaluate to get the final answer

Let us simplify in this way,

(2,1,2)+(−3,9,7)=(2−3,1+9,2+7)

=(−1,10,9)

Therefore, the required solution is (−1,10,9)

Page 7 Problem 13 Answer

Given : 1/2(8,4,1)+2(5,−7,1/4)

To find : Single vector a=(a₁,a₂,a₃) in R³

Evaluate to get the final answer

Let us simplify in this way,

​1/2(8,4,1)+2(5,−7,1/4)=(4,2,1/2)+(10,−14,1/2)

=(14,−12,1)

Therefore, the required solution is (14,−12,1)

Page 7 Problem 14 Answer

Given : −2((2,0,1)−6(1/2,−4,1))

To find : Single vector a=(a₁,a₂,a₃) in R³

Evaluate to get the final answer

Let us simplify in this way,

​−2((2,0,1)−6(1/2,−4,1))=−2((2,0,1)−(3,−24,6))

​=−2(−1,24,−5)

Therefore, the required solution is (2,−48,10)

Page 7 Problem 15 Answer

Given : a=(1,2),

b=(−2,5), and

a+b=(1,2)+(−2,5)

​To find: Parallelogram law and the head-to-tail methodEvaluate to get the final answer

Addition of vectors using parallelogram law.

Resultant vector is CD

Addition of vectors using head-to-tail method :

Therefore, the graph is plotted using parallelogram law and the head-to-tail method.

Page 7 Problem 16 Answer

Given : a=(3,2)

b=(−1,1)

​To find: Calculate and graph a−b,1/2a, and a+2b

Evaluate to get the final answer

Hence, all the required graphs has been plotted.

Page 7 Problem 17 Answer

Given : Let A be the point with coordinates (1,0,2),let B be the point with coordinates (−3,3,1)

and let C be the point with coordinates(2,1,5)

To find : Vectors AB and BA

Evaluate to get the final answer

Each vector is determined with initial and terminal point.

That is, two points – one where it starts and one where it ends.

Vector AB starts at point A and ends at point B

Vector BA starts at point B and ends at point A.

Therefore,

Vector AB starts at point A and ends at point B and,

Vector BA starts at point B and ends at point A

Page 7 Problem 18 Answer

Given : Let A be the point with coordinates (1,0,2),let B be the point with coordinates(−3,3,1) and let C

be the point with coordinates(2,1,5)

To find : Vectors AC,BC, and AC+CB

Evaluate to get the final answer

Let us simplify,Vector AC starts at point A and ends at point C.

Vector BC starts at point B and ends at point C.

Vector AC+CB is sum of two vectors. Notice that first vector ends at point C and second vector starts at point C.

This means that the resulting vector starts at point A and ends at point B

Hence, we have described all the 3 given vectors.

Page 7 Problem 19 Answer

Given :  Let A be the point with coordinates (1,0,2), let B be the point with coordinates (−3,3,1),and let C be the point with coordinates (2,1,5)

To find : Explain with pictures why AC+CB=AB

Evaluate to get the final answer

Let us plot a graph:

Hence, the vector is solved with the help of a picture.

Page 7 Problem 20 Answer

Given : (1,2,1) and (0,−2,3),

To find : Calculate and graph (1,2,1)+(0,−2,3),−1(1,2,1), and 4(1,2,1)

Evaluate to get the final answer

Let us calculate,

(1,2,1)+(0,−2,3)=(1,0,4)−1(1,2,1)

=(−1,−2,−1)

4(1,2,1)=(4,8,4)

Hence, we have calculated and graphed the given vectors.

Page 7 Problem 21 Answer

Given: The equation(−12,9,z)+(x,7,−3)=(2,y,5)

To find : Values of X,Y&Z

Apply addition of vectors to get the result.

Let us evaluate the given equation,

(−12,9,z)+(x,7,−3)=(2,y,5)

(−12+x,9+7,z−3)=(2,y,5)

(−12+x,16,z−3)=(2,y,5)

−12+x=2

So, we get

x=14

16=y

z−3=5

And, z=8

Therefore, the required values of X,Y and Z are 14,16 and 8.

Page 7 Problem 22 Answer

Given: The vector (3,1)

To find : What is the length (magnitude) of the vector (3,1)

Use Pythagorous theorem to get the length.

Given: The vector (3,1)

To find : What is the length (magnitude) of the vector (3,1)

Use Pythagorous theorem to get the length.

A vector  from a origin to point (3,1)

The length of the vector is d=√32+12=√10

Therefore, the required length of the vector is √10.

Page 7 Problem 23 Answer

Given : The vectors, a=(1,2) and b=(5,10)

To sketch: The vectors and explain why they point in the same direction.

Explain with the help of a graph.

The graph of the given vectors a=(1,2) and  b=(5,10)

As we see in the graph

It is true that a and b point in the same direction, because b is a multiple of a.

So, we can say that : b=5a

Hence, a and b point in the same direction ,because b is a multiple of a.

Page 7 Problem 24 Answer

Given : a=(a₁,a₂,…,a_n)

b=(b₁,b₂,…,b_n) are two vectors in  Rn  and k ∈ R is a scalar.To find : Add the vectors (1,2,3,4)

and (5,−1,2,0) in R⁴ and the value of 2(7,6,−3,1)

Evaluate to get the final solution.

We add vectors in any dimension : (1,2,3,4)+(5,−1,2,0)=(6,1,5,4)

When we multiply with scalar, we multiply each component:

2(7,6,−3,1)=(14,12,−6,2)

So,(a₁,a₂,…,a_n)+(b₁,b₂,…,b_n)=(a₁+b₁,a₂+b₂,…,a_n+b_n)

k(a₁,a₂,…,a_n)=(ka₁,ka₂,…,ka_n)

Hence, the required solution is(1,2,3,4)+(5,−1,2,0)=(6,1,5,4)

And 2(7,6,−3,1)=(14,12,−6,2)

Page 7 Problem 25 Answer

Given : P₁(1,0,2),P2(2,1,7)

To find:  Displacement vectors from P₁ to P₂

To sketch :  P₁,P₂, and P₁/P₂ .

Evaluate to get the final solution.

We can find displacement vector :

P₁/P₂=(x₂−x₁,y₂−y₁,z₂−z₁)

Where P₁(x₁,y₁,z₁) and P₂(x₂,y₂,z₂) are two points.

Let us solve now

P₁/P₂=(2−1,1−0,7−2)

=(1,1,5)​

Hence, the required solution Is P₁/P₂=(1,1,5)

Page 7 Problem 26 Answer

Given :  P₁ (1,6,−1),P₂ (0,4,2)

To find: Displacement vectors P₁ to P₂

To sketch : P₁,P₂ , and P₁ /P₂ .

Evaluate to get the final answer

We can find displacement vector as follows

P₁/P₂=(x₂−x₁,y₂−y₁,z₂−z₁)

Where P₁(x₁,y₁,z₁) and P₂(x₂,y₂,z₂)

Evaluating we get

P₁/P₂=(1−0,6−4,−1−2)

=(1,2,−3)

​Hence, the required solution is P₁/P₂=(1,2,−3)

Page 7 Problem 27 Answer

Given : P₁ (0,4,2),P₂ (1,6,−1)

To find: The displacement vectors from P₁ to P₂

Evaluate to get the final answer.

We can find displacement vector :

P₁/P₂=(x₂−x₁,y₂−y1,z₂−z₁)

Where P₁(x₁,y₁,z₁) and P₂(x₂,y₂,z₂)

We will do the evaluation now

P₁/P₂ =(0−1,4−6,2+1)

=(−1,−2,3)​

Hence, the required displacement vector P₁/P₂

=(−1,−2,3)

Page 7 Problem 28 Answer

Given : P₁(3,1),P₂(2,−1)

To find : The displacement vectors from P₁ to P₂.

To sketch 😛₁,P₂ , and P₁P₂

Evaluate to get the final answer.

We can find displacement vector :

P₁/P₂=(x₂−x₁,y₂−y₁,z₂−z₁)

Where P1(x₁,y₁,z₁) and P₂(x₂,y₂,z₂)

Evaluating we get

P₁/P₂=(3−2,1+1)

=(1,2)​

Hence, the required displacement vector is P₁/P₂=(1,2)

Page 7 Problem 29 Answer

Given : P₁ (2,5,−1,6) and P₂ (3,1,−2,7)

To calculate : The displacement vector from P₁ to P₂

Evaluate to get the final answer.

We can find displacement vector :

P₁/P₂=(x₂−x₁, y₂−y₁, z₂−z₁)

Where P₁(x₁,y₁,z₁) and P₂(x₂,y₂,z₂)

We define displacement the same way as in R³.

So Displacement:

P₁/P₂=(3−2,1−5,−2+1,7−6)

=(1,−4,−1,1)

hence, the required displacement is P₁/P₂

=(1,−4,−1,1)

Page 7 Problem 30 Answer

Given : A is the point in R3 with coordinates (2,5,−6) The displacement vector from A to a second point B is (12,−3,7)

To find : Coordinates of B? Evaluate to get the final answer.

Let us find the coordinates of point B.

We can use displacement vector:

SupposeB=(x,y,z), then (12,−3,7)=(x−2,y−5,z+6)

Thus,

x−2=12

x=14

y−5=−3

y=2

z+6=7

z=1

Coordinates of B are: (14,2,1).

Hence, the coordinates of B are: (14,2,1).

Page 7 Problem 31 Answer

Given : Suppose that you and your friend talking on cellular phones.

You inform each other of your own displacement vectors.

To explain : How to determine the displacement vector from you to your friend.

Evaluate to get the final solution.

Let coordinate system represents origin.

Then, our displacements vectors coincide with our coordinates.

Thus, a⃗=A and   b⃗=B.

Now, we find the displacement vector as

d⃗=B−A

Hence, the required displacement vector is d⃗=B−A

Page 7 Problem 32 Answer

Given: Properties 2 and 3 of vector addition.

To find : Give the details of the proofs of properties Two vectors can be added together by placing them together.

Let us evaluate

a+(b+c)=

=(a₁,a₂,a₃)+((b₁,b₂,b₃)+(c₁,c₂,c₃))

=(a₁,a₂,a₃)+(b₁+c₁,b₂+c₂,b₃+c₃)

=(a₁+b₁+c₁,a₂+b₂+c₂,a₃+b₃+c₃)

=(a1+b₁,a₂+b₂, =a₃+b₃)+(c₁,c₂,c₃)

=(a+b)+c​

Further evaluating,a+0=

=(a₁,a₂,a₃)+(0,0,0)

=(a₁+0,a₂+0,a₃+0)

=(a₁,a₂,a₃)

=a

Hence, we have given the details of the proofs of properties 2 and 3 of vector addition(a+b)+c.

Page 7 Problem 33 Answer

Given: Properties of scalar multiplication

To prove : The properties of scalar multiplication Evaluate to get the final answer.

We can prove this as follows

k(la)=k(la₁,la₂,la₃)

=kl(a₁,a₂,a₃)

=(kl)a

=(lk)a

=l(ka)​

Hence, we have proved the properties of scalar multiplication.

Page 7 Problem 34 Answer

Given: A vector a in R2 or R3.To Find: Calculate the value of 0a and prove the answer.

By doing scalar multiplication of vector a, we can calculate the value.

Firstly,0a is zero vector in R2 or R3 depending on where a came from.

A zero vector is a vector having a magnitude of zero.

Now,

0a=0(a₁,a₂,a₃)

⇒0a=(0⋅a₁,0⋅a₂,0⋅a₃)

0a=(0,0,0)

Therefore, 0a is a zero vector having magnitude 0.

Page 7 Problem 35 Answer

Given: A vector a in R² and R³.To Find: The value of 1a

and prove the answer. By doing the scalar multiplication, we can calculate the value.

From Scalar multiplication, we know that the value of 1a is a.

Now,1a=1(a₁,a₂,a₃)

⇒1a=(1⋅a₁,1⋅a₂,1⋅a₃)

⇒1a=(a₁,a₂,a₃)

∴1a=a

Therefore, the required value of 1a is a.

Page 7 Problem 36 Answer

Given: A vector x=sa+tb where 0≤s≤1 and 0≤t≤1,along with the coordinates of a and b.

To Explain: The reason for vector x lying in the parallelogram determined by a and b.

A sketch of the vectors described will help in determining the answer.

A simple sketch explains why the vectors of the described set are in fact a parallelogram.

The most distant point from (0,0) you can reach with vectors a and b is exactly the end point of vector g=a+b.

On the other hand, using any other, smaller coefficients on a and b will land the new vector somewhere inside or on the edge of parallelogram depending on what coefficients we use.

For example, vector 0.5a+0.2b will be inside of parallelogram since both coefficients in front of a and b are smaller then l.

On the other hand, vector 0.5a+b will have it’s end point on the edge of parallelogram since the coefficient in front of b is equal to 1.

Therefore, we have explained the reason for x lying in the parallelogram determined by a and b.

Page 7 Problem 37 Answer

Given: A set of vectors, {x=sa+tb∣0≤s≤1,0≤t≤1} along with the coordinates of a and b.

To Describe: The set of vectors, {x=sa+tb∣0≤s≤1,0≤t≤1}.

From the coordinates of a and b, we know that the given vector is in 3-D, so we can explain accordingly.

The explanation is similar to the part a) of the task.

The only difference is that we now have two vectors in 3-D space.

However, any linear combination of these two vectors with the coefficients being between zero and one will again yield a parallelogram, but this time in three dimensional space.

Therefore, we have described the given set of vectors.