Vector Calculus

Integral Transformations Exercise 7.3

1. Verify Stokes theorem for the function F=zi+xj+yk where the curve is the unit circle in the xy – plane bounding the hemispherez=\(\sqrt{\left.1-x^2-y^2\right)}\)

Solution:  

Given \(\oint_C(3 x+4 y) d x+(2 x-3 y) d y\) . Here \(\mathbf{P}=3 x+4 y, \mathbf{Q}=2 x-3 y\)

By Green’s theorem \(\int_C \mathbf{P} d x+\mathbf{Q} d y=\iint_S\left(\frac{\partial \mathbf{Q}}{\partial x}-\frac{\partial \mathbf{P}}{\partial y}\right) d x d y\)

= \(\iint_S(2-4) d x d y=-2 \int_S d \mathrm{~A}=-2 \mathrm{~A}=-2 \pi(2)^2=-8 \pi\)

∴ \(\int_C \mathbf{F} . d \mathbf{r}=\int_C x d y\) because z=0, d z=0

Let  x = \(\cos \theta, y=\sin \theta \quad \int \mathbf{F} . d \mathbf{r}=\int_0^{2 \pi} \cos ^2 \theta d \theta\)

= \(4 \int_0^{2 \pi} \cos ^2 \theta \cdot d \theta=4 \cdot \frac{1}{2} \cdot \frac{\pi}{2}=\pi\)……….(1)

Now let \(\int_S \text{curl} \mathbf{F} \cdot \mathbf{N} d \mathbf{S}\).

⇒ \(\nabla \times \mathbf{F}=\mathbf{i}+\mathbf{j}+\mathbf{k}\)

If \(\mathbf{S}_1\) is the plane region bounded by the circle C then unit normal N=k.

∴ \(\int_S \text{curl} \mathbf{F} . \mathbf{N} d \mathbf{S}=\int_{\mathrm{S}_1}(\nabla \times \mathbf{F}) \cdot \mathbf{k} d \mathbf{S}=\int_{\mathrm{S}_1} 1 . d \mathbf{S}=\mathbf{S}_1\)

But \(\mathbf{S}_1=\) area of the circle of radius unity \(=\pi\)

∴ \(\int_S \text{curl} \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\pi\)……….(2)

Hence from (1) and (2) the theorem is verified.

Integral Calculus Exercise 7.3 Problems

2. Evaluate \(\int_C\)F.dr by Stokes theorem , if F=(x²+y²)i- 2xyj where C is the rectangle formed x=±a, y=0, y=b

Solution:

curl F = (-4 y) k

In the xy-plane N =k

∴ \(\int_C \mathbf{F} . d \mathbf{r}=\int_S \text{curl} \mathbf{F} . \mathbf{N} d \mathbf{S}\)

= \(\int^x(\nabla \times \mathbf{F}) \cdot \mathbf{k} d s\)

= \(\int_{y=0}^b \int_{x=-a}^a-4 y d x d y=-4[x]_{-a}^a\left[\frac{y^2}{2}\right]_0^b=-4 a b^2\)

3. Evaluate by Stokes theorem \(\int_C\)F.dr where F= yzi+zxj+xyk and C is the curve x²+y²=1,z=y²

Solution:

F = \(y z \mathbf{i}+z x \mathbf{j}+x y \mathbf{k}\)

∴ \(\text{curl} \mathbf{F}=0\)

By Stokes theorem, \(\oint \mathbf{F} \cdot d \mathbf{r}=\int(\text{curl} \mathbf{F}) \cdot \mathbf{N} d \mathbf{S}=0\)

4. Evaluate by Stokes theorem \(\int_C\)sinz dx-cos x dy + sin y dz where C is the boundary of the rectangle 0 ≤ x≤π, 0<y≤1, z=3 [Hint: Unit normal vector N=k since rectangle lies in the plane z=3].

Solution:

Here \(\mathbf{F}=(\sin z) \mathbf{i}-\cos x \mathbf{j}+\sin y \mathbf{k}\)

∴ \(\text{curl} \mathbf{F}=(\cos y) \mathbf{i}+(\cos z) \mathbf{j}+(\sin x) \mathbf{k}\)

∴ The rectangle lies in the plane z=3

N = k\(\mathbf{F} . \mathbf{N}=\sin x\)

By Stokes theorem, \(\oint_C \mathbf{F} \cdot d \mathbf{r}=\int_{\mathbf{S}} \text{curl} \mathbf{F} \cdot \mathbf{N} d \mathbf{S}\)

= \(\int_{y=0}^1 \int_{x=0}^\pi \sin x d x d y=\int_0^1 d y \cdot \int_0^{S_\pi} \sin x d x=2\)

Integral Techniques Used In Exercise 7.3

5.Prove that \(\int_S\)r× dr=2\(\int_S\)dS [Hint: Apply Stokes theorem for a×r where a is a constant vector]

Solution:  Let F=a×r where a is a constant vector. Then ∇× F = ∇× (a×r)=2a

∴ By Stokes theorem \(\Rightarrow \int_C(\mathbf{a} \times \mathbf{r}) \cdot d \mathbf{r}=\int_S 2 \mathbf{a} \cdot \mathbf{N} d \mathbf{S}\)

a. \(\int(\mathbf{r} \times d \mathbf{r})=2 \mathbf{a} \cdot \int \mathbf{N} d \mathbf{S} \Rightarrow \int \mathbf{r} \times d \mathbf{r}=2 \int d \mathbf{S}\)

6. Evaluate by Stokes theorem \(\oint_C\)(e^x dx+2y dy-dz) where C is the curve x²+y²=0,z=2.

Solution:

∴ \(\oint_C\left(e^x d x+2 y d y-d z\right)=\oint_C\left(e^x \mathrm{i}+2 y \mathrm{j}-\mathrm{k}\right) \cdot(\mathrm{i} d x+\mathrm{j} d y+\mathrm{k} d z)=\oint \mathrm{F} \cdot d \mathrm{r}\)

Hence \(\mathrm{F}=e^x \mathrm{i}+2 y \mathrm{j}-\mathrm{k}\)

∴ \(\nabla \times \mathbf{F}=0\)

By Stokes theorem \(\int_C \mathbf{F}. d \mathbf{r}=\int_S(\nabla \times \mathbf{F}) \cdot \mathbf{N} d s=0\)

Integral Transformations Green’s Theorem In A Plane

Let S be a closed region in xy- xy-plane enclosed by a curve C. Let P and Q be continuous and differentiable scalar functions of x and y in S . Then \(\oint_C P \mathrm{dx}+\mathrm{Q} \mathrm{dy}\)=\(\iiint_S\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y\) The line integral being taken round C such that S is on the left as one advance along C.

Proof: Let any line parallel to either coordinate axes cut C in at most two points. Let S lie between the lines x = a, x = b, and y = c, y = d.

Let y = f(x) be the curve C₁ (i.e. AEB) and y = g (x) be the curve C₂ (i.e. ADB), where f(x) ≤ g(x)

Consider \(\iint_S \frac{\partial \mathrm{P}}{\partial y} d x d y=\int_{x=a}^b \int_{y=f(x)}^{g(x)} \frac{\partial \mathrm{P}}{\partial y} d x d y\)

= \(\int_a^b[\mathrm{P}(x, y)]_{y=f(x)}^{g(x)} d x=\int_a^b[\mathrm{P}(x, g)-\mathrm{P}(x, f)] d x\)

= \(\int_a^b \mathrm{P}(x, g) d x-\int_a^b \mathrm{P}(x, f) d x\)

= \(-\int_b^a \mathrm{P}(x, y) d x-\int_a^b \mathrm{P}(x, y) d x=-\int_{C_2} \mathrm{P}(x, y) d x-\int_{C_1} \mathrm{P}(x, y) d x\)

∴ \(\iint_S \frac{\partial \mathrm{P}}{\partial y} d x d y=-\oint_C \mathrm{P} d x\)……(1)

Similarly we can prove that \(\iint_S \frac{\partial \mathrm{Q}}{\partial x} d x d y=\oint_C \mathrm{Q} d y\)…….(2)

Hence adding (1) and (2), we get \(\oint_C \mathrm{P} d x+\mathrm{Q} d y=\iint_S\left(\ \frac {\partial \mathrm{Q}}{\partial x}-\frac{\partial \mathrm{P}}{\partial y}\right) d x d y\)

If the line parallel to either axis cuts in more than two points then we divide S into such regions satisfying our condition. Now we apply the formula obtained to each subregion and take the sum of integrals which is the same as the line integral over C This is because the line integrals along the boundary curves will cancel in pairs.

Integral Transformations Using Green’S And Stokes’ Theorem

Integral Transformations Stokes, Theorem

Let S be a surface bounded by a closed, nonintersecting curve C. If F is any differentiable vector point function, the \(\oint_c \mathbf{F} \cdot d \mathbf{r}=\int_s \text{curl} \mathbf{F} \cdot \mathbf{N} d \mathbf{S}\)

where C is traversed in the positive direction. The direction of C is called positive if the person, walking on the boundary of S in this direction, with his head pointing in the direction of outward drawn normal N to S, has the surface on his left.

Cartesian Form Let F = F₁i + F₂ j + F₃k

Let the unit normal vector N, of the x, y, z axes. drawn outward make angles α,β,γ with the positive direction of the x,y, and z axes.

∴ \(\mathbf{N}=\mathbf{i} \cos \alpha+\mathbf{j} \cos \beta+\mathbf{k} \cos \gamma\)

∴ \(\mathbf{F} \cdot d \mathbf{r}=\left(F_1 \mathbf{i}+F_2 \mathbf{j}+F_3 \mathbf{k}\right) \cdot(\mathbf{i} d x+\mathbf{j} d y+\mathbf{k} d z)=F_1 d x+F_2 d y+F_3 d z\)

Also \(\nabla \times \mathbf{F}=\left|\begin{array}{ccc}\mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ F_1 & F_2 & F_3\end{array}\right|\)

= \(\left(\frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z}\right) \mathbf{i}+\left(\frac{\partial F_1}{\partial z}-\frac{\partial F_3}{\partial x}\right) \mathbf{j}+\left(\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right) \mathbf{k}\)

∴ \((\nabla \times \mathbf{F}) \cdot \mathbf{N}=\left(\frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z}\right) \cos \alpha+\left(\frac{\partial F_1}{\partial z}-\frac{\partial F_3}{\partial x}\right) \cos \beta+\left(\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right) \cos \gamma\)

∴ Stokes theorem is equivalent to \(\oint_c F_1 d x+F_2 d y+F_3 d z\)

= \(\int_s\left[\left(\frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z}\right) \cos \alpha+\left(\frac{\partial F_1}{\partial z}-\frac{\partial F_3}{\partial x}\right) \cos \beta+\left(\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right) \cos \gamma\right] d \mathbf{S}\)

Proof: Let S be a surface which is such that its projections on xy, yz, and zx planes are regions bounded by simple closed curves.

Let S have the equations z=f(x,y) or z=g(y,z) or z=h(z,x) where f,g,h are simple values continuous and differentiable functions.

Now to prove \(\int_s(\nabla \times \mathbf{F}) \cdot \mathbf{N} d \mathbf{S}=\int_s \nabla \times\left(F_1 \mathbf{i}+F_2 \mathbf{j}+F_3 \mathbf{k}\right) \cdot \mathbf{N} d \mathbf{S}=\oint_c \mathbf{F} \cdot d \mathbf{r}\)

Let us consider \(\int\left[\nabla \times\left(F_{\mathbf{1}} \mathbf{i}\right)\right] . \mathbf{N} d \mathbf{S}\)

Now \(\nabla \times\left(F_1 \mathbf{i}\right)=\left|\begin{array}{ccc}\mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ F_1 & 0 & 0\end{array}\right|=\frac{\partial F_1}{\partial z} \mathbf{j}-\frac{\partial F_1}{\partial y} \mathbf{k}\)

∴ \(\left[\nabla \times\left(F_1 \mathbf{i}\right) \cdot \mathbf{N}\right] d \mathbf{S}=\left(\frac{\partial F_1}{\partial z} \mathbf{j}-\frac{\partial F_1}{\partial y} \mathbf{k}\right) \cdot \mathbf{N} d \mathbf{S}=\left[\frac{\partial F_1}{\partial z}(\mathbf{N} \cdot \mathbf{j})-\frac{\partial F_1}{\partial y}(\mathbf{N} \cdot \mathbf{k})\right] d \mathbf{S}\)

Let z=f(x, y) be the equation of S. For any point S \(\mathbf{r}=x \mathbf{i}+y \mathbf{j}+z \mathbf{k}=x \mathbf{i}+y \mathbf{j}+f(x, y) \mathbf{k}=\frac{\partial \mathbf{r}}{\partial y}=\mathbf{j}+\frac{\partial z}{\partial y} \mathbf{k}\)

because \(\frac{\partial \mathbf{r}}{\partial y}\) is the tangent vector to \(\mathbf{S}, \mathbf{N} \cdot \frac{\partial \mathbf{r}}{\partial y}=0\)

⇒ \(\mathbf{N} \cdot \mathbf{j}+(\mathbf{N} \cdot \mathbf{k}) \frac{\partial z}{\partial y}=0 \Rightarrow \mathbf{N} \cdot \mathbf{j}=-(\mathbf{N} \cdot \mathbf{k}) \frac{\partial z}{\partial y}\)

Substituting in (1) \(\nabla \times\left(F_1 \mathbf{i}\right) \cdot \mathbf{N}=-(\mathbf{N} \cdot \mathbf{k}) \frac{\partial F_1}{\partial z} \frac{\partial z}{\partial y}-(\mathbf{N} \cdot \mathbf{k}) \frac{\partial F_1}{\partial y}\)

⇒ \({\left[\nabla \times\left(F_1 \mathbf{i}\right) \cdot \mathbf{N}\right] d \mathbf{S}=-\left(\frac{\partial F_1}{\partial v}+\frac{\partial F_1}{\partial z} \frac{\partial z}{\partial v}\right)(\mathbf{N} \cdot \mathbf{k}) d \mathbf{S} }\)

= \(-\frac{\partial}{\partial y} F_1(x, y, z)(\cos \gamma) d \mathbf{S}=-\frac{\partial}{\partial y} F_1 \cdot d x d y\)

Let R be the projection of S on x y-plane and \(\sigma\) be the boundary of R

∴ \(\int_s\left[\nabla \times\left(F_1 \mathbf{i}\right)\right] \cdot \mathbf{N} d \mathbf{S}=\iint_R-\frac{\partial F_1}{\partial y} d x d y\)

By Green’s theorem in$x y-plane \(\iint_R\left(0-\frac{\partial F_1}{\partial y}\right) d x d y=\int_\sigma F_1 d x+0 d y\)

Since \(F_1(x, y, z)\) of \(\mathbf{C}\) is same as \(F_1\left(x, y, f(x, y)\right.\)of \(\sigma\) we have \(\oint_\sigma F_1 d x=\oint_c F_1 d x\)

Hence \(\oint_s\left[\nabla \times\left(F_1\right)\right] . \mathrm{N} d \mathrm{~S}=\oint_c F_1 d x\)

Similarly, by projections on the other y z, z x planes \(\oint_s\left[\nabla \times\left(F_2 \mathrm{j}\right)\right] . \mathrm{N} d \mathrm{~S}=\oint_c F_2 d y\)

⇒ \(\oint_s\left[\nabla \times\left(F_3 \mathrm{k}\right)\right] \cdot \mathrm{N} d \mathrm{~S}=\oint_c F_3 d z\)

Hence in addition, we have \(\int_s \nabla \times\left(F_1 \mathbf{i}+F_2 \mathbf{j}+F_3 \mathbf{k}\right) \cdot \mathbf{N} d \mathbf{S}=\int F_1 d x+F_2 d y+F_3 d z \text { i.e. } \int \nabla \times \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\int_c \mathbf{F} . d \mathbf{r}\)

Applying Stokes’ Theorem In The Plane

Integral Transformations Stokes Theorem In A Plane

Let the surface S lie in the xy-plane. Then the z-axis will be along the normal i.e. N=K

Let \(\mathbf{F}=F_1 \mathbf{i}+F_2 \mathbf{j}\) and \(\mathbf{r}=x \mathbf{i}+y \mathbf{j}\)

∴ \(\mathbf{F} . d \mathbf{r}=\left(F_1 \mathbf{i}+F_2 \mathbf{j}\right) \cdot(\mathbf{i} d x+\mathbf{j} d y)=F_1 d x+F_2 d y\)

and \(\nabla \times \mathbf{F}=\left|\begin{array}{ccc}\mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ F_1 & F_2 & 0\end{array}\right|\)

= \(-\frac{\partial F_2}{\partial z} \mathrm{i}+\frac{\partial F_1}{\partial z} \mathrm{j}+\left(\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right) \mathrm{k}\)

∴ \((\nabla \times \mathbf{F}) . \mathbf{N}=(\nabla \times \mathbf{F}) . \mathbf{k}=\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\)

In x y- plane, \(d \mathbf{S}=d x d y\)

⇒ \(\int_c \mathbf{F} \cdot d \mathbf{r}=\int_s(\nabla \times \mathbf{F}) \cdot \mathbf{N} d \mathbf{S} \Rightarrow \int_c F_1 d x+F_2 d y=\iint_s\left(\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right) d x d y\)

This is the same as Green’s theorem in a plane.

Integral Transformations Solved Problems

Example.1 If F=yi+(x-2xz)j-xyk evaluate\(\int_s(\nabla \times \mathbf{F})\) .Nds where S is the surface of the sphere x²+y²+z²=a² above the XY-plane

Solution:

Given \(\mathbf{F}=y \mathbf{i}+(x-2 x z) \mathbf{j}-x y \mathbf{k}\)

By stokes theorem \(\int_s \nabla \times \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\int_c \mathbf{F} \cdot d \mathbf{r}=\int_c \mathbf{F}_1 d x+\mathbf{F}_2 d y+\mathbf{F}_3 d z\)

= \(\int_c y d x+(x-2 x z) d y-x y d z\)

Above the x y – plane the sphere is \(z=0, x^2+y^2=a^2\)

∴ \(\int_c \mathbf{F} . d \mathbf{r}=\int_c y d x+x d y\) put \(x=a \cos \theta, y=a \sin \theta, d x=-a \sin \theta, d y=a \cos \theta d \theta\) and \(\theta\) varies from 0 to 2π

∴ \(\int_c \mathrm{~F} . d \mathbf{r}=\int_0^{2 \pi}[(a \sin \theta)(-a \sin \theta)+(a \cos \theta)(a \cos \theta)] d \theta\)

= \(a^2 \int_0^{2 \pi} \cos 2 \theta \cdot d \theta=a^2\left[\frac{\sin 2 \theta}{2}\right]_0^{2 \pi}=0\)

Applications Of Stokes’ Theorem In Plane Integral Transformations

Example.2 Prove by Stokes theorem that curl brad Φ=0.

Solution:

Stokes theorem

Let S be a surface enclosed by a simple closed curve C.

∴ By Stokes theorem \(\int_s(curl. \text{grad} \phi). \mathbf{N} d \mathbf{S}=\int_c[\nabla \times(\vee \phi)] . \mathbf{N} d \mathbf{S}=\oint_c \nabla \phi . d \mathbf{r}\)

= \(\int_c\left(\mathbf{i} \frac{\partial \phi}{d x}+\mathbf{j} \frac{\partial \phi}{d y}+\mathbf{k} \frac{\partial \phi}{d z}\right) \cdot(\mathbf{i} d x+\mathbf{j} d y+\mathbf{k} d z)\)

= \(\int_c\left(\frac{\partial \phi}{d x} d x+\frac{\partial \phi}{d y} d y+\frac{\partial \phi}{d z} d z\right)=\int_c d \phi=[\phi]_p^p\) where P is any p t on C=0.

∴ \(\int_c(\text{curl} \text{grad} \phi) \cdot \mathbf{N} d \mathbf{S}=0 \Rightarrow \text{curlgrad} \phi=0\)

Example.3 Verify Stokes theorem for A=(2x-y)i-yz²j-y²zk, where S is the upper half surface of the sphere x²+y²+z²=1 and C is its boundary.

Solution: The boundary C of S is a circle in xy-plane i.e. x+y=1,z=0

The parametric equation. Is x=cos t, y= sin t , z=0 for 0≤ t ≤ 2π

⇒ \(\int_c \mathbf{A} \cdot d \mathbf{r}\)=\(\int_c \mathbf{F}_1 d x+\mathbf{F}_2 d y+\mathbf{F}_3 d z\) = \(\int_c(2 x-y) d x-y z^2 d y-y^2 z d z\)

= \(\int_c(2 x-y) d x\) ∴ \(z=0, d z=0\)

= \(-\int_0^{2 \pi}(2 \cos t-\sin t) \sin t d t=\int_0^{2 \pi} \sin ^2 t d t-\int_0^{2 \pi} \sin 2 t d t\)

= \(4 \int_0^{\pi / 2} \sin ^2 t \cdot d t+\left[\frac{\cos 2 t}{2}\right]_0^{2 \pi}=4 \frac{1}{2} \cdot \frac{\pi}{2}+\frac{1}{2}(1-1)=\pi\)

Also \(\nabla \times \mathbf{A}=\left|\begin{array}{ccc}\mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ 2 x-y & -y z^2 & -y^2 z\end{array}\right|\) = k

∴ \(\int_z(\nabla \times \mathbf{A}) \cdot \mathbf{N} d \mathbf{S}=\int_z \mathbf{k} \cdot \mathbf{N} d \mathbf{S}=\int_R \int d x d y\)

Since \(\mathbf{k} \cdot \mathbf{N} d \mathbf{S}=d x d y\) and \(\mathbf{R}\) is the projection of S on x y-plane.

Now \(\iint_R d x d y=4 \int_{x=0}^1 \int_{y=0}^{\sqrt{\left(1-x^2\right)}} d y d x=4 \int_0^1 \sqrt{\left(1-x^2\right)} d x\) put \(x=\sin \theta, d x=\cos \theta d \theta\)

= \(4 \int_0^{\pi / 2} \cos ^2 \theta \cdot d \theta=4 \cdot \frac{1}{2} \frac{\pi}{2}=\pi\)

Thus Stokes’s theorem is verified.

Practical Examples Of Stokes’ Theorem In A Plane

Example.4 Verify Sokes theorem for F=-y³ i+x³ j, where S is the circular disc x²+y²≤1, z=0

Solution:

Given \(\mathrm{F}=-y^3 \mathbf{i}+x^3 \mathbf{j}\)

The boundary C of S is a circle in xy-plane

⇒ \(x^3+y^2=1,\)

In parametric form \(x=\cos \theta, y \sin \theta, z=0\) where \(0 \leq \theta \leq 2 \pi\)

∴ \(\int_c \mathrm{~F} . d \bar{r}=\int_c \mathrm{~F}_1 d x+\mathrm{F}_2 d y+\mathrm{F}_3 d z=\int_c\left(-y^3 d x+x^3 d y\right)\)

= \(\int_{2 \pi}^{2 \pi}\left[-\sin ^3 \theta(-\sin \theta)+\cos ^3 \theta \cos \theta\right] d \theta=\int_0^{\pi / 2}\left(1-2 \sin ^2 \theta \cos ^2 \theta\right) d \theta\)

= \(\int_0^{2 \pi} 1 d \theta-2 \int_0^{2 \pi} \sin ^2 \theta \cos ^2 \theta d \theta=2 \pi-2(4) \int_0^2 \sin ^2 \theta \cos ^2 \theta d \theta=2 \pi-8 \cdot \frac{1}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2}=\frac{3 \pi}{2}\)

⇒ \(\nabla \times F=\left|\begin{array}{ccc}
i & j & k \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
-y^3 & x^3 & 0
\end{array}\right|\)

= \(k\left(3 x^2+3 y^2\right)\)

∴ \(\int(\nabla \times \mathrm{F}) \mathbf{N} d \mathrm{~S}=3 \int_s\left(x^2+y^2\right) \mathbf{k} \cdot \mathbf{N} d \mathrm{~S}\)

= \(3 \iint_R\left(x^2+y^2\right) d x d y\)…………(1)

Since \((\mathbf{k} . \mathbf{N}) d \mathrm{~S}=d x d y\) and R is the region of xy – plane

For solving (1) put x = \(r \cos \phi, y=r \sin \phi\)

∴ dx dy = \(r d r d \phi\) and r varies from 0 to 1 and \(0 \leq \phi \leq 2 \pi\)

∴ \(\int(\nabla \times \mathrm{F}) \mathbf{N} d \mathrm{~S}=3 \int_{\phi=0}^{2 \pi} \int_{r=0}^1 r^2 \cdot r d r d \phi=\frac{3 \pi}{2}\),

Hence the verification of the theorem.

Example.5 If F= (y²+z²-x²)i+(z²+x²-y²)j+(x²+y²-z²)k, evaluate ∫curl F.Nds taken over the portion of the surface x²+y²-2ax+az=0 above the plane z=0.

Solution:

Given \(F=\left(y^2+z^2-x^2\right) \mathbf{i}+\left(z^2+x^2-y^2\right) \mathbf{j}+\left(x^2+y^2-z^2\right) \mathbf{k}\)

By Stokes theorem \(\int_S(\nabla \times \mathrm{F}) \cdot \mathrm{N} d \mathrm{~S}=\int_C \mathrm{~F} \cdot d r\)

where C is the circle given by \(x^2+y^2-2 a x=0, z=0\) i.e. \((x-a)^2+y^2=a^2, z=0\)

In parameters the equation of the circle C is

x = \(a+a \cos \theta\),

y = \(a \sin \theta \text {, }\)

z = 0

∴ dx = \(-a \sin \theta d \theta \text {, }\)

dy = \(a \cos \theta d \theta\),

dz=0

∴ \(F. d r=F_1 d x+F_2 d y+F_3 d z\)

= \(\left(y^2+z^2-x^2\right) d x+\left(z^2+x^2-y^2\right) d y+\left(x^2+y^2-z^2\right) d z\)

= \(\left(y^2-x^2\right) d x+\left(x^2-y^2\right) d y\) on the circle C=\(\left(x^2-y^2\right)(d y-d x)\)

= \(\left[(a+a \cos \theta)^2-a^2 \sin ^2 \theta\right][a \cos \theta+a \sin \theta] d \theta\)

= \(a^3\left(1+2 \cos \theta+\cos ^2 \theta-\sin ^2 \theta\right)(\cos \theta+\sin \theta) d \theta\)

∴ \(\int_C F \cdot d r=a^3 \int_0^{2 \pi}\left(1+2 \cos \theta+\cos ^2 \theta-\sin ^2 \theta\right)(\cos \theta+\sin \theta) d \theta\)

= \(a^3 \int_0^{2 \pi}\left(1+2 \cos \theta+\cos ^2 \theta-\sin ^2 \theta\right) \cos \theta d \theta\) the other integrals vanish

= \(2 a^3 \int_0^\pi\left(1+2 \cos \theta+\cos ^2 \theta-\sin ^2 \theta\right) \cos \theta d \theta\)

= \(2 a^3 \int_0^\pi 2 \cos ^2 \theta \cdot d \theta\) the other integrals vanish

= \(8 a^3 \int_0^{\pi / 2} \cos ^2 \theta \cdot d \theta=8 a^3 \frac{1}{2} \cdot \frac{\pi}{2}=2 a^3 \pi\)

Integration Techniques Using Stokes’ Theorem In A Plane

Example.6 Evaluate \( \int_Cy \)dx + z dy + x dz where C is the curve of the Intersection of x²+y²+z²=a² and x+z=a.

Solution:

y dx+z dy+x dz = \((y \bar{i}+z \bar{j}+x \bar{k}) \cdot(\bar{i} d x+\bar{j} d y+\bar{k} d z)=\bar{F} \cdot d \bar{r}\) where \(\bar{F}=y \bar{i}+z \bar{j}+x \bar{k}\)

by Stokes theorem \(\int_C F \cdot d \bar{r}=\int_S \text{curl} \bar{F} \cdot \overline{\mathrm{N}} d S\)

∴ \(\text{curl} \bar{F}=\nabla \times \bar{F}\) =\(\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
y & z & x
\end{array}\right|\) = \(-(\bar{i}+j+\bar{k})\)

Let the projection be taken in xy-plane

⇒ \(\overline{\mathrm{N}}=\bar{k}\)

∴ \(\int_C \bar{F} \cdot d \bar{r}=-\int_S(\bar{i}+\bar{j}+\bar{k}) \cdot \bar{k} d s=-\int_S d s=-S\)

where S is the surface area of the sphere

⇒ \(\mathrm{S}=4 \pi a^2\)

∴ \(\int \bar{F} . d \bar{r}=-4 \pi a^2\)

Example.7 Prove that \(\oint_c(f \nabla g) \cdot d r\)=\(\int_S[\nabla \times(f \nabla g)] . \mathrm{N} d \mathrm{~S}\)

Solution:

By Stokes theorem \(\oint_c(f \nabla g). d r=\int_S[\nabla \times(f \nabla g)]\). NdS

= \(\int_S[\nabla f \times \nabla g+f \quad curl\quad grad \quad g] \cdot \mathrm{N} d \mathrm{~S}=\int_S(\nabla f \times \nabla g) \cdot \mathrm{N} d \mathrm{~S}\)

Example.8 Prove that\(\int_S \phi \text { curlf. } d S\)=\(=\int_C \phi \mathrm{f} \cdot d r\) – \(\begin{equation}\int_S\end{equation}\) grad Φ ×f.dS

Solution:

Applying Stokes theorem to the function \(\phi \mathrm{f}\)

⇒ \(\int_C \phi \mathrm{f} . d r=\int \text{curl}(\phi f) \cdot \mathrm{N} d \mathrm{~S}=\int_S(\text{grad} \phi \times \mathrm{f}+\phi \text{curlf}) \cdot d S\) using the formula

∴ \(\int_S \phi \text{curl} \mathrm{f} . d \mathrm{~S}=\int_C \phi \mathrm{f} . d r-\int_S \nabla \phi \times \mathrm{f} . d S\)

Vector Calculus Problems Using Stokes’ Theorem

Example.9 Prove that\(\oint_C(f \nabla f) \cdot d r\)=0

Solution:

By Stokes theorem \(\int_{\mathrm{C}}(f \nabla f) \cdot d r=\int_{\mathrm{S}}(\text{curl} f \nabla f) \cdot \mathrm{N} d \mathrm{~S}=\int_{\mathrm{S}}[f \text{curl} \nabla f+\nabla f \times \nabla f] . \mathrm{N} d \mathrm{~S}\)

= \(\int 0 \cdot \mathrm{N} d \mathrm{~S}=0\)

(because curl \(\nabla f=0\) and \(\nabla f \times \nabla f=0\))

Example.10 Verify Stokes’s theorem for F=(y-z+2)i+(yz+4)j-xzk where S is the surface of the cube x=0,y=0,z=0,x=2,y=2,z=2 above the xy-plane.

Solution:

Given \(\mathbf{F}=(y-z+2) \mathbf{i}+(y z+4) \mathbf{j}-x z \mathbf{k}\) where S is the surface of the cube. \(x=0, y=0, z=0\), and x=2, y=2, z=2 above the xy-plane.

By Stoke’s theorem, we have \(\int \text{Curl} \mathbf{F} \cdot \mathbf{n} d s=\int \mathbf{F} \cdot d \mathbf{r}\)

⇒ \(\nabla \times \mathbf{F}\)=\(\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\hat{o}}{\partial z} \\
y-z+2 & y z+4 & -x z
\end{array}\right|\)

= \(\mathbf{i}(0-y)-\mathbf{j}(-z+1)+\mathbf{k}(0-1)=-y \mathbf{i}-(1-z) \mathbf{j}-\mathbf{k}\)

∴ \(\nabla \times \mathbf{F} \cdot \mathbf{n}=\nabla \times \mathbf{F} \cdot \mathbf{k}=(y \mathbf{i}-(1-z) \mathbf{j}-\mathbf{k}) \cdot \mathbf{k}=-1\)

∴ \(\int \nabla \times \mathbf{F} \cdot \mathbf{n} d s=\int_0^2 \int_0^2-1 d x d y\) (because z=0, d z=0) =-4…….(1)

To find \(\int F \cdot d r\)

⇒ \(\int \mathbf{F} \cdot d \mathbf{r}=\int((y-z+2) \mathbf{i}+(y z+4) \mathbf{j}-x z \mathbf{k}) \cdot(d x \mathbf{i}+d y \mathbf{j}+d z \mathbf{k})\)

= \(\int[(y-z+2) d x+(y z+4) d y-(x z) d z]\)

S is the surface of the cube above the XY plane

∴ \(z=0 \quad \Rightarrow d z=0\)

∴ \(\int \mathbf{F} \cdot d \mathbf{r}=\int(y+2) d x+\int 4 d y\)……(1)

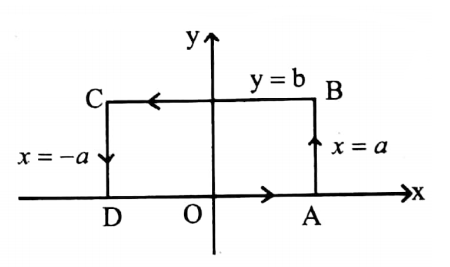
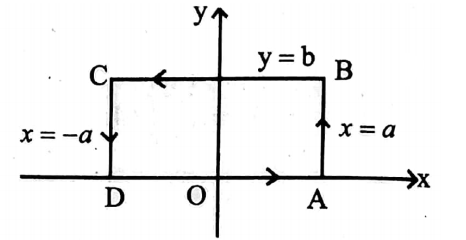
Along \(\overline{O A}, y=0, z=0, d y=0, d z=0, x\) changes from 0 to 2 .

⇒ \(\int_0^2 2 d x=2[x]_0^2=4\)……(2)

Along \(\overline{B C}, y=2, z=0, d y=0, d z=0, x\) changes from 2 to 0 .

⇒ \(\int_2^0 4 d x=4[x]_2^0=-8\)…..(3)

Along \(\overline{A B}, x=2, z=0, d x=0, d z=0, y\) changes from 0 to 2 .

⇒ \(\int \mathbf{F} \cdot d \mathbf{r}=\int_0^2 4 d y=[4 y]_0^2=8\)……(4)

Along \(\overline{C O}, x=0, z=0, d x=0, d z=0, y\) changes from 2 to 0 .

⇒ \(\int_2^0 4 d y=-8\)……(5)

Above the surface when z=2

Along \(O^{\prime} A^{\prime}, \int_0^2 \mathbf{F} d \mathbf{r}=0\)….(6)

Along \(A^{\prime} B^{\prime}, x=2, z=2, d x=0, d z=0, y\) changes from 0 to 2 .

⇒ \(\left.\left.\int_0^2 \bar{F} \cdot \bar{r}=\int_0^2(2 y+4) d y=2 \cdot \frac{y^2}{2}\right]_0^2+4 y\right]_0^2=4+8=12\)…..(7)

Along \(B^{\prime} C^{\prime}, y=2, z=2, d y=0, d z=0, x\) changes from 2 to 0 .

⇒ \(\int_2^0 \mathbf{F} \cdot d \mathbf{r}=0\)……(8)

Along \(C^{\prime} D^{\prime}, x=0, z=2, d x=0, d z=0, y\) changes from 2 to 0 .

⇒ \(\left.\left.\int_2^0(2 y+4)=2 \cdot \frac{y^2}{2}\right]_2^0+4 y\right]_2^0=-12\)…….(9)

(2)+(3)+(4)+(5)+(6)+(7)+(8)+(9) gives

⇒ \(\int_C \mathbf{F} \cdot d \mathbf{r}=4-8+8-8+0+12+0-12=-4\)…..(10)

By Stoke’s theorem, we have \(\int \mathbf{F} \cdot d \mathbf{r}=\int \text{curl} \mathbf{F} \cdot \mathbf{n} d s=-4\)

Hence Stoke’s theorem is verified.

Integral Transformations Exercise 7(b)

1. Evaluate \(\oint_C\)(3x+4y) dx+(2x-3y) dy where C is a circle x²+y²=4

Solution:

Given \(\oint_C(3 x+4 y) d x+(2 x-3 y) d y\). Here \(\mathbf{P}=3 x+4 y, \mathbf{Q}=2 x-3 y\)

By Green’s theorem \(\int_C \mathbf{P} d x+\mathbf{Q} d y=\iint_S\left(\frac{\partial \mathbf{Q}}{\partial x}-\frac{\partial \mathbf{P}}{\partial y}\right) d x d y\)

= \(\iint_S(2-4) d x d y=-2 \int_S d \mathrm{~A}=-2 \mathrm{~A}=-2 \pi(2)^2=-8 \pi\)

2. Find \(\oint_C\)(x²-2xy)dx+(x²y+z)dy around the boundary C of the regeion defined by y²= 8x and x=2 by Green’s theorem.

Solution: 

Given \(\oint\left(x^2-2 x y\right) d x+\left(x^2 y+2\right) d y\) .

P = \(x^2-2 x y, \mathrm{Q}=x^2 y+2\)

By Green’s theorem the given integral

= \(\iint_S\left(\frac{\partial \mathbf{Q}}{\partial x}-\frac{\partial \mathbf{P}}{\partial y}\right) d x d y=\iint_S(2 x y+2 x) d x d y\)

For the region \(y^2=8 x\) and x=2

x varies from 0 to 2 . y varies from \(-\sqrt{8 x}\) to \(\sqrt{8 x}\).

⇒ \(\int_{x=0}^2 \int_{y=-\sqrt{8 x}}^{\sqrt{8 x}} 2 x(y+1) d x d y=\int_0^2 2 x\left[\frac{y^2}{2}+y\right]_{-\sqrt{8 x}}^{\sqrt{8 x}} d x=+8 \sqrt{2} \int_0^2 x^{3 / 2} d x=\frac{128}{5}
\)

Examples From Integrals Exercise 7.2

3. Find the area bounded by one arc of the cycloid x=a(θ-sin). y=a(1-cosθ), a>0 and the axis.

Solution:

The area of the curve \(\mathbf{A}=\frac{1}{2} \oint_C(x d y-y d x)\)

Now \(x=a(\theta-\sin \theta), y=a(1-\cos \theta) \theta\) varies from 0 to \(2 \pi\).

∴ A = \(\frac{1}{2} \int_{\mathcal{C}}^{2 \pi}\left[a(\theta-\sin \theta) a \sin \theta-a^2(1-\cos \theta)^2\right] d \theta\)

= \(\frac{a^3}{2} \int_0^{2 \pi} \theta \sin \theta-\frac{a^2}{2} \int_0^{2 \pi} 2(1-\cos \theta) d \theta\)

= \(\frac{a^2}{2}[-\theta \cos \theta+\sin \theta]_0^{2 \pi}-2 \frac{a^2}{2}[\theta-\sin \theta]_0^{2 \pi}=3 \pi a^2\)

4. Find the area bounded by the hypocycloid x^2/3+y^2/3=a^2/3, a>0 [Hint: Take x=a cos³ θ,y= a sin³θ ].

Solution:

Here x=a cos³  θ, y= asin³ θ and varies from 0 to  π/2

A = \(\int_C x d y-y d x=\int\left(a \cos ^3 \theta\right) \cdot\left(3 a \sin ^2 \theta \cos \theta\right)+\left(a \sin ^3 \theta\right)\left(3 a \cos ^2 \sin \theta\right) d \theta\)

= \(3 a^2 \cdot 2 \int_0^{\pi / 2} \sin ^2 \theta \cos ^2 \theta d \theta=\frac{3}{8} \pi a^2\)

5. Find \(\oint_C\)(3x²– 8y²)dx+ (4y-6xy)  dy by Green’s theorem where C is the boundary defined by x=0, y=0,  x+y=1.

Solution:

P = \(3 x^2-8 y^2, \mathbf{Q}=4 y-6 x y\)

⇒ \(\frac{\partial \mathbf{P}}{\partial y}=-16 y \quad \frac{\partial \mathbf{Q}}{\partial x}=-6 y\)

⇒ \(\int_C \mathbf{P} d x+\mathbf{Q} d y=\iint_S\left(\frac{\partial \mathbf{Q}}{\partial x}-\frac{\partial \mathbf{P}}{\partial y}\right) d x d y\)

= \(\int_{x=0}^1 \int_{y=0}^{1-x}(10 y) d y d x=10 \int_0^1\left[\frac{y^2}{2}\right]_0^{1-x} d x=5 \int_0^1(1-x)^2 d x=\frac{5}{3}\)

Integral Calculus Exercise 7.2 Problems

6. Find \(\oint_C\)(2x²-y²) dx+(x²+y²) dy where C is the boundary of the surface in the xy-plane enclosed by the x-axis and the circle x²+y²=1.

Solution:

⇒ \(\frac{\partial \mathbf{P}}{\partial y}=-2 y \quad \frac{\partial \mathbf{Q}}{\partial x}=2 x\)

= \(\iint_S\left(\frac{\partial \mathbf{Q}}{\partial x}-\frac{\partial \mathbf{P}}{\partial y}\right) d x d y=\int_{x=-1}^1 \int_{y=0}^{\sqrt{1-x^2}}(2 y+2 x) d x d y\)

= \(\int_{-1}^1\left[2 x y+y^2 \int_{y=0}^{\sqrt{1-x^2}} d x=\int_{-1}^1\left[2 x \sqrt{1-x^2}+1-x^2\right] d x\right.\)

= \(\left[-\frac{2}{3}\left(1-x^2\right)^{3 / 2}+x-\frac{x^3}{3}\right]_{-1}^1=\frac{4}{3}\)

7. Find \(\oint_C\)(x²+y²)dx+3xy² dy whre C is the circle x²+y²=4 in xy-plane.

Solution:

⇒ \(\int \int\left(\frac{\partial \mathbf{Q}}{\partial x}-\frac{\partial \mathbf{P}}{\partial y}\right) d x d y=\iint_S\left(3 y^2-2 y\right) d x d y\)

= \(\int_{x=-2}^2 \int_{y=-\sqrt{4-x^2}}^{\sqrt{4-x^2}}\left(3 y^2-2 y\right) d y d x=\int_{-2}^2\left[y^3-y^2\right]_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} d x\)

= \(2 \int_{-2}^2\left(4-x^2\right)^{3 / 2} d x=2.2 \int_0^2\left(4-x^2\right)^{3 / 2} d x\)

= \(64 \int_0^{\pi / 2} \cos ^4 \theta \cdot d \theta=64 \cdot \frac{3}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2}=12 \pi\)

Integral Transformations Exercise 7.1

1. if N is the unit outward drawn normally to any closed surface, show that \(\int_V\) div N dV=S [Hint: Apply Gauss’s theorem for the unit vector N]

Solution: By Gauss’s Theorem \(\int_{\mathbf{V}}(\nabla \cdot \mathbf{N}) d \mathbf{V}=\int_{\mathbf{V}} \mathbf{N} \cdot \mathbf{N} d \mathbf{S}=\int_{\mathbf{V}} d \mathbf{S}\)

2. Apply the divergence theorem to evaluate ∫ \(\int_S\) (x+z)dy dz +(y+z)dz dx +(x+y)dx dy where is the surface of the sphere x²+y²+z²=4.

Solution:

Given \(\iint_S(x+z) d y d z+(y+z) d z d x+(z+x) d x d y\)

Here \(\mathbf{F}_1 \stackrel{s}{=} x+z, \mathbf{F}_2=y+z, \mathbf{F}_3=x+y\)

∴ \(\frac{\partial \mathbf{F}_1}{\partial x}=1, \frac{\partial \mathbf{F}_2}{\partial y}=1, \frac{\partial \mathbf{F}_3}{\partial z}=0\)

∴ \(\frac{\partial \mathbf{F}_1}{\partial x}+\frac{\partial \mathbf{F}_2}{\partial y}+\frac{\partial \mathbf{F}_3}{\partial z}=1+1+0=2\)

By Gauss’s theorem \(\iint_S \mathbf{F}_1 d y d z+\mathbf{F}_2 d z d x+\mathbf{F}_3 d x d y\)

= \(\iiint_V\left(\frac{\partial \mathbf{F}_1}{\partial x}+\frac{\partial \mathbf{F}_2}{\partial y}+\frac{\partial \mathbf{F}_3}{\partial z}\right) d x d y d z=\iiint 2 d x d y d z=2 \int_V d \mathbf{V}=2 \mathbf{V}\)

= \(2\left[\frac{4}{3} \pi(2)^3\right]=\frac{64 \pi}{3}\) [because For the sphere radius =2]

Examples From Integrals Exercise 7.1

3. Evalute ∫ \(\int_S\)x dydz + y dzdx + z dxdy where S- is the surface x²+y²+z²=1.

Solution:

Given

∫ \(\int_S\)x dydz + y dzdx + z dxdy where S- is the surface x²+y²+z²=1

Here \(\mathbf{F}_1=x, \mathbf{F}_2=y, \mathbf{F}_3=z\)

∴ \(\frac{\partial \mathbf{F}_1}{\partial x}+\frac{\partial \mathbf{F}_2}{\partial y}+\frac{\partial \mathbf{F}_3}{\partial z}=1+1+1=3\)

⇒ \(\mathrm{div} \mathbf{F}=3\)

∴ \(\iint_S x d y d z+y d z d x+z d x d y=\int_V \mathrm{div} \mathbf{F} d \mathbf{V}\)

⇒ \(\int_V 3 d \mathbf{V}=3 \mathbf{V}=3 \frac{4}{3} \pi=4 \pi\)……..[radius =1]

4. Find \(\int_S\) F.N dS where F= 2x²-y²j+4xzk and S is the region in the first octant bounded by y²+z²=9 and x=0, x=2

Solution:

⇒ \(\int_S \mathbf{F} . \mathbf{N} d \mathbf{S}=\int_V \text{div} \mathbf{F} d \mathbf{V}\)

= \(\int_V\left[\frac{\partial}{\partial x}\left(2 x^2\right)+\frac{\partial}{\partial y}\left(-y^2\right)+\frac{\partial}{\partial z}(4 x z)\right] d x d y d z\)

= \(\int_{x=0}^2 \int_{y=0}^3 \int_{z=0}^{\sqrt{\left(9-y^2\right)}}(8 x-2 y) d x d y d z=\int_{x=0}^2 \int_{y=0}^3(8 x-2 y) \sqrt{\left(9-y^2\right)} d x d y\)

= \(\int_0^2 8 x\left[\frac{1}{2} y \sqrt{\left(9-y^2\right)}+\frac{1}{2} \cdot 9 \text{Sin}^{-1} \frac{y}{3}\right]_0^3+\left[\frac{2}{3}\left(9-y^2\right)^{3 / 2}\right]_0^3 d x\)

= \(\int_0^2 8 x\left(\frac{9}{2} \cdot \frac{\pi}{2}\right)+\left(0-\frac{2}{3} \cdot 27\right) d x=\left[18 \pi \cdot \frac{x^2}{2}-18 x\right]_0^2=36 \pi-36\)

Integral Calculus Exercise 7.1 Problems

5. Evalute \(\int_S\) F.N dS where F= 2x²yi-y²j+4xzk taken over the region in the first octant bounded by y²+z²=9 and x=2.

Solution:

Given \(\mathbf{F}=2 x^2 y \mathbf{i}-y^2 \mathbf{j}+4 x z^2 \mathbf{k}\) . ∴ \(\text{div} \mathbf{F}=4 x y-2 y+8 x z\)

∴ \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\int_V \text{div} \mathbf{F} d \mathbf{V}=\int_{x=0}^2 \int_{y=0}^3 \cdot \int_{z=0}^{\sqrt{9-y^2}}(4 x y-2 y+8 x z) d x d y d z\)

= \(\int_{x=0}^2 \int_{y=0}^3[4 x y z-2 y z+4 x z^2 \int_0^{\sqrt{9-y^2}} d x^{\prime} d y\)

= \(\int_{x=0}^2 \int_{y=0}^3\left[4 x y \sqrt{9-y^2}-2 y \sqrt{9-y^2}+4 x\left(9-y^2\right) d x\right] d y\)

= \(\int_{y=0}^3\left[2 x^2 y \sqrt{9-y^2}-2 y \sqrt{9-y^2}+2 x^2\left(9-y^2\right)\right]_{x=0}^2 d y\)

= \(\int_0^3\left[8 y \sqrt{9-y^2}-4 y \sqrt{9-y^2}+8\left(9-y^2\right)\right] d y\)

= \(\int_0^3\left[4 y \sqrt{9-y^2}+8\left(9-y^2\right)\right] d y\)

= \(\left[-\frac{4}{3}\left(9-y^2\right)^{3 / 2}+8\left(9 y-\frac{y^3}{3}\right)\right]^3=36+144=180\)

6. Find \(\int_S\)(4xi-2y²j+z²k .N.dS where S is the region bounded by x²+y=4, z=0 and z=3.

Solution:

Given \(\mathbf{F}=4 x \mathbf{i}-2 y^2 \mathbf{j}+z^2 \mathbf{k}\)

∴ \(\text{div} \mathbf{F}=(4-4 y+2 z)\)

⇒ \(\int_S \mathrm{~F} \cdot \mathrm{N} d \mathrm{~S}=\int_V \text{div} \mathrm{F} d \mathrm{~V}=\int_{x=-2}^2 \int_{y=-\sqrt{4-x^2}}^{\sqrt{4-x^2}} \int_{z=0}^3(4-4 y+2 z) d x d y d z\)

= \(\int_{x=-2}^2 \int_{y=-\sqrt{4-x^2}}^{\sqrt{4-x^2}}\left[4 z-4 y z+z^2\right]_{z=0}^3 d x d y\)

= \(\int_{x=-2}^2 \int_{y=-\sqrt{4-x^2}}^{\sqrt{4-x^2}}(21-12 y) d x d y=\int_{x=-2}^2 42 \sqrt{4-x^2} d x=84 \pi\)

7. Using the divergence theorem, show that the volume V of the region bounded by surface S is V = ∫\(\int_S\)x dx dy = ∫\(\int_S\)y dx dz = ∫\(\int_S\)z dx dy =\(\frac{1}{3}\) ∫\(\int_S\)x dx dy + y dx dz + z dx dy

Solution:

By Gauss’s theorem \(\iint_S x d y d z=\int_V \frac{\partial}{\partial x}(x) d \mathbf{V}=\int_V d \boldsymbol{V}=\mathbf{V}\)

Similarly \(\iint_S y d z d x=\int_S^S z d x d y=\mathbf{V}\)

∴ Adding \(3 \mathbf{V}=\iint_S(x d y d z+y d z d x+z d x d y)\)

⇒ \(\mathbf{V}=\frac{1}{3} \iint_S(x d y d z+y d z d x+z d x d y)\)

Integral Techniques Used In Exercise 7.1

8. If F= 2xyi-yzj+x²k find \(\int_S\)F.NdS where S is the entire surface of the cube bounded by the coordinate planes and the planes x=a, y=a, z=a by the application of Gauss’s theorem.

Solution:

= \(\int_0^a \int_0^a \int_0^a(2 y-z) d x d y d z=\int_0^a \int_0^a(2 y-z)[x]_0^a d y . d z\)

= \(a \int_0^a\left[y^2-y z\right]_{y=0}^a d z=a \int_0^a\left(a^2-a z\right) d z=a\left[a^2 z-a \frac{z^2}{2}\right]_0^a=\frac{1}{2} a^4\)

9. If F= 4xz\(\overline{\mathrm{i}}\)-y\(\overline{\mathrm{j}}\) =yz\(\overline{\mathrm{k}}\) find \(\int_S\)F.Nds by divergence theorem where S is the surface of the cube bounded by x=0, x=1, y=0,y=1,z=0, z=1.

Solution:

⇒ \(\int_V \text{div} \mathbf{F} d \mathbf{V}=\int_0^1 \int_0^1 \int_0^1(4 z-y) d x d y d z=\int_0^1 \int_0^1(4 z-y) d y d z\)

= \(\int_0^1\left[4 z y-\frac{y^2}{2}\right]_{\nu=0}^1 d z=\int_0^1\left(4 z-\frac{1}{2}\right) d z=\frac{3}{2}\)

Integral Transformations Solved Problems

Example.1 Show that the area bounded by a simple closed curve C is given by \(\frac{1}{2} \oint_C\)xdy-ydx and hence find the area of the ellipse x=a cos θ,y= bsinθ, 0 ≤ θ ≤ 2π

Solution:

By Green’s theorem \(\int_C \mathrm{P} d x+\mathrm{Q} d y=\iint_S\left(\frac{\partial \mathrm{Q}}{\partial x}-\frac{\partial \mathrm{P}}{\partial y}\right) d x d y\)

Put \(\mathrm{P}=-y\) and \(\mathrm{Q}=+x \frac{\partial \mathrm{P}}{\partial y}=-1, \frac{\partial \mathrm{Q}}{\partial x}=+1\)

∴ \(\oint_C x d y-y d x=2 \int_S d x d y=2 \mathrm{~A}\) where A is the area of the surface S

∴ \(\frac{1}{2} \int_C x d y-y d x=\mathrm{A}\)

Now for the ellipse x = \(a \cos \theta, y=b \sin \theta\).

Area = \(\frac{1}{2} \oint_C x d y-y d x\)

= \(\frac{1}{2} \int_0^{2 \pi}(a \cos \theta)(b \cos \theta)-(b \sin \theta)(-a \sin \theta) d \theta=\frac{1}{2} a b \int_0^{2 \pi} d \theta=\pi a b\)

Example.2 Evaluate \(\oint_C\)(cos x sin y – xy) dx+ sin x cos y dy, by Green’s theorem where C is the circle x²+y² =1

Solution:

Given

\(\oint_C\)(cos x sin y – xy) dx+ sin x cos y dy

By Green’s theorem, we have \(\int_C \mathrm{P} d x+\mathrm{Q} d y=\iint_S\left(\frac{\partial \mathrm{Q}}{\partial x}-\frac{\partial \mathrm{P}}{\partial y}\right) d x d y\)

Here \(\mathrm{P}=\cos x \sin y-x y, \mathrm{Q}=\sin x \cos y\)

∴ \(\frac{\partial \mathrm{P}}{\partial y}=\cos x \cos y-x, \frac{\partial \mathrm{Q}}{\partial x}=\cos x \cos y\)

for the circle, \(x^2+y^2=1\). Changing to polar coordinates.

x = \(r \cos \theta, y=r \sin \theta, d x d y=r d r d \theta\)

∴ \(\oint_C(\cos x \sin y-x y) d x+\sin x \cos y d y \int_S[\cos x \cos y-(\cos x \cos y-x)] d x d y\)

= \(\iint_S x d x d y=\int_{\theta=0}^{2 \pi} \int_{r=0}^1 r \cos \theta \cdot r d r d \theta=\int_0^{2 \pi}\left[\frac{r^3}{3}\right]_0^1 \cos \theta d \theta=\frac{1}{3} \int_0^{2 \pi} \cos \theta d \theta=\frac{1}{3}[\sin \theta]_0^{2 \pi}=0\)

Practical Examples Of Green’S Theorem In Vector Calculus

Example.3 Verify Green’s theorem in the plane for \(\oint_C\)(3x²-8y²)dx+(4x-6xy) dy where C is the region bounded by y=\(\sqrt{x}\)  and y=x²

Solution:

Here \(\mathrm{P}=3 x^2-8 y^2 \quad \frac{\partial \mathrm{P}}{\partial y}=-16 y \quad \mathrm{Q}=4 y-6 x y \quad \frac{\partial \mathrm{Q}}{\partial x}=-6 y\)

Hence to Green’s theorem

1. \(\int_C\left(3 x^2-8 y^2\right) d x+(4 y-6 x y) d y\)

= \(\iint_S(-6 y+16 y) d x d y=10 \int_{x=0}^1 \int_{y=x^2}^C y d y d x\)

=\(10 \int_0^1\left[\frac{y^2}{2}\right]_{x^2}^{\sqrt{x}} d x=5 \int_0^1\left(x-x^4\right) d x=\frac{3}{2}\)

2. Verification.

The line integral along C

= Line integral along y = \(x^2\) (from O to A) + line integral along \(y^2=x\) (from A to O) = \(\mathrm{I}_1+\mathrm{I}_2\)

∴ \(\mathrm{I}=\int_{x=0}^1\left[3 x^2-8\left(x^2\right)^2\right] d x+\left[4 x^2-6 x\left(x^2\right)\right] 2 x d x=\int_0^1\left(3 x^2+8 x^2-20 x^4\right) d x=-1\)

⇒ \(\mathrm{I}_2=\int_1^0\left(3 x^2-8 x\right) d x+\left(4 \sqrt{x}-6 x^{3 / 2}\right) \frac{1}{2 \sqrt{x}} d x\)

y = \(\sqrt{x}\)

= \(\int_1^0\left(3 x^2-11 x+2\right) d x=\frac{5}{2}\)

∴ \(\mathrm{I}_1+\mathrm{I}_2=-1+\frac{5}{2}=\frac{3}{2}\)

Hence the theorem is verified.

Example.4 Evaluate by Green’s theorem \(\oint_C\)(y-sinx)+cos x dy where C is the triangle enclosed by the lines x=0,x=\(\frac{\pi}{2}\), πy=2x.

Solution:

Here P = \(y-\sin x, \mathrm{Q}=\cos x \quad \frac{\partial \mathrm{P}}{\partial y}=1, \frac{\partial \mathrm{Q}}{\partial x}=-\sin x\)

Hence by Green’s theorem \(\int_C(y-\sin x) d x+\cos x d y=\iint_S(-1-\sin x) d x d y\)

= \(-\int_{x=0}^{\pi / 2} \int_{y=0}^{2 x / \pi}(1+\sin x) d x d y=-\int_0^{\pi / 2}(1+\sin x) \frac{2 x}{\pi} d x\)

= \(-\frac{2}{\pi} \int_0^{\pi / 2}(x+x \sin x) d x=-\left(\frac{\pi}{4}+\frac{2}{\pi}\right)\)

Example.5 Evaluate by greens theorem \(\oint_C\)(x-cosh y) dx +(y +sin x) dy where C is the rectangle with vertices (0,0),(π,0) (π,1) and (0,1)

Solution:

Here \(\mathrm{P}=x^2-\cosh y, \quad \mathrm{Q}=y+\sin x \quad \frac{\partial \mathrm{P}}{\partial y}=-\sinh y, \quad \frac{\partial \mathrm{Q}}{\partial x}=\cos x\)

By Green’s theorem \(\int_C\left(x^2-\cosh y\right) d x+(y+\sin x) d y=\iint_S(\cos x+\sinh y) d x d y\)

= \(\int_{x=0}^\pi \int_{y=0}^1(\cos x+\sinh y) d x d y=\int_0^\pi[(y \cos x+\cosh y)]_0^1 d x=\int_0^\pi[\cos x+\cosh 1-1] d x\)

= \([\sin x+x \cosh 1-x]_0^\pi=\pi[\cosh 1-1]\)

Examples Of Green’S Theorem In Physics And Engineering

Example.6 Verify Greens theorem in the plane for \(\oint_C\)(xy+y²) dx+x²dy where C is the closed curve of the region bounded by y=x and y=x²

Solution:  Solving the curves y=x and y=x² we get the points  of intersection are (0,0) and (1,1)

On the curve y=x²

The limits for x are 0 to 1

y²= x  ⇒ dy =2x dx

⇒ \(\int_{C_1}\left(x y+y^2\right) d x+x^2 d y\)

= \(\int_{x=0}^1\left(x\left(x^2\right)+x^4\right) d x+x^2 2 x d x\)

= \(\int_0^1\left(x^3+x^4+2 x^3\right) d x=\int_0^1\left(3 x^3+x^4\right) d x\)

= \(3 \frac{x^4}{4}+\frac{x^5}{5}_0^1=\frac{3}{4}+\frac{1}{5}-0=\frac{19}{20}\)

On the curve y=x

The limits of x are \(1 \rightarrow 0\)

y = \(x \Rightarrow d y=d x\)

⇒ \(\left.\oint_C\left(x y+y^2\right) d x+x^2 d y=\int_{x=1}^0\left(x(x)+x^2\right) d x+x^2 d x=\int_1^0 3 x^2=\frac{3 x^3}{3}\right]_1^0=-1\)

Adding (1) and (2) : \(\oint_C\left(x y+y^2\right) d x+x^2 d y=\frac{19}{20}-1=-\frac{1}{20}\)

By Green’s theorem, \(\oint_C P d x+Q d y=\iint_R\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\)

R. H. S. \(=\int_{x=0}^1 \int_{y=x^2}^x\left[\frac{\partial}{\partial x}\left(x^2\right)-\frac{\partial}{\partial y}\left(x y+y^2\right)\right] d x d y\)

= \(\int_{x=0}^1 \cdot \int_{y=x^2}^x(2 x-x-2 y) d x d y=\int_{x=0}^1 \int_{y=x^2}^x(x-2 y) d x d y\)

= \(\left.\int_{x=0}^1 x y-y^2\right]_{x^2}^x d x=\int_0^1\left[\left(x^2-x^2\right)-\left(x^3-x^4\right)\right] d x\)

= \(\int_{x=0}^1\left(x^4-x^3\right) d x=\frac{x^5}{5}-\frac{x^4}{4}_0^1=\frac{1}{5}-\frac{1}{4}=-\frac{1}{20}=\text { L. H. S. }\)

∴ Green’s theorem is verified.

Integral Transformations Solved Problems

Example.1 Show that \(\int_S\)(axi+byj+czk).N.dS=4\(\frac{\pi}{3}\) (a+b+c) where S is the surface of the sphere x²+y²+z²=1.

Solution:

Here \(\mathbf{F}=a x \mathbf{i}+b y \mathbf{j}+c z \mathbf{k} \quad \text{div} \mathbf{F}=\nabla . \mathbf{F}=\frac{\partial \mathbf{F}_1}{\partial x}+\frac{\partial \mathbf{F}_2}{\partial y}+\frac{\partial \mathbf{F}_3}{\partial z}=a+b+c\)

By Gauss’s Theorem \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\int_V \nabla \cdot \mathbf{F} d \mathbf{V}=\int_V(a+b+c) d \mathbf{V}=(a+b+c) \mathbf{V}=\frac{4 \pi}{3}(a+b+c)\)

V = \(\frac{4 \pi}{3}\), for the given sphere

Example.2 Verify Gauss’s divergence theorem to evaluate (x³-yz)i-2x²yj+zk).NdS over the surface of a cube bounded by the coordinate planes x=y=z=a.

Solution:

Gauss’s theorem states that \(\iint_{\mathrm{S}} \mathbf{F}_1 d y d z+\mathbf{F}_2 d z d x+\mathbf{F}_3 d x d y=\iiint_V\left(\frac{\partial \mathbf{F}_1}{\partial x}+\frac{\partial \mathbf{F}_2}{\partial y}+\frac{\partial \mathbf{F}_3}{\partial z}\right) d x d y d z\)

From the problem \(\mathbf{F}_1=x^3-y z, \mathbf{F}_2=-2 x^2 y, \mathbf{F}_3=z\)

⇒ \(\frac{\partial \mathbf{F}_1}{\partial x}=3 x^2, \frac{\partial \mathbf{F}_2}{\partial y}=-2 x^2, \frac{\partial \mathbf{F}_3}{\partial z}=1\)

∴ RHS = \(\iiint_V\left(3 x^2-2 x^2+1\right) d x d y d z\)

= \(\int_0^a \int_0^a \int_0^a\left(x^2+1\right) d x d y d z\)

= \(\int_0^a \int_0^a\left[\frac{x^3}{3}+x\right]_0^a d y d z=\frac{1}{3} a^5+a^3\)

Integral Transformations For Spherical Surfaces Using Divergence Theorem

Verification: Let us calculate the value of \(\int \mathbf{F} \cdot \mathbf{N} d \mathbf{S}\) over the six faces of the cube directly

1. For the face PQAR \(\mathbf{N}=\mathbf{i}, d \mathbf{S}=d z d y\) and x=a

∴ \(\int_{S_1} \mathbf{F} . \mathbf{N} d \mathbf{S}=\iint_{S_1}\left[\left(x^3-y z\right) \mathbf{i}-2 x^2 y \mathbf{j}+z \mathbf{k}\right] . \mathbf{i} d z d y\)

= \(\int_{z=0}^a \int_{y=0}^a\left(x^3-y z\right) d z d y=\int_{z=0}^a \int_{y=0}^a\left(a^3-y z\right) d z d y=a^3\left[[y]_0^a[z]_0^a\right]-\left[\frac{y^2}{2}\right]_0^a\left[\frac{z^2}{2}\right]_0^a=a^5-\frac{1}{4} a^4\)

2. For the face OBSC \(\mathbf{N}=-\mathbf{i}, d \mathbf{S}=d y d z\) and x=0

∴ \(\int_{S_2} \mathbf{F} . \mathbf{N} d \mathbf{S}=-\int_{y=0}^a \int_{z=0}^a\left(x^3-y z\right) d y d z=\int_0^a \int_0^a y z d y d z=\left[\frac{y^2}{2}\right]_0^a\left[\frac{z^2}{2}\right]_0^a=\frac{1}{4} a^4\)

because x=0 for this face

3. For the face \(\text{PQBS} \mathbf{N}=\mathbf{j}, d \mathbf{S}=d z d x\) and y=a

∴ \(\int_{S_3} \mathbf{F} . \mathbf{N} d \mathbf{S}=-\int_{x=0}^a \int_{z=0}^a\left(2 x^2 y\right) d x d z=-2 a \int_0^a \int_0^a x^2 d x d z\)

because y = a for this face

= \(-2 a\left[\frac{x^3}{3}\right]_0^a[z]_0^a=-\frac{2}{3} a^5\)

4. For the face OARC \(\mathbf{N}=-\mathbf{j}, d \mathbf{S}=d z d x\) and y=0

⇒ \(\int_{S_4} \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\iint_{S_4} 2 x^2 y d x d z=0\) because on this face y=0

5. For the face PRCS \(\mathbf{N}=\mathbf{k}, d \mathbf{S}=d x d y\) and z=a

∴ \(\int_S \mathbf{F} . \mathbf{N} d \mathbf{S}=\int_{x=0}^a \int_{y=0}^a z d x d y=a \int_0^a \int_0^a d x d y\)

because z=a on this face

= \(a[x]_0^a[y]_0^a=a^3\)

6. For the face OBQA \(\mathbf{N}=-\mathbf{k}, d \mathbf{S}=d x d y\) and z=0

∴ \(\int_S \mathbf{F} . \mathbf{N} d \mathbf{S}=-\int_{x=0}^a \int_{y=0}^a z d x d y=0\) because on this face z=0

Hence for the total faces \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=a^5-\frac{1}{4} a^4+\frac{1}{4} a^4-\frac{2}{3} a^5+0+a^3=\frac{1}{3} a^5+a^3\)

Example.3 Apply Gauss’s theorem to prove that \(\int_S\)r.N.dS=3V

Solution:  By Gauss’s theorem \(\int_S\)r.N.dS=\(\int_V\) div r dv

div \(\mathbf{r}=\nabla \cdot \mathbf{r}=\left(\mathbf{i} \frac{\partial}{\partial x}+\mathbf{j} \frac{\partial}{\partial y}+\mathbf{k} \frac{\partial}{\partial z}\right) \cdot(x \mathbf{i}+y \mathbf{j}+z \mathbf{k})=1+1+1=3\)

∴ \(\int_V \text{div} \mathbf{r} d \mathbf{V}=\int_V 3 d \mathbf{V}=3 V\)

Surface Integral Problems With Gauss’S Divergence On Spheres

Example.4 By transforming into a triple integral, evaluate (x³ dy dz+x²y dz dy+x²z dx dy) where S is the closed surface consisting of the cylinder x²+y²=a² and the circular discs z=0 and z=b.

Solution:

Here \(\mathbf{F}_1=x^3, \mathbf{F}_2=x^2 y, \mathbf{F}_3=x^2 z\)

⇒ \(\frac{\partial \mathbf{F}_1}{\partial x}=3 x^2, \frac{\partial \mathbf{F}_2}{\partial y}=x^2, \frac{\partial \mathbf{F}_3}{\partial z}=x^2\)

∴ \(\frac{\partial \mathbf{F}_1}{\partial x}+\frac{\partial \mathbf{F}_2}{\partial y}+\frac{\partial \mathbf{F}_3}{\partial z}=3 x^2+x^2+x^2=5 x^2\)

By Gauss’s theorem \(\iint_{\mathrm{S}} \mathbf{F}_1 d y d z+\mathbf{F}_2 d z d x+\mathbf{F}_3 d x d y=\iiint_V\left(\frac{\partial \mathbf{F}_1}{\partial x}+\frac{\partial \mathbf{F}_2}{\partial y}+\frac{\partial \mathbf{F}_3}{\partial z}\right) d x d y d z\)

∴ \(\iint_{\mathrm{S}} x^3 d y d z+x^2 y d z d x+x^2 z d x d y\)

= \(\iiint_V 5 x^2 d x d y d z=5(4) \int_{x=0}^a \int_{y=0}^{\sqrt{a^2-x^2}} \int_{z=0}^b x^2 d x d y d z\)

= \(20 \int_{x=0}^a \int_{y=0}^{\sqrt{a^2-x^2}} x^2(b) d x d y=20 b \int_0^a x^2 \sqrt{a^2-x^2} \cdot d x\)

Put x = \(a \sin \theta, d x=a \cos \theta d \theta\)

x = \(0 \Rightarrow \theta=0 \quad x=a \Rightarrow \theta=\pi / 2\)

= \(20 b a^4 \int_0^{\pi / 2} \sin ^2 \theta \cdot \cos ^2 \theta d \theta=20 a^4 b \int_0^{\pi / 2}\left(\sin ^2 \theta-\sin ^4 \theta\right) d \theta\)

= \(20 a^4 b\left[\frac{1}{2} \frac{\pi}{2}-\frac{3}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2}\right]=\frac{5}{4} \pi a^4 b\)

Example.5 Prove that ∫f.curl F dV =∫F×f.dS+∫F.curlf dV

Solution:

Consider the vector function \(\mathbf{F} \times \mathbf{f}\)

By Gauss’s theorem \(\int_S(\mathrm{~F} \times \mathrm{f}) \cdot \overline{\mathrm{N}} d \mathrm{~S}=\int_V \text{div}(\mathrm{F} \times \mathrm{f}) d \mathrm{~V}\)

⇒ \(\int_S(\mathrm{~F} \times \mathbf{f}) \cdot \mathrm{N} d \mathrm{~S}=\int_V \text{div}(\mathrm{F} \times \mathbf{f}) d \mathrm{~V}=\int(\mathbf{F} \times \mathbf{f}) \cdot d \mathbf{S}=\int_V \nabla \cdot(\mathbf{F} \times \mathbf{f}) d \mathbf{V}\)

because \(\mathbf{N} d \mathbf{S}=d \mathbf{S}\)

∴ \(\int(F \times \bar{f}) d \overline{\mathrm{S}}=\int_V(\mathrm{f} . \mathrm{curlF}-\mathrm{F} \text { curlf }) d \mathrm{~V}\)

∴ \(\int \mathbf{f} . \text{curl} \mathbf{F} d \mathbf{V}=\int(\mathbf{F} \times \mathbf{f}) \cdot d \mathbf{S}+\int \mathbf{F} . \text{curl} \mathbf{f} d \mathbf{V}\)

Integration Techniques For Surface Of The Sphere Using Gauss’S Theorem

Example.6 Compute \(\int_S\) (ax²+by²+cz²) ds over the sphere x² +y²+z²=1

Solution:

By divergence theorem \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\int_V \nabla \cdot \mathbf{F} d \mathbf{V}\)

Given \(\mathbf{F}. \mathbf{N}=a x^2+b y^2+c z^2\)

Let \(\phi=x^2+y^2+z^2-1\)

∴ Normal vector N to the surface \(\phi\) is \(\nabla \phi=\left(\mathbf{i} \frac{\partial}{\partial x}+\mathbf{j} \frac{\partial}{\partial y}+\mathbf{k} \frac{\partial}{\partial z}\right)\left(x^2+y^2+z^2-1\right)=2(x \mathbf{i}+y \mathbf{j}+z \mathbf{k})\)

∴ Unit normal vector \(\mathbf{N}=\frac{2(x \mathbf{i}+y \mathbf{j}+z \mathbf{k})}{2 \sqrt{\left(x^2+y^2+z^2\right)}}=x \mathbf{i}+y \mathbf{j}+z \mathbf{k}\)

∴ \(\mathbf{F} . \mathbf{N}=\mathbf{F} .(x \mathbf{i}+y \mathbf{j}+z \mathbf{k})=a x^2+b y^2+c z^2\)

i.e. \(\mathbf{F}=a x \mathbf{i}+b y \mathbf{j}+c z \mathbf{k}\)

∴ \(\nabla . \mathbf{F}=a+b+c\)

Hence by Gauss theorem \(\oint_S\left(a x^2+b y^2+c z^2\right) d \mathbf{S}=\int_V(a+b+c) d \mathbf{V}\)

=(a+b+c) \(\mathbf{V}=\frac{4 \pi}{3}(a+b+c)\) as \(\mathbf{V}=\frac{4}{3} \pi\) being the volume of the sphere of unit radius.

Example.7 By converting the surface integral to volume integral show that ∫\(\int_S\) x³dy dz + y³dz dx+ z³dx dy= \(\frac{12 \pi}{5}\)where S is the surface of the sphere x²+y²+z²=1

Solution:

Consider the sphere \(x^2+y^2+z^2=a^2\) and

⇒ \(\bar{F}=x^3 \bar{i}+y^3 \bar{j}+z^3 \bar{k}=F_1 \bar{i}+F_2 \bar{j}+F_3 \bar{k}\)

div \(\bar{F}=\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}=3 x^2+3 y^2+3 z^2=3\left(x^2+y^2+z^2\right)=3 r^2\)

where r is the radius of the sphere.

We have by divergence theorem \(\iint_S \bar{F} \cdot \bar{n} d s=\iiint_{d i v} \bar{F} d \nu\)

i.e. \(\iint_{\text {S }} F_1 d y d z+F_2 d z d x+F_3 d x d y=\iiint_V d i v F d v=3 \iiint_S r^2 d v\)

Changing into a spherical coordinator

x = \(r \sin \theta \cos \phi \quad y=r \sin \theta \sin \phi \quad z=r \cos \theta\)

then \(d V=r^2 \sin \theta d r d \theta d \phi\)

L.H.S. = \(3 \int_{\phi=0}^{2 \pi} \int_{\theta=0}^\pi \int_{r=0}^a r^4 \sin \theta d r d \theta d \phi=3 \int_0^{2 \pi} d \phi \int_0^\pi \sin \theta d \theta \int_0^a r^4 d r\)

= \(3[\phi]_0^{2 \pi}[-\cos \theta]_0^\pi\left[\frac{r^5}{5}\right]_0^a=\frac{12}{5} \pi a^5\)

Taking a=1 we get the value as \(\frac{12}{5} \pi\)

Example.8 Find \(\iint_S \overline{\mathbf{F}} \cdot \overline{\mathbf{N}} d \mathrm{~s}\) where \(\overline{\mathrm{F}}\) =2xy\(\overline{\mathrm{i}}\) +yz2\(\overline{\mathrm{j}}\) +xz\(\overline{\mathrm{k}}\) and S is the surface of the parallelopiped formed by x=0,y=0,z=0,x=0,x=2,y=1,z=3.

Solution:

By Gauss’s theorem \(\iint_S \overline{\mathbf{F}} \cdot \overline{\mathbf{N}} d \mathbf{s}=\iiint_V \nabla \cdot \overline{\mathbf{F}} d \mathbf{v}\)

⇒ \(\nabla. \overline{\mathbf{F}}=\frac{\partial \mathbf{f}_1}{\partial x}+\frac{\partial \mathbf{f}_2}{\partial y}+\frac{\partial \mathbf{f}_3}{\partial z}=2 y+z^2+x\)

⇒ \(\iiint_V(\nabla . \overline{\mathbf{F}}) d \mathbf{v}=\int_{x=0}^2 \int_{y=0}^1 \int_{z=0}^3\left(x+2 y+z^2\right) d x d y d z=\int_{x=0}^2 \int_{y=0}^1\left[x z+2 y z+\frac{z^3}{3}\right]_0^3 d x d y\)

= \(\int_{x=0}^2 \int_{y=0}^1(3 x+6 y+9) d x d y=\int_{x=0}^2\left[3 x y+3 y^2+9 y\right]_{y=0}^1 d x\)

= \(\int_{x=0}^2(3 x+12) d x=\left[\frac{3 x^2}{2}+12 x\right]_0^2=6+24=30\)

Example.9 Valuate by Gauss divergence theorem∫ \(\int_S\)4xz dy dz-y² dz dx+yz x dy where S is the surface of the cube bounded by the planes x=0,x=1, y=0,y=1,z=0,z=1.

Solution:

By divergence theorem \(\int_S \overline{\mathbf{F}} \cdot \mathbf{N} d \mathbf{S}=\int_V d i v \overline{\mathbf{F}} d \mathbf{V}\)

⇒ \(\iint_S \mathbf{f}_1 d y d z+\mathbf{f}_2 d z d x+\mathbf{f}_3 d x d y=\iiint_V\left(\frac{\partial \mathbf{f}_1}{\partial x}+\frac{\partial \mathbf{f}_2}{\partial y}+\frac{\partial \mathbf{f}_3}{\partial z}\right) d x d y d z\)

From the given problem \(\mathbf{f}_1=4 x z, \mathbf{f}_2=-y^2\) and \(\mathbf{f}_3=y z\)

We get \(\iiint_V\left[\frac{\partial}{\partial x}(4 x z)+\frac{\partial}{\partial y}\left(-y^2\right)+\frac{\partial}{\partial z}(y z)\right] d x d y d z\)

= \(\iiint_{x=0}^1(4 z-2 y+y) d x d y d z=\int_{x=0}^1 \int_{y=0}^1 \int_{z=0}^1(4 z-y) d z d y d x\)

= \(\int_{x=0}^1 \int_{x=0}^1\left[2 z^2-y z z_{z=0} d y d x=\int_{x=0}^1 \int_{y=0}^1(2-y) d y d x\)

= \(\int_{x=0}^1\left[2 y-\frac{y^2}{2}\right]_0^1 d x=\int_{x=0}^1\left(2-\frac{1}{2}\right) d x\right.\)

= \(\frac{3}{2} \int_0^1 d x=\frac{3}{2}[x]_0^1=\frac{3}{2}\)

Understanding Integral Transformations On Spherical Surfaces

Example.10 If\(\overline{\mathrm{F}}\) =(2x²-3z)\(\overline{\mathrm{i}}\)-2xy\(\overline{\mathrm{j}}\)-4x\(\overline{\mathrm{k}}\) then evaluate \(\int_S\)div\(\overline{\mathrm{F}}\) dv where V is the closed region bounded by the planes x=0, y=0,z=0 and 2x+2y+z=4.

Solution:

div \(\overline{\mathbf{F}}=\nabla \cdot \overline{\mathbf{F}}=\frac{\partial \mathbf{f}_1}{\partial x}+\frac{\partial \mathbf{f}_2}{\partial y}+\frac{\partial \mathbf{f}_3}{\partial z}=4 x-2 x=2 x\)

Limits of z are 0 to 4-(2 x+2 y)

Limits of y are 0 to 2-x

Limits of x are 0 to 2

∴ \(\int_V \nabla \cdot \overline{\mathbf{F}} d \mathbf{V}=\int_{x=0}^2 \int_{y=0}^{2-x} \int_{z=0}^{4-2 x-2 y} 2 x d x d y d z=\int_{x=0}^2 \int_{y=0}^{2-x}[2 x z]_{z=0}^{4-2 x-2 y} d y d x\)

= \(\int_{x=0}^2 \int_{y=0}^{2-x} 2 x(4-2 x-2 y) d y d x=\int_{x=0}^2 \int_{y=0}^{2-x}\left(8 x-4 x^2-4 x y\right) d y d x\)

= \(\int_{x=0}^2\left[8 x y-4 x^2 y-2 x y^2\right]_{y=0}^{2-x} d x=\int_0^2\left[8 x(2-x)-4 x^2(2-x)-2 x(2-x)^2\right] d x\)

= \(\int_0^2\left(2 x^3-8 x^2+8 x\right) d x=\left[\frac{2 x^4}{4}-\frac{8 x^3}{3}+\frac{8 x^2}{2}\right]_0^2=\frac{1}{2} \cdot 2^4-\frac{8}{3} \cdot 2^3+4 \cdot 2^2=\frac{8}{3}\)

Integral Transformations Gauss’s Divergence Theorem

Let S be a closed surface enclosed in a volume V . If F is a continuously differentiable vector point function, then \(\int_V d i v \mathbf{F} d \mathbf{V}=\int_S \mathbf{F} \cdot \mathbf{N} d S\)

Where N is the outward drawn unit normal vector at any point of S.

Green’s identities And Gauss’s Divergence Relation

Cartesian Form

Let F =F₁i+F₂ j+F₃ k and N=i cos α+j cos β+k cos γ

where \(\cos \alpha, \cos \beta, \cos \gamma\) are the direction cosines of N. \(\mathbf{F} . \mathbf{N}=\mathbf{F}_1 \cos \alpha+\mathbf{F}_2 \cos \beta+\mathbf{F}_3 \cos \gamma\)

Also div \(\mathbf{F}=\nabla . \mathbf{F}=\frac{\partial \mathbf{F}_1}{\partial x}+\frac{\partial \mathbf{F}_2}{\partial y}+\frac{\partial \mathbf{F}_3}{\partial z}\)

Hence the divergence theorem can be written as \(\iiint\left(\frac{\partial \mathbf{F}_1}{\partial x}+\frac{\partial \mathbf{F}_2}{\partial y}+\frac{\partial \mathbf{F}_3}{\partial z}\right) d x d y d z\)

= \(\int_S\left(\mathrm{~F}_1 \cos \alpha+\mathrm{F}_2 \cos \beta+\mathrm{F}_3 \cos \gamma\right) d S\)

= \(\iint_S\left(\mathbf{F}_1 d y d z+\mathbf{F}_2 d z d x+\mathbf{F}_3 d x d y\right)\)

Proof: Let s be a closed surface. Let us choose the coordinate axes so that any line parallel to the coordinate axes cuts S in at most two points.  Let R be the projection of S on xy-plane. S and S are the lower and upper parts of S.

z=f(x,y) and z=g(x,y) be the  equations of S₁ and S₂. The relation can be put in the form f(x,y) ≤ z ≤ g(x,y).

∴  \(\int_V \frac{\partial \mathbf{F}_3}{\partial z} d \mathbf{V}\)\(=\iiint_V \frac{\partial \mathbf{F}_3}{\partial z}\) dx dy =\(=\iint_R\left[\frac{\partial \mathbf{F}_3}{\partial z} d z\right]_{z=f(x, y)}^{z=g(x, y)}\) dx dy

= \(\iint_R\left[\mathbf{F}_3(x, y, z)\right]_f^g d x d y=\iint_R\left[\mathbf{F}_3(x, y, g)-\mathbf{F}_3(x, y, f)\right] d x d y\)

= \(\iint_R \mathrm{~F}_3(x, y, g) d x d y-\mathrm{F}_3(x, y, f) d x d y\) …….. (1)

For the upper part \(\mathbf{S}_2 \quad d x d y=d S \cdot \cos \gamma=\mathbf{N} \cdot \mathbf{k} d S\)

Since the normal to \(\mathbf{S}_2\) makes an acute \(\gamma\) with \(\mathbf{k}\).

∴ \(\iint_R \mathbf{F}_3(x, y, g) d x d y=\int_{S_1} \mathbf{F}_{\mathbf{3}} \mathbf{N} \cdot \mathbf{k} d S\)

For the lower portion \(\mathbf{S}_1 \quad d x d y=-\cos \gamma d S=-\mathbf{N} \cdot \mathbf{k} d S\)

Since the normal to \(\mathbf{S}_1\) makes an obtuse angle \(\gamma\) with \(\mathbf{k}\)

∴ \(\iint_R \mathbf{F}_3(x, y, f) d x d y=-\int_{S_3} \mathbf{F}_3 \mathbf{N} \cdot \mathbf{k} d S\)

Hence from (1)

∴ \(\int_V \frac{\partial \mathbf{F}_3}{\partial z} d \mathbf{V}=\int_{S_2} \mathbf{F}_3 \mathbf{k} \cdot \mathbf{N} d S+\int_{S_1} \mathbf{F}_3 \mathbf{k} \cdot \mathbf{N} d S=\int_S \mathbf{F}_3 \mathbf{k} \cdot \mathbf{N} d S\)

The theorem can be extended to surfaces which are such that lines parallel to coordinate axes meet them in more than two points. In such a case, we subdivided the region bounded by S into subregions whose surfaces satisfy this condition. Applying the same procedure we can prove the Theorem.

Green’s Identities Explained With Examples

Integral Transformations Deduction From Gauss’s Theorem

1. Prove that\(\int_S\)N × F ds=\(\int_V\) ∇×F dv

Proof: Let f=a × F, where a is a constant vector.

Applying Gauss’s Theorem on f we have \(\int_S\)f.Nds= \(\int_V\)∇f dv ⇒ \(\int_S\)(a×f).Nds=\(\int_V\)∇.(a×f) dv

⇒ \(\int \mathbf{a} \cdot(\mathbf{F} \times \mathbf{N}) d \mathbf{S}=-\int \nabla \cdot(\mathbf{F} \times \mathbf{a}) d \mathbf{V}=-\int(\nabla \times \mathbf{F}) \cdot \mathbf{a} d \mathbf{V}\)

because \(\mathbf{a}\) is constant

⇒ \({\mathbf{a} \cdot \int_S}(\mathbf{N} \times \mathbf{F}) d \mathbf{S}=\mathbf{a} \cdot \int_S \nabla \times \mathbf{F} d \mathbf{V}\)

⇒ \(\mathbf{a} \cdot\left[\int_S(\mathbf{N} \times \mathbf{F}) d \mathbf{S}-\int_V \nabla \times \mathbf{F} d \mathbf{V}\right]=0\)

Since a is a constant vector

⇒ \(\int_S(\mathbf{N} \times \mathbf{F}) d \mathbf{S}-\int_V \nabla \times \mathbf{F} d \mathbf{V}=0 \Rightarrow \int(\mathbf{N} \times \mathbf{F}) d \mathbf{S}=\int \nabla \times \mathbf{F} d \mathbf{V}\)

2. Prove that \(\int_S\)NΦ ds=\(\int_V\)∇Φ dv

Proof:

Applying Gauss theorem to \(\mathbf{a} \phi\) we have

⇒ \(\int_S(\mathbf{a} \phi) \cdot \mathbf{N} d \mathbf{s}=\int_V \text{div}(\mathbf{a} \phi) d \mathbf{V}=\int_V \nabla \cdot(\mathbf{a} \phi) d \mathbf{V}\)

a. \(\int_S(\phi \mathbf{N}) \cdot \mathbf{N} d \mathbf{s}=\mathbf{a} \cdot \int_V(\nabla \phi) d \mathbf{V} \Rightarrow \mathbf{a} \cdot\left[\int_S \phi \mathbf{N} d \mathbf{S}-\int_V \nabla \phi d \mathbf{V}\right]=0\)

Since a is a constant vector.

⇒ \(\int_S \phi \mathbf{N} d \mathbf{S}-\int_V \nabla \phi d \mathbf{V}=0\)

∴ \(\int_S \mathbf{N} \phi d \mathbf{S}-\int_V \nabla \phi d \mathbf{V}=0\)

Note. The result proved above can be rewritten as follows.

1.\(\int_S\)Φ N.F dS = ∫∇.F dV

2.\(\int_S\)N× F dS=\(\int_V\)∇× F dV

3.∫NΦ dS=∫∇Φ dv

Here N is written before the function in L.H.S ∇ displaces N in R.H.S

Relationship Between Gauss’S Divergence Theorem And Green’S Identities

Integral Transformations  Green Identities

If f and g are two continuous and differentiable scalar point functions over the region V enclosed by the surfaces S. then

1. \(\int_V\)[f∇² g+∇ f.∇ g]dV=\(\int_S\)(f.∇ g).N dS
2. \(\int_V\)[f∇² g-g∇² f]dV=\(\int_S\)(f∇g-g∇f).N S

Proof: By Gauss’s divergence theorem we have \(\int_V\)∇. F dV=\(\int_S\)F.N dS

Now substituting \(\overline{\mathrm{F}}\)=f ∇g, we get

∇.F ∇(f∇g)=f(∇.∇g)∇f+∇g

∴ Divergence theorem gives \(\int_V\)[f∇²g+∇f.g]dV=\(\int_S\)(f∇g).N dS      ……………….(1)

This is called Green’s first identity or theorem.

2. Interchanging f and g in (1), we get

∫[g∇²f+∇g.∇f]dV=(g∇f).N dS     ………………(2)

Subtracting (2) from(1) we, get

∫(f∇²g-g∇²f)dV=∫f∇g-g∇f). N dS

This is called Green’s second identity or Green’s theorem in symmetrical form.

Subrings, Ideals, Quotient Rings & Euclidean Rings Quotient Rings Or Factor Rings

The concept of a quotient ring is analogous to that of quotient groups. If U is an ideal of a ring (R,+,•) then (U,+) is a normal subgroup of the commutative group (R,+).

From group theory, we know that the set R/U.= {x+U =U+ x | x ∈ R} of all cosets of U In R is a group with respect to the addition of two cosets defined by (a+U) + (b+U) = (a+b)+U for a+U,b +U ∈(R/U).

We know further that these costs are disjoint.

As addition operation is commutative left coset a+llis equal to right coset u + a In order to impose ring structure in R/U we can define multiplication of two of cosets as (a+U) (b+U) = ab +U for a+U,b +U ∈ R /U

Subrings, Ideals, Quotient Rings, And Euclidean Rings Theorems

Theorem.1 If U is an ideal of a ring R then the set R/U ={x+U|x ∈R} is a ring with respect to the induced operations of addition (+ ) and multiplication ( • ) of cosets defined : (a+ u)+(b+u)=(a+b)+U and (a+U). (b+U)=ab+U for a+Ub+u R/U.

Proof. Since (R,+) is a commutative group, the quotient group (R/U,+) is also commutative, In order to show that (R,+,•) is a ring we must show that

(1) multiplication of cosets is well defined,
(2) multiplication is associative and (3) distributive laws hold.

(1) Let \(a+U=a_1+U\) and \(b+U=b_1+U \text {. }\)

Then \(a=a_1+u_1\) and \(b=b_1+u_2\) for \(u_1, u_2 \in U \text {. }\)

ab = \(\left(a_1+u_1\right)\left(b_1+u_2\right)=a_1 b_1+a_1 u_2+u_1 b_1+u_1 u_2\)

Since U is an ideal, \(a_1 u_2, u_1 b_1, u_1 u_2 \in U\)

∴ \(a b-a_1 b_1 \in U\) and hence \(a b+U=a_1 b_1+U \Rightarrow(a+U) \cdot(b+U)=\left(a_1+U\right) \cdot\left(b_1+U\right)\)

Therefore multiplication of cosets is well defined.

Let a+U,b+U,c+U ∈R/U

(2) [(a+U).(b+U)] .(c+U) = (ab+U).(c+U) = (ab) c+U = a'(bc) +U (v a,b,c∈R) = (a +U). (bc+U) = (a+U) . [(b+U).(c+U)]

(3) (a+U). [(b+U)+(c+U)] = (a+U).[(b+ c)+U] = a(b+ c)+U = (ab+ ac)+U (v a,b,c∈R)

(ab+U)(ac+U) = (a+U) .(b+U)+(a+U). (c+U)

Similarly we can prove that [(b+U)+ (c+ U)].(a+U) = (b+U).(a+U)+(c+U).(a+U) Hence (R/U,+,•) is a ring

Examples Of Factor Rings In Abstract Algebra

Definition Of Addition And Multiplication Cosets

Definition. Let R be a ring and U be an ideal of R. Then the set R/U = {x+U\x∈R] with respect to induced operations of addition and multiplication of cosets defined by (a+U)+(b+U)-(a+b) +U;(a+U). (b+U) = ab +Ufor a+U,b+U eR/U is a ring.

This ring (R/U,+,•)is called the quotient ring or factor ring, or residue class ring of R modulo U.

Note.

1. It is convenient, sometimes, to denote coset a+U in R/U by the symbol a or.[a]. Then we write the sum and product of two cosets as [a]+[b] =[a+b] and [a].[b] = [ab].
2. o+U = U is the zero element in the ring R/U.
3. Every ring R has two improper ideals, namely, the trivial ideal {0} and the ideal R. The quotient ring of the ideal {0} is R/{0} or R /(0) = {x+ (0)| x∈ R}The quotient ring of the ideal R is R / R or Rt(l) = {x+(l) | x ∈ R}
4. (a+U)+ (b+U) = (a+b)+U-,(a+U)(b+U) = ab+U
5. (a+U)² =(a+U)(a+U) = a²+U
6. a+U = b+U ⇔(a-b)∈U.
7. a +U =U ⇔ a ∈ U

Theorem. 2. If R/U is the quotient ring prove that (1) R/U is commutative if R is commutative and (2) R/u has a unity element if R has a unity element.

Proof. (2) R is commutative => ab = ba∀ a,b ∈ R.

Let a+U,b+U ∈ R/U. (a+U) (b+U) = ab+U = ba+U =(b+U).(a+U)

∴ R/U is commutative.

(2) R has unity element => there exists 1 ∈ R so that a1 = 1a- a∀ a∈R.

Let a+U ∈ R/U.  For 1∈R we have 1+U ∈R/U

We now prove that 1 +U is the unity element.

(a+U)(l+U) = a1+U = a+U and (X+U)(a+U)*=la+U = a+U V a+U eR/U

1+U is the unity element in R/U.

Note. In the quotient ring R/U, the unity element = 1 +U.

Rings Examples Of Addition And Multiplication Cosets

Example. 1 Consider Z6 = {0,1, 2,3,4,5}, the ring of integers modulo 6.

U= {0,3} is an ideal of Z6. The costs of Uin R are as follows :

0+U = {0 + 0, 0+ 3} = {0,3};l+t/ = {1 + 0,1+ 3} = {1,4}

2+U = {2 +02 + 3} = {2,5};3+t/ = {3+0, 3+ 3} = {3,0} =0+ 17

4+U = {4+ 0, 4+ 3} = {4, 1} – 1 +U and 5+U {5 + 0, 5+3} = {5, 2} = 2+U

(Z6/U) = {0+U,l+U,2+U} is the quotientring.

Note. We observe that two cosets are identical or disjoint and the union of all cosets = Z6.

Quotient Rings And Their Properties Explained

Example 2. For the ring Z of all integers, we know that nZ = {nx| x∈ Z} for any n∈ Z is an additive subgroup of Z.

Let m ∈ nZ and r ∈ Z  Then m = na where a∈ Z.

mr = (na)r = n (ar) and rm =r (na) = n (ar)

so that mr = rm = n (ar) = nb∈nZ where b = ar∈Z Thus nZ is an ideal of Z.

The set of all cosets of nZ in Z, namely, (Z/nZ) = {x+nZ |x∈ Z} forms a ring under the induced operations of addition and multiplication.

Euclidean Rings

Definition. An integral domain R is said to be a Euclidean ring or Euclidean domain if for every a(≠0)∈ R there is defined a non-negative integer d(a) such that

(1)for all a,b∈ R, a≠ 0,b≠ 0;d (a) < d (ab) and

(2)for any a,b∈R,b≠ 0 there exist q,r∈R such that a = bq +r where either r = 0 or d (r) <d(b) .

Note

1. For any a(≠ 0)∈R,d (a)> 0.
2. For the zero element 0 of R,d{0) is not defined. However, some authors defined d(0) = 0, integer.
3. The property (2) in the above definition is called the division algorithm.
4. From the above definition, we note that d: R- {0} -> Z is a mapping such that

(1) d (a) > 0 ∀ R— {0} .
(2) d (a) < d (a,b)∀1 a,b∈R- {0} and
(3) there exist q,r∈R so that a-bq+r where either r = 0 or d (r) < d (b) for any a b∈R and b≠0.

Subrings, Ideals, Quotient Rings, And Euclidean Rings Theorems

Theorem 1. Every field is a Euclidean ring

Proof. Let F be a field and F be the set of all non-zero elements of F. Since F is a field, F is an integral domain

Define the mapping d:FZ by d(a) = 0 (zero integer) for all a ϵ F

d (a) ≥0 ∀ a ϵF

Let a bϵF.

Then a,b, and ab are non-zero elements of F

d (a) = 0 and d (ab) = 0 => d (a) <,d (ab)

Let aϵF and bϵF.

Now a = a 1 where 1 is the unity element of F.

=a(b^-1b) = (ab^-1)b  ( b^-1b=1)

= (ab^-1]) b+ 0 where ‘O’ is the zero element of the field F.

a = qb +r where q = ab^-1,r = 0 1

Hence, for a ϵ F,b ϵ F there exists q,r ϵ F so that a = qb+r where r= 0. F is an Euclidean ring.

Note. We can prove the above theorem by defining d: F -> Z by d(a) = 1 (integer) ∀ a ϵ F

Theorems On Subrings And Their Applications

Theorem 2. Every Euclidean ring is a principal ideal ring (or) Every ideal of an Euclidean ring is a principal ideal

Proof. Let R be an Euclidean ring.

Let U = {0} where ‘O’ is the zero element of R. Then U = {0} is the ideal generated by QϵR.

U is a principal ideal of R.

Let U be an ideal of R.

Let u≠ {0}. there exists xϵU and x≠0 so that the set {d (x) | x≠ 0} is a non-empty set of nonnegative integers.

By well ordering principle there exists b≠0 ϵ U so that d(b)<d (x) where x≠0ϵU.

We now prove that U = (b). Let ‘a’ be any element of U.

By division algorithm, there exists q,rϵR so that a -bq +r where r = 0 or d (r) < d (b). bϵU,qϵR, and U is an ideal => bqϵU. aϵU,bq ϵU => a-bq =r ϵU

If r≠ 0 then d (r) < d (b) so that we have a contradiction as d (b) < d (x) V x≠ 0 ϵU

r = 0 and hence a=b q.

U- {bq| qϵR} = (b) is the principal ideal generated by b(≠ 0) ϵU. Hence every ideal U of R is a principal ideal.

R is a principal ideal ring.

Note 1. If U is an ideal of a Euclidean ring R then U is a principal ideal of R so that U = (b) = {bq |q ϵF}

For,’ the ring R = \(\left\{a+b\left(\frac{1+\sqrt{19 i}}{2}\right): a, b \in Z\right\}\) of complex numbers is a principal ideal ring but not Euclidean