Geometry Homework Practice Workbook 1st Edition Chapter 1 Points Lines and Planes
Page 3 Problem 1 Answer
Given,
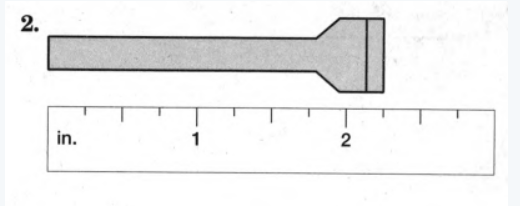
We need to determine the length of the object.
Given,
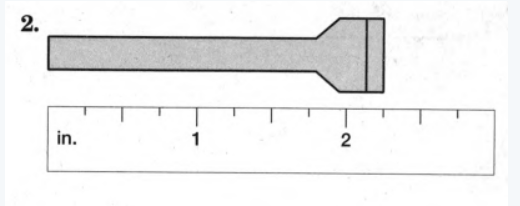
The ruler is marked in inches. The distance between two consecutive numbers is divided into 4 equal parts.
One end of the object starts at the zero mark of the ruler, and the other endpoint is 1/4 marks after 2.
So the length of the object is 2×1/4in.
So the length of the object is 2×1/4in.
Page 3 Problem 2 Answer
Given,
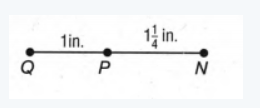
We need to find the length of the segment NQ.
Given,
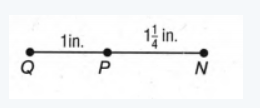
The length of NQ= The length of NP+ the length of PQ
=1×1/4in+1in
=(1×1/4+1)in
=2×1/4in
The length of the segment NQ is 2×1/4in.
Page 3 Problem 3 Answer
Given.
We need to find the length of the segment AC.
Given,
The length of AC= the length of AB + the length of BC
= 4.9cm+5.2cm
= (4.9+5.2)cm
= 10.1cm
The length of the segment AC is 10.1cm
Page 3 Problem 4 Answer
Given,
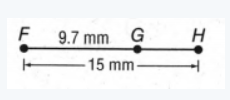
We need to find the value of the segment GH.
Given,
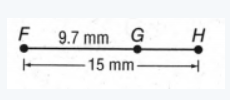
The value of the segment GH= the value of FH- the value of FG
=15mm−9.7mm
= (15−9.7)mm
= 5.3mm
The value of the given segment GH is 5.3mm.
Page 3 Problem 5 Answer
Here, the given values are XY=5x, YZ=x, and XY=25.
We need to find the value of x and YZ.
Here, Y is between X and Z.
Given values of XY are 2x and 25.
By equalling both the values, we get,
∴ 5x=25( required linear equation)
⇒ x=25/5
⇒ x=5
Therefore, the value of YZ=5. (putting the value of x).
The value of x is 5 and the value of YZ is 5.
Page 3 Problem 6 Answer
Here, the given values of XY = 12, YZ = 2x, and XZ = 28.
We need to find the value of x and YZ.
Here, Y is between X and Z.
So the value of XZ = the value of XY + the value of YZ.
∴ 28=12+2x(reaquired linear equation).
By solving the equation, we get,
∴ 28=12+2x
⇒ 28−12=2x
⇒ 16=2x
⇒ x=16/2
⇒ x=8
Therefore, the value of YZ,
= 2×8( putting the value of x)
= 16
The value of x is 8 and the value of YZ is 16.
Page 3 Problem 7 Answer
Here, the given values of XY = 4x, YZ = 3x, XZ = 42. We need to find the value of x and YZ.
Here, Y is between X and Z.
So the value of XZ = the value of XY + the value of YZ.
∴ 42=4x+3x(reaquired linear equation).
By solving the equation, we get,
∴ 42=4x+3x
⇒ 42=7x
⇒ 42/7
= x
⇒ x = 6
Therefore, the value of YZ,
= 3x
= 3×6(putting the value of x)
= 18
The value of x is 6 and the value of YZ is 18.
Page 3 Problem 8 Answer
Here, the given values of XY =2x+1, YZ = 6x and XZ = 81.
We need to find the value of x and YZ.
Here, Y is between X and Z.
So the value of XZ = the value of XY + the value of YZ.
∴ 81=2x+1+6x( reaquired linear equation).
By solving the equation, we get,
∴ 81=2x+1+6x
⇒ 81−1 = 8x
⇒ 80=8x
⇒ 80/8
= x
⇒ x=10
Therefore, the value of YZ,
= 6x
= 6×10( putting the value of x)
= 60
The value of x is 10 and the value of YZ is 60.
Page 3 Problem 9 Answer
Given,
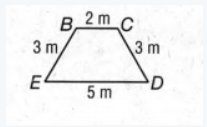
We need to determine whether the given pair of segments BE, and CD are congruent.
Segments that have the same measure are called congruent segments.
Given,
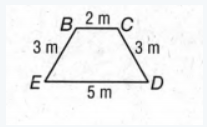
Here, BE=3cm and CD =3cm.
Therefore, BE=CD.
So. the given pair of segments BE, CD is congruent.
The given pair of segments BE, CD is congruent.
Page 3 Problem 10 Answer
We are given the figure,
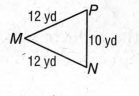
and we have to find whether segments MP and NP are congruent or not.
Now, we can clearly see that the segment MP has a length of 12 yds, and the length of the segment NP is 10 yds.
Hence, as these are different, they are not congruent.
Finally, we can conclude that the two segments MP and NP are not congruent.
Page 3 Problem 11 Answer
We are given the figure,
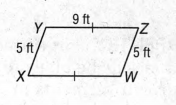
and we have to find whether segments WX and WZ are congruent or not.
Now, we can clearly see that the segment WX is parallel and equal to YZ i.e. it has a length of 9ft.
Also, it is given that the length of the segment WZ is 5ft.
Hence, they have different lengths, so they are not congruent.
Finally, we can conclude that the two segments WX and WZ are not congruent.
Page 4 Problem 12 Answer
We are given the figure,
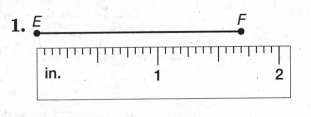
We match the line with the measuring scale to find the number of small segments combinedly refer to the length of the line EF.
We have the line EF and a measuring scale (in inches) as,
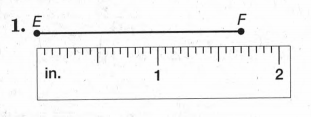
Now, we can notice that in the scale every inch is segmented into 16 small portions.
The line lies in a way that its starting point is matching with the starting point of the measuring scale.
Now, we can measure that the line is long enough to cover 1 inch and 11 small segments in the scale.
Therefore, the length of the line EF can be written as,
EF=1+11/16 in.
=111/16 in.
Finally, we can conclude that the length of line EF is given as 111/16 in.
Page 4 Problem 13 Answer
We are given the figure,
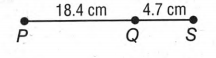
We can see that the line PS is made of two segments PQ and QS. We add the lengths of these segments to obtain the final length of the line PS.
We have the figure
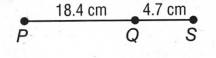
The length of the segment PQ is 18.4 cm and the length of the segment QS is 4.7 cm.
Now, the line PS is made of these two consecutive segments, hence, length of PS=length of PQ+length of QS
⇒ length of PS=(18.4+4.7)
⇒ length of PS=23.1 cm.
Finally, we can conclude that the length of the line PS is 23.1 cm.
Page 4 Problem 14 Answer
Given
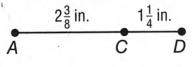
To find AD.
The value of AD can be calculated as AD=AC+CD.
AD = AC + CD
⇒ AD = 2×3/8 + 1×1/4
⇒ AD =19/8 +5/4
⇒ AD =19 + 2 × 5/8
⇒ AD =29/8 = 3.625in.
Hence the measurement of WX is 35/8in or 3.625in.
Page 4 Problem 15 Answer
Given,
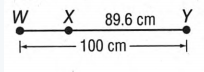
To find WX.
WY=WX+XY
⇒ WX=WY−XY.
WX = WY − XY
⇒ WX = 100 − 89.6
⇒ WX = 10.4cm.
Hence the measurement of WX is 10.4cm.
Page 4 Problem 16 Answer
Given, JK=6x, KL=3x, JL=27, and K is between JL.
To find x and KL.
Since K is between JL, JK+KL=JL.
Since K is between J and L, thereforeJL=JK+KL
⇒ 27=6x+3x
⇒ 9x=27
⇒ x=27/9
⇒ x=3.
HenceKL=3x
= 3×3
= 9.
Hence we can conclude that the values of x=3, KL =9.
Page 4 Problem 17 Answer
Given,JK=2x,KL=x+2,andJL=5x−10.
K is between J and L.
To find x and KL.
Since K is between J&L, JK+KL=JL.
Since K is between J&L, therefore JL=JK+KL
⇒ 5x−10=(2x)+(x+2)
⇒ 2x=10+2
⇒ x=12/2
⇒ x=6.
Hence KL=x+2
= 6+2
= 8.
Hence we can conclude that the values of x=6,KL=8.
Page 4 Problem 18 Answer
Given
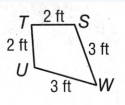
To check whether the line segments TU&SW are congruent or not.
Two line segments are congruent when they are of equal lengths.Length of TU=2ft,
Length of SW=3ft.
Since the two segments do not have equal lengths hence they are not congruent.
Hence we can conclude that since the two segments TU&SW do not have equal lengths hence they are not congruent.
Page 4 Problem 19 Answer
Given
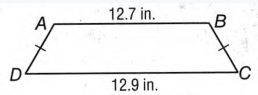
To check whether AD&BC are congruent.
Two line segments are congruent when they are of equal lengths.
The given figure shows two marks on the lengths AD&BC which indicate they are equal.
Since both the line segments are equal they are congruent.
Hence we can conclude that since the two segments AD&BC
have equal lengths hence they are congruent.
Page 4 Problem 20 Answer
Given
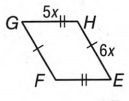
To check whether GF&FE are congruent.
Two line segments are congruent when they are of equal lengths.
The similar marks on two different line segments indicate that they are equal.
Hence GF≡HE=6x and GH≡FE=5x.
Thus GF&FE are not equal, hence they are not congruent.
Hence we can conclude that since the two segments GF&FE do not have equal lengths hence they are not congruent.
Page 4 Problem 21 Answer
Given
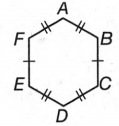
To find all the congruent pairs of line segments.
The similar marks on two different line segments indicate that they are equal.HenceAF≡AB, EF≡CB, DE≡DC.
All these pairs are congruent. Hence AF≅AB, EF≅CB, DE≅DC.
These are the pairs of congruent segments.
Hence the pairs of congruent segments are AF and AB, EF and CB, DE and DC.