Geometry Homework Practice Workbook 1st Edition Chapter 1 Points Lines and Planes
Geometry Homework Practice Workbook 1st Edition Chapter 1 Exercise 1.3 Solution Page 5 Problem 1 Answer
Given

To find the length of LN.
The absolute value difference between the coordinates of the endpoints will give the length.
Let the coordinate of the endpointL=(l) and the coordinate of N=(n).
The length ofLN=∣l−n∣
=∣3−9∣
=∣−6∣
=6 units.
Hence we can conclude that the length of LN is 6 units.
Read and Learn More Geometry, Homework Practice Workbook 1st Edition Solutions
Geometry Homework Practice Workbook Chapter 1 Page 5 Problem 2 Answer
Here given a number line
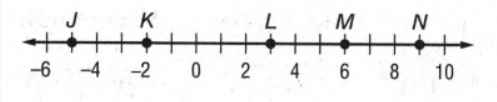
By using this number line we have to measure KN.
Now we will consider K as point x1 and N as point x2.
Then we will find the distance between K
And N by using the distance formula that is ∣x2−x1∣.
Given that a number line
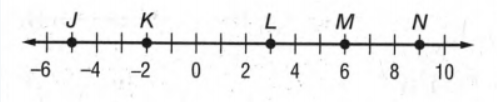
Now we will consider K as point x1 and N as point x2 and to measure the distance we will use the formula of distance that is ∣x2−x1∣.
If we give a closer look at this number line we can say x1 is on −2 and x2 is on 9.
So, KN= ∣x2−x1∣
=∣9−(−2)∣Unit
=∣11∣Unit
=11Unit.
Hence, the length of KN on the number line is 11 units.
Solutions For Points, Lines, And Planes Exercise 1.3 Page 5 Problem 3 Answer
Here given a number line
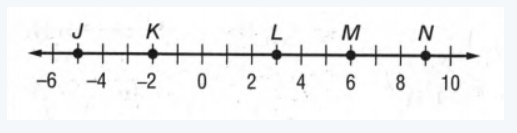
By using this number line we have to measure MN.
Now we will consider M as point x1 and N as point x2.
Then we will find the distance between M and N by using the distance formula that is∣x2−x1.

Hence, the length of MN on the number line is 3 units.
Geometry Homework Practice Workbook Chapter 1 Page 5 Problem 4 Answer
Given two points K(2,3) and F(4,4).
Let’s assume (x1,y1) and(x2,y2) be the coordinates of those points respectively.
Finally, we are going to use the formula∣√(x2−x1)2+(y2−y1)2∣to measure the distance between those points.
Given that two points are K(2,3) and F(4,4).
Now to calculate the distance between them from the formula that is∣√(x2−x1)2+(y2−y1)2∣
we will replace the value of x1,y1,x2,y2.
So KF=∣√(4−2)2+(4−3)2Unit
=∣√22+1/2∣Unit
=∣√5∣Unit
=∣2.23∣Unit
=2.23Unit.
Hence, the distance between the two points is 2.23Unit.
Page 5 Problem 5 Answer
Given two points C(−3,−1) and Q(−2,3).
Let’s assume (x1,y1) and (x2,y2) be the coordinates of those points respectively.
Finally, we are going to use the formula∣√(x2−x1)2+(y2−y1)2∣to measure the distance between those points.
Given that two points are C(−3,−1) and Q(−2,3).
Now to calculate the distance between them from the formula that is ∣√(x2−x1)2+(y2−y1)2∣
we will replace the value of x1,y1,x2,y2.
So, CQ= ∣√{(−2)−(−3)2+{3−(−1)}2∣Unit
= ∣√12+4/2∣Unit
= ∣√17∣Unit
= ∣4.12∣Unit
= 4.12Unit.
Hence, the distance between the two points is 4.12Unit.
Geometry Workbook 1st Edition Exercise 1.3 Solutions Page 5 Problem 6 Answer
Given two pointsY(2,0) and P(2,6).
Let’s assume (x1,y1) and (x2,y2) be the coordinates of those points respectively.
Finally, we are going to use the formula∣√(x2−x1)2+(y2−y1)2∣to measure the distance between those points.
Given that two points are Y(2,0) and P(2,6).
Now to calculate the distance between them from the formula that is∣√(x2−x1)2+(y2−y1)2∣
we will replace the value of x1,y1,x2,y2.
So, YP=∣√(2−2)2+(6−0)2∣Unit
=∣√6/2∣Unit
=∣6∣ Unit
=6 Unit.
Hence, the distance between the two points is 6 units.
Page 5 Problem 7 Answer
Given two points W(−2,2) and R(5,2).
Let’s assume (x1,y1) and (x2,y2) be the coordinates of those points respectively.
Finally, we are going to use the formula∣√(x2−x1)2+(y2−y1)2| to measure the distance between those points.
Given that two points are W(−2,2) and R(5,2).
Now to calculate the distance between them from the formula that is∣√(x2−x1)2+(y2−y1)2∣
we will replace the value of x1,y1,x2,y2.
So,WR=∣√{5−(−2)}2+(2−2)2∣Unit
= ∣√72+0/2∣Unit
= ∣√49∣Unit
= ∣7∣Unit
= 7Unit
Hence, the distance between the two points is 7 units.
Geometry Homework Practice Workbook Chapter 1 Page 5 Problem 8 Answer
Given two points A(−7,−3) and B(5,2). Let’s assume (x1,y1) and(x2,y2) be the coordinates of those points respectively.
Finally, we are going to use the formula∣(x2−x1)2+(y2−y1)2∣to measure the distance between those points.
Given that two points are A(−7,−3) and B(5,2).
Now to calculate the distance between them from the formula that is∣√(x2−x1)2+(y2−y1)2∣
we will replace the value of x1,y1,x2,y2.
So, AB=∣√{5−(−7)}2+{2−(−3)}2∣Unit
= ∣√122+5/2∣Unit
= ∣√144+25∣Unit
= ∣√169∣Unit
= ∣13∣Unit
= 13 Unit.
Hence, the distance between the two points is 13 Units.
Points, Lines, And Planes Solutions Chapter 1 Exercise 1.3 Geometry Workbook Page 5 Problem 9 Answer
Given two points C(−3,1) and Q(2,6).
Let’s assume(x1,y1) and (x2,y2) be the coordinates of those points respectively.
Finally, we are going to use the formula∣√(x2−x1)2+(y2−y1)2∣to measure the distance between those points.
Given that two points are C(−3,1) and Q(2,6).
Now to calculate the distance between them from the formula that is∣√(x2−x1)2+(y2−y1)2∣
we will replace the value of x1,y1,x2,y2.
So CQ=∣√{2−(−3)}2+(6−1)2∣Unit
= ∣√52+5/2∣Unit
= ∣√25+25∣Unit
= ∣√50∣Unit
= ∣7.07∣Unit
= 7.07Unit.
Hence, the distance between the two points is 7.07 Units.
Step-By-Step Solutions For Geometry Homework Practice Workbook Chapter 1 Exercise 1.3 Page 5 Problem 10 Answer
Given

To find the coordinate of the midpoint of DE.
The midpoint of a line with end coordinates x1 and x2 is given by the formula \(\frac{x_1+y_1}{2}\)
The coordinate of the endpoint D is x1=7.
The coordinate of the endpoint E is y1=11.
Hence the coordinate of the midpoint of the line DE is \(\frac{x_1+y_1}{2}\)=\(\frac{7+11}{2}\)
=\(\frac{8}{2}\)
=9.
Hence we can conclude that the coordinate of the midpoint of DE is 9.
Page 5 Problem 11 Answer
Given

To find the coordinate of the midpoint of BC.
The midpoint of a line with end coordinates x1 and y1 is given by the formula \(\frac{x_1+y_1}{2}\)
The coordinate of the endpoint B is −1.
The coordinate of the endpoint C is 3.
Hence the coordinate of the midpoint of line BC is
⇒ \(\frac{x_1+y_1}{2}\)
= \(\frac{-1+3}{2}\)
= \(\frac{2}{2}\)
=1.
Hence we can conclude that the coordinate of the midpoint of BC is 1.
Geometry Chapter 1 Exercise 1.3 Free Solutions Page 5 Problem 12 Answer
Given

To find the coordinate of the midpoint of BD.
The midpoint of a line with end coordinates x1 and y1 is given by the formula \(\frac{x_1+y_1}{2}\)
The coordinate of the endpoint B is −1.
The coordinate of the endpoint D is 7.
Hence the coordinate of the midpoint of the line BD is \(\frac{x_1+y_1}{2}\)
= \(\frac{-1+7}{2}\)
= \(\frac{6}{2}\)
= 3.
Hence we can conclude that the coordinate of the midpoint of BD is 3.
Page 5 Problem 13 Answer
Given

To find the coordinate of the midpoint of AD.
The midpoint of a line with end coordinates x1 and y1 is given by the formula \(\frac{x_1+y_1}{2}\)
The coordinate of the endpoint A is −4.
The coordinate of the endpoint D is 7.
Hence the coordinate of the midpoint of the line AD is \(\frac{x_1+y_1}{2}\)
= \(\frac{-4+7}{2}\)
= \(\frac{3}{2}\)
=1.5
Hence we can conclude that the coordinate of the midpoint of AD is 1.5.
Geometry Homework Practice Workbook Chapter 1 Page 5 Problem 14 Answer
Given endpoints T(3,1) and U(5,3).
To find the coordinates of the midpoint of a segment with the given endpoints.
The midpoint of a line with end coordinates(x1,y1)and(x2,y2) is given by the formula \(\frac{x_1+x_2}{2}\), \(\frac{y_1+y_2}{2}\)
The coordinates of the endpoint T is (3,1).
The coordinates of the endpoint U is (5,3).
Hence the coordinates of the midpoint of the line TU are \(\frac{x_1+x_2}{2}\), \(\frac{y_1+y_2}{2}\)
= \(\frac{3+5}{2}\), \(\frac{1+3}{2}\)
= \(\frac{8}{2}\), \(\frac{4}{2}\)
=(4,2).
Hence we can conclude that the coordinates of the midpoint of TU is (4,2).
Geometry Homework Practice Workbook Exercise 1.3 Student Solutions Page 5 Problem 15 Answer
Given endpoints J(−4,2) and F(5,−2).
To find the coordinates of the midpoint of a segment with the given endpoints.
The midpoint of a line with end coordinates(x1,y1) and (x2,y2) is given by the formula \(\frac{x_1+x_2}{2}\), \(\frac{y_1+y_2}{2}\)
The coordinates of the endpoint J are (−4,2).
The coordinates of the endpoint F is (5,−2).
Hence the coordinates of the midpoint of the line JF are \(\frac{x_1+x_2}{2}\), \(\frac{y_1+y_2}{2}\)
= \(\frac{-4+5}{2}\), \(\frac{2-2}{2}\)
= \(\frac{1}{2},0\)
Hence we can conclude that the coordinates of the midpoint of JF are \(\frac{1}{2},0\)
Geometry Homework Practice Workbook Chapter 1 Page 5 Problem 16 Answer
Given endpoint N (2,0) and the midpoint of the line NQ is P(5,2).
To find the coordinates of the missing endpoint.
The midpoint of a line with end coordinates(x1,y1) and (x2,y2) is given by the formula \(\frac{x_1+x_2}{2}\), \(\frac{y_1+y_2}{2}\)
Let the coordinates of Q be (x,y).
The coordinates of the endpoint N are (2,0).
The coordinates of the midpoint P is (5,2).
Hence the coordinates of the midpoint of the line NQ
are \(\frac{x_1+x_2}{2}\), \(\frac{y_1+y_2}{2}\) =(5,2)
⇒ \(\frac{2+x}{2}\), \(\frac{0+y}{2}\) =(5,2)
⇒ 2+x=10, y=4
⇒ x=8, y=4.
Thus, the coordinates of Q are (8,4).
Hence we can conclude that the coordinates of the missing endpoint are(8,4).
Points, Lines, And Planes Exercise 1.3 Geometry Workbook Answers Page 5 Problem 17 Answer
Given endpoint N(5,4) and the midpoint of the line NQ is P(6,3).
To find the coordinates of the missing endpoint.The midpoint of a line with end coordinates(x1,y1)
And (x2,y2) is given by the formula \(\frac{x_1+x_2}{2}\), \(\frac{y_1+y_2}{2}\)
Let the coordinates of Q be (x,y).
The coordinates of the endpoint N are (5,4).
The coordinates of the midpoint P are (6,3).
Hence the coordinates of the midpoint of the line NQ
are \(\frac{x_1+x_2}{2}\), \(\frac{y_1+y_2}{2}\) =(6,3)
⇒ \(\frac{5+x}{2}\), \(\frac{4+y}{2}\) =(6,3)
⇒ 5+x=12,4+y=6
⇒ x=7,y=2.
Thus, the coordinates of Q are (7,2).
Hence we can conclude that the coordinates of the missing endpoint are(7,2).
Geometry Homework Practice Workbook Chapter 1 Page 5 Problem 18 Answer
Given endpoint Q(3,9) and the midpoint of the line NQ is P(−1,5).
To find the coordinates of the missing endpoint.
The midpoint of a line with end coordinates (x1,y1) and (x2,y2) is given by the formula \(\frac{x_1+x_2}{2}\), \(\frac{y_1+y_2}{2}\)
Let the coordinates of N be(x,y).
The coordinates of the endpoint Q are (3,9).
The coordinates of the midpoint P are (−1,5).
Hence the coordinates of the midpoint of the line NQ are \(\frac{x_1+x_2}{2}\), \(\frac{y_1+y_2}{2}\)=(−1,5)
⇒ \(\frac{x+3}{2}\), \(\frac{y+9}{2}\) =(−1,5)
⇒ x+3=−2,y+9=10
⇒ x=−5,y=1.
Thus, the coordinates of N are (−5,1).
Hence we can conclude that the coordinates of the missing endpoint are (−5,1).
Page 6 Problem 19 Answer
Given

To find the length of VW.
The absolute value difference between the coordinates of the endpoints will give the length.
Let the coordinate of the endpoint V=(v) and the coordinate of W=(w).
The length of VW=∣v−w∣
= ∣1−5∣
= ∣−4∣
= 4 units.
Hence we can conclude that the length of VW is 4 units.
Geometry Homework Practice Workbook Chapter 1 Page 6 Problem 20 Answer
Here given a number line By using this number line we have to measure TV.
Now we will consider T as point x1 and V as point x2.
Then we will find the distance between T and V by using the distance formula that is ∣x2−x1∣.
Given that a number line
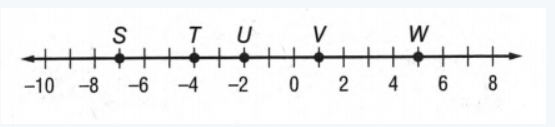
Now we will consider T as point x1 and V as point x2 and to measure the distance we will use the formula of distance that is ∣x2−x1∣.
If we give a closer look at this number line we can say T is on −4 and V is on 1.
So, TV= ∣x2−x1∣
= ∣−4−1∣Unit
= ∣−5∣Unit
= 5Unit.
Hence the length of TV on the number line is 5 units.
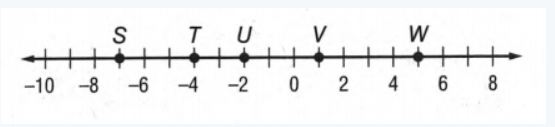
Page 6 Problem 21 Answer
Here given a number line By using this number line we have to measure ST
Now we will consider S as point x1 and T as point x2.
Then we will find the distance between S And T by using the distance formula that is ∣x2−x1∣.
Given that a number line
Now we will consider S as point x1 and T as point x2 and to measure the distance we will use the formula of distance that is ∣x2−x1∣.
If we give a closer look at this number line we can say x1 is on−7 and x2 is on−4.
So, ST= ∣x2−x1∣
= ∣−7−(−4)∣Unit
= ∣−3∣Unit
= 3Unit.
Hence the length of ST on the number line is 3 Units.
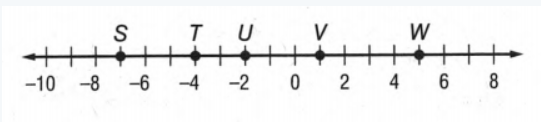
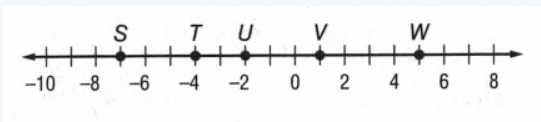
Geometry Homework Practice Workbook Chapter 1 Page 6 Problem 22 Answer
Here given a number line By using this number line we have to measure SV.
Now we will consider S as point x1 and V as point x2.
Then we will find the distance between S and V
by using the distance formula that is ∣x2−x1∣.
Given that a number line
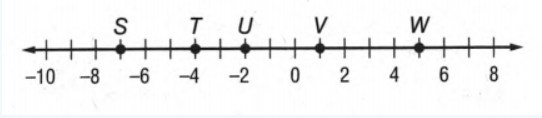
Now we will consider S as point x1 and V as point x2 and to measure the distance we will use the formula of distance that is ∣x2−x1∣.
If we give a closer look at this number line we can say S is on −7 and V is on 1.
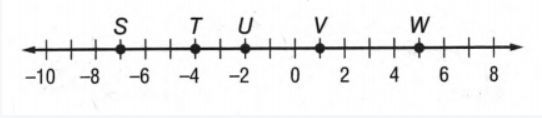
So SV=∣x2−x1∣
= ∣−7−1∣Unit
= ∣−8∣Unit
= 8 Unit.
Hence the length of SV on the number line is 8Unit.
Page 6 Problem 23 Answer
Given that

By using this graph we have to measure the distance between two given points.
Now find the coordinates of those points and find out the distance between them using∣√(x2−x1)2+(y2−y1)2∣
where(x1,y1) and (x2,y2) are the coordinates of S and E respectively.
Given that
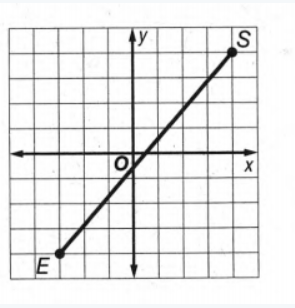
By using this graph we have to measure the distance between two given points.
From the graph the coordinates of S and E respectively (4,4) and (−3,−4).
Now we are going to use the formula ∣√(x2−x1)2+(y2−y1)2∣ to calculate the distance between each pair of points.
Putting the value of x1,x2,y1,y2
The distance of SE
GF= ∣√(−3−4)2+(−4−4)2∣Unit
= ∣√(−7)2+(−8)2∣Unit
= ∣√49+64∣Unit
= ∣√113∣Unit
= 10.630Unit
≈10.6Unit.
Hence, the distance between each pair of points is 10.6 Units.
Geometry Homework Practice Workbook Chapter 1 Page 6 Problem 24 Answer
The given points are.
We need to find the distance between the two points.
The distance can be calculated as d=2√(x2−x1)2+(y2−y1)2.
Using the formula d=2√(x2−x1)2+(y2−y1)2
we can say that,
d= 2 √(5+7)2+(9−0)2
= 2√(12)2+(9)2
= √144+81
= √225
= 15
The total distance is found to be 15 units.
Page 6 Problem 25 Answer
The given points are U(1,3),B(4,6). We need to find the distance between the two points.
The distance can be calculated as d = 2/√(x2−x1)2+(y2−y1)2.
Using the formula d = 2/√(x2−x1)2+(y2−y1)2
we can say that,
d=2/√(4−1)2+(6−3)2
=2√32+32
=√9+9
=√18
=3/√2
The total distance is found to be 3/√2 units.
Geometry Homework Practice Workbook Chapter 1 Page 6 Problem 26 Answer
The given points are V(−2,5),M(0,−4). We need to find the distance between the two points.
The distance can be calculated as d = 2/√(x2−x1)2+(y2−y1)2.
Using the formula we can say that,
d = 2/√(x2−x1)2+(y2−y1)2
=2/√(0+2)2+(−4−5)2
=2/√(2)2+(−9)2
=2/√4+81
=√85
The total distance is found to be √85 units.
Page 6 Problem 27 Answer
The given points are C(−2,−1),K(8,3). We need to find the distance between the two points.
The distance can be calculated as d=2√(x2−x1)2+(y2−y1)2.
Using the formula we can say that,
d=2√(x2−x1)2+(y2−y1)2 or,d=2√(8+2)2+(3+1)2=2
√(10)2+(4)2=√100+16
=√116
=2/√29
The total distance is found to be 2/√29 units.
Geometry Homework Practice Workbook Chapter 1 Page 6 Problem 28 Answer
The given line is RT.
We must find the endpoints of the line.
The midpoint can be found using the formula m= \(\frac{x_1+x_2}{2}\)
We can see that the line has endpoints as−2 and 4.
Thereby using the formula m=\(\frac{x_1+x_2}{2}\),
m= \(\frac{-2+4}{2}\)
m=\(\frac{2}{2}\)
m=1.
The midpoint is found to be (1,0).
Page 6 Problem 29 Answer
The given line is QR.
We must find the endpoints of the line.
The midpoint can be found using the formula m= \(\frac{x_1+x_2}{2}\)
We can see that the line has endpoints as−6and−2,
Thereby using the formula m=\(\frac{x_1+x_2}{2}\)
m= \(\frac{-6-2}{2}\)
= \(\frac{-8}{2}\)
=−4
The midpoint is found to be (−4,0).
Geometry Homework Practice Workbook Chapter 1 Page 6 Problem 30 Answer
The given line is ST.
We must find the endpoints of the line.
The midpoint can be found using the formula m= x1+x2/2.
We can see that the line has endpoints 1 and 4.
Thereby using the formula m= \(\frac{x_1+x_2}{2}\)
m= \(\frac{1+4}{2}\)
= \(\frac{5}{2}\)
The midpoint is found to be \(\frac{5}{2},0\)
Page 6 Problem 31 Answer
The given line is PR.
We must find the endpoints of the line.
The midpoint can be found using the formula m = \(\frac{x_1+x_2}{2}\)
We can see that the line has endpoints as −9 and −2.
Thereby using the formula m = \(\frac{x_1+x_2}{2}\),m = \(\frac{-9-2}{2}\)
= \(\frac{-11}{2}\)
The midpoint is found to be \(\frac{-11}{2},0\)
Geometry Homework Practice Workbook Chapter 1 Page 6 Problem 32 Answer
The given points are K(−9,3) and H(5,7).
We must find the endpoints of the line.
The midpoint can be found using the formula m= \(\frac{x_1+x_2}{2}\), \(\frac{y_1+y_2}{2}\)
Using the formula,
m = \(\frac{x_1+x_2}{2}\), \(\frac{y_1+y_2}{2}\) or,m=(−9+5)
(2,3+\(\frac{7}{2}\)) or,m= \(\frac{-4}{2}\), \(\frac{10}{2}\)or,m=(−2,5)
The midpoint is found to be (−2,5).
Page 6 Problem 33 Answer
The given points are W(−12,−7);T(−8,−4).We must find the endpoints of the line.
The midpoint can be found using the formula m=\(\frac{x_1+x_2}{2}\), \(\frac{y_1+y_2}{2}\)
Using the formula,
m= \(\frac{x_1+x_2}{2}\), \(\frac{y_1+y_2}{2}\) or,m=(−12−8/2,−7−4/2)
or,m= \(\frac{-20}{2}\)\(\frac{-11}{2}\)or,m=(−10,\(\frac{-11}{2}\))
The midpoint is found to be (−10,−11/2).
Geometry Homework Practice Workbook Chapter 1 Page 6 Problem 34 Answer
The given points are R(−1,3),S(3,3),T(5,−1),U(−2,−1) and.
We must find the length of each side.
The perimeter can be found by summing up all the lengths of the sides.
The perimeter The length found is given below,
RS= √(3+1)2+(3−3)2
=√42
=4
ST=√(5−3)2+(−1−3)2
=√22+(−4)2
=√20
TU=√(5+2)2+(1−1)2
=√72
=7
RU=√(−2+1)2+(−1−3)2
=√1+42
=√17
Perimeter of quadrilateral RSTU=4+7+√20+√17
=19.59
The perimeter is found to be 19.59 sq. units.
