Glencoe Math Course 3 Volume 2 Student Chapter 7 Congruence And Similarity Exercise
Glencoe Math Course 3 Volume 2 Chapter 7 Congruence And Similarity Exercise Solutions Page 504 Exercise 1, Problem1
The given equation is (x/15) = (7/30).
We apply cross multiplication i.e. multiply the numerator of one ratio to the denominator of the other ratio to obtain the value of the unknown variable.
We have the proportion \(\frac{x}{15}=\frac{7}{30}\),
⇒ \(\frac{x}{15}=\frac{7}{30}\)
⇒ x x 30 = 7 x 15 [applying cross multiplication]
⇒ x x 30 = 105
⇒ x = \(\frac{105}{30}\)
⇒ x = 3.5. Hence, the value of x is 3.5.
Finally, we can conclude that the value of the unknown variable is x = 3.5.
Read and Learn More Glencoe Math Course 2 Volume 1 Common Core Student Edition Solutions
Glencoe Math Course 3 Volume 2 Student Chapter 7 Page 504 Exercise 2 Problem1
The given equation is (4/9) = (14/y).
We apply cross multiplication i.e. multiply the numerator of one ratio to the denominator of the other ratio to obtain the value of the unknown variable.
We have the proportion \(\frac{4}{9}=\frac{14}{y}\),

⇒ 4 x y = 14 x 9 [applying cross-multiplication]
⇒ 4 x y = 126
⇒ y = \(\frac{126}{4}\)
⇒ y = 31.5.
Finally, we can conclude that the value of the unknown variable is y=31.5.
Chapter 7 Congruence And Similarity Answers Glencoe Math Course 3 Volume 2 Page 504 Exercise 3, Problem1
The given equation is (12/Z) = (30/37).
We apply cross multiplication i.e. multiply the numerator of one ratio to the denominator of the other ratio to obtain the value of the unknown variable.
We have the proportion \(\frac{12}{Z}=\frac{30}{37}\),
⇒ 12 x 37 = 30 x z [applying cross-multiplication]
⇒ 30 x z = 444
⇒ z = \(\frac{444}{30}\)
⇒ z = 14.8.
Hence, the value of z is 14.8.
Finally, we can conclude that the value of the unknown variable is Z=14.8
Glencoe Math Course 3 Volume 2 Student Chapter 7 Page 504 Exercise 4 Problem1
The given equation is (8/15) = (m/21).
We apply cross multiplication i.e. multiply the numerator of one ratio to the denominator of the other ratio to obtain the value of the unknown variable.
We have the proportion \(\frac{8}{15}=\frac{m}{21}\),
⇒ 8 x 21 = m x15 [applying cross-multiplication]
⇒ 168 = m x 15
⇒ m = \(\frac{168}{15}\)
⇒ m = 11.2.
Hence, the value of m is 11.2.
Finally, we can conclude that the value of the unknown variable is m=112.
Step-By-Step Solutions For Chapter 7 Congruence And Similarity Exercises In Glencoe Math Course 3 Page 504 Exercise 5, Problem1
The given equation is (n/5) = (18/45).
We apply cross multiplication i.e. multiply the numerator of one ratio to the denominator of the other ratio to obtain the value of the unknown variable.
We have the proportion \(\frac{n}{5}=\frac{18}{45}\),
⇒ n x 45 = 18 x 5 [applying cross-multiplication]
⇒ n x 45 = 90
⇒ n = \(\frac{90}{45}\)
⇒ n = 2.
Hence, the value of n is 2.
Finally, we can conclude that the value of the unknown variable is n=2.
Glencoe Math Course 3 Volume 2 Student Chapter 7 Page 504 Exercise 6 Problem1
The given equation is (3/7) = (21/p).
We apply cross multiplication i.e. multiply the numerator of one ratio to the denominator of the other ratio to obtain the value of the unknown variable.
We have the proportion \(\frac{3}{7}=\frac{21}{p}\),
⇒ 3 x p = 21 x 7 [applying cross-multiplication]
⇒ 3 x p = 147
⇒ p = \(\frac{147}{3}\)
⇒ p = 49.
Hence, the value of p is 49.
Finally, we can conclude that the value of the unknown variable is p=49.
Exercise Solutions For Chapter 7 Congruence And Similarity Glencoe Math Course 3 Volume 2 Page 504 Exercise 7, Problem1
The given statement is to find the slope of the line that passes through each pair of points (-1,1),(-3,7).
We apply the formula, m=(y2−y1)/(x2−x1) for determining the slope.
m = \(\underline{y_2-y_1}, \text { where, } x_1=-1, x_2=-3, y_1=1, y_2=7\). Therefore,
m = \(\frac{7-1}{-3-(-1)}\)
⇒ m = \(\frac{6}{-3+1}\)
⇒ m = \(\frac{6}{-2}\)
⇒ m = -3.
Hence, the slope of the line is m = -3.
Finally, we can conclude that the slope of the line that passes through each pair of points (−1,1),(−3,7) is m=−3.
Glencoe Math Course 3 Volume 2 Student Chapter 7 Page 504 Exercise 8 Problem1
The given statement is to find the slope of the line that passes through each pair of points (2,0), (0,2).
We apply the formula, m=(y2−y1)/(x2−x1) for determining the slope.
We have to find the slope of the line that passes through the two points (2,0),(0,2).
Let the slope be m, then we can write the formula,
m = \(\frac{y_2-y_1}{x_2-x_1} \text {, where, } x_1=2, x_2=0, y_1=0, y_2=2\). Therefore,
m = \(\frac{2-0}{0-2}\)
⇒ m = \(\frac{2}{-2}\)
⇒ m = -1.
Hence, the slope of the line is m = -1.
Finally, we can conclude that the slope of the line that passes through each pair of points (2,0),(0,2)is m=−1.
Examples Of Problems From Chapter 7 Congruence And Similarity Exercises In Glencoe Math Course 3 Page 504 Exercise 9, Problem1
The given statement is to find the slope of the line that passes through each pair of points (−6,−1),(−3,4).
We apply the formula, m=(y2−y1)/(x2−x1)for determining the slope.
We have to find the slope of the line that passes through the two points (−6,−1),(−3,4).
Let the slope be m, then we can write the formula,
m = \(\frac{y_2-y_1}{x_2-x_1}, \text { where, } x_1=-6, x_2=-3, y_1=-1, y_2=4\). Therefore,
m = \(\frac{4-(-1)}{-3-(-6)}\)
⇒ m = \(\frac{4+1}{-3+6}\)
⇒ m = \(\frac{5}{3}\).
Hence, the slope of the line is m = \(\frac{5}{3}\).
Finally, we can conclude that the slope of the line that passes through each pair of points (−6,−1),(−3,4))is m=5/3.
Glencoe Math Course 3 Volume 2 Student Chapter 7 Page 505 Exercise 1 Problem1
We have the instruction to fold the given page vertically into three parts.We can denote the folding lines in dotted fashion as,
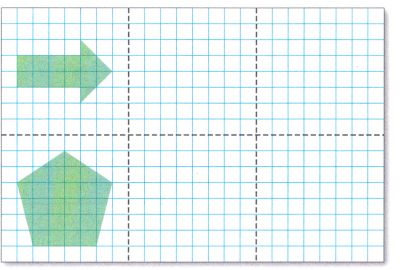
Finally, we can conclude that after folding the page vertically into three sections we get,

Common Core Chapter 7 Congruence And Similarity Exercise Detailed Solutions Glencoe Math Course 3 Volume 2 Page 505 Exercise 1, Problem2
We have a page that is folded vertically into three sections
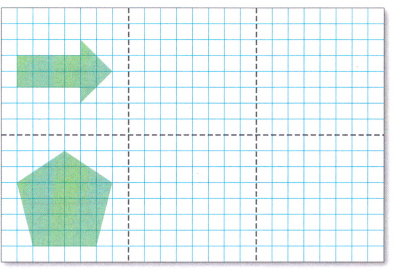
Now we draw the reflection of the arrow over the fold in the middle section.
We draw the reflected image of the arrow as the distance of each point of the previous arrow and its image with the folded line be the same.
As we know the distance of each point of an image and its preimage from the line of reflection is the same.
Here, the vertical folded line is referred to as the line of reflection.
So, we can draw as
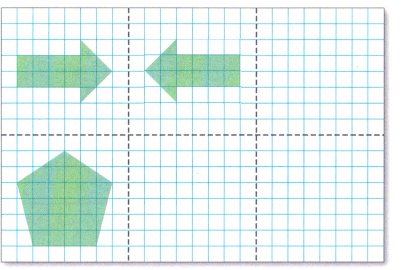
Finally, we can conclude that after drawing the reflection of the arrow over the fold in the middle section we get

Glencoe Math Course 3 Volume 2 Student Chapter 7 Page 505 Exercise 1 Problem3
We have a page that is folded vertically into three sections
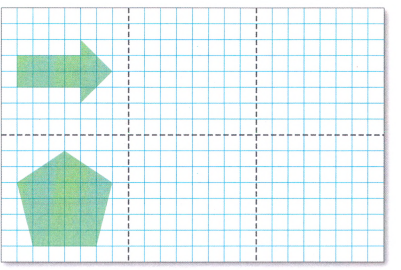
Then we draw the reflection of the arrow over the fold in the middle section
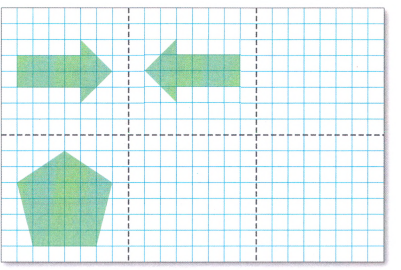
Now, we draw the reflection of the second arrow in the right-most section in a similar way.
As we know that the distance of each point of an image and its preimage from the line of reflection is the same.
Here, the vertical folded line is referred to as the line of reflection.
So, we can draw as
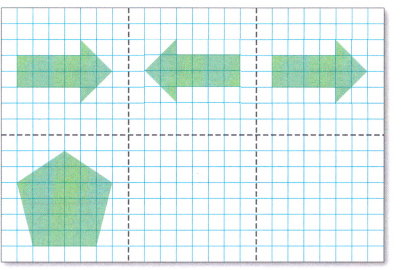
Finally, we can conclude that after drawing the reflection of the second arrow over the fold in the right-hand section we get,

Glencoe Math Course 3 Volume 2 Student Chapter 7 Page 505 Exercise 1 Problem4
When both images are reflected over the vertical line the resulting images of the pentagon are identical but that of the arrow is not.
Both the first and the second reflection produce the same shapes. The reflection is shown below.
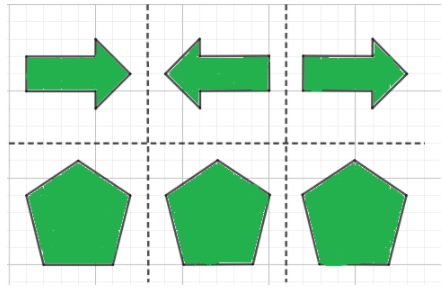
When the reflection is done first over the vertical axis followed by the horizontal axis, the original and the final image of the arrow are different. Only the image formed after the horizontal reflection is the same as the preimage.
This is because the arrow possesses horizontal symmetry.
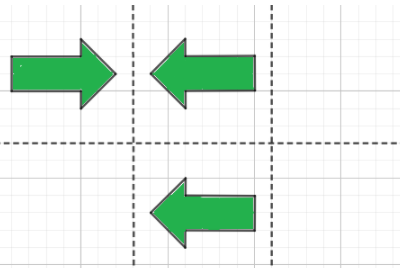
When the reflection is done first over the vertical axis followed by the horizontal axis, the original and the final image of the pentagon are different.
Only the image formed after the first reflection along the vertical axis is the same as the original image.
This is because the pentagon possesses only vertical symmetry.
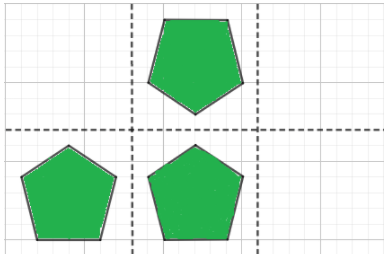
When both images are reflected over the vertical line the resulting images of the pentagon are identical but that of the arrow is not.
When the reflection is done first over the vertical axis followed by the horizontal axis, the original and the final image of the pentagon are different.
Only the image formed after the first reflection along the vertical axis is the same as the original image and in the case of the arrow, the original and the last reflected image is the same.
Glencoe Math Course 3 Volume 2 Student Chapter 7 Page 507 Exercise 1 Problem1
First, we need to apply translation to the given figure. Translation refers to the movement of shapes from one location to another. The foot on the left side is to be slid down beside the right foot.
Then a vertical line is drawn between them and the left foot is reflected along this line. This results in the formation of the right foot.

So, translation followed by reflection gives the required transformation.
We get the transformation by applying translation followed by reflection.

Student Edition Chapter 7 Congruence and Similarity Solutions Guide Glencoe Math Course 3 Volume 2 Page 507 Exercise 2, Problem1
The blue triangle is first flipped along the horizontal line. This is known as reflection.
A reflection is a metamorphosis that depicts a figure being flipped.
After this, the figure is translated down and then to the right side. This results in the pink triangle.
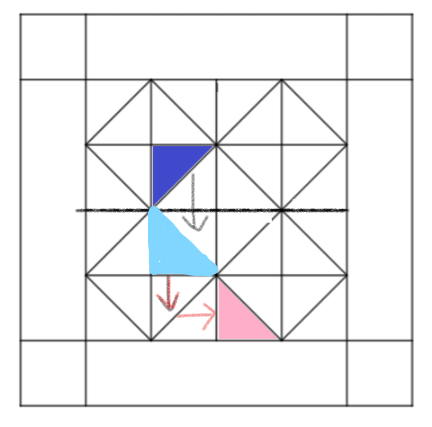
So the transformation is reflection followed by the translation.
Reflection followed by translation results in the given transformation.
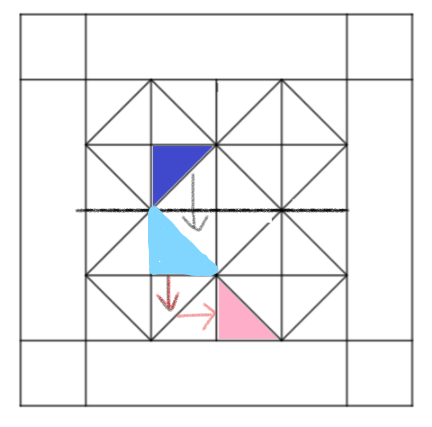
Glencoe Math Course 3 Volume 2 Student Chapter 7 Page 507 Exercise 3 Problem1
At first, the figure on the lower side is to be reflected along a vertical line.
A reflection is a metamorphosis that depicts a figure being flipped.
Now this reflected figure is to be translated to get the final figure.
The final figure is given in the following image.
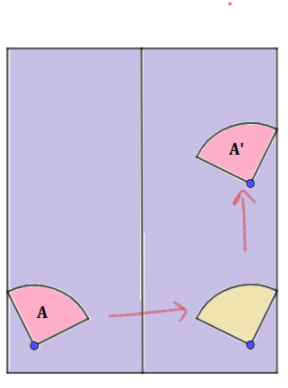
So, reflection followed by translation gives the final image.
The required transformation results from reflection followed by the translation.

Step-By-Step Answers For Chapter 7 Congruence And Similarity In Glencoe Math Course 3 Volume 2 Page 507 Exercise 4, Problem1
At first, using circles and sections the preimage is created.
Then, this preimage is constantly reflected first over the horizontal plane and then over the vertical plane.
At last, the small circle is rotated repeated at a right angle in the clockwise direction.
This results in the formation of a logo.
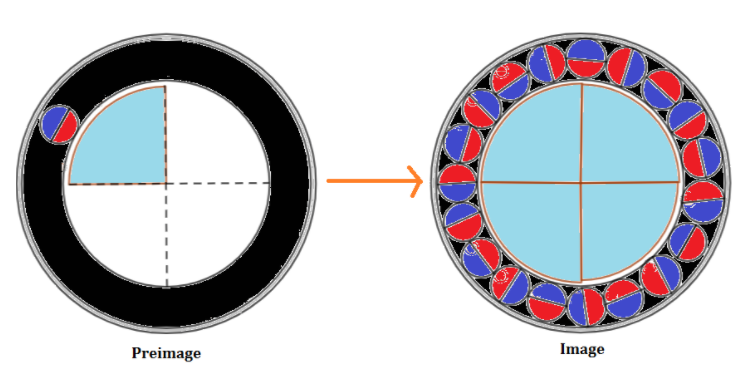
The logo formed by using reflection and rotation is given in the image below.
image
Glencoe Math Course 3 Volume 2 Student Chapter 7 Page 508 Exercise 5 Problem1
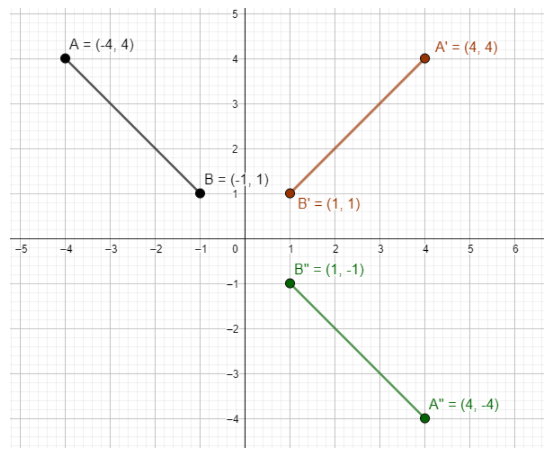
Let us consider the initial position of the line segment as (−4,4)and (−1,1).
After reflection from the x-axis, the x coordinates of the original image remain intact while they coordinates will be multiplied by −1.
After reflection from the y-axis, the x coordinates of the original image remain intact while the y coordinates will be multiplied by −1.
The resultant figure is given in the image below.
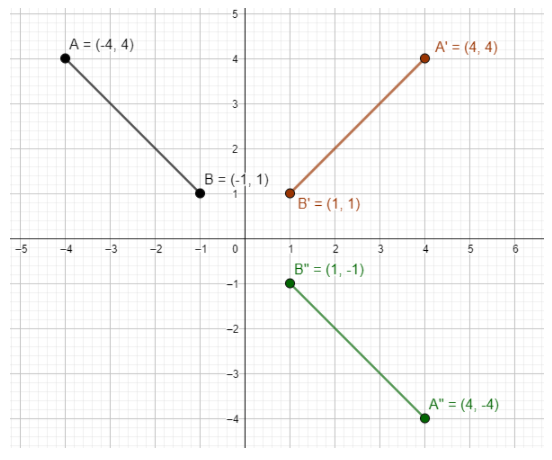
The final transformation is given in the image below.
Glencoe Math Course 3 Volume 2 Student Chapter 7 Page 508 Exercise 6 Problem1
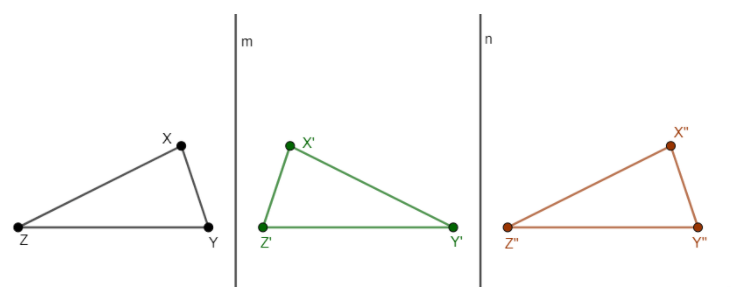
We consider two vertical axes. The ΔXYZ is first reflected over the first vertical axis and then, over the second axis.
The single transformation that could be used to obtain the final position of the triangle is by translating the original figure to the right-hand side.
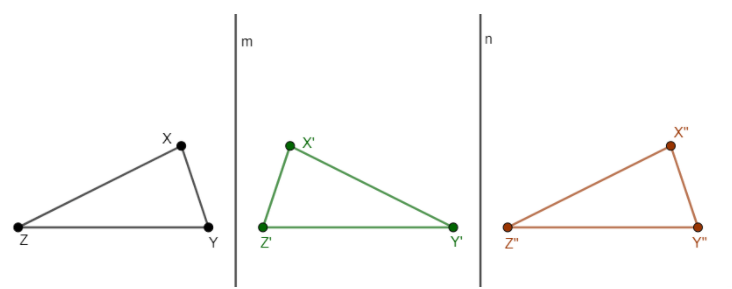
The single transformation that can be used to obtain the following image is translation.
Glencoe Math Course 3 Volume 2 Student Chapter 7 Page 508 Exercise 7 Problem1
A dilation is a stretching or shrinking of an image that alters its location but does not change its shape.
To get the coordinates of the picture, we multiply each preimage coordinate by a scale factor when the coordinate plane’s centre of dilatation is the origin.When the scale factor is more than one, the size of the image is enlarged.
When the scale factor is less than one, the size of the image is reduced.When the scale factor is equal to one, the size of the image is unchanged.
A dilation is a stretching or shrinking of an image that alters its location but does not change its shape.
Page 504 Exercise 8, Problem1
After an object has been modified, the image of that object can be transformed again to create a new image. A combination of transformations is the name for such a transformation.
A single transformation can explain the transformation from a single object to the final image after a series of transformations.
An object’s image can be transformed again to generate a new image after it has been transformed. A combination of transformations is a type of transformation.
A single transformation can explain the transformation from a single object to the final image after a number of transformations have been applied.
