Integral Transformations Solved Problems
Example.1 Show that the area bounded by a simple closed curve C is given by \(\frac{1}{2} \oint_C\)xdy-ydx and hence find the area of the ellipse x=a cos θ,y= bsinθ, 0 ≤ θ ≤ 2π
Solution:
By Green’s theorem \(\int_C \mathrm{P} d x+\mathrm{Q} d y=\iint_S\left(\frac{\partial \mathrm{Q}}{\partial x}-\frac{\partial \mathrm{P}}{\partial y}\right) d x d y\)
Put \(\mathrm{P}=-y\) and \(\mathrm{Q}=+x \frac{\partial \mathrm{P}}{\partial y}=-1, \frac{\partial \mathrm{Q}}{\partial x}=+1\)
∴ \(\oint_C x d y-y d x=2 \int_S d x d y=2 \mathrm{~A}\) where A is the area of the surface S
∴ \(\frac{1}{2} \int_C x d y-y d x=\mathrm{A}\)
Now for the ellipse x = \(a \cos \theta, y=b \sin \theta\).
Area = \(\frac{1}{2} \oint_C x d y-y d x\)
= \(\frac{1}{2} \int_0^{2 \pi}(a \cos \theta)(b \cos \theta)-(b \sin \theta)(-a \sin \theta) d \theta=\frac{1}{2} a b \int_0^{2 \pi} d \theta=\pi a b\)
Example.2 Evaluate \(\oint_C\)(cos x sin y – xy) dx+ sin x cos y dy, by Green’s theorem where C is the circle x2+y2 =1
Solution:
By Green’s theorem, we have \(\int_C \mathrm{P} d x+\mathrm{Q} d y=\iint_S\left(\frac{\partial \mathrm{Q}}{\partial x}-\frac{\partial \mathrm{P}}{\partial y}\right) d x d y\)
Here \(\mathrm{P}=\cos x \sin y-x y, \mathrm{Q}=\sin x \cos y\)
∴ \(\frac{\partial \mathrm{P}}{\partial y}=\cos x \cos y-x, \frac{\partial \mathrm{Q}}{\partial x}=\cos x \cos y\)
for the circle, \(x^2+y^2=1\). Changing to polar coordinates.
x = \(r \cos \theta, y=r \sin \theta, d x d y=r d r d \theta\)
∴ \(\oint_C(\cos x \sin y-x y) d x+\sin x \cos y d y \int_S[\cos x \cos y-(\cos x \cos y-x)] d x d y\)
= \(\iint_S x d x d y=\int_{\theta=0}^{2 \pi} \int_{r=0}^1 r \cos \theta \cdot r d r d \theta=\int_0^{2 \pi}\left[\frac{r^3}{3}\right]_0^1 \cos \theta d \theta=\frac{1}{3} \int_0^{2 \pi} \cos \theta d \theta=\frac{1}{3}[\sin \theta]_0^{2 \pi}=0\)
Example.3 Verify Green’s theorem in the plane for \(\oint_C\)(3x2-8y2)dx+(4x-6xy) dy where C is the region bounded by y=\(\sqrt{x}\) and y=x2
Solution:
Here \(\mathrm{P}=3 x^2-8 y^2 \quad \frac{\partial \mathrm{P}}{\partial y}=-16 y \quad \mathrm{Q}=4 y-6 x y \quad \frac{\partial \mathrm{Q}}{\partial x}=-6 y\)
Hence to Green’s theorem
1. \(\int_C\left(3 x^2-8 y^2\right) d x+(4 y-6 x y) d y\)
= \(\iint_S(-6 y+16 y) d x d y=10 \int_{x=0}^1 \int_{y=x^2}^C y d y d x\)
=\(10 \int_0^1\left[\frac{y^2}{2}\right]_{x^2}^{\sqrt{x}} d x=5 \int_0^1\left(x-x^4\right) d x=\frac{3}{2}\)
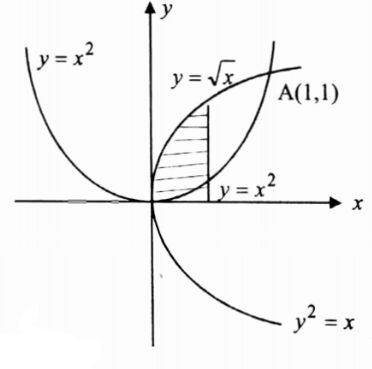
2. Verification.
The line integral along C
= Line integral along y = \(x^2\) (from O to A) + line integral along \(y^2=x\) (from A to O) = \(\mathrm{I}_1+\mathrm{I}_2\)
∴ \(\mathrm{I}=\int_{x=0}^1\left[3 x^2-8\left(x^2\right)^2\right] d x+\left[4 x^2-6 x\left(x^2\right)\right] 2 x d x=\int_0^1\left(3 x^2+8 x^2-20 x^4\right) d x=-1\)
⇒ \(\mathrm{I}_2=\int_1^0\left(3 x^2-8 x\right) d x+\left(4 \sqrt{x}-6 x^{3 / 2}\right) \frac{1}{2 \sqrt{x}} d x\)
y = \(\sqrt{x}\)
= \(\int_1^0\left(3 x^2-11 x+2\right) d x=\frac{5}{2}\)
∴ \(\mathrm{I}_1+\mathrm{I}_2=-1+\frac{5}{2}=\frac{3}{2}\)
Hence the theorem is verified.
Example.4 Evaluate by Green’s theorem \(\oint_C\)(y-sinx)+cos x dy where C is the triangle enclosed by the lines x=0,x=\(\frac{\pi}{2}\), πy=2x.
Solution:
Here P = \(y-\sin x, \mathrm{Q}=\cos x \quad \frac{\partial \mathrm{P}}{\partial y}=1, \frac{\partial \mathrm{Q}}{\partial x}=-\sin x\)
Hence by Green’s theorem \(\int_C(y-\sin x) d x+\cos x d y=\iint_S(-1-\sin x) d x d y\)
= \(-\int_{x=0}^{\pi / 2} \int_{y=0}^{2 x / \pi}(1+\sin x) d x d y=-\int_0^{\pi / 2}(1+\sin x) \frac{2 x}{\pi} d x\)
= \(-\frac{2}{\pi} \int_0^{\pi / 2}(x+x \sin x) d x=-\left(\frac{\pi}{4}+\frac{2}{\pi}\right)\)
Example.5 Evaluate by greens theorem \(\oint_C\)(x-cosh y) dx +(y +sin x) dy where C is the rectangle with vertices (0,0),(π,0) (π,1) and (0,1)
Solution:
Here \(\mathrm{P}=x^2-\cosh y, \quad \mathrm{Q}=y+\sin x \quad \frac{\partial \mathrm{P}}{\partial y}=-\sinh y, \quad \frac{\partial \mathrm{Q}}{\partial x}=\cos x\)
By Green’s theorem \(\int_C\left(x^2-\cosh y\right) d x+(y+\sin x) d y=\iint_S(\cos x+\sinh y) d x d y\)
= \(\int_{x=0}^\pi \int_{y=0}^1(\cos x+\sinh y) d x d y=\int_0^\pi[(y \cos x+\cosh y)]_0^1 d x=\int_0^\pi[\cos x+\cosh 1-1] d x\)
= \([\sin x+x \cosh 1-x]_0^\pi=\pi[\cosh 1-1]\)
Example.6 Verify Greens theorem in the plane for \(\oint_C\)(xy+y2) dx+x2dy where C is the closed curve of the region bounded by y=x and y=x2
Solution: Solving the curves y=x and y=x2 we get the points of intersection are (0,0) and (1,1)
On the curve y=x2
The limits for x are 0 to 1
y2= x ⇒ dy =2x dx
⇒ \(\int_{C_1}\left(x y+y^2\right) d x+x^2 d y\)
= \(\int_{x=0}^1\left(x\left(x^2\right)+x^4\right) d x+x^2 2 x d x\)
= \(\int_0^1\left(x^3+x^4+2 x^3\right) d x=\int_0^1\left(3 x^3+x^4\right) d x\)
= \(3 \frac{x^4}{4}+\frac{x^5}{5}_0^1=\frac{3}{4}+\frac{1}{5}-0=\frac{19}{20}\)
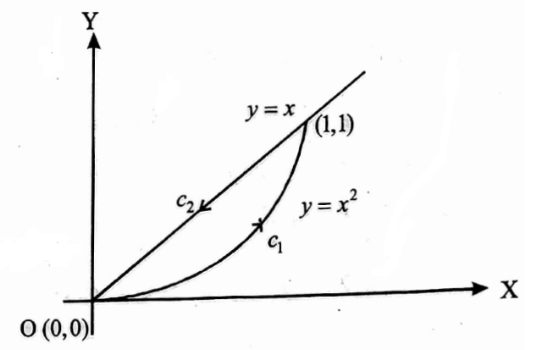
On the curve y=x
The limits of x are \(1 \rightarrow 0\)
y = \(x \Rightarrow d y=d x\)
⇒ \(\left.\oint_C\left(x y+y^2\right) d x+x^2 d y=\int_{x=1}^0\left(x(x)+x^2\right) d x+x^2 d x=\int_1^0 3 x^2=\frac{3 x^3}{3}\right]_1^0=-1\)
Adding (1) and (2) : \(\oint_C\left(x y+y^2\right) d x+x^2 d y=\frac{19}{20}-1=-\frac{1}{20}\)
By Green’s theorem, \(\oint_C P d x+Q d y=\iint_R\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\)
R. H. S. \(=\int_{x=0}^1 \int_{y=x^2}^x\left[\frac{\partial}{\partial x}\left(x^2\right)-\frac{\partial}{\partial y}\left(x y+y^2\right)\right] d x d y\)
= \(\int_{x=0}^1 \cdot \int_{y=x^2}^x(2 x-x-2 y) d x d y=\int_{x=0}^1 \int_{y=x^2}^x(x-2 y) d x d y\)
= \(\left.\int_{x=0}^1 x y-y^2\right]_{x^2}^x d x=\int_0^1\left[\left(x^2-x^2\right)-\left(x^3-x^4\right)\right] d x\)
= \(\int_{x=0}^1\left(x^4-x^3\right) d x=\frac{x^5}{5}-\frac{x^4}{4}_0^1=\frac{1}{5}-\frac{1}{4}=-\frac{1}{20}=\text { L. H. S. }\)
∴ Green’s theorem is verified.