Integral Transformations Green’s Theorem In A Plane
Let S be a closed region in xy- xy-plane enclosed by a curve C. Let P and Q be continuous and differentiable scalar functions of x and y in S . Then \(\oint_C P \mathrm{dx}+\mathrm{Q} \mathrm{dy}\)=\(\iiint_S\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y\) The line integral being taken round C such that S is on the left as one advance along C.
Proof: Let any line parallel to either coordinate axes cut C in at most two points. Let S lie between the lines x = a, x = b, and y = c, y = d.
Let y = f(x) be the curve C1 (i.e. AEB) and y = g (x) be the curve C2 (i.e. ADB), where f(x) ≤ g(x)
Consider \(\iint_S \frac{\partial \mathrm{P}}{\partial y} d x d y=\int_{x=a}^b \int_{y=f(x)}^{g(x)} \frac{\partial \mathrm{P}}{\partial y} d x d y\)
= \(\int_a^b[\mathrm{P}(x, y)]_{y=f(x)}^{g(x)} d x=\int_a^b[\mathrm{P}(x, g)-\mathrm{P}(x, f)] d x\)
= \(\int_a^b \mathrm{P}(x, g) d x-\int_a^b \mathrm{P}(x, f) d x\)
= \(-\int_b^a \mathrm{P}(x, y) d x-\int_a^b \mathrm{P}(x, y) d x=-\int_{C_2} \mathrm{P}(x, y) d x-\int_{C_1} \mathrm{P}(x, y) d x\)
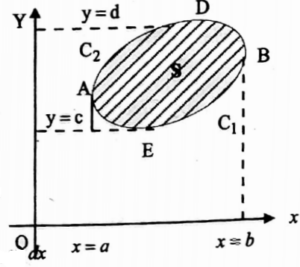
∴ \(\iint_S \frac{\partial \mathrm{P}}{\partial y} d x d y=-\oint_C \mathrm{P} d x\)……(1)
Similarly we can prove that \(\iint_S \frac{\partial \mathrm{Q}}{\partial x} d x d y=\oint_C \mathrm{Q} d y\)…….(2)
Hence adding (1) and (2), we get \(\oint_C \mathrm{P} d x+\mathrm{Q} d y=\iint_S\left(\ \frac {\partial \mathrm{Q}}{\partial x}-\frac{\partial \mathrm{P}}{\partial y}\right) d x d y\)
If the line parallel to either axis cuts in more than two points then we divide S into such regions satisfying our condition. Now we apply the formula obtained to each subregion and take the sum of integrals which is the same as the line integral over C This is because the line integrals along the boundary curves will cancel in pairs.
Integral Transformations Using Green’S And Stokes’ Theorem
Integral Transformations Stokes, Theorem
Let S be a surface bounded by a closed, nonintersecting curve C. If F is any differentiable vector point function, the \(\oint_c \mathbf{F} \cdot d \mathbf{r}=\int_s \text{curl} \mathbf{F} \cdot \mathbf{N} d \mathbf{S}\)
where C is traversed in the positive direction. The direction of C is called positive if the person, walking on the boundary of S in this direction, with his head pointing in the direction of outward drawn normal N to S, has the surface on his left.
Cartesian Form Let F = F1i + F2 j + F3k
Let the unit normal vector N, of the x, y, z axes. drawn outward make angles α,β,γ with the positive direction of the x,y, and z axes.
∴ \(\mathbf{N}=\mathbf{i} \cos \alpha+\mathbf{j} \cos \beta+\mathbf{k} \cos \gamma\)
∴ \(\mathbf{F} \cdot d \mathbf{r}=\left(F_1 \mathbf{i}+F_2 \mathbf{j}+F_3 \mathbf{k}\right) \cdot(\mathbf{i} d x+\mathbf{j} d y+\mathbf{k} d z)=F_1 d x+F_2 d y+F_3 d z\)
Also \(\nabla \times \mathbf{F}=\left|\begin{array}{ccc}\mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ F_1 & F_2 & F_3\end{array}\right|\)
= \(\left(\frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z}\right) \mathbf{i}+\left(\frac{\partial F_1}{\partial z}-\frac{\partial F_3}{\partial x}\right) \mathbf{j}+\left(\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right) \mathbf{k}\)
∴ \((\nabla \times \mathbf{F}) \cdot \mathbf{N}=\left(\frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z}\right) \cos \alpha+\left(\frac{\partial F_1}{\partial z}-\frac{\partial F_3}{\partial x}\right) \cos \beta+\left(\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right) \cos \gamma\)
∴ Stokes theorem is equivalent to \(\oint_c F_1 d x+F_2 d y+F_3 d z\)
= \(\int_s\left[\left(\frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z}\right) \cos \alpha+\left(\frac{\partial F_1}{\partial z}-\frac{\partial F_3}{\partial x}\right) \cos \beta+\left(\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right) \cos \gamma\right] d \mathbf{S}\)
Proof: Let S be a surface which is such that its projections on xy, yz, and zx planes are regions bounded by simple closed curves.
Let S have the equations z=f(x,y) or z=g(y,z) or z=h(z,x) where f,g,h are simple values continuous and differentiable functions.
Now to prove \(\int_s(\nabla \times \mathbf{F}) \cdot \mathbf{N} d \mathbf{S}=\int_s \nabla \times\left(F_1 \mathbf{i}+F_2 \mathbf{j}+F_3 \mathbf{k}\right) \cdot \mathbf{N} d \mathbf{S}=\oint_c \mathbf{F} \cdot d \mathbf{r}\)
Let us consider \(\int\left[\nabla \times\left(F_{\mathbf{1}} \mathbf{i}\right)\right] . \mathbf{N} d \mathbf{S}\)
Now \(\nabla \times\left(F_1 \mathbf{i}\right)=\left|\begin{array}{ccc}\mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ F_1 & 0 & 0\end{array}\right|=\frac{\partial F_1}{\partial z} \mathbf{j}-\frac{\partial F_1}{\partial y} \mathbf{k}\)
∴ \(\left[\nabla \times\left(F_1 \mathbf{i}\right) \cdot \mathbf{N}\right] d \mathbf{S}=\left(\frac{\partial F_1}{\partial z} \mathbf{j}-\frac{\partial F_1}{\partial y} \mathbf{k}\right) \cdot \mathbf{N} d \mathbf{S}=\left[\frac{\partial F_1}{\partial z}(\mathbf{N} \cdot \mathbf{j})-\frac{\partial F_1}{\partial y}(\mathbf{N} \cdot \mathbf{k})\right] d \mathbf{S}\)
Let z=f(x, y) be the equation of S. For any point S \(\mathbf{r}=x \mathbf{i}+y \mathbf{j}+z \mathbf{k}=x \mathbf{i}+y \mathbf{j}+f(x, y) \mathbf{k}=\frac{\partial \mathbf{r}}{\partial y}=\mathbf{j}+\frac{\partial z}{\partial y} \mathbf{k}\)
because \(\frac{\partial \mathbf{r}}{\partial y}\) is the tangent vector to \(\mathbf{S}, \mathbf{N} \cdot \frac{\partial \mathbf{r}}{\partial y}=0\)
⇒ \(\mathbf{N} \cdot \mathbf{j}+(\mathbf{N} \cdot \mathbf{k}) \frac{\partial z}{\partial y}=0 \Rightarrow \mathbf{N} \cdot \mathbf{j}=-(\mathbf{N} \cdot \mathbf{k}) \frac{\partial z}{\partial y}\)
Substituting in (1) \(\nabla \times\left(F_1 \mathbf{i}\right) \cdot \mathbf{N}=-(\mathbf{N} \cdot \mathbf{k}) \frac{\partial F_1}{\partial z} \frac{\partial z}{\partial y}-(\mathbf{N} \cdot \mathbf{k}) \frac{\partial F_1}{\partial y}\)
⇒ \({\left[\nabla \times\left(F_1 \mathbf{i}\right) \cdot \mathbf{N}\right] d \mathbf{S}=-\left(\frac{\partial F_1}{\partial v}+\frac{\partial F_1}{\partial z} \frac{\partial z}{\partial v}\right)(\mathbf{N} \cdot \mathbf{k}) d \mathbf{S} }\)
= \(-\frac{\partial}{\partial y} F_1(x, y, z)(\cos \gamma) d \mathbf{S}=-\frac{\partial}{\partial y} F_1 \cdot d x d y\)
Let R be the projection of S on x y-plane and \(\sigma\) be the boundary of R
∴ \(\int_s\left[\nabla \times\left(F_1 \mathbf{i}\right)\right] \cdot \mathbf{N} d \mathbf{S}=\iint_R-\frac{\partial F_1}{\partial y} d x d y\)
By Green’s theorem in$x y-plane \(\iint_R\left(0-\frac{\partial F_1}{\partial y}\right) d x d y=\int_\sigma F_1 d x+0 d y\)
Since \(F_1(x, y, z)\) of \(\mathbf{C}\) is same as \(F_1\left(x, y, f(x, y)\right.\)of \(\sigma\) we have \(\oint_\sigma F_1 d x=\oint_c F_1 d x\)
Hence \(\oint_s\left[\nabla \times\left(F_1\right)\right] . \mathrm{N} d \mathrm{~S}=\oint_c F_1 d x\)
Similarly, by projections on the other y z, z x planes \(\oint_s\left[\nabla \times\left(F_2 \mathrm{j}\right)\right] . \mathrm{N} d \mathrm{~S}=\oint_c F_2 d y\)
⇒ \(\oint_s\left[\nabla \times\left(F_3 \mathrm{k}\right)\right] \cdot \mathrm{N} d \mathrm{~S}=\oint_c F_3 d z\)
Hence in addition, we have \(\int_s \nabla \times\left(F_1 \mathbf{i}+F_2 \mathbf{j}+F_3 \mathbf{k}\right) \cdot \mathbf{N} d \mathbf{S}=\int F_1 d x+F_2 d y+F_3 d z \text { i.e. } \int \nabla \times \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\int_c \mathbf{F} . d \mathbf{r}\)
Applying Stokes’ Theorem In The Plane
Integral Transformations Stokes Theorem In A Plane
Let the surface S lie in the xy-plane. Then the z-axis will be along the normal i.e. N=K
Let \(\mathbf{F}=F_1 \mathbf{i}+F_2 \mathbf{j}\) and \(\mathbf{r}=x \mathbf{i}+y \mathbf{j}\)
∴ \(\mathbf{F} . d \mathbf{r}=\left(F_1 \mathbf{i}+F_2 \mathbf{j}\right) \cdot(\mathbf{i} d x+\mathbf{j} d y)=F_1 d x+F_2 d y\)
and \(\nabla \times \mathbf{F}=\left|\begin{array}{ccc}\mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ F_1 & F_2 & 0\end{array}\right|\)
= \(-\frac{\partial F_2}{\partial z} \mathrm{i}+\frac{\partial F_1}{\partial z} \mathrm{j}+\left(\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right) \mathrm{k}\)
∴ \((\nabla \times \mathbf{F}) . \mathbf{N}=(\nabla \times \mathbf{F}) . \mathbf{k}=\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\)
In x y- plane, \(d \mathbf{S}=d x d y\)
⇒ \(\int_c \mathbf{F} \cdot d \mathbf{r}=\int_s(\nabla \times \mathbf{F}) \cdot \mathbf{N} d \mathbf{S} \Rightarrow \int_c F_1 d x+F_2 d y=\iint_s\left(\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right) d x d y\)
This is the same as Green’s theorem in a plane.
