Integral Transformations Exercise 7.3
1. Verify Stokes theorem for the function F=zi+xj+yk where the curve is the unit circle in the xy – plane bounding the hemispherez=\(\sqrt{\left.1-x^2-y^2\right)}\)
Solution:
Given \(\oint_C(3 x+4 y) d x+(2 x-3 y) d y\) . Here \(\mathbf{P}=3 x+4 y, \mathbf{Q}=2 x-3 y\)
By Green’s theorem \(\int_C \mathbf{P} d x+\mathbf{Q} d y=\iint_S\left(\frac{\partial \mathbf{Q}}{\partial x}-\frac{\partial \mathbf{P}}{\partial y}\right) d x d y\)
= \(\iint_S(2-4) d x d y=-2 \int_S d \mathrm{~A}=-2 \mathrm{~A}=-2 \pi(2)^2=-8 \pi\)
∴ \(\int_C \mathbf{F} . d \mathbf{r}=\int_C x d y\) because z=0, d z=0
Let x = \(\cos \theta, y=\sin \theta \quad \int \mathbf{F} . d \mathbf{r}=\int_0^{2 \pi} \cos ^2 \theta d \theta\)
= \(4 \int_0^{2 \pi} \cos ^2 \theta \cdot d \theta=4 \cdot \frac{1}{2} \cdot \frac{\pi}{2}=\pi\)……….(1)
Now let \(\int_S \text{curl} \mathbf{F} \cdot \mathbf{N} d \mathbf{S}\).
⇒ \(\nabla \times \mathbf{F}=\mathbf{i}+\mathbf{j}+\mathbf{k}\)
If \(\mathbf{S}_1\) is the plane region bounded by the circle C then unit normal N=k.
∴ \(\int_S \text{curl} \mathbf{F} . \mathbf{N} d \mathbf{S}=\int_{\mathrm{S}_1}(\nabla \times \mathbf{F}) \cdot \mathbf{k} d \mathbf{S}=\int_{\mathrm{S}_1} 1 . d \mathbf{S}=\mathbf{S}_1\)
But \(\mathbf{S}_1=\) area of the circle of radius unity \(=\pi\)
∴ \(\int_S \text{curl} \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\pi\)……….(2)
Hence from (1) and (2) the theorem is verified.
2. Evaluate \(\int_C\)F.dr by Stokes theorem , if F=(x2+y2)i- 2xyj where C is the rectangle formed x=±a, y=0, y=b
Solution:
curl F = (-4 y) k
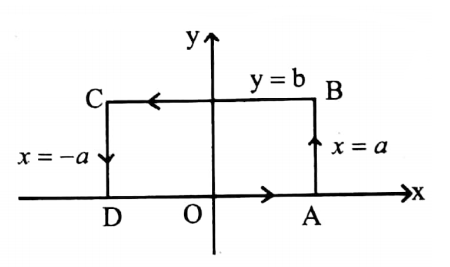
In the xy-plane N =k
∴ \(\int_C \mathbf{F} . d \mathbf{r}=\int_S \text{curl} \mathbf{F} . \mathbf{N} d \mathbf{S}\)
= \(\int^x(\nabla \times \mathbf{F}) \cdot \mathbf{k} d s\)
= \(\int_{y=0}^b \int_{x=-a}^a-4 y d x d y=-4[x]_{-a}^a\left[\frac{y^2}{2}\right]_0^b=-4 a b^2\)
3. Evaluate by Stokes theorem \(\int_C\)F.dr where F= yzi+zxj+xyk and C is the curve x²+y²=1,z=y²
Solution:
F = \(y z \mathbf{i}+z x \mathbf{j}+x y \mathbf{k}\)
∴ \(\text{curl} \mathbf{F}=0\)
By Stokes theorem, \(\oint \mathbf{F} \cdot d \mathbf{r}=\int(\text{curl} \mathbf{F}) \cdot \mathbf{N} d \mathbf{S}=0\)
4. Evaluate by Stokes theorem \(\int_C\)sinz dx-cos x dy + sin y dz where C is the boundary of the rectangle 0 ≤ x≤π, 0<y≤1, z=3 [Hint: Unit normal vector N=k since rectangle lies in the plane z=3].
Solution:
Here \(\mathbf{F}=(\sin z) \mathbf{i}-\cos x \mathbf{j}+\sin y \mathbf{k}\)
∴ \(\text{curl} \mathbf{F}=(\cos y) \mathbf{i}+(\cos z) \mathbf{j}+(\sin x) \mathbf{k}\)
∴ The rectangle lies in the plane z=3
N = k\(\mathbf{F} . \mathbf{N}=\sin x\)
By Stokes theorem, \(\oint_C \mathbf{F} \cdot d \mathbf{r}=\int_{\mathbf{S}} \text{curl} \mathbf{F} \cdot \mathbf{N} d \mathbf{S}\)
= \(\int_{y=0}^1 \int_{x=0}^\pi \sin x d x d y=\int_0^1 d y \cdot \int_0^{S_\pi} \sin x d x=2\)
5.Prove that \(\int_S\)r× dr=2\(\int_S\)dS [Hint: Apply Stokes theorem for a×r where a is a constant vector]
Solution: Let F=a×r where a is a constant vector. Then ∇× F = ∇× (a×r)=2a
∴ By Stokes theorem \(\Rightarrow \int_C(\mathbf{a} \times \mathbf{r}) \cdot d \mathbf{r}=\int_S 2 \mathbf{a} \cdot \mathbf{N} d \mathbf{S}\)
a. \(\int(\mathbf{r} \times d \mathbf{r})=2 \mathbf{a} \cdot \int \mathbf{N} d \mathbf{S} \Rightarrow \int \mathbf{r} \times d \mathbf{r}=2 \int d \mathbf{S}\)
6. Evaluate by Stokes theorem \(\oint_C\)(ex dx+2y dy-dz) where C is the curve x2+y2=0,z=2.
Solution:
∴ \(\oint_C\left(e^x d x+2 y d y-d z\right)=\oint_C\left(e^x \mathrm{i}+2 y \mathrm{j}-\mathrm{k}\right) \cdot(\mathrm{i} d x+\mathrm{j} d y+\mathrm{k} d z)=\oint \mathrm{F} \cdot d \mathrm{r}\)
Hence \(\mathrm{F}=e^x \mathrm{i}+2 y \mathrm{j}-\mathrm{k}\)
∴ \(\nabla \times \mathbf{F}=0\)
By Stokes theorem \(\int_C \mathbf{F}. d \mathbf{r}=\int_S(\nabla \times \mathbf{F}) \cdot \mathbf{N} d s=0\)