Integration Of Vectors
Integration is the inverse operation of differentiation. Let F (t) be a differentiable vector function of a scalar variable t and
Let \(\frac{d}{d t} \mathbf{F}(t)\)=\(\mathbf{f}(t)\). Then \(\int \mathbf{f}(t) d t\)= F(t)
F (t) is called the primitive of f (t)
The set of all primitives of f (t), that is\(\int \mathbf{f}(t) d t\) = F (t) + C where C is any arbitrary constant vector, is called the indefinite integral of f (t).
Hence, the indefinite integral of F (t) is not unique.
Note. If f(t)= f1(t)i + f2(t)j + f3(t)k , then
∫f(t)dt = i∫f1(t)dt +j∫f2(t)dt + k ∫f3(t)dt + C
Integration Of Vectors Examples And Solutions
Integration Of Vectors Definite Integral
Let ∫f(t)dt = F (t) . Then F (b)- F (a) is called the definite integral of F (t) between
The limits, t = a and t = b. This is denoted\(\int_a^b \mathbf{f}(t) dt \)=\([\mathbf{F}(t)]_a^b\) =F(b)-F(a)
This integral can also be defined as a limit of a sum in a manner analogous to that of elementary integral calculus.
Note. Let f(t)=f1(t)i + f2(t)j + f3(t)k .
Then \(\int_a^b \mathbf{f}(t) d t\)=\(\mathbf{i} \int_a^b f_1(t) d t+\mathbf{j} \int_a^b f_2(t) d t+\mathbf{k} \int_a^b f_3(t) d t\)
Standard Results
1. We have \(\frac{d}{d t}(\mathbf{r} \cdot \mathbf{s})\)=\(\frac{d \mathbf{r}}{d t} \cdot \mathbf{s}+\mathbf{r} \cdot \frac{d \mathbf{s}}{d t}\)
∴ \(\int\left(\frac{d \mathbf{r}}{d t} \cdot \mathbf{s}+\mathbf{r} \cdot \frac{d \mathbf{s}}{d t}\right) d t\) = r.s + c
Here c is a scalar constant, since the integrand is a scalar
We have \(\frac{d}{d t}\left(\mathbf{r}^2\right)\)=\(2 \mathbf{r} \cdot \frac{d \mathbf{r}}{d t}\)
∴ \(\int\left(2 \mathbf{r} \cdot \frac{d \mathbf{r}}{d t}\right) d t\) = r2+c
2.\(\frac{d}{d t}\left(\frac{d \mathbf{r}}{d t}\right)^2\)=\(2 \frac{d \mathbf{r}}{d t} \cdot \frac{d^2 \mathbf{r}}{d t^2}\)
∴\(\int\left(2 \frac{d \mathbf{r}}{d t} \cdot \frac{d^2 \mathbf{r}}{d t^2}\right) d t\)=\(\left(\frac{d \mathbf{r}}{d t}\right)^2+c\)
where c is a scalar constant
3.We have\(\frac{d}{d t}(\mathbf{r} \times \mathbf{s})\)=\(\frac{d \mathbf{r}}{d t} \times \mathbf{s}+\mathbf{r} \times \frac{d \mathbf{s}}{d t}\)
∴\(\int\left(\frac{d \mathbf{r}}{d t} \times \mathbf{s}+\mathbf{r} \times \frac{d \mathbf{s}}{d t}\right) d t\)=\(\mathbf{r} \times \mathbf{s}+\mathbf{c}\)
Here the constant c is a vector quantity since the integrand is also a vector quantity.
4. If an Inconstant vector, we have \(\frac{d}{d t}(\mathbf{a} \times \mathbf{r})\)=\(\mathbf{a} \times \frac{d \mathbf{r}}{d t}\)
∴ \(\int\left(\mathbf{a} \times \frac{d \mathbf{r}}{d t}\right) d t=\mathbf{a} \times \int \frac{d \mathbf{r}}{d t} d t\)=\(\mathbf{a} \times \mathbf{r}+\mathbf{c}\)
5. Now \(\frac{d}{d t}\left(\mathbf{r} \times \frac{d \mathbf{r}}{d t}\right)\)=\(\frac{d \mathbf{r}}{d t} \times \frac{d \mathbf{r}}{d t}+\mathbf{r} \times \frac{d^2 \mathbf{r}}{d t^2}\)=\(\mathbf{r} \times \frac{d^2 \mathbf{r}}{d t^2}\)
∴ \(\int\left(\mathbf{r} \times \frac{d^2 \mathbf{r}}{d t^2}\right) d t\)=\(\mathbf{r} \times \frac{d \mathbf{r}}{d t}+\mathbf{c}\)
6. Ifr = |r|, then \(\frac{d}{d t}\left(\frac{\mathbf{r}}{r}\right)\)=\(\frac{1}{r} \frac{d \mathbf{r}}{d t}-\frac{1}{\dot{r}^2} \frac{d r}{d t} \mathbf{r}\)
∴ \(\int\left(\frac{1}{r} \frac{d \mathbf{r}}{d t}-\frac{1}{r^2} \frac{d r}{d t} \mathbf{r}\right) d t\)=\(\frac{\mathbf{r}}{r}+\mathbf{c}\)
7. If c is a scalar constant then c is a scalar constant then∫ cr dt=c∫r dt
8. If r and s are any two vector functions of a scalar t, then ∫(r+s) dt= ∫r dt+ ∫ s dt
Integration Of Vectors Solved Problems
Exmple.1. Evaluate \(\int_0^1\left(e^t \mathbf{i}+e^{-2 t} \mathbf{j}+t \mathbf{k}\right) d t\)
Solution:
Given
\(\int_0^1\left(e^t \mathbf{i}+e^{-2 t} \mathbf{j}+t \mathbf{k}\right) d t\) \(\int_0^1\left(e^t \mathbf{i}+e^{-2 t} \mathbf{j}+t \mathbf{k}\right) d t=\mathbf{i} \int_0^1 e^t d t+\mathbf{j} \int_0^1 e^{-2 t} d t+\mathbf{k} \int_0^1 t d t\)= \(\mathbf{i}\left[e^t\right]_0^1+\mathbf{j}\left[-\frac{1}{2} e^{-2 t}\right]_0^1+\mathbf{k}\left[\frac{t^2}{2}\right]_0^1=(e-1) \mathbf{i}-\frac{1}{2}\left(e^{-2}-1\right) \mathbf{j}+\frac{1}{2} \mathbf{k}\)
Solved Problems On Vector Integration Step-By-Step
Example. 2. Evaluate \(\int_2^3 \mathbf{f} \cdot \frac{d \mathbf{f}}{d t} d t\) if f(2) = 2i – i+2k and f(3)= 4i-2j+3k
Solution:
Given
\(\int_2^3 \mathbf{f} \cdot \frac{d \mathbf{f}}{d t} d t\)(2) = 2i – i+2k and f(3)= 4i-2j+3k
We know that \(\int\left(2 \mathbf{f} \cdot \frac{d \mathbf{f}}{d t}\right) d t=\mathbf{f}^2+c\)
∴ \(\int_2^3(\mathrm{f} \cdot \frac{d \mathrm{f}}{d t}) d t=\frac{1}{2}[\mathrm{f}^2{ }_2^3=\frac{1}{2}[\mathrm{f}^2(3)-\mathrm{f}^2(2)]\)
= \(\frac{1}{2}\left[(4 \mathbf{i}-2 \mathbf{j}+3 \mathbf{k})^2-(2 \mathbf{i}-\mathbf{j}+2 \mathbf{k})^2\right]=\frac{1}{2}[(16+4+3)-(4+1+4)]=10\)
Example. 3. Find the value of \(\frac{d \mathbf{r}}{d t}\) by integrating \(\frac{d^2 \mathbf{r}}{d t^2}\) = -n2r
Solution:
The given equation is \(\frac{d^2 \mathbf{r}}{d t^2}=-n^2 \mathbf{r}\)
Taking the dot product with \(2 \frac{d \mathrm{r}}{d t}\) both sides
and integrating we have \(\int\left(2 \frac{d \mathbf{r}}{d t} \cdot \frac{d^2 \mathbf{r}}{d t^2}\right) d t=-n^2 \int\left(2 r \cdot \frac{d \mathbf{r}}{d t}\right) d t\)
⇒ \(\left(\frac{d \mathbf{r}}{d t}\right)^2=n^2 \mathbf{r}^2+\mathbf{c}\)
where c is any constant vector.
Exercises On Line, Surface, And Volume Integrals With Solutions
Example. 4. If f(t) =5t2 i+tj-t3k find \(\int_1^2\left(\bar{f} \times \frac{d^2 \tilde{f}}{d t^2}\right) d t\)
Solution: \(\int_1^2\left(\mathbf{f} \times \frac{d^2 \mathbf{f}}{d t^2}\right\} d t=\left[\mathbf{f} \times \frac{d \mathbf{f}}{d t}\right]_1^2\)
Given \(\mathbf{f}(t)=5 t^2 \mathbf{i}+t \mathbf{j}-t^3 \mathbf{k}\)
∴ \(\frac{d \mathbf{f}}{d t}=10 t \mathbf{i}+\mathbf{j}-3 t^2 \mathbf{k}\)
f x \(\frac{d \mathbf{f}}{d t}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
5 t^2 & t & -t^3 \\
10 t & 1 & -3 t^2
\end{array}\right|\)
= \(-2 t^3 \mathbf{i}+5 t^4 \mathbf{j}-5 t^2 \mathbf{k}\)
∴ \(\left[\mathbf{f} \times \frac{d \mathbf{f}}{d t}\right]_1^2=\left[-2 t^3 \mathbf{i}+5 t^4 \mathbf{j}-5 t^2 \mathbf{k}\right]_1^2=-14 \mathbf{i}+75 \mathbf{j}-15 \mathbf{k}\)
∴ \(\int_1^2\left(\mathbf{f} \times \frac{d^2 \mathbf{f}}{d t^2}\right) d t=-14 \mathbf{i}+75 \mathbf{j}-15 \mathbf{k}\)
Integration Of Vectors Exercise 6(a)
1. If F(t) = (t-t2)i+2t3j-3k find \(\int_1^2 \mathbf{F}(t) d t\)
Solution:
Given
F(t) = (t-t2)i+2t3j-3k
⇒ \(\int_1^2\left[\left(t-t^2\right) \mathrm{i}+2 t^3 \mathrm{j}-3 \mathrm{k}\right] d t\)
= \(\left[\left(\frac{t^2}{2}-\frac{t^3}{3}\right) \mathrm{i}+\frac{2 t^4 \mathrm{j}}{4}-3 t \mathrm{k}\right]_1^2=-\frac{5}{6} \mathrm{i}+\frac{15}{2} \mathrm{j}-3 \mathrm{k}\)
Surface Integrals Of Vectors Examples And Solutions
2.If F(t) =ti+(t2-2t)j+(3t2+3t3)k find \(\int_0^1 f(t) d t\)
Solution:
Given
F(t) =ti+(t2-2t)j+(3t2+3t3)k
⇒ \(\int_0^1 f(t) d t=\int_0^1\left[t \mathbf{i}+\left(t^2-2 t\right) \mathbf{j}+\left(3 t^2+3 t^3\right) \mathbf{k}\right] d t\)
= \(\left[\frac{t^2}{2} \mathbf{i}+\left(\frac{t^3}{3}-t^2\right) \mathbf{j}+\left(t^3+\frac{3}{4} t^4\right) \mathbf{k}\right]_0^1=\frac{1}{2} \mathbf{i}-\frac{2}{3} \mathbf{j}+\frac{7}{4} \mathbf{k}\)
= \(\frac{1}{12}[6 \mathbf{i}-8 \mathbf{j}+21 \mathbf{k}]\)
3. If A=ti-t2j+(t-1)k and B= 2t2i+6tK find \(\int_1^2(\mathbf{A} \cdot \mathbf{B}) d t\)
Solution:
Given
A=ti-t2j+(t-1)k and B= 2t2i+6tK
A . B = \(t\left(2 t^3\right)+6 t(t-1)\)
∴ \(\int_0^2(\mathbf{A} \cdot \mathbf{B}) d t=\int_0^2\left(2 t^3+6 t^2-6 t\right) d t=12\)
4. If a=ti-3j+2tk : B= i-2j+2k : C= 3i+tj-k find
(1)\(\int_1^2[\mathbf{A B C}] d t\)
(2) \(\int_1^2[\mathrm{~A} \times(\mathrm{B} \times \mathrm{C})]dt\)
Solution:
Given
a=ti-3j+2tk : B= i-2j+2k : C= 3i+tj-k
(1) [А B C] = \(\left|\begin{array}{ccc}
t & -3 & 2 t \\
1 & -2 & 2 \\
3 & t & -1
\end{array}\right|\) =14 t-21
∴ \(\int_1^2[\mathbf{A ~ B ~ C}] d t=\int_1^2(14 t-21) d t=0\)
(2) Use \(\mathbf{A} \times(\mathbf{B} \times \mathbf{C})=(\mathbf{A} \cdot \mathbf{C}) \mathbf{B}-(\mathbf{A} \cdot \mathbf{B}) \mathbf{C}\) and then integrate.
5. If \(\frac{d^2 \mathbf{r}}{d t^2}\)=6ti-24t2j+4 sin tk find r given thatr= 2i+j and \(\frac{d \mathbf{r}}{d t}\)=-i-3k at t=0
Solution:
Given
\(\frac{d^2 \mathbf{r}}{d t^2}\)=6ti-24t2j+4 sin tk
∫ \(\frac{d^2 \mathbf{r}}{d t^2} \cdot d t=\int\left(6 t \mathbf{i}-24 t^2 \mathbf{j}+4 \sin t \mathbf{k}\right) d t\)
⇒ \(\frac{d \mathbf{r}}{d t}=3 t^2 \mathbf{i}-8 t^3 \mathbf{j}-4 \cos t \mathbf{k}+\mathbf{A}\) when t = \(0 \quad \frac{d \mathbf{r}}{d t}=-\mathbf{i}-3 \mathbf{k}\)
–\(\mathbf{i}-3 \mathbf{k}=-4 \mathbf{k}+\mathbf{A} \Rightarrow \mathbf{A}=-\mathbf{i}+\mathbf{k}\)
Hence \(\frac{d \mathrm{r}}{d t}=\left(3 t^2-1\right) \mathbf{i}-8 t^3 \mathbf{j}+(1-4 \cos t) \mathbf{k}\)
Again integrating \(\mathbf{r}=\int \frac{d \mathbf{r}}{d t} d t=\left(t^3-t\right) \mathbf{i}-2 t^4 \mathbf{j}+(t-4 \sin t) \mathbf{k}+\mathbf{B}\) when t=0,2 i+j=B
∴ \(\mathbf{r}=\left(t^2-t+2\right) \mathbf{i}+\left(1-2 t^4\right) \mathbf{j}+(t-4 \sin t) \mathbf{k}\)
Volume Integrals Solved Problems With Step-By-Step Explanations
6. Find F(t), given \(\frac{d \mathbf{F}}{d t}\) =12 cos 2ti-8 sin 2tj+2tk and F(0)=0
Solution:
F(t) = \(\int d \mathbf{F}=\int(12 \cos 2 t \mathbf{i}-8 \sin 2 t \mathbf{j}+2 t \mathbf{k}) d t\)
F(t) = \(6 \sin 2 t \mathbf{i}+4 \cos 2 t \mathbf{j}+t^2 \mathbf{k}+\mathbf{C}\)
Given \(\mathbf{F}(0)=0 \Rightarrow 4 \mathbf{j}+\mathbf{C}=0 \Rightarrow \mathbf{C}=-4 \mathbf{j}\)
∴ \(\mathrm{F}(t)=6 \sin 2 t \mathrm{i}+(4 \cos 2 t-4) \mathrm{j}+t^2 \mathrm{k}\)
7. If a,b, and n are constants and r= a cos nt+b sin nt. Show that \(\frac{d^2 \mathbf{r}}{d t^2}+n^2 \mathbf{r}\)=0
Solution:
Given
a,b, and n are constants and r= a cos nt+b sin nt
⇒ \(\frac{d \mathbf{r}}{d t}=-\mathbf{a} n \sin n t+\mathbf{b} n \cos n t\)
⇒ \(\frac{d^2 \mathbf{r}}{d t^2}=-\mathbf{a} n^2 \cos n t-\mathbf{b} n^2 \sin n t=-n^2 \mathbf{r}\)
∴ \(\frac{d^2 \mathbf{r}}{d t^2}+n^2 \mathbf{r}=0\)
Applications Of Vector Integration In Physics And Engineering
8. Given \(\frac{d^2 \mathbf{r}}{d t^2}\)=-k2r show that \(\left(\frac{d \mathbf{r}}{d t}\right)^2\)=c-k2r2
Solution:
The given equation is \(\frac{d^2 \mathbf{r}}{d t^2}=-n^2 \mathbf{r}\)
Taking the dot product with \(2 \frac{d \mathbf{r}}{d t}\) both sides and integrating we have \(\int\left(2 \frac{d \mathbf{r}}{d t} \cdot \frac{d^2 \mathbf{r}}{d t^2}\right) d t=-n^2 \int\left(2 r \cdot \frac{d \mathbf{r}}{d t}\right) d t \quad\left(\frac{d \mathbf{r}}{d t}\right)^2=n^2 \mathbf{r}^2+\mathbf{c}\)
where c is any constant vector.
Integration Of Vectors Line, Surface, Volume, Integrals Oriented Curve
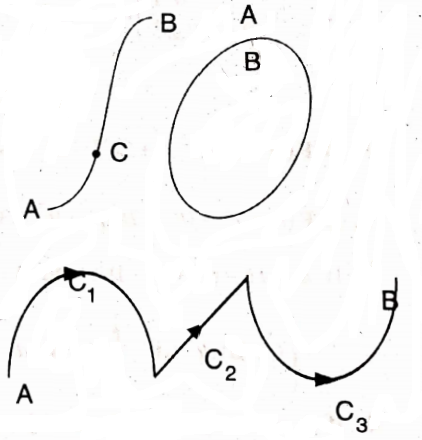
Let C be a curve in space. A be the initial point and B be the terminal point of curve C . When the direction along C oriented
from A to B is positive then the direction B to A is then called the negative direction. If the two points coincide, curve C is called the closed curve.
Integration Of Vectors Smooth Curve
A curve r = F (t) is called a smooth curve if F (t) is continuously differentiable. A curve C is said to be piecewise smooth if it consists of a finite number of smooth curves. The curve of is composed of three smooth curves C1, C2, and C3.
Integration Of Vectors Line Integrals
Let r = f (t) define a smooth curve C joining points A and B. Let us be the differential of arc length at P e C.
Then \(\frac{d \mathbf{r}}{d s}\)=T, is the unit vector along the tangent to the curve C at P.
Let F (r) be a vector point, a function defined and continuous along C. The component of F (r) along the tangent at P is F (r). T.
The integral ∫F.Tds taken along the curve C is called the Linear integral of F along
C. This is written as\(\int_A^B \mathbf{F} \cdot \mathbf{T} d s\)=\(\int_C\left(\mathbf{F} \cdot \frac{d \mathbf{r}}{d s}\right) d s\)=\(\int_C \mathbf{F} \cdot d \mathbf{r}\)
This is also called the tangential line integral of F along C.
Note. The other types of line integrals are \(\int_C \mathbf{F} \times d \mathbf{r} \text { and } \int_C \phi d \mathbf{r}\)
where F is a continuous vector and Φ a continuous scalar point function. In general, any integral which is to be evaluated along a curve is called a line integral. Such integrals can be defined in terms of limits of sums as are the integrals of elementary calculus.
Integration Of Vectors Circulation
Let C be a simple closed curve (i.e. a curve that does not intersect itself anywhere). The line integral of F along C is called the circulation of F along C. It is often denoted by
∴ \(\oint_{\mathrm{C}} \mathrm{F} \cdot d \bar{r}\)=\(\oint_{\mathrm{C}}\left(\mathrm{F}_1 d x+\mathrm{F}_2 d y+\mathrm{F}_3 d z\right)\)
Integration Of Vectors Cartesian Form
LetF(r) = F1i+F2j+F3k (r) = xi+yj+zk
Then \(\oint_{\mathbf{C}} \mathbf{F} \cdot d \mathbf{r}\)=\(\oint_{\mathbf{C}}\left(\mathrm{F}_1 d x+\mathrm{F}_2 d y+\mathrm{F}_3 d z\right) \cdot(\mathbf{i} d x+\mathbf{j} d y+\mathbf{k} d z)\)
⇒ \(\oint_C\left(\mathrm{~F}_1 d x+\mathrm{F}_2 d y+\mathrm{F}_3 d z\right)\) is the line integral in cartesian form. If, x,y, and z are functions of t, then
⇒ \(\oint_{\mathbf{C}} \mathbf{F} \cdot d \mathbf{r}\)=\(\oint_{\mathbf{C}} \mathrm{F}_1 d x+\mathrm{F}_2 d y+\mathrm{F}_3 d z\)
= \(\oint_{\mathbf{C}}\left(\mathrm{F}_1 \frac{d x}{d t}+\mathrm{F}_2 \frac{d y}{d t}+\mathrm{F}_3 \frac{d z}{d t}\right) d t\)
Integration Of Vectors Work Done By A Force
If A is the force F acting on a particle moving along C, then \(\int_C \mathbf{A} d \mathbf{r}\) denotes the work done by the force.
Integration Of Vectors Solved Problems
Example. 1. Find \(\int_{\mathbf{C}} \mathbf{F} \cdot d \mathbf{r}\) where F= xyi+yzj+ zx+k and the curve C is r= ti+t2j+t3k , t varying from -1 to 1.
Solution:
Given \(\mathbf{r}=t \mathbf{i}+t^2 \mathbf{j}+t^3 \mathbf{k}\), for the curve \(\mathbf{C}\)
∴ \(\frac{d \mathbf{r}}{d t}=\mathbf{i}+2 t \mathbf{j}+3 t^2 \mathbf{k}\)
Also \(\mathbf{r}=x \mathbf{i}+y \mathbf{j}+z \mathbf{k}\)
∴ x=t, y=t^2, z = \(t^3\), is the curve C
Again F = \(x y \mathbf{i}+y z \mathbf{j}+z x \mathbf{k}\)
∴ F over the curve C is F = \(t\left(t^2\right) \mathbf{i}+\left(t^2\right)\left(t^3\right) \mathbf{j}+\left(t^3\right)(t) \mathbf{k}=t^3 \mathbf{i}+t^5 \mathbf{j}+t^4 \mathbf{k}\)
∴ \(\mathrm{F} \cdot \frac{d \mathrm{r}}{d t}=\left(t^3 \mathrm{i}+t^5 \mathrm{j}+t^4 \mathrm{k}\right) \cdot\left(\mathrm{i}+2 t \mathrm{j}+3 t^2 \mathrm{k}\right)=t^3+2 t^6+3 t^6=t^3+5 t^6\)
∴ \(\oint_{\mathrm{C}} \mathrm{F} \cdot d \mathrm{r}=\int_C\left(\mathrm{~F} \cdot \frac{d \mathrm{r}}{d t}\right) d t=\int_{t=-1}^1\left(t^3+5 t^6\right) d t=\left[\frac{t^4}{4}+\frac{5 t^7}{7}\right]_{-1}^1=\frac{10}{7}\)
Step-By-Step Guide To Vector Surface Integrals
Example.2. Evaluate \(\int_C \mathbf{A} d \mathbf{r}\) where F= 3x2i=92xy-y)j=zk along the straight line C from (0,0,0) to (2,1,3)
Solution:
The equation to the line joining (0,0,0) and (2,1,3) is \(\frac{x}{2}=\frac{y}{1}=\frac{z}{3}=t\)
Then along the line C
x=2 t, y=t, z=3 t
Also \(\mathbf{r}=x \mathbf{i}+y \mathbf{j}+z \mathbf{k}=2 t \mathbf{i}+t \mathbf{j}+3 t \mathbf{k}\)
∴ \(d \mathbf{r}=(2 \mathbf{i}+\mathbf{j}+3 \mathbf{k}) d t\)
Given \(\mathrm{F}=3 x^2 \mathrm{i}+(2 x z-y) \mathrm{j}+z \mathrm{k}\)
And along C
F = \(3(2 t)^2 \mathbf{i}+[2(2 t)(3 t)-t] \mathbf{j}+3 t \mathbf{k}=12 t^2 \mathbf{i}+\left(12 t^2-t\right) \mathbf{i}+3 t \mathbf{k}\)
F. dr = \(\left[24 t^2+\left(12 t^2-t\right)+9 t\right] d t=\left(36 t^2+8 t\right) d t\)
At (0,0,0) and at (2,1,3), t=1.
∴ \(\int_{\mathbf{C}} \mathbf{F} . d \mathbf{r}=\int_{t=0}^1\left(36 t^2+8 t\right) d t=\left[12 t^3+4 t^2\right]_0^1=16\)
Example.3. If F= (3x2+6y)i-14yz j +20 xz2 k calculate \(\int_{\mathbf{C}} \mathbf{F} \cdot d \mathbf{r}\) along the lines from (0,0,0), to (1,0,0,) , then to (1,1,0) , and then to (1,1,1).
Solution:
Given F = \(\left(3 x^2+6 y\right) \mathrm{i}-14 y z \mathrm{j}+20 x z^2 \mathrm{k}\)
r = \(x \mathbf{i}+y \mathbf{j}+z \mathbf{k} \quad d \mathbf{r}=\mathbf{i} d x+\mathbf{j} d y+\mathbf{k} d z\)
∴ \(\int_{\mathbf{C}} \mathbf{F} \cdot d \mathbf{r}=\int_{\mathbf{C}}\left(3 x^2+6 y\right) d x-14 y z d y+20 x z^2 d z\)
1. Along the line from (0,0,0) to (1,0,0)
y = \(0, z=0 \Rightarrow \quad d y=0, d z=0\)
x varies from 0 to 1
The integral over this part of the path
∴ \(\int_{\mathrm{C}_1} \mathrm{~F} \cdot d \bar{r}=\int_{x=0}^1 3 x^2 d x=\left[x^3\right]_0=1\)
2. Along the line (1,0,0) to (1,1,0) x=1, z=0 ⇒ dx=0, dz=0
y varies from 0 to 1. The integral over this part of the path
∴ \(\int_{C_2} \mathbf{F} \cdot d \mathbf{r}=\int_{y=0}^1(0-0+0) d y=0\)
3. Along the line (1,1,0) to (1,1,1), x=1, y=1
dx=0, dy=0
z varies from 0 to 1
The integral over this part of the path
∴ \(\int_{\mathbf{C}_3} \mathbf{F} \cdot d \mathbf{r}=\int_{z=0}^1 20 z^2 d z=\left[\frac{20 z^3}{3}\right]_0^1=\frac{20}{3}\)
∴ Adding \(\int_{\mathbf{C}} \mathbf{F} \cdot d \mathbf{r}=1+0+\frac{20}{3}=\frac{23}{3}\)
Example.4. If F = 3xyi-y2j evaluates \(\int_{\mathbf{C}} \mathbf{F} \cdot d \mathbf{r}\) where C is curved y= 2x2 in xy plane from (0,0) to (1,2).
Solution:
Given
F = 3xyi-y2j
The equation of the curve C is y=\(2 x^2\)
dy = 4x d x
Given \(\mathbf{F}=3 x y \mathbf{i}-y^2 \mathbf{j}\)
Since the integration is performed in the xy plane (z=0) and x varies from 0 to 1.
∴ \(\int_{\mathbf{C}} \mathbf{F} . d \mathbf{r}=\int_{z=0}^1 \mathbf{F}_1 d x+\mathbf{F}_2 d y=\int_{\mathbf{C}} 3 x y d x-y^2 d y\)
= \(\int_{x=0}^1 3 x\left(2 x^2\right) d x-4 x^4(4 x) d x\)
= \(\int_0^1\left(6 x^3-16 x^5\right) d x=\left[\frac{6 x^4}{4}-\frac{16 x^6}{6}\right]_0^1=-\frac{7}{6}\)
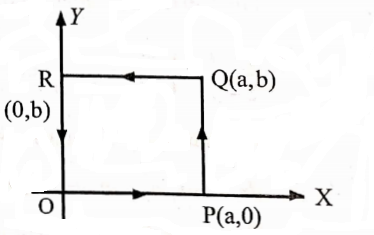
Example.5 If F(x2+y2)i-2xyz evaluate \(\int_{\mathbf{C}} \mathbf{F} \cdot d \mathbf{r}\) where the curve C is the rectangle in the xy plane bounded by y=0, y=b, x=0, x=a
Solution:
Equation to the curve C \(x^2+y^2=1, z=0\) ∴ dz=0
In parametric form, \(x=\cos \theta, y=\sin \theta, z=0\)
The circulation of F = \(y \mathbf{i}+z \mathbf{j}+x \mathbf{k}\), along C is \(\oint_{\mathbf{C}} \mathbf{F} \cdot d \mathbf{r}=\oint_{\mathbf{C}} \mathbf{F}_1 d x+\mathbf{F}_2 d y+\mathbf{F}_3 d z=\oint_{\mathbf{C}} y d x+z d y+x d z=\oint_{\mathbf{C}} y d x\)
For the circle \(\theta\) varies from 0 to \(2 \pi\)
∴ \(\oint \mathbf{F} \cdot d \mathbf{r}=\int_0^{2 \pi} \sin \theta(-\sin \theta) d \theta=-4 \int_0^{\pi / 2} \sin ^2 \theta d \theta=-4\left(\frac{1}{2}\right) \frac{\pi}{2}=-\pi\)
Worked Examples Of Vector Line And Volume Integrals
Example.6. If F=yi+ zj+xk find the circulation of f around the curve C where C is the circle x2+y2=1, z=0
Solution:
Equation to the curve C \(x^2+y^2=1, z=0\) ∴ dz=0
in parametric form, \(x=\cos \theta, y=\sin \theta, z=0\)
The circulation of \(\mathbf{F}=y \mathbf{i}+z \mathbf{j}+x \mathbf{k}\), along \(\mathbf{C}\) is \(\oint_{\mathbf{C}} \mathbf{F} \cdot d \mathbf{r}=\oint_{\mathbf{C}} \mathbf{F}_1 d x+\mathbf{F}_2 d y+\mathbf{F}_3 d z=\oint_{\mathbf{C}} y d x+z d y+x d z=\oint_{\mathbf{C}} y d x\)
For the circle \(\theta\) varies from 0 to \(2 \pi\)
∴ \(\oint \mathbf{F} . d \mathbf{r}=\int_0^{2 \pi} \sin \theta(-\sin \theta) d \theta=-4 \int_0^{\pi / 2} \sin ^2 \theta d \theta=-4\left(\frac{1}{2}\right) \frac{\pi}{2}=-\pi\)
Example.7. Find the work done in moving a particle force field F=3xi+(2xz-y)j+zk along the straight line form (0,0,0) to (2,1,3)
Solution:
Given curve is \(\mathbf{F}=3 x^2 \mathbf{i}+(2 x z-y) \mathbf{j}+z \mathbf{k}\)
Let \(\mathbf{r}=x \mathbf{i}+y \mathbf{j}+3 \mathbf{k} \Rightarrow d \mathbf{r}=d x \mathbf{i}+d y \mathbf{j}+d \mathbf{k}\)
F. \(d \mathbf{r}=3 x^2 d x+(2 x z-y) d y+z d z\)
The Cartesian equation of line through the points (0,0,0),(2,1,3) is \(\frac{x-0}{2-0}=\frac{y-0}{1-0}=\frac{z-0}{3-0}\) i.e. \(\frac{x}{2}=\frac{y}{1}=\frac{z}{3}=t\) (say)
The parametric equations are, x=2t, y=t, z=3t.
dx = 2 dt, dy=dt, dz=3 dt on C, t varies from 0 to 1.
The work done by particles in the force field is
= \(\int_C \mathbf{F} \cdot d \mathbf{r}=\int_{t=0}^1 3\left(2 t^2\right)^2 2 d t+(2.2 t .3 t-t) d t+(3 t) 3 d t\)
= \(\left.\left.\int_0^1\left(24 t^2+12 t^2-t+9 t\right) d t=\int_0^1\left(3 \dot{6} \dot{t}^2+8 t\right) d t\)
= \(36 \frac{t^3}{3}+\frac{8 t^2}{2}\right]_0^1=12 t^3+4 t^2\right]_0^1=1^7+4=16\)
Integration Of Vectors Exercise6 ( b )
1. Evaluate \(\int_{\mathbf{C}} \mathbf{F} \cdot d \mathbf{r}\)where F = x2y2i + yj and the curve C is y2 = 4x in the xy plane from (0,0) to (4,4).
Solution:
The equation of the curve C is \(4 x=y^2\) ∴4 dx=2y dy
Given F = \(x^2 y^2 \mathbf{i}+y \mathbf{j}\)
The integration is performed in xy – plane (z=0) and y varies from 0 to 4.
∴ \(\int_c \mathbf{F} . d \mathbf{r}=\int_c \mathbf{F}_1 d x+\mathbf{F}_2 d y=\int_c x^2 y^2 d x+y d y\)
= \(\int_{y=0}^4\left(\frac{y^2}{4}\right)^2 y^2\left(\frac{1}{2} y\right) d y+y d y=\int_0^4\left(\frac{y^7}{32}+y\right) d y=\left[\frac{y^8}{256}+\frac{y^2}{2}\right]_0^4=264\)
2. If F = (3x2 + 6y) i- 14yzj + 20xz2k evaluate ∫F.dr along the straight line joining (0,0,0) and (1,1,1).
Solution:
Equation to the line joining (0,0,0) and (1,1,1) is \(\frac{x}{1}=\frac{y}{1}=\frac{z}{1}=t\).
∴ \(\mathbf{r}=x \mathbf{i}+y \mathbf{j}+z \mathbf{k}=(\overline{\mathbf{i}}+\mathbf{j}+\mathbf{k}) t\)
d \(\mathbf{r}=(\mathbf{i}+\mathbf{j}+\mathbf{k}) d t\)
Given \(\mathrm{F}=\left(3 x^2+6 y\right) \mathbf{i}-14 y z \mathbf{j}+20 x z^2 \mathbf{k}\)
Along the straight line x=y=z=t
F = \(\left(3 t^2+6 t\right) \mathbf{i}-14 t^2 \mathbf{j}+20 t^3 \mathbf{k}\)
At (0,0,0), t=0 and at (1,1,1), t=1
⇒ \(\overline{\mathrm{F}} \cdot d \bar{r}=\left[\left(3 t^2+6 t\right)-14 t^2+20 t^3\right] d t\)
∴ \(\left.\int_C \overline{\mathrm{F}} \cdot d \bar{r}=3 t^2-\frac{11 t^3}{3}+5 t^4\right]_0^1=\frac{13}{3}\)
Examples Of Vector Integration In Electromagnetism
3. If F = 3xyi- 5zj+ l0xk evaluate ∫F.dr along the curve x = t2+l, y=2t2, z = t3 from t=1 to t=2
Solution:
Given x = \(t^2+1, y=2 t^2, z=t^3\)
r = \(x \mathbf{i}+y \mathbf{j}+z \mathbf{k}=\left(t^2+1\right) \mathbf{i}+2 t^2 \mathbf{j}+t^3 \mathbf{k}\)
dr = \(\left(2 t \mathbf{i}+4 t \mathbf{j}+3 t^2\right) d t\)
Along the given curve C
4. If F = (2y + 3)i + xzj + (yz – x)k evaluate ∫F.dr along the curve C given x = t2, y = t, z =t3 from t = 0 to t = 1 (or) c is the line joining (0,0,0) and (2,1,1)
Solution:
F.dr = \([(2 y+3) \mathbf{i}+x z \mathbf{j}+(y z-x) \mathbf{k}] \cdot(\mathbf{i} d x+\mathbf{j} d y+\mathbf{k} d z)\)
= \((2 y+3) d x+x z d y+(y z-x) d x\)
= \((2 t+3)(4 t)+\left(2 t^2\right)\left(t^3\right)+\left[(t) t^3-2 t^2\right]\left(3 t^2\right)\)
= \(3 t^6+2 t^5-6 t^4+8 t^2+12 t\)
∴ \(\int_0^1 \mathbf{F} \cdot d \mathbf{r}=\int_0^1\left[3 t^6+2 t^5-6 t^4+8 t^2+12 t\right] d t\)
= \(\left[\frac{3}{7} \boldsymbol{t}^7+\frac{2}{6} \boldsymbol{t}^6-\frac{\mathbf{6}}{5} \boldsymbol{t}^5+\frac{8}{3} \boldsymbol{t}^3+\mathbf{6} t^2\right]_0^1=\frac{288}{35}\)
5. Find the line integral of the vector F = zi + xj+ yk over the curve C given by x = a cost, y = a sin t,z = from z = t/2π from z=0 to z = 1.
Solution:
F = \(z \mathbf{i}+x \mathbf{j}+y \mathbf{k}\)
Given x = \(a \cos t, y=a \sin t, z=\frac{t}{2 \pi}\)
∴ dx = \(-a \sin t d t, d y=a \cos t d t, d z=\frac{1}{2 \pi} d t\)
z = \(0 \Rightarrow t=0\) and \(z=1 \Rightarrow t=2 \pi\)
∴ \(\int \mathbf{F} \cdot d \mathbf{r}=\int z d x+x d y+y d z\)
= \(\frac{a}{2 \pi} \int_0^{2 \pi}\left(\frac{t}{2 \pi}(-a \sin t)+a \cos t-\sin t\right) t \cdot d t+a^2 \int_0^{2 \pi} \cos ^2 t \cdot d t\)
= \(\frac{a}{2 \pi}(t \sin t+\cos t)-\frac{a}{2 \pi}[-\cos t+\sin t]_0^{2 \pi}+4 a^2 \int_0^{2 \pi} \cos ^2 t \cdot d t\)
= \(\frac{a}{2 \pi}(2 \pi)-0+4 a^2=\left(\frac{1}{2} \cdot \frac{\pi}{2}\right)=a+\pi a^2\)
6. Evaluate \(\int_{\mathbf{C}}\)(x2 + xy) dx + (x2 + y2)dy where C is the square formed by the lines x = ± 1, y = ± 1
Solution:
Given F. dr = \(\int\left(x^2+x y\right) d x+\left(x^2+y^2\right) d y\)
(1) Along \(\mathbf{A B}, y=1, d y=0\)
and x changes from 1 to -1.
∴ \(\int \mathbf{F} \cdot d \mathbf{r}=\int_1^{-1}\left(x^2+x\right) d x\)
= \(\left[\frac{x^3}{3}+\frac{x^2}{2}\right]_1^{-1}=-\frac{2}{3} .\)
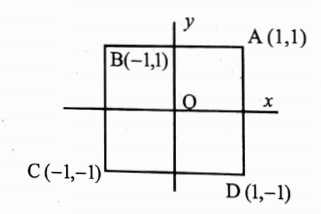
(2) Along B C, x=-1, d x=0, changes from 1 to -1
∴ \(\int \mathbf{F} \cdot d \mathbf{r}=\int_1^{-1}\left(1+y^2\right) d y=\left[y+\frac{y^3}{3}\right]_1^{-1}=-\frac{8}{3}\)
(3) Along CD, \(y=-1, d y=0\) and x changes from -1 to 1 .
∴ \(\int \mathbf{F} . d \mathrm{r}=\int_{-1}^1\left(x^2-x\right) d x=\left[\frac{x^3}{3}+\frac{y^2}{2}\right]_{-1}^1=\frac{2}{3}\)
(4) Along D A, \(x=1, d x=0\) and y changes from -1 to 1 .
∴ \(\int \mathbf{F} . d \mathbf{r}=\int_{-1}^1\left(1+y^2\right) d y=\left[y+\frac{y^3}{3}\right]_{-1}^1=\frac{8}{3}\)
∴ \(\int \mathbf{F} . d \mathbf{r}\) along \(x= \pm, y= \pm 1\) is \(\left[-\frac{2}{3}-\frac{8}{3}+\frac{2}{3}+\frac{8}{3}\right]=0\)
Properties Of Vector Integrals With Solved Problems
7. Find the circulation of F = (2x- y + 2z) i + (x + y- z) j + (3x- 2y- 5z)k along the circle x2+ y2 = 4, z = 0 . [Hint: Take x = 2 cos t, y = 2sint and t from 0 to 2π ].
Solution:
The equation to the curve C \(x^3+y^3=4, z=0\)
In parametric form \(z=0, x=2 \cos \theta_1, y=2 \sin \theta\)
For the circle \(\theta\) varies from 0 to \(2 \pi\)
∴ The circulation of \(\mathbf{F}\) along C is \(\oint_C \mathbf{F} \cdot d \mathbf{r}=\oint_C \mathbf{F}_1 d x+\mathbf{F}_2 d y+\mathbf{F}_3 d z\)
= \(\oint_c(2 x-y+2 z) d x+(x+y-z) d y+(3 x-2 y-5 z) d z\)
= \(\int_0^{2 \pi}(4 \cos \theta-2 \sin \theta)(-2 \sin \theta) d \theta+(2 \cos \theta+2 \sin \theta) 2 \cos \theta\)
= \(\int_0^{2 \pi}(4-\sin 2 \theta) d \theta=4(2 \pi)-\int_0^{2 \pi} \sin \theta=8 \pi-0=8 \pi\)
8. Evaluate \(\int_{\mathbf{C}}\)F.dr along the line joining (0, 0, 0) to (2,1,4) where c F = yz i + (xz + 1) j + xy k .
Solution:
Equation to the line joining (1,0,0) to (2,1,4) is \(\frac{x-1}{1}=\frac{y}{1}=\frac{z}{4}=t\)
∴ \(x=t+1, y=t, z=4 t \Rightarrow d x=d t, d y=d t, d z=4 d t\)
t varies from 0 to 1
⇒ \(\mathbf{F} \cdot d \mathbf{r}=(y z \mathbf{i}+(x z+1) \mathbf{j}+x y \mathbf{k}) \cdot(\mathbf{i} d x+\mathbf{j} d y+\mathbf{k} d z)\)
= \(y z d x+(x z+1) d y+x y d z\)
∴ \(\int_C \mathbf{F} . d \mathbf{r}=\int_0^1 t(4 t) d t+[(t+1) 4 t+1] d t+(t+1) t(4 d t)\)
+ \(\int_0^1\left(12 t^2+8 t+1\right) d t=\left[4 t^3+4 t^2+t\right]=9\)
9. If F = (x- 3y)i + (y- 2x) j find\(\int_{\mathbf{C}}\)F.dr where C is the closed curve in the c xy plane, x = 2 cos t, y = 3 sin t from t = 0 to t = 2π .
Solution:
x = \(2 \cos t \Rightarrow d x=-2 \sin t . d t, \quad y=3 \sin t d t \Rightarrow d y=3 \cos t d t\)
F. dr = (x-3 y) d x+(y-2 x) d y
(2 cos t-9 sin t)(-2 sin t) d t+(3 sin t-4 cos t)(3 cos t) d t
= \(\left(\frac{5}{2} \sin 2 t+18 \sin ^2 t-12 \cos ^2 t\right) d t\)
= \(\left(\frac{5}{2} \sin 2 t-12 \cos 2 t+6 \sin ^2 t\right) d t\)
∴ \(\int_C \mathbf{F} . d \mathbf{r}=\int_0^{2 \pi}\left(6 \sin ^2 t+\frac{5}{2} \sin 2 t-12 \cos 2 t\right) d t\)
= \(6 \cdot \int_0^{2 \pi} \sin ^2 t+\int_0^{2 \pi}\left(+\frac{5}{2} \sin 2 t-12 \cos 2 t\right) d t\)
= \(6.4 \int_0^{\pi / 2} \sin ^2 t+0=6.4 \cdot \frac{1}{2} \frac{\pi}{2}=6 \pi\)
Integration Of Vectors Surface Integrals
A surface r = f (w, v) is called a smooth surface if f (u, V) is continuous and possesses partial derivatives. Let F (r) be a continuous vector point function,
defined over the smooth surface r = f (w, v) Let S be a region of the surface. Divide the region into m sub-regions of areas δS1 δS2, …, δSi… δSm. Let Pi be point of Si and Nj be the unit normal to δSi at Pi.
Let δ Ai be the vector area of δSi, then Ai = Ni δ S1
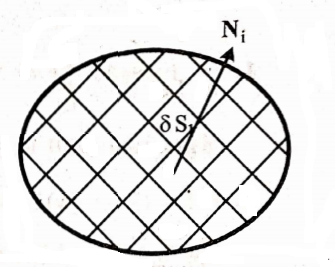
Now from the sum Im\(=\sum_{i=1}^m \mathbf{F}\left(\mathbf{r}_{\mathrm{i}}\right) \cdot \delta \mathbf{A}_{\mathrm{i}} \quad \text { or } \Sigma \mathbf{F}\left(\mathbf{r}_{\mathrm{i}}\right) \mathbf{N}_{\mathrm{i}} \delta \mathbf{S}_{\mathrm{i}}\)
Let m tend to infinity in such a way that each 8 Sj shrinks to a point. The limit of Im
if it exists, is called the normal surface integral of F (r) over the region S of the surface :
⇒ \(\bar{r}\)=\(\bar{f}(u, v)\)and is denoted by \(\int_S \mathrm{~F}(\bar{r}) \cdot d \mathrm{~A} \text { or } \int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S}\)
Note. The other types of surface integrals are \(\int_S \mathbf{F} \times d \mathbf{A}, \quad \int \phi d \mathbf{A}\)
where F is a continuous vector and Φ a continuous scalar point function.
Integration Of Vectors Flux
Let S be a closed surface. Then the normal surface integral \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S} \text { or } \int_S \mathbf{F} \cdot d \mathbf{A}\) called the flux of F over S.
Cartesian form
Let F(r) =F1i+ F2j+F3k where F1, F2, and F3 are continuous and differentiable functions of x, y, and z.
Let cosα, cos β, cos γ be the directions cosines of the unit normal N.
N = i cos α + j cos β + k cos γ and F . N = F1 cos α + F2 cos β + F3 cos γ
∴ \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S}\)=\(\int_S\left(F_1 \cos \alpha+\mathrm{F}_2 \cos \beta+\mathrm{F}_3 \cos \gamma\right) d \mathbf{S}\)
But dScos α, dScosβ, and dScos γ are the projections of dS on yz, zx and xy planes. If dx, dy, dz are the differentials along the axes then
dS cos α= dy dz, dS cos β= dz dx, dS cos ϒ = dx dy
∴ \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\iint_S\left(\mathrm{~F}_1 d y d z+\mathrm{F}_2 d z d x+\mathrm{F}_3 d x d y\right)\)
Note. Let R1 be the projection of S on xy plane. then
⇒ \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\iint_{R_1} \mathbf{F} \cdot \mathbf{N} \frac{d x d y}{\cos \gamma}=\iint_{R_1} \mathrm{~F} \cdot \mathrm{N} \frac{d x d y}{|\mathrm{~N} \cdot \overline{\mathrm{K}}|}\)
Thus the surface integral S can be evaluated with the help of the double integral integrated over in R1 xy plane.
Similarly , \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S}\)=\(\iint_{R_2} \mathbf{F} \cdot \mathbf{N} \frac{d y d z}{|\mathbf{N} \cdot \mathbf{i}|}\)=\(\iint_{R_3} \mathbf{F} \cdot \mathbf{N} \frac{d z d x}{|\mathbf{N} \cdot \mathbf{j}|}\)
Integration Of Vectors Solved problems
Example. 1. Evaluate \(\int_S\)F.Nds, where \(\int_S\)F=zi+xj-3y2zk and is the surface x2+y2=16 included in the first octant between z=0 and z=5.
Solution:
Given
\(\int_S\)F.Nds
Let \(\phi=x^2+y^2-16\)
∴ The normal to the surface \(\mathbf{S}\) is grad \(\phi\) (i.e. \(\nabla \phi\))
∴ normal = \(\nabla \phi=\mathbf{i} \frac{\partial \phi}{\partial x}+\mathbf{j} \frac{\partial \phi}{\partial y}+\mathbf{k} \frac{\partial \phi}{\partial z}=2 x \mathbf{i}+2 y \mathbf{j}\)
∴ Unit normal \(\mathbf{N}=\frac{2 x \mathbf{i}+2 y \mathbf{j}}{\sqrt{\left(4 x^2+4 y^2\right)}}=\frac{x \mathbf{i}+y \mathbf{j}}{\sqrt{\left(x^2+y^2\right)}}=\frac{x \mathbf{i}+y \mathbf{j}}{4}\) because \(x^2+y^2=16\) on S.
Let R be the projection of S on Y Z plane, then \(\iint_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\iint_S \mathbf{F} \cdot \mathbf{N} \frac{d y d z}{|\mathbf{N} \cdot \mathbf{i}|}\)
Given \(\mathbf{F}=z \mathbf{i}+x \mathbf{j}-3 y^2 z \mathbf{k}\)
∴ \(\mathbf{F} \cdot \mathbf{N}=\left(z \mathbf{i}+x \mathbf{j}-3 y^2 z \mathbf{k}\right) \cdot \frac{(x \mathbf{i}+y \mathbf{j})}{4}=\frac{1}{4}(x z+x y)\) and \(\mathbf{N} \cdot \mathbf{i}=\frac{1}{4}(x \mathbf{i}+y \mathbf{j}) \cdot \mathbf{i}=\frac{x}{4}\)
For the surface \(x^2+y^2=16\) in yz plane x=0 ⇒ y=4
Hence in first octant y varies from 0 to 4 z varies from 0 to 5
Then the surface integral \(\iint_R \mathbf{F} \cdot \mathbf{N} \frac{d y d z}{|\mathbf{N} \cdot \mathbf{i}|}=\iint_R\left(\frac{x z+x \dot{y}}{4}\right)\left(\frac{4}{x}\right) d y d z=\int_{y=0}^4 \int_{z=0}^5(y+z) d y d z\)
= \(\int_{y=0}^4 \int_0^5(y d y)^1 d z+\int_{y=0}^4 \int_{z=0}^5 d y(z d z)=\int_0^4 y d y \int_0^5 d z+\int_0^4 d y \int_0^5 z d z\)
= \({\left[\frac{y^2}{2}\right]_0^4[z]_0^5+[y]_0^4\left[\frac{z^2}{2}\right]_0^5=8 \cdot 5+4 \cdot \frac{25}{2}=90 }\)
Vector Integration Problems In Calculus And Physics
Example.2. Evaluate \(\int_S\)F.Nds where F= 18zi-12j+3yk and Sis the part of the plane 2x+3y+6z=12 located in the first octant
Solution:
Let \(\phi=2 x+3 y+6 z-12\)
∴ Normal to the plane \(\phi\) is \(\nabla \phi\)
⇒ \(\nabla \phi=\mathbf{i} \frac{\partial \phi}{\partial x}+\mathbf{j} \frac{\partial \phi}{\partial y}+\mathbf{k} \frac{\partial \phi}{\partial z} \quad=2 \mathbf{i}+3 \mathbf{j}+6 \mathbf{k}\)
∴ unit normal, \(\mathbf{N}=\frac{2 \mathbf{i}+3 \mathbf{j}+6 \mathbf{k}}{\sqrt{(4+9+36)}}=\frac{1}{7}(2 \mathbf{i}+3 \mathbf{j}+6 \mathbf{h}\) ।
Let R be the projection of S on X Y plane, then \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\iint_R \mathbf{F} \cdot \mathbf{N} \frac{d x d y}{|(\mathbf{N} \cdot \mathbf{k})|}\)
Given \(\mathbf{F}=18 z \mathbf{i}-12 \mathbf{j}+3 y \mathbf{k}\)
∴ \(\mathbf{F} \cdot \mathbf{N}=(8 z \mathbf{i}-12 \mathbf{j}+3 y \mathbf{k}) \cdot \frac{1}{7}(2 \mathbf{i}+3 \mathbf{j}+6 \mathbf{k})=\frac{1}{7}(36 z+36+18 y)=\frac{6}{7}(6 z-6+3 y)\)
⇒ \(\mathrm{N} \cdot \overline{\mathbf{k}} \cdot=\frac{1}{7}(2 \mathrm{i}+3 \mathrm{j}+6 \mathrm{k}) \cdot \mathbf{k}=\frac{6}{7}\)
Given surface S is 2 x+3 y+6 z=12 ∴ R of x y plane is 2 x+3 y=12
⇒ \(y=\frac{12-2 x}{3}\)
∴ y=0 ⇒ x=6
∴ x varies from 0 to 6 and y varies from 0 to \(\frac{12-2 x}{3}\)
The surface integral \(\iint_R \mathbf{F} \cdot \mathbf{N} \frac{d x d y}{|\mathbf{N} \cdot \mathbf{k}|}=\iint_R^6 \frac{7}{7}(6 z-6+3 y) \cdot \frac{7}{6} d x d y\)
= \(\iint_R(12-2 x-3 y-6+3 y) d x d y\) because 6 z=12-2 x-3 y
= \(\iint_R(6-2 x) d x d y=2 \int_0^6(3-x)\left[\int_0^{\frac{1}{3}(12-2 x)} d y d x\right.\)
= \(2 \int_0^6(3-x)[y]_0^{\frac{1}{3}(12-2 x)} d x=2 \int_0^6(3-x) \frac{1}{3}(12-2 x) d x\)
= \(\frac{4}{3} \int_0^6\left(18-9 x+x^2\right) d x=\frac{4}{3}\left[18 x-\frac{9}{2} x^2+\frac{1}{3} x^3\right]_0^6=24\)
Example.3.If f=4xzi-y2j+yzk, evaluate where S is the surface of the cube bounded by x=0,x=a,y=0,y=a,z=0,z=a.
Solution: Consider the cube surrounded by the following faces.
(1) For the face PQRS, i is the outward normal
∴ \(\mathbf{N}=\mathrm{i}, x=a, d \mathbf{S}=d y d z\)
∴ \(\int_0 \mathrm{~F} \cdot \mathrm{N} d \mathrm{~S}=\int_{y=0}^a \int_{z=0}^a\left(4 x z \mathrm{i}-y^2 \mathrm{j}+y z \mathrm{k}\right) \cdot \overline{\mathrm{i}} d y d z \)
= \(\int_{y=0}^a \int_{z=0}^a 4 x z d y d z=4 a \int_{y=0}^a d y \cdot \int_0^a z d z\)
because x = a on this face = \(4 a[y]_0^a\left[\frac{z^2}{2}\right]_0^a=2 a^4\)
(2) For the face OABC, \(-\overline{\mathrm{i}}\) is the outward normal
∴ \(\mathbf{N}=-\mathrm{i}, x=0\), and \(d \mathbf{S}=d y d z\)
∴ \(\int_{R_2} \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\iint_{R_2}\left(4 x z \mathbf{i}-y^2 \mathbf{j}+y z \mathbf{k}\right) \cdot(-\mathbf{i}) d y d z=-\iint_{R_2} 4 x z d y d z=0\)
because x=0 on this face
(3) For the face BPQC, \(\bar{j}\) is the outward normal
∴ \(\mathrm{N}=\bar{j}, y=a\), and \(d \mathbf{S}=d x d z\)
∴ \(\int_{R_3} \mathrm{~F} \cdot \mathrm{N} d \mathrm{~S}=\iint_{R_3}\left(4 x z \mathrm{i}-y^2 \mathrm{j}+y z \mathrm{k}\right) \cdot \overline{\mathrm{j}} d x d z=-\iint_{R_3} y^2 d x d z\)
= \(-a^2 \int_{x=0}^a \int_{z=0}^a d y d z\) because y=a, on this face \(=-a^2[x]_0^a[z]_0^a=-a^4\)
(4) For the face ORSA, \(-\overline{\mathrm{j}}\) is the outward normal
∴ \(\mathrm{N}=-\overline{\mathrm{j}}, y=0\) and \(d \mathbf{S}=d x d z\)
F. \(\mathrm{N}=\left(4 x z \mathrm{i}-y^2 \mathrm{j}+y z \mathrm{k}\right) \cdot(-\mathrm{j})=y^2\)
∴ \(\int_{R_4} \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\iint_{R_4} y^2 d x d z=0\)
because y=0, on this face
(5) For the face ABPS; \(\overline{\mathrm{k}}\) is the outward normal
∴ \(\mathrm{N}=\overrightarrow{\mathrm{k}}, z=a\), and \(d \mathbf{S}=d x d y\)
F. \(\mathrm{N}=\left(4 x z \mathrm{i}-y^2 \mathrm{j}+y z \mathrm{k}\right) \cdot \overline{\mathrm{k}}=y z\)
∴ \(\int_{R_5} \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\iint_{R_5} y z d x d y=\int_{z=0}^a \int_{y=0}^a a y d x d y=a[x]_0^a \cdot\left[\frac{y^2}{2}\right]_0^a=\frac{a^4}{4}\)
(6) For the face OCQR,\(-\overline{\mathrm{k}}\) is the outward normal
∴ \(\mathrm{N}=-\overline{\mathrm{k}}, z=0\) and \(d \mathrm{~S}=d x d y\)
F . \(\mathrm{N}=\left(4 x z \mathrm{i}-y^2 \mathrm{j}+y z \mathrm{k}\right) \cdot(-\overline{\mathrm{k}})=-y z\)
∴ \(\int_{R_6} \mathbf{F} . \mathbf{N} d \mathbf{S}=-\iint_{R_6} y z d x d y=0\)
because z=0, on this face
Hence adding all we get \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=2 a^4+0-a^4+0+\frac{1}{2} a^4+0=\frac{3}{2} a^4\).
Example.4. If F=(x+y2)i-2xj+2yzk evaluate \(\int_S\)F.Nds where S is the surface of the plane 2x+y+2z=6 in the first octant.
Solution:
Let \(\phi=2 x+y+2 z-6\)
∴ The vector normal to surface \(\mathbf{S}\) is \(\nabla \phi\)
i.e. \(\nabla \phi=\mathbf{i} \frac{\partial \phi}{\partial x}+\mathbf{j} \frac{\partial \phi}{\partial y}+\mathbf{k} \frac{\partial \phi}{\partial z}=2 \mathbf{i}+\mathbf{j}+2 \mathbf{k}\)
∴ Unit normal, \(\mathbf{N}=\frac{2 \mathbf{i}+\mathbf{j}+2 \mathbf{k}}{\sqrt{(4+1+4)}}=\frac{1}{3}(2 \mathbf{i}+\mathbf{j}+2 \mathbf{k})\)
Let R be the projection of S over XY – plane. Now R is bounded by x-axis, y-axis, and the line 2 x+y=6, z=0.
we have \(\mathbf{F} \cdot \mathbf{N}=\left[\left(x+y^2\right) \mathbf{i}-2 x \mathbf{j}+2 y z \mathbf{k}\right] \cdot \frac{1}{3}(2 \mathbf{i}+\mathbf{j}+2 \mathbf{k})\)
= \(\frac{1}{3}\left[2 x+2 y^2-2 x+4 y z\right]=\frac{2}{3}\left(y^2+2 y z\right)\)
N \(\cdot \overline{\mathbf{k}}=\frac{1}{3}(2 \mathrm{i}+\mathrm{j}+2 \mathrm{k}) \cdot \mathbf{k}=\frac{2}{3}\)
∴ \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\iint_R \mathbf{F} \cdot \mathbf{N} \frac{d x d y}{|\mathbf{N} \cdot \mathbf{k}|}\)
= \(\iint_R^2 \frac{2}{3}\left(y^2+2 y z\right)\left(\frac{3}{2}\right) d x d y=\iint_R\left[y^2+2 y\left(\frac{6-2 x-y}{2}\right)\right] d x d y\)
= \(2 \iint_R y(3-x) d x d y\) because \(z=\frac{6-2 x-y}{2}\) on S
To evaluate the double integral keep x fixed and integrate with respect to y from y=0 to y=6-2x, then integrate y function from x=0 to x=3.
∴ The surface integral \(=2 \int_{x=0}^3 \int_{y=0}^{6-2 x} y(3-x) d x d y=\int_{x=0}^3\left[\int_{y=0}^{6-2 x} y d y\right](3-x) d x\)
= \(2 \int_0^3\left[\frac{y^2}{2}\right]_0^5(3-x) d x=\int_0^3(6-2 x)^2(3-x) d x=4 \int_0^3(3-x)^3 d x=4\left[\frac{(3-x)^4}{4}\right]_0^3=81\)
Integration Of Vectors Volume Integrals
Let V be a volume bounded by a surface r = f (w, v).F (r) be a vector point function defined over V .
Divide V into m sub-regions of volumes (δV1,δV2,….δVi,…δV,) let Pi (ri) be a point δVi then form the sum Im =\(\sum_{i=1}^m \mathbf{F}\left(\mathbf{r}_{\mathrm{i}}\right) \delta \mathbf{V}_{\mathrm{i}}\)
Let m→ ∝ in such a way that δVi. Shrinks to a point. The limit of Im if it exists, is called the volume integrals of F (r) in the region V and is denoted by\(\int_V \mathbf{F}(\mathbf{r}) d \mathbf{V} \text { or } \int_V \mathbf{F} d \mathbf{V}\)
Cartesian form
Let F (r) = F1i + F2 j + F3k where F1, F2 , F3 are functions of x,y,z
Also, we have dV= dx dy dz The volume integral is then given by
The volume integral is then given by\(\int_V \mathbf{F} d \mathbf{V}\)=\(\iiint\left(\mathbf{F}_1 \mathbf{i}+\mathbf{F}_2 \mathbf{j}+\mathbf{F}_3 \mathbf{k}\right) d x d y d z\)
= \(\mathbf{i} \iiint \mathbf{F}_1 d x d y d z+\mathbf{j} \iiint \mathbf{F}_2 d x d y d z+\mathbf{k} \iiint \mathbf{F}_3 d x d y d z\)
Integration Of Vectors Solved problems
Example.1. 2xzi-xj+y2k evaluate \(\int_V\)F.dv where V is the region bounded by the surfaces x=0,x=2,y=0,y=6,z=x2,z=4
Solution:
Given \(\mathbf{F}=2 x z \mathbf{i}-x \mathbf{j}+y^2 \mathbf{k}\)
∴ The volume integral is \(\int_V \mathrm{~F} . d \mathrm{~V}=\iiint_V\left(2 x z \mathrm{i}-x \mathrm{j}+y^2 \mathrm{k}\right) d x d y d z\)
= \(\mathbf{i} \int_{x=0}^2 \int_{y=0}^6 \int_{z=x^2}^4 2 x z d x d y d z-\mathbf{j} \iiint x d x d y d z+\mathbf{k} \iiint y^2 d x d y d z\)
= \(\mathbf{i} \int_{x=0}^2 \int_{y=0}^6 2 x\left[\frac{z^2}{2}\right]_{x^2}^4 d x d y-\mathbf{j} \int_{x=0}^2 \int_{y=0}^6 x\left[z \int_{x^2}^4 d x d y+\mathbf{k} \int_{x=0}^2 \int_{y=0}^6 y^2[z]_{x^2}^4 d x d y\right.\)
= \(\mathbf{i} \int_0^2 x\left(16-x^4\right) d x \int_0^6 d y-\mathbf{j} \int_0^2 x\left(4-x^2\right) d x \int_0^6 d y+\mathbf{k} \int_{x=0}^2\left(4-x^2\right) d x \int_0^6 y^2 d y\)
= \(\mathbf{i}\left[8 x^2-\frac{x^6}{6}\right]_0^2[y]_0^6-\mathbf{j}\left[2 x^2-\frac{x^4}{4}\right]_0^2[y]_0^6+\mathbf{k}\left[4 x-\frac{x^3}{3}\right]_0^2\left[\frac{y^3}{3}\right]_0^6=128 \mathbf{i}-24 \mathbf{j}+384 \mathbf{k}\)
Example.2. If F = (2x2 – 3z)i- 2xyj- 4x k evaluate (1) \(\int_V\)∇F.dv and v (2)\(\int_V\)∇×F.dv where V is the closed region bounded by x = 0, y = 0, z = 0,2x + 2y + z = 4.
Solution: (1) ∇. F =\(\left(\mathbf{i} \cdot \frac{\partial \mathbf{F}}{\partial x}+\mathbf{j} \cdot \frac{\partial \mathbf{F}}{\partial y}+\mathbf{k} \cdot \frac{\partial \mathbf{F}}{\partial z}\right)\) 4x-2x=2x
The limits are z=0 to z=4-2x-2y
y = 0 to \(\frac{4-2 x}{2}\) i.e. (2-x) x=0 to \(\frac{4}{2}\) i.e. 2
∴ \(\int_V \nabla . \overline{\mathrm{F}} d \mathrm{~V}=\int_{x=0}^2 \int_{y=0}^{2-x} \int_{z=0}^{4-2 x-2 y} 2 x d x d y d z\)
= \(\int_{x=0}^2 \int_{y=0}^{2-x} 2 x[z]_0^{4-2 x-2 y} d x d y\)
= \(\int_{x=0}^2 \int_{y=0}^{2-x} 2 x(4-2 x-2 y) d x d y=4 \int_{x=0}^2 \int_{y=0}^{2-x}\left(2 x-x^2-x y\right) d x d y\)
= \(4 \int_0^2\left[\left(2 x-x^2\right) y-x \frac{y^2}{2}\right]_0^{2-x} d x=4 \int_0^2\left[\left(2 x-x^2\right)(2-x)-\frac{x}{2}(2-x)^2\right] d x\)
= \(\int_0^2\left(2 x^3-8 x^2+8 x\right) d x=\left[\frac{x^4}{2}-\frac{8 x^3}{3}+4 x^2\right]_0^2=\frac{8}{3}\)
(2) \(\nabla \times \mathbf{F}=\left|\begin{array}{ccc}\mathbf{i} & \mathbf{j} & \mathbf{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ 2 x^2-3 z & -2 x y & -4 x\end{array}\right|=\mathbf{j}-2 y \mathbf{k}\)
∴ \(\int_V \nabla \times \mathbf{F} d \mathbf{V}=\iiint_V(\mathbf{j}-2 y \mathbf{k}) d x d y d z=\int_{x=0}^2 \int_{y=0}^{2-x} \int(\mathbf{j}-2 y \mathbf{k})[z]_0^{4-2 x-2 y} d x d y\)
= \(\int_{x=0}^2 \int_{y=0}^{2-x}(\mathbf{j}-2 y \mathbf{k})(4-2 x-2 y) d x d y\)
= \(\int_{x=0}^2 \mathbf{j}\left[(4-2 x) y-y^2\right]_0^{2-x} d x-\mathbf{k} \int_{x=0}^2\left[(4-2 x) y^2-\frac{4 y^3}{3}\right] d x\)
= \(\mathbf{j} \int_0^2(2-x)^2 d x-\mathbf{k} \int_0^2 \frac{2}{3}(2-x)^3 d x=\mathbf{j}\left[\frac{(2-x)^3}{3}\right]_0^2 \frac{-2 \mathbf{k}}{3}\left[\frac{(2-x)^4}{4}\right]_0^2=\frac{8}{3}(\mathbf{j}-\mathbf{k})\)
Integration Of Vectors Exercise 6(c)
1. Evaluate \(\int_{\mathbf{S}}\)F.NdS, where F = y i + 2xj-z k and S is the surface of the plane 2x + y = 6 in the first octant, cut off by the plane z = 4 . [Take R the projection of S on yz plane].
Solution:
Let \(\phi=2 x+y-6\)
∴ The vector normal to the surface is \(\nabla \phi=2 \mathbf{i}+\mathbf{j}\)
∴ Unit normal N = \(\frac{2 \mathbf{i}+\mathbf{j}}{\sqrt{5}}\)
Let R be the projection of \(\mathbf{S}\) over the y z-plane. Here the surface S is \(\perp r\) to y – plane and hence cannot be projected on x y – plane.
∴ Now \(\mathbf{F} \cdot \mathbf{N}=(y \mathbf{i}+2 x \mathbf{j}-z \mathbf{k}) \cdot \frac{1}{\sqrt{5}}(2 \mathbf{i}+\mathbf{j})=\frac{2}{\sqrt{5}}(x+y)\)
∴ We have \(\oint_S \mathbf{F} . \mathbf{N} d \mathbf{S}=\int \oint_R \mathbf{F} \cdot \mathbf{N} \frac{d y d z}{|\mathbf{N} . i|}=\int \oint_R \frac{2}{\sqrt{5}}(x+y) \frac{\sqrt{5}}{2} d y d z\)
= \(\int \oint_R\left(\frac{6-y}{2}+y\right) d y d z\)…….. (because x=\(\frac{6-y}{2}\))
= \(\frac{1}{2} \int_{y=0}^6 \int_{y=0}^4(6+y) d y d z=\frac{1}{2} \int_{y=0}^6(6+y) d y \int_{y=0}^4 d z\)
= \(\frac{1}{2}\left[6 y+\frac{y^3}{2}\right]_0^6[z]_0^4=108\)
2. If F = 2yi- 3 j + x2k and S is the surface y2 = 8x in the first octant bounded by the planes y= 4 and z = 6, evaluate\(\int_{\mathbf{S}}\)F.NdS. [Take R by projecting S on yz plane]
Solution:
Let \(\phi=y^2-8 x\) be the surface S. Normal to S = \(\nabla \phi=-8 \mathbf{i}+2 y \mathbf{j}\)
∴ \(\mathbf{N}=\frac{-4 \mathbf{i}+y \mathbf{j}}{\sqrt{\left(16+y^2\right)}}\)
∴ \(\mathbf{N} . \mathbf{i}=\frac{-4}{\sqrt{16+y^2}}\)
∴ \(\mathrm{F} . \mathbf{N}=\frac{-8 y-3 y}{\sqrt{\left(16+y^2\right)}}=\frac{-11 y}{\sqrt{16+y^2}}\)
Let R be the projection of S over the y z-plane. Then
= \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S} \iint_R \mathbf{F} \cdot \mathbf{N} \frac{d y d z}{|\mathbf{N} \cdot \mathbf{i}|}=\frac{11}{4} \iint_R y d y d z\)
= \(\frac{11}{4} \int_{y=0}^4 y d y \int_{z=0}^6 d z=132\)
3. Find \(\int_{\mathbf{S}}\)F.NdS over the entire surface of the region bounded by x2 + z2 = 9, x = 0, y = 0, z = 0 and y = 8 if F = 6zi + (2x + y)- xk .
Solution:
Let \(\varphi=x^2+z^2-9[/late] be the surface S.
Normal vector to S = [latex]\nabla \phi=2 x \mathbf{i}+2 z \mathbf{k}\)
∴ Unit normal \(\mathbf{N}=\frac{x \mathbf{i}+z \mathbf{k}}{\sqrt{x^3+z^3}}=\frac{1}{3}(x \mathbf{i}+z \mathbf{k})\)
Now \(\mathbf{N}=\frac{1}{3}(6 z x-z x)=\frac{5}{3} z x\)
Let R be the projection of S over the y z-plane. Then
= \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S} \iint_R \mathbf{F} \cdot \mathbf{N} \frac{d y d z}{|\mathbf{N} \cdot \mathbf{i}|}=\frac{5}{3} \iint_R z x\left(\frac{3}{x}\right) d y d z\)
= \(5 \int_0^3 z d z \int_0^8 d y=180\)
4. If F = yz i + zx j + xy k evaluate \(\int_{\mathbf{S}}\)F.NdS over the surface of x2 + y2 + z2= 1 in the first octant.
Solution:
Let \(\phi=x^2+y^2+z^2-1\) be the surface S.
Normal vector to \(\mathrm{S}, \nabla \phi=2(x \mathbf{i}+y \mathbf{j}+\mathbf{z k})\)
∴ Unit normal \(\mathbf{N}=\frac{x \mathbf{i}+y \mathbf{j}+z \mathbf{k}}{\sqrt{x^3+y^3+z^3}}=\frac{x \mathbf{i}+y \mathbf{j}+z \mathbf{k}}{1}\)
∴ \(\mathbf{F} . \mathbf{N}=3 x y z, \mathbf{N} \cdot \mathbf{i}=x\)
Let R be the projection of S over the y z-plane. Then \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\iint_R \mathbf{F} \cdot \mathbf{N} \frac{d y d z}{|\mathbf{N} \cdot \mathbf{i}|}=\iint_R(3 x y z) \frac{d y d z}{x}\)
Now in the y z-plane x=0, hence the equation of the surface becomes \(x^2+y^2+z^2=1\)
∴ \(\int \mathbf{F} . \mathbf{N} d \mathbf{S}=3 \int_{y=0}^1 y \int_{z=0}^{\sqrt{1-y^2}} z d z d y\)
= \(\frac{3}{2} \int_0^1 y\left(1-y^2\right) d y=\frac{3}{2}\left[\frac{y^2}{2}-\frac{y^4}{4}\right]_0^1=\frac{3}{8}\)
5. Find ∫F.NdS Where F = 4xi- 2y2 j+ z2 k over the region bounded by x2 + y2 = 4, z = 0 and z = 3
Solution:
Let \(\phi=x^2+y^2-4, \mathbf{F}=4 x \mathbf{i}-2 y^2 \mathbf{j}+z^2 \mathbf{k}\)
Normal = \(\nabla \phi=2 x \mathbf{i}+2 y \mathbf{j}\)
∴ Unit normal \(\mathbf{N}=\frac{2 x \mathbf{i}+2 y \mathbf{j}}{\sqrt{4 x^2+4 y^2}}=\frac{1}{2}(x \mathbf{i}+y \mathbf{j})\)
Let R be the projection of S over the y z-plane. Then \(\int_S \mathbf{F} \cdot \mathbf{N} d \mathbf{S}=\iint_R \mathbf{F} \cdot \mathbf{N} \frac{d y d z}{|\mathbf{N} \cdot \mathbf{i}|}\)
Now \(\mathbf{F} \cdot \mathbf{N}=\left(4 x \mathbf{i}-2 y^2 \mathbf{j}+z^2 \mathbf{k}\right) \cdot \frac{1}{2}(x \mathbf{i}+y \mathbf{j})=2 x^2-y^3\) and \(\mathbf{N} \cdot \mathbf{i}=\frac{1}{2}(x \mathbf{i}+y \mathbf{j}) \cdot \mathbf{i}=\frac{x}{2}\)
For the surface \(x^2+y^2=4\) in y z-plane. x=0 ⇒ \(y= \pm 2\)
Hence y varies from -2 to 2.
z varies from 0 to 3
∴ The surface integral = \(\iint_R \mathbf{F} \cdot \mathbf{N} \frac{d y d z}{|\mathbf{N} \cdot \mathbf{i}|}=\iint_R\left(2 x^2-y^3\right)\left(\frac{2}{x}\right) d y d z\)
= \(\int_{y=-2}^2\left(4 x-\frac{2 y^3}{x}\right) d y \cdot \int_0^3 d z=3 \int_{y=-2}^2\left(4 \sqrt{4-y^2}-\frac{2 y^3}{\sqrt{4-y^2}}\right) d y\)
= \(12 \int_2^2 \sqrt{4-y^2} d y-6 \int_2^2 \frac{y^3}{\sqrt{4-y^2}} d y=24 \int_0^2 \sqrt{4-y^2} d y-0\)
Put \(y=2 \sin \theta, d y=2 \cos \theta, d \theta\)
6. If Φ = 45x2,y evaluate \(\begin{equation}
\iiint_V \phi d \mathbf{V}\end{equation}\)where V is the closed region bounded by the planes 4x + 2y + z = 8, x = 0, y = 0, z = 0.
Solution:
The limits are
z=0 to z=8-4 x-2 y
y=0 to y=4-2 x
x=0 to x=2
∴ \(\iiint_V \phi d \mathrm{~V}=\int_{x=0}^2 \int_{y=0}^{4-2 x} \int_{z=0}^{8-4 x-2 y} 45 x^2 y d z d y d x\)
= \(45 \int_{x=0}^2 \int_{y=0}^{4-2 x} x^2 y[z]_0^{8-4 x-2 y} d y \cdot d x\)
= \(45 \int_{x=0}^2 \int_{y=0}^{4-2 x} x^2 y(8-4 x-2 y) d x d y\)
= \(45 \int_0^2 x^2\left[\frac{8 y^2}{2}-\frac{4 x y^2}{2}-\frac{2 y^3}{3}\right]_0^{4-2 x} d x\)
