Pre-Calculus 11 Student Edition Chapter 1 Sequences and Series
Page 58 Problem 1 Answer
Given that a big square is given (as shown in the following figure) it is divided into two equal parts and one of the portions is shaded.
Then the unshaded portion is again divided in half and one of the halves is shaded.
This process is continued.
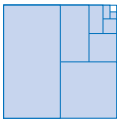
To find: A sequence that represents the area of the newly shaded region as a fraction of the entire region.
Let the total area be A square units.
The area of first shaded region = A/2
A=1/2.
Now, this half region is again divided into two halves, and one half is shaded, therefore area of 2nd shaded region is:
A/4
A=1/4
Similarly area of the third shaded region = 1/8
Area of fourth shaded region = 1/16
Area of fifth shaded region = 1/32
Therefore, the sequence is 1/2,1/4,1/8,1/16,1/32.
The answer is 1/2,1/4,1/8,1/16,1/32.
Read and Learn More Precalculus Textbook Mcgraw Hill Answers
Page 58 Problem 2 Answer
As we find in the previous question the sequence that is given here is:-
A geometric series as 1/2,1/4,1/8,1/16,1/32., with
First term, t1=1/2 and
Common ratio,r=1/2.
We have to find: The 6th and 7th term.
Let us use the formula for a general term to find the answer.
Applying the formula and putting the values, we have:
Precalculus Textbook Mcgraw Hill Answers
Sixth term:
t6=1/2⋅(1/2)6−1⇒t6
=1/2⋅(1/2)5⇒t6
=1/64
Seventh term:
t7=1/2⋅(1/2)7−1
⇒t7 =1/2⋅(1/2) 6
⇒ t7 =1/128
The answer is 1/64,1/128.
Page 59 Problem 3 Answer
Given that, start with a square piece of paper draw a line dividing it in half, and shade one of the halves.
In the unshaded half of the square, draw a line to divide it in half, and shade one of the halves. Repeat this process.
We need to verify whether the sequence of these shaded regions is arithmetic, geometric, or neither.
For this, check whether a constant is added or multiplied to get the successive terms of the sequence.
Since we draw a line that divides the square as two equal parts, therefore each shaded region is half of its previous shaded region.
So 1/2 is multiplied by each term of the sequence to get the successive terms of the sequence.
Hence the sequence is geometric.
The sequence is geometric.
Page 59 Problem 4 Answer
Given that, start with a square piece of paper draw a line dividing it in half, and shade one of the halves. In the unshaded half of the square, draw a line to divide it in half, and shade one of the halves. Repeat this process.
We need to verify whether it is an infinite sequence.
By ignoring physical conditions, we can continuously divide the square into two equal parts indefinitely.
As we repeat the process continuously again and again, the area of the resulting square approaches zero.
Hence the given sequence can be an infinite sequence.
The given sequence can be an infinite sequence.
Precalculus Textbook Mcgraw Hill Answers
Page 59 Problem 5 Answer
Given that, start with a square piece of paper draw a line dividing it in half, and shade one of the halves. In the unshaded half of the square, draw a line to divide it in half, shade one of the halves. Repeat this process.
We need to write the conclusion that can be made about the area of the square that would remain unshaded as the number of terms in the sequence approaches infinity.
As we repeat the process of dividing the square into two equal parts by drawing a line continuously again and again, the resulting squares will get smaller and smaller and the area of the square that would remain unshaded approaches zero.
The area of the square that would remain unshaded approaches to zero.
Page 59 Problem 6 Answer
Given function is y=(1/2)x.
We need to draw the graph of a given function using a graphing calculator and make a conclusion about the value of y=(1/2)x as x gets larger and larger.
For this, use the graphing calculator and input the given function.
The graph and the table of values is,
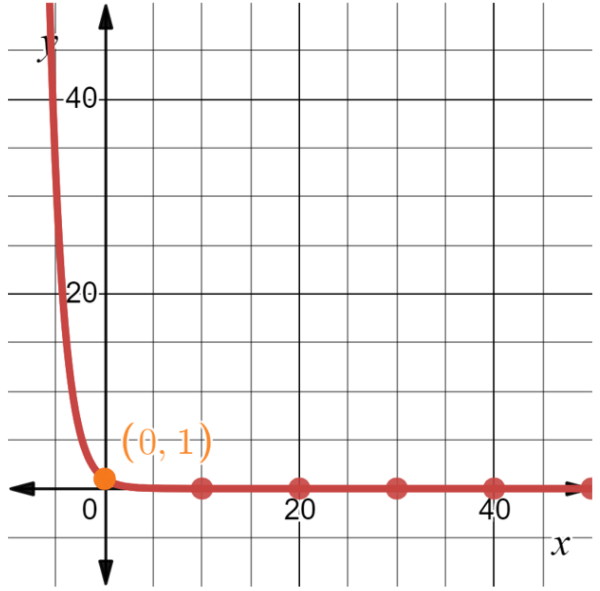
From the above table of values and graph, we can conclude that the value of y=(1/2)x
approaches to zero as x gets larger and larger.
The value of y=(1/2)x approaches to zero as x gets larger and larger.
Page 59 Problem 7 Answer
We need to find if the value of (1/2)x can become equal to zero.
Assume that there exists some value at which the value (1/2)x equals zero and then show that the consequences of this are not possible.
This would imply that there exists no x where(1/2)x equals zero.
Precalculus Textbook Mcgraw Hill Answers
The graph of the functiony=(1/2)x is:
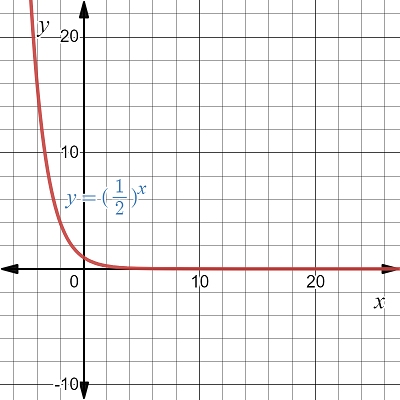
From the graph, we observe that the value (1/2)x approaches zero for greater values of x.
Suppose there exists a point say x1 at which the value of the function y=(1/2)x equals zero.
Then, x1 ≠ 0.
For if, x1=0, then,(1/2) 0=1, which is not equal to 0.
Therefore, x1>0 or x1<0.
Now,(1/2)x1=0, where x1≠0
Raising both sides to the power of 1/x1, we get,
((1/2)x1)1/x1=01/x1
1/2=0, which is not possible.
Therefore, there exists no x where the value of (1/2)x equals zero.
Therefore, it is not possible for the value of (1/2)x to equal zero.
Page 59 Problem 8 Answer
Given infinite geometric series is 1/2+1/4+1/8+1/16+….. and the formula to determine the sum of this series is given to be Sx=1−(1/2)x.
We need to observe the behavior of the function Sx=1−(1)x as x gets larger.
Precalculus Textbook Mcgraw Hill Answers
\(\begin{array}{|l|l|}\hline x & S_x=1-\left(\frac{1}{2}\right)^x \\
\hline 2 & 0.75 \\
\hline 5 & 0.96875 \\
\hline 10 & 0.999023 \\
\hline 15 & 0.999969 \\
\hline 20 & 0.999999046 \\
\hline 30 & 0.999999999068 \\
\hline
\end{array}\)
Enter the function into the calculator and use the table feature to find the sum Sx =1−(1/2)x for increasing values of x.
The value of the function Sx = 1−(1/2)x for increasing values of x is shown in the table below:
We observe that as x gets larger, the value of Sx approaches 1.
Therefore, as x gets larger, the sum Sx = 1−(1/2)x goes closer and closer to 1.
Page 59 Problem 9 Answer
Given geometric series is 1/2+1/4+1/8+1/16+.… and the formula to determine the sum of this series is Sx =1−(1/2)x.
We need to find if the sum increases without limit.
The formula to find the sum of the geometric series
2+1/4+1/8+1/16+.…is S1 =1−(1/2)x.
The sum Sx=1+(−(1/2)x) increases without limit provided the amount being added to 1 which is−(1/2)x increases without limit.
Now, −(1/2)x increases without limit, provided (1/2)x decreases without limit.
Now, as x increases, the denominator of (1/2)x increases, as a result, the value of(1/2)x decreases below 1 but never becomes negative.
Therefore,(1/2)x does not decrease without limit.
Therefore, it is not possible for the sum to increase without limit.
Therefore, it is not possible for the sum Sx
=1−(1/2)x to increase without limit.
Page 59 Problem 10 Answer
Given an expression rx
\(\begin{array}{|l|ll|}\hline x & r^x \\
\hline 1 & \frac{1}{2} \\
\hline 2 & \frac{1}{4} & \\
\hline 5 & \frac{1}{64}=0.015625 & \\
\hline 10 & \frac{1}{1024}=0.000976 & \\
\hline
\end{array}\)
To find as the value of x gets very large, what value does rx come close to.
When−1<r<1, say when r=1/2.
We observe that as x increases, the value of(1/2)x approaches 0.
Therefore, based on this, we assume that when −1<r<1, the value of rx Approaches 0.
Mcgraw Hill Precalculus Textbook Answers
If, r>1,say when r=10
We observe that as the value of x increases, the value of (10)x approaches infinity.
Therefore, based on this we conclude that when r >1, the value of rx approaches∞.
As the value of x gets very large, the value of rx
for −1<r<1 becomes close to 0 and for r>1 the value of rx comes close to ∞
\(\begin{array}{|l|l|}\hline x & r^x \\
\hline 1 & 10 \\
\hline 2 & 100 \\
\hline 5 & 100000 \\
\hline 10 & 10000000000 \\
\hline
\end{array}\)
Page 59 Problem 11 Answer
We need to find the formula for the sum of an infinite geometric series, using the answer from parta.
The formula to determine the sum of a geometric series is Sx=a(1−rx)/1−r
Where a is the first term and r is the common ratio.
In an infinite geometric series,−1<r<1.
Now from part a, we have,rx approaches 0 as x becomes large when−1<r<1.
Therefore, as x gets large, the partial sum Sx
Approaches a/1−r.
Therefore, the sum of an infinite geometric series is S∞=a/1−r, where−1<r<1.
The sum of an infinite geometric series is,S∞=a/1−r, where−1<r<1.
Page 59 Problem 12 Answer
The sum of an infinite geometric series is S=a/1−r,where−1<r<1
We need to find the sum of the given infinite series.
Given geometric series;1/2+(1/2)2+(1/2)3+(1/2)4….
Now,r=(1/2)2
1/2=1/2 and a=1/2
Therefore,
S=a/1−r=1/2
1−1/2
S=1/2
2−1/2=1/2⋅2/1=1
Therefore, the sum of the infinite geometric series is 1.
Page 61 Problem 13 Answer
The objective of the problem is to determine whether the given geometric series converges or diverges and calculate the sum if it exists.
Given: 1+1/5+1/25+…
Given series is 1+1/5+1/25+…
Here,
t1=1
r=1/5
As −1<r<1, the series is convergent.
Mcgraw Hill Precalculus Textbook Answers
Using the formula for the sum of an infinite geometric series,
S∞=t1/1−r
S∞=1/1−1/5
S∞ = 5/5−1
S∞ = 5/4
Hence, the given series is convergent and a sum of the given infinite geometric series is 5/4.
Page 61 Problem 14 Answer
The objective of the problem is to determine whether the given geometric series converges or diverges and calculate the sum if it exists.
Given: 4+8+16+…
Given: 4+8+16+…
Here, t1=4 and r=2
As r>1, the series is divergent and has no sum.
Hence, the given series is divergent and there is no sum exists.
Page 63 Problem 15 Answer
The given values are:
t1 = 8
r=−1/4
First, we need to find whether the infinite geometric series is convergent or divergent.
If it is convergent, then we will use the formula of the sum of an infinite geometric series.
We know that, −1/4=−0.25 and −1<−0.25<1.
Since −1<r<1, therefore the series is convergent and the sum of infinite geometric series exists.
Using the formula of the sum of an infinite geometric series, we get
S∞=8/1−(−1/4)
S∞=8/1+1/4
S∞=8/4+1/4
S∞ =8×4/5
S∞=32/5
The sum of infinite geometric series is 32/5.
Mcgraw Hill Precalculus Textbook Answers
Page 63 Problem 16 Answer
Given: t1=3 and r=4/3
To find: The sum of an infinite geometric series.
First, we need to check whether an infinite geometric series is convergent or divergent.
If it is convergent, then we will use the formula of the sum of an infinite geometric series.
We have t1=3 and r=4/3
First, we will check that the value of ris lies between −1/ to 1 or not :
Since r=4/3=1.3333
Thus,1.3333>1
So the value of r doesn’t lie between −1 to 1.
Therefore, the series is divergent and it has no sum.
Sincer>1, the series is divergent and it has no sum.
Page 63 Problem 17 Answer
Given: t1=5 and r=1
To find: The sum of an infinite geometric series.
First, we need to check whether an infinite geometric series is convergent or divergent.
If it is convergent, then we will use the formula of the sum of an infinite geometric series.
We have t1=5 and r=1.
First, we will check that the value of r is lies between −1 to 1 or not :
Since r=1
Then all of the terms of the series are the same and the series is infinite.
Thus, if r=1 then the series does not converge.
Since r=1, the series is divergent and it has no sum.
Mcgraw Hill Precalculus Textbook Answers
Page 63 Problem 18 Answer
Given: The series 1+0.5+0.25+⋯
To find: The sum of an infinite geometric series.
First, we need to find the value of rand and then check whether an infinite geometric series is convergent or divergent.
If it is convergent, then we will use the formula of the sum of an infinite geometric series.
We have the series1+0.5+0.25+⋯
First, find r:
r=0.5
1 =0.5
Now we have t1=1 andr=0.5and we know that−1<0.5<1
Since −1<r<1, the series is convergent and the sum of an infinite geometric series exists.
Using the formula for the sum of an infinite geometric series, we get
S∞ = t1/1−r
=1/1−0.5
=1/0.5
=2
∴S∞=2
Thus, the sum of an infinite geometric series is 2.
Page 63 Problem 19 Answer
Given: The series 4−12/5+36/25−108/125+⋯
To find: The sum of an infinite geometric series.
First we need to find the value of r and then check whether an infinite geometric series is convergent or divergent.
If it is convergent, then we will use the formula of the sum of an infinite geometric series.
We have the series 4−12/5+36/25−108/125+⋯
First, find r:
r=−12/5
4 =−12/5×1
4 =−3/5
=−0.6
Now we have t1 = 4 and r=−0.6 and we know that −1<−0.6<1.
Since −1<r<1, the series is convergent and the sum of an infinite geometric series exists.
Using the formula for the sum of an infinite geometric series, we get
S∞=t1/1−r
=4/1−(−0.6)
=4/1+0.6
=4/1.6
=2.5
∴ S∞=2.5
Thus, the sum of an infinite geometric series is 2.5.
Page 63 Problem 20 Answer
Given: 0.87
0.87 can be expressed as an infinite geometric series.
i.e.,0.87 =0.87878787…
=0.87+0.0087+0.000087+0.00000087+⋯
To find: The sum of an infinite geometric series.
First, we need to find the value of r and then check whether an infinite geometric series is convergent or divergent.
If it is convergent, then we will use the formula of the sum of an infinite geometric series.
We have the series0.87+0.0087+0.000087+0.00000087+⋯
By rewriting each term as a fraction,
87/100+87/10000+87/1000000+87/100000000+⋯
=87/100+87/100(1/100)+87/100(1/10000)+87/100(1/1000000)+…
=87/100+87/100(1/100)+87/100(1/100)2+87/100(1/100)3+⋯
So herer=1/100
=0.01
Now we have t1=87/100 and r=0.01 and w know that −1<0.01<1.
Since −1<r<1, the series is convergent and the sum of an infinite geometric series exists.
Using the formula for the sum of an infinite geometric series, we get
S∞=t1/1−r
=87/100/1−1/100
=87/100/99/100
=87/99
∴ S∞=87/99
Thus, the sum of an infinite geometric series is 87/99.
Mcgraw Hill Precalculus Textbook Answers
Page 63 Problem 21 Answer
0.437 can be written as a geometric progression of an infinite series
0.437 =0.437+0.000437+0.000000437+−−−−−−
t1=0.437
r=1/103
find the sum of this given series
0.437 =0.437+0.000437+0.000000437+−−−−−−
437 =0.437/1 − 0.001
0.437 =0.437/0.999
0.437 = 437/999
hence,the sum of the infinite geometric series is 437/999
Page 63 Problem 22 Answer
Given statement: 0.9999=1 this is absolutely wrong because when we extend this number to infinite then also 0.9999 will tend to 1 that doesn’t mean that it is equal to 1.
hence we can say clearly that0.999≠1
Page 63 Problem 23 Answer
Given:S∞=5+5(2/3)+5(2/3)2+5(2/3)3−−−−∞
t1 = 5
r=2/3
find the sum of this given series.
S∞ = 5 + 5(2/3 ) + 5(2/3 )2 + 5(2/3 )3 −−−− ∞
S∞ =5/1 −2/3
S∞ = 15
hence the sum of an infinite given geometric series is 15.
Page 63 Problem 24 Answer
Given:
S∞ = 1+(−1/4)+(−1/4)2+5(−1/4)3−−−−∞
t1=1
r = −1/4
find the sum of the given series.
S∞ = 1 + (−1/4 ) + (−1/4 )2 + 5(−1/4 )3 −−−− ∞
S∞ =1/1 − (−1/4 )
S∞ =4/5
hence the sum of infinite geometric series is 4/5
Page 63 Problem 25 Answer
Given: S∞=7+7(1/2)+7(1/2)2+7(1/2)3−−−−∞
Where t1=7 r=1/2 find S∞
S∞ = 7 + 7(1/2 ) + 7(1/2 )2 + 7(1/2 )3 −−−− ∞
S∞ =7/1 − 1/2
S∞ = 14
hence the sum of this infinite geometric series is 14.