Multiple Integrals – 1 Exercise 1 Solved Problems
1. Evaluate \(\int_0^2 \int_0^3 x y d x d y\)
Solution: \(\int_0^2 \int_0^3 x y d x d y=\int_0^2 x d x \int_0^3 y d y\)
= \(\left[\frac{x^2}{2}\right]\left[\frac{y^2}{2}\right]=(2-0)\left(\frac{9}{2}-0\right)=9\)
2. Evaluate \(\int_0^3 \int_{-1}^1 x^2 y^2 d x d y\)
Solution: \(\left.\int_0^3 \int_{-1}^1 x^2 y^2 d x d y=\int_0^3 \int_{-1}^1 \int_{-1}^2 y^2 d y\right] d x\)
= \(\int_0^3 2\left[\int_0^1 x^2 y^2 d y\right] d x=2 \int_0^3\left[\frac{x^2 y^3}{3}\right] d x=2 \int_0^3 \frac{x^2}{3} d x\)
= \(2\left[\frac{x^3}{9}\right]_b^3=6\)
3. Evaluate \(\int_0^3 \int_1^2 x y(x+y) d y d x\)
Solution: \(\int_0^3 \int_1^2 x y(x+y) d y d x=\int_0^3\left[\int_1^2\left(x^2 y+x y^2\right) d x\right] d y\)
= \(\int_0^3\left[\frac{x^3 y}{3}+\frac{x^2 y^2}{2}\right]_0^2 d y\)
= \(\int_0^3\left(\frac{7 y}{3}+\frac{3 y^2}{2}\right) d y\)
= \(\left[\frac{7 y^2}{6}+\frac{y^3}{2}\right]=\frac{63}{6}+\frac{27}{2}=\frac{48}{2}=24\)
4. Evaluate \(\int_0^1 \int_0^1 \frac{d x d y}{\sqrt{1-x^2} \sqrt{1-y^2}}\)
Solution: \(I=\int_0^1 \int_0^1 \frac{d x d y}{\sqrt{1-x^2} \sqrt{1-y^2}}\)
= \(\int_0^1 \frac{d x}{\sqrt{1-x^2}} \int_0^1 \frac{d y}{\sqrt{1-y^2}}=\left[\ Sin ^-1 x \right]\left[\ Sin ^-1 y\right]\)
= \(\left(\ Sin^-1 1-\ Sin^-1 0\right)\left(\ Sin^-1 1-\ Sin^-1 0\right)=\frac{\pi}{2} \frac{\pi}{2}=\frac{\pi^2}{4}\)
5. Evaluate \(\iint x y\left(x^2+y^2\right) d x d y \text { over }[0, a ; 0, b]\)
Solution: \(\iint_R x y\left(x^2+y^2\right) d x d y=\int_0^a \int_0^b x y\left(x^2+y^2\right) d x d y\)
= \(\int_0^a\left[\int_0^b x y\left(x^2+y^2\right) d y\right] d x\)
= \(\int_0^a\left[\int_0^b\left(x^3 y+x y^3\right) d y\right] d x=\int_0^a\left[\frac{x^3 y^3}{2}+\frac{x y^4}{4}\right]_0^b d x\)
= \(\int_0^a\left[\frac{b^2 x^3}{2}+\frac{b^4 x}{4}\right] d x=\left[\frac{b^2 x^4}{8}+\frac{b^4 x^2}{8}\right]_0^a\)
= \(\frac{a^4 b^2+a^2 b^4}{8}=\frac{1}{8} a^2 b^2\left(a^2+b^2\right)\)
6. Evaluate \(\iint_R \frac{d x d y}{\left(1+x^2\right)\left(1+y^2\right)} \text { over }[0,1 ; 0,1]\)
Solution: \(\iint_R \frac{d x d y}{\left(1+x^2\right)\left(1+y^2\right)}\)
= \(\int_0^1 \int_0^1 \frac{d x d y}{\left(1+x^2\right)\left(1+y^2\right)}=\int_0^1 \frac{1}{1+x^2} d x \int_0^1 \frac{1}{1+y^2} d y\)
= \(\left[\text{Tan}^{-1} x\right]_{x=0}^{x=1}\left[\text{Sin}^{-1} y\right]_{y=0}^{y=1}=\frac{\pi}{4} \frac{\pi}{4}=\frac{\pi^2}{16}\)
7. Evaluate \(\iint y e^{x y} d x d y \text { over }[0, a ; 0, b]\)
Solution: \(\iint y e^{x y} d x d y=\int_0^a \int_0^b y e^{x y} d x d y=\int_0^b\left[\int_0^a y e^{x y} d x\right] d y\)
= \(\int_0^b\left[y \frac{e^{x y}}{y}\right]_{x=0}^{x=a} d y=\int_0^b\left(e^{a y}-1\right) d y\)
= \(\left[\frac{e^{a y}}{a}-y\right]_0^b=\frac{e^{a b}-1}{a}-b\)
8. Evaluate \(\iint \frac{x-y}{x+y} d x d y \text { over }[0,1 ; 0,1]\)
Solution: \(\iint \frac{x-y}{x+y} d x d y=\int_0^1 \int_0^1 \frac{x-y}{x+y} d x d y\)
= \(\int_0^1\left[\int_0^1 \frac{2 x-(x+y)}{x+y} d y\right] d x=\int_0^1\left[\int_0^1\left(\frac{2 x}{x+y}-1\right) d y\right] d x\)
= \(\int_0^1[2 x \log (x+y)-y] \int_{y=0}^{y=1} d x=\int_0^1[2 x \log (x+1)-1-2 x \log x] d x\)
= \(\left[\log (x+1) x^2\right]-\int_0^1 \frac{x^2}{x+1} d x-[x]-\left[\log \left(x^2\right)\right]_0^1+\int_0^1 \frac{x^2}{x} d x\)
= \(\log 2-\int_0^1\left(x-1+\frac{1}{x+1}\right) d x-1+\left[\frac{x^2}{2}\right]_0^1\)
= \(\log 2-\left[\frac{x^2}{2}-x+\log (x+1)\right]-1+\frac{1}{2}\)
= \(\log 2-\frac{1}{2}+1-\log 2-\frac{1}{2}=0\)
9. Evaluate \(\int_0^2 \int_0^x y d x d y\)
Solution: \(\int_0^2 \int_0^x y d x d y=\int_0^2\left[\int_0^x y d y\right] d x\)
= \(\int_0^2\left[\frac{y^2}{2}\right]=\int_0^2 \frac{x^2}{2} d x=\left[\frac{x^3}{6}\right]=\frac{8}{6}=\frac{4}{3} .\)
10. Evaluate \(\int_1^2 \int_1^x x y^2 d x d y\)
Solution: \(\int_1^2 \int_1^x x y^2 d x d y=\int_1^2\left[\int_1^x x y^2 d y\right] d x\)
= \(\int_1^2\left[x \frac{y^3}{3}\right]_1^x d x=\int_1^2\left[\frac{x^4}{3}-\frac{x}{3}\right] d x\)
= \(\left[\frac{x^5}{15}-\frac{x^2}{6}\right]^2=\frac{32}{15}-\frac{4}{6}-\frac{1}{15}+\frac{1}{6}\)
= \(\frac{31}{15}-\frac{3}{6}=\frac{62-15}{30}=\frac{47}{30}\)
11. Evaluate \(\int_0^2 \int_{x^2}^{2 x}(2 x+3 y) d x d y\)
Solution: \(\left.\int_0^2 \int_{x^2}^{2 x}(2 x+3 y) d x d y=\int_0^2 \int_{x^2}^{2 x}(2 x+3 y) d y\right] d x\)
= \(\int_0^2\left[2 x y+\frac{3 y^2}{2}\right]_{x^2}^{2 x} d x\)
= \(\int_0^2\left(4 x^2+6 x^2-2 x^3-\frac{3 x^4}{2}\right) d x\)
= \(\int_0^2\left[10 x^2-2 x^3-\frac{3 x^4}{2}\right] d x=\left[\frac{10 x^3}{3}-\frac{x^4}{2}-\frac{3 x^5}{10}\right]_0^2\)
= \(\frac{80}{3}-8-\frac{48}{5}=\frac{400-120-144}{15}=\frac{136}{15}\)
12. Evaluate \(\int_0^4 \int_0^{x^2} e^{y / x} d x d y\)
Solution: \(\int_0^4 \int_0^{x^2} e^{y / x} d x d y\)
= \(\int_0^4\left[\int_0^{x^2} e^{y / x} d y\right]\)dx
= \(\int_0^4\left[x e^{y / x}\right]_0^{x^2} d x\)
= \(\int_0^4\left(x e^x-x\right) d x\)
= \(\left[x e^x-e^x-\frac{x^2}{2}\right]_0^4\)
= \(\left(4 e^4-e^4-8\right)-(0-1-0)=3 e^4-7\)
13. Evaluate \(\int_0^1 \int_x^{\sqrt{x}}\left(x^2+y^2\right) d x d y\)
Solution: \(\int_0^1 \int_x^{\sqrt{x}}\left(x^2+y^2\right) d x d y\)
= \(\int_0^1\left[\int_x^{\sqrt{x}}\left(x^2+y^2\right) d y\right] d x=\int_0^1\left[x^2 y+\frac{y^3}{3}\right]_x^{\sqrt{x}} d x\)
= \(\int_0^1\left[x^{5 / 2}+\frac{x^{3 / 2}}{3}-x^3-\frac{x^3}{3}\right] d x\)
= \(\int_0^1\left[x^{5 / 2}+\frac{x^{3 / 2}}{3}-\frac{4 x^3}{3}\right] d x\)
= \(\left[\frac{x^{7 / 2}}{7 / 2}+\frac{x^{5 / 2}}{3(5 / 2)}-\frac{x^4}{3}\right]=\frac{2}{7}+\frac{2}{15}-\frac{1}{3}\)
= \(\frac{30+14-35}{105}=\frac{9}{105}=\frac{3}{35}\)
14. Evaluate \(\int_0^5 \int_0^{x^2} x\left(x^2+y^2\right) d x d y\).
Solution: \(\int_0^5 \int_0^{x^2} x\left(x^2+y^2\right) d x d y=\int_0^5\left[x^3 y+\frac{x y^3}{3}\right]_0^{x^2} d x\)
= \(\int_0^5\left[x^5+\frac{x^7}{3}\right] d x=\left[\frac{x^6}{6}+\frac{x^8}{24}\right]_0^5\)
= \(5^6\left[\frac{1}{6}+\frac{25}{24}\right]=\frac{29 \times 5^6}{24}\)
15. Evaluate \(\int_0^1 \int_x^{\sqrt{x}} x^2 y^2(x+y) d y d x\)
Solution: \(\int_0^1 \int_x^{\sqrt{x}} x^2 y^2(x+y) d x d y\)
= \(\int_0^1\left[\int_x^{\sqrt{x}}\left(x^3 y^2+x^2 y^3\right) d y\right] d x\)
= \(\int_0^1\left[\frac{x^3 y^3}{3}+\frac{x^2 y^4}{4}\right]_x^{\sqrt{x}} d x\)
= \(\int_0^1\left(\frac{x^{9 / 2}}{3}+\frac{x^4}{4}-\frac{x^6}{3}-\frac{x^6}{4}\right) d x\)
= \(\left[\frac{x^{11 / 2}}{3(11 / 2)}+\frac{x^5}{20}-\frac{x^7}{21}-\frac{x^7}{28}\right]_0^1\)
= \(\frac{2}{23}+\frac{1}{20}-\frac{1}{21}-\frac{1}{28}\)
= \(\frac{73}{660}-\frac{7}{84}=\frac{73}{660}-\frac{1}{12}=\frac{18}{660}=\frac{3}{110}\)
16. Evaluate \(\int_0^a \int_0^{\sqrt{a^2-x^2}} \sqrt{a^2-x^2-y^2} d x d y\).
Solution: \(\int_0^a \int_0^{\sqrt{a^2-x^2}} \sqrt{a^2-x^2-y^2} d x d y\)
= \(\int_0^a\left[\int_0^{\sqrt{a^2-x^2}} \cdot \sqrt{\left(a^2-x^2\right)-y^2} d y\right] d x\)
= \(\int_0^a\left[\frac{y}{2} \sqrt{a^2-x^2-y^2}+\frac{a^2-x^2}{2} \sin ^{-1} \frac{y}{\sqrt{a^2-x^2}}\right]_0^{\sqrt{a^2-x^2}} d x\)
= \(\int_0^a \frac{a^2-x^2}{2} \cdot \frac{\pi}{2} d x=\frac{\pi}{4} \int_0^a\left(a^2-x^2\right) d x\)
= \(\frac{\pi}{4}\left[a^2 x-\frac{x^3}{3}\right]_0^a=\frac{\pi}{4}\left[a^3-\frac{a^3}{3}\right]=\frac{\pi a^3}{6} .\)
17. Evaluate \(\int_0^1 \int_{\sqrt{y}}^{2-y} x^2 d x d y\).
Solution: \(\int_0^1 \int_{\sqrt{y}}^{2-y} x^2 d x d y=\int_0^1\left[\int_{\sqrt{y}}^{2-y} x^2 d x\right] d y\)
= \(\int_0^1\left[\frac{x^3}{3}\right]_{\sqrt{y}}^{2-y} d y=\int_0^1 \frac{(2-y)^3-y \sqrt{y}}{3} d y\)
= \(\left[\frac{-(2-y)^4}{12}-\frac{y^{5 / 2}}{3(5 / 2)}\right]_0^1\)
= \(-\frac{1}{12}-\frac{2}{15}+\frac{16}{12}=\frac{5}{4}-\frac{2}{15}=\frac{67}{60} .\)
18. Evaluate \(\int_1^{\log 8} \int_0^{\log y} e^{x+y} d x d y\).
Solution: \(\int_1^{\log 8} \int_0^{\log y} e^{x+y} d x d y\)
= \(\int_1^{\log 8}\left[\int_0^{\log y} e^{x+y} d x\right] d y=\int_1^{\log 8}\left[e^{x+y}\right]_0^{\log y} d y\)
= \(\int_1^{\log 8}\left(y e^y-e^y\right) d y\)
= \(\int_0^{\log 8}(y-1) e^y d y=\left[(y-1) e^y\right]_1^{\log 8}-\int_1^{\log 8} e^y d y=8(\log 8-1)-\left[e^y\right]_1^{\log 8}\)
= \(8 \log 8-8-8+e=8 \log 8-16+e\)
19. Prove that \(\int_0^1\left\{\int_0^1 \frac{x-y}{(x+y)^3} d y\right\} d x=\frac{1}{2} \neq-\frac{1}{2}=\int_0^1\left\{\int_0^1 \frac{x-y}{(x+y)^3} d x\right\} d y\).
Solution: \(\int_0^1\left\{\int_0^1 \frac{x-y}{(x+y)^3} d y\right\} d x\)
= \(\int_0^1\left\{\int_0^1\left[\frac{2 x}{(x+y)^3}-\frac{1}{(x+y)^2}\right] d y\right\} d x\)
= \(\int_0^1\left[\frac{1}{x+y}-\frac{x}{(x+y)^2}\right] d x\)
= \(\int_0^1\left[\frac{y}{(x+y)^2}\right]_0^1 d x=\int_0^1 \frac{1}{(1+x)^2} d x\)
= \(\left[-\frac{1}{1+x}\right]=-\frac{1}{2}+1=\frac{1}{2}\)
= \(\int_0^1\left[\int_0^1 \frac{x-y}{(x+y)^3} d x\right] d y\)
= \(\int_0^1\left[\int_0^1\left\{\frac{1}{(x+y)^2}-\frac{2 y}{(x+y)^3}\right\} d x\right] d y\)
= \(\int_0^1\left[-\frac{1}{x+y}+\frac{y}{(x+y)^2}\right]_0^1 d y\)
= \(\int_0^1\left[-\frac{x}{(x+y)^2}\right]_0^1 d y=-\int_0^1 \frac{1}{(1+y)^2} d y=\left[\frac{1}{1+y}\right]=\frac{1}{2}-1=-\frac{1}{2} .\)
20. Evaluate \(\iint(5-2 x-y) d x d y \text { where } \mathrm{R} \text { is given by } y=0, x+2 y=3, x=y^2 \text {. }\).
Solution: The region R bounded by \(y=0, x+2 y=3, x=y^2\) is shown in the figure.
It is convenient to consider a horizontal strip, with one end moving on x=y^2 and another end moving on x=3-2y.
To cover the region, this strip has to be slid from y=0 to y=1.
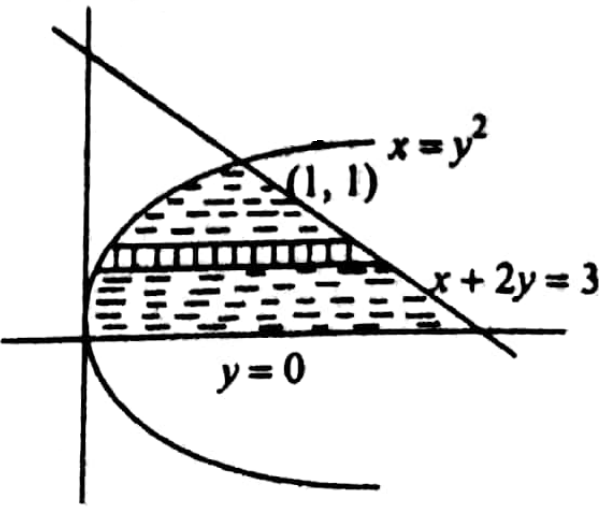
Hence \(\iint_R(5-2 x-y) d x d y=\int_0^1 \int_{y^2}^{3-2 y}(5-2 x-y) d y d x\)
= \(\int_0^1\left[\int_{y^2}^{3-2 y}(5-2 x-y) d x\right] d y=\int_0^1\left[5 x-x^2-x y\right]_2^{3-2 y} d y\)
= \(\int_0^1\left[5(3-2 y)-(3-2 y)^2-(3-2 y) y-5 y^2+y^4+y^3\right] d y\)
= \(\int_0^1\left(y^4+y^3-7 y^2-y+6\right) d y\)
= \(\left[\frac{y^5}{5}+\frac{y^4}{4}-\frac{7 y^3}{3}-\frac{y^2}{2}+6 y\right]_0^1\)
= \(\frac{1}{5}+\frac{1}{4}-\frac{7}{3}-\frac{1}{2}+6=\frac{217}{60} .\)
21. Evaluate \(\iint x y(x+y) d x d y \text { over the area between } y=x^2 \text { and } y=x\).
Solution:The curves y=x^2 and y=x intersect at (0,0),(1,1).
The region of integration is 0≤x≤1,x^2≤y≤x.
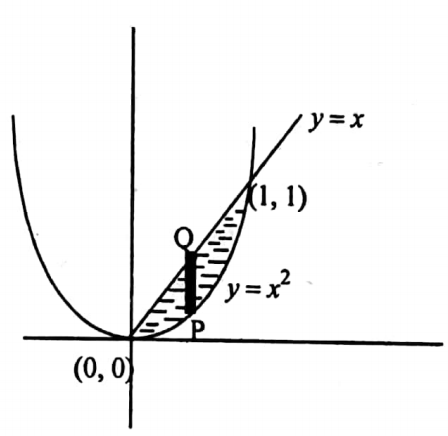
∴ \(\iint x y(x+y) d x d y=\int_0^1\left[\int_x^2[x y(x+y) d y]\right] d x\)
= \(\int_0^1\left[\int_{x^2}^x\left(x^2 y+x y^2\right) d y\right] d x=\int_0^1\left[\frac{x^2 y^2}{2}+\frac{x y^3}{3}\right]_{x^2}^x d x\)
= \(\int_0^1\left[\frac{x^4}{2}+\frac{x^4}{3}-\frac{x^6}{2}-\frac{x^7}{3}\right] d x=\int_0^1\left(\frac{5 x^4}{6}-\frac{x^6}{2}-\frac{x^7}{3}\right) d x\)
= \(\left[\frac{x^5}{6}-\frac{x^7}{14}-\frac{x^8}{24}\right]_0^1=\frac{1}{6}-\frac{1}{14}-\frac{1}{24}=\frac{9}{162}=\frac{3}{56}\)
22. Evaluate \(\iint e^{2 x+3 y} d x d y\) over the triangle bounded by x=0,y=0, and x+y=1.
Solution: The region of integration R is the shaded area shown in the figure.
The integral can be evaluated over R by considering either a horizontal strip or a vertical strip.
Imagine a vertical strip such that one end is moving on y=0 and the other end is moving on y=1-x.
By sliding this strip from x=0 to x=1 the region can be covered.
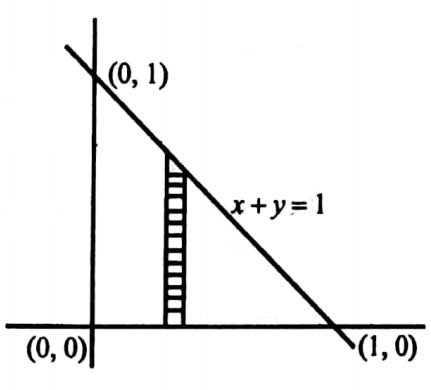
Hence \(\iint_R e^{2 x+3 y} d x d y=\int_0^1 \int_0^{1-x} e^{2 x+3 y} d x d y=\int_0^1\left[\int_0^{1-x} e^{2 x+3 y} d y\right] d x\)
= \(\int_0^1\left[\frac{e^{2 x+3 y}}{3}\right]_0^{1-x} d x\)
= \(\int_0^1 \frac{1}{3}\left(e^{3-x}-e^{2 x}\right) d x=\frac{1}{3}\left[-e^{3-x}-\frac{e^{2 x}}{2}\right]_0^1\)
= \(\frac{1}{3}\left[-e^2-\frac{e^2}{2}+e^3+\frac{1}{2}\right]=\frac{1}{3}\left[\frac{2 e^3-3 e^2+1}{2}\right]\)
= \(\frac{1}{6}(e-1)^2(2 e+1) .\)
23. Evaluate \(\iint_R x^2 d x d y\) where R is the region in the first quadrant bounded by the hyperbola xy=16 and the lines y=x,y=0, and x=8.
Solution:
The region is as a shaded area. It may be noted that the entire region can’t be covered with a single horizontal strip or a vertical strip.
Let us divide the region into two regions R1 and R2 and evaluate. Hence
∴ \(\iint_{\boldsymbol{R}} x^2 d x d y\) =\(\iint_{R_1} x^2 d x d y+\iint_{R_2} x^2 d x d y\)
Imagine a vertical strip in R1 ∋ one end moves on the x-axis and another end moves on y = x. Thus the limits of y are 0 to x
And the strip must be slid from x = 0 to x = 4 to cover R1
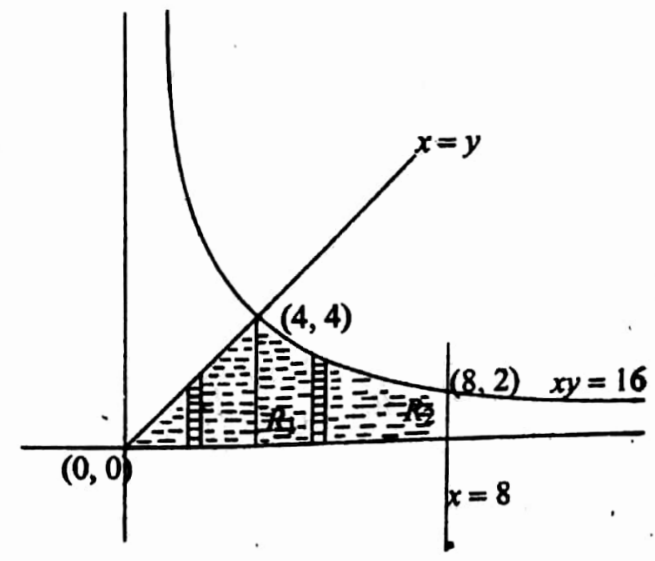
Imagine a vertical strip in R2 ∋ one end moves on the x-axis and another end moves on = 16/x. Thus the limits of y are 0, 16/x.
This strip must be moved from x = 4 tox = 8 to cover R2
Hence \(\iint_R x^2 d x d y=\iint_{R_1} x^2 d x d y+\iint_{R_2} x^2 d x d y\)
= \(\int_0^4 \int_0^x x^2 d x d y+\int_4^8 \int_{10}^{16 / x} x^2 d x d y \cdot\)
= \(\int_0^4\left[\int_0^x x^2 d y\right] d x+\int_4^8\left[\int_{10}^{16 / x} x^2 d y\right] d x\)
= \(\int_0^4\left[x^2 \cdot y\right]_0^x d x+\int_4^8\left[x^2 y\right]_0^{16 / x} d x=\int_0^4 x^3 d x+\int_4^8 16 x d x\)
= \(\left[\frac{x^4}{4}\right]_0^4+\left[\frac{16 x^2}{2}\right]_4^8=\frac{256}{4}+\frac{16 \cdot 64}{2}-\frac{16 \cdot 16}{2}=64+512-128=448\).
24. Evaluate \(\iint\left(x^2+y^2\right) d x d y\) over the area bounded by x+y≤1 in the first quadrant.
Solution:
⇒ \(\iint_R\left(x^2+y^2\right) d x d y=\int_{x=0}^1 \int_{y=0}^{1-x}\left(x^2+y^2\right) d x d y\)
= \(\int_{x=0}^1\left[\int_{y=0}^{1-x}\left(x^2+y^2\right) d y\right] d x\)
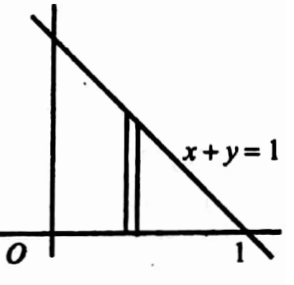
= \(\int_0^1\left[x^2 y+\frac{y^3}{3}\right]_0^{1-x} d x d y=\int_0^1\left[x^2(1-x)+\frac{1}{3}(1-x)^3\right] d x\)
= \(\left[\frac{x^3}{3}-\frac{x^4}{4}-\frac{1}{12}(1-x)^4\right]_0^1=\left[\frac{1}{3}-\frac{1}{4}-0\right]-\left[0-0-\frac{1}{12}\right]\)
= \(\frac{4-3+1}{12}=\frac{1}{6} .\)
25. Evaluate \(\iint\left(x^2+y^2\right) d x d y\) over the region bounded by y=x,y=2x,x=1 in the first quadrant .
Solution:
⇒ \(\iint_R\left(x^2+y^2\right) d x d y=\int_{x=0}^1 \int_{y=x}^{y=2 x}\left(x^2+y^2\right) d x d y\)
= \(\int_{x=0}^1\left[\int_{y=x}^{y=2 x}\left(x^2+y^2\right) d y\right] d x\)
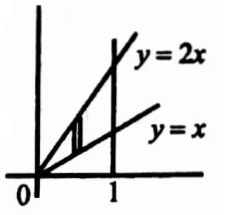
= \(\int_0^1\left[x^2 y+\frac{y^3}{3}\right]_{y=x}^{2 x} d x=\int_0^1\left[2 x^3+\frac{8 x^3}{3}-x^3-\frac{x^3}{3}\right] d x\)
= \(\int_0^1 \frac{10}{3} x^3 d x=\frac{10}{3}\left[\frac{x^4}{4}\right]_0^1=\frac{5}{6}\)
26. Evaluate \(\iint x y d x d y\) taken over the positive quadrant of the circle \(x^2+y^2=a^2\).
Solution: The region of integration is the positive quadrant of the circle x2+y2=a2
⇒ y various from 0 to \(\sqrt{a^2-x^2}\) and x varies from 0 to a.
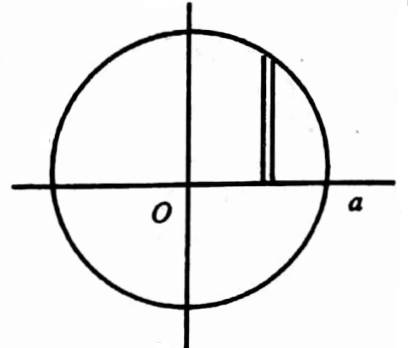
∴ \(\iint_0 x y d x d y=\int_0^a \int_0^{\sqrt{a^2-x^2}} x y d x d y=\int_0^a\left[\int_0^{\sqrt{a^2-x^2}} x y d y\right] d x\)
= \(\int_0^a\left[x \frac{y^2}{2}\right] d x=\int_0^{\sqrt{a^2-x^2}} \frac{x\left(a^2-x^2\right)}{2} d x=\frac{a^4}{8 .}\)
27. Evaluate \(\iint(x+y)^2 d x d y\) over the area bounded by the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\).
Solution:
Given \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \Rightarrow \frac{y^2}{b^2}=\frac{a^2-x^2}{a^2} \Rightarrow y= \pm \frac{b}{a} \sqrt{a^2-x^2}\)
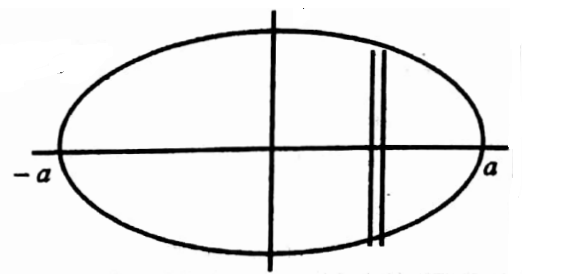
The region of integration is \(-a \leq x \leq a\),
– \(\frac{b}{a} \sqrt{a^2-x^2} \leq y \leq \frac{b}{a} \sqrt{a^2-x^2} \text {. }\)
⇒ \(\iint_R(x+y)^2 d x d y=\iint_R\left(x^2+y^2+2 x y\right) d x d y\)
= \(\int_{x=-a}^a \int_{-\frac{b}{a} \sqrt{a^2-x^2}}^{\frac{b}{a} \sqrt{a^2-x^2}}\left(x^2+y^2+2 x y\right) d x d y\)
= \(\int_{-a}^a\left[\int_{-\frac{b}{a} \sqrt{a^2-x^2}}^{\frac{b}{a} \sqrt{a^2-x^2}}\left(x^2+y^2+2 x y\right) d y\right] d x\)
= \(\int_{-a}^a\left[x^2 y+\frac{y^3}{3}+x y^2\right]_{-\frac{b}{a}}^{\frac{b}{a} \sqrt{a^2-x^2}-x^2} d x \int_{-a}^a\left[x^2\left(\frac{2 b}{a} \sqrt{a^2-x^2}\right)+\frac{2}{3} \frac{b^3}{a^3}\left(a^2-x^2\right)^{3 / 2}+0\right] d x\)
= \(2 \int_0^a\left[x^2\left(\frac{2 b}{a} \sqrt{a^2-x^2}\right)+\frac{2}{3} \frac{b^3}{a^3}\left(a^2-x^2\right)^{3 / 2}\right] d x\)
Put x = \(a \sin \theta\) so that
dx = \(a \cos \theta d \theta\)
= \(4 \int_0^{\pi / 2}\left[\frac{b}{a} a^2 \sin ^2 \theta a \cos \theta+\frac{b^3}{3 a^3} a^3 \cos ^3 \theta\right] a \cos \theta d \theta\)
= \(4 b a^3 \int_0^{\pi / 2} \sin ^2 \theta \cos ^2 \theta d \theta+\frac{4 a b^3}{3} \int_0^{\pi / 2} \cos ^4 \theta d \theta\)
= \(4 a^3 b \cdot \frac{1}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2}+4 \frac{a b^3}{3} \cdot \frac{3}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2}\)
= \(\left(a^3 b+a b^3\right) \frac{\pi}{4}=\frac{a b\left(a^2+b^2\right) \pi}{4}\)
28. Evaluate \(\int_0^{\pi / 4} \int_0^{\sqrt{\cos 2 \theta}} \frac{r}{\left(1+r^2\right)^2} d \theta d r\)
Solution:
⇒ \(\int_0^{\pi / 4} \int_0^{\sqrt{\cos 2 \theta}} \frac{r}{\left(1+r^2\right)^2} d \theta d r\)
= \(\int_0^{\pi / 4}\left[\int_0^{\sqrt{\cos 2 \theta}} \frac{r}{\left(1+r^2\right)^2} d r\right] d \theta\)
= \(\int_0^{\pi / 4} \frac{1}{2}\left[-\frac{1}{1+r^2}\right]_0^{\sqrt{\cos 2 \theta}} d \theta\)
= \(\frac{1}{2} \int_0^{\pi / 4}\left(\frac{-1}{1+\cos 2 \theta}+1\right) d \theta=\frac{1}{2} \int_0^{\pi / 4}\left(1-\frac{1}{2} \sec ^2 \theta\right) d \theta\)
= \(\frac{1}{2}\left[\theta-\frac{1}{2} \tan \theta\right]_0^{\pi / 4}=\frac{1}{2}\left[\frac{\pi}{4}-\frac{1}{2}\right]\)
= \(\frac{\pi-2}{8}\)
29. Evaluate \(\int_0^{\pi / 4} \int_0^{a \sin \theta} \frac{r d \theta d r}{\sqrt{a^2-r^2}}\).
Solution: \(\int_0^{\pi / 4} \int_0^{a \sin \theta}\left[\frac{r d r}{\sqrt{a^2-r^2}}\right] d \theta\)
= \(\int_0^{\pi / 4}\left[-\left(a^2-r^2\right)^{1 / 2}\right]_0^{a \sin \theta} d \theta=\int_0^{\pi / 4}[-a \cos \theta+a] d \theta\)
= \([-a \sin \theta+a \theta]{ }_0^{\pi / 4}=a\left[\frac{\pi}{4}-\sin \frac{\pi}{4}\right]=a\left(\frac{\pi}{4}-\frac{1}{\sqrt{2}}\right)\)
30. Evaluate \(\int_0^\pi \int_0^{a \sin \theta} r d \theta d r\)
Solution: \(\int_0^\pi \int_0^{a \sin \theta} r d r d \theta=\int_0^\pi\left[\int_0^{a \sin \theta} r d r\right] d \theta\)
= \(\int_0^\pi\left[\frac{r^2}{2}\right]_0^{a \sin \theta} d \theta=\int_0^\pi \frac{a^2}{2} \sin ^2 \theta d \theta=a^2 \int_0^{\pi / 2} \sin ^2 \theta d \theta\)
= \(a^2\left(\frac{1}{2}\right)\left(\frac{\pi}{2}\right)=\frac{\pi a^2}{4}\)
31. Evaluate \(\int_0^{\pi / 2} \int_0^{2 a \cos \theta} r^2 \sin \theta d \theta d r\)
Solution: \(\int_0^{\pi / 2} \int_0^{2 a \cos \theta} r^2 \sin \theta d r d \theta\)
= \(\int_0^{\pi / 2}\left[\int_0^{2 a \cos \theta} r^2 \sin \theta d r\right] d \theta\)
= \(\int_0^{\pi / 2}\left[\frac{r^3}{3} \sin \theta\right]_0^{2 a \cos \theta} d \theta\)
⇒ \(\int_0^{\pi / 2}\left[\frac{8 a^3}{3} \cos ^3 \theta \sin \theta\right] d \theta\)
= \(\frac{8 a^3}{3}\left[\frac{-\cos ^4 \theta}{4}\right]_0^{\pi / 2}\)=\(\frac{2 a^3}{3}\)
32. Evaluate \(\int_0^{\pi / 2} \int_{a(1-\cos \theta)}^a r^2 d \theta d r\)
Solution: \(\int_0^{\pi / 2} \int_{a(1-\cos \theta)}^a r^2 d \theta d r=\int_0^{\pi / 2}\left[\int_{a(1-\cos \theta)}^a r^2 d r\right] d \theta\)
= \(\int_0^{\pi / 2} d \theta[\frac{r^3}{3}]=\frac{1}{a} \int_0^{\pi / 2}[a^3-a^3(1-\cos \theta)\)
= \(\frac{a^3}{3} \int_0^{\pi / 2}\left[1-(1-\cos \theta)^3\right] d \theta\)
= \(\frac{a^3}{3} \int_0^{\pi / 2}\left[1-\left(1-3 \cos \theta+3 \cos ^2 \theta-\cos ^3 \theta\right)\right] d \theta\)
= \(\frac{a^3}{3} \int_0^{\pi / 2}\left[3 \cos \theta-3 \cos ^2 \theta+\cos ^3 \theta\right] d \theta\)
= \(\frac{a^3}{3}\left[3(\sin \theta)-3 \int_0^{\pi / 2} \cos ^2 \theta d \theta+\int_0^{\pi / 2} \cos ^3 \theta d \theta\right]\)
= \(\frac{a^3}{3}\left[3-3 \cdot \frac{1}{2} \cdot \frac{\pi}{2}+\frac{2}{3} \cdot 1\right]\)
= \(\frac{a^3}{3}\left[3-\frac{3 \pi}{4}+\frac{2}{3}\right]=\frac{a^3}{36}(44-9 \pi) .\)
33. Evaluate \(\iint r \sin \theta d \theta d r\) over the cardioid r=a(1-cosθ) above the initial line.
Solution: The cardioid is symmetric about the initial line and through the pole O. Above the initial line the region of integration is r=0, r=a(1-a cosθ) and θ=0, θ=π
⇒ \(\iint_R r \sin \theta d r d \theta=\int_{r=0}^{a(1-\cos \theta)} \int_{\theta=0}^\pi r \sin \theta d r d \theta\)
= \(\int_{\theta=0}^\pi \sin \theta\left[\frac{r^2}{2}\right]_0^{a(1-\cos \theta)} d \theta\)
= \(\int_0^\pi \frac{a^2(1-\cos \theta)^2}{2} \sin \theta d \theta\)
= \(\frac{a^2}{2}\left[\frac{(1-\cos \theta)^3}{3}\right]_0^\pi\)
= \(\frac{a^2}{6}\left[(1-\cos \pi)^3-(1-\cos 0)^3\right]=\frac{a^2}{6}[8-0]=\frac{4 a^2}{3}\)
34. Evaluate \(\iint r \sqrt{a^2-r^2} d \theta d r\)over the upper half of the circle r=a cosθ.
Solution:
The required integral = \(\int_0^{\pi / 2} \int_{r=0}^{r=a \cos \theta} r \sqrt{a^2-r^2} d r d \theta\)
= \(\int_0^{\pi / 2}\left[-\frac{1}{3}\left(a^2-r^2\right)^{3 / 2}\right]_0^{a \cos \theta} d \theta\)
= \(-\frac{1}{3} \int_0^{\pi / 2}\left\{\left(a^2-a^2 \cos ^2 \theta\right)^{3 / 2}-\left(a^2\right)^{3 / 2}\right\} d \theta\)
= \(\frac{a^3}{3} \int_0^{\pi / 2}\left(1-\sin ^3 \theta\right) d \theta=\frac{a^3(3 \pi-4)}{18} .\)
35. Evaluate \(\iint \frac{\sqrt{\left(a^2 b^2-b^2 x^2-a^2 y^2\right)}}{\sqrt{\left(a^2 b^2+b^2 x^2+a^2 y^2\right)}} d x d y\) the field of integration being the positive quadrant of the ellipse \(x^2 / a^2+y^2 / b^2=1\).
Solution: Changing the variables x,y to , where x=aX,y=bY
We see that, since ∂ (x,y)/ ∂ (x,y)= ab, the integral = \(a b\iint \sqrt{\left(\frac{1-X^2-Y^2}{1+X^2+Y^2}\right)}\)dX dY,
The new field of integration is the positive quadrant of the circle X2+Y2=1.
Changing X,Y to r, where X= r cosθ , Y= =r sinθ , so that(X,Y)/(r,θ )=r,
We see that the integral = ab\(=a b \iint \frac{\sqrt{\left(1-r^2\right)}}{\sqrt{\left(1+r^2\right)}}\)r dr dθ.
It is easily seen that the positive quadrant of the circle X2+Y2= 1, will be described if 0 varies from 0 to π/2 and corresponds to each value of θ between 0 and π/2, r varies from 0 to 1.
This new domain of integration, therefore, is the rectangle [ 0, 1:0, 1/2π].
Thus the integral = \(a b \int_0^{\pi / 2} d \theta \int_0^1 \frac{\sqrt{\left(1-r^2\right)}}{\sqrt{\left(1+r^2\right)}} r d r\)
= \(\frac{\pi}{2} a b \int_0^1 \frac{\sqrt{\left(1-r^2\right)}}{\sqrt{\left(1+r^2\right)}} r d r=\frac{1}{2} \pi(\pi-2) a b\)
where the integral has been evaluated by putting \(r^2=\cos t\).
36. Integrate the function \(\frac{1}{x y}\) over the area bounded by the four circles \(x^2+y^2=a x, a^{\prime} x, b y, b^{\prime} y \text { where } a, a^{\prime}, b, b^{\prime}\) are all positive.
Solution: The integration is to be carried over the shaded area. We have supposed a’> a and b’ > b.
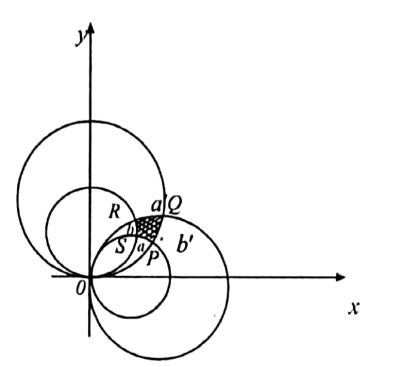
The region of integration is defined by ax≤ x+y ≤ a’ x; by≤x+y≤ b’y. We change the variables to u, v, where
u = \(\frac{\left(x^2+y^2\right)}{x, v}=\frac{\left(x^2+y^2\right)}{y} \Rightarrow x=\frac{u v^2}{u^2+v^2} ; y=\frac{u^2 v}{u^2+v^2}\)
It is easy to see that \(\frac{\partial(u, v)}{\partial(x, y)}=-\frac{\left(x^2+y^2\right)^2}{x^2 y^2}\)
∴ \(\frac{\partial(x, y)}{\partial(u, v)}=-\frac{x^2 y^2}{\left(x^2+y^2\right)^2}\).
Since the Jacobian is negative, the transformation is inverse. This fact may also be directly verified. The new field of integration is determined by the boundaries u=a, u=a’, v=b,v=b’, and is, therefore, the rectangle [a, a’; b, b’].
Thus we see that the integral = \(\iint \frac{1}{x y}|J| d u d v=\iint \frac{x y}{\left(x^2+y^2\right)^2} d u d v\)‘
= \(\iint \frac{1}{u v} d u d v=\int_a^{a^{\prime}} \frac{1}{u} d u \int_b^{b^{\prime}} \frac{1}{v} d v=\log \frac{a^{\prime}}{a} \cdot \log \frac{b^{\prime}}{b} .\)
37. By substituting x+y=u,x=uv, prove that the value of \(\iint \sqrt{[x y(1-x-y)]} d x d y\) taken over the interior of the triangle bounded by the lines x=0,y=0,x+y-1=0 is 2π/105.
Solution:
Now x=uv,y=u (1-v)⇒ ∂(x,y)/∂(u,v)=-u, so that the jacobian≤ 0.
The jacobian vanishes when u=0, i.e when x=y=0, but not otherwise.
It is easy to see that to the origin of the xy-plane corresponds to the whole line u=0 of the uv- plane so that the correspondence ceases to be one-to-one.
In order to exclude x=0, y=0, we look upon the given integral, which certainly exists, as the limit, when h→0, of the integral over the region bounded by x+y=1, x=0, y=h. (h>0)
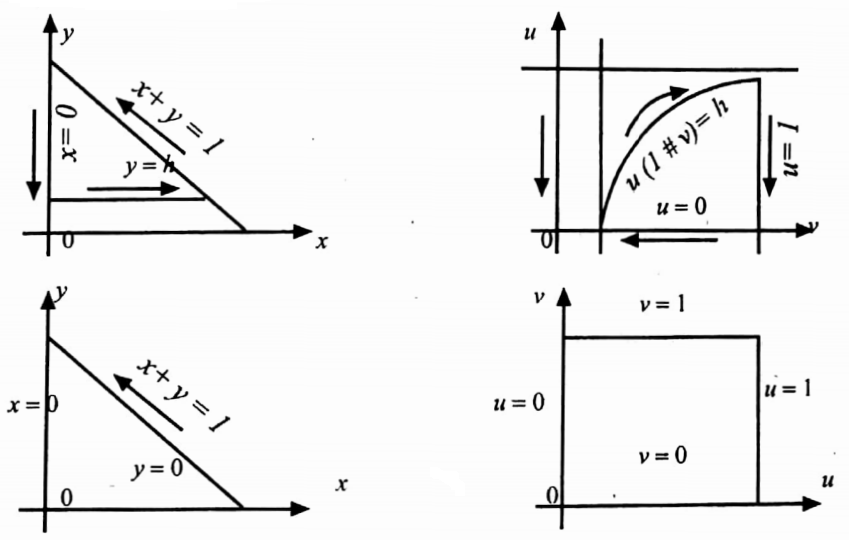
The transformed region is, then, bounded by the lines u=1,v=0,u(1-v)=h, which correspond to the three boundaries of the region in the xy-plane. When h→0, this new region of the UV-plane tends, as the limit, to the square bounded by the lines u=1, v=1,u=0,v=0.
Thus the Integral
= \(\iint \sqrt{[u \nu u(1-v)(1-u)} u d u d v=\int_0^1 u^2 \sqrt{1-u} d u \int_0^1 \sqrt{[v(1-v)]} d v\)
Putting \(u=\sin ^2 \theta\) and \(v=\sin ^2 \psi\), we see that
⇒ \(\int_0^1 u^2 \sqrt{(1-u)} d u=2 \int_0^{\pi / 2} \sin ^5 \theta \cos ^2 \theta d \theta\)
= \(\frac{2 \cdot 4 \cdot 2 \cdot 1}{\not \cdot 5 \cdot 3 \cdot 1}=\frac{16}{105}\),
∴ \( \int_0^1 \sqrt{v(1-v)} d v=2 \int_0^{\pi / 2} \sin ^3 \psi \cos ^2 \psi d x=\frac{2 \cdot 1 \cdot 1}{4 \cdot 2} \cdot \frac{\pi}{2}=\frac{\pi}{8}\).
Note: We have u=x+y, v=x/(x+y) and x= uv, y= u(1-v).
38. Using the transformation x+y=u,x-y=ν, evaluate \(\iint e^{\frac{x-y}{x+y}} d x d y\) over the region bounded by x=0,y=0,x+y=1.
Solution:
Solving x+y=u, x-y=v, we have x=\(\frac{u+v}{2}, y=\frac{u-v}{2}\)
We transform the function, curves in to u, v plane with this substitution. xy plane
Curves :
x=0
y=0
x+y=1
u v plane
u=-v
u=v
u=1
Now, \(f(x, y)=e^{\frac{x-y}{x+y}}\) is . \(f(u, v)=e^{\frac{v}{u}}\) . \(J\left(\begin{array}{ll}x & y \\ u & v\end{array}\right)\)
= \(\left|\begin{array}{ll}\frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v}\end{array}\right|\)
= \(\left|\begin{array}{cc}\frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2}\end{array}\right|=-\frac{1}{2}\).
Hence dx dy = \(\left|J\left(\begin{array}{ll}
x & y \\
u & v
\end{array}\right)\right| d u d v=\frac{1}{2} d u d v\)
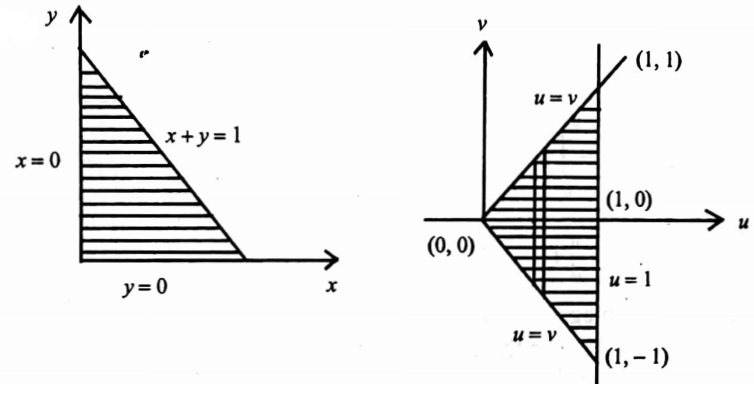
⇒ \(\int_0^1 \int_{-u}^u e^{v / u} \cdot \frac{1}{2} d v d u\)
= \(\frac{1}{2} \int_0^1\left[u e^{v / u}\right]_{-u}^u d u=\frac{1}{2} \int_0^1\left(u \cdot e-u \cdot e^{-1}\right) d u\)
= \(\frac{1}{2} \int_0^1\left(u e-\frac{u}{e}\right) d u\)
= \(\frac{1}{2}\left(e-\frac{1}{e}\right)\left[\frac{u^2}{2}\right]_0^1=\frac{1}{4}\left(e-\frac{1}{e}\right)\).
In the new region of the u-v plane imagine a vertical strip with one end on v=-u and the other end on v=u. This has, to be slid from u=0 to u=1, to cover the region. With the transformation, the integral becomes
39. By changing into polar coordinates evaluate the integral \(\int_0^{2 a} \int_0^\sqrt{2 a x-x^2}\left(x^2+y^2\right) d x d y\).
Solution: The region of integration is the semi-circle x+y=2ax above the x-axis. Changing into polar, the region becomes r=0 to r=2a cos θ from θ=0 to θ= π/2. Hence the required integral
= \(\int_0^{\pi / 2} \int_0^{2 a \cos \theta}\left(r^2 \cos ^2 \theta+r^2 \sin ^2 \theta\right) r d r d \theta\)
=\(\int_0^{\pi / 2} \cdot \int_0^{2 a \cos \theta} r^2 d r d \theta\)
= \(\int_0^{\pi / 2}\left[\frac{r^4}{4}\right]_0^{2 a \cos \theta} d \theta=4 a^4 \int_0^{\pi / 2} \cos ^4 \theta d \theta=\frac{3 \pi a^4}{4} .\)
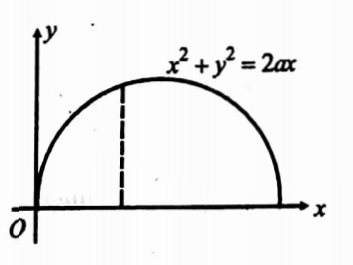
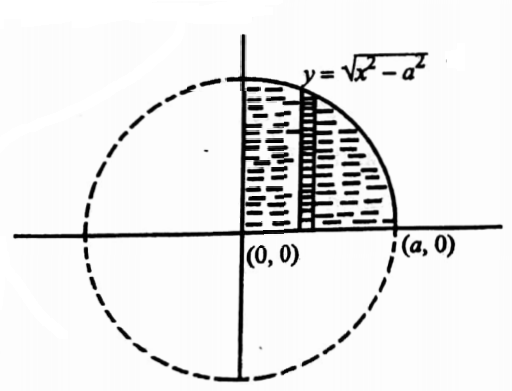
40. Change into polar coordinates and evaluate \(\int_0^a \int_0^{\sqrt{a^2-x^2}} e^{-\left(x^2+y^2\right)} d x d y\).
Solution:
Here f(x,y) =e-(x2+y2) and the region is bounded by y=0, y=\(\sqrt{a^2-x^2}\), x=0,x=a.
The region is shown in the figure. Substitute x=r cosθ,y=r sinθ. f(x,y)= e-(r2cos2θ+r sin2θ) = e-r2.
The curve y= \(\sqrt{a^2-x^2}\) is a circle whose equation is x2+y2=a2.
Substituting x= r cosθ , y= r sinθ, this becomes r=a
Imagine a wedge with one end at the pole O and the other end moving on r=a.To cover the region the wedge has to be moved from θ=0 to θ= π/2
Thus \(\int_0^a \int_0^{\sqrt{a^2-x^2}} e^{-\left(x^2+y^2\right)} d x d y=\int_0^{\pi / 2} \int_0^a e^{-r^2} r d r d \theta\)
= \(\int_0^{\pi / 2}\left[-\frac{e^{-r^2}}{2}\right]_0^a d \theta\)
= \(\int_0^{\pi / 2}\left[-\frac{e^{-a^2}}{2}+\frac{1}{2}\right] d \theta\)
= \(\frac{1-e^{-a^2}}{2}[\theta]_0^{\pi / 2}=\frac{\pi}{4}\left(1-e^{-a^2}\right)\)
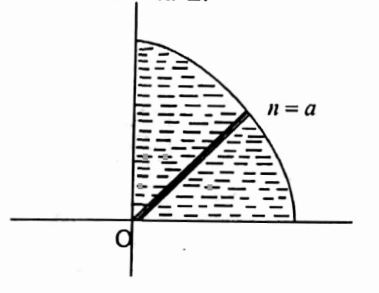
41. Change into polar coordinates and evaluate \(\int_0^{\infty} \int_0^{\infty} \frac{1}{\left(a^2+x^2+y^2\right)^{3 / 2}} d x d y\).
Solution:
The region of integration is y-=0, y = ∞ , x = 0, x = ∞ , and hence the entire region lies in the first quadrant. Put x = r cos θ, y = r sin θ.
Now \(\frac{1}{\left(a^2+x^2+y^2\right)^{3 / 2}}\)
= \(\frac{1}{\left(a^2+r^2 \cos ^2 \theta+r^2 \sin ^2 \theta\right)^3 / 2}\)\(=\frac{1}{\left(a^2+r^2\right)^{3 / 2}}\)
Imagine a wedge of angular thickness δθ with one end at pole r=0 and the other end on r=∞. To cover the first quadrant this wedge has to be moved from θ =0 to θ =π/2.
Hence \(\int_0^{\infty} \int_0^{\infty} \frac{1}{\left(a^2+x^2+y^2\right)^{3 / 2}} d x d y\)
= \(\int_0^{\pi / 2} \int_0^{\infty} \frac{1}{\left(a^2+r^2\right)^{3 / 2}} r d r d \theta\)
= \(\int_0^{\pi / 2}-\left[\frac{1}{\left(a^2+r^2\right)^{1 / 2}}\right]_0^{\infty} d \theta\)
= \(\int_0^{\pi / 2} \frac{1}{a} d \theta=\frac{1}{a} \cdot \frac{\pi}{2}=\frac{\pi}{2 a}\)
42. Change into polar coordinates and evaluate \(\int_0^a \int_{\sqrt{a x-x^2}}^{\sqrt{a^2-x^2}} \frac{1}{\sqrt{a^2-x^2-y^2}} d x d y\).
Solution:
The region of integration is surrounded by y = \(\sqrt{a x-x^2}, y=\sqrt{a^2-x^2}, x=0, x=a\).
y = \(\sqrt{a x-x^2}\) i.e., \(y^2=a x-x^2\) i.e., \(\left(x-\frac{a}{2}\right)^2+y^2=\frac{a^2}{4}\) represents a circle with center (a/2,0), radius a/2.
y = \(\sqrt{a^2-x^2}\) represents a circle with center (0,0) and radius a.
The region of integration is shown in the figure
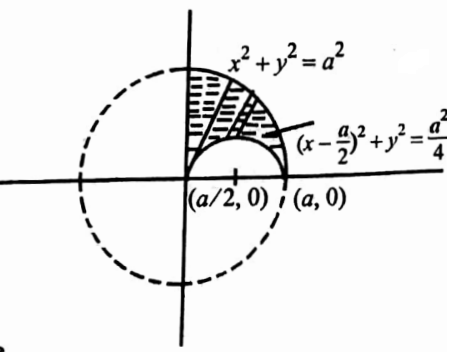
Put x = \(r \cos \theta, y=r \sin \theta\) so that \(\frac{1}{\sqrt{a^2-x^2-y^2}}=\frac{1}{\sqrt{a^2-r^2}}, x^2+y^2=a^2\) is r=a \(\left(x-\frac{a}{2}\right)^2+y^2=\frac{a^2}{4}\) is \(r=a \cos \theta\)
Imagine a wedge of angular thickness δθ with one end on r = a cos θ and another end on r = a. To cover the region this wedge has to be moved from θ = 0 to 0 = π/2. Thus the given integral in polar coordinates is
⇒ \(\int_0^{\pi / 2} \int_{a \cos \theta}^a \frac{1}{\sqrt{\left.a^2-r^2\right)}} r d r d \theta\)
= \(\int_0^{\pi / 2}\left[-\sqrt{a^2-r^2}\right]_{a \cos \theta}^a d \theta\)
= \(\int_0^{\pi / 2} a \sin \theta d \theta\)\(=a[-\cos \theta]_0^{\pi / 2}\)=a
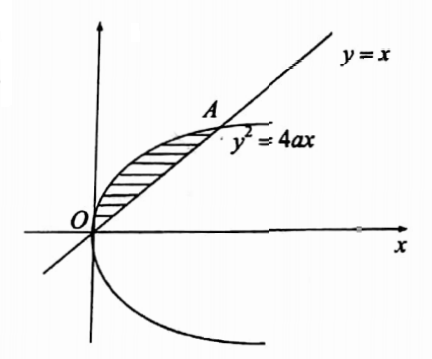
43. Evaluate the integral \(\int_0^{4 a} \int_{y^2 / 4 a}^y \frac{x^2-y^2}{x^2+y^2} d x d y\) by changing to polar coordinates.
Solution: The region of integration is y= 0,y=4a,x=y/4a, x=y
∴ The regions is bounded by the line y=x and the parabola y= 4ax.
Put x = \(r \cos \theta, y=r \sin \theta\).
Then dx dy = r dr dθ
⇒ \(y^2=4 a x \Rightarrow r^2 \sin ^2 \theta=4 a \cdot r \cos \theta\)
⇒ r = \(\frac{4 a \cos \theta}{\sin ^2 \theta}\)
The limits of integration are r=0 to r = \(\frac{4 a \cos \theta}{\sin ^2 \theta}\) and for the line x=y, slope, \(\tan \theta=1 \Rightarrow \theta=\pi / 4\).
∴ limits for θ are θ = \(\pi / 4\) to \(\theta=\pi / 2\)
Also \(x^2+y^2=r^2, x^2-y^2=r^2\left(\cos ^2 \theta-\sin ^2 \theta\right)\).
∴ \(\int_0^{4 a} \int_{y^2 / 4 a}^y \frac{x^2-y^2}{x^2+y^2} d x d y\)
= \(\int_{\theta=\pi / 4}^{\pi / 2} \int_{r=0}^{4 a \cos \theta / \sin ^2 \theta}\left(\cos ^2 \theta-\sin ^2 \theta\right) r d r d \theta\)
= \(\int_{\pi / 4}^{\pi / 2}\left(\cos ^2 \theta-\sin ^2 \theta\right)\left[\frac{r^2}{2}\right]_0^{4 a \cos \theta / \sin ^2 \theta} d \theta\)
= \(8 a^2 \int_{\pi / 4}^{\pi / 2}\left(\cos ^2 \theta-\sin ^2 \theta\right) \frac{\cos ^2 \theta}{\sin ^4 \theta} d \theta\)
= \(8 a^2 \int_{\pi / 4}^{\pi / 2}\left(\cot ^4 \theta-\cot ^2 \theta\right) d \theta=8 a^2\left[-\frac{\cot ^3 \theta}{3}+2 \cot \theta+2 \theta\right]_{/ 4}^{\pi / 2}\)
= \(8 a^2\left[\pi+\frac{1}{3}-2-\frac{\pi}{2}\right]=\frac{4 a^2}{3}[3 \pi-10]\)
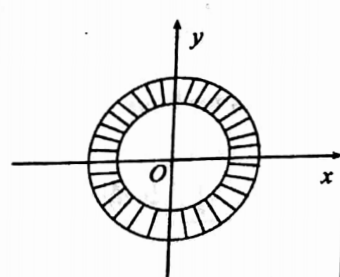
44. By changing into polar coordinates evaluate \(\iint \frac{x^2 y^2}{x^2+y^2} d x d y\) over the angular region between the circles.
Solution:
Put x=r cos θ,y= r sin θ.
Then dx dy=r dr dθ and x+y=r.
For the circle x+y=a ⇒ r=a
⇒ r=a and x+y=b ⇒ r=b ⇒ r=b.
∴ \(\iint \frac{x^2 y^2}{x^2+y^2}\) dx dy \(=\int_{\theta=0}^{2 \pi} \int_{r=a}^b \frac{r^2 \cos ^2 \theta r^2 \sin ^2 \theta}{r^2} r d r d \theta\)
= \(\int_{\theta=0}^{2 \pi} \int_{r=a}^b \sin ^2 \theta \cos ^2 \theta \cdot r^3 d r d \theta\)
= \(\int_{\theta=0}^{2 \pi}\left[\frac{r^4}{4}\right]_a^b \sin ^2 \theta \cos ^2 \theta d \theta\)
= \(\frac{b^4-a^4}{4} \int_0^{2 \pi} \sin ^2 \theta \cos ^2 \theta d \theta\)
= \(\frac{b^4-a^4}{4} \cdot 2 \int_0^\pi \sin ^2 \theta \cos ^2 \theta d \theta\)
= \(\frac{b^4-a^4}{2} \times 2 \int_0^{\pi / 2} \sin ^2 \theta \cos ^2 \theta d \theta\)
= \(\left(b^4-a^4\right) \cdot \frac{1}{4} \times \frac{1}{2} \times \frac{\pi}{2}=\frac{\left(b^4-a^4\right) \pi}{16}\)
45. By changing the variables evaluate \(\iint_R(x+y)^2 d x d y\) where R is the region bounded by the parallelogram x+y=0,x+y=1,2x-y=0,2x-y=4.
Solution: Put x+y =u,2x-y=v.Then the given parallelogram reduces to a rectangle.
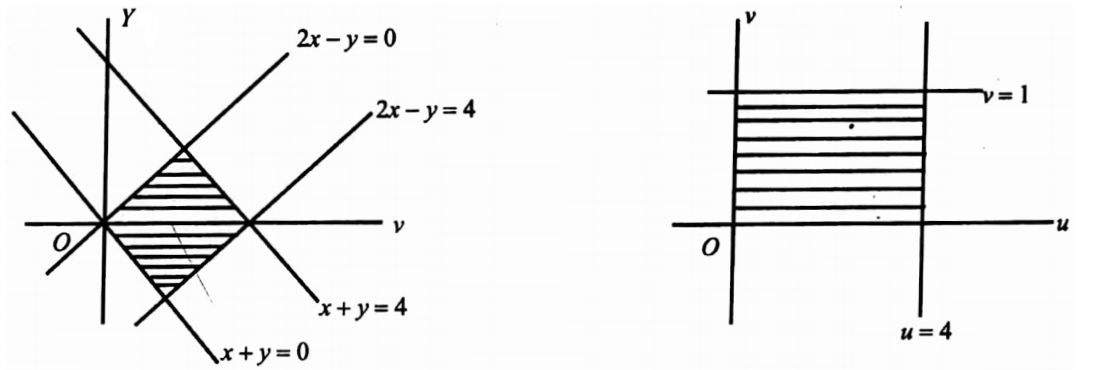
⇒ \(\frac{\partial(u, v)}{\partial(x, y)}\)
= \(\left|\begin{array}{ll}
\frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} \\
\frac{\partial v}{\partial x} & \frac{\partial v}{\partial y}
\end{array}\right|\)
= \(\left|\begin{array}{rr}
1 & 1 \\
2 & -1
\end{array}\right|\)=-3 .
∴ Jacobian J = \(\frac{\partial(x, y)}{\partial(u, v)}=-\frac{1}{3}\) .
u.varies from 0 to 1 and v varies from 0 to 4.
∴ \(\iint_R(x+y)^2 d x d y=\int_{u=0}^1 \int_{v=0}^4 u^2\left(\frac{1}{3}\right) d u d v\)
= \(\frac{1}{3} \int_{v=0}^4 \frac{u^3}{3} d v=\frac{1}{9} \int_0^4 d v=\frac{4}{9} \text {. }\)
46. Change the order of integration in the double integral \(\int_0^{2 a} \int_{\sqrt{2 a x-x^2}}^{\sqrt{(2 a x)}} f(x, y) d x d y\).
Solution: The given domain of integration is described by a line that starts from x=0 and moving parallel to itself, goes over to x=2a; the extremities of the moving line on the parts of the parabola y= 2ax and the circle xy=2ax in the first quadrant.
We now regard the same region as described by a line moving parallel to the x-axis instead of the y-axis. In this way, the domain of integration is subdivided into three sub-regions to each of which corresponds a double integral. Thus we have
⇒ \(\int_0^{2 a} \frac{\sqrt{2 a x}}{\sqrt{2 a x-x^2}} f d x d y\)
= \(\int_0^a \int_{y^2 / 2 a}^{a-\sqrt{\left(a^2-y^2\right)}} f d y d x\)
+\(\int_0^{2 a} \int_{a+\sqrt{a^2-y^2}}^{2 a} f d y d x+\int_a^{2 a} \int_{y^2 / 2 a}^{2 a} f d y d x\)
47. Change the order of integration in \(\int_0^{\rho \cos a} \int_{\tan a}^{\sqrt{\left(a^2-x^2\right)}} f(x, y) d x d y\) and verify result when f(x,y)=1.
Solution: The limits of integration are given by y = x tan α (a straight line), y= \(\sqrt{\left(a^2-x^2\right)}\), i.e., x2+y2= a2 (a circle); x = 0 (y-axis) and x = a cos α (a straight line). Clearly, the area of integration is OMNO.
The strips parallel to x- x-axis change their character at point M. Draw a straight line AM parallel to the x-axis and this divides the area OMNO into two portions OMA and AMN.
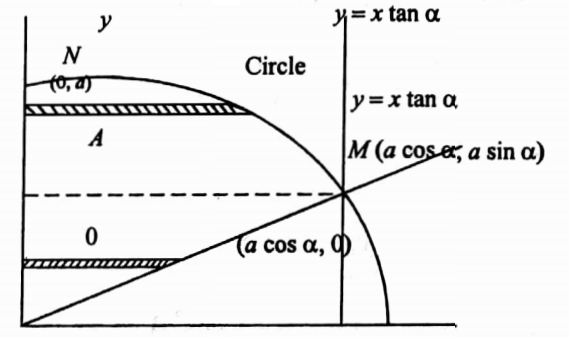
For the area OMA, the limits of x are from 0 to y cot α, and the limits of y are from 0 to y sin α. For the area AMN, the limits of x are from 0 to \(\sqrt{\left(a^2-y^2\right)}\), and the limits for are from a sin α to a.
Hence changing the order of integration, we have \(\int_0^{\cos \alpha} \int_{x \tan \alpha}^{\sqrt{\left(a^2-x^2\right)}} f(x, y) d x d y\)
= \(\int_0^{\sin \alpha} \int_0^{y \cot \alpha} f(x, y) \cdot d x d y+\int_{a \sin \alpha}^\rho \int_0^{\sqrt{\left(a^2-y^2\right)}} f(x, y) d x d y\)
To verify result when f(x, y)=1,
L.H.S. =\(\int_0^{\cos \alpha} \int_{x \tan \alpha}^{\sqrt{\left(a^2-x^2\right)}} d x d y=\int_0^{\cos \alpha}\left\{\sqrt{\left(a^2-x^2\right)}-x \tan \alpha\right\} d x\)
= \(\frac{a}{2} \cos \alpha \cdot a \sin \alpha+\frac{a^2}{2} \text{Sin}^{-1}(\cos \alpha)-\frac{a^2 \cos ^2 \alpha}{2} \tan \alpha\)
= \(\frac{1}{2} a^2 \text{Sin}^{-1}\left\{\sin \left(\frac{\pi}{2}-\alpha\right)\right\}=\frac{1}{2} a^2\left(\frac{\pi}{2}-\alpha\right)\)
R.H.S. = \(\int_0^{\sin \alpha} \int_0^{\cot \alpha} d y d x+\int_{a \sin \alpha}^{\infty} \int_0^{\left.\sqrt{\left(a^2-y^2\right.}\right)} d y d x\)
= \(\int_0^{\sin \alpha} y \cot \alpha d y+\int_{a \sin \alpha}^0 \sqrt{\left(a^2-y^2\right)} d x\)
= \(\frac{1}{2} a^2 \sin \alpha \cot \alpha+\frac{a^2}{2} \cdot \frac{\pi}{2}-\left\{\frac{a}{2} \sin \alpha \cdot a \cos \alpha+\frac{a^2}{2} \cdot \alpha\right\}\)
= \(\frac{a^2}{2}\left(\frac{\pi}{2}-\alpha\right)\)
48. Change the order of integration in the double integral \(\int_0^{\infty} \int_x^{\infty} \frac{e^{-y}}{y} d x d y\) and hence find the value.
Solution: The limits of integration are given by the straight line y = x, y = ∞ x=0, and x= ∞ i.e., the region of integration is bounded by x = 0,y = x, and an ‘infinite boundary. Hence taking the strips parallel to the x-axis, the limits for y are from 0 to ∞.
Hence changing the order of integration, we have \(\int_0^{\infty} \int_x^{\infty} \frac{e^{-y}}{y} d x d y\)
= \(\int_0^{\infty} \int_0^y \frac{e^{-y}}{y} d y d x\) \(=\int_0^{\infty} \frac{e^{-y}}{y}[x]_0^y d y\)
= \(\int_0^{\infty} e^{-y} d y\)=1
49. Change the order of integration in double integral \(\int_0^p \int_0^x \frac{\phi^{\prime}(y) d x d y}{\sqrt{(a-x)(x-y)}}\) and hence find its value.
Solution: The region of integration is ONM. The limit for x are from y to a and limits for y are from 0 to a.
Hence \(\int_0^e \int_0^x \frac{\phi^{\prime}(y) d x d y}{\sqrt{(a-x)(x-y)}}\) \(=\int_0^a \int_y^g \frac{\phi^{\prime}(y) d y d x}{\sqrt{(a-x)(x-y)}}\)
To find the value, let x=a sin2θ +y cos2θ
Also (a-x)=(a-y) cos2θ, x-y=(a-y) sin2θ.
For the limits of θ, when x=y, we have y=a sin2θ+y cos2θ =(y-a) sin2 θ=0
⇒θ=0 and when x=a,we have a=a sin 2θ+y cos2 θ
⇒ (a-y) cos2 θ =0 ⇒ θ =π/2
Thus the limits of θ bare from 0 to π/2
∴ Given integral = \(\int_0^2 \int_y^{\infty} \frac{\phi^{\prime}(y) d y d x}{\sqrt{(a-x)(x-y)}}\)
= \(\int_0^\pi \int_0^{\pi / 2} \frac{\phi^{\prime}(y) \cdot 2(a-y)(\sin \theta \cos \theta) d y d \theta}{(a-y)(\sin \theta \cos \theta)}\)
= \(2 \int_0^e \int_0^{\pi / 2} \phi^{\prime}(y) d y d \theta=2 \int_0^{\infty} \phi^{\prime}(y) \cdot \frac{\pi}{2} d y\)
= \(\pi[\phi(y)]_0^a=\pi[\phi(a)-\phi(0)]\)
50. Change the order of integration in \(\int_0^{2 a} \int_0^{\sqrt{2a x-x}} \frac{\phi^{\prime}(y)\left(x^2+y^2\right) x d x d y}{\sqrt{4 a^2 x^2-\left(x^2+y^2\right)}}\) and hence evaluate it.
Solution: Clearly, the area of integration is OMNO.
Solving x2-2ax+y2=0 for x, we get x=a ± \(\sqrt{\left(a^2-y^2\right)}\)
hence limits of x are from a-\(\sqrt{\left(a^2-y^2\right)}\) to a+ \(\sqrt{\left(a^2-y^2\right)}\)
The limits of y are from 0 t0 a.
Hence, given integral becomes \(\int_0^e \int_{a-\sqrt{\left(a^2-y^2\right)}}^{a+\sqrt{\left(a^2-y\right)}} \frac{\phi^{\prime}(y)\left(x^2+y^2\right) x d y d x}{\sqrt{4 a^2 x^2-\left(x^2+y^2\right)^2}}\)
To evaluate the integral, put \(x^2+y^2=t\).
2 x d x=d t.
Then = \(\int_0^2 \int_{a-\sqrt{2}+\sqrt{\left(a^2-y^2\right)}}^{\left.a^2-y^2\right)} \frac{\phi^{\prime}(y)\left(x^2+y^2\right) x d y d x}{\sqrt{4 a^2 x^2-\left(x^2+y^2\right)^2}} \)
= \(\frac{1}{2} \int_0^1 \int_{t_1}^{t^2} \frac{\phi^{\prime}(y) t d y d x}{\sqrt{4 a^2\left(t-y^2\right)-t^2}}\)
= \(-\frac{1}{4} \int_0^2 \int_{t_1}^2 \frac{\phi^{\prime}(y)\left(4 a^2-2 t\right) d y d t}{\sqrt{\left(4 a^2 t-t^2-4 a^2 y^2\right)}}+\int_0^2 \int_{t_1}^2 \frac{\phi^{\prime}(y) \cdot a^2 d y d t}{\sqrt{4 a^2\left(a^2-y^2\right)-\left(2 a^2+t^2\right)}}\)
= \(-\frac{1}{2} \int_0^\rho \phi^{\prime}(y)\left[\sqrt{4 a^2 t-t^2-4 a^2 y^2}+a^2 \text{Sin}^{-1}\left\{\frac{-2 a^2+t}{\sqrt{4 a^2\left(a^2-y^2\right)}}\right\}\right]_{t_1}^{t_2} d y\)
51. Show how the change in the order of integration leads to the evaluation of \(\int_0^{\infty} \frac{\sin r x}{x} d x \text { from } \int_0^{\infty} \int_0^{\infty} e^{-x y} \sin r x d x d y\)
Solution:
Let \(I=\int_0^{\infty} \int_0^{\infty} e^{-x y} \sin r x d x d y\)
= \(\int_0^{\infty} \sin r\left[\frac{e^{-x y}}{-x}\right] d x=\int_0^{\infty} \frac{\sin r x}{x} d x=x\)…..(1)
Again, \(I=\int_0^{\infty} \int_0^{\infty} e^{-x y} \sin r x d x d y=\int_0^{\infty}\left[\int_0^{\infty} e^{-x y} \sin r x d x\right] d y\)
= \(\int_0^{\infty} \frac{r d y}{\left(r^2+y^2\right)}=\left[\text{Tan}^{-1}\frac{y}{r}\right]_0^{\infty}=\pi / 2\)……(2)
Hence from (1) and (2) we have \(\int_0^{\infty} \frac{\sin r x}{x} d x=\pi / 2\).
52. Change the order of integration in \(\int_0^a \int_0^{\sqrt{a^2-y^2}}\left(x^2+y^2\right) d y d x\).
Solution: The limits on the inner integrals are functions of y and these are x limits. These limits are obtained by considering horizontal strips. This region of integration is surrounded by x=0, x=\(\sqrt{a^2-y^2}\), y=0, y=a, and this region is shown as a shaded area in the figure.
Now we have to consider vertical strips for changing the order of integration. Imagine a vertical strip with one end on the axis (y=0) and the other end on the curve x2+y2=a2 (y=\(\sqrt{a^2-y^2}\)). To cover the region, this strip has to be moved from x=0 to x=a.
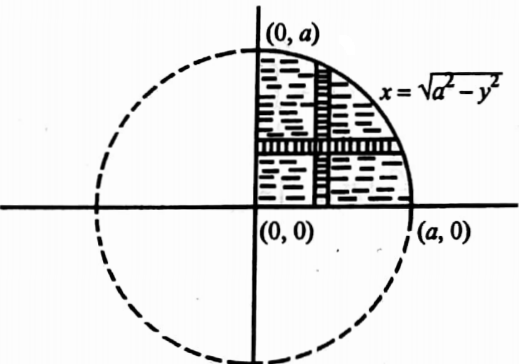
Hence the new equivalent double integral is \(\int_0^a \int_0^{\sqrt{a^2-x^2}}\left(x^2+y^2\right) d y d x\)
= \(\int_0^a\left[x^2 y+\frac{y^3}{3}\right]_0^{\sqrt{a^2-x^2}} d x\)
= \(\int_0^a x^2 \sqrt{a^2-x^2} d x+\int_0^a \frac{\left(a^2-x^2\right)^{3 / 2}}{3} d x\)
⇒ \(\int_0^a x^2 \sqrt{a^2-x^2} d x=\int_0^{\pi / 2} a^2 \sin ^2 \theta \cdot a \cos \theta \cdot a \cos \theta d \theta\)(where x=\(a \sin \theta\))
= \(a^4 \int_0^{\pi / 2} \sin ^2 \theta \cos ^2 \theta d \theta=a^4 \cdot \frac{1}{4} \cdot \frac{1}{2} \frac{\pi}{2}=\frac{\pi a^4}{16}\)
⇒ \(\int_0^a \frac{\left(a^2-x^2\right)^{3 / 2}}{3} d x\)
= \(\int_0^{\pi / 2} \frac{a^3 \cos ^3 \theta a \cos \theta}{3} d \theta=\frac{a^{4^{\pi / 2}}}{3} \int_0 \cos ^4 \theta d \theta\)
= \(\frac{a^4}{3} \cdot \frac{3}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2}=\frac{\pi a^4}{16}\)
Hence \(\int_0^a \int_0^{\sqrt{a^2-x^2}}\left(x^2+y^2\right) d y d x=\frac{\pi a^4}{16}+\frac{\pi a^4}{16}=\frac{\pi a^4}{8}\).
53. Change the order of integration and evaluate \(\int_0^4 a \int_{x^2 / 4 a}^{2 \sqrt{a x}} d x d y\).
Solution: The limits on the inner integral are functions of x= and these are y limits.
These limits are obtained by considering vertical strips. The region is bounded by y\(=\frac{x^2}{4 a}\),y=\(\sqrt{a x}\),x=0,x=4a and the
To change the order of integration we consider a horizontal strip with one end on the y2=4ax i..e. x=\(=\frac{y^2}{4 a}\) and the other end on x2=4ay i.e, x=2\(\sqrt{a y}\)
This strip has to be slid be from y=0 to y= 4a to cover the region.
Hence the double integral with new limits is \(\int_0^{4 a} \int_{y^2 / 4 a}^{2 \sqrt{a y}} d y d x=\int_0^{4 a}\left[\int_{y^2 / 4 a}^{2 \sqrt{a y}} d x\right] d y\)
= \(\int_0^{4 a}[x]_{y^2 / 4 a}^{2 \sqrt{a y}} d y=\int_0^{4 a} 2 \sqrt{a y}-\frac{y^2}{4 a} d y\)
= \(2 \sqrt{a} \cdot\left[\frac{y^{3 / 2}}{3 / 2}\right]_0^{4 a}-\frac{1}{4 a}\left[\frac{y^3}{3}\right]_0^{4 a}\)
= \(\frac{4 \sqrt{a}}{3}\left[2^3 a^{3 / 2}\right]-\frac{1}{4 a}\left[\frac{64 a^3}{3}\right]\)
= \(\frac{32 a^2}{3}-\frac{16 a^2}{3}=\frac{16 a^2}{3}\).
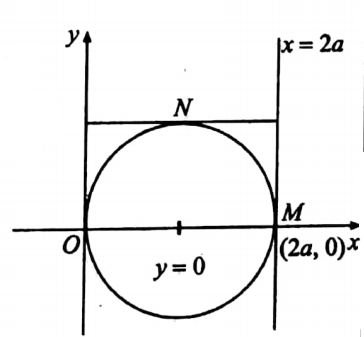
54. Change the order of integration and evaluate \(\int_0^a \int_2^{2 a-x} x y d y d x\).
Solution: The limits on the inner integral are functions of x and these are limits of y. These are obtained by considering vertical strips. The region is bounded by
y\(=\frac{x^2}{ a}\) , y=2a-x, x=0, x=a and this is
To change the order of integration we consider horizontal strips. Since two different curves surround the region let us divide the region into two regions R1, and R2, and in each region, we consider a horizontal strip.
Integral over \(R_1=\int_0^a \int_0^{\sqrt{a y}} x y d x d y\).
Integral over \(R_2=\int_a^{2 a} \int_0^{2 a-y} x y d x d y\)
Thus given the integral of changing the order of integration, it becomes \(\int_0^a \int_0^{\sqrt{a y}} x y d x d y+\int_a^{2 a} \int_0^{2 a-y} x y d x d y\)
= \(\int_0^a\left[\frac{x^2 y}{2}\right]_0^{\sqrt{a y}} d y+\int_a^{2 a}\left[\frac{x^2 y}{2}\right]_0^{2 a-y} d y\)
= \(\int_0^a \frac{a y^2}{2} d y+\int_a^{2 a} \frac{y(2 a-y)^2}{2} d y\)
= \(\frac{a}{2} \int_0^a y^2 d y+\int_a^{2 a} \frac{y\left(4 a^2+y^2-4 a y\right)}{2} d y\)
= \(\frac{a}{2}\left[\frac{y^3}{3}\right]_0^a+\frac{1}{2}\left[\frac{4 a^2 y^2}{2}+\frac{y^4}{4}-\frac{4 a y^3}{3}\right]_a^{2 a}\)
= \(\frac{a^4}{6}+\frac{1}{2}\left[\frac{4 a^2 4 a^2}{2}+\frac{4 a^2 \cdot 4 a^2}{4}-\frac{32 a^4}{3}-\frac{4 a^4}{2}-\frac{a^4}{4}+\frac{4 a^4}{3}\right]\)
= \(\frac{a^4}{6}+\frac{5 a^4}{24}=\frac{9 a^4}{24}=\frac{3}{8} a^4\).
55. Change the order of integration and evaluate \(\int_0^{2 a} \int_0^{\sqrt{a^2-(x-a)^2}} d x d y\)
Solution: The region of integrals is surrounded by
y=0,y=\(\sqrt{a^2-(x-a)^2}\) , x= 0 and x=2a.
y=\(\sqrt{a^2-(x-a)^2}\) ⇒y2=a2-(x-a)2
⇒ (x-a)2+ y2=a2.
This represents a circle with center (a,0) and radius a.
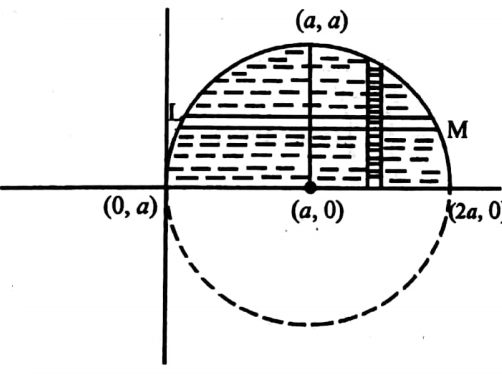
The region is in the given integral the limits are obtained by considering the vertical strip.
Now imagine a horizontal strip where both ends slide on two parts of the circle in the first quadrant.
(x-a)2+y2=a2 ⇒ (x-a)2= a2-y2 ⇒ x-a =± \(\sqrt{a^2-y^2}\) ⇒ x=a±\(\sqrt{a^2-y^2}\)
Thus the end L of the horizontal strip moves on a-\(\sqrt{a^2-y^2}\) whereas the end M of the horizontal strip moves on a + \(\sqrt{a^2-y^2}\).
To cover the region this strip slides from y = 0 to y = a.
Thus the given double integral with the change of order of integration becomes
⇒ \(\int_0^a \int_{a-\sqrt{a^2-y^2}}^{a+\sqrt{a^2-y^2}} d x d y=\int_0^a[x] \frac{a-\sqrt{a^2-y^2-y^2}}{[x} d y\)
= \(\int_0^a a+\sqrt{a^2-y^2}-a+\sqrt{a^2-y^2} d y\)
= \(2 \int_0^a \sqrt{a^2-y^2} d y=2 \cdot\left[\frac{y \sqrt{a^2-y^2}}{2}+\frac{a^2}{2} \text{Sin}^{-1} \frac{y}{a}\right]_0^a\)
= \( 2\left[\frac{a^2}{2} \cdot \frac{\pi}{2}\right]=\frac{\pi a^2}{2}\) .
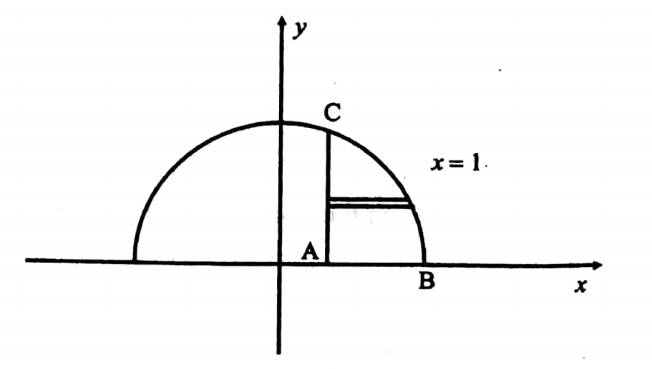
56. Evaluate the following integral by changing the order \(\int_0^3 \int_1^{\sqrt{4-y}}(x+y) d x d y\).
Solution: I=\(\int_0^3 \int_1^{\sqrt{4-y}}(x+y) d x d y\)
The integration first w.r.t. ‘x’ then w.r.t. ‘x’ The integration w.r.t. ‘x’ corresponds to along one edge of the horizontal strip and the integration w.r.t. ‘y’ corresponds to sliding the strip from y = 0 to y = 3. Horizontal strip ends lie on x = 1, x =\(\sqrt{4-y}\) i.e., y = 4- x2. The region of integration is ABC.
Change of order of integration: On change of order of integration, we integrate first w.r.t. y from y=0 to y=4-x2 then w.r.t x from x=1 to x=2
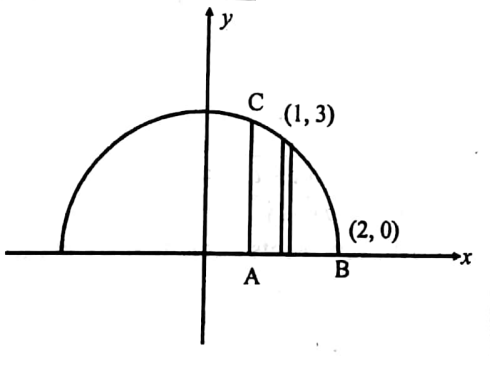
I = \(\int_1^2 \int_0^{4-x^2}(x+y) d y d x=\int_1^2\left[x y+\frac{y^2}{2}\right]_0^{4-x^2} d x\)
= \(\int_1^1\left[x\left(4-\dot{x}^2\right)+\frac{\left(4-x^2\right)^2}{2}\right] d x\)
= \(\int_1^2\left(4 x-x^3+\frac{x^4+16-8 x^2}{2}\right) d x\)
= \(\left[2 x^2-\frac{x^4}{4}+\frac{x^5}{10}+8 x-\frac{4 x^3}{3}\right]_1^2\)
= \(\left(8-4+\frac{16}{5}+16-\frac{32}{3}\right)-\left(\frac{1}{10}+2-\frac{1}{4}+8-\frac{4}{3}\right)=\frac{241}{60}\)
57. By changing the order of integration, evaluate \(\int_0^a \int_y^a \frac{x}{x^2+y^2} d x d y\)
Solution: The limits on the inner integral are functions of y and these are limits of x. These are obtained by considering horizontal strips. The region is a triangle bounded by y = 0, x = a, and y=x.
To change the order of integration, we consider the vertical strip.
So the limits of integration are y = 0 to y=x and x = 0 to x = a. On changing the order of integration, given integral becomes
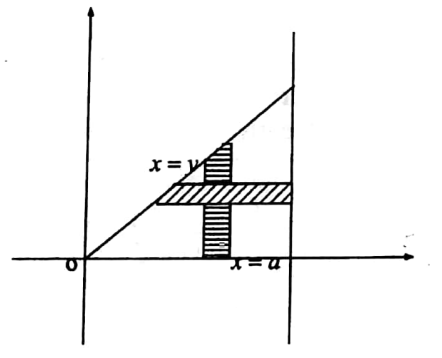
⇒ \(\int_0^a \int_0^a \frac{x}{x^2+y^2} d y d x\)
= \(\int_0^a\left[\frac{1}{x} \text{Tan}^{-1} \frac{y}{x}\right]_0^x \cdot x d x\)
= \(\int_0^a \frac{1}{2} \text{Tan}^{-1}(1) \cdot x d x=\int_0^a \frac{\pi}{4} d x=\frac{\pi a}{4}\) .
58. Change the order of integration and evaluate the double integral \(\int_0^1 \int_1^{e^x} d y d x\).
Solution: The limits on the inner integral are functions of x and these are limits of y. These are obtained by considering the vertical strip. The region of integration is bounded by y=1, x=1 y =ex To change the order of integration we consider the horizontal strip. So the limits of integration are x = 1 to x = log y and y = 1 to y = e.
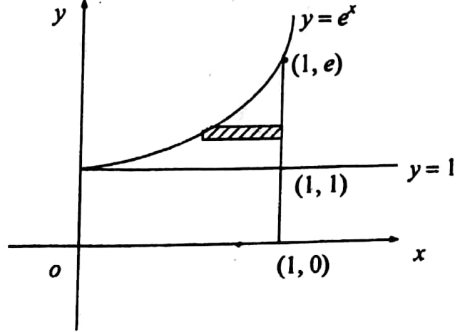
By changing the order of integration the given integral becomes \(\int_1^e \int_{\log y}^1 d x d y=\int_1^e[x]_{\log y}^1 d y=\int_1^e[1-\log y] d y=[y-y \log y+y]_1^e=e-2\).