Probability and Statistics for Engineering and the Sciences 8th Edition Chapter 2 Probability
Page 80 Problem 1 Answer
Given: The population of a particular country consists of three ethnic groups. Each individual belongs to one of the four major blood groups.
Given probability table is:
| Blood Group | O | A | B | AB | |
| Ethnic Group | 1 | 0.082 | 0.106 | 0.008 | 0.004 |
| 2 | 0.135 | 0.141 | 0.018 | 0.006 | |
| 3 | 0.215 | 0.2 | 0.065 | 0.02 |
Given events:A={ type A selected },B={ type B selected }, and C={ ethnic group 3 selected }
To calculate P(A),P(C), and P(A∩C)
We will make use of the given table in order to find the probabilities.
The probability of selecting type A is the sum of column A of joint probability table.
P(A)=0.106+0.141+0.2
=0.447
The probability of selecting group 3 is the sum of row 3 of the given joint probability table.
The probability of A∩C is row 3 and column A
P(A∩C)=0.2
We obtain:
P(A)=0.447
P(C)=0.5
P(A∩C)=0.2
Page 80 Problem 2 Answer
Given: The population of a particular country consists of three ethnic groups. Each individual belongs to one of the four major blood groups.
Given: Joint probability table:
| Blood Group | O | A | B | AB | |
| Ethinc Group | 1 | 0.082 | 0.106 | 0.008 | 0.004 |
| 2 | 0.135 | 0.141 | 0.018 | 0.006 | |
| 3 | 0.215 | 0.2 | 0.065 | 0.02 |
Given events:
A={ type A selected }
B ={ type B selected }
and C={ ethnic group 3 selected }
To calculate: P(A∣C) and P(C∣A)
To explain in context what each of these probabilities represents.
We will calculate the required conditional probabilities by using the formula: P(A∣B)=P(A∩B)
P(B) where P(B)>0.
From previous part P(A∩C)=0.2
By using the definition of conditional probability
P(A∣C)=P(A∩C)/P(C)
=0.2/0.5
=0.4
This represents that if we know that an individual comes from ethnic group 3, the probability that the individual has blood type A is 0.4.
and P(C∣A)= P(C∩A)/P(A)
0.2/0.447
= 0.447
This represents that if we know that an individual has blood type A the probability that the individual comes from ethnic group 3 is 0.447.
We obtain:
P(A∣C)=0.4
P(C∣A)=0.447
P(A∣C) represents that if we know that an individual comes from ethnic group 3 , the probability that the individual has blood type A is 0.4.
P(C∣A) represents that if we know that an individual has blood type A the probability that the individual comes from ethnic group3 is 0.447.
Page 80 Problem 3 Answer
Given: The population of a particular country consists of three ethnic groups. Each individual belongs to one of the four major blood groups.
We are given the table:
| Blood Group | O | A | B | AB | |
| Ethnic Group | 1 | 82 | 0.106 | 0.008 | 0.004 |
| 2 | 0.135 | 0.141 | 0.018 | 0.006 | |
| 3 | 0.215 | 0.2 | 0.065 | 0.02 |
Given events:
A={ type A selected }
B={ type B selected } and C={ ethnic group 3 selected }
To find the probability a given individual is from ethnic group 1 if he or she does not have type B blood.
We will first find the probability of not have a B blood then use conditional probability.
We need to find P(D∣B′).
P(D∩B′)=0.082+0.106+0.004
=0.192
We know P(B′)=1−P(B)
=1−(0.008+0.018+0.065)
=0.909
By using the definition of conditional probability, we get
P(D∣B′)=P(D∩B′)
P(B′)= 0.192/0.909
=0.211
The probability that the given individual is from ethnic group 1 given that he or she does not have type B blood is 0.211.
Page 80 Problem 4 Answer
Given: An individual is randomly selected from the population of all adult males living in the United States Given the following events:
A={ Individual person is 6 feet tall }
B={ Individual person is a professional basketball player}
To check among P(A∣B) and P(B∣A), which is larger.We will check using the conditional probability formula: P(A∣B)=P(A∩B)
P(B),P(B)>0
We are not given the exact data of how many people are taller than 6 feet.
By logic, we can say that number of people who are taller than 6 feet are more than the number of professional basketball players.
So, N(A)>N(B)
N(A)>N(B)
We know P(A)= Number of favourable outcomes of A/ Number of outcomes in sample space
=N(A)/N>N(B)/N
=P(B)
Therefore,⇒P(A)>P(B)
⇒1
P(A)<1/P(B)
Obviously, P(A∩B)>0
So, P(A∩B)
P(A)<P(A∩B)
P(B) which is equivalent to P(B∣A)<P(A∣B)
For events
A={ Individual person is 6 feet tall }
B={ Individual person is a professional basketball player}
we obtain P(B∣A)<P(A∣B) because N(A)>N(B)
Page 80 Problem 5 Answer
Given: A certain system can experience three different types of defects. Given: that Ai={ event of the type i ;=1,2,3}
Given probabilities:
P(A1)=0.12
P(A2)=0.07
P(A3)=0.05
P(A1∪A2)=0.13
P(A1∪A3)=0.14
P(A2∪A3)=0.1
P(A1∩A2∩A3)=0.01
To find the probability that the system has type 2 defect, given that it has type 1 defect.
We will use the Conditional probability formula P(A∣B)=P(A∩B)
P(B),P(B)>0
We need to find P(A2∣A1).
By using conditional probability and data given in the question, we get
P(A2∩A1) =0.06
=P(A1)+P(A2)−P(A1∪A2)
= 0.12+0.07−0.13
= P(A2∣A1)=P(A2∩A1)/P(A1)
=0.06/0.12
=0.5
The probability that the system have a defect of type 2 given that the system has type 1 defect is 0.5
Page 80 Problem 6 Answer
Given: A certain system can experience three different types of defects.
Given: that Ai ={ event of the type i ;=1,2,3}
Given probabilities:
P(A1)=0.12
P(A2)=0.07
P(A3)=0.05
P(A1∪A2)=0.13
P(A1∪A3)=0.14
P(A2∪A3)=0.1
P(A1∩A2∩A3)=0.01
To find the probability the system has all three types of defects given that it has type 1
defect. We will use the conditional prob
We need to find P(A1∩A2∩A3∣A3).
Using the definition of conditional probability and the data given in the question, we get
P(A1∩A2∩A3∣A1)=P[(A1∩A2∩A3)∩A3]/P(A1)
=P(A1∩A2∩A3)/P(A1)
=0.01/0.12
=0.0833
The probability that system has all three types of defects given that it has the type 1 defect is 0.0833.
Page 80 Problem 7 Answer
Given: A certain system can experience three different types of defects.
Given: that Ai ={ event of the type i ;=1,2,3}
Given probabilities:
P(A1)=0.12
P(A2)=0.07
P(A3)=0.05
P(A1∪A2)=0.13
P(A1∪A3)=0.14
P(A2∪A3)=0.1
P(A1∩A2∩A3)=0.01
To find the probability that the system has exactly one type of defect given that it has at least one type of defect.
We will use the Venn diagrams to obtain the probabilities of the individual events and then use the conditional probability.
We will obtain the following probabilities in order to solve further.
P(A1∩A2)=P(A1)+P(A2)−P(A1∪A2)
=0.12+0.07−0.13
=0.06
P(A1∩A3)=P(A1)+P(A3)−P(A1∪A3)
=0.12+0.05−0.14
=0
P(A2∩A3)=P(A2)+P(A3)−P(A2∪A3)
=0.07+0.05−0.1
=0.02
We observe that A∩B=B as B⊂A.
We also see that B is the union of A1∩A2′∩A3′,A1′∩A2∩A3′,A1′∩A2′∩A3.
We will now find the value of probabilities of these individual events and unite then in order to get.P(B).
For,A1∩A2′∩A3′
we will first draw the Venn diagram as follows.
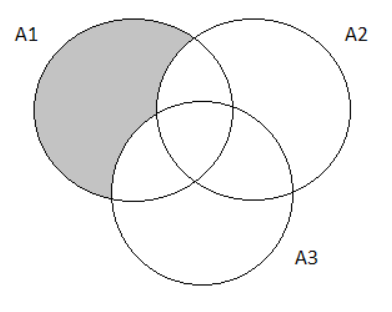
Using the data given in the question, we get
P(A1∩A2′∩A3′)=
=0.04
P(A1)−P(A1∩A2)−P(A1∩A3)+P(A1∩A2∩A3)
= 0.12−0.06−0.03+0.01
For, we will first draw the Venn diagram as follows.
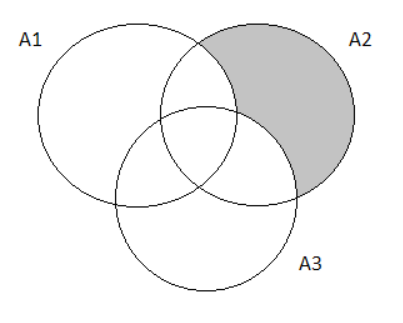
Using the data given in the question, we get
P(A1′∩A2∩A3′)
=0.07−0.06−0.02+0.01
=0
=P(A2)−P(A1∩A2)−P(A2∩A3)+P(A1∩A2∩A3)
For, we will first draw the Venn diagram as follows.
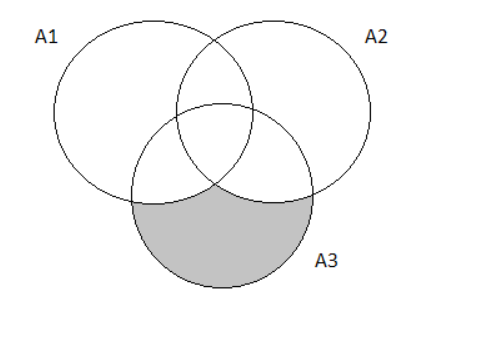
Using the data given in the question, we get
P(A1′∩A2′∩A3)=P(A3)−P(A1∩A3)−P(A2∩A3)+P(A1∩A2∩A3)
=0.05−0.03−0.02+0.01
=0.01
We will combine all these to get P(B)
P(B)=0.04+0+0.01
=0.05
Using the definition of conditional probability, we get
P(B∣A)=P(B∩A)/P(A)
=P(B)/P(A)
=0.05/0.14
=0.3571
Given that the system has at least one type of defect, the probability that it has exactly one type of defect is 0.3571.
Page 80 Problem 8 Answer
Given: A certain system can experience three different types of defects. Given: that Ai={ event of the type i ;=1,2,3}
Given probabilities:
P(A1)=0.12P(A2)=0.07P(A3)=0.05
P(A1∪A2)=0.13
P(A1∪A3)=0.14
P(A2∪A3)=0.1
P(A1∩A2∩A3)=0.01
To find the probability that the system does not have third type of defect given that it has both of the first two ty
We need to find P(A3′∣A1∩A2). we will first construct its Venn diagram to get the desired formula.
By using the definition of conditional probability, we get
P(A3′∣A1∩A2)=P(A1∩A2∩A3′)
P(A1∩A2)=P(A1∩A2)−P(A1∩A2∩A3)
P(A1∩A2)=0.06−0.01/0.06
=0.833
The probability that it does not have the third type of defect given that it has both of the first two types of defects is 0.833.
Page 81 Problem 9 Answer
Given: Deer ticks can be carriers of either Lyme disease or human granulocytic ehrlichiosis (HGE).
Based on a recent study, suppose that 16% of all ticks in a certain location carry Lyme disease, 10% carry HGE, and 10% of the ticks that carry at least one of these diseases in fact carry both of them.
Given: A randomly selected tick is found to have carried HGE.
To find the probability that the selected tick is also a carrier of Lyme disease.
We will find this using the conditional probability formula: P(A∣B)=P(A∩B)/P(B)
We define,
A={ Carrier of Lyme disease }
B={ Carrier of HGE disease }
So, we have
P(A)=0.16
P(B)=0.1
P(A∩B∣A∪B)=0.1
We will calculate the probability of A given that B has already occurred.
We haveP(A∩B∣A∪B)
=P[(A∩B)∩(A∪B)]/P(A∪B)
=P(A∩B)
P(A∪B) ( as intersection is the subset of union ).
Given, P(A∩B∣A∪B)=0.1.
Putting this in above equation, we get
P(A∩B)/P(A∪B)
=0.1
Applying the formula of union of two sets, we get
P(A∩B)=0.1⋅P(A∪B)
P(A∩B)=0.1⋅[P(A)+P(B)−P(A∩B)]
=0.1⋅[0.16+0.1−P(A∩B)]
=0.016+0.01−0.1⋅P(A∩B)
=0.026−0.1⋅P(A∩B)
Hence, 1.1⋅P(A∩B)=0.026
P(A∩B)=0.026/1.1
=0.02364
Putting this value in the formula for conditional property,
P(A∣B)
=0.02364/0.1
=P(A∩B)/P(B)
=0.2364
The probability that is also a carrier of Lymph disease given that it is a carrier of HGE is 0.2364.
Page 81 Problem 10 Answer
Given any events A and B.
To show that: P(A∣B)+P(A′∣B)=1
We will use the conditional probability formula: P(A∣B)=P(A∩B)/P(B),P(B)>0
We have P(B∣A)=P(A∩B)/P(A).
Also, we know that A′represents the complement of A.
Hence, we obtain
P(A∣B)=P(A∩B)
P(B)⋯(1)
P(B∣A)=P(A′∩B)/P(B)
Also,A′∩B is that part of B where no element of A is present.
So, P(A′∩B)=P(B)−P(A∩B)
On combining the results,
We get P(A∣B)+P(A′∣B)=P(A∩B)
P(B)+P(A′∩B)
P(B)=P(A∩B)
P(B)+P(B)−P(A∩B)
P(B)=P(A∩B)+P(B)−P(A∩B)/P(B)
=P(B)/P(B)
=1
Hence, P(A∣B)+P
(A′∣B)=P(B)/P(B)=1
We proved that P(A∣B)+P(A′∣B)=1
Page 81 Problem 11 Answer
Given: Any three events A,B,C with P(C)>0.
To show that: P(A∪B∣C)=P(A∣C)+P(B∣C)−P(A∩B∣C).
We will use the conditional probability and P(A∪B)=P(A)+P(B)−P(A∩B).
We will find the value of P(A∪B∣C).
P(A∪B∣C)=P[(A∪B)∩C]/P(C)
[Now using the property (A∪B)∩C=(A∩C)∪(B∩C)
P(A∪B∣C)=P[(A∪B)∩C]/P(C)
=P[(A∩C)∪(B∩C)]/P(C)
=P(A∣C)+P(B∣C)+P(A∩B∣C)
=P(A∩C)+P(B∩C)−P(A∩B∩C)/P(C)
= P(A∩C)/P(C)+P(B∩C)
P(C)−P(A∩B)∩C/P(C)
Hence,P(A∪B∣C)=P(A∣C)+P(B∣C)+P(A∩B∣C)
We have shown that P(A∪B∣C)=P(A∣C)+P(B∣C)+P(A∩B∣C)
Page 81 Problem 12 Answer
Given: Seventy percent of the light aircraft that disappear while in flight in a certain country are subsequently discovered.
Of the aircraft that are discovered, 60% have an emergency locator, whereas 90% of the aircraft not discovered do not have such a locator.
Given : a light aircraft has disappeared.
To find that the aircraft will not be discovered if it has an emergency locator.We will use conditional probability P(A∣B)=P(B∣A)P(A)
P(B),P(B)>0
The given data is, D=0.7,L∣D=0.6 and NL∣ND=0.9
Finding the probability of the airplane being not discovered, and has an emergency locator,
P(ND∣L)=P(L∣ND)P(ND)/P(L)
P(ND)=1−P(D)
P(ND)=1−0.7
P(ND)=0.3
The probability assembly rule can be used,
P(L)=P(L∣D)P(D)+P(L∣ND)P(ND)
P(L∣ND)=1−P(NL∣ND)
P(L∣ND)=1−0.90
P(L∣ND)=0.10
Substitute the values in the equation,
P(L)=(0.6)(0.7)+(0.1)(0.3)
P(L)=0.45
Find the value of P(ND) by subtracting the value of P(D) from 1,
P(ND)=1−P(D)
P(ND)=1−0.45
P(ND)=0.55
Substitute the values in the conditional probability formula,
P(ND∣L)=(0.1)(0.3)/(0.45)
P(ND∣L)=0.067
The probability that the aircraft will not be discovered, but has an emergency locator is 0.067.
Page 81 Problem 13 Answer
Given: Seventy percent of the light aircraft that disappear while in flight in a certain country are subsequently discovered.
Of the aircraft that are discovered, 60% have an emergency locator, whereas 90% of the aircraft not discovered do not have such a locator.
Given : a light aircraft has disappeared.To find the probability that the plane will be discovered given that it does not have an emergency locator.
We will use the conditional probability
P(A|B)=P(B|A)P(A)/P(B),P(B)>0
The formula can be rewritten too suit the situation,
P(D∣NL)=P(NL∣D)P(D)/P(NL)
Find the rest of the unknown values,
P(NL∣D)=1−P(L∣D)
P(NL∣D)=1−0.6
P(NL∣D)=0.4
Now substitute all the calculated values in the equation,
P(D∣NL)=P(NL∣D)P(D)/P(NL)
P(D∣NL)=(0.4)⋅(0.7)/0.55
P(D∣NL)=0.509
The probability that it will be discovered and did not have an emergency locator is 0.509
Page 82 Problem 14 Answer
Given: A company that manufactures video cameras produces a basic model and a deluxe model.
Over the past year, 40% of the cameras sold have been of the basic model.
Of those buying the basic model, 30% purchase an extended warranty, whereas 50% of all deluxe purchasers do so.
A randomly selected purchaser has an extended warranty.
To find the probability that he or she has a basic model.
We will use law of total probability.
Let B be the event that the basic model has been produced.
Let D be the event that the deluxe model has be produces.
Let EW be the evet that the extended warranty is chosen by the customer.
Then we can see:
P(B)/E(D)=0.4,
P(EW∣B)=0.6,
P(EW∣D)=0.3,=0.5.
The required probability is of the event B∣EW
We get: P(B∣EW)=P(B∩EW)/P(Ew)
Using the property P(A∩B)=P(A∣B)⋅P(B)
we get: P(B∣EW)=P(B∣EW)
Now using law of total probability we get:
P(B∣EW)=P(EW∣B)P(B)
P(EW∣B)P(B)+P(EW∣D)P(D)
=0.3⋅0.4/0.3⋅0.4+0.5⋅0.6
=0.29.
The probability that the purchaser has a basic model given that he or she has an extended warranty is 0.29.
Page 82 Problem 15 Answer
Given: For customers purchasing a refrigerator at a certain appliance store, let A be the event that the refrigerator was manufactured in the U.S.,
B be the event that the refrigerator had an ice maker, and C be the event that the customer purchased an extended warranty.
Given probabilities are :
P(A)=.75
P(B∣A)=.9
P(B∣A′)=.8
P(C∣A∩B)=.8
P(C∣A∩B′)=.6
P(C∣A′∩B)=.7
P(C∣A′∩B′)=.3
To construct a tree diagram consisting of first-, second-, and third-generation branches, and place an event label and appropriate probability next to each branch.
We will first find the required probabilities to draw the diagram and then draw it.
In tree diagram,
In the initial branch there will be first layer of events , and in the diagram the adequate probabilities are given.
In the second branch there will be second layer of events with the given adequate conditional probabilities.
And in the third branch there will be third layer of events with the given adequate conditional probabilities.
The first layer probabilities :
P(A)=0.75
P(A′)=1−P(A)
P(A′)=0.25
The second layer probabilities :
P(B∣A)=0.9
P(B′∣A)=1−P(B∣A)
P(B′∣A)=0.1
P(B∣A′)=0.8
P(B′∣A′)=1−P(B∣A′)
P(B′∣A′)=0.2
The third layer probabilities : All the events in this will be the probability of intersection of adequate three three events that leads to that point.
P(C∣A∩B)=0.8
P(C′∣A∩B)=0.2
P(C∣A∩B′)=0.6
P(C′∣A∩B′)=0.4
P(C∣A′∩B)=0.7
P(C′∣A′∩B)=0.3
P(C∣A′∩B′)=0.3
P(C′∣A′∩B′)=0.7
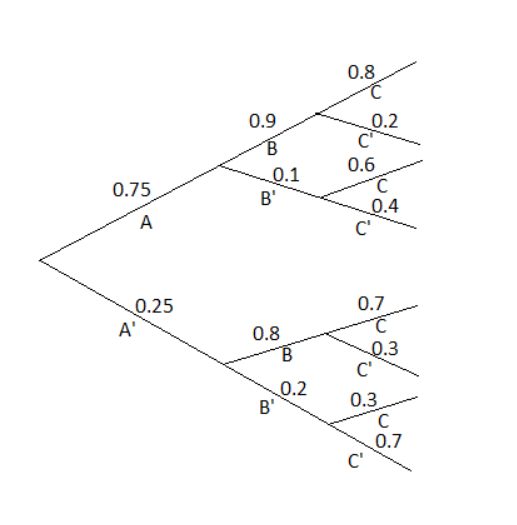
The tree diagram is :
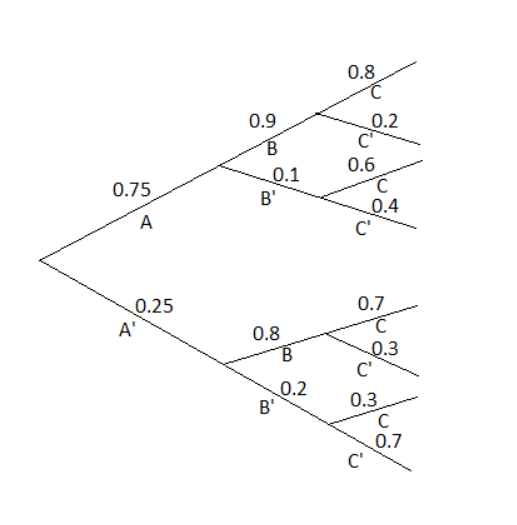
The tree diagram is :
Page 82 Problem 16 Answer
Given: For customers purchasing a refrigerator at a certain appliance store, let A be the event that the refrigerator was manufactured in the U.S.,B be the event that the refrigerator had an ice maker, and C be the event that the customer purchased an extended warranty.
Given probabilities are :
P(A)=.75
P(B∣A)=.9
P(B∣A′)=.8
P(C∣A∩B)=.8
P(C∣A∩B′)=.6
P(C∣A′∩B)=.7
P(C∣A′∩B′)=.3
To compute : P(A∩B∩C)
We will use the multiplication rule P(A∩B)=P(A∣B)⋅P(B)
If there are three events then we will use multiplication rule twice.
Now, using multiplication rule :
P(A∩B∩C)=P(C∣A∩B)⋅P(A∩B)
=P(C∣A∩B)⋅P(B∣A)⋅P(A)∣
=0.75⋅0.9⋅0.8
=0.54
Hence, P(A∩B∩C)=0.54
We obtain: P(A∩B∩C)=0.54
Page 82 Problem 17 Answer
Given: For customers purchasing a refrigerator at a certain appliance store, let A be the event that the refrigerator was manufactured in the U.S.,B be the event that the refrigerator had an ice maker, and C be the event that the customer purchased an extended warranty.
Given probabilities are :
P(A)=.75
P(B∣A)=.9
P(B∣A′)=.8
P(C∣A∩B)=.8
P(C∣A∩B′)=.6
P(C∣A′∩B)=.7
P(C∣A′∩B′)=.3
To compute: P(B∩C)
We will use the multiplication rule and the property P(B∩C)=P(B∩C∩A)+P(B∩C∩A′)
for three events.
Using property :
P(B∩C)=P(B∩C∩A)+P(B∩C∩A′)
Now, we will use the multiplication rule twice we get :
=0.54+0.25⋅0.8⋅0.7
=0.68
Hence, P(B∩C)=0.68
We obtain: P(B∩C)=0.68
Page 82 Problem 18 Answer
Given: For customers purchasing a refrigerator at a certain appliance store, let A be the event that the refrigerator was manufactured in the U.S., B be the event that the refrigerator had an ice maker, and C be the event that the customer purchased an extended warranty.
Given probabilities are :
P(A)=.75
P(B∣A)=.9
P(B∣A′)=.8
P(C∣A∩B)=.8
P(C∣A∩B′)=.6
P(C∣A′∩B)=.7
P(C∣A′∩B′)=.3
To compute P(C).
We will use the property P(C)=P(A∩B∩C)+P(A′∩B∩C)+P(A∩B′∩C)+P(A′∩B′∩C)
Using property ,
P(C)=P(A∩B∩C)+P(A′
∩B∩C)+P(A∩B′∩C)+P(A′∩B′∩C)
=0.75⋅0.9⋅0.8+0.75⋅0.1⋅0.6+0.25⋅0.8⋅0.7+0.25⋅0.2⋅0.3
=0.54+0.045+0.14+0.015
=0.74
Hence, P(C)=0.74
We obtain: P(C)=0.74
Page 82 Problem 19 Answer
Given: For customers purchasing a refrigerator at a certain appliance store, let A be the event that the refrigerator was manufactured in the U.S., B be the event that the refrigerator had an ice maker, and C be the event that the customer purchased an extended warranty.
Given probabilities are :
P(A)=.75
P(B∣A)=.9
P(B∣A′)=.8
P(C∣A∩B)=.8
P(C∣A∩B′)=.6
P(C∣A′∩B)=.7
P(C∣A′∩B′)=.3
To compute P(A∣B∩C), the probability of U.S purchase given that an icemaker and an extended warranty are also purchased.
We will use the conditional property given by: P(A∣B)=P(A∩B)
P(B) where P(B)>0.
Using conditional property,
P(A∣B∩C)=P(A∩B∩C)/P(B∩C)
=0.54/0.68
=0.7941
Hence, P(A∣B∩C)=0.7941.
The probability of a U.S purchase given that an icemaker and an extended warranty are also purchased is: P(A∣B∩C)=0.7941.
Page 82 Problem 20 Answer
Given : The Reviews editor for a certain scientific journal decides whether the review for any particular book should be short (1−2pages), medium (3−4 pages), or long (5−6pages).
Data on recent reviews indicates that 60% of them are short, 30% are medium, and the other 10% are long.
Reviews are submitted in either Word or LaTeX.
For short reviews, 80% are in Word, whereas 50%of medium reviews are in Word and 30% of long reviews are in Word.
Given: a recent review is randomly selected.To find the probability that the selected review was submitted in Word format.
We will draw a tree diagram and then with the help of that use that law total of total probability.
In tree diagram,
In the initial branch there will be first layer of events , and in the diagram the adequate probabilities are given.
In the second branch there will be second layer of events with the given adequate conditional probabilities.
Then, using the multiplication rule to the right of the second generation branches then we will display the product of the particular probabilities that leads to the point which is the probability of intersections.
The first layer of events are given below :
A1={ short book }
A2={ medium book }
A3={ long book }
Their adequate properties are :
P(A1)=0.6
P(A2)=0.3
P(A3)=0.1
The second layer of events are given below :
W={ submited in word }
L={ submited in LaTeX }
Now, the adequate conditional probabilities are :
P(W∣A1)=0.8
P(L∣A1)=1−P(W∣A1)∣
P(L∣A1)=0.2
P(W∣A2)=0.5
P(L∣A2)=1−P(W∣A2)
P(L∣A2)=0.5
P(W∣A3)=0.3
P(L∣A3)=1−P(W∣A3)
P(L∣A3)=0.7
Now, we will calculate the every of the four intersections using the multiplication rule :
P(A1∩W)=P(A1)⋅P(W∣A1)
=0.6⋅0.8
=0.48
P(A1∩L)=P(A1)⋅P(L∣A1)
=0.6⋅0.2
=0.12
Similarly, P(A2∩W)=0.15P(A2∩L)=0.15
P(A3∩W)=0.03
P(A3∩L)=0.07
Now, the tree diagram is :
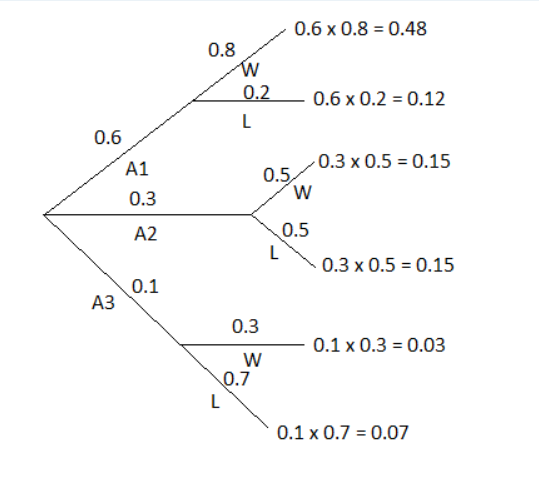
Now, using the law of total probability :
P(W)=P(W∣A1)P(A1)+P(W∣A2)P(A2)+P(W∣A3)P(A3)
=0.48+0.15+0.03
=0.66
Hence, P(W)=0.66
The probability that the selected review was submitted in Word format is
P(W)=0.66
Page 82 Problem 21 Answer
Given : The Reviews editor for a certain scientific journal decides whether the review for any particular book should be short ( 1−2pages), medium (3−4pages), or long ( 5−6pages).
Data on recent reviews indicates that60% of them are short, 30%are medium, and the other 10% are long.
Reviews are submitted in either Word or LaTeX.
For short reviews, 80% are in Word, whereas 50%
of medium reviews are in Word and 30% of long reviews are in Word.
Given: a recent review is randomly selected.To find the probabilities for the review to be short , medium and long given that it was submitted in Word format.
We will draw the tree diagram and then use Bayes’ theorem in order to get the answer.
In tree diagram,
In the initial branch there will be first layer of events , and in the diagram the adequate probabilities are given.
In the second branch there will be second layer of events with the given adequate conditional probabilities.
Then, using the multiplication rule to the right of the second generation branches then we will display the product of the particular probabilities that leads to the point which is the probability of intersections.
The first layer of events are given below :
A1={ short book }
A2={ medium book
A3={ long book }
Their adequate properties are :
P(A1)=0.6
P(A2)=0.3
P(A3)=0.1
The second layer of events are given below :
W={ submited in word }
L={ submited in LaTeX }
Now, the adequate conditional probabilities are :
P(W∣A1)=0.8
P(L∣A1)=1−P(W∣A1)
P(L∣A1)=0.2
P(W∣A2)=0.5
P(L∣A2)=1−P(W∣A2)
P(L∣A2)=0.5
P(W∣A3)=0.3
P(L∣A3)=1−P(W∣A3)
P(L∣A3)=0.7
Now, we will calculate the every of the four intersections using the multiplication rule :
P(A1∩W)=P(A1)⋅P(W∣A1)
=0.6⋅0.8
=0.48
P(A1∩L)=P(A1)⋅P(L∣A1)
=0.6⋅0.2
=0.12
Similarly, P(A2∩W)=0.15
P(A2∩L)=0.15
P(A3∩W)=0.03
P(A3∩L)=0.07
Now, the tree diagram is :
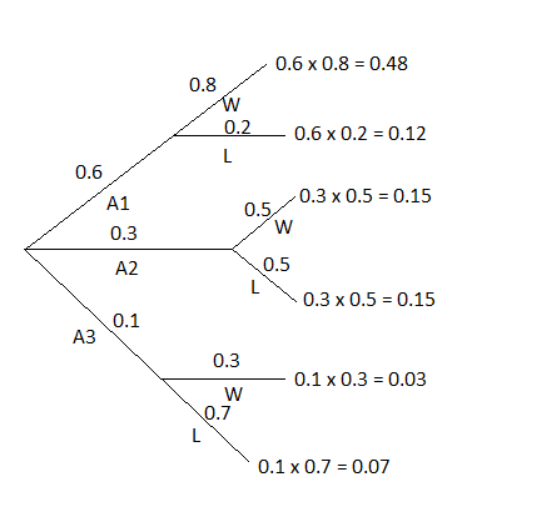
Now using Bayes’ theorem,
The posterior probabilities are :
P(A1∣W)=P(A1∩W)/P(W)
=0.48/0.66
=0.727
P(A2∣W)=P(A2∩W)/P(W)
=0.15/0.66
=0.227
P(A3∣W)=P(A3∩W)/P(W)
=0.03/0.66
=0.046
The posterior probability for the review to be short given that it is submitted in Word is:0.727
The posterior probability for the review to be medium given that it is submitted in Word is:0.227
The posterior probability for the review to be long given that it is submitted in Word is:0.046