Ring Theory And Vector Calculus
Definition of Homomorphism – Homomorphic Image – Elementary Properties of Homomorphism -Kernel of a Homomorphism – Fundamental theorem of Homomorphism – Maximal Ideals – Prime Ideals.
2 Homomorphism of Rings, Maximal and Prime Ideals
3 Homomorphism of Rings, Maximal and Prime Ideals
In groups, we have learned that one way of knowing more information about a group is to examine its interaction with other groups by using homomorphism.
The concept of homomorphism in rings is analogous to that of homomorphism in groups. The homomorphism in rings is a mapping that preserves the relations a + b = c and ab = d, the addition and multiplication operations.
Definition. (Homomorphism). Let R, R0 be two rings. A mapping f: R → R0 is – said to be a homomorphism if (a)f(a + b) = f(a) + f(b) and (b)f(ab) = f(a)f(b) for all a, b ∈ R.
Note 1. The operations +, · on the left-hand side of the properties (a), (b) are that of the ring R, while the operations +, · on the right-hand side of the properties (a), (b) are that of the ring R0.
Note 2. Since R, R0 are commutative groups under addition clearly property (a) shows that a ring homomorphism is a group homomorphism from (R, +) to (R0, +).
Definition. If f: R → R0 is a homomorphism of a ring R into R0 then the image set f(R) = R¯ = {f(x) | x ∈ R} is called the f – homomorphic image of R.
Definition. Let R, R0 be two rings. A homomorphism f: R → R0 is called an epimorphism or onto homomorphism if f is onto mapping.
A homomorphism f: R → R0 is called a monomorphism if f is one-one mapping
A homomorphism f: R → R0 is called an isomorphism if f is both one-one and onto mapping.
A homomorphism f: R → R of a ring R into itself is called an endomorphism.
A homomorphism f: R → R which is both one-one and onto is called an automorphism.
Notation. 1. If f: R → R0 is an onto homomorphism or epimorphism then R 0 is the homomorphic image of R and we write R ‘ R0.
If f: R → R0 is an isomorphism then we say that R is isomorphic to R 0 or R, R 0 are isomorphic and we write R ∼= R0.
Note:
1. If f: R → R0 is an onto homomorphism then f(R) = R0.
2. If U is an ideal of the ring R, then R/U = {x + U | x ∈ R} is also a ring w.r.t. addition and multiplication of cosets. Then the mapping f: R → R/U defined by f(x) = x + U for all x ∈ R is called the natural homomorphism from R onto R/U.
3. A homomorphism is used to simplify a ring while retaining certain of its features. An isomorphism is used to show that two rings are algebraically identical.
Example 1. Let R, R0 be two rings, and f: R → R0 be defined by f(x) = 00∀x ∈ R, where 00 ∈ R0 is the zero element.
Let a, b ∈ R. Then f(a) = 00, f(b) = 00 and hence f(a + b) = 00, f(ab) = 00.
Then a + b, ab ∈ R.
f(a + b) = 00 = 00 + 00 = f(a) + f(b) and f(ab) = 00 = 00.00 = f(a) · f(b).
∴ f is a homomorphism from R into R0. This is called Zero homomorphism.
Example 2. Let R be a ring and f: R → R be defined by f(x) = x∀x ∈ R.
Let a, b ∈ R so that a + b, ab ∈ R.
By definition, f(a + b) = a + b = f(a) + f(b) and f(ab) = ab = f(a)f(b).
Also for each y ∈ R (codomain), there exists y ∈ R (domain) so that f(y) = y
⇒ f is onto mapping.
Further for a, b ∈ R, f(a) = f(b) ⇒ a = b ⇒ f is one-one mapping.
Hence f is an automorphism. This is called Identity homomorphism.
Example 3. Let Z be the ring of integers and f: Z → 2Z be defined by f(n) = 2n∀n ∈ Z.
Let m, n ∈ Z. Then m+n, mn ∈ Z. Then f(m+n) = 2(m+n) = 2m+2n = f(m) + f(n). But f(mn) = 2(mn) 6= (2m)(2n) = f(m)f(n).
∴ f is not a ring homomorphism.
Although, the group (Z, +) is isomorphic to the group (2Z, +), the ring
(Z, +, ·) is not isomorphic to the ring (2Z, +, ·).
Theorem 1. Let f: R → R 0 be a homomorphism of a ring R into the ring R 0 and 0 ∈ R, 00 ∈ R0 be the zero elements. Then (1) f(0) = 0 f(−a) = −f(a)∀a ∈ R and (3) f(a − b) = f(a) − f(b) for all a,b ∈ R.
Proof. (1) For 0 ∈ R we have 0 + 0 = 0.
∴ f(0 + 0) = f(0) ⇒ f(0) + f(0) = f(0) + 00 ( ∵ f is homomorphism )
∴ f(0) = 00 ( by left cancellation law in R0 ) (2) For a ∈ R there exists −a ∈ R so that a + (−a) = 0.
∴ f(a + (−a)) = f(0) ⇒ f(a) + f(−a) = f(0) = 00. ( ∵ f is homomorphism)
∴ f(−a) = −f(a).
( ∵ f(a),f(−a) ∈ R0 , ring )
(3) For a,b ∈ R; f(a − b) = f(a + (−b)) = f(a) + f(−b) = f(a) − f(b) (f(−b) = −f(b)By(2))
Note 1. A homomorphism maps the zero element of R into the zero element of R0.
2. A homomorphism maps the negative ’ −a ’ of each element a ∈ R into the negative in R0 of the corresponding element a’.
Remark. If the rings R, R’ have unity elements 1, and 10 respectively then it does not necessarily follow that f(1) = 10 is true.
However, if R0 is an integral domain then f(1) = 10 is true.
Theorem 2. The homomorphic image of a ring is a ring.
Proof. Let R, R’ be two rings and f: R → R0 be a homomorphism.
By definition, homomorphic image of R = R¯ = f(R) = {f(x) ∈ R0 | x ∈ R}.
To prove that f(R) is a ring, we show that f(R) = R¯ is a subring of R0.
For 0 ∈ R, f(0) = 00 ∈ R0.
∴ f(0) = 00 ∈ R¯ and hence R¯ ⊂ R0.
Let a0, b0 ∈ R¯.
∴ There exists a,b ∈ R so that f(a) = a’,f(b) = b’.
Since a, b ∈ R we have a − b, ab ∈ R and hence f(a − b), f(ab) ∈ R¯.
Now a’ − b’ = f(a) − f(b) = f(a − b) ∈ R¯ (Theorem (1))
a0b0 = f(a)f(b) = f(ab) ∈ R.¯ (Homomorphism property (2))
Thus a’,b; ∈ R¯ ⇒ a’ − b’,a’b’ ∈ R¯.
∴ R¯ is a subring of R0 and hence R¯ is a ring.
Corollary. The homomorphic image of a commutative ring is a commutative ring.
Proof. Let R be a commutative ring and R¯ = f(R) be its holomorphic image.
a0,b0 ∈ R¯ ⇒ a0b0 = f(a)f(b) where a,b ∈ R
= f(ab) = f(ba) = f(b)f(a) = b0a0.
( ∵ R is commutative )
∴ f(R) = R¯ is commutative.
Theorem 3. If f: R → R0 be an isomorphism from the ring R to the ring R0 then
- f(0) = 00 where 0, 00 are the zero elements of R, R’.
- For each a ∈ R, f(−a) = −f(a).
- R0 is a commutative ring if R is a commutative ring,
- R0 is an integral domain if R is an integral domain. and
- R0 is a field if R is a field.
Proof. For (1), (2), and (3) see the proof of Theorem (1) of Art 3.1 and its corollary.
(4) Since f(0) = 0′ and f is one-one we have that 0 ∈ R is the only element whose image is 0′ ∈ R’.
∴ Let a’, b’ ∈ R’ and a’ ≠ 0′, b’ ≠0′.
Then there exists a, b ∈ R and a≠0, b 6= 0 so that f(a) = a’, f(b) = b0.
a, b ∈ R, a ≠ 0, b ≠ 0 and R has no zero divisors ⇒ ab ≠ 0.
⇒ f(ab) ≠ f(0) ( ∵ f is one-one )
⇒ f(a)f(b) ≠ 00 ⇒ a0b0 6= 00.
∴ R0 is without zero divisors.
Let 1 ∈ R be the unity element.
Then f(1) ∈ R0 and say f(1) = 10.
For a0 ∈ R0 there exists unique a ∈ R so that f(a) = a0.
For each a0 ∈ R0, a010 = f(a)f(1) = f(a1) = f(a) = a0.
∴ a010 = 10a0 = a0 ⇒ f(1) = 10 is the unity element of R0.
Hence R0 is an integral domain.
(5) If R is a field then
- R is commutative,
- R has a unity element and
- Every non-zero element of R has a multiplicative inverse.
By (3) and (5) R0 is commutative and has unity element 10 = f(1) for 1 ∈ R.
Let a’ ∈ R’ and a’ ≠ 0′. There exists a ∈ R so that f(a) = a0.
a = 0 ⇒ f(a) = f(0) ⇒ a0 = 00 and hence a ≠ 0.
Since R is a field, there exists a− 1 ∈ R so that aa− 1 = 1 = a− 1a.
∴ f a’− 1 = f(1) ⇒ f(a)f a− 1 = 10 = f a− 1 f(a).
Hence f a− 1 = f(a)− 1 is the multiplicative inverse of f(a) = a0.
∴ R’ is a field.
Theorem 4. Let R, R0 be two rings and f: R → R0 be a homomorphism. For every ideal U’ in the ring R’, f− 1 (U’) is an ideal in R.
Proof. Let U = f− 1 (U’) = {x ∈ R | f(x) ∈ U0}.
f(0) = 0′ ∈ U’ ⇒ 0 ∈ f− 1(U’) = U.
∴ U ≠ φ and U ⊂ R.
Let a, b ∈ U. By the def. of U = f− 1 (U’); f(a), f(b) ∈ U’.
U’ is an ideal, f(a), f(b) ∈ U0 ⇒ f(a) − f(b) ∈ U’
⇒ f(a − b) ∈ U’ ⇒ a − b ∈ f− 1 (U’) = U
∴ a, b ∈ U ⇒ a − b ∈ U
Let a ∈ U, r ∈ R. Then f(a) ∈ U’ and f(r) ∈ R’.
Since U0 is an ideal in R’; f(a)f(r), f(r)f(a) ∈ U’
⇒ f(ar), f(ra) ∈ U ⇒ ar, ra ∈ U, ∴ a ∈ U, r ∈ R ⇒ ar, ra ∈ U
Hence U = f− 1 (U) is an ideal in R.
Note. If S0 is a subring of R0 then f− 1 (S’) is a subring of R.
Theorem. 5. Let R, R0 be two rings and f: R → R’ be a homomorphism. For every ideal U in R,f(U) is an ideal in R¯ = f(R)
Proof. f(U) = {f(x) | x ∈ U}.
0 ∈ U ⇒ f(0) = 0′ ∈ f(U) ⇒ f(U) 6= φ and f(U) ⊂ f(R).
Let a’,b’ ∈ f(U). ’There exist a,b ∈ U such that f(a) = a0,f(b) = b0.
∴ a’ − b’ = f(a) − f(b) = f(a − b) ∈ f(U) ( ∵ a,b ∈ U and U is an ideal )
Let a’ ∈ f(U) and r’ ∈ f(R) = R¯.
There exist a ∈ U,r ∈ R such that f(a) = a’,f(r) = r’
a ∈ U,r ∈ R and U is an ideal ⇒ ar,ra ∈ U ⇒ f(ar),f(ra) ∈ f(U)
⇒ f(a) · f(r),f(r) · f(a) ∈ f(U) ( ∵ f is homomorphism )
⇒ a’r’,r ‘a’ ∈ f(U)
From (1) and (2): f(U) is an ideal in f(R) = R¯.
Note 1. If f: R → R’ is onto homomorphism then for every ideal U in R,f(U) is an ideal in R’.
2. The above theorem is true for a subring.
Ring Theory And Vector Calculus Kernel Of A Homomorphism
Definition. (Kernel). Let R, R’ be two rings and f: R → R’ be a homomorphism. The set {x ∈ R | f(x) = 0′} where 00 ∈ R’ is the zero element, is defined as the Kernel of the homomorphism f. The kernel of the homomorphism f: R → R’ is denoted by Ker for I(f).
Note 1. If f: R → R’ is a homomorphism then Ker f = f− 1 {00} ⊂ R.
2. For 0 ∈ R we have f(0) = 0′. Therefore 0 ∈ Ker f and hence Ker f 6= φ.
Example 1. Consider the Zero homomorphism f: R → R0 defined by f(x) = 0’∀x ∈ R.
Ker f = {x ∈ R | f(x) = 0′} = {x ∈ R | ∀x ∈ R} = R.
Example 2. Consider the identity homomorphism f: R → R defined by f(x) = x∀x ∈ R.
Ker f = {x ∈ R | f(x) = 0} = {x ∈ R | x = 0 only }( ∵ f(0) = 0) = {0}.
Theorem 1. If f is a homomorphism of a ring R into a ring R’ then Ker f is an ideal of R.
Proof. If 0 ∈ R is the zero element of R then f(0) = 0′ the zero element of R’.
∴ 0 ∈ Ker f and hence Ker f 6= φ, Ker f ⊂ R.
Let a,b ∈ Ker f and r ∈ R. Then f(a) = 0’f(b) = 0′.
f(a − b) = f(a) − f(b) = 0′ − 0′ = 0′ ⇒ a − b ∈ Ker f
f(ar) = f(a)f(r) = 0’f(r) = 0′ and f(ra) = f(r)f(a) = f(r)00 = 00 ⇒ ar,ra ∈ Ker f.
∴ a,b ∈ Ker f,r ∈ R ⇒ a − b ∈ Ker f and ar,ra ∈ Ker f.
Hence Ker f is an ideal of R.
Theorem 2. If f is a homomorphism of a ring R into the ring R 0 then f is an isomorphism if and only if Ker f = {0}.
Proof. Let f be an into isomorphism. That is, f is one-one homomorphism.
We prove that Ker f = {0}.
a ∈ R, f(a) = 0′ ⇒ f(a) = f(0) ⇒ a = 0 ( ∵ f is one-one )
∴ 0 ∈ R is the only element in R so that f(0) = 0′.
∴ By definition, Ker f = {0}.
Conversely, let Ker f = {0}. We now prove that f is one-one.
a, b ∈ R and f(a) = f(b) ⇒ f(a) − .f(b) = 0′ ⇒ f(a − b) = 00
⇒ a − b ∈ Ker f = {0} ⇒ a − b = 0 ⇒ a = b. ∴ f is one-one.
Note. Ker f = {0} ⇔ f is one-one.
Theorem 3. If U is an ideal of a ring R then the quotient ring R/U is a homomorphic image of R. or Every quotient ring of a ring is a homomorphic image of the ring.
Proof.
We know that R/U = {x + U | x ∈ R} is a ring with respect to the addition and multiplication of cosets defined as (a + U) + (b + U) = (a + b) + U and (a + U) : (b + U) = ab + U where a + U, b + U ∈ R/U.
Let f: R → R/U be a mapping defined by f(a) = a + U for all a ∈ R.
For a, b ∈ R, a = b ⇒ a + U = b + U ⇒ f(a) = f(b).
∴ the mapping f is well-defined.
For a, b ∈ R; f(a + b) = (a + b) + U = (a + U) + (b + U) = f(a) + f(b)
and f(ab) = ab + U = (a + U) · (b + U) = f(a) · f(b)
∴ f is a homomorphism.
Let x + U ∈ R/U. Then x ∈ R and for this x ∈ R we have f(x) = x + U.
∴ for each x + U ∈ R/U there exists x ∈ R so that f(x) = x + U.
∴ f is onto mapping.
Hence f: R → R/U is an onto homomorphism.
Note. Ker f = {x ∈ R | f(x) = 0 + U} = {x ∈ R | x + U = 0 + U} = {x ∈ R | x ∈ U} = U.
In view of this result, the above theorem can also be stated as follows: “Every ideal in a ring R is the Kernel of some homomorphism defined on R”.
f: R → R/U is called Canonical homomorphism.
Example Z6 = {0, 1, 2, 3, 4, 5} under addition and multiplication modulo −6 is a ring.
U = {0, 3} is an ideal of Z6 and Z6/U = {0 + U, 1 + U, 2 + U} = set of 3 elements.
Take Z3 = {0, 1, 2}.
By the correspondence f(0) = 0 + U, f(1) = 1 + U and f(2) = 2 + U; Z 3 and Z6/U are isomorphic.
4 Theorem 4. (Fundamental theorem of homomorphism)
Let R, R’ be two rings and f: R → R ‘ be homomorphism with Kernel U. Then R is isomorphic to R/U.
Proof. a ∈ Ker f = U ⇒ f(a) = 00 where 00 is the zero element of R’.
Since U is an ideal of R, R/U = {x + U | x ∈ R} is the quotient ring of cosets under the addition and multiplication of cosets.
Since f: R → R’ is a homomorphism, f(R) = R¯ is a ring.
That is, for each f(x) ∈ R¯ we have x ∈ R.
Define φ = R/U → R¯ by φ(x + U) = f(x)∀x + U ∈ R/U a + U,b + U ∈ R/U and a + U = b + U ⇔ a − b ∈ U
⇔ f(a − b) = 00 ⇔ f(a) − f(b) = 00 = f(0) ⇔ f(a) = f(b) ⇔ φ(a + U) = φ(b + U).
∴ φ is well-defined and one-one mapping.
Let y ∈ R¯.
Since f: R → R¯ is onto, there exists x ∈ R so that f(x) = y. For this x ∈ R
we have x + U ∈ R/U.
∴ for each y ∈ R¯ there exists x + U ∈ R/U so that φ(x + U) = f(x) = y.
∴ φ is onto mapping.
Let a + U,b + U ∈ R/U. Then a,b ∈ R
φ[(a + U) + (b + U)] = φ[(a + b) + U] = f˙(a + b) (Definition of φ )
= f(a) + f(b) = φ(a + U) + φ(b + U) ( ∵ f is homomorphism )
φ[(a + U)(b + U)] = φ[a.b + U] = f(ab)
= f(a)f(b) = φ(a + U)φ(b + U) ( ∵ f is homomorphism )
∴ φ is a homomorphism.
Hence φ is an isomorphism from R/U to R¯ = f(R).
Note. 1. Every homomorphic image of a ring R is isomorphic to some quotient ring thereof.
2. If f: R → R0 is onto homomorphism from a ring R to the ring R’ and U is an ideal of R then R/U is isomorphic to R0. Then f(R) = R¯ = R0. In the above proof replace R¯ by R0.
3. R¯ = f(R) = the homomorphic image of R.
Let Ψ: R → R/U be the Canonical homomorphism. By fundamental theorem φ: R/U → R¯ is isomorphism.
For x ∈ R we have Ψ(x) = x + U ∈ R/U.
For this x + U ∈ R/U we have φ(x + U) = f(x) ∈ f(R) = R¯
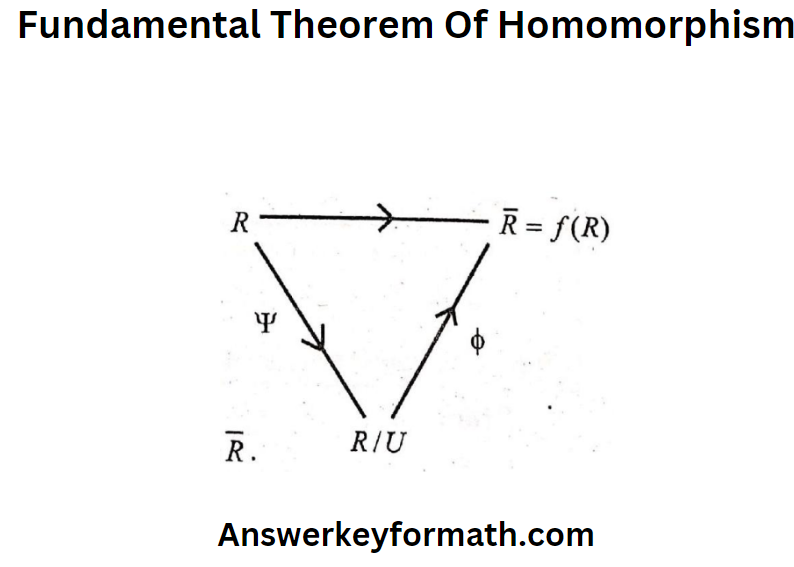
Also, for x ∈ R we have f(x) ∈ f(R) = R¯. Therefore, φ · Ψ = f.
Ring Theory And Vector Calculus Solved Problems
Example. 1. Is the ring 2Z isomorphic to ring 3Z?
Solution. 2Z = {2n | r ∈ Z} and 3Z = {3n | n ∈ Z}.
Define f : 2Z → 3Z by f(2x) = 3x∀2x ∈ 2Z. Let 2m, 2n ∈ 2Z.
f(2m + 2n) = f(2(m + n)) = 3(m + n) = 3m + 3n = f(2m) + f(2n)
f(2m.2n) = f(2(2mn)) = 3(2mn) 6= 3m.3n = f(2m)f(2n)
∴ The correspondence f does not preserve multiplication.
∴ Ring 2Z is not isomorphic to ring 3Z.
Example. 2. Let Z4, Z10 be modulo-4 and modulo – 10 rings. If f: Z4 → Z10 is defined by f(x) = 5x∀x ∈ Z4 then prove that f is a homomorphism.
Solution. Let a, b ∈ Z4.
Let a+b = 4q1+r1 and a·b = 4q2+r2 where 0 ≤ r1 , r2 < 4.
f(a + b) =f (r1) = 5r1 = 5 (a + b − 4q1) =5a + 5b − 20q1 = 5a + 5b( modulo 10) = f(a) + f(b) in Z10.
f(a : b) =f (r2) = 5r2 = 5 (ab − 4q2) = 5ab − 20q2 =5ab(mod10) = 25ab(mod10) = 5a · 5b = f(a) · f(b) in Z10.
∴ Z4 is homomorphic to Z10.
Example. 3. Prove or disprove that f: M2(Z) → Z defined by
⇒ \(f\left(\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]\right)=a \forall\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right] \in \mathrm{M}_2(\mathrm{Z}) \text { is a ringhomomorphism. } \)
⇒ \(\text { Sol. Let } \mathrm{A}_1=\left[\begin{array}{ll}
a_1 & b_1 \\
c_1 & d_1
\end{array}\right], \mathrm{A}_2=\left[\begin{array}{ll}
a_2 & b_2 \\
c_2 & d_2
\end{array}\right] \in \mathrm{M}_2(\mathrm{Z})\)
where a1,b1,c1,d1,a2,b2,c2,d2 ∈
Z. By definition of f,f ( A1) = a1,f ( A2) = a2.
f ( A1 + A2) = f \( \left(\begin{array}{ll}
a_1+a_2 & b_1+b_2 \\
c_1+c_2 & d_1+d_2
\end{array}\right)\) = a1 + a2 = f ( A1) + f ( A2)
∴ f preserves addition.
f ( A1 · A2) = f \(\left(\begin{array}{cc}
a_1 a_2+b_1 c_2 & a_1 b_2+b_1 d_2 \\
c_1 a_2+d_1 c_2 & c_1 b_2+d_1 d_2
\end{array}\right) \) = a1a2 + b1c2 6= a1a2 =
f ( A1) · f ( A2) f does not preserve multiplication.
∴ f is not a homomorphism.
Example. 4. Let Z(√2) = {m + n√2 | m,n ∈ Z} be a ring under addition and multiplication of numbers. Prove that f : Z(√2) → Z(√2) defined by f(m + n√2) = m − n√2∀m + n√2 ∈ Z(√2) is an automorphism. Also, find Ker f.
Solution. Let a,b ∈ Z(√2) so that a = m1 + n1√2,b = m2 + n2√2 where m1,n1,m2,n2 ∈ Z.
Then we have a+b = (m1 + m2)+(n1 + n2) √2 and ab = (m1m2 + 2n1n2)+ (m1n2 + m2n1) √2. Clearly, f is well-defined.
By definition of f;
f(a + b) = (m1 + m2) − (n1 + n2) √2 = m1 − n1√2 + m2 − n2√2 = f(a) + f(b) and f(ab) = (m1m2 + 2n1n2)−(m1n2 + m2n1) √2 =(m1 − n1√2 m2 − n2√2 )= f(a)f(b)
∴ f is an endomorphism.
a,b ∈ Z(√2); f(a) = f(b) ⇒ m1 − n1√2 = m2 − n2√2
⇒ m1 = m2 and n1 = n2 ⇒ m1 + n1√2 = m2 + n2√2 ⇒ a = b
∴ f is one-one.
Let y = m + n√2 ∈ Z(√2), the co-domain of f.
Then x = m − n√2 ∈ Z(√2), the domain of f, exists so that
f˙(x) = f(m − n√2) = m − (−n√2) = m + n√2 = y.
∴ For each y ∈ Z(√2) there exists x ∈ Z(√2) so that f(x) = y.
∴ f is onto. Hence f is an automorphism.
f(m+n√2) = m−n√2 = 0, zero element of Z(√2) ⇒ m = 0,n = 0 ⇒ m+n√2 = 0, zero element.
∴ ker f = {0}.
Example. 5. L et Zb e is the ring of integers and Zn is the ring of residue classes modulo n. If a mapping f: Z → Zn is defined by f(x) = ¯r∀x ∈ Z where x ≡ r(modn) proves that f is a homomorphism. Also, find Ker f.
Solution. Let x, y ∈ Z.
By the definition of f; f(x) = ¯r, f(y) = ¯s where x ∼= r(modn) and y ≡ s(modn).
Clearly, f is well-defined.
We know that (1)x ≡ r(modn),
y ≡ s(modn) ⇒ x + y ≡ r + s(modn) and xy ≡ rs(modn) and (2)r + s = r¯ + ¯s, rs = ¯rs¯.
Now f(x+y) = r + s = ¯r+¯s = f(x)+f(y) and f(xy) = rs = ¯rs¯ = f(x)f(y).
∴ f is a homomorphism.
Hence Zn is a homomorphic image of Z.
This is called the natural homomorphism from Z to Zn.
Example. 6. Let C be the ring of Complex numbers and M2(R) be the ring of 2 × 2 matrices. If f : C → M2(R) is defined by f(a + ib) =\(\left(\begin{array}{cc}a & b \\ -b & a\end{array}\right)\) prove that f is an into isomorphism or monomorphism. Also, find Ker f
Solution. Let Z1, Z2 ∈ C and Z1 = x1 + iy 1, Z2 = x2 + iy2 where x1, y1, x2, y2 ∈ R.
Then f (Z1) = f (x1 + iy1) = \(\left(\begin{array}{cc}
x_1 & y_1 \\
-y_1 & x_1
\end{array}\right) \) and f (Z2) = f (x2 + iy2) = \( \left(\begin{array}{cc}
x_2 & y_2 \\
-y_2 & x_2
\end{array}\right)\)
f (Z1 + Z2) = f ((x1 + x2) + i (y1 + y2)) = \( \left(\begin{array}{cc}
x_1+x_2 & y_1+y_2 \\
-\left(y_1+y_2\right) & x_1+x_2
\end{array}\right) \)=
⇒ \(\left(\begin{array}{cc}
x_1 & y_1 \\
-y_1 & x_1
\end{array}\right)+\left(\begin{array}{cc}
x_2 & y_2 \\
-y_2 & x_2
\end{array}\right) \) = f (Z1) + f (Z2)
f (Z1 · Z2) = f ((x1x2 − y1y2) + i (x1y2 + x2y1)) =\( \left(\begin{array}{cc}
x_1 x_2-y_1 y_2 & x_1 y_2+x_2 y_1 \\
-\left(x_1 y_2+x_2 y_1\right) & x_1 x_2-y_1 y_2
\end{array}\right)\)
⇒ \(\left(\begin{array}{cc}
x_1 & y_1 \\
-y_1 & x_1
\end{array}\right) \cdot\left(\begin{array}{cc}
x_2 & y_2 \\
-y_2 & x_2
\end{array}\right)\) = f (Z1) · f (Z2)
∴ f is a homomorphism from C to M2(R).
f (Z1) = f (Z2) ⇒ \(\left(\begin{array}{cc}
x_1 & y_1 \\
-y_1 & x_1
\end{array}\right)=\left(\begin{array}{cc}
x_2 & y_2 \\
-y_2 & x_2
\end{array}\right)\) ⇒ x1 = x2, y1 = y2
⇒ x1 + iy1 = x2+ iy2⇒ Z1 = Z2.
∴ f is one-one.
⇒ \(\text { For }\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right) \in \mathrm{M}_2(\mathrm{Z}) \text { and }\left(\begin{array}{ll}
a & b \\
c & d
\end{array}\right) \neq\left(\begin{array}{cc}
a & b \\
-b & a
\end{array}\right)\)
there is no complex number a + ib ∈ C satisfying the correspondence.
∴ f is not onto. Hence f is a monomorphism or an isomorphism.
Note. Instead of M2(R) if we take ring of 2×2 matrices = S =\(\left\{\left(\begin{array}{cc}a & b \\ -b & a\end{array}\right) \mid a, b \in \mathrm{R}\right\}\)
then f: C → S will be isomorphism onto. 1 = 1 + 0i ∈ C is the unity in C, and
f(1) = f(1 + 0i) = \(\left(\begin{array}{cc}1 & 0 \\ -0 & 1\end{array}\right)=\left(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array}\right)\) = unit matrix in M2 (R)
f(a + ib) =\(\left(\begin{array}{cc}a & b \\ -b & a\end{array}\right)=\left(\begin{array}{ll}0 & 0 \\ 0 & 0\end{array}\right)\) = zero element in M2(R) ⇒ a = 0, b = 0
⇒ a + ib = 0 + i0 = 0 = Zero element in C.
∴ Ker f = {0}
Example. 7. Let R be the ring of integers and R 0 be the set of even integers in which addition is the same as that of integers and multiplication (∗) is defined by a ∗ b = ab/2∀a, b ∈ R 0. Prove that R is isomorphic to R’.
Solution. We know that R0 = {2n | n ∈ Z} is a commutative group under addition.
Let a, b, c ∈ R0 so that a = 2m, b = 2n, c = 2p where m, n, p ∈ Z.
a, b ∈ R0 ⇒ a ∗ b = (ab/2) = (2m)(2n)/2 = 2(mn) = 2q where q ∈ Z.
∴ ∗ is a binary operation in R0.
∴ ∗ is a binary operation in R0. a, b, c ∈ R0 ⇒ (a ∗ b) ∗ c = ab2 ∗ c = (ab/22)c = ABC 4 = a(bc/2)2 = a ∗ bc2 = a ∗ (b ∗ c)
∴ ∗ is associative in R’.
a, b, c ∈ R’ ⇒ a ∗ (b + c) = a(b2+c) = ab2 + ac2 = a ∗ b + a ∗ c.
Similarly, (b + c) ∗ a = b ∗ a + c ∗ a. ∴ ∗ is distributive over addition.
a, b ∈ R 0 and a ∗ b = ab2 = ba2 = b ∗ a ⇒ ∗ is commutative in R 0.
Hence (R0, +, ∗) is a commutative ring.
Define f: R → R0 by f(x) = 2x∀x ∈ R.. Obviously f is well defined.
Let x, y ∈ R so that x + y, xy ∈ R. Then f(x) = 2x, f(y) = 2y.
Now f(x + y) = 2(x + y) = 2x + 2y = f(x) + f(y) and
f(xy) = 2(xy) = (2x)(22 y) = 2x ∗ 2y = f(x) ∗ f(y).
∴ f is a homomorphism from R into R 0.
x, y ∈ R, f(x) = f(y) ⇒ 2x = 2y ⇒ x = y ⇒ f is one-one.
Let b ∈ R0. Then b = 2a where a ∈ R and for a ∈ R we have f(a) = 2a = b.
∴ for each b ∈ R 0 there exists a ∈ R so that b = f(a) ⇒ f is onto .
Hence f is an isomorphism from R to R 0.
Example. 8. Prove that any homomorphism defined on a field is either isomorphism or zero homomorphism. Or, prove that a field has no proper homomorphic image.
Solution. Let F be a field R be a ring and f: F → R be a homomorphism.
Then we know that Ker f is an ideal of the field F.
Since a field has no proper ideals either Ker f = F or Ker f = {0} where ’ 0 ’ is the zero element of F.
Let Ker f = F.
By definition of Ker f., we have f(x) = 00∀x ∈ F where 00 ∈ R is the zero element.
∴ homomorphic image of F = f(F) = {0′}.
Hence, in this case, f is a zero homomorphism. Let Ker f = {0}.
∴ By theorem (2) Art. 3.2, f is an isomorphism from F to R.
Hence, in this case, a homomorphic image of F = f(F) is also a field.
Example. 9. Prove that Z/hnior Z/nZ is isomorphic to Zn:
Solution. Define f: Z → Zn as f(x) = ¯r∀x ∈ Z.
Then f is a homomorphism
∀r¯ ∈ Zn we have r ∈ Z and for this r ∈ Z, f(r) = ¯r ( ∵ r ≡ r mod n).
∴ f: Z → Zn is onto homomorphism. But Ker f = nZ = hni.
By fundamental theorem; Z/ Ker f ∼= Zn(i.e.,) Z/hni ∼= Zn.
Further, if n is a prime = p then Zp is a field.
Z/hpi ∼= Zp ⇒ that a quotient ring of an integral domain is isomorphic to the field Zp.
Hence a quotient ring of an integral domain may be a field.
Note. Z6= {0, 1, 2, 3, 4, 5} is a ring and U = {0, 3} is an ideal of Z6.
Z6/U = {0 + U, 1 + U, 2 + U} contains only 3 elements.
If we define φ : Z3 → Z6/N as φ(0) = 0 + U, φ(1) = 1 + U, φ(2) = 2 + U, then φ is an isomorphism.
Ring Theory And Vector Calculus Maximal Ideals
The concept of a maximal ideal of a ring is analogous to the idea of the maximum normal subgroup in Group Theory.
Definition. (Maximal Ideal). A maximal ideal M of a ring R is an ideal different from R such that there is no proper ideal U of R properly containing M.
(or)
Let R be a ring and M be an ideal of R so that M 6= R. M is said to be a maximal ideal of R if whenever U is an ideal of R such that M ⊂ U ⊂ R then either R = U or U = M.
Note 1. M is a maximal ideal of R if any ideal U of R containing M is either R or M.
2. An ideal M of a ring R is called a maximal ideal if M is not included in any other ideal of R except R itself. That is, the only ideal that properly contains a maximal ideal is the entire ring.
3. If M is a maximal ideal of the ring R then there exists no ideal U of R so that M ⊂ U ⊂ R
Theorem. 1. In the ring Z of integers the ideal generated by a prime integer is a maximal ideal.
Proof. Let p be the prime integer and M = HPI = pZ = {pn | n ∈ Z} be the ideal generated by p.
Let U be any ideal so that M ⊂ U ⊂ Z
Since every ideal of Z is a principal ideal, U is a principal ideal so U = hqi where q is an integer.
M ⊂ U ⊂ Z ⇒ hpi ⊂ hqi ⊂ Z ⇒ p ∈ hqi ⇒ p = qm, m ∈ Z.
Since p is a prime, either q = 1 or m = 1
m = 1 ⇒ p = q ⇒ hpi = hqi ⇒ M = U; q = 1 ⇒ hqi = Z ⇒ U = Z
∴ M is a maximal ideal.
Note. An ideal generated by a composite integer is not a maximal ideal.
Consider M = h6i = {. . . , −12, −6, 0, 6, 12, . . .}, the ideal generated by composite integer 6.
There exists ideal U = h3i = {. . . , −12, −9, −6, −3, 0, 3, 6, . . .} so that M ⊂ U ⊂ Z
Theorem. 2. If M is a maximal ideal of the ring of integers Z then M is generated by prime integer.
Proof. Let M = hni where n ∈ Z be a maximal ideal of Z.
We prove that n is a prime integer.
If possible, suppose that n = ab where a, and b are prime integers.
Then U = hai is an ideal of Z and U ⊃ M so that M ⊂ U ⊂ Z
Since M is the maximal ideal of Z, by the definition either U = Z or M = U.
Case (1). Let U = Z. Then U = hai = h1i so that a = 1
∴ n = ab = b ⇒ n is a prime integer.
Case (2). Let M = U
Then U = hai = M ⇒ a ∈ M ⇒ a ∈ hni ⇒ a = rn for some r ∈ Z.
∴ n = ab = (rn)b = n(rb) ⇒ 1 = rb ⇒ r = 1, b = 1.
∴ n = a(1) = a ⇒ n is a prime integer.
From cases (1) and (2) we have that n is a prime integer.
Note. 1. For the ring of integers Z, any ideal generated by a prime integer is a maximal ideal.
2. A ring may have more than one maximal ideal. For example, the ring Z has h2i, h3i, h5i, . . . as maximal ideals.
Theorem. 3. An ideal in Z is a maximal ideal if and only if it is generated by a prime integer.
Proof. Write the proofs of Theorems (1) and (2).
Theorem. 4. An ideal U of a commutative ring R with unity is maximal if and only if the quotient ring RU is a field.
Proof. R is a commutative ring with unity and U is an ideal ⇒ the quotient ring R/U = {x + U | x ∈ R} is commutative and has a unity element.
Zero element of R/U = 0 + U = U where 0 ∈ R is the zero element in R.
Unity element of R/U = 1 + U where 1 ∈ R is the unity element in R. It is to be noted that a + U = U zero element of R/U ⇔ a ∈ U
(1) Suppose that U is a maximal ideal of R. We prove that R/U is a field.
To prove that R/U is a field we have to show that every non-zero element of R/U has a multiplicative inverse.
Let x + U ∈ R/U and x + U be non-zero elements. Then x /∈ U
If hxi is the principal ideal of R then hxi + U is also an ideal of R.
( ∵ The sum of two ideals is also an ideal. Ex. 4)
x /∈ U ⇒ U ⊂ hxi + U
Now we have, U ⊂ hxi + U ⊆ R and U is maximal ideal ⇒ hxi + U = R = h1i
⇒ there exists a ∈ U and α ∈ R such that a + xα = 1
∴ 1 + U = (a + xα) + U = (a + U) + (xα + U) (sum of cosets)
= U + (xα + U) = (0 + U) + (xα + U)
( ∵ a ∈ U ⇒ a + U = U)
= xα + U = (x + U)(α + U) (Product of cosets)
∴ for non-zero element x + U ∈ R/U there exists α + U ∈ R/U such that (x + U)(α + U) = 1 + U.
Hence every non-zero element of R/U is invertible.
∴ R/U is a field.
(2) suppose that R/U is a field. We prove that U is the maximal ideal.
Let U0 be an ideal of R so that U 0 ⊃ U and U 0 6= U
Now we show that U0 = R
Since U0 ⊃ U and U0 6= U, there exists α ∈ U0 such that α /∈ U
α /∈ U ⇒ α + U is non-zero element of R/U
R/U is a field of α + U is a non-zero element of R/U
⇒ α + U has multiplicative inverse, say x + U.
∴ (α + U)(x + U) = 1 + U
⇒ αx + U = 1 + U ⇒ 1 − αx ∈ U ⊂ U 0 ( ∵ a + U = b + U ⇒ a − b ∈ U)
x ∈ R, α ∈ U0 and U0 is an ideal ⇒ αx ∈ U0.
αx ∈ U0, 1 − αx ∈ U0 ⇒ αx + (1 − αx) = 1 ∈ U0
∴ 1 ∈ U0 and U 0 is an ideal ⇒ U0 = R.
Hence U is a maximal ideal.
Ring Theory And Vector Calculus Prime Ideals
Definition. (Prime Ideal) An ideal U6= R of a commutative ring R is said to be prime ideal if for all a, b ∈ R and a, b ∈ U ⇒ a ∈ U or b ∈ U.
Example. For an integral domain R, the null ideal is a prime ideal.
∵ a, b ∈ R, ab ∈ h0i ⇒ ab = 0 ⇒ a = 0 or b = 0
Theorem. An ideal U≠ R of a commutative ring R, is a prime idea if and only if R/U is an integral domain.
Proof. Let R/U be an integral domain.
We now prove that U is a prime ideal of R.
∀a, b ∈ R and a, b ∈ U ⇒ ab + U = U ⇒ (a + U).(b + U) = 0 + U
⇒ a + U = 0 + U or b + U = 0 + U (0 + U is the zero element of R/U)
⇒ a ∈ U or b ∈ U.
∴ U is a prime ideal of R.
Conversely, let U be a prime ideal of R.
We now prove that R/U is an integral domain.
a + U, b + U ∈ R/U and (a + U) · (b + U) = 0 + U
⇒ ab + U = 0 + U ⇒ ab ∈ U ⇒ a ∈ U or b ∈ U ( ∵ U is prime ideal)
⇒ a + U = 0 +. U or b + U = 0 + U.
∴ R/U has no zero divisors and hence is an integral domain.
Corollary. Every maximal ideal of a commutative ring R with unity is a prime ideal.
Proof. Let U be a maximal ideal of a ring R.
By Theorem (3) of Art. 3.3; R/U is a field. ⇒ R/U is an integral domain.
By Theorem (4) of Art. 3.3; U is a prime ideal.
Thus every maximal ideal of R is a prime ideal.
Note. 1. The converse of the above corollary is not true.
That is, a prime ideal of a commutative ring with unity need not be a maximal ideal.
Consider the integral domain Z of integers.
The null ideal = h0i of Z is a prime ideal. But the h0i ideal is not the maximal ideal.
There exists ideal = h2i of Z such that h0i ⊂ h2i ⊂ Z and h2i 6= h0i, h2i 6= Z.
Example. If R = {0, 2, 4, 6} is a ring with respect to addition and multiplication modulo 8, then show that M = {0, 4} is a maximal ideal of R but not a prime ideal.
Solution. For 0, 0 ∈ M, 0 − 0 = 0 ∈ M, For 0,4 or 4, 0 ∈ M,
0 − 4 = 8 − 4 = 4 ∈ M, 4 − 0 = 4 ∈ M. For 4, 4 ∈ M, 4 − 4 = 0 ∈ M.
For 0 ∈ M, 0, 2, 4, 6 ∈ R we have 0.0 = 0, 0.2 = 0, 0.4 = 0, 0.6 = 0 ∈ M For
4 ∈ M, 0, 2, 4, 6 ∈ R we have 4.0 = 0 ∈ M, 4.2 = 8 = 0 ∈ M, 4.4 = 16 = 0 ∈ M,
4.6 = 24 = 0 ∈ M.
∴ M is an ideal of R.
U1 = {0, 2, 4} is not an ideal, for, 2, 4 ∈ U1 we have 2 − 4 = −2 = 6 ∈/ U1
U2 = {0, 4, 6} is not ideal, for, 6, 4 ∈ U 2 we have 6 − 4 = 2 ∈/ U2.
∴ There is no ideal U of R such that M ⊂ U ⊂ R.
∴ M = {0, 4} is a maximal ideal.
For 2, 6 ∈ R and 2.6 = 12 = 4 ∈ M does not imply either 2 ∈ M or 6 ∈ M
∴ M is not a prime ideal.
Ring Theory And Vector Calculus Field Of Quotients Of An Integral Domain
If an integral domain is such that every non-zero element of it has a multiplicative inverse the n it is a field. However many integral domains do not form fields.
Though the integral domain of integers is not a field, it is such that it can be embedded in the field of rational numbers. In this section, we show that every integral domain can be regarded as being contained in a certain field. The minimal field containing an integral domain is called a field of quotients of an integral domain.
Theorem. Every integral domain can be embedded in a field. (or) An integral domain D can be embedded in a field F such that every element of F can be regarded a quotient of two elements of D.
Proof. Let D be an integral domain with at least two elements.
Consider S = {(a, b) | a, b ∈ D, b 6= 0}. Then S 6= φ and S ⊂ D × D.
For all (a, b), (c, d) ∈ S define a relation ∼ on S as (a, b) ∼ (c, d) if and only if ad = bc. We now prove that ∼ is an equivalence relation on S.
(1) For each (a, b) ∈ S we have ab = ba which implies that (a, b) ∼ (a, b).
(2) (a, b), (c, d) ∈ S and (a, b) ∼ (c, d) ⇒ ad = bc ⇒ cb = da ⇒ (c, d) ∼ (a, b).
(3) (a, b), (c, d), (e, f) ∈ S and (a, b) ∼ (c, d), (c, d) ∼ (e, f) ⇒ ad = bc, cf = de.
⇒ (ad)f = (bc)f; cf = de ⇒ (af)d = b(de) = d(be) ⇒ af = be ( ∵ d 6= 0)
⇒ (a, b) ∼ (e, f)
∴ ’ 0 ’ is an equivalence relation on S.
The equivalence relation partitions the set S into equivalence classes which are either identical or disjoint.
For (a, b) ∈ S let a/b denote the equivalence class of (a, b). Then a/b = {(x, y) ∈ S | (x, y) ∼ (a, b)}. If a/b, c/d are the equivalence classes of (a, b), (c, d) ∈ S then either a/b = c/d or a/b ∩ c/d = φ. It is evident that a/b = c/d if and only if ad = bc.
Let F denote the set of all the equivalence classes or the set of quotients.
Then F = {n a/b | (a, b)} ∈ S˙ o.
Since D has at least two elements, say, 0, a ∈ D
we have quotients \(\frac{0}{a}, \frac{a}{a} \in F and \frac{0}{a} \neq \frac{a}{a}\)
∴ the set F has at least two elements.
For a/b, c/d ∈ F define addition (+) and multiplication ( · ) as
⇒ \(\frac{a}{b}+\frac{c}{d}=\frac{a d+b c}{b d} and \frac{a}{b}, \frac{c}{d}=\frac{a c}{b d}\)
Since D is without zero divisors, b ≠ 0, d ≠ 0 ∈ D ⇒ bd≠ 0
So \(\frac{a d+b c}{b d}, \frac{a c}{b d} \in F\)
Now we prove that the addition and multiplication defined above are well defined.
Let \(\frac{a}{b}=\frac{a^{\prime}}{b^{\prime}} and \frac{c}{d}=\frac{c^{\prime}}{d^{\prime}}. Then a b^{\prime}=a^{\prime} b$ and c d^{\prime}=c^{\prime} d\)
⇒ \(Now (I) \Rightarrow a b^{\prime} d d^{\prime}=a^{\prime} b d d^{\prime} and b b^{\prime} c d^{\prime}=b b^{\prime} c^{\prime} d\)
⇒ \(\text { (2) For } \frac{a}{b}, \frac{c}{d} \in F ; \frac{a}{b}+\frac{c}{d}=\frac{a d+b c}{b d}=\frac{b c+a d}{d b}=\frac{c}{d}+\frac{a}{b} \Rightarrow\)
⇒ \((3) For $u \neq 0 \in D$ we have $\frac{0}{u} \in F$ such that $\frac{0}{u}+\frac{a}{b}=\frac{0 b+u a}{u b}=\frac{u a}{u b}=\frac{a}{b} \forall \frac{a}{b} \in F. \therefore \frac{0}{u} \\)in F is the zero element.
⇒ \( \frac{a d+b c}{b d}=\frac{a^d d+b c}{b^{\prime} d^{\prime}} \)
Also (I) ⇒\( a b^{\prime} c d^{\prime}=a^{\prime} b c^{\prime} d \Rightarrow(a c)\left(b^{\prime} d^{\prime}\right)=\left(a^{\prime} c^{\prime}\right)(b d) \Rightarrow \frac{a c}{b d}=\frac{a^{\prime} c^{\prime}}{b^{\prime} d^{\prime}} \)
∴ The addition and multiplication of quotients are well-defined binary operations on F.
We now prove that (F, +, ·) is a field.
⇒ \(\text { (1) For } \frac{a}{b}, \frac{c}{d}, \frac{c}{f} \in F ;\left(\frac{a}{b}+\frac{c}{d}\right)+\frac{c}{f}=\frac{a d+b c}{b d}+\frac{c}{b}=\frac{(a d+b c) f+(b d) e}{(b d) f}=\frac{a(d f)+(c f+d e) b}{b(d f)}= \)
⇒ \(\frac{a}{b}+\frac{c f+d c}{d f}=\frac{a}{b}+\left(\frac{c}{d}+\frac{c}{f}\right) \Rightarrow \) addition is assocative.
⇒ \(\text { (2) For } \frac{a}{b}, \frac{c}{d} \in F ; \frac{a}{b}+\frac{c}{d}=\frac{a d+b c}{b d}=\frac{b c+a d}{d h}=\frac{c}{d}+\frac{a}{b} \Rightarrow \text { addition is commutative. } \)
(3) For \(u \neq 0 \in D we have \frac{0}{u} \in F such that \frac{0}{u}+\frac{a}{b}=\frac{0 b+u a}{u b}=\frac{u a}{u b}=\frac{a}{b} \forall \frac{a}{b} \in F. therefore \frac{0}{u} \in F\)is the zero element.
(4) Let\(\frac{a}{b} \in F. Then \frac{-a}{b} \in F such that \frac{a}{b}+\frac{-a}{b}=\frac{a b+(-a) b}{b^2}=\frac{0}{b^2}=\frac{0}{u}\left(because 0 u=0 b^2\right)\) therefore every element in F has additive inverse.
(5) For \(\frac{a}{b}, \frac{c}{d}, \frac{c}{f} \in F ;\left(\frac{a}{b}, \frac{c}{d}\right) \cdot \frac{c}{f}=\)
⇒ \(\frac{a c}{b d} \cdot \frac{c}{f}=\frac{(a c) c}{(b d) f}=\frac{a(c)}{b(d f)}=\frac{a}{b} \cdot \frac{c c}{d f}=\frac{a}{b} \cdot\left(\frac{c}{d} \cdot \frac{c}{f}\right)\)
∴ multiplication is associative.
⇒ \(\text { (6) For } \frac{a}{b}, \frac{c}{d} \in F ; \frac{a}{b} \cdot \frac{c}{d}=\frac{a c}{b d}=\frac{c a}{d b}=\frac{c}{d} \cdot \frac{a}{b}\)
∴ multiplication is commutative
(7) for \(u \neq 0 \in D we have frac{u}{u} \in Fsuch that \frac{a}{b} \cdot \frac{u}{u}=\frac{a u}{b u}=\frac{a}{b} \forall \frac{a}{b} \in Ftherefore frac{u}{u} \in F\) is the unity element.
(8) Let\(\frac{a}{b} \in F and \frac{a}{b} \neq \frac{\underline{0}}{u}.\)
⇒ \(Then a u \neq 0 which implies that a \neq 0 asu \neq 0. therefore b \neq 0 and a \neq 0 \Rightarrow \frac{b}{a} \in F\)
⇒ \(therefore for \frac{a}{b}\left(\neq \frac{a}{u}\right) \in F there exists\frac{b}{a} \in F such that\)
⇒ \( \frac{a}{b} \cdot \frac{b}{a}=\frac{a b}{b a}=\frac{u}{u} \quad(because(a b) u=(b a) u)\)
∴ every non-zero element in F has multiplicative inverse
⇒ \(\text { (9) For } \frac{a}{b}, \frac{c}{d}, \frac{c}{f} \in F ; \frac{a}{b} \cdot\left(\frac{c}{d}+\frac{c}{f}\right)=\frac{a}{b} \cdot \frac{c f+d c}{d f}=\frac{a(c f+d c)}{b(d f)}=\frac{(a c f+a d c)(b d f)}{(b d f) b d f)}\)
⇒ \(\frac{a c f \text { bdf+adebdf }}{(b a d) b d f)}=\frac{a c f}{b d f}+\frac{a d e}{b d f}=\frac{a c}{b d}+\frac{a c}{b f}=\frac{a}{b} \cdot \frac{c}{d}+\frac{a}{b} \cdot \frac{c}{f}\)
Similarly we can prove that \( \left(\frac{c}{d}+\frac{c}{f}\right) \cdot \frac{a}{b}=\frac{c}{d} \cdot \frac{a}{b}+\frac{e}{f} \cdot \frac{a}{b}\)
∴ Multiplication is distributive over addition.
In view of (1), (2), (3), (4), (5), (6), (7), (8) and (9) (F, +, ·) is a field.
Now we have to prove that D is embedded in the field F, that is, we have to show that there exists an isomorphism of D into F.
Define the mapping φ : D → F by φ(a) = ax/x ∀a ∈ D and x(6= 0) ∈ D.
⇒ \(a, b \in D \text { and } \phi(a)=\phi(b) \Rightarrow \frac{a x}{x}=\frac{b x}{\tau} \Rightarrow(a x)^x x=(b x) x\)
⇒ \(\Rightarrow(a-b) x^2=0 \Rightarrow a-b=0 \text { since } x^2 \neq 0 \Rightarrow a=b . \quad therefore \phi \text { is one – one. }\)
⇒ \(\text { For } a, b \in D ; \phi(a+b)=\frac{(a+b) x}{x}=\frac{(a+b) x x}{x x}=\frac{a x x+b x x}{x x}=\frac{a x}{x}+\frac{b x}{x}=\phi(a)+\phi(b)\)
⇒ \(\phi(a b)=\frac{(a b) x}{x}=\frac{(a b) x x}{x x}=\frac{a x}{x}, \frac{b x}{x}=\phi(a) \phi(b)\)
∴ φ is a homomorphism. Hence φ is an isomorphism of D into F.
∴ the integral domain D is embedded in the field F.
Note. 1. Every element in the field F is in the form of a quotient of two elements in D. So, the field F is called the “field of quotients of D ”
2. The equivalence class of (a, b) ∈ S is also denoted as [(a, b)] or [a, b] or (a, b) Then [(a, b)] = [(c, d)] ⇔ ad = bc, [(a, b)] + [(c, d)] = [(ad + bc, bd)], [(a, b)] · [(c, d)] = [(ac, bd)], the zero element of F = [(0, 1)] and the unity element of F = [(1, 1)]
3. If D is the ring of integers then the field F, constructed in the above theorem, would be the field Q of rational numbers.
Ring Theory And Vector Calculus Prime Fields
Definition. A field is said to be prime if it has no subfield other than itself.
The field Zp = {0, 1, 2, . . . , p − 1} where p is a prime and the field Q, of the set of all rational numbers, are prime fields. The field of real numbers R is not a prime field.
We now establish that any field F contains a subfield isomorphic to Zp or contains a subfield isomorphic to Q.
Theorem. 1. If R is a ring with unity element ’ 1 ’ then f: Z → R defined by f(x) = n · 1∀n ∈ Z is a homomorphism.
Proof. Let m, n ∈ Z. Then f(m) = m.1, f(n) = n.1.
f(m + n) = (m + n) · 1 = m · 1 + n · 1 = f(m) + f(n)
Let m > 0, n > 0.
(mn) · 1 = 1 + 1 + . . . + 1(mn times ) = {(1 + 1 + . . . + 1)m times } {(1 +1 + . . . + 1)n times } = (m.1)(n.1) (using Distributivity in the ring R )
Similarly, ∀m, n ∈ Z we can prove that (mn).1 = (m.1)(n.1) using Distributivity.
∴ f(mn) = (mn) · 1 = (m · 1)(n · 1) = f(m)f(n).
Hence f: Z → R is a homomorphism.
Theorem. 2. If R is a ring with unity element ’ I ’ and characteristic of R = n > 0 Then R contains a subring isomorphic to Zn.
Proof. Consider the homomorphism f: Z → R defined by f(m) = m.1∀m ∈ Z.
∴ Ker f is an ideal of Z.
But every ideal in Z is the form hsi = sZ where s ∈ Z.
Characteristic of ring R = n > 0 ⇒ n is the least positive integer such that n.1 = 0.
∴ Ker f = nZ = hni By fundamental Theorem, f(Z) ⊆ R is isomorphic to Z/nz = Z/hni.
But Z/nz = Z/hni is isomorphic to Zn.
∴ f(Z) ⊆ R is isomorphic to Zn.
Theorem.3. If R is a ring with unity element ’ 1 ’ and characteristic of R = 0 then R contains a subring isomorphic to Z.
Proof. Consider the homomorphism f: Z → R defined by f(m) = m: 1∀m ∈ Z.
Characteristic of R = 0 ⇒ m.1 ≠ 0∀m ∈ Z and m≠ 0.
Ker f = {m ∈ Z | f(m) = m.1 = 0} = {0}.
∴ f(Z) ⊆ R is isomorphic to Z.
Corollary. A field F of prime characteristic = p contains a subfield isomorphic to Zp and a field F of characteristic zero contains a subfield isomorphic to Q, the field of rational numbers.
Proof. Let F be the field of characteristic = p, a prime.
Then p is the least positive integer such that p.1 = 0.
∴ Ker f = pZ = hpi,
Hence, by the above theorem; F contains a subfield isomorphic to Zp.
Let F be the field of characteristic = 0.
By the above Theorem; F contains a subring isomorphic to Z.
But the field F contains a field of quotients of Z which is the field Q of rational numbers. Thus we have established that apart from isomorphism the only prime fields are Q and Zp.
Ring Theory And Vector Calculus Multiple Choice Questions:
1. For any two elements a,b in a ring, a(−b) =
(1) −(ab)
(2) ab
(3) −(ba)
(4) None
Answer: 1. −(ab)
2. If (R, +, ·) is a ring then (R, +) is
(1) A group
(2) An abelian group
(3) A finite group
(4) Semigroup
Answer: (2) An abelian group
3. The residue classes modulo 11 with respect to addition and multiplication modulo 11 is
(1) Commutative ring
(2) An integral domain
(3) A field
(4) Skew field
Answer: (3) A field
4. The characteristic of the residue classes mod 8 is
(1) 0
(2) 2
(3) 8
(4) none
Answer: (3) 8
5. If F is a field then the number of ideals in F is
(1) 0
(2) 1
(3) 2
(4) Infinite
Answer: (3) 2
6. If a, b are nilpotent elements in a commutative ring then ab is
(1) Nilpotent
(2) Not nilpotent
(3) Idempotent
(4) Zero
Answer: (1) nilpotent
7. The characteristic of the field of rational numbers is.
(1) 0
(2) ∞
(3) A prime
(4) None
Answer: (1) 0
8. With the usual addition and multiplication, the set of all even integers is
(1) A ring
(2) A field
(3) An integral domain
(4) None
Answer: (1) a ring
9. The number of proper ideals of a field is
(1) 0
(2) 1
(3) 2
(4) None of these
Answer: (3) 2
10. The set a + bi | a, b ∈ Z, i 2 = −1 of Gaussian integers is
(1) Ring
(2) Integral do ain
(3) Field
(4) None
Answer: (1) Ring
11. A commutative ring satisfying cancellation laws is a
(1) Field
(2) Skew field
(3) Integral domain
(4) None
Answer: (3) integral domain
12. In the ring Z of integers the ideal generated by 7 is
(1) Prime ideal
(2) Maximal ideal
(3) Not maximal
(4) None
Answer: (4) none
13. For the homomorphism f : R → R defined by f(x) = x∀x ∈ R Ker f =
(1) {0}
(2) R
(3){0, 1}
(4) none
Answer: (1) {0}
14. In the ring of integers Z, the units are (1) 0,1 (2).1 only (3) 1, −1 only (4) none 17. If a, b are two non-zero elements of a Euclidean ring R and b is a unit in R, then
(1) d(ab) = d(1)
(2) d(ab) > d(1)
(3) d(ab) < d(1)
(4) None
Answer: (3) d(ab) < d(1)
15. If F is a field and f: F → R is a homomorphism so that Ker f = {0} then f is
(1) Isomorphism
(2) Monomorphism
(3) Zero homomorphism
(4) None
Answer: (3) zero homomorphism
16. In the ring Z[i] of Gaussian integers 1 + i is
(1) Unit
(2) Unity element
(3) Prime element
(4) None
Answer: (3) prime element
17. If U is an ideal of ring R with unity 1 such that 1 ∈ U then U is
(1) U
(2) R
(3) ⊆ R
(4) none
Answer: (1) U
18. Let R be a commutative ring with unity and a ∈ R, then U = {ra | r ∈ R} is
(1) left ideal only
(2) ideal only
(3) prime ideal
(4) smallest ideal containing ’ a ’
Answer: (3) prime ideal
19. Every ring of numbers with unity is
(1) integral domain
(2) division ring
(3) field
(4) none
Answer: (1) integral domain
20. The ring R = {a + b√2 | a, b ∈ Q} is
(1) Integral domain
(2) Skew field
(3) Field
(4) None
Answer: (2) Skew field
21. If S1, S2 are two subrings of a ring R then S1 + S2 is
(1) Subring
(2) Ideal
(3) Need not be a subring
Answer: (3) need not be a subring
22. A subring S of a ring R is called ideal if
(1) α ∈ S, a ∈ R ⇒ αa ∈ S
(2) α ∈ S, a ∈ R ⇒ aα ∈ S
(3) α ∈ S, a ∈ R ⇒ αa, aα ∈ S
(4) none
Answer: (1) α ∈ S, a ∈ R ⇒ αa ∈ S
23. The set Q of rational numbers is
(1) subring
(2) ideal
(3) not subring
(4) not ideal, for the ring of real numbers
Answer: (1) subring
24. A homomorphic image of an integral domain is
(1) a ring
(2) integral domain
(3) need not be an integral domain
(4) none
Answer: (1) a ring
25. If R is a non-zero ring so that a2 = a∀∈ R then the characteristic of R =
(1) 0
(2) 1
(3) 2
(4) Prime
Answer: (3) 2
26. If the characteristic of a ring R is 2 and a, b ∈ R then (a + b) 2 =
(1) a2 + 2ab + b2
(2) a2 + ab + ba + b2
(3) a2 + b2
(4) none
Answer: (1) a2 + 2ab + b2
27. If p is a prime, the ring of integers modulo p is.
(1) Field
(2) Integral domain
(3) Skew field
(4) None
Answer: (1) Field
Ring Theory & Vector Calculus Fill In The Blanks:
1. If R is a ring without zero divisors then hold in R.
Answer: Cancellation laws
2. A ring R has no zero divisors if
Answer: There exist a, b ∈ R and ab = 0 ⇒ a = 0 or b = 0
3. A division ring has divisors.
Answer: No zero-divisors
4. A finite integral domain is a
Answer: Field
5. In a ring R if a2 = a for a ∈ R0 a0 is called w. r. t. multiplication.
Answer: Idempotent element
6. a ∈ 0 ∈ R, R is a ring, is called nilpotent element if there exists
Answer: There exist a, b ∈ R and ab = 0 ⇒ a = 0 or b = 0
7. If characteristic of a ring R = 2 and a, b ∈ R commute then (a − b)2 =
Answer: n ∈ N so that an = 0 46. a2 + b2
8. A subring of (Z6, +6, × 6) is
Answer: {0, 3}
9. A field has ideals.
Answer: Need not be an ideal
10. The union of two ideals of a ring R, of R.
Answer: No proper
11. For a field every ideal is
Answer: Need not be an ideal
12. A subring of (R, +, ·) which is not an ideal is
Answer: A principal ideal
13. In the quotient ring R/U the zero element is and the unity element is
Answer: (Q, +, ·) 52. U, 1 + U
14. An ideal U of a ring R is a prime ideal if.
Answer: U ⊂ U 0 ⊂ R
15. For the ring of integers any ideal generated by a prime integer is a
Answer: an ideal of R
16. For a commutative ring R, with unity if U is a maximal ideal then R/U is a
Answer: Maximal ideal
17. If f: R → R’ is a ring isomorphism and R is an integral domain then R’ is
Answer: associates