Savvas Learning Co Geometry Student Edition Chapter 2 Reasoning And Proof Exercise 2.1 Patterns and Inductive Reasoning
Savvas Learning Co Geometry Student Edition Chapter 2 Exercise 2.1 Patterns And Inductive Reasoning Solutions Page 85 Exercise 1 Problem 1
Given: All four-sided figures are squares.
To find – What is a counterexample for the given conjecture.
Given
All four- sided figures are squares.
A counterexample is one that proves the statement false.
Therefore, by saying that a rectangle is a four-sided figure we prove the statement incorrect.
So, the counterexample is
A rectangle is a four-sided figure.
The answer is a rectangle is a four-sided figure.
Savvas Learning Co Geometry Student Edition Chapter 2 Exercise 2.1 Patterns And Inductive Reasoning Solutions Page 85 Exercise 2 Problem 2
The counter is something opposite from the given statement. A counterexample is used to show that conjecture is false.
A counterexample to a mathematical statement is an example that satisfies the statement’s condition(s) but does not lead to the statement’s conclusion.
Identifying counterexamples is a way to show that a mathematical statement is false.
These opposing positions are called counterarguments.
Think of it this way: if my argument is that dogs are better pets than cats because they are more social, but you argue that cats are better pets because they are more self-sufficient, your position is a counterargument to my position.
The counter is something opposite from the given statement. A counterexample is used to show that conjecture is false.
Read and Learn More Savvas Learning Co Geometry Student Edition Solutions
Exercise 2.1 Patterns And Inductive Reasoning Savvas Geometry Answers Page 85 Exercise 3 Problem 3
Given: The sequence 5,10,20,40
To find – Find the next two-term in the sequence.
Given

The answer is 80,160
Exercise 2.1 Patterns And Inductive Reasoning Savvas Geometry Answers Page 85 Exercise 4 Problem 4
Given: 1,4,9,16,25,…
To find – Find a pattern for each sequence.
Here, the pattern is 12,22,32,42,52
So the next two patterns will be 62,72
The next two patterns will be 62,72.
Patterns And Inductive Reasoning Solutions Chapter 2 Exercise 2.1 Savvas Geometry Page 85 Exercise 5 Problem 5
Given: 1,−1,2,−2,3,………..
To find – Find a pattern for each sequence.
Use the pattern to show the next two terms.
A sequence or number pattern is an ordered set of numbers or diagrams that follow a rule.
The pattern for terms starts at 1, then goes to the opposite of this number.
Then one is added to the opposite of this new term. Continue in this pattern of alternating, making it the opposite or making it the opposite and adding one.
The next two terms of this sequence are −3,4.
Chapter 2 Exercise 2.1 Patterns And Inductive Reasoning Savvas Learning Co Geometry Explanation Page 85 Exercise 6 Problem 6
Given: A series 1, \(1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}\)….. is given.
To find – A pattern in the series and the next two terms.
Given series 1, \(1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}\)
Divide the second term by the first term to find the pattern
\(\frac{\frac{1}{2}}{1}=\frac{1}{2}\)Each term is being multiplied by \(\frac{1}{2}\)in the series
Next term after \(\frac{1}{8}\) ⇒ \(\frac{1}{8}\) ×\(\frac{1}{2}\) = \(\frac{1}{16}\)
Next term after \(\frac{1}{16}\) ⇒ \(\frac{1}{16}\) ×\(\frac{1}{2}\) = \(\frac{1}{32}\)
Each term is being multiplied by \(\frac{1}{2}\) in the series and the next two terms in the series \(\frac{1}{16}\) and \(\frac{1}{32}\)
Chapter 2 Exercise 2.1 Patterns And Inductive Reasoning Savvas Learning Co Geometry Explanation Page 85 Exercise 7 Problem 7
Given: A series 1, \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}\) ………… is given.
To find – A pattern in the series and the next two terms.
Given series 1, \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}\) ………..
We can see that in the denominator of each term, one is being added.
So next term after \(\frac{1}{4}\) ⇒ \(\frac{1}{4+1}\) = \(\frac{1}{5}\)
And the next term after \(\frac{1}{5}\) ⇒ \(\frac{1}{5+1}\) = \(\frac{1}{6}\).
In the sequence 1, \(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}\) ………..
one is being added in the denominator of each term and the next two terms of the sequence are \(\frac{1}{5}\) and \(\frac{1}{6}\)
Chapter 2 Exercise 2.1 Patterns And Inductive Reasoning Savvas Learning Co Geometry Explanation Page 85 Exercise 8 Problem 8
Given: A series 15,12,9,6, ……. is given.
To Find – A pattern in the series and the next two terms.
Given series 15,12,9,6 ……………..
Subtract the second term from the first term to find the pattern.
15 − 12 = 3
So 3 is being subtracted from each term.
The next term after 6 ⇒ 6 − 3 = 3 and the next term after 3 ⇒ 3 − 3 = 0
In the sequence15,12,9,6… ……, 3 is being subtracted from each term and the next two terms of the sequence are 3 and 0.
Solutions For Patterns And Inductive Reasoning Exercise 2.1 In Savvas Geometry Chapter 2 Student Edition Page 85 Exercise 9 Problem 9
Given: A series O, T, T, F, F, S, E, …….. is given
To find – A pattern in the series and the next two terms.
Given series O, T, T, F, F, S, E, ……….
The letters given in the series are the first letter of numbers
One = O
Two = T
Three = T
Four = F
Five = F
Six = S
Eight = E
So next letter in the series will be Nine = Nand Ten = T
The next two terms in the series O, T, T, F, F, S, E,… will be N and T.
Solutions For Patterns And Inductive Reasoning Exercise 2.1 In Savvas Geometry Chapter 2 Student Edition Page 85 Exercise 10 Problem 10
Given: A series- Dollar coin, half a dollar, quarter,…….. is given.
To find – A pattern in the series and the next two terms.
Given series- Dollar coin, half a dollar, quarter,……..
We can see that the dollar is being divided in half in every term.
So the next two terms in the series will be⇒
one-eighth and one-sixteenth.
The next two terms in the series- Dollar coin, half a dollar, quarter,….. are ⇒ one-eighth and one-sixteenth.
Exercise 2.1 Patterns And Inductive Reasoning Savvas Learning Co Geometry Detailed Answers Page 85 Exercise 11 Problem 11
Given: A series AL, AK, AZ, AR, CA ………. is given.
To find – A pattern in the series and the next two terms.
Given series AL, AK, AZ, AR, CA ……
These are the short form of the states name of the U.S.
AL = Alabama
AK = Alaska
AZ = Arizona
AR = Arkansas
CA = California
So the next two terms in the series will be
CO = Colarado
CT = Connecticut
The next two terms in the series AL, AK, AZ, AR, CA ……. are CO and CT
Exercise 2.1 Patterns And Inductive Reasoning Savvas Learning Co Geometry Detailed Answers Page 85 Exercise 12 Problem 12
Given: A series is given

To Find A pattern in the series and the next two terms.
In the given series the semicircle is being divided into equal parts.
So the next two terms in the series will be
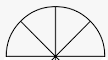
And
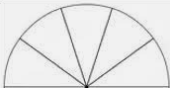
The next two terms in the series are
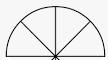
And
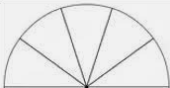
Geometry Chapter 2 Patterns And Inductive Reasoning Savvas Learning Co Explanation Guide Page 85 Exercise 13 Problem 13
Given: Sequence of figures.
To find: The shape of the fortieth figure
We are given a sequence of figures. We need to find the shape of the fortieth figure.
In terms of shape, there are four shapes that repeat in a cycle of circle-triangle-square-star.
Using this pattern, the fortieth figure will be a star.
The fortieth figure will be a star.
Geometry Chapter 2 Patterns And Inductive Reasoning Savvas Learning Co Explanation Guide Page 85 Exercise 14 Problem 14
Given: The sum of the first 100 positive odd numbers.
To find a conjecture for each scenario
We make the following conjecture.
The sum of the first 100 positive odd numbers is 10,000.
The first 100 positive odd numbers are 1,3,5,…,199.
Let their sum be S.
⇒ S = 1 + 3 + 5 + ⋯+ 199
We write the sum in two ways.
⇒ S = 199 + 197 + ⋯+ 3 + 1
We add the two equations side by side.
⇒ S + S = (1 + 199) + (3 + 197) +…+(197 + 3) + (199 + 1)
⇒ 2S = 200 + 200 + ⋯ + 200
⇒ 2S = 200.100
⇒ S = 10000
The sum of the first 100 positive odd numbers is 10000.
Savvas Learning Co Geometry Student Edition Chapter 2 Reasoning And Proof Exercise 2.1 Patterns and Inductive Reasoning Page 85 Exercise 15 Problem 15
Given: The sum of the first 100 positive even numbers.
To find: A conjecture for each scenario
We start by considering a small number, and we will use a form of deduction to come up with a conjecture.
Consider first 10 even numbers. 2 + 4 + 6 + ⋯ + 20
Rearranging the terms: (2 + 20)+(4 + 16)+(6 + 14) + (8 + 12) + (10 + 12)
⇒ 5(22) = 110
We can use a similar trick for the first 100 even numbers, except each pair will equal 202, instead of 22.
Since there were 5 terms when we found the sum of the first 10 odd numbers, there are 50 terms for the sum of first 100 even numbers.
That gives, S = 202(50) = 10100
The sum of first 100 positive even numbers is 10100.
Page 85 Exercise 16 Problem 16
Given: The sum of an even and odd number.
To find: A conjecture for each scenario
The sum of an even and odd number is odd.
This is always true, because even and odd numbers are adjacent have the form n, n + 1,n + 2,…
Since the sum of consecutive even or odd numbers is even.
The sum of an even and odd number is odd.
The sum of an even and odd number is odd.
Savvas Learning Co Geometry Student Edition Chapter 2 Reasoning And Proof Exercise 2.1 Patterns and Inductive Reasoning Page 85 Exercise 17 Problem 17
Given: The product of two odd numbers
To find: A conjecture for each scenario
Since odd numbers are not divisible by two.
If multiplying two odd numbers got us an even number, then we would have the product of 2 and some number.
However, this is not right, because of the previous statement that odd numbers cannot be divisible by two.
So, the product of two odd numbers is odd.
The product of two odd numbers is odd.
