Savvas Learning Co Geometry Student Edition Chapter 9 Transformations Exercise
Page 541 Exercise 1 Problem 1
The given two triangle are congruent.
To complete the congruence statement for the given pair △ABC≅.
Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal
Congruent triangles have congruent corresponding sides.
Triangles share the side \(\overline{A C}\).
Corresponding side to \(\overline{A B}\) is \(\overline{A D}\)
Since the triangles are congruent , it follows that ⇒ \(\overline{A B}\) ≅ s \(\overline{A D}\)
Corresponding side to \(\overline{C B}\) is \(\overline{C D}\)
Since the triangles are congruent , it follows that \(\overline{C B}\) ≅ \(\overline{C D}\)
The congruence statement is
⇒ △ABC ≅ △ADC
The congruence statement is △ABC ≅ △ADC
Page 541 Exercise 2 Problem 2
The given two triangle are congruent.
To complete the congruence statement for the given pair △ABC≅.
Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal
Congruent triangles have congruent corresponding sides.
Corresponding side to \(\overline{A C}\) is \(\overline{L K}\).
Since the triangles are congruent, it follows that ⇒ \(\overline{A C}\) ≅ \(\overline{L K}\)
Corresponding side to \(\overline{C B}\) is \(\overline{K J}\)
Since the triangles are congruent, it follows that ⇒ \(\overline{C B}\) ≅ \(\overline{K J}\)
Corresponding side to \(\overline{B A}\) is \(\overline{J L}\).
Since the triangles are corresponding, it follows that ⇒ \(\overline{B A}\) ≅ \(\overline{J L}\)
The congruence statement is ⇒ △ABC≅△LJK
The congruence statement is △ABC≅△LJK
Page 541 Exercise 3 Problem 3
The given two triangle are congruent.
To complete the congruence statement for the given pair △ABC≅.
Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal
Congruent triangles have congruent corresponding sides.
Corresponding side to \(\overline{A C}\) is \(\overline{R S}\).
Since the triangles are congruent, it follows that ⇒ \(\overline{A C}\) ≅ \(\overline{R S}\).
Corresponding side to \(\overline{A B}\) is \(\overline{R T}\).
Since the triangles are congruent, it follows that ⇒ \(\overline{A B}\) ≅ \(\overline{R T}\).
Corresponding side to \(\overline{B C}\) is \(\overline{T S}\).
Since the triangles are congruent, it follows that ⇒ \(\overline{B C}\) ≅ \(\overline{T S}\)
The congruence statement is ⇒△ABC ≅ △RTS
The congruence statement is △ABC ≅ △RTS
Page 541 Exercise 4 Problem 4
The given two triangle are congruent.
To complete the congruence statement for the given pair △ABC≅
Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal
Congruent triangles have congruent corresponding sides and angles.
Corresponding side to \(\overline{A B}\) is \(\overline{H L}\).
Since the triangles are congruent, it follows that ⇒ \(\overline{A B}\) ≅\(\overline{H L}\)
Corresponding side to \(\overline{B C}\) is \(\overline{H C}\).
Since the triangles are congruent, it follows that ⇒ \(\overline{B C}\) ≅ \(\overline{H C}\).
Corresponding side to \(\overline{A C}\) is \(\overline{C L}\).
Since the triangles are congruent, it follows that ⇒ \(\overline{A C}\) ≅ \(\overline{C L}\)
The congruence statement is ⇒ ΔABC ≅ △LHC
The congruence statement is ΔABC ≅ △LHC
Page 541 Exercise 5 Problem 5
The given regular polygon is decagon.
To find – The measure of an angle of the given regular polygon.
The measure of interior angle of a regular n-polygon is given by (n−2)⋅180° .
A regular decagon is a regular polygon with 10 sides.
Substitute n=10 into the formula from the Polygon Interior Angles Sum Theorem to calculate the sum of the measures of the angles
⇒ (10−2)⋅180
Calculate the sum of the angles:
⇒ (10−2 ) × 180
⇒ 1440°
Since the angles of a regular polygon are all equal in measure, divide the sum by the number of angles to find the measure of one angle:
⇒ \(\frac{1440}{10}\)
Divide the numbers ⇒ 144°
Therefore, the measure of the interior angle of a regular decagon is 144°.
The measure of the interior angle of a regular decagon is 144°.
Page 541 Exercise 6 Problem 6
The given regular polygon is 18 -polygon.
To find – The measure of an angle of the given regular polygon.
The measure of interior angle of a regular n-polygon is given by \(\frac{(n-2) \cdot 180^{\circ}}{n}\)
The formula for the measure $m$ of an interior angle of a regular n-polygon is m = \(\frac{(n-2) \cdot 180^{\circ}}{n}\)
Since the given regular polygon is an n = 18 into the equation. m = \(\frac{(18-2) \cdot 180^{\circ}}{18}\)
Calculate the value of m:
m = \(\frac{(18-2) \times 180}{18}\)
m = 160
⇒ 160°
The measure of an interior angle of an 18 – polygon is 160°.
Page 541 Exercise 7 Problem 7
The given quadrilateral is rectangle.
To find whether a diagonal of the given quadrilateral always, sometimes, or never produces congruent triangles.
Two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other.
The rectangle ABCD is a parallelogram with four right angles.
The diagonal \(\overline{A C}\) is separating the rectangle ABCD into two right triangles △ABC and △ADC
The diagonal AC is the hypotenuse of both triangles △ABC and △ADC.
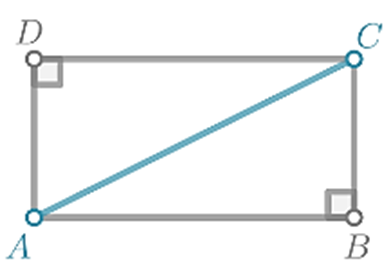
The leg \(\overline{A B}\) is congruent with \(\overline{C D}\).
Since conditions for the Hypotenuse-Leg (HL)
Theorem are met, triangles △ABC and △ADC are congruent.
It follows that the diagonal of any rectangle will split the rectangle into two right, congruent triangles.
The diagonal of the rectangle will always separate the rectangle into two congruent triangles.
The diagonal of the rectangle will always separate the rectangle into two congruent triangles.
Page 541 Exercise 8 Problem 8
The given quadrilateral is isosceles trapezoid.
To find whether a diagonal of the given quadrilateral always, sometimes, or never produces congruent triangles.
Two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other.
The diagonal AC is separating the isosceles trapezoid ABCD into two triangles △ABC and △ADC.
The diagonal AC is the side of both triangles △ABC and △ADC.
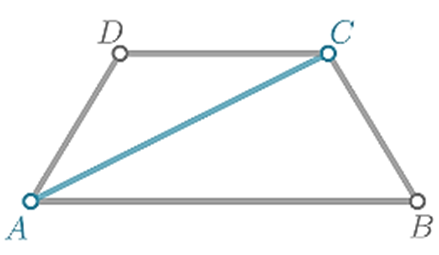
The leg h \(\overline{A D}\) is congruent with \(\overline{B C}\).
Since the bases AB and CD never have equal length, the triangles will never be congruent.
The diagonal of the isosceles trapezoid will never separate the trapezoid into two congruent triangles.
The diagonal of the isosceles trapezoid will never separate the trapezoid into two congruent triangles.
Page 541 Exercise 9 Problem 9
The given quadrilateral is kite.
To find whether a diagonal of the given quadrilateral always, sometimes, or never produces congruent triangles.
Two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other.
Kite has 2 diagonals.
The diagonal \(\overline{A C}\) is separating the kite ABCD into two triangles △ABC and △ADC.
The diagonal\(\overline{A C}\) is the side of both triangles △ABC and △ADC.
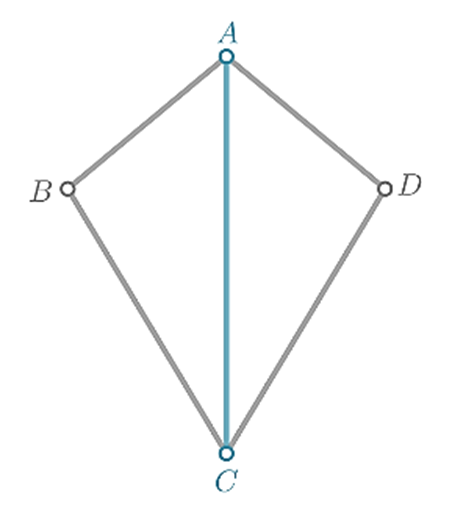
The side \(\overline{A C}\) is congruent with \(\overline{A D}\) . The side \(\overline{B C}\) is congruent with \(\overline{D C}\) .
Since conditions for the Side-Side-Side Postulate are met, triangles △ABC and △ADC are congruent.
The diagonal \(\overline{B D}\) is separating the kite ABCD in to two triangles △ABD and △BCD.
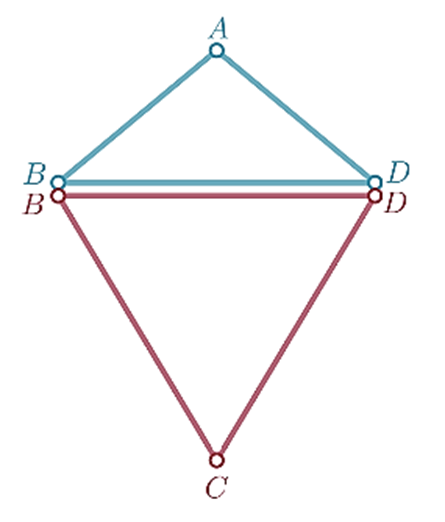
If the legs of triangle △BCD are not the same length as the legs of triangle △ABD , the triangles are not congruent.
The diagonal of the kite will sometimes separate the kite into two congruent triangles.
The diagonal of the kite will sometimes separate the kite into two congruent triangles.
Page 541 Exercise 10 Problem 10
To find whether a diagonal of the given quadrilateral always, sometimes, or never produces congruent triangles.
Two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other.
The diagonal AC is separating the parallelogram ABCD into two triangles △ABC and △ADC . The diagonal \(\overline{A C}\) is the side of both triangles △ABC and △ADC.
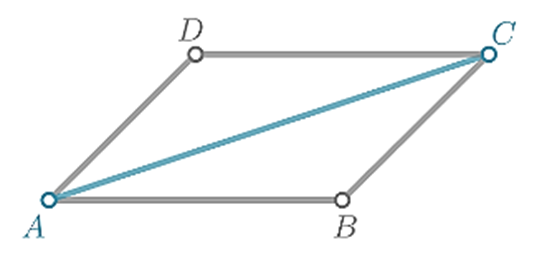
The side \(\overline{A B}\) is congruent with \(\overline{C D}\) . The side \(\overline{A D}\) is congruent with \(\overline{B C}\).
Since conditions for the Side-Side-Side Postulate are met, triangles △ABC and △ADC
are congruent.
It follows that the diagonal of any parallelogram will split the parallelogram into two congruent triangles.
The diagonal of the parallelogram will always separate the parallelogram into two congruent triangles.
The diagonal of the parallelogram will always separate the parallelogram into two congruent triangles.
Page 541 Exercise 11 Problem 11
The given length of a wall in the blueprint is 2.5in.
To find the length of the actual wall.
The given scale of a blueprint is 1in. = 20ft
The length of a wall in the blueprint is ⇒ 2.5in
Substitute scale1in.=20ft to convert to actual length ⇒ 2.5 × 20ft
Multiply the numbers ⇒ 2.5 × 20
⇒ 50
The actully length of the well is 50 ft.
Page 541 Exercise 12 Problem 12
The given entrance is wide.
To find the blueprint length of an entrance that is 5ft wide.
The given scale of a blueprint is 1in.=20ft
Let w be the width of the door on the image.
Using the scale and given width, write the proportion for the width w:
⇒ \(\frac{1}{20}\) = \(\frac{w}{5}\)
Calculate the value of w:
⇒ \(\frac{1}{20}\) = \(\frac{w}{5}\)
⇒ w = 0.25
The width of the door on the image is 0.25in.
The width is 0.25in
The width is 0.25in.
Page 541 Exercise 13 Problem 13
Given: A mirror and a person
To find if you raise your right hand, which hand appears to be raised in your reflection and If you are standing 2ft from the mirror, how far away from you does your reflection appear to be?
If you raise your right hand, left hand appears to be raised in your reflection If you are standing 2ft from the mirror, your reflection appear to be at a distance 4ft of from you
Therefore ,If you raise your right hand, left hand appears to be raised in your reflection If you are standing 2ft from the mirror, your reflection appear to be at a distance 4ft of from you.
Page 541 Exercise 14 Problem 14
Given:
The minute hand of a clock rotates as the minutes go by.
To find – That what point of the minute hand stays fixed as the hand rotates
The back end of the minute hand or the beginning part of the minute hand stays fixed as the hand rotates
The back end of the minute hand or the beginning part of the minute hand stays fixed as the hand rotates.
Page 541 Exercise 15 Problem 15
Given:
The pupils in your eyes dilate in the dark
To find – That what it means to dilate a geometric
To dilate a geometric, means to change the size of a given figure, without changing its shape.
For example: An equilateral triangle of side 3 units can be dilated to an equilateral triangle with side 9 units.
Therefore, Dilation is the process of increasing the size of an object while maintaining its shape.
Page 541 Exercise 16 Problem 16
The given that an interior designer used a repeating pattern when planning the tiling of a bathroom floor.
To describe your thinking about a tiling is in geometry.
A repeating pattern is a type of pattern where the rule just keeps on repeating over and over.
In real life, tiles used in floors should have the same pattern for it to be aesthetically pleasing.
Tiles are connected side by side to fill a certain floor area.
In geometry , tilling means a repeating patter of shapes that completely fills a plane.