Vector Calculus 4th Edition Chapter 1 Vectors
Page 38 Problem 1 Answer
Given :
|2 1|
| 4 3 |
Evaluate to get the final answer.
Definition 4.2, gives a formula for evaluating determinants.
|2 1|
|4 3|
=(2)(3)−(1)(4)
=6−4
=2.
Hence, the required solution is 2.
Page 38 Problem 2 Answer
Given :
|0 −1|
|5 6|.
Evaluate to get the final answer.
Definition 4.2,
gives a formula for evaluating determinants.
=|0 −1|
|5 6|
=(0)(6)−(5)(−1)
=0+5
=5
Hence, the required solution is 5.
Read and Learn More Susan Colley Vector Calculus Solutions
Page 38 Problem 3 Answer
Given :
|1 0 −1|
|3 2 0|
|5 7 3|
Evaluate to get the final answer.
Definition 4.2, gives a formula for evaluating determinants.
∴ \(\left|\begin{array}{ccc}
1 & 3 & 5 \\
0 & 2 & 7 \\
-1 & 0 & 3
\end{array}\right|=1\left|\begin{array}{ll}
2 & 7 \\
0 & 3
\end{array}\right|-3\left|\begin{array}{cc}
0 & 7 \\
-1 & 3
\end{array}\right|+5\left|\begin{array}{cc}
0 & 2 \\
-1 & 0
\end{array}\right|\)
= 1(6-0) -3(0+7)+5(0+2)
= 6-21+10
= -5
Hence, the required solution is −5.
Page 38 Problem 4 Answer
Given :
|−2 3 4|
|0 6 −8|
|1/2 −1 2|
Evaluate to get the final answer.
Definition 4.2, gives a formula for evaluating determinants.
∴ \(\left|\begin{array}{ccc}
-2 & 0 & 1 / 2 \\
3 & 6 & -1 \\
4 & -8 & 2
\end{array}\right|=-2\left|\begin{array}{cc}
6 & -1 \\
-8 & 2
\end{array}\right|-0\left|\begin{array}{cc}
3 & -1 \\
4 & 2
\end{array}\right|+\frac{1}{2}\left|\begin{array}{cc}
3 & 6 \\
4 & -8
\end{array}\right|\)
= -2(12-8) – 0 + 1/2(-24-24)
= -8-24
= -32
Hence, the required solution is −32.
Page 38 Problem 5 Answer
Given : (3i−2j+k)×(i+j+k).
Evaluate to get the final answer.
Let us consider and simplify,
Apply Formula 2:
a×b=(a2b3−a3b2)i+(a3b1−a1b3)j+(a1b2−a2b1)k
Evaluate cross product using formula (2):
=(3,−2,1)×(1,1,1)
=(−2−1)i+(1−3)j+(3+2)k
=−3i−2j+5k
Formula 3:
∴ \(a \times b=\left|\begin{array}{ccc}
i & j & k \\
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3
\end{array}\right|\)
Evaluate cross-product using formula (3):
= (3, -2, 1) x (1, 1, 1)
= \(\left|\begin{array}{ccc}
i & j & k \\
3 & -2 & 1 \\
1 & 1 & 1
\end{array}\right|\)
= -3i – 2j + 5k
Hence, the required answer is −3i−2j+5k.
Page 38 Problem 6 Answer
Given : (i+j)×(−3i+2j).
Evaluate to get the final answer.
Let us consider and simplify,
Formula (2):
a×b=(a2b3−a3b2)i+(a3b1−a1b3)j+(a1b2−a2b1)k
Evaluate cross product using formula (2):
=(1,1,0)×(−3,2,0)
=(0−0)i+(0−0)j+(2+3)k
=5k
Apply Formula (3):
∴ \(a \times b=\left|\begin{array}{ccc}
i & j & k \\
a_1 & a_2 & a_3 \\
b_1 & b_2 & b_3
\end{array}\right|\)
Evaluate cross-product using formula (3):
= (1, 1, 0) x (-3, 2, 0)
= \(\begin{gathered}
\left|\begin{array}{ccc}
i & j & k \\
1 & 1 & 0 \\
-3 & 2 & 0
\end{array}\right| \\
\end{gathered}\)
= 5k
Hence, the required solution is 5k.
Page 38 Problem 7 Answer
To Prove property 3 of cross products.
Using properties 1 and 2
Evaluate to get the final answer.
We have to prove that (a+b)×c=a×c+b×c using properties 1 and 2.
Proof:
(a+b)×c=(1)−c×(a+b)=(2)−c×a−c×b=(1)a×c+b×c
Hence using property (1) and (2) we have proved.
Page 38 Problem 8 Answer
Given: If vector a×b=3i−7j−2k.
To find: Value of(a+b)×(a−b).
Evaluate to get the final answer.
For solve this problem, first we find the Cross Product of (a+b)(a−b), and then we put the value of ab=3i−7j−2k into this Cross Product.
First we use the property of Cross Product
(a+b)c=ac+bc(distributivity)…(1)
Hence,(a+b)(a−b)=a(a−b)+b(a−b)
=a(a+(−b))+b(a+(−b))…(1)
Now we use the property of Cross Product
a(b+c)=ab+ac(distributivity) into (1),
we get,(a+b)(a−b)=a(a+(−b))+b(a+(−b))
=aa+a(−b)+ba+b(−b)
=aa−ab+ba+bb…(2)
Now we use the property of Cross Product
aa=0 into (1), we get (a+b)(a−b)=0−ab+ba+0
=−ab+ba…(3)
Now we use the property of Cross Product
ab=−b a (anticommutativity), into (3),
we get,(a+b)(a−b)=−ab−ab
=−2(ab)…(4)
Now, put the value ofab=3i−7j−2k into (iv), we get (a+b)(a−b)=−2(3i−7j−2k)
=−6i+14j+4k
(a+b)(a−b)=−6i+14j+4k
Hence, the required solution is (a+b)(a−b)=−6i+14j+4k.
Page 38 Problem 9 Answer
Given : The parallelogram have vertices(1,1),(3,2),(1,3),(−1,2).
To calculate: The area of the parallelogram of given vertices.
Evaluate to get the final answer.
We need to form vectors from two adjacent sides.
Drawing a picture, we see that the side with vertices (1,1) and(3,2) and the side with vertices (1,1)and(−1,2) are adjacent.
The vectors corresponding to these sides area=(3,2)−(1,1)=(2,1) and b=(−1,2)−(1,1)=(−2,1).
Now we just need to find the length of the cross product of these.
Except these vectors are in R2, not R3.
No worries, just embed these vectors in R3 by setting their z-components equal to 0 (i.e. a=2i+j+0k=2i+j and similarly for b)Then,
Area of Parallelogram
=∥a×b∥
=∥(2i+j)×(−2i+j)∥
=∥−4i×i+2i×j−2j×i+j×j∥
=∥4i×j∥
=∥4k∥
=4
The area of the given parallelogram is 4.
Page 38 Problem 10 Answer
Given : The parallelogram have vertices(1,2,3),(4,−2,1),(−3,1,0),(0,−3,−2).
To calculate: The area of parallelogram having above vertices.
Evaluate to get the final answer.
We need two adjacent sides to form vectors.
A bit of thought shows that the side with vertices(1,2,3) and(4,−2,1) and the side with vertices(1,2,3) and(−3,1,0) are adjacent.
The vectors corresponding to these sides area=(4,−2,1)−(1,2,3)=(3,−4,−2) and b=(−3,1,0)−(1,2,3)=(−4,−1,−3).
Now we use the fact that the length of the cross product is equal to the area of the parallelogram determined by the vectors:
Area of Parallelogram
=∥a×b∥
=∥(3i−4j−2k)×(−4i−j−3k)∥
=∥−3i×j−9i×k+16j×i+12j×k+8k×i+2k×j∥
=∥−3k+9j−16k+12i+8j−2i∥
=∥10i+17j−19k∥
=√102+172+(−19)2
=5√30
The area of given parallelogram is 5√30.
Page 38 Problem 11 Answer
Given: Vector is perpendicular to indices 2i+j−3k and i+k.
To find: The unit of vector having both indices.
Evaluate to get the final answer.
The cross product will give us the right direction; if we then divide this result by its length we will get a unit vector.
Let, the desired vector,
=(2,1,−3)×(1,0,1)
∥(2,1,−3)×(1,0,1)∥=(1,−5,−1)
∥(1,−5,−1)∥=1/√27(1,−5,−1)
Hence, The desired vector is 1/√27(1,−5,−1).
Page 38 Problem 12 Answer
Given :(a×b)⋅c=0
To determine: The geometric relation between a,b, and c.
Evaluate to get the final answer.
For (a×b)⋅c to be zero either of the following conditions are true:
One or more of the three vectors is 0
a×b=0 which would happen if a=kb for some real k, or c is in the plane determined by a and b.
Hence, For (a×b)⋅c to be zero either of the following conditions are true:
One or more of the three vectors is 0a×b=0 which would happen ifa=kb for some real k, orc is in the plane determined by a and b.
Page 38 Problem 13 Answer
Given: The triangle is determined by vectors a=i+j andb=2i−j.
To Compute: The area of triangle determined by above vectors.
Evaluate to get the final answer.
We know that the magnitude of the cross product of these two vectors will give the area of a parallelogram spanned by them as shown in the adjacent figure.
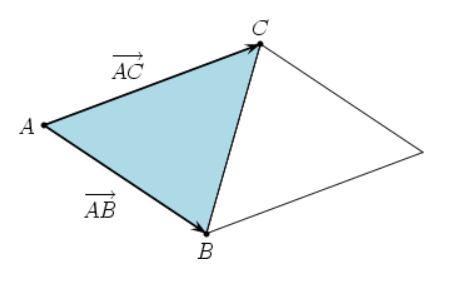
It follows that area of the triangle is half of the magnitude of the cross product.
The area is half of the magnitude of the cross product of the two vectors−(1,1,0) and(2,−1,0)
Area of triangle :
=(1/2)∗∥(1,1,0)×(2,−10)∥
=(1/2)∗∥(0,0,−3)∥
=3/2
Hence, we get that the area of triangle is 3/2.
Page 38 Problem 14 Answer
Given: The triangle is determined by vectors a=i−2j+6k and b=4i+3j−k.
To compute: The area of triangle determined by above vectors.
Evaluate to get the final answer.
We know that the magnitude of the cross product of these two vectors will give the area of a parallelogram spanned by them as shown in the adjacent figure.
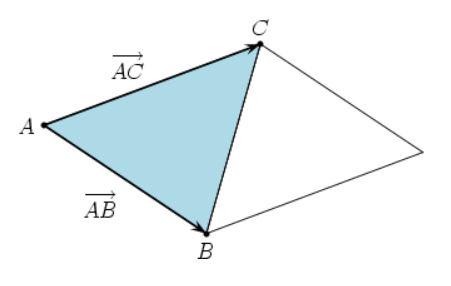
It follows that area of the triangle is half of the magnitude of the cross product.
The area is half of the magnitude of the cross product of the two vectors−(1,−2,6) and (2,−1,0)(4, 3, −1)
The area of triangle is :
=(1/2)∗∥(1,−2,6)×(4,3,−1)∥
=(1/2)∥(−16,25,11)∥
=√1002/2
Hence, we get that the area of triangle is =√1002/2.