Vector Calculus 4th Edition Chapter 2 Differentiation in Several Variables
Page 95 Problem 1 Answer
Given : f: R→R be given by f(x)=2x2+1.
To find : The domain and range of function.Evaluate the function to get solution.
Consider given function,
f:R→R be given by f(x)=2x2+1 .
The domain and codomain of f are explicitly R.
Since 0≤x2 for all x∈R we have that 0≤2x2 for all x∈R.
Thus,1≤2x2+1=f(x) for all x∈R and therefore the range of f is {y∈R:y≥1}.
Hence, the domain of function f is R and range of function is {y∈R:y≥1}.
Page 95 Problem 2 Answer
Given : f:R→R be given by f(x)=2x2+1
To find : Whether the function is one-one or not .Evaluate the given function to find solution.
Consider above function,
f:R→R be given by f(x)=2x2+1
Observe that f(−1)=3=f(1) which gives us that f is not one-to-one.
Therefore, the given function f is not one-to-one.
Read and Learn More Susan Colley Vector Calculus Solutions
Page 95 Problem 3 Answer
Given : f:R→R be given by f(x)=2x2+1 .
To find : If the function is onto.Evaluate above function to find solution.
Consider the above function ,
Let f:R→R be given by f(x)=2x2+1 .
By the item (a) we have that the range of f is not R.
Therefore f is not onto.
Therefore, f is not onto.
Solutions To Chapter 2.1 Differentiation Bu Susan Colley Page 95 Problem 4 Answer
Given:f(x,y)=ln(x+y)
To find: Domain and Range of the given function.
Evaluate to get the final answer.
From the given function f(x,y)=ln(x+y).
Observe that the expression,
ln(x+y) is well defined if and only ifx+y>0.
Thus, the domain of f is {(x,y)∈R2:x+y>0}
given x∈R we have that 0<ex=ex+0.
Hence, we get f(ex,0)=ln(ex+0)
=ln(ex)
=x.
Therefore, range off isR.
Therefore, domain of fis{(x,y)∈R2:x+y>0}.and range of f is R
Page 95 Problem 5 Answer
Given: g(x,y,z)=√x2+(y−2)2+(z+1)2
To find: Domain and range of the function Evaluate to get the final answer.
We Consider the function,
⇒ g(x,y,z)=√x2+(y−2)2+(z+1)2.
From the function we can observe that 0≤x2+(y−2)2+(z+1)2 for all (x,y,z)∈R and therefore the expression,
⇒ √x2+(y−2)2+(z+1)2 is well defined for all(x,y,z)∈R3
Thus, the domain of g is R3.
We now observe that 0≤√x2+(y−2)2+(z+1)2 } for all (x,y,z)∈R3
Given x∈R we have,
⇒ g(x,2,−1)=√x2+(2−2)2+(−1+1)2
=√x2
=∣x∣.
Thus, the range of g is [0,∞).
Hence, domain of g is R3 and range of g is [0,∞).
Page 96 Problem 6 Answer
Given: g(x,y,z)=1
⇒ √4−x2−y2−z2
To find: Domain and range of the given function.
Evaluate to get the final result.
From the given function, we observe that the function is always positive i.e.
√4−x2−y2−z2>0⇒x2+y2+z2<4 as long as the inequality above holds, the function will be well defined.
Hence, the domain of the function is a subset of R3 with the following properties:{(x,y,z)=x2+y2+z2<4}
As for the range of the function, we determine it by assigning y and z on 0.
The smaller the denominator the larger the expression will be, hence the biggest denominator is achieved if we set x=0.
Therefore, the lowest value we can get in this case is 1/2
Since we can make denominator arbitrary small, we can consider any other real number larger than 1/2 by adjusting x and keeping the other two values intact.
Hence the range of the function is [1/2,∞⟩
Therefore, the given function has following,
Domain:{(x,y,z)=x2+y2+z2<4} and range: [1/2,∞⟩
Susan Colley Chapter 2.1 Partial Differentiation Solved Problems Page 96 Problem 7 Answer
Given:f(x,y)=(x+y,1/y−1,x2+y2)
To Find: Domain and Range of the given functionEvaluate to get the final answer.
Let us denote the components like below and discuss each of it separately.
⇒ f1(x,y)=x+y
⇒ f2(x,y)=1/y−1
⇒ f{3}(x,y)=x{2}+y{2}
The functions f1 and f3 are well defined for every pair (x,y).
except the entire domain of f is the function f2 which is not well defined if y=1 since we can not divide by zero.
Therefore the range of f is the following set:
{(x,y)∈R2:y≠1}
We now write the range of f in terms of it’s components.
The first component of range, x, can be any real number.
This is due to the property of the function f1, you can find two real numbers that, when added, yield a fixed real number.
The second component is a typical one variable rational function. It will yield all real number except 0 .
The third component, z, will yield a positive real number or zero if both x and y are zero.
Hence the range of f is:{(x,y,z):x∈R,y∈R,y≠1,z∈[0,∞⟩} which is not well defined if y=1 since we can not divide by zero.
Therefore the range of f is the following set: {(x,y)∈R2:y≠1}
Therefore, the range of f is : {(x,y,z):x∈R,y∈R,y≠1,z∈[0,∞⟩}
Page 96 Problem 8 Answer
Given: f:R2→R3 and f(x,y)=(x+y,yex,x2y+7)
To find: Component function of f Evaluate to get the final answer.
Since f is the vector function, it’s components are separated by comma.
We can further simplify the given functions as,
⇒ f1(x,y)=x+y
⇒ f2(x,y)=yex
⇒ f3 (x,y)=x2y+7
Hence, component functions of f are:
⇒ f1(x,y)=x+y
⇒ f2(x,y)=yex
⇒ f3(x,y)=x2y+7
Page 96 Problem 9 Answer
Given: v(x,y,z,t) = (xy zt ,x2−y2,3z+t)
To find the component function for the given function.Evaluate to get the final answer.
The function in the given example is derived from the following formula:
⇒ v(x,y,z,t) = (xyzt,x2−y2,3z+t)
Rewriting the components we get:
⇒ v1(x,y,z,t)=xyzt
⇒ v2(x,y,z,t)=x2−y2
⇒ v3(x,y,z,t)=(3z+t)
Hence, component functions of the given expression are:
⇒ v1(x,y,z,t)=xyzt
⇒ v2(x,y,z,t)=x2−y2
⇒ v3(x,y,z,t)=(3z+t)
Page 96 Problem 10 Answer
Given:- f(x)=x+3j
To find:- The component functions off in terms of the components of the vector x
Evaluate to get the final answer.
Let us evaluate the vectors
Pay attention to two things.
First, f takes values from R3 and outputs the values in the same set.
This means that a vectorx∈R3 can be written as x=(x1,x2,x3)
Second recall that j=(0,1,0)
We can rewrite the components of f now like this:
⇒ f1 (x1,x2,x3)=x1
⇒ f2 (x1,x2,x3)=x2+3
⇒ f3 (x1,x2,x3)=x3
Note that this is in fact equal to the expression given to us in task,
But the only difference is that the f is rewritten in terms of its components.
Hence, the component functions of f in terms of the components of the vector x is f1
(x1,x2,x3)=x1 ,f2(x1,x2,x3)=x2+3 and f3(x1,x2,x3)= x3
Differentiation In Several Variables Susan Colley Chapter 2.1 Examples Page 96 Problem 11 Answer
Given:- A nonzero vector x in R3 the vector of length 2 that points in the direction opposite to x.
To find:- An analytic (symbolic) description of mapping Evaluate to get the final answer.
Let us evaluate the vectors
Analytically, take a vector and then return the vector of the exact same direction with an opposite orientation and the length of two.
Therefore, To turn x into a unit vector and then multiply the unit vector with−2.
The symbolic description of this operation is given below:−2x
⇒ ∥x∥
Hence, the analytic (symbolic) description of mapping is −2x
⇒ ∥x∥.
Page 96 Problem 12 Answer
Given:- a nonzero vector x in R3 the vector of length 2 that points in the direction opposite to x.
To find:- the component functions of x=(x,y,z) mapping.
Let us evaluate the vectors
Apply the analytic explanation given above.
Recall that for vector (x,y,z) a norm function (∥⋅∥) representing it’s length is usually defined like this:
⇒ (x,y,z)∥=√x2+y2+z2
Scale every component by the factor of−2
⇒ √x2+y2+z2
therefore :
⇒ f1(x,y,z)=−2x
⇒ √x2+y2+z2
⇒ f2(x,y,z)=−2y
⇒ √x2+y2+z2
⇒ f3(x,y,z)=−2z
⇒ √x2+y2+z2
Hence, the component function of x is f1
⇒ (x,y,z)=−2x
⇒ √x2+y2+z2, f2(x,y,z)=−2y
⇒ √x2+y2+z2 and f3(x,y,z)=−2z
⇒ √x2+y2+z2
Page 96 Problem 13 Answer
Given:- f(x)=Ax
Where, A=[2/5 −6−1 0/3] and x=[x1/x2]
To find:- the component functions of f in terms of the components x1, x2 of the vector x.
Let us evaluate the vectors,
Consider the given function f(x1,x2)=A(x1,x2)
Where A=[2/5−6−1 0/3]
Substitute A in the above function, to get;
⇒ f(x1,x2)&=[2/5−6−1/0 3][x1/x2]
=[2x1−x2/5×1−6×1+3×2]
Thus, f(x1,x2)=(2×1−x2,5×1,−6×1+3×2)
Hence, the component functions of f in terms of x1,x2 are (2x1−x2,5×1,−6×1+3×2).
Page 96 Problem 14 Answer
Given:- f(x)=Ax
Where, A=[2/5−6−1 0/3] & x=[x1/x2]
To find:- Range of f
Let us evaluate the vectors
The range of f is ;{(2×1−x2,5×1,−6×1+3×2):x1,x2∈R}
As linear combination of first and third component gives;
3(2x−y)+(−6x+3y)=0.
The range of f is the plane 3u+w=0.
Hence, the range of f is the plane 3u+w=0.
Page 96 Problem 15 Answer
Given: A=[2/0 2/0 3/0 −1/0−1/0 1]
⇒ x=⎣x1 x2 x3 x4 ⎤
To find: Component functions of f in terms of x1, x2, x3, and x4.Multiply A with x to determine f1, f2, f3.
Let us simplify the given exercise.
⇒ f1(x1,x2,x3,x4)=2x1−x3+ x4
⇒ f2(x1,x2=2,x3,x4)=3×2
⇒ f3(x1,x2,x3,x4)=f1(x1,x2,x3,x4)
Hence, the obtained expression is
⇒ f1=2×1−x3+x4,
⇒ f2=3 x 2 and f3=f1(x1,x2,x3,x4)
Susan Colley Vector Calculus Exercise 2.1 Problem Explanations Page 96 Problem 16 Answer
Given: A=[2 /0 2/0 3/0−1/0 −1/1 0/1]
⇒ X =⎣x1 x2 x3 x4⎤
To describe: The range of f. Evaluate to get the final answer.
Let us solve the given exercise,
The range is the plane in R3
which contains the origin that is said to be parallel to both (1,0,1) (and thus (2,0,2) and (−1,0,−1)
which are both parallel to this vector) and they-axis (hence the vector (0,3,0)).
The range of f is plane in R3
Page 96 Problem 17 Answer
Given: Function f(x,y)=3
To find: Several level curves of the function f
Evaluate to get the final answer.
Let us solve the given exercise.
The entire graph is in the contour curve (on the actual contour surface).
This is the plane parallel to xy plane at z=3
Therefore, we can conclude that the entire graph for Function f(x,y)=3 is in the contour curve.
Page 96 Problem 18 Answer
Given: Function f(x,y)=3
To obtain: Sketch of the graph off
Evaluate to get the final answer.
Following is the graph,
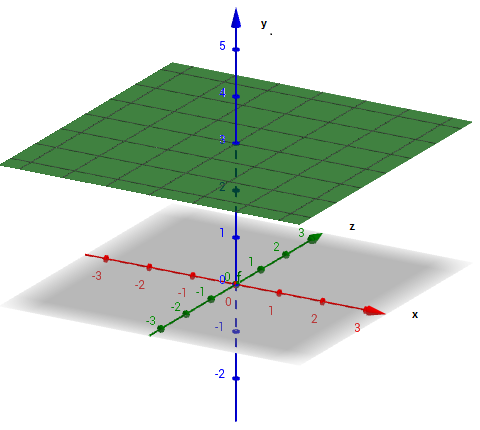
Therefore, we conclude that the entire graph for function f(x,y)=3 is in the contour curve.
Page 96 Problem 19 Answer
Given: Function f(x,y)=x2+y2
To find: Several level curves of the given function f
Evaluate to get the final answer.
Let us solve the exercise.
For a fixed z we can observe that the curve is defined by x and y
The function given in the task is zero if and only if both x and y are zero.
Hence, let us pick a height (level) in such a way that the value of the level is positive.
For example,c By rewriting the curve equation, we can see that a level surface in question is in fact a circle of a radius√c.
⇒ x2+y2=c
Hence, the obtained expression is x2+y2=c
Page 96 Problem 20 Answer
Given: f(x,y)=x2+y2
To Find: sketch the graph of f.Evaluate to get the result.
For a fixed z we observe the curve defined by x and y.
Obviously, the function given in the task is zero if and only if both x and y are zero.
Therefore, let us pick a height (level) such that the value of level is positive, for example c.
By rewriting the curve equation, we can see that a level surface in question is in fact a circle of a radius √c.x2+y2=c
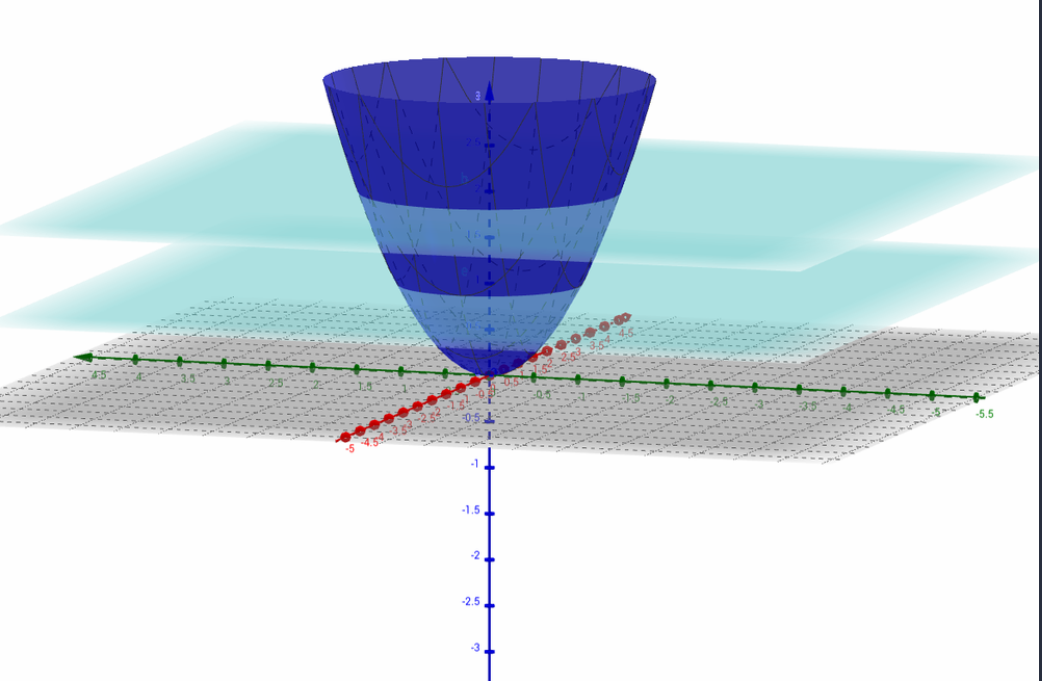
You can imagine a level curve in this case an intersection between the graph of a given surface and the plane z=c.
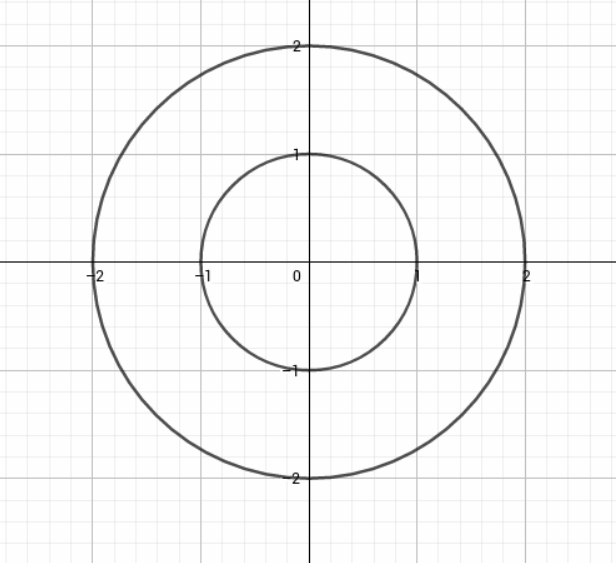
The example is given on the picture for c=1andc=2. The sketches of the level curves are then circles of radius 1 and√2 in the xy plane.
Let us plot a graph :
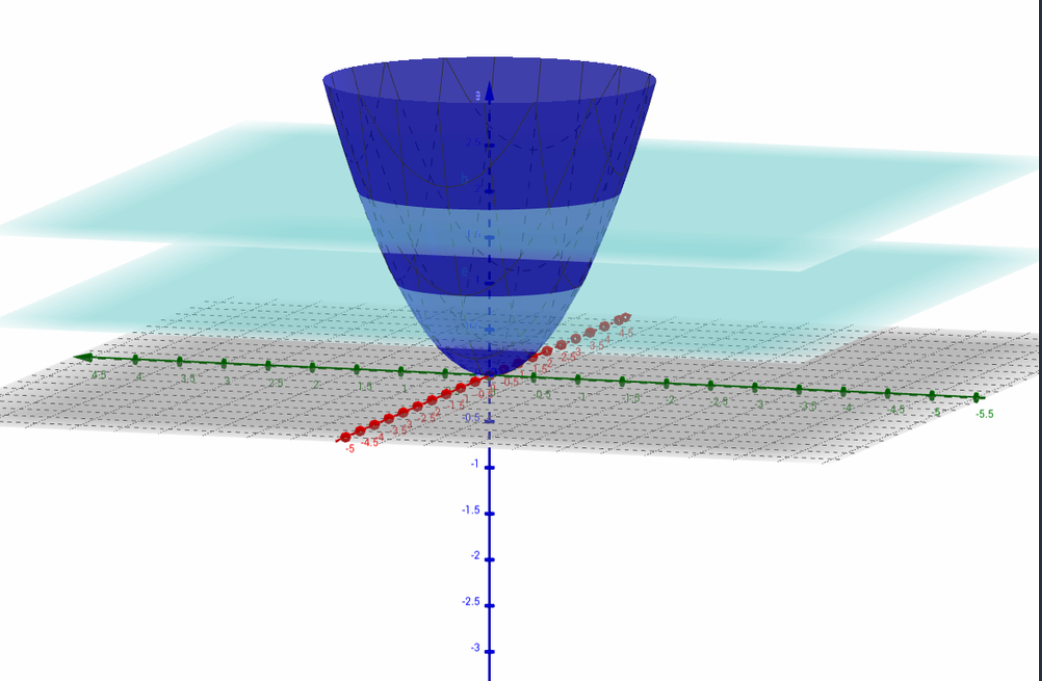
Hence, the required graph of f is :
Practice Problems For Differentiation In Several Variables Chapter 2.1 Page 96 Problem 21 Answer
Given : f(x,y)=x2+y2−9
To find : Determine several level curves of the given function f (make sure to indicate the height c of each curve).
Evaluate to get the result.
To find the type of the level curve, in this case it is enough to check the condition for the given function to be zero.
In fact one can easily observe that x2+y2−9=0 ⇒ x2+y2=9
The second equation is in fact the equation describing a circle with radius 3 and it’s center at origin.
All of the other level curves will in fact be circles, as shown on the image in step two.
If set the surface height on z=2,
Let us plot a graph :

View from the top will in fact show all three circles :
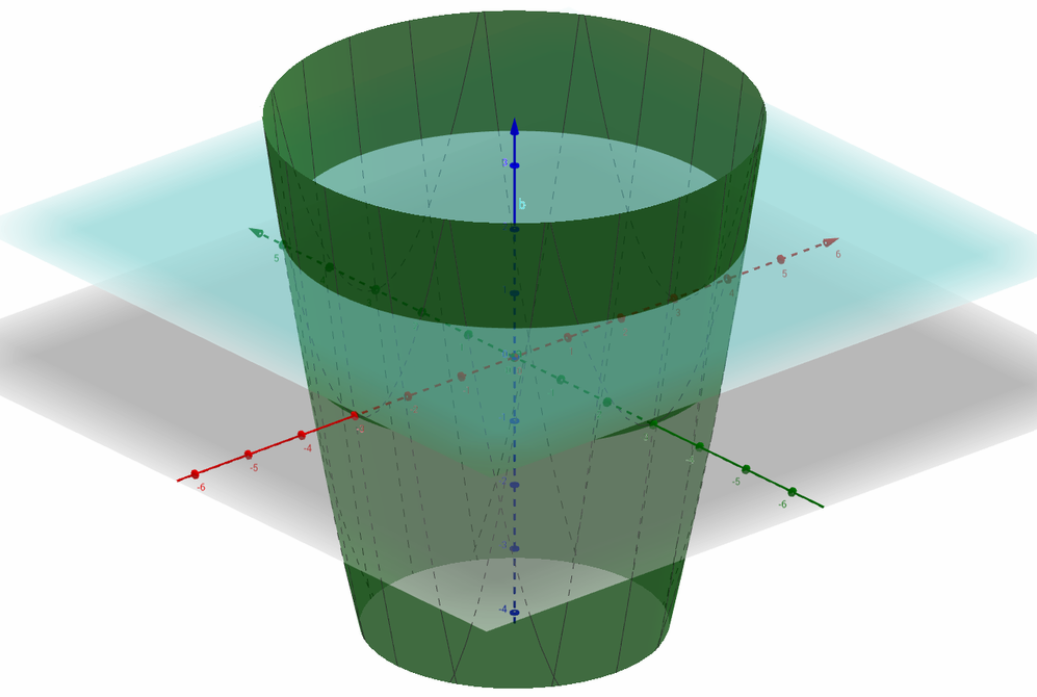
Note that there are infinitely many level curves that can be obtained like this and all of them are circles.
The bottom one is, however the smallest circle.
Hence, through the following images we determined several levels of curves of the given function.
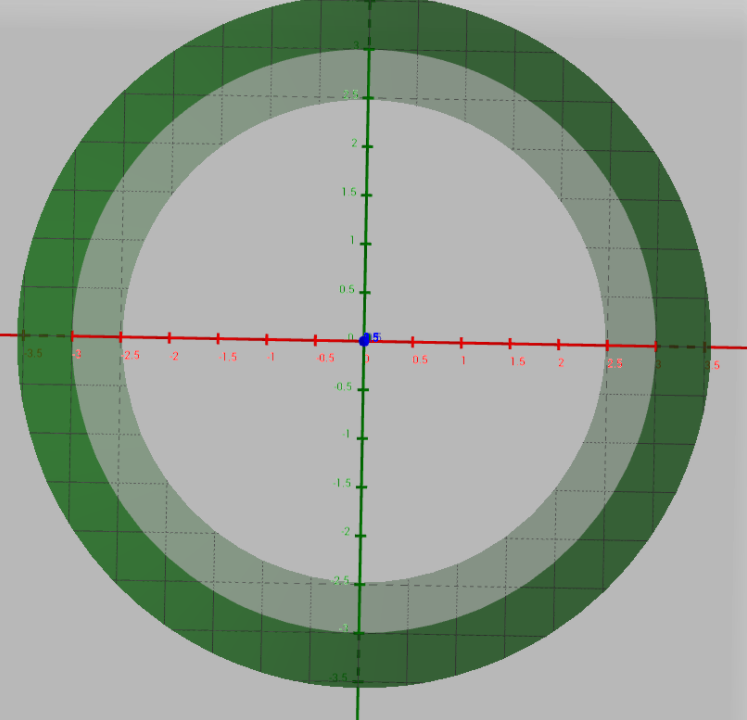
Page 96 Problem 22 Answer
Given :f(x,y)=x2+y2−9
To find : Use the information obtained in part (a) to sketch the graph of f.

Evaluate to get the result.
Finding the type of the level curve, in this case it is enough to check the condition for the given function to be zero.
In fact one can easily observe that
x2+y2−9=0 ⇒ x2+y2=9
The second equation is in fact the equation describing a circle with radius 3 and it’s center at origin.
All of the other level curves will in fact be circles, as shown on the image in step two.
If set the surface height on z=2, we get another circle with a larger radius,
Hence, the graph of f is:

Page 96 Problem 23 Answer
Given : f(x,y)=√x2+y2
To find : (a) Determine several level curves of the given function f (make sure to indicate the height c of each curve).
Evaluate to get the result.
This time, the given surface is a cone.
Intersecting the surface at any level other than zero will again yield the circle.
Let c be a level of a curve.
Then the equation of the curve is given by the following relation:
√x2+y2
=c ⇒ x2+y2
=c2
As you can see, a level curve on any height c is in fact a circle.
Below are sketches of circles on height 1 and 2.
Let us plot a graph:
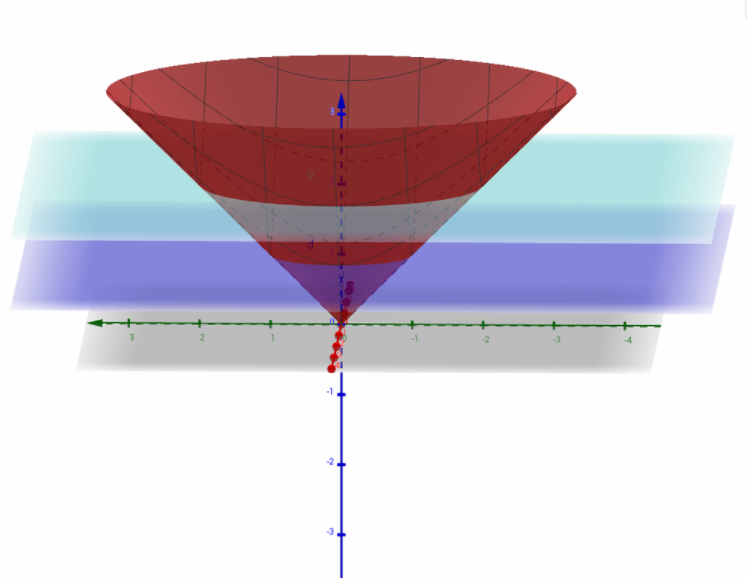
Now
Technically, the correct sketches of the level curves are on picture number two.
Imagine that we fix the height c on a plane z=c. For z=1 in a smaller circle.
For height z=2 is the larger one. This is exactly the situation depicted on a picture one.
So level curves are in fact drawn as a projections on xy plane with assumption that z is fixed.
Hence, Determined several levels of curves of the given function of f
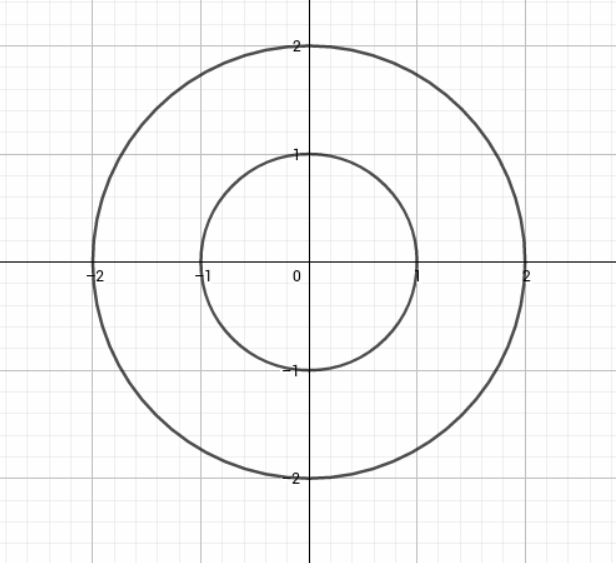
Susan Colley Vector Calculus Chapter 2.1 Differentiation Solutions Page 96 Problem 24 Answer
Given :f(x,y)=√x2+y2
To find : (b) use the information obtained in part (a) to sketch the graph off.
Evaluate to get the result
This time, the given surface is a cone.
Intersecting the surface at any level other than zero will again yield the circle Let be a level of a curve.
Then the equation of the curve is given by the following relation:
As you can see, a level curve on any height is in fact a circle. Below are sketches of circles on height 1 and 2.
Let us plot a graph :
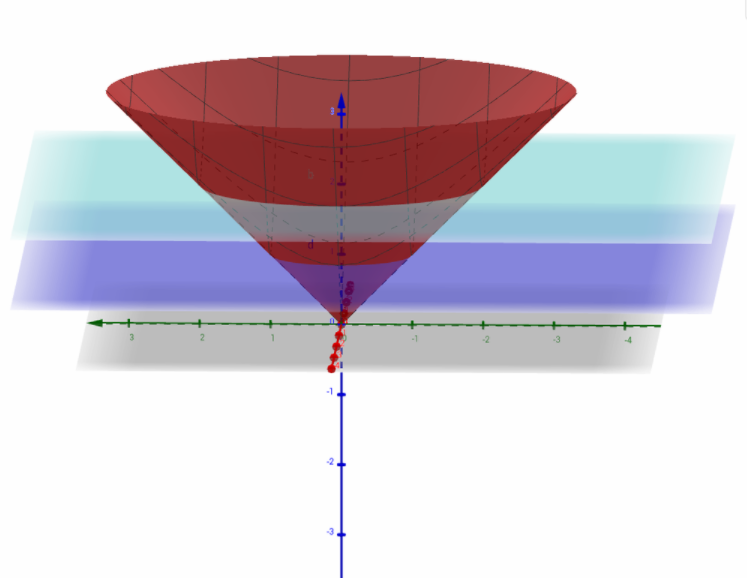
Next,
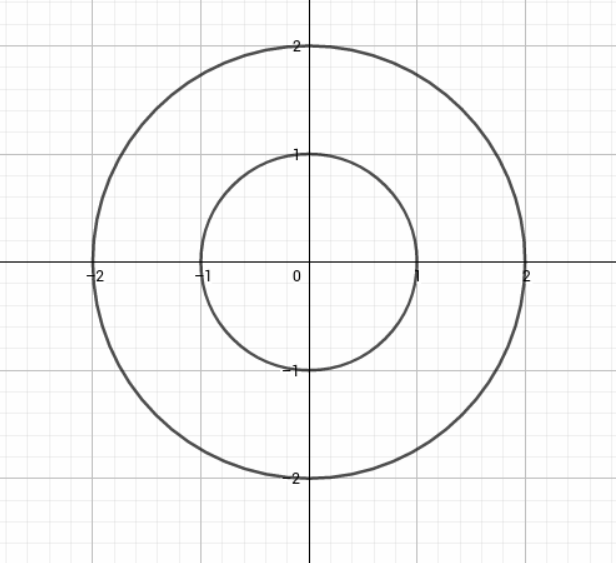
Hence, the graph of f is,