Susan Colley Vector Calculus 4th Edition Chapter 2 Exercise 2.2 Differentiation in Several Variables

Vector Calculus 4th Edition Chapter 2 Differentiation in Several Variables

Page 114 Problem 1 Answer

Given: {(x,y)∈R²∣1≤x²+y²≤4}

To determine whether the given set is open or closed.

Evaluate to find the answer.

Let us consider the given set and simplify,

X={(x,y)∈R²∣1≤x²+y²≤4}

This set is closed in R², since, it contains all of its boundary points.

The boundary of X consist the circumference of circles of radius 1, and 2

Finally, it can be seen from the image

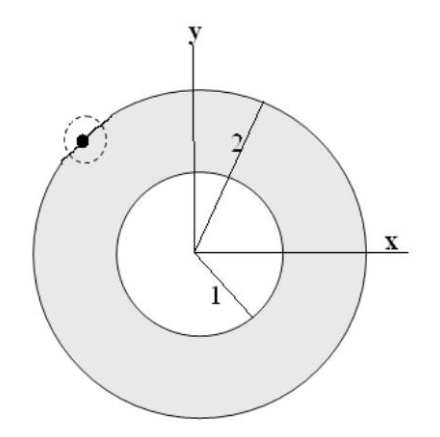
Hence, the given set is closed.

Page 114 Problem 2 Answer

Given: {(x,y)∈R²∣1≤x²+y²<4}

To determine the given set is open or closed.

Evaluate to find the answer.

Let us consider the given set and simplify.

This set contains the points on the circle described with an equation.

Read and Learn More Susan Colley Vector Calculus Solutions

x²+y²=1

but does not contain the points described with an equation,

x²+y²=4

So this set is neither open nor closed because it does not contain all of its boundaries.

Hence, the given set is neither open nor closed.

Page 114 Problem 3 Answer

Given: {(x,y,z)∈Rs

∣1≤x²+y²+z²≤4}

To determine whether the given set is open or closed.

Evaluate to find the solution.

Let us consider the given set and simplify

X={(x,y,z)∈R3∣1≤x²+y²+z²≤4}

This set is closed in R2,

As it can be seen it contains all of its boundary points.

The boundary of X consist of surfaces of spheres of radius 1 and 2

Similarly, we have the image here.

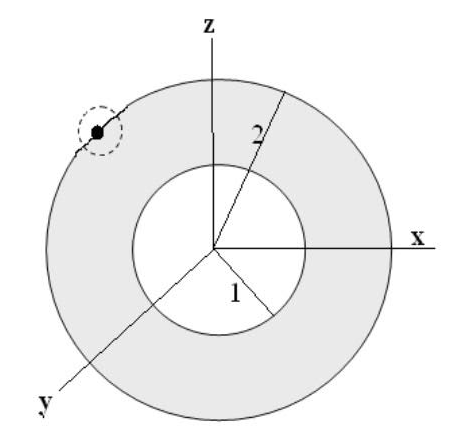
Hence, the given set is closed.

Page 114 Problem 4 Answer

Given: {(x,y,z)∈R3

∣1<x²+y²<4}

To determine whether the given set is open or closed.

Evaluate to find the solution.

Let us consider the given set and state.

First, the given set does not contain any restriction on z.

Also, the given set does not include its boundaries. So it should be the open set.

Hence, the given set is open.

Page 114 Problem 5 Answer

Given: [x​y]→[0,0]_I’m∣y∣√x²+y²

To find: Whether the limit exists or not.

Evaluate to find the solution.

Let us consider the given expression and simplify

Let us approach the value of y from the side where x=0 we get: (0,p)→(0,0)_lim f(x,y)=1

Nevertheless, let us see what happens when we set x=t and y=2t. If we approach the limit from this side we get: (x=t,p=2t)→(0,0)_lim f(x,y)=2∣t∣√5∣t∣

By cancelling out the terms t in the fraction above we can clearly see that the limit along these paths is not zero.

Hence, the limit does not exist.

Page 114 Problem 6 Answer

Given: A limit, (x,y)→(0,0)_lim ex ey x+y+2

To Find: The value of the limit or why does the given limit not exist.

Evaluate the given limit by plugging in the approaching values of x and y.

⇒ (x,y)→(0,0) _limex ey x+y+2

= (x,y)→(0,0)_lim e0 e0

0+0+2

⇒ (x,y)→(0,0)_limex ey x+y+2

=1/2

Hence, the value of the given limit is 1/2.

Page 114 Problem 7 Answer

Given: A limit, (x,y)→(−1,2)_lim 2x²+y²

x²+y²

To Find: The value of the limit or why does the given limit not exist.

In the given case, just plug in the values for x andy.

Since the given expression is well defined for (x,y)= (−1,2) the limit’s value can be calculated.

x,y)→(−1,2)_lim

2x²+y²

x²+y²

⇒ 2(−1)²+2(−1)²+2

= 6/5

Hence, the value of the given limit is 6/5.

Page 114 Problem 8 Answer

Given: A limit, (x,y)→(0,0)_lim x²+2xy+y²x+y

To Find: The value of the limit or why does the given limit not exist.

Solve the given limit using the standard formula:

(x+y)²=x²+2xy+y²

Apply the formula on the numerator:

(x,y)→(0,0)_lim (x+y)²

x+y⇒x+y=0

Hence, the value of the given limit is 0.

Page 114 Problem 9 Answer

Given: A limit, (x,y)→(0,0)_lim xy/x²+y²

To Find: The value of the limit or why does the given limit not exist.

It is known that the limit exists if the limit is the same when approached to it along all paths.

Consider the limit along the pathx=y :(x,y)→(0,0)_lim xy/x²+y²

⇒ y²2y²

= 1/2

Now take limit along the path x=0:

(x,y)→(0,0)_lim

xyx²+y²⇒0

y²=0

As the limits are not the same. Hence the limit does not exist

Hence, the given limit does not exist.

Page 114 Problem 10 Answer

Given: A limit, (x,y)→(0,0)_lim

x⁴−y⁴

x²+y²

To Find: The value of the limit or why does the given limit not exist.

The given limit can be easily solved by factoring and canceling out one factor with denominator we get:

(x,y)→(0,0) _lim

x⁴−y⁴

x²+y² ⇒ (x²−y²)(x²+y²)

x²+y²=0

Hence, the value of the given limit is 0.

Page 114 Problem 11 Answer

Given: A limit, (x,y)→(0.0)_limx²

x²+y²

To Find: The value of the limit or why does the given limit not exist.

It is known that the limit exists if the limit is the same when approached it from every path. Consider the pathx=y

(x,y) → (0,0)_limx²

x²+y² ⇒ y²

2y² = 1/2

On the other hand, along the path x=0, the result is:

(x,y) → (0,0) _limx²

x² + y² ⇒ 0

y² = 0

Since the results are different when we approach from the different parts, the limit does not exist.

Hence, the given limit does not exist.

Page 114 Problem 12 Answer

Given: A limit, (x,y)→(0,0),x≠y

_limx²−xy√x−√y

To Find: The value of the limit or why does the given limit not exist.

Here, firstly factor out the x

term in numerator. Then rewrite the other term as factors:

(x,y)→(0,0)_lim

x²−xy√x−√y

⇒x(x−y)/√x−√y

=x(√x−√y)(√x+√y)√x−√y

Now cancel out the terms and calculate limit effortlessly:

(x,y)→(0,0)_lim x(√x+√y)=0

The value of the given limit is 0.

Page 114 Problem 13 Answer

Given: A limit, (x,y)→(2,0)_lim

x²−y²−4x+4

x²+y²−4x+4

To Find: The value of the limit or why does the given limit not exist.

It is known that the limit exists if the limit of the expression is the same when approached it from any path.

Examine the case then we approach to the limit along the pathx=2

xy)→(2,0)_lim x²−y²−4x+4

x²+y²−4x+4 ⇒ −y²/y²

=−1

However, if it is approached along the path y=0 the expressions in the numerator and denominator become the same and they cancel out.

In that case, the limit is equal to 1.

Hence, the limit does not exist.

Hence, the given limit does not exist.

Page 114 Problem 14 Answer

Given: (x,y,z)→(0,√​π,1)_lim exz cosy²−x

To find: The limit and explain why the limit fails to exist.

Evaluate to get the answer.

The expression given in this task is well-defined for all triplets of real numbers.

Therefore we obtain the limit by simply plugging in the values in the expression:

(x,y,z)→(0,√​π,1)_lim e xz cos y²−x=e0⋅(−1)−0

=−1

Therefore, the required limit is −1.

Page 114 Problem 15 Answer

Given: (x,y,z)→(0,0,0)_lim2x²+3y²+z²

x²+y²+z²

To find: The limit or explain why the limit fails to exist.

Evaluate to get the answer.

This case is the same as the previous cases in two variables.

We again try to find two different paths that will give the different limit as a result.

If we manage to do this, the limit does not exist.

First, we take the path (x,y,z)=(t,t,t)

(x,y,z)→(0,0,0)_lim 2x²+3y²+z²

x²+y²+z²=6t²/3t²

=2

If we inspect the path (x,y,z)=(t,0,t)

We get the result:

(x,y,z)→(0,0,0)_lim 2x²+3y²+z²

x²+y²+z²= 3t²/2t²

=3/2

So, we found that the limits are different for the paths that lead to the same point and thus the limit does not exist.