Theorems Integral Transformations Deduction From gauss’s Gauss’s Divergence Green Identities

Integral Transformations Gauss’s Divergence Theorem

Let S be a closed surface enclosed in a volume V . If F is a continuously differentiable vector point function, then \(\int_V d i v \mathbf{F} d \mathbf{V}=\int_S \mathbf{F} \cdot \mathbf{N} d S\)

Where N is the outward drawn unit normal vector at any point of S.

Cartesian Form

Let F =F₁i+F₂ j+F₃ k and N=i cos α+j cos β+k cos γ

where \(\cos \alpha, \cos \beta, \cos \gamma\) are the direction cosines of N. \(\mathbf{F} . \mathbf{N}=\mathbf{F}_1 \cos \alpha+\mathbf{F}_2 \cos \beta+\mathbf{F}_3 \cos \gamma\)

Also div \(\mathbf{F}=\nabla . \mathbf{F}=\frac{\partial \mathbf{F}_1}{\partial x}+\frac{\partial \mathbf{F}_2}{\partial y}+\frac{\partial \mathbf{F}_3}{\partial z}\)

Hence the divergence theorem can be written as \(\iiint\left(\frac{\partial \mathbf{F}_1}{\partial x}+\frac{\partial \mathbf{F}_2}{\partial y}+\frac{\partial \mathbf{F}_3}{\partial z}\right) d x d y d z\)

= \(\int_S\left(\mathrm{~F}_1 \cos \alpha+\mathrm{F}_2 \cos \beta+\mathrm{F}_3 \cos \gamma\right) d S\)

= \(\iint_S\left(\mathbf{F}_1 d y d z+\mathbf{F}_2 d z d x+\mathbf{F}_3 d x d y\right)\)

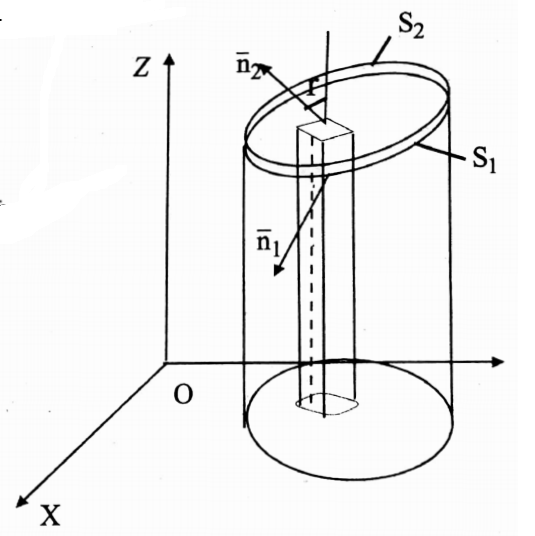
Proof: Let s be a closed surface. Let us choose the coordinate axes so that any line parallel to the coordinate axes cuts S in at most two points.  Let R be the projection of S on xy-plane. S and S are the lower and upper parts of S.

z=f(x,y) and z=g(x,y) be the  equations of S₁ and S₂. The relation can be put in the form f(x,y) ≤ z ≤ g(x,y).

∴  \(\int_V \frac{\partial \mathbf{F}_3}{\partial z} d \mathbf{V}\)\(=\iiint_V \frac{\partial \mathbf{F}_3}{\partial z}\) dx dy =\(=\iint_R\left[\frac{\partial \mathbf{F}_3}{\partial z} d z\right]_{z=f(x, y)}^{z=g(x, y)}\) dx dy

= \(\iint_R\left[\mathbf{F}_3(x, y, z)\right]_f^g d x d y=\iint_R\left[\mathbf{F}_3(x, y, g)-\mathbf{F}_3(x, y, f)\right] d x d y\)

= \(\iint_R \mathrm{~F}_3(x, y, g) d x d y-\mathrm{F}_3(x, y, f) d x d y\) …….. (1)

For the upper part \(\mathbf{S}_2 \quad d x d y=d S \cdot \cos \gamma=\mathbf{N} \cdot \mathbf{k} d S\)

Since the normal to \(\mathbf{S}_2\) makes an acute \(\gamma\) with \(\mathbf{k}\).

∴ \(\iint_R \mathbf{F}_3(x, y, g) d x d y=\int_{S_1} \mathbf{F}_{\mathbf{3}} \mathbf{N} \cdot \mathbf{k} d S\)

For the lower portion \(\mathbf{S}_1 \quad d x d y=-\cos \gamma d S=-\mathbf{N} \cdot \mathbf{k} d S\)

Since the normal to \(\mathbf{S}_1\) makes an obtuse angle \(\gamma\) with \(\mathbf{k}\)

∴ \(\iint_R \mathbf{F}_3(x, y, f) d x d y=-\int_{S_3} \mathbf{F}_3 \mathbf{N} \cdot \mathbf{k} d S\)

Hence from (1)

∴ \(\int_V \frac{\partial \mathbf{F}_3}{\partial z} d \mathbf{V}=\int_{S_2} \mathbf{F}_3 \mathbf{k} \cdot \mathbf{N} d S+\int_{S_1} \mathbf{F}_3 \mathbf{k} \cdot \mathbf{N} d S=\int_S \mathbf{F}_3 \mathbf{k} \cdot \mathbf{N} d S\)

The theorem can be extended to surfaces which are such that lines parallel to coordinate axes meet them in more than two points. In such a case, we subdivided the region bounded by S into subregions whose surfaces satisfy this condition. Applying the same procedure we can prove the Theorem.

Integral Transformations Deduction From Gauss’s Theorem

1. Prove that\(\int_S\)N × F ds=\(\int_V\) ∇×F dv

Proof: Let f=a × F, where a is a constant vector.

Applying Gauss’s Theorem on f we have \(\int_S\)f.Nds= \(\int_V\)∇f dv ⇒ \(\int_S\)(a×f).Nds=\(\int_V\)∇.(a×f) dv

⇒ \(\int \mathbf{a} \cdot(\mathbf{F} \times \mathbf{N}) d \mathbf{S}=-\int \nabla \cdot(\mathbf{F} \times \mathbf{a}) d \mathbf{V}=-\int(\nabla \times \mathbf{F}) \cdot \mathbf{a} d \mathbf{V}\)

because \(\mathbf{a}\) is constant

⇒ \({\mathbf{a} \cdot \int_S}(\mathbf{N} \times \mathbf{F}) d \mathbf{S}=\mathbf{a} \cdot \int_S \nabla \times \mathbf{F} d \mathbf{V}\)

⇒ \(\mathbf{a} \cdot\left[\int_S(\mathbf{N} \times \mathbf{F}) d \mathbf{S}-\int_V \nabla \times \mathbf{F} d \mathbf{V}\right]=0\)

Since a is a constant vector

⇒ \(\int_S(\mathbf{N} \times \mathbf{F}) d \mathbf{S}-\int_V \nabla \times \mathbf{F} d \mathbf{V}=0 \Rightarrow \int(\mathbf{N} \times \mathbf{F}) d \mathbf{S}=\int \nabla \times \mathbf{F} d \mathbf{V}\)

2. Prove that \(\int_S\)NΦ ds=\(\int_V\)∇Φ dv

Proof:

Applying Gauss theorem to \(\mathbf{a} \phi\) we have

⇒ \(\int_S(\mathbf{a} \phi) \cdot \mathbf{N} d \mathbf{s}=\int_V \text{div}(\mathbf{a} \phi) d \mathbf{V}=\int_V \nabla \cdot(\mathbf{a} \phi) d \mathbf{V}\)

a. \(\int_S(\phi \mathbf{N}) \cdot \mathbf{N} d \mathbf{s}=\mathbf{a} \cdot \int_V(\nabla \phi) d \mathbf{V} \Rightarrow \mathbf{a} \cdot\left[\int_S \phi \mathbf{N} d \mathbf{S}-\int_V \nabla \phi d \mathbf{V}\right]=0\)

Since a is a constant vector.

⇒ \(\int_S \phi \mathbf{N} d \mathbf{S}-\int_V \nabla \phi d \mathbf{V}=0\)

∴ \(\int_S \mathbf{N} \phi d \mathbf{S}-\int_V \nabla \phi d \mathbf{V}=0\)

Note. The result proved above can be rewritten as follows.

1.\(\int_S\)Φ N.F dS = ∫∇.F dV

2.\(\int_S\)N× F dS=\(\int_V\)∇× F dV

3.∫NΦ dS=∫∇Φ dv

Here N is written before the function in L.H.S ∇ displaces N in R.H.S

Integral Transformations  Green Identities

If f and g are two continuous and differentiable scalar point functions over the region V enclosed by the surfaces S. then

1. \(\int_V\)[f∇² g+∇ f.∇ g]dV=\(\int_S\)(f.∇ g).N dS
2. \(\int_V\)[f∇² g-g∇² f]dV=\(\int_S\)(f∇g-g∇f).N S

Proof: By Gauss’s divergence theorem we have \(\int_V\)∇. F dV=\(\int_S\)F.N dS

Now substituting \(\overline{\mathrm{F}}\)=f ∇g, we get

∇.F ∇(f∇g)=f(∇.∇g)∇f+∇g

∴ Divergence theorem gives \(\int_V\)[f∇²g+∇f.g]dV=\(\int_S\)(f∇g).N dS      ……………….(1)

This is called Green’s first identity or theorem.

2. Interchanging f and g in (1), we get

∫[g∇²f+∇g.∇f]dV=(g∇f).N dS     ………………(2)

Subtracting (2) from(1) we, get

∫(f∇²g-g∇²f)dV=∫f∇g-g∇f). N dS

This is called Green’s second identity or Green’s theorem in symmetrical form.