Triple Integral Problems And Solutions

Multiple Integrals 2 Exercise 2 Solved Problems

 

1. Evaluate \(\begin{equation}\int_0^1 \int_0^2 \int_1^2 x^2 y z d x d y d z\end{equation}\).

Solution: \(\int_0^1 \int_0^2 \int_1^2 x^2 y z d x d y d z\)

= \(\int_0^1\left[\int_0^2\left\{\int_0^2 x^2 y z d z\right\} d y\right] d x=\int_0^1\left\{\int\left[x^2 y \frac{z^2}{2}\right] d y\right\} d x\)

= \(\int_0^1\left[\int_0^2 x^2 y\left(2-\frac{1}{2}\right) d y\right] d x\)

= \(\int_0^1 \frac{3}{2} x^2\left[\frac{y^2}{2}\right] d x=\int_0^1 \frac{3 x^2}{2}(2) d x=\int_0^1 3 x^2 d x=\left[x^3\right]_0^1=1\)

2. Evaluate\(\int_0^{2 a} \int_0^x \int_y^x x y z\) dx dy dz.

Solution: \(\int_0^{2 a} \int_0^x \int_y^x x y z d x d y d z\)

= \(\int_0^{2 a}\left[\int_0^x\left[\int_y^x x y z d z\right] d y\right] d x=\int_0^{2 a x} \int x y\left[\frac{z^2}{2}\right]_0^x d y d x\)

= \(\int_0^{2 a} \int_0^x \frac{x y}{2}\left(x^2-y^2\right) d y d x\)

= \(\int_0^{2 a}\left[\frac{x^3 y^2}{4}-\frac{x y^4}{8}\right]_0^x d x=\int_0^{2 a}\left[\frac{x^5}{4}-\frac{x^5}{8}\right] d x\)

= \(\int_0^{2 a} \frac{x^5}{8} d x=\left[\frac{x^6}{48}\right]_0^{2 a}=\frac{64 a^6}{48}=\frac{4 a^6}{3}\)

3. Evaluate \(\int_0^1 \int_y^1 \int_0^{1-x} x\)dz dx dy.

Solution: \(\int_0^1 \int_y^1 \int_0^{1-x} x d z d x d y\)

= \(\int_{z=0}^{z=1}\left\{\int_{x=y}^{x=1}\left[\int_{y=0}^{y=1-x} x d y\right] d x\right\} d z\)

= \(\int_{z=0}^{z=1}\left\{\int_{x=y}^{x=1}[x y]{ }_{y=0}^{y=1-x} d x\right\} d z\)

= \(\int_{z=0}^{z=1}\left\{\int_{x=y}^{x=1} x(1-x) d x\right\} d z=\int_{z=0}^{z=1}\left[\int_{x=y}^{x=1}\left(x-x^2\right) d x\right] d z\)

= \(\int_{z=0}^{x=1}\left[\frac{x^2}{2}-\frac{x^3}{3}\right]_{x=y}^1 d z\)

= \(\int_{z=0}^{z=1}\left(\frac{1}{2}-\frac{1}{3}-\frac{y^2}{2}+\frac{y^3}{3}\right) d z=\int_0^1\left(\frac{1}{6}-\frac{y^2}{2}+\frac{y^3}{3}\right) d y\)

= \(\left[\frac{y}{6}-\frac{y^3}{6}+\frac{y^4}{12}\right]=\frac{1}{6}-\frac{1}{6}+\frac{1}{12}=\frac{1}{12}\)

4. Evaluate\(\int_{-1}^1 \int_0^z \int_{x-z}^{x+z}(x+y+z)\)dz dx dy.

Solution: \(\int_{-1}^1 \int_0^z \int_{x-z}^{x+z}(x+y+z) d z d x d y\)

= \(\int_{z=-1}^{z=1}\left[\int_{x=0}^{x=z}\left\{\int_{y=x-z}^{y=x+z}(x+y+z) d y\right\} d x\right] d z\)

= \(\int_{z=-1}^{z=1}\left[\int_{x=0}^{x=z}\left(x y+\frac{y^2}{2}+z y\right)_{y=x-z}^{y=x+z} d x\right] d z\)

= \(\int_{z=-1}^{z=1}\left[\int_{x=0}^{x=z}\left\{x(x+z)+\frac{(x+z)^2}{2}+z(x+z)-x(x-z)-\frac{(x-z)^2}{2}-z(x-z)\right\} d x\right] d z\)

= \(\int_{z=-1}^{z=1}\left[\int_{x=0}^{x=z}\left(2 x z+2 x z+2 z^2\right) d x\right] dz=\int_{z=-1}^{z=1}[x^2 z+x^2 z+2 x z_{x=0}^{x=z} d x\)

= \(\int_{z=-1}^{z=1}\left(z^2+z^3+2 z^3\right) d z\)

= \(\int_{-1}^1 4 z^3 d z=0\)

5. Evaluate \(\int_1^e \int_1^{\log y} \int_1^{e^x} \log z\) dy dx dz.

Solution: \(\int_1^e \int_1^{\log y} \int_1^{e^x} \log z d y d x d z\)

= \(\int_1^e\left\{\int_1^{\log y}\left[\int_1^{e^x} \log z d z\right] d x\right\} d y\)

= \(\int_1^e\left\{\int_1^{\log y}[z \log z-z]_1^{e^x} d x\right\} d y\)

= \(\int_1^e\left[\int_1^{\log y}\left(x e^x-e^x+1\right) d x\right] d y=\int_1^e\left[x e^x-e^x-e^x+x\right] d y\)

= \(\int_1^e(y \log y+\log y-2 y+e-1) d y=\left[\left(\frac{y^2}{2}+y\right) \log y-\left(\frac{y^2}{4}+y\right)-y^2+(e-1) y\right]\)

= \(\frac{e^2}{4}-2 e+\frac{13}{4}=\frac{1}{4}\left(e^2-8 e+13\right)\).

6. Evaluate\(\int_0^a \int_0^x \int_0^{x+y} e^{x+y+z}\) dx dy dz.

Solution: \(\int_0^a \int_0^x \int_0^{x+y} e^{x+y+z} d x d y d z\)

= \(\int_0^a\left[\int_0^x\left[\int_a^{x+y+z} e^{x+y+z} d z\right\} d y\right] d x\)

= \(\int_0^a\left[\int_0^x\left(e^{x+y+z}\right)_0^{x+y} d y\right] d x\)

= \(\int_0^a\left[\int_0^x\left(e^{2 x+2 y}-e^{x+y}\right) d y\right] d x\)

= \(\int_0^a\left[\frac{e^{2 x+2 y}}{2}-e^{x+y}\right]_0^x d x=\int_0^{4 x}\left(\frac{e^{4 x}}{2}-e^{2 x}-\frac{e^{2 x}}{2}+e^x\right) d x\)

= \(\left[\frac{e^{4 x}}{8}-\frac{e^{2 x}}{2}-\frac{e^{2 x}}{4}+e^x\right]_0^a\)

= \(\frac{e^{4 a}}{8}-\frac{e^{2 a}}{2}-\frac{e^{2 a}}{4}+e^a=\frac{e^{4 a}}{8}-\frac{3}{4} e^{2 a}+e^a\) .

7. Evaluate \(\int_0^{\log 2} \int_0^x \int_0^{x+\log y} e^{x+y+z}\)dx dy dz

Solution: \(\int_0^{\log 2} \int_0^x \int_0^{x+\log y} e^{x+y+z} d x d y d z\)

= \(\int_0^{\log 2}\left(\int_0^x\left[\int_0^{x+\log y} e^{x+y+z} d z\right] d y\right) d x\)

= \(\int_0^{\log 2}\left(\int_0^x\left[e^{x+y+z}\right] d y\right) d x\)

= \(\int_0^{\log 2}\left(\int_0^x\left(e^{2 x+y+\log y}-e^{x+y}\right) d y\right) d x\)

= \(\int_0^{\log 2}\left(\int_0^x\left[y e^{2 x+y}-e^{x+y}\right] d y\right) d x\)

= \(\int_0^{\log 2}\left[y e^{2 x+y}-e^{2 x+y}-e^{x+y}\right]_{y=0}^{y=x} d x\)

= \(\int_0^{\log 2}\left(x e^{3 x}-e^{3 x}-e^{2 x}+e^{2 x}+e^x\right) d x\)

= \(\int_0^{\log 2}\left[(x-1) e^{3 x}+e^x\right] d x=\left[(x-1) \frac{e^{3 x}}{3}-\frac{e^{3 x}}{9}+e^x\right]_0^{\log 2}\)

= \(\frac{8}{3}(\log 2-1)-\frac{8}{9}+2+\frac{1}{3}+\frac{1}{9}-1=\frac{8}{3}(\log 2-1)+\frac{5}{9}=\frac{8}{3} \log 2-\frac{19}{9}\)

8. Evaluate \(\int_0^1 \int_0^{1-x} \int_0^{1-x-y} \frac{d x d y d z}{(x+y+z+1)^3}\)

Solution:

I = \(\int_0^1 \int_0^{1-x 1} \int_0^{1-x-y} \frac{d x d y d z}{(x+y+z+1)^3}\)

= \(\int_0^1 \int_0^{1-x}\left[-\frac{1}{2} \frac{1}{(x+y+z+1)^2}\right]_0^{1-x-y} d x d y\)

= \(-\frac{1}{2} \int_0^1 \int_0^{1-x}\left[\frac{1}{4}-\frac{1}{(x+y+1)^2}\right] d x d y\)

= \(-\frac{1}{2} \int_0^1\left[\frac{1}{4} y+\frac{1}{x+y+1}\right]_0^{1-x} d x\)

= \(-\frac{1}{2} \int_0^1\left[\frac{1}{4}(1-x)+\frac{1}{2}-\frac{1}{x+1}\right] d x\)

= \(\frac{1}{2}\left[\frac{3}{4} x-\frac{1}{8} x^2-\log (x+1)\right]=\frac{1}{2}\left(\log 2-\frac{5}{8}\right)\)

9. Evaluate \(\int_0^a \int_0^{\sqrt{a}-x^2} \int_0^{\sqrt{a^2-x}-y} \frac{d x d y d z}{\sqrt{a^2-x^2-y^2-z^2}}\)

Solution: \(\int_0^a \int_0^{\sqrt{a^2-x^2}} \int_0^{\sqrt{a}^2-x^2-y^2} \frac{d x d y d z}{\sqrt{a^2-x^2-y^2-z^2}}\)

= \(\int_0^a\left\{\int_0^{\sqrt{a^2-x^2}}\left[\int_0^{\sqrt{a^2-x^2-y^2}} \frac{1}{\sqrt{a^2-x^2-y^2-z^2}} d z\right] d y\right\} d x\)

= \(\int_0^a\left\{\int_0^{\sqrt{a^2-x^2}}\left[\text{Sin}^{-1} \frac{z}{\sqrt{a^2-x^2-y^2}}\right] d y\right\} d x\)

= \(\int_0^a\left\{\int_0^{\sqrt{a^2-x^2}}\left[\text{Sin}^{-1} 1-\text{Sin}^{-1} 0\right] d y\right\} d x\)

= \(\int_0^a\left\{\int_0^{\sqrt{a^2-x^2}} \frac{\pi}{2} d y\right\} d x\)

= \(\int_0^a\left[\frac{\pi}{2} y\right]_0^{\sqrt{a^2-x^2}} d x=\frac{\pi}{2} \int_0^a \sqrt{a^2-x^2} d x\)

= \(\frac{\pi}{2}\left[\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2} \text{Sin}^{-1} \frac{x}{a}\right]_0^a\)

= \(\frac{\pi}{2} \frac{a^2}{2} \frac{\pi}{2}=\frac{\pi^2 a^2}{8}\)

10. Evaluate \(\int_0^4 \int_0^{2 \sqrt{2}} \int_0^{\sqrt{4 z-x^2}} d z d x d y\) dx dy dz

Solution: \(\int_0^4 \int_0^{2 \sqrt{z}} \int_0^{\sqrt{4 z-x^2}} d z d x d y\)

= \(\int_0^4\left[\int_0^{2 \sqrt{z}}\left\{\int_0^{\sqrt{4 z-x^2}} d y\right\} d x\right] d z\)

= \(\int_0^4\left[\int_0^{2 \sqrt{z}}[y]_0^{\sqrt{4 z-x^2}} d x\right] d z=\int_0^4\left[\int_0^{2 \sqrt{z}} \sqrt{4 z-x^2} d x\right] d z\)

= \(\int_0^4\left[\frac{x}{2} \sqrt{4 z-x^2}+2 z \text{Sin}^{-1} \frac{x^{2 \sqrt{2}}}{2 \sqrt{z}}\right]_{x=0}^4 d z\)

= \(\int_0^4\left(2 z \frac{\pi}{2}\right) d z=\frac{\pi}{2}\left[z^2\right]=8 \pi\).

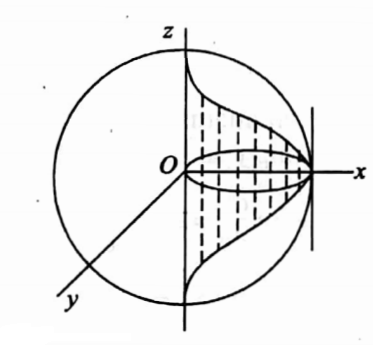
11. Evaluate \(\iint_D∫\) dx dy dz over the region D taken through the positive octant of the sphere x² +y² + z² = a².

Solution: To cover the region of positive octant of the sphere x² + y² + z² = a², z varies from \(\sqrt{a^2-x^2-y^2}\)

y varies from 0 to\(\) and x varies from 0 to a.

 

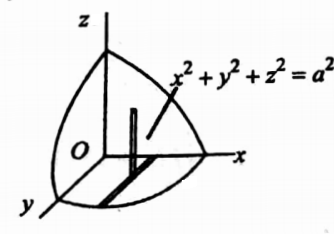
Hence the required integral is \(\int_0^a \int_0^{\sqrt{a^3-x^2}} \cdot \int_0^{\sqrt{a^2-x^2-y^2}} x y z\)  dz dy dx

= \(\int_0^a \int_0^{\sqrt{a^2-x^2}}\left[\frac{x y z^2}{2}\right]_0^{\sqrt{a^2-x^2-y^2}} d y d x\)

= \(\int_0^a \int_0^{\sqrt{a^2-x^2}} \frac{x y\left(a^2-x^2-y^2\right)}{2} d y d x\)

= \(\frac{1}{2} \int_0^a \int_0^{\sqrt{a^2-x^2}}\left(x y a^2-x^3 y-x y^3\right) d y d x\)

= \(\frac{1}{2} \int_0^a\left[\frac{x y^2 a^2}{2}-\frac{x^3 y^2}{2}-\frac{x y^4}{4}\right]_0^{\sqrt{a^2-x^2}} d x\)

= \(\frac{1}{2} \int_0^a\left\{\frac{x\left(a^2-x^2\right) a^2-x^3\left(a^2-x^2\right)}{2}-\frac{x\left(a^2-x^2\right)^2}{4}\right\} d x\)

= \(\frac{a^6}{48}\)

= \(\int_0^a \int_0^{\sqrt{a^2-x^2}}\left[\frac{x y z^2}{2}\right]_0^{\sqrt{a^2-x^2-y^2}} d y d x\)

= \(\int_0^a \int_0^{\sqrt{a^2-x^2}} \frac{x y\left(a^2-x^2-y^2\right)}{2} d y d x\)

= \(\frac{1}{2} \int_0^a \int_0^{\sqrt{a^2-x^2}}\left(x y a^2-x^3 y-x y^3\right) d y d x\)

= \(\frac{1}{2} \int_0^a\left[\frac{x y^2 a^2}{2}-\frac{x^3 y^2}{2}-\frac{x y^4}{4}\right]_0^{\sqrt{a^2-x^2}} d x\)

= \(\frac{1}{2} \int_0^a\left\{\frac{x\left(a^2-x^2\right) a^2-x^3\left(a^2-x^2\right)}{2}-\frac{x\left(a^2-x^2\right)^2}{4}\right\} d x\)=\(\frac{a^6}{48}\)

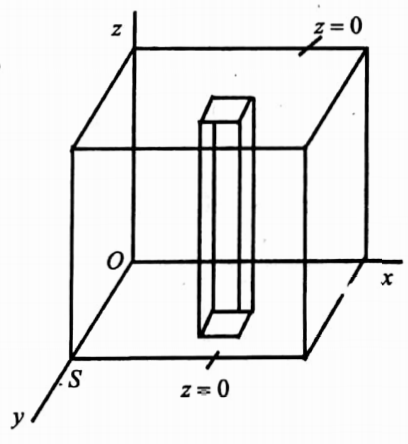
12. Evaluate \(\iiint_V\left(x^2+y^2+z^2\right)\) dx dy dz where V is the volume of the cube bounded by the coordinate planes and the planes x=y = z = a.

Solution: Hence a column parallel to the z-axis is bounded by the planes z=0 and z=a.

Here the region S above which the volume V stands is the region in the xy-plane bounded by the lines x=0,x=a,y=0,y=a.

Hence the given integral

= \(\int_0^a \int_0^a \int_0^a\left(x^2+y^2+z^2\right) d x d y d z\)

= \(\int_0^a \int_0^a\left[x^2 z+y^2 z+\frac{z^3}{3}\right] d x d y\)

= \(\int_0^a \int_0^a\left(x^2 a+y^2 a+\frac{1}{3} a^3\right) d x d y=\int_0^a\left[x^2 a y+\frac{1}{3} y^3 a+\frac{1}{3} a^3 y\right] d x\)

= \(\int_0^a\left(x^2 a^2+\frac{1}{3} a^4+\frac{1}{3} a^4\right) d x=\left[\frac{1}{3} x^3 a^2+\frac{1}{3} a^4 x+\frac{1}{3} a^4 x\right]=a^5\)

 

13. Evaluate \(\iiint_V(2 x+y)\)dxdy dz, where V is the closed region bounded by the cylinder z = 4- x² and the planes  x= 0, y = 0, y = 2 and z = 0.

Solution: Here a column parallel to the z-axis is bounded by the plane z=0 and the surface z=4-x of the cylinder.

This cylinder z=4-x meets the z-axis,x=0,y=0, at(0,0,4) and the x-axis , y=0, z=0 at (2,0,0) in the given region.

 

 

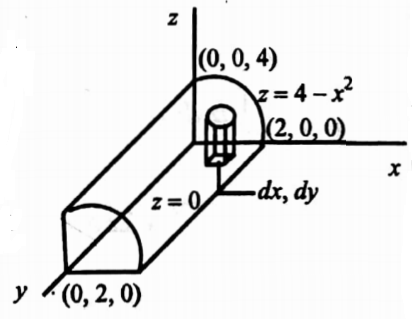
Therefore, it is evident that the limits of integration for z are from 0 to 4-x, for from 0 to 2 and for x from 0 to 2.

Hence the given integral

= \(\int_{x=0}^2 \int_{y=0}^2 \int_{z=0}^{4-x^2}(2 x+y) d x d y d z=\int_{x=0}^2 \int_{y=0}^2(2 x+y)[z]_0^{4-x^2} d x d y\)

= \(\int_{x=0}^2 \int_{y=0}^2(2 x+y)\left(4-x^2\right) d x d y=\int_{x=0}^2 \int_{y=0}^2\left[8 x-2 x^3+\left(4-x^2\right) y\right] d x d y\)

14. Use the substitution x+y + z = u,y + z = uv, z = uvw to evaluate the integral \(\iiint[x y z(1-x-y-z)]^{1 / 2}\)dx dy dz taken over the tetrahedral volume enclosed by the planes x=0, y = 0, z = 0 and x+y + z= 1.

Solution:

Here x = \(u(1-v), y=u v(1-u v), z=u v w\).

∴ \(\frac{\partial(x, y, z)}{\partial(u, v, w)}\)

= \(\left|\begin{array}{ccc}
1-v & -u & 0 \\
v(1-w) & u(1-w) & -u v \\
v w & u w & u v
\end{array}\right|=u^2 v\)

The tetrahedral volume is covered by taking the limits for u from 0 to 1, v from 0 to and w from 0 to 1.

Required integral = \(\int_0^1 \int_0^1 \int_0^1\left[u^3 v^{2 w}(1-u)(1-v)(1-w)\right]^{1 / 2} u^2 v d u d v d w\)

= \(\int_0^1 u^{7 / 2}(1-u)^{1 / 2} d u \int_0^1 v^2(1-v)^{1 / 2} d v \int_0^1 w^{1 / 2}(1-w)^{1 / 2} d w \text {. }\)

Putting u = \(\sin ^2 \theta, \nu=\sin ^2 \phi, w=\sin ^2 t\) the integral becomes

∴ \(\int_0^{\pi / 2} 2 \sin ^2 \theta \cos ^2 \theta d \theta \int_0^{\pi / 2} 2 \sin ^5 \phi \cos \phi d \phi \int_0^{\pi / 2} 2 \sin ^2 t \cos ^2 t d t=\frac{\pi^2}{1920}\)

15. Evaluate ∫∫∫ xyz dx dy dz over the positive octant of the sphere x² + y² + z² = a² by transforming it into spherical coordinates.

Solution:  x= r sinθ cos Φ, y= r sin θ sin Φ, z= r cosθ.

dx dy dz \(=\frac{\partial(x, y, z)}{\partial(r, \theta, \phi)}\) dr dθ dΦ=-r² sin dr dθ dΦ

To cover the positive octant of the sphere r varies from 0 to 0 varies from 0 to π/2 and θ varies from π /2  to 0.

Required integral = \(\int_{r=0}^a \int_{\phi=0}^{\pi / 2} \int_{\theta=\pi / 2}^0 r^3 \sin ^2 \theta \cos \theta \sin \phi \cos \phi\left(-r^2 \sin ^2 \theta\right) d r d \theta d \phi\)

= \(\int_{r=0}^a \int_{\theta=0 \phi=0}^{\pi / 2} \int^{\pi / 2} r^5 \sin \phi \cos \phi \sin ^3 \theta \cos \theta d r d \theta d \phi\)

= \(\int_0^a r^5 d r \int_0^{\pi / 2} \sin \phi \cos \phi d \phi \int_0^{\pi / 2} \sin ^2 \theta \cos \theta d \theta=\frac{a^6}{48}\)

16. Evaluate ∫∫∫ (x²+y² + z² )dx dy dz taken over the volume enclosed by the sphere x²+y² + z²= 1.

Solution: \(\iint_R\)∫(x²+y² + z² )dx dy dz

R is the region bounded by the sphere x²+y² + z² +  = 1

Change to spherical polar co-ordinates, we have

x = r sin θ  cos Φ , y=sin θ  sin Φ, z = r cos θ  , dx dy dz = r² sinθ  dr dθ  dΦ

I = \(\iiint_{R^{\prime}} r^2 \cdot r^2 \sin \theta d r d \theta d \phi\)

Over the region \(R^1: r\) varies from 0 to 1, θ varies from 0 to \(\pi, \phi\) varies from 0 to \(2 \pi\)

I = \(\int_{\phi=0}^{2 \pi} \int_{\theta=0}^\pi \int_0^1 r^4 \sin \theta d r d \theta d \phi\)

= \(\int_{\phi=0}^{2 \pi} \int_{\theta=0}^\pi \frac{r^5}{5} \sin \theta d \theta d \phi\)

= \(\frac{1}{5} \int_{\phi=0}^{2 \pi} \int_{\theta=0}^\pi \sin \theta d \theta d \phi\)

= \(\frac{1}{5} \int_{\phi=0}^{2 \pi}(-\cos \theta)_0^\pi d \phi=\int_{\phi=0}^{2 \pi} \frac{2}{5} d \phi\)

= \(\left(\frac{2}{5} \phi\right)_0^{2 \pi}=\frac{4 \pi}{5}\)

17. Evaluate \(\int_0^1 \int_0^{\sqrt{1-x^2}} \int_0^{\sqrt{1-x^2-y^2}} \frac{d z d y d x}{\sqrt{1-x^2-y^2-z^2}}\) dz dy dx coordinates. 0 by changing to a spherical polar

Solution:
Here the regeion of integration is bounded by z=0, z=\(\sqrt{1-x^2-y^2}\): y=0, y=\(\sqrt{1-x^2}\); x=0, x=1 which is the sphere x+y+z=1 is the positive octant.

To change spherical polar coordinates,

Put x=r sin θ cos Φ, y= r sin θ sin Φ, z= r cos θ  so that x²+y²+z²=r²

∴ f(x,y,z) \(=\frac{1}{\sqrt{1-x^2-y^2-z^2}}\)=\(\frac{1}{\sqrt{1-r^2}}\)

Note that r varies from 0 to 1,θ varies from 0 t0 π/2 and Φ varies from 0 to π/2.

Hence the given triple integral is equivalent to \(\int_0^{\pi / 2} \int_0^{\pi / 2} \int_0^1 r^2 \sin \theta \cdot \frac{1}{\sqrt{1-r^2}} d r d \theta d \phi\)

= \(\int_0^{\pi / 2} \int_0^{\pi / 2} \int_0^1(\frac{1}{\sqrt{1-r^2}}-\sqrt{1-r^2})) \sin \theta d r d \theta d \phi\)

= \(\int_0^{\pi / 2} \int_0^{\pi / 2} \sin \theta\left[\text{Sin}^{-1} r-\left(\frac{r \sqrt{1-r^2}}{2}+\frac{1}{2} \text{Sin}^{-1} r\right)\right]_0^1 d \theta d \phi\)

= \(\int_0^{\pi / 2} \int_0^{\pi / 2} \sin \theta \cdot \frac{\pi}{4} d \theta d \phi=\frac{\pi}{4} \int_0^{\pi / 2}[-\cos \theta]_0^{\pi / 2} d \phi\)

= \(\frac{\pi}{4} \int_0^{\pi / 2} d \phi=\frac{\pi}{4} \cdot \frac{\pi}{2}=\frac{\pi^2}{8}\)

18. Evaluate ∫∫∫ z² dx dy dz taken over the volume bounded by the surfaces x² +y² = a², x² +y² = z and z = 0.

Solution: The limits of z=0 are z= x+y   the limits of y and the limits of x are x=-a to x=a.

∴ I = \(\iiint z^2 d x d y d z=\int_{x=-a}^{x=a}\left[\int_{y=-\sqrt{a^2-x^2}}^{y=\sqrt{a^2-x^2}}\left\{\int_{z=0}^{z=x^2+y^2} z^2 d z\right\} d y\right] d x\)

= \(\int_{x=-a}^{x=a}\left\{\int_{y=-\sqrt{a^2-x^2}}^{y=\sqrt{a^2-x^2}}\left[\frac{z^3}{3}\right]_{z=0}^{z=x^2+y^2} d y\right\} d x\)

= \(\int_{x=-a}^{x=a}\left[\int_{y=-\sqrt{a^2-x^2}}^{\sqrt{a^2-x^2}} \frac{\left(x^2+y^2\right)^3}{3}\right] d x\)

= \(\int_{x=-a}^{x=a} \iint_{y=-\sqrt{a^2-x^2}}^{y=x^2} \frac{1}{3}\left(x^6+3 x^4 y^2+3 x^2 y^4+y^6\right) d y d x\)

= \(\frac{2}{3} \int_{x=-a}^{x=a}\left[x^6 y+3 x^4 \frac{y^3}{3}+3 x^2 \frac{y^5}{5}+\frac{y^7}{7}\right] d x\)

= \(\frac{4}{3} \int_0^a\left[x^6+3 x^4 \frac{\left(a^2-x^2\right)}{3}+\frac{3 x^2\left(a^2-x^2\right)}{5}+\frac{\left(a^2-x^2\right)^3}{7}\right] \sqrt{a^2-x^2} d x\)

Put \(x=a \sin \theta\).

Then \(d x=a \cos \theta d \theta. x=0, a \Rightarrow \theta=0, \pi / 2\).

∴ I = \(\frac{4}{3} \int_0^{\pi / 2}\left[a^6 \sin ^6 \theta+a^6 \sin ^4 \theta \cos ^2 \theta+\frac{3}{5} a^6 \sin ^2 \theta \cos ^4 \theta+\frac{a^6}{7} \cos ^6 \theta\right] a \cos \theta a \cos \theta d \theta\)

= \(\frac{4 a^8}{3} \int_{\theta=0}^{\theta=\pi / 2}\left(\sin ^6 \theta \cos ^2 \theta+\sin ^4 \theta \cos ^4 \theta+\frac{3}{5} \sin ^2 \theta \cos ^6 \theta+\frac{1}{7} \cos ^8 \theta\right) d \theta\)

= \(\frac{4 a^8}{3}[\frac{1}{8} \times \frac{5}{6} \times \frac{3}{4} \times \frac{1}{2} \times \frac{\pi}{2}+\frac{3}{8} \times \frac{1}{6} \times \frac{3}{4} \times \frac{1}{2}\)

x \(\frac{\pi}{2}+\frac{3}{5} \times \frac{5}{8} \times \frac{3}{6} \times \frac{1}{4} \times \frac{1}{2} \times \frac{\pi}{2}+\frac{1}{7} \times \frac{7}{8}\)

x \(\frac{5}{6} \times \frac{3}{4} \times \frac{1}{2} \times \frac{\pi}{2}]\)

= \(\frac{4 a^8}{3}\left[\frac{15 \pi+9 \pi+9 \pi+15 \pi}{8 \times 6 \times 4 \times 2 \times 2}\right]=\frac{48 \pi a^8}{3(8 \times 6 \times 2 \times 2)}=\frac{\pi a^8}{12}\)

19. Using double integral find the area enclosed by the curves y = 2x² and y² = 4x.

Solution:
The region of integration is the region bounded by y² = 4x and y = 2x²

To find A, solve the equations y² = 4x and y = 2x²

y = 2x² ⇒ y² = 4x⁴⇒4x⁴ = 4 ⇒ x(x³-l) = 0

⇒x = 0, 1.

∴A is (1,1)

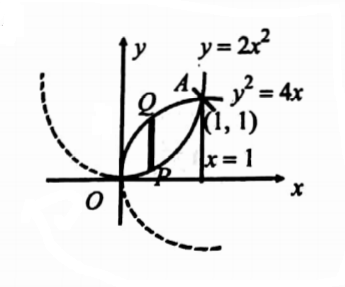
Required area =\(\iint_R d x d y\)

Take a strip PQ parallel toy axis with P lies only = 2x², Q lies on y² = 4x ⇒ y = 2\(\sqrt{x}\)

The limits of are y = 2x² to y = 2\(\sqrt{x}\) and the limits ofx are x = 0 to x = 1.

Required Area = \(\int_0^1 \int_{2 x^2}^{2 \sqrt{x}} d x d y=\int_0^1 [y x_{2 x^2}^{2 \sqrt{x}} d x=\int_0^1\left[2 \sqrt{x}-2 x^2\right] d x\)

= \(\left[\frac{2 x^{3 / 2}}{3 / 2}-2 \frac{x^3}{3}\right]_0^1=\frac{4}{3}-\frac{2}{3}=\frac{2}{3}.\)

20. Find the smaller of the areas bounded by y = 2- x and x² +y² = 4 using double integral.

Solution:
Region R is the upper part of the.

Required area A = \(\iint_R d x d y\)

To find limits for y, take a strip PQ parallel to the they-axis with P lies on y = 2 -x and Q lies on the circle x²+y² = 4.

y limits are \(y=2-x\) to \(y=\sqrt{4-x^2}\) and x limits are x=0 to x=2.

∴ A = \(\int_0^2 \int_{2-x}^{\sqrt{4-x^2}} d x d y=\int_0^2\left[\int_{2-x}^{\sqrt{4-x^2}} d y\right] d x=\int_0^2[y] d x\)

= \(\int_0^{\sqrt{4-x^2}}\left[\sqrt{4-x^2}-(2-x)\right] d x\)

= \(\left[\frac{x}{2} \sqrt{4-x^2}+\frac{4}{2} \text{Sin}^{-1} \frac{x}{2}-2 x+\frac{x^2}{2}\right]\)

= \(0+2\left(\text{Sin}^{-1} 1-\text{Sin}^{-1} 0\right)-2 \cdot 2+\frac{4}{2}\)

=2.π/2-4+2=π-2.

21. Find the area bounded by the parabola y² = 4-x and y² = 4 -4x as a double integral and evaluate it.

Solution: Given y² = 4− x =− (x- 4) is a parabola with vertex (4, 0) and towards the negative x-axis, axis of symmetry the x-axis. y² = 4 − 4x = − 4(x − 1) is a parabola with vertex (1,0) and towards the negative x-axis, axis of symmetry the x-axis.

To find the points of intersection, solve y² = 4- x and y² = 4- 4x.

∴ 4 −x = 4- 4x ⇒ 3x = 0 ⇒ x = 0 and y² = 4- x ⇒  y² = 4  ⇒ y = ±4 and the points of intersection are (0, 2), (0,- 2).

 

 

 

 

 

 

 

 

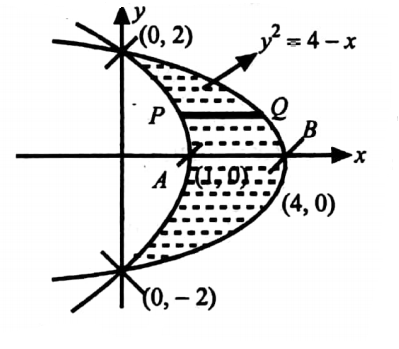
The region is the shaded region in the figure.

Both curves are symmetric about x-axis.

Required area A=2 (Area above the x-axis)=2∫\(\int_R\)dx dy

It is convenient to take strip PQ  parallel to the x-axis with P lies on y² = 4− 4x and Q lies on y² = 4−x.

Now y² = 4− 4x ⇒ x = 1 −y² /4 and y² = 4− x ⇒ x = 4 −y² and the limits of y are y = 0,y = 2.

Required area, A = \(2 \int_0^2\left[\int_{1-y^2 / 4}^{4-y^2} d x\right] d y=2 \int_0^2[x] y_{1-y^2 / 4}^{4-y^2} d y=2 \int_0^2\left[4-y^2-\left(1-\frac{y^2}{4}\right)\right] d y \)

= \(2 \int_0^2\left(3-\frac{3}{4} y^2\right) d y=2\left[3 y-\frac{3}{4} \frac{y^3}{3}\right]=2\left[3 \times 2-\frac{8}{4}\right]=2[6-2]=8\)

22. Find the area bounded by x² = 4y and x− 2y + 4 = 0 using double integral.

Solution: Solving the given curves x² = 4y, x −2y + 4 = 0;

We get x² =4 \(\left(\frac{x+4}{2}\right)\) ⇒. x² −  2x- 8 = 0

⇒ (x- 4)(x + 2) = 0 ⇒ x = 4 or −2.

Ifx = 4 theny = 4; Ifx =− 2 then y = 1.

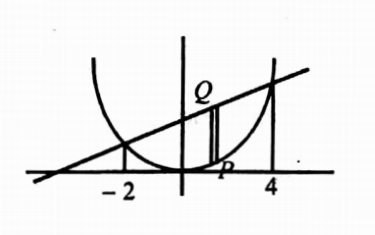
The points of intersection are (−2, 1) and (4, 4).

Take strip PQ parallel to y-axis with P lies on x2 = 4y and Q lies on x − 2y + 4 = 0.

∴ The limits of y are \(y=\frac{x^2}{4}\) to \(y=\frac{x+4}{2}\) and the limits of x are x=-2 to x=4.

Required area = \(\int_{-2}^4 \int_{x^2 / 4}^{(x+4) / 2} d x d y=\int_{x=-2}^{x=4}\left[\int_{y=x^2 / 4}^{y=(x+4) / 2} d y\right] d x=\int_{-2}^4[y] \int_{y=x / 4}^{y=(x+4) / 2} d x\)

= \(\int_{-2}^4\left(\frac{x+4}{2}-\frac{x^2}{4}\right) d x=\left[\frac{x^2}{4}+2 x-\frac{x^3}{12}\right]_{-2}^4=\left(4+8-\frac{16}{3}\right)-\left(1-4+\frac{2}{3}\right)=15-\frac{18}{3}=9\) .

23. Find the smaller area bounded \(\frac{x^2}{9}+\frac{y^2}{4}\) = 1 and \(\frac{x}{3}+\frac{y}{2}\) = 1 using double integral.

Solution:

The curves \(\frac{x^2}{9}+\frac{y^2}{4}\)=1, \(\frac{x}{3}+\frac{y}{2}\) =1 intersect at A(3,0), B(0,2).

Take strip PQ parallel to y-axis with P lies on \(\frac{x^2}{9}+\frac{y^2}{4}\) =1 and Q lies on \(\frac{x}{3}+\frac{y}{2}\) =1.

The limits of integration are y-varies from

y = \(2(1-x / 3)\) to \(y=2 \sqrt{1-x^2 / 9}\) and x varies from x=0 to x=3.

= \(\int_0^3\left[2 \sqrt{1-\frac{x^2}{9}}-2\left(1-\frac{x}{3}\right)\right] d x\)

= \(2\left[\frac{x}{6} \sqrt{1-\frac{x^2}{9}}+\frac{3}{2} \text{Sin}^{-1} \frac{x}{3}-x+\frac{x^2}{6}\right]\)

= \(\frac{3 \pi}{2}-6+3=\frac{3 \pi}{2}-3=\frac{3(\pi-2)}{2}\)

24. Find the smaller area bounded by y² = 4x, x +y = 3 and x-axis using double integral

Solution: Solving y= 4x², x+y=3, we get y²= 4(3-y) = y²+4y-12=0

= (y+6)(y-2) =0 = y=-6 or 2

Take strip parallel to x-axis with P lies on y²=4x and Q lies on x+y=3.

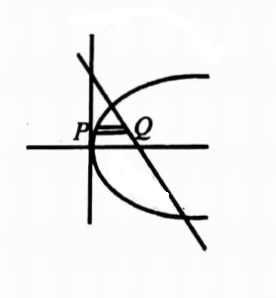
To find the smaller area bounded by y=4x²,x+y=3 and x-axis, the limits of integration are x varies from x=y²/4 x=3-y and y varies from y=0 to y=2.

The required area = \(\int_0^2 \int_{y^2 / 4}^{3-3} d y d x=\int_0^2[\int_{y^2 / 4}^{3-y} d x d y\)

= \(\int_0^2[x] \cdot d y=\int_0^{3-y}\left[3-y-\frac{y^2}{4}\right] d y=\left[3 y-\frac{y^2}{2}-\frac{y^3}{12}\right]\)

= \(6-2-\frac{2}{3}=\frac{10}{3}\)

25. Find the area of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\)= 1 by double integration.

Solution: The area of the ellipse = 4 (Area in the first quadrant)

Take strip PQ parallel toy-axis with P on x-axis and Q on the ellipse.

The limits of integration are y varies from y = 0 to y = \(b \sqrt{1-x^2 / a^2}\) and x varies from x = 0 to x = a.

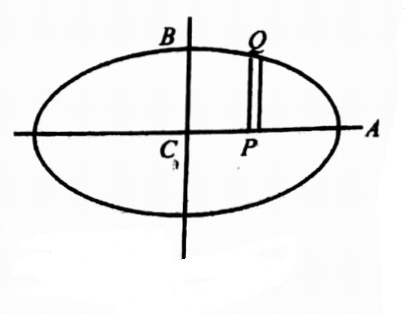
∴ Area of the ellipse = \(4 \int_0^a \int_0^{b \sqrt{1-x^2 / a^2}} d x d y\)

= \(4 \int_0^a[y]_0^{b \sqrt{1-x^2 / a^2}} d x=4 \int_0^a b \sqrt{1-\frac{x^2}{a^2}} d x\)

= \(\frac{4 b}{d} \int_0^a \sqrt{a^2-x^2} d x=\frac{4 b}{a}\left[\frac{x}{a} \sqrt{a^2-x^2}+\frac{a^2}{2} \text{Sin}^{-1} \frac{x}{a}\right]\)

= \(\frac{4 b}{a}\left(\frac{a^2}{2} \frac{\pi}{2}\right)=\pi a b\) .

26. Using double integration find the area of the parallelogram whose vertices are A (1,0), B (3, 1), C (2, 2), and D (0, 1).

Solution: The given points A (1, 0), B (3, 1), C (2, 2) and D (0, 1) are the vertices of a parallelogram ABCD.

The required area is the area of the parallelogram ABCD. Area of the parallelogram ABCD

We shall find the equations of AB and AD.

 

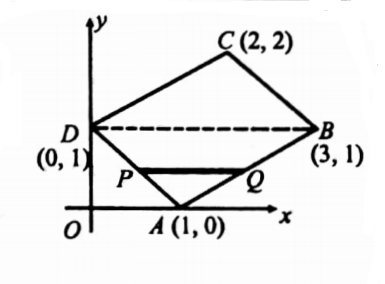
Equation of \(\stackrel{\leftrightarrow}{A B}\)is \(\frac{y-0}{0-1}\)=\(\frac{x-1}{1-3}\)  ⇒ y=1/2(x-1)……. (1)

Equation of \(\stackrel{\leftrightarrow}{A D}\)  is \(\frac{y-0}{0-1}\)= \(\frac{x-1}{1-0}\)……. (2)

Area of \(\triangle A B D=\iint_{A B D} d x d y\).

Take a strip PQ parallel to the x-axis with P on (2) and Q is on (1).

∴ x=-y+1 and x=2 y+1 and y varies from 0 to 1.

= \(\int_0^1 3 y d y=3\left[\frac{y^2}{2}\right]=\frac{3}{2}\) .

∴ Area of the parallelogram A B C D is = \(2 \times \frac{3}{2}=3\)

27. Find the area bounded between ∫r = 2 cos θ and r = 4 cos θ .

Solution: Area A = \(\iint_R r d r d \theta\)where the region R is the region between the circles r = 2 cos θ and r = 4 cos θ

The area is the region outside the circle r = 2 cos θ and inside, the circle r = 4 cos θ.

We first integrate w.r.to r and so, we take the radius vector OPQ.

 

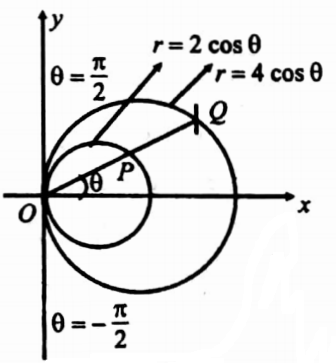
When PQ is moved to cover the area A, r varies from r = 2 cosθ to r = 4 cos θ, and 0 varies from 0 =- π/2 to θ = π/2.

∴ Area  A = \(\int_{-\pi / 2}^{\pi / 2} \int_{2 \cos \theta}^{4 \cos \theta} r d r d \theta\)

= \(\int_{-\pi / 2}^{\pi / 2}\left[\frac{r^2}{2}\right]_{2 \cos \theta}^{4 \cos \theta} d \theta\)

= \(\frac{1}{2} \int_{-\pi / 2}^{\pi / 2}\left(4^2 \cos ^2 \theta-2^2 \cos ^2 \theta\right) d \theta\)

= \(6 \int_{-\pi / 2}^{\pi / 2} \cos ^2 \theta d \theta=6 \times 2 \int_0^{\pi / 2} \cos ^2 \theta d \theta=12 \frac{1}{2} \frac{\pi}{2}=3 \pi \text {. }\)

28. Find the area of one loop of the lemniscate r² = a² cos 2θ.

Solution:

Given r² = a² cos 2 θ

Area of the loop = \(\iint_R r d r d \theta\), where R is the region as in the figure.

Since the loop is symmetric about the initial line, the required area is twice the area above the initial line. First, we integrate w.r.to r.

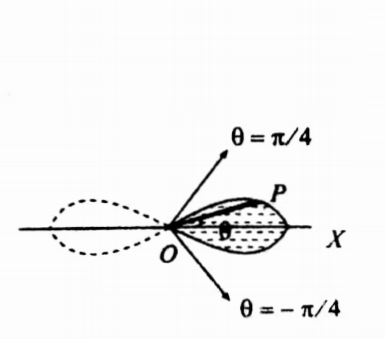
In the region, take a radical strip OP, its ends are r=0 and r= a\(\sqrt{\cos 2 \theta}\)

When the strip is moved to cover the region R, θ varies from 0 to π/4

Required area A = \(2 \int_0^{\pi / 4} \int_0^{a \sqrt{\cos 2 \theta}} r d r d \theta=2 \int_0^{\pi / 4}\left[\left(\frac{r^2}{2}\right)\right]_0^{a \sqrt{\cos 2 \theta}} d \theta\)

= \(\int_0^{\pi / 4} a^2 \cos 2 \theta d \theta\)

= \(a^2 \int_0^{\pi / 4} \cos 2 \theta d \theta=a^2\left[\frac{\sin 2 \theta}{2}\right]\)

= \(\frac{a^2}{2}\left(\sin \frac{\pi}{2}-\sin 0\right)=\frac{a^2}{2}\)

29. Find the area of a the loop of the curve r = a sin 3θ.

Solution:

Given r = a sin 3θ.

The area of the \(\iint_R r d r d \theta\)

But the loop is formed by two consecutive values of θ  when r = 0.

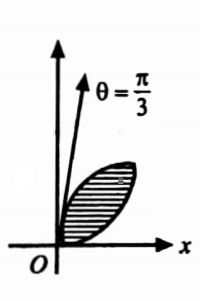
When r = 0, a sin 3θ  = 0⇒ 3θ = 0 or π⇒0 = 0 or π /3 and r varies from r = 0 to r = a sin 3θ

Area of the loop = \(\int_0^{\pi / 3} \int_0^{a \sin 3 \theta} r d r d \theta\)

= \(\int_0^{\pi / 3}\left[\frac{r^2}{2}\right]_0^{a \sin 3 \theta} d \theta=\frac{1}{2} \int_0^{\pi / 3} a^2 \sin ^2 3 \theta d \theta\)

= \(\frac{a^2}{2} \int_0^{\pi / 3} \frac{1-\cos 6 \theta}{2} d \theta=\frac{a^2}{4}\left[\theta-\frac{\sin 6 \theta}{6}\right]_0^{\pi / 3}\)

= \(\frac{a^2}{4}\left[\frac{\pi}{3}-\frac{\sin 2 \pi-\sin 0}{6}\right]=\frac{\pi a^2}{12}\)

30. Find the area of the cardioid r = a(1+ cos θ).

Solution: Given r = a (1 + cos θ)

Area = ∫\(\int_R r d r d \theta\)

 

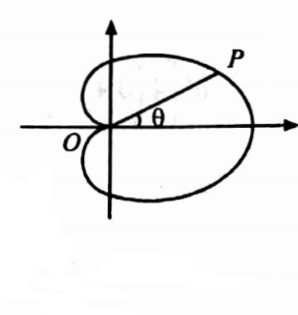
Now r varies from 0 to a (1 + cosθ ) and θ varies from −π to π

Required area = \(\int_{\theta=-\pi}^{\theta=\pi}\left[\int_{r=0}^{r=a(1+\cos \theta)} r d r\right] d \theta\)

= \(\int_{\theta=-\pi}^{\theta=\pi}\left[\frac{r^2}{2}\right]_{r=0}^{r=a(1+\cos \theta)} d \theta\)

= \(\int_{-\pi}^\pi \frac{a^2}{2}(1+\cos \theta)^2 d \theta=a^2 \int_0^\pi\left(1+2 \cos \theta+\cos ^2 \theta\right) d \theta\)

= \(a^2 \int_0^\pi\left[1+2 \cos \theta+\frac{1+\cos \theta}{2}\right] d \theta\)

= \(a^2 \int_0^\pi\left[\frac{3}{2}+2 \cos \theta+\frac{1}{2} \cos 2 \theta\right] d \theta\)

= \(a^2\left[\frac{3 \theta}{2}+2 \sin \theta+\frac{1}{4} \sin 2 \theta\right]=\frac{3 \pi a^2}{2} \)

31. Find the area which is inside the circle r = 3a cos θ and outside the cardioid r =a(1+cos θ).

Solution:

Given r = 3a cos θ  → (1) and r = a (1 + cos θ)  → (2)

Required area A = ∫∫r dr dθ

Eliminating r from (1) and (2), we get 3a cos θ = a (1 + cos θ) ⇒ 2 cos θ = 1

⇒  cos θ = 1/2 ⇒  θ=−π/3 or π/3.

 

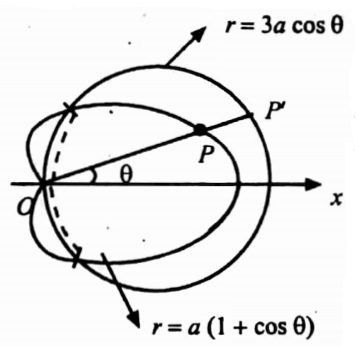
The required area is the region shown in the figure. Since both curves are symmetrical about the initial line, the required area is twice the area above the initial line.

In this region take a radial strip OPP where P lies on (2) and P’ lies on (1).

When it moves, it will cover the required area.

∴  r varies from a (1 + cos θ) to 3a cos θ and 0 varies from 0 to π/3

Required area = \(2 \int_0^{\pi / 3} \int_{r=a(1+\cos \theta)}^{r=3 a \cos \theta} r d r d \theta\)

= \(2 \int_0^{\pi / 3}\left[\frac{r^2}{2}\right]_{a(1+\cos \theta)}^{3 a \cos \theta} d \theta\)

= \(\int_0^{\pi / 3}\left[9 a^2 \cos ^2 \theta-a^2(1+\cos \theta)^2\right] d \theta\)

= \(a^2 \int_0^{\pi / 3}\left[9 \cos ^2 \theta-\left(1+2 \cos \theta+\cos ^2 \theta\right)\right] d \theta\)

= \(a^2 \int_0^{\pi / 3}\left[8 \cos ^2 \theta-1-2 \cos \theta\right] d \theta=a^2 \int_0^{\pi / 3}\left[8\left\{\frac{1+\cos 2 \theta}{2}\right\}-1-2 \cos \theta\right] d \theta\)

= \(a^2\left[4\left(\theta+\frac{\sin 2 \theta}{2}\right)-\theta-2 \sin \theta\right]_0^{\pi / 3}\)

= \(a^2\left[4\left(\frac{\pi}{3}+\frac{\sin \frac{2 \pi}{3}}{2}\right)-\frac{\pi}{3}-2 \sin \frac{\pi}{3}-0\right]\)

= \(a^2\left[\frac{4 \pi}{3}+2 \frac{\sqrt{3}}{2}-\frac{\pi}{3}-2 \frac{\sqrt{3}}{2}\right]=a^2\left[\frac{4 \pi}{3}-\frac{\pi}{3}\right]=\pi a^2\)

32. Find the area common to r = \(a \sqrt{2}\) and r- 2a cosθ .

Solution: Given r = a\(\sqrt{2}\) → (1) and r = 2a cosθ  → (2)

(1) is a circle with centre (0, 0) and radius a\(\sqrt{2}\)

(2) is a circle with centre (a, 0) and radius a.

Solve (1) and (2) to find the point of intersection.

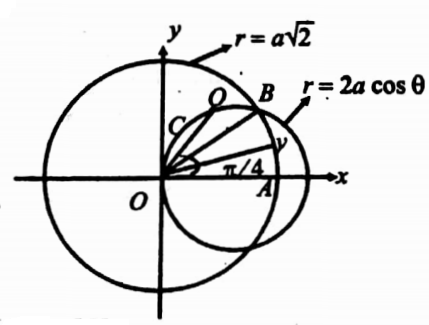
∴ a\(\sqrt{2}\) 2a cosθ ⇒ cosθ \(\frac{1}{\sqrt{2}}\) ⇒ θ=π/4.

Since the circles are symmetrical about the initial line OX, the required area = 2 [area OABC]- 2[area OAB+ area OBC]

In OAB, take a strip OP. When OP moves it covers the area OAR Ends of OP we, r = 0 and r = a\(\sqrt{2}\).

∴ r varies from 0 to a\(\sqrt{2}\) and 0 varies from 0 toπ/4 . In the area, OBC, take a strip OQ.

When OQ moves it covers the area OBC. Ends of OQ are, r = 0 and r = 2a cos θ

Required area = \(2\left[\int_{0^{-}}^{\pi / 4} \int_0^{\sqrt{2}} r d r d \theta+\int_{\pi / 4}^{\pi / 2} \int_0^{2 a \cos \theta} r d r d \theta\right]\)

= \(2 \int_0^{\pi / 4}\left[\frac{r^2}{2}\right]_0^{a \sqrt{2}} d \theta+2 \int_{\pi / 4}^{\pi / 2}\left[\frac{r^2}{2}\right]_0^{2 a \cos \theta} d \theta\)

= \(\int_0^{\pi / 4} 2 a^2 d \theta+\int_{\pi / 4}^{\pi / 2} 4 a^2 \cos ^2 \theta d \theta\)

= \(2 a^2[\theta]+4 a^2 \int_{\pi / 4}^{\pi / 4}\left(\frac{1+\cos 2 \theta}{2}\right) d \theta\)

= \(2 a^2 \frac{\pi}{4}+2 a^2\left[\theta+\frac{\sin 2 \theta}{2}\right]_{\pi / 4}^{\pi / 2}\)

= \(\frac{\pi a^2}{2}+2 a^2\left[\frac{\pi}{2}-\frac{\pi}{4}+\frac{1}{2}\left(\sin \pi-\sin \frac{\pi}{2}\right)\right]\)

= \(\frac{\pi a^2}{2}+2 a^2\left[\frac{\pi}{4}-\frac{1}{2}\right]=\frac{\pi a^2}{2}+\frac{\pi a^2}{2}-a^2=a^2(\pi-1)\)

33. Find the area inside the circle r = a sin θ but lying outside the cardioid r = a (1 – cos θ).

Solution: Given r= a sin θ →(1) and r= a(1- cos θ) →(2)

Area=∫∫ r dr dθ

Eliminating r from (1) and (2), we get a sin o a=(1- cos θ)= sin θ+ cos θ=1

sin² θ+ cos² θ + 2 sin θ cos θ =1⇒ 1+2 sin 2θ=1= sin 2θ=0

2θ =0, π⇒ θ=0 or π/2

 

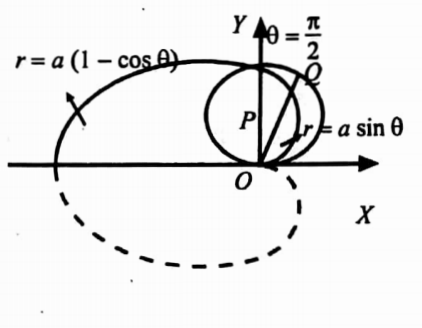
Area = \(\int_0^{\pi / 2} \int_{a(1-\cos \theta)}^{a \sin \theta} r d \theta=\int_0^{\pi / 2}\left[\frac{r^2}{2}\right]_{a(1-\cos \theta)}^{a \sin \theta} d \theta\)

= \(\frac{1}{2} \int_0^{\pi / 2}\left[a^2 \sin ^2 \theta-a^2(1-\cos \theta)^2\right] d \theta\)

= \(\frac{a^{2^{\pi / 2}}}{2} \int_0^2\left[\sin ^2 \theta-\left(1-2 \cos \theta+\cos ^2 \theta\right)\right] d \theta\)

= \(\frac{a^2}{2} \int_0^{2 / 2}\left\{-1+2 \cos \theta-\left(\cos ^2 \theta-\sin ^2 \theta\right)\right\} d \theta\)

= \(\frac{a^2}{2}\left[\int_0^{\pi / 2}[-1+2 \cos \theta\} d \theta-\int_0^{\pi / 2}\left\{\cos ^2 \theta-\sin ^2 \theta\right] d \theta\right]\)

= \(\frac{a^2}{2} \int_0^{\pi / 2}(-1+2 \cos \theta) d \theta\)

= \(\frac{a^2}{2}[-\theta+2 \sin \theta]=\frac{\pi / 2}{0}=\frac{a^2}{2}\left[-\frac{\pi}{2}+2 \sin \frac{\pi}{2}\right]\)

= \(\frac{a^2}{2}\left[-\frac{\pi}{2}+2\right]=\frac{a^2}{4}[4-\pi] \text {. }\)

 

34. Find the area of the surface of the sphere of radius r.

Solution:
Taking the origin as the centre and radius r, the equation of the sphere is x² +y² + z²= r². Let us consider the surface of the sphere in the first octant. It will be 1/8 of the surface of the sphere. The orthogonal projection of this surface area on the XOY plane is the quadrant of the circle x² +y² − r² in that plane.

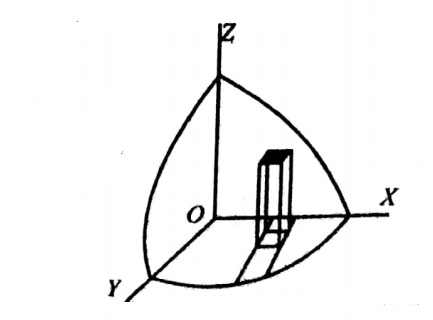
Hence this surface area = \(\iint\left\{\left(\frac{\partial z}{\partial x}\right)^2+\left(\frac{\partial z}{\partial y}\right)^2+1\right\}^{1 / 2} d y d x\) taken over the area of the quarter of the circle \(x^2+y^2=r^2\) on the positivequadrant.

Now \(\frac{\partial z}{\partial x}=-\frac{x}{z}, \frac{\partial y}{\partial z}=-\frac{y}{z}\).

Surface area of the sphere = \(8 \iint\left(\frac{x^2}{z^2}+\frac{y^2}{z^2}+1\right)^{1 / 2} d x d y\)

= \(8 \iint \frac{\left(x^2+y^2+z^2\right)^{1 / 2}}{z} d x d y=8 \iint \frac{r}{z} d x d y=8 \int_0^r \int_0^{\sqrt{r^2-x^2}} \frac{r d x d y}{\sqrt{r^2-x^2-y^2}}\)

= \(8 \times \frac{\pi r^2}{2}=4 \pi r^2\)

35. Find the area of the surface of the sphere x² +y² + Z² = 9a² cut off by the cylinder x² +y² =3ax.

Solution: The Projection of the required area S on the xy-plane is the circle x²+y²=3ax.

 

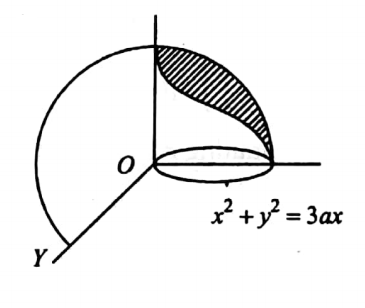
On the sphere z = \(\sqrt{9 a^2-x^2-y^2}\),

⇒ \(\frac{\partial z}{\partial x}=-\frac{x}{\sqrt{9 a^2-x^2-y^2}}, \frac{\partial z}{\partial y}=-\frac{y}{\sqrt{9 a^2-x^2-y^2}}\)

S = \(\iint_R \sqrt{1+\left(\frac{\partial z}{\partial x}\right)^2+\left(\frac{\partial z}{\partial y}\right)^2} d x d y\)

where R is the region enclosed by the circle \(x^2+y^2=3 a x\).

= \(\iint_R \sqrt{1+\frac{x^2}{9 a^2-x^2-y^2}+\frac{y^2}{9 a^2-x^2-y^2}} d x d y=\iint_R \frac{3 a}{\sqrt{9 a^2-x^2-y^2}} d x d y\)

= \(3 a \iint_R \frac{r d r d \theta}{\sqrt{9 a^2-r^2}}\) changing to polars.

The polar equation of the circle is r= 3a cos θ.

To cover the area of this circle t varies from 0 to 3a cos θ  and θ from −π/2 to π/2.

∴ S = \(3 a \int_{-\pi / 2}^{\pi / 2} \int_0^{3 a \cos \theta} \frac{r d r d \theta}{\sqrt{9 a^2-r^2}}\)

= \(3 a \int_{-\pi / 2}^{\pi / 2}\left[-\sqrt{9 a^2-r^2}\right]{ }_0^{3 a \cos \theta}=9 a^2 \int_{-\pi / 2}^{\pi / 2}\left[1-\sqrt{1-\cos ^2 \theta}\right] d \theta\)

= \(18 a^2 \int_0^{\pi / 2}\left[1-\sqrt{1-\cos ^2 \theta}\right] d \theta=18 a^2 \int_0^{\pi / 2}[1-\sin \theta] d \theta=18 a^2\left(\frac{\pi}{2}-1\right)=9 a^2(\pi-2)\)

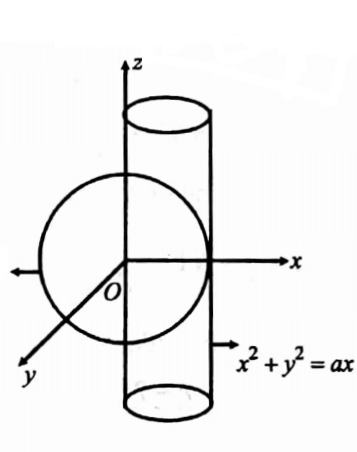
36. Find the surface area of the cylinder x² +y² =ax cut off by the sphere x² +y² + Z² = a² 

Solution: The equation of the sphere is x² + y² + z²= a² → (1)

The equation of the cylinder is x² +y²= ax  →(2)

The surface area of the cylinder cut off by the sphere is required.

Projecting the surface on the xz-plane, we get the required surface area of S.

∴ S= 2 \(\iint_{D_1} \sqrt{\left(\frac{\partial y}{\partial x}\right)^2+\left(\frac{\partial y}{\partial z}\right)^2}\) +1dx dz

Where D₁ is the region obtained by eliminating y² from (1) and (2).

∴ z²+ax=a²→(3)

The surface is x²+y²=ax

Differentiating partially w. r. to x and z, treating y as function of x and z, we get

2x+2y \(\frac{\partial y}{\partial x}=a \Rightarrow \frac{\partial y}{\partial x}=\frac{a-2 x}{2 y}\) and

2y \(\frac{\partial y}{\partial z}=0 \Rightarrow \frac{\partial y}{\partial z}=0\)

∴ \(\left(\frac{\partial y}{\partial x}\right)^2+\left(\frac{\partial y}{\partial z}\right)^2+1\)

= \(\frac{(a-2 x)^2}{4 y^2}+1=\frac{(a-2 x)^2+4 y^2}{4 y^2}\)

= \(\frac{a^2-4 a x+4 x^2+4\left(a x-x^2\right)}{4 y^2}=\frac{a^2}{4 y^2}\)

∴ \( \sqrt{\left(\frac{\partial y}{\partial x}\right)^2+\left(\frac{\partial y}{\partial z}\right)^2+1}=\frac{a}{2 y}=\frac{a}{2 \sqrt{a x-x^2}}\)

We have \(z^2+a x=a^2 \Rightarrow z^2=a^2-a x \Rightarrow z= \pm \sqrt{a^2-a x}\)

∴ S = \(2 \iint_{D_1}^{2 \sqrt{a x-x^2}} d x d z=a \int_0^a \int_{-\sqrt{a^2-a x}}^{\sqrt{a^2-a x}} \frac{1}{\sqrt{a x-x^2}} d x d z\)

= \(a \int_0^a\left[\int_{-\sqrt{a^2-a x}}^{\sqrt{a^2-a x}} \frac{1}{\sqrt{a x-x^2}} d z\right] d x\)

= \(a \int_0^a\left[\frac{1}{\sqrt{a x-x^2}}[z]-\sqrt{a^2-a x}\right] d x\)

= \(a \int_0^{\sqrt{a^2-a x}}\left\{\frac{1}{\sqrt{a x-x^2}}\left[\sqrt{a^2-a x}+\sqrt{a^2-a x}\right]\right\} d x\)

= \(2 a \int_0^a \frac{\sqrt{a^2-a x}}{\sqrt{a x-x^2}} d x=2 a \int_0^a \sqrt{\frac{a(a-x)}{x(a-x)}} d x\)

= \(2 a \int_0^a \sqrt{\frac{a}{x}} d x=2 a \sqrt{a} \int_0^a x^{-1 / 2} d x\)

= \(2 a \sqrt{a}\left[\frac{x^{1 / 2}}{1 / 2}\right]=4 a \sqrt{a}\left(a^{1 / 2}-0\right)=4 a^2\)

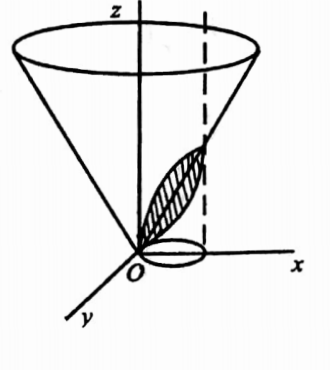
37. Find the portion of the cone x² +y² = 4z² lying above the xy-plane and inside the cylinder x² +y² = 3y.

Solution:
The projection of the required area on the x,y plane is the circle x² +y² =3y.

Given cone is x²+y²= 4z² ⇒  z = 1/2\(\sqrt{x^2+y^2}\).

 

⇒ \(\frac{\partial z}{\partial x}=\frac{1}{2} \frac{x}{\sqrt{x^2+y^2}}, \frac{\partial z}{\partial y}=\frac{1}{2} \frac{y}{\sqrt{x^2+y^2}}\)

∴ S = \(\iint_k \sqrt{1+\frac{1}{4} \frac{x^2}{x^2+y^2}+\frac{1}{4} \frac{y^2}{x^2+y^2}} d x d y\)

= \(\frac{\sqrt{5}}{2} \iint_R d x d y\), where R is the circle \(x^2+y^2=3 y\)

= \(\frac{\sqrt{5}}{2}\)(area of the circle \(x^2+y^2=3 y\))=\(\frac{\sqrt{5}}{2} \pi\left(\frac{3 a}{2}\right)^2=\frac{9 \sqrt{5}}{8} \pi a^2\)

38. The centre of a sphere of radius r is on the surface of a right cylinder, the radius of whose base is r/2. Find the area of the surface of the cylinder intercepted by the sphere.

Solution: The equation of the sphere is x² +y² +z² =r² and the equation of the cylinder is

⇒ \(\left(x-\frac{r}{2}\right)^2+y^2=\left(\frac{r}{2}\right)^2 \Rightarrow x^2+y^2=r x \text {. }\)

Projecting on the zx-plane, we have

S = \(\iint_R \sqrt{1+\left(\frac{\partial y}{\partial x}\right)^2+\left(\frac{\partial y}{\partial z}\right)^2} d x d z \text {. }\)

On the cylinder \(y^2=r x-x^2\).

∴ \(\frac{\partial y}{\partial x}=\frac{r-2 x}{2 y}, \frac{\partial y}{\partial z}=0 \text {. }\)

The projection of the area on the zx-plane is the curve by eliminating y from x² +y² =rx and x² +y² +z² =r², i.e, z² +rx=r².

Hence the required area = \(2 \iint_R \sqrt{1+\frac{(r-2 x)^2}{4 y^2}} d x d z\)

= \(2 \iint \frac{\sqrt{4 y^2+4 x^2-4 r x+r^2}}{2 y} d x d z=2 r \iint \frac{d x d z}{2 y}=r \iint \frac{d x d z}{\sqrt{r x-x^2}}\)

= \(r \int_0^r \int_{-\sqrt{r^2-r x}}^{\sqrt{r^2-r x}} \frac{d x d z}{\sqrt{r x-x^2}}=2 r \int_0^r\left[\int_0^{\sqrt{r^2-r x}} \frac{d z}{\sqrt{r x-x^2}}\right] d x\)

= \(2 r \int_0^r \frac{1}{\sqrt{r x-x^2}}[z] \int_0^{\sqrt{r^2-r x}} d x\)

= \(2 r \int_0^r \frac{\sqrt{r^2-r x}}{\sqrt{r x-x^2}} d x=2 r \int_0^r \frac{\sqrt{r}}{\sqrt{x}} d x=4 r^2\)

39. Find the volume of the ellipsoid \(\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}\) =1 by using a double integral.

Solution: Note that the” ellipsoid is symmetrical about axes and hence the required volume is 8 times the volume of the ellipsoid in the positive octant.

The region above which the volume lies is bounded by x = 0, x = a, y = 0 andy=b \(\sqrt{1-\frac{x^2}{a^2}}\).

Hence the required volume of the ellipsoid

= \(8 \int_0^a \int_0^{b \sqrt{1-x^2 / a^2}} z d y d x=8 \int_0^a \int_0^b c \sqrt{1-x^2 / a^2} \frac{x^2}{a^2}-\frac{y^2}{b^2} d y d x\)

= \(8 \int_0^t \int_0^t c \sqrt{\left.\frac{t^2}{b^2}-\frac{y^2}{b^2}\right]} d y d x \text {, where } b^2\left(1-\frac{x^2}{a^2}\right)=t^2\)

= \(8 \int_0^a \int \frac{c}{b} \sqrt{t^2-y^2} d y d x=8 \int_0^a \frac{c}{b}\left[y \frac{\sqrt{t^2-y^2}}{2}+\frac{t^2}{2} \text{Sin}^{-1} \frac{y}{t}\right]_0^t d x\)

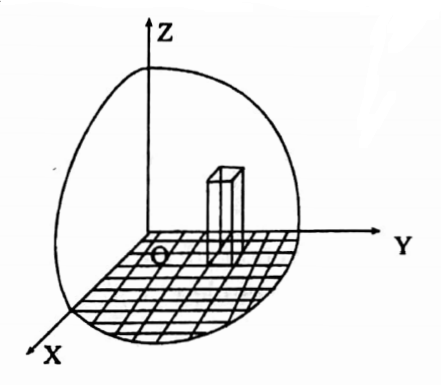
40. Find the volume bounded by the cylinder X² +y² = 4 and the planes y + z = 3 and z = 0 by using double integral.

Solution: From the it is clear that to get the required volume z=3-y is to be integrated over the circle x² +y² =4 in the XOY plane.

Note that x varies from –\(\sqrt{4-y^2}\) to \(\sqrt{4-y^2}\) and y varies from-2 to +2.

 

∴ Required volume

= \(\int_{-2}^2 \int_{-\sqrt{4-y^2}}^{\sqrt{4-y^2}} z d x d y=\int_{-2}^2 \int_{-\sqrt{4-y^2}:}^{\sqrt{4-y^2}}(3-y) d x d y\)

= \(\int_{-2}^2(3-y)[x]_{-\sqrt{4-y^2}}^{\sqrt{4-y^2}} d y=2 \int_{-2}^2(3-y) \sqrt{4-y^2} d y\)

= \(6 \int_{-2}^2 \sqrt{4-y^2} d y-2 \int_{-2}^2 y \sqrt{4-y^2} d y=12 \int_0^2 \sqrt{4-y^2} d y-0\)

= \(12 \int_0^{\pi / 2} 4 \cos ^2 \theta d \theta=48 \cdot \frac{1}{2} \cdot \frac{\pi}{2}=12 \pi \text {. }\)

41. Find the volume of the tetrahedron bounded by coordinate planes and the plane \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\)=1

Solution: The region of integration is the region bounded by \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\)=1, x=0,y=0,z=0.

Its projection in the xy-plane is the ΔOAB bounded by x=0, y=0 and \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\)=1.

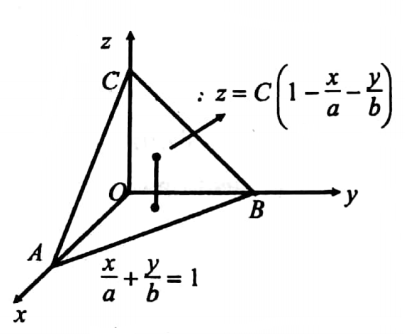
Volume V = \(\iiint_D \int d x d y d z\)

= \(\int_0^a \int_0^{b\left(1-\frac{x}{a}\right) c\left(1-\frac{x}{a}-\frac{y}{b}\right)} \int_0^a d z d y d x\)

= \(\int_0^b \int_0^{b\left(1-\frac{x}{a}\right)}[z]_0^{c\left(1-\frac{x}{a}-\frac{y}{b}\right)} d y d x\)

= \(\int_0^{a^b\left(1-\frac{x}{a}\right)} \int_0^c c\left(1-\frac{x}{a}-\frac{y}{b}\right) d y d x\)

= \(c \int_0^a\left[\left(1-\frac{x}{a}\right) y-\frac{y^2}{2 b}\right]_0^{b\left(1-\frac{x}{a}\right)} d x\)

= \(c \int_0^a\left[\left(1-\frac{x}{a}\right) b\left(1-\frac{x}{a}\right)-\frac{1}{2 b} b^2\left(1-\frac{x}{a}\right)^2\right] d x\)

= \(\frac{b c}{2} \int_0^a\left(1-\frac{x}{a}\right)^2 d x=\frac{b c}{2}\left[\frac{\left(1-\frac{x}{a}\right)^3}{-\frac{1}{a} 3}\right]^a\)

= \(\frac{-a b c}{6}[0-1]=\frac{a b c}{6}\)

42. Find the volume of the sphere x² + y² + Z² = a².

Solution: The sphere x² +y² +z² =a² is symmetric about the coordinate planes

The volume of the sphere=8 (Volume of the sphere in the first octant).
x² +y² +z² =a² ⇒ z² =a² -x² -y² ⇒ z=± \(\sqrt{a^2-x^2-y^2}\)

In the first octant z varies from z=0 to z \(\sqrt{a^2-x^2-y^2}\)

The section of the sphere by the xy-plane z=0 is the circle x²+y²=a²

⇒y²=a²-x^2⇒ y=±\(\sqrt{a^2-x^2}\).

∴ y varies from 0 to \(\sqrt{a^2-x^2}\) and x varies from 0 to a.

∴ Volume of the sphere = \(8 \int_0^a \int_0^{\sqrt{a^2-x^2} \sqrt{a^2-x^2-y^2}} \int_0^a d x d y d z\)

= \(8 \int_0^{\sqrt{a^2-x^2}}\left\{\int_0^{\sqrt{a^2-x^2}}\left[\int_0^d d z\right] d y\right\} d x\)

= \(8 \int_0^a\left\{\int_0^{\sqrt{a^2-x^2}}[z]_{z=0}^{z=\sqrt{a^2-x^2-y^2}} d y\right\} d x=8 \int_0^a\left[\int_0^{\sqrt{a^2-x^2}} \sqrt{a^2-x^2-y^2} d y\right] d x\)

= \(8 \int_0^a\left[\frac{y}{2} \sqrt{a^2-x^2-y^2}+\frac{a^2-x^2}{2} \text{Sin}^{-1} \frac{y}{\sqrt{a^2-x^2}}\right] d x\)

= \(8 \int_0^{y=\sqrt{a^2-x^2}} \frac{a^2-x^2}{2} \frac{\pi}{2} d x\)

= \(2 \pi \int_0^a\left(a^2-x^2\right) d x=2 \pi\left[a^2 x-\frac{x^3}{3}\right]=2 \pi\left(a^3-\frac{a^3}{3}\right)=\frac{4 \pi a^3}{3}\)

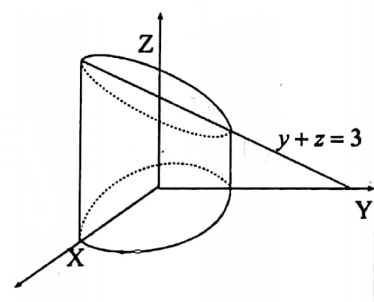
43. Find the volume bounded by the cylinder x² +y²  = 4 and the planes y + z-4 and z = 0 by using double integral.

Solution: The required volume of the cylinder x²+y²=4, cut off between the planes z=0 and y+z =4 is V ∫\(\int_D\)∫ dx dy dz.

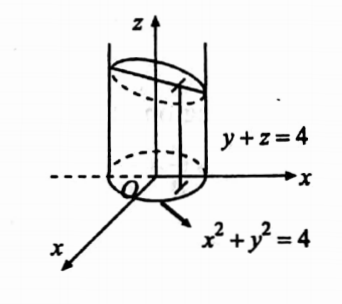
∴  z varies from z=0 to z=4-y

∴ The projection of the region in the plane is x²+y²=4 =y=± \(\sqrt{4-x^2}\)

∴ y varies from \(-\sqrt{4-x^2}\) to \(+\sqrt{4-x^2}\) and x-varies from -2 to 2

Volume V = \(\int_{-2}^2 \int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}}[z]_0^{4-y} d y d x=\int_{-2}^2 \int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}}(4-y) d y d x\)

= \(\int_{-2}^2\left[4 y-\frac{y^2}{2}\right]_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} d x\)

= \(\int_{-2}^2\left\{4\left[\sqrt{4-x^2}-\left(-\sqrt{4-x^2}\right)-\frac{1}{2}\left[4-x^2-\left(4-x^2\right)\right]\right\} d x=8 \int_{-2}^2 \sqrt{4-x^2} d x\right.\)

= \(8 \cdot 2 \int_0^2 \sqrt{4-x^2} d x=16\left[\frac{x \sqrt{4-x^2}}{2}+\frac{4}{2} \text{Sin}^{-1} \frac{x}{2}\right]=16\left[0+2 \text{Sin}^{-1} 1-(0+0)\right]\)

= \(16 \cdot 2 \frac{\pi}{2}=16 \pi\)

44. Find the volume common to the cylinders x² + y²= a² and x²+ z² = a².

Solution:  Given cylinder x²+y²=a² →(1)

⇒ y²=a²-x² or y=±  \(\sqrt{a^2-x^2}\) and

x²+z² =a² →(2)= z²=a²-x²  0r  z= ±\(\sqrt{a^2-x^2}\)

The required volume can be covered as follows:

z: from-\(\sqrt{a^2-x^2}\) to \(\sqrt{a^2-x^2}\) : y: from – \(\sqrt{a^2-x^2}\) to \(\sqrt{a^2-x^2}\) : x: from  − a to a.

Thus the volume V enclosed by the cylinders

V = \(\int_{-a-\sqrt{a^2-x^2}}^a \int_{-\sqrt{a^2-x^2}}^{\sqrt{a^2-x^2}} d z d x=2 \int_{-a}^a \int_{-\sqrt{a^2-x^2}}^{\sqrt{a^2-x^2}}[z]_0^{\sqrt{a^2-x^2}} d y d x\)

= \(4 \int_{-a}^{a \sqrt{a^2-x^2}} \int_0^{\sqrt{2}} \sqrt{\left(a^2-x^2\right)} d y d x\)

= \(4 \int_{-a}^a \sqrt{a^2-x^2}[y] d x=8 \int_0^{\sqrt{a^2-x^2}}\left(a^2-x^2\right) d x\)

= \(8(a^2 x-\frac{x^3}{3} \int_0^a=8 (a^3-\frac{a^3}{3})\)

= \(8 a^3\left(1-\frac{1}{3}\right)=\frac{16 a^3}{3}\) cubic units

45. Find the volume of the portion of the sphere x² +y² + z² = a² lying inside the cylinder x² + y² = ax.

Solution: We solve the problem by transforming it into cylindrical coordinates.

Putx-p cos Φ , y = ρ sin Φ, z = z.

Required volume = ∫∫∫ρ dz dρ dΦ.

The equation of the sphere is ρ² + z² = a² and the equation of the cylinder is  ρ= a cos Φ.

The volume inside the cylinder bounded by the sphere

= 2 x volume shown shaded in the.

Note that z varies from 0 to\(\sqrt{a^2-\rho^2}\),ρ varies from 0 to a cosΦ and Φ varies from 0 to π.

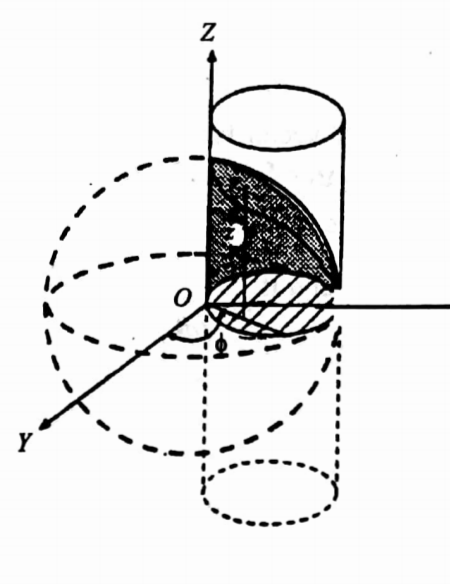
Required volume

= \(2 \int_0^\pi \int_0^{a \cos \phi} \int_0^{\sqrt{a^2-\rho^2}} \rho d z d \rho d \phi\)

= \(2 \int_0^\pi \int_0^{a \cos \phi} \rho \sqrt{a^2-\rho^2} d \rho d \phi\)

= \(2 \int_0^\pi\left[-\frac{\left(a^2-\rho^2\right)^{3 / 2}}{3}\right]_0^{a \cos \phi} d \phi\)

= \(\frac{2 a^3}{3} \int_0^\pi\left(1-\sin ^3 \phi\right) d \phi\)

= \(\frac{2 a^3}{9}(3 \pi-4) .\)