Vector Integration Applications Gauss Theorem And Applications Gauss Theorem In Plane And Applications Stokes Theorem And Applications Solved Problems Exercise 5

Vector Integration Application Exercise -5

 

1. State and prove Gauss’s divergence theorem.

Solution:

Gauss’s divergence theorem: If F is a differentiable vector point function and S is a closed surface enclosing a region V, then \(\int_S\)F. N dS \(\int_V\)  div F dV, where N is the outward drawn unit normal vector to S.

Proof: Let S be a closed surface. Let us choose the coordinate axes so that any line parallel to the axes meets the surface in almost two points. Let R be the projection of S on xy-plane.  Let S₁ and S₂ be the lower and upper parts of S.

 

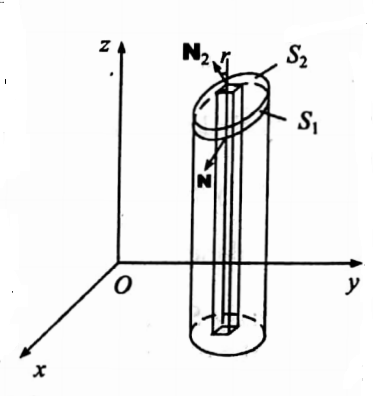
Let z=f(x,y) and z = g(x, y) be the equations of S₁ and S₂ which can be put in the form f(x,y)≤z≤ g(x, y)
Let F = F₁i+F₂ j+F₃k where F_1, F₂, and F₃ are scalar point functions.

∴ \(\int_v \text{div} \mathbf{F} d V=\int_V \nabla \cdot \mathbf{F} d V=\iint_V\left(\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}\right) d V=\int_V \frac{\partial F_1}{\partial x} d V+\int_V \frac{\partial F_2}{\partial y}+\int_V \frac{\partial F_3}{\partial z} d V .\)

Now \(\int_V \frac{\partial F_3}{\partial z} d V=\iiint_V \frac{\partial F_3}{\partial z} d x d y d z=\iiint_R\left[F_3(x, y, z)\right]_f^g d x d y\)

⇒ \(\iint_R\left[F_3(x, y, g)-F_3(x, y, f)\right] d x d y .\)

For the upper part S₂, dx dy = dS cos γ = N . k dS, since the normal to S₂ makes an acute angle y with k.

∴ \(\iint_R F_3(x, y, g) d x d y=\int_{s_2} F_3 \mathbf{N} \cdot \mathbf{k} d S\)

For the lower part S₁ dx dy =- cos γ dS =− N . k dS, since the normal to S₁ makes an obtuse angle y with k.

∴ \(\iint_R F_3(x, y, f) d x d y=-\int_{s_1} F_3 \mathbf{N} . \mathbf{k} d S\)

⇒ \(\int_V \frac{\partial F_3}{\partial z} d V=\int_{s_2} F_3 \mathbf{N} . \mathbf{k} d S+\int_{s_1} F_3 \mathbf{N} \cdot \mathbf{k} d S=\int_S F_3 \mathbf{k} . \mathbf{N} d S\)

Similarly \(\int_V \frac{\partial F_2}{\partial y} d V=\int_S F_2 \mathbf{j} \cdot \mathbf{N} d S \text { and } \int_V \frac{\partial F_1}{\partial x} d V=\int_S F_1 \mathbf{i} \cdot \mathbf{N} d S\)

∴ \(\int_V\left(\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}\right) d V=\int_S F_1 \mathbf{i} \cdot \mathbf{N} d S+\int_S F_2 \mathbf{j} \cdot \mathbf{N} d S+\int_S F_3 \mathbf{k} \cdot \mathbf{N} d S\)

⇒ \(\int_V \nabla \cdot \mathbf{F} d V=\int_S\left(F_1 \mathbf{i}+F_2 \mathbf{j}+F_3 \mathbf{k}\right) \cdot \mathbf{N} d S \Rightarrow \int_V \nabla \cdot \mathbf{F} d V=\int_S \mathbf{F} \cdot \mathbf{N} d S\)

2. If F is a continuously differentiable vector point function and S is a closed surface enclosing a region V then prove that \(\int_S\)N×F dS=\(\int_V\) ∇×F dV.

Solution: Let f=a×F where a is any constant vector.

By Gauss’s divergence theorem \(\int_S\)f.N dS= \(\int_V\)∇.f dV.

⇒ \(\int_S(\mathbf{a} \times \mathbf{F}) \cdot \mathbf{N} d S=\int_V \nabla \cdot(\mathbf{a} \times \mathbf{F}) d V \Rightarrow \int_S \mathbf{a} \cdot(\mathbf{F} \times \mathbf{N}) d S=-\int_V \nabla \cdot(\mathbf{F} \times \mathbf{a}) d v\)

⇒ \(-\int_S \mathbf{a} \cdot(\mathbf{N} \times \mathbf{F}) d S=-\int_V(\nabla \times \mathbf{F}) \cdot \mathbf{a} d V \Rightarrow \mathbf{a} \cdot \int_S(\mathbf{N} \times \mathbf{F}) d S=\mathbf{a} \cdot \int_V \nabla \times \mathbf{F} d V\)

⇒ \(\int_S(\mathbf{N} \times \mathbf{F}) d S=\int_V \nabla \times \mathbf{F} d V\) [∵ a is any constant vector]

3. If φ  is a continuously differentiable scalar point function and S is a closed surface enclosing a region V then prove that \(\int_S\)N φ dS= \(\int_V\) ∇φ dV.

Solution: Let f=a φ where a is any constant vector.

By Gauss’s divergence theorem, \(\int_S \mathbf{f} \cdot \mathbf{N} d S=\int_V \nabla \cdot \mathbf{f} d V\)

⇒ \(\int_S a \varphi \cdot \mathbf{N} d S=\int_V \nabla \cdot \mathbf{a} \varphi d V \Rightarrow \int_S \mathbf{a} \cdot \varphi \mathbf{N} d S=\int_V \nabla \varphi \cdot \mathbf{a} d V\)

⇒ \(\mathbf{a} \cdot \int_S \varphi \mathbf{N} d S=\mathbf{a} \cdot \int_V \nabla \varphi d V \Rightarrow \int_S \varphi \mathbf{N} d S=\int_V \nabla \varphi d V\) [∵ a is any constant vector]

4. Apply Gauss’s theorem to prove that  \(\int_S\)r. N dS = 3 V.

Solution: \(\int_S\)r.NdS=\(\int_V\)div r dV=\(\int_V\)∇.r dV=\(\int_V\)3 dV=3V, where V is the volume of the region bounded by the closed surface S.

5. Prove that for any closed surface S, \(\iint_S\)N dS = 0.

Solution:\(\iint_S\)N dS=\(\iint_S\)N 1 dS=\(\int_V\)(∇ 1)dV=\(\int_V\)0 dV=0

6. For any closed surface S, prove that \(\iint_S\)Curl F . N dS = 0.

Solution: By Gauss’s  divergence theorem,

\(\iint_S\)F.N dS=\(\iint_S\)(∇×F).N dS=\(\int_V\)div(∇×F) dV=\(\int_V\)0 dV=0.

7. If S is any closed surface enclosing a volume V and F = xi + 2yj+ 3zk, prove that \(\iint_S\)F.N dS=6v.

Solution:  By Gauss’s divergence theorem,

∴ \(\iint_S \mathbf{F} \cdot \mathbf{N} d S=\int_V \nabla \cdot \mathbf{F} d V=\int_V\left[\frac{\partial}{\partial x}\{x\}+\frac{\partial}{\partial y}\{2 y\}+\frac{\partial}{\partial z}\{3 z\}\right] d V=\int_V(1+2+3) d V=6 V\)

8. If F = xi- 2yi + 3zk and S is a closed surface enclosing a volume V, show that \(\int_S\)F.N dS=2v.

Solution: 

By Gauss’s divergence theorem,

⇒ \(\int_S \mathbf{F} \cdot \mathbf{N} d S=\int_V \text{div} \mathbf{F} d V=\int_V(\nabla \cdot \mathbf{F}) d V=\int_V\left[\frac{\partial}{\partial x}\{x\}+\frac{\partial}{\partial y}\{-2 y\}+\frac{\partial}{\partial z}\{3 z\}\right] d V\)

⇒ \(\int_V(1-2+3) d V=2 \int_V d V=2 V\)

9. Computed \(\oint_S\)(ax²+by²+cz²) dS over the sphere x² +y² + z² = 1.

Solution: Let φ =x²+y²+z²-1

Normal vector to the surface, ∇φ =\(\mathbf{i} \frac{\partial \varphi}{\partial x}+\mathbf{j} \frac{\partial \varphi}{\partial y}+\mathbf{k} \frac{\partial \varphi}{\partial z}\)

=2xi+2yj+2zk

Unit normal vector, \(\mathbf{N}=\frac{2 x \mathbf{i}+2 y \mathbf{j}+2 z \mathbf{k}}{\sqrt{4 x^2+4 y^2+4 z^2}}=\frac{2 x \mathbf{i}+2 y \mathbf{j}+2 z \mathbf{k}}{2 \sqrt{x^2+y^2+z^2}}=x \mathbf{i}+y \mathbf{j}+z \mathbf{k}\)

⇒ \(\mathbf{F} \cdot \mathbf{N}=a x^2+b y^2+c z^2 \Rightarrow \mathbf{F} \cdot(x \mathbf{i}+y \mathbf{j}+z \mathbf{k})=a x^2+b y^2+c z^2 \Rightarrow \mathbf{F}=a x \mathbf{i}+b y \mathbf{j}+c z \mathbf{k}\)

⇒ \(\nabla \cdot \mathbf{F}=\frac{\partial}{\partial x}(a x)+\frac{\partial}{\partial y}(b y)+\frac{\partial}{\partial z}(c z)=a+b+c\)

Volume of the sphere \(x^2+y^2+z^2=1 \text { is } 4 \pi / 3\)

By Gauss’s divergence theorem,

⇒ \(\oint_S\left(a x^2+b y^2+c z^2\right) d S=\int_S \mathbf{F} \cdot \mathbf{N} d S=\int_V \nabla \cdot \mathbf{F} d V=\int_V(a+b+c) d V=(a+b+c) V\)

⇒ \((a+b+c) \frac{4}{3} \pi=\frac{4 \pi}{3}(a+b+c)\)

10. If F = axi + byj+ czk and a, b, c are constants, show that ∫F.N dS =\(\frac{4}{3} \pi\) (a + b + c) where S is the surface of the  unit sphere.

Solution:

∴ \(\nabla \cdot \mathbf{F}=\frac{\partial}{\partial x}\{a x\}+\frac{\partial}{\partial y}\{b y\}+\frac{\partial}{\partial z}\{c z\}=a+b+c\)

Volume of the sphere, \(V=\frac{4}{3} \pi(1)^3=\frac{4}{3} \pi\)

By Gauss’s divergence theorem, \(\int_S \mathbf{F} \cdot \mathbf{N} d S=\int_V \nabla \cdot \mathbf{F} d V=\int_V(a+b+c) d V\)

⇒ \((a+b+c) \int_V d V=(a+b+c) V=\frac{4}{3} \pi(a+b+c)\)

11. Show that \(\iint_S\)(ax dy dz + by dz dx + cz dx dy) = \(\frac{4}{3} \pi\)(a + b + c), where S is the surface of the sphere x² +y² + z²=1. where S is the surface of the sphere.

Solution: 

By Gauss’s divergence theorem,

⇒ \(\iint_S(a x d y d z+b y d z d x+c z d x d y)=\int_s[a x \mathbf{N} \cdot \mathbf{i} d S+\text { by N.j } d S+c z \mathbf{N} \cdot \mathbf{k} d S]\)

⇒ \(\int_s(a x \mathbf{i}+b y \mathbf{j}+c z \mathbf{k}) \cdot \mathbf{N} d S=\int_V\left[\frac{\partial}{\partial x}(a x)+\frac{\partial}{\partial y}(b y)+\frac{\partial}{\partial z}(c z)\right] d V=(a+b+c) \int_V d V\)

⇒ \((a+b+c) V \text { where } V \text { is the volume of } x^2+y^2+z^2 = 1\)

⇒ \((a+b+c) \frac{4}{3} \pi=\frac{4 \pi}{3}(a+b+c) \text {. }\)

12. Apply divergence theorem to evaluate \(\iint_S\) x dy dz+y dz dx + z dx dy where S is the surface x² +y² + z² = 1

Solution: By Gauss’s divergence Theorem,

\(\iint_S\)(x dy dz+y dz dy+z dx dy)= \(\int_S\)[x N.idS+y N.jdS+z N.k dS]

⇒ \(\int_S(x \mathbf{i}+y \mathbf{j}+z \mathbf{k}) \cdot \mathbf{N} d S=\int_V\left[\frac{\partial}{\partial x}(x)+\frac{\partial}{\partial y}(y)+\frac{\partial}{\partial z}(z)\right] d V=(1+1+1) \int_V d V\)

⇒ \(3 V \text { where } V \text { is the volume of } x^2+y^2+z^2=1=3 \times \frac{4}{3} \pi=4 \pi \text {. }\)

13. Apply Gauss’s divergence theorem to compute the double integral\(\iint_S\) (x+z) dy dz+(y+z) dz dx+(x+y) dxdy where S is the surface of the sphere x² +y² + z² = 4.

Solution: 

By Gauss’s divergence theorem, \(\iint_S(x+z) d y d z+(y+z) d z d x+(x+y) d x d y\)

⇒ \(\int_S(x+z) \mathbf{N} \cdot \mathbf{i} d S+(y+z) \mathbf{N} \cdot \mathbf{j} d S+(x+y) \mathbf{N} \cdot \mathbf{k} d S\)

⇒ \(\int_S[(x+z) \mathbf{i}+(y+z) \mathbf{j}+(x+y) \mathbf{k}] \cdot \mathbf{N} d S\)

⇒ \(\int_v\left[\frac{\partial}{\partial x}(x+z)+\frac{\partial}{\partial y}(y+z)+\frac{\partial}{\partial z}(x+y)\right] d V=\int_V(1+1+0) d V=2 V=2 \frac{4 \pi}{3}(8)=\frac{64 \pi}{3}\)

14. If F = xi−yj+ (z²−1)k find the value of \(\int_S\) F . N dS where S is the closed surface bounded by the planes z = 0, z = 1 and the cylinder x² +y² = 4

Solution: 

∴ \(\mathbf{F}=x \mathbf{i}-y \mathbf{j}+\left(z^2-1\right) \mathbf{k}\)

⇒ \(\text{div} \mathbf{F}=\nabla \cdot \mathbf{F}=\frac{\partial}{\partial x}\{x\}+\frac{\partial}{\partial y}\{-y\}+\frac{\partial}{\partial z}\left\{z^2-1\right\}=1-1+2 z=2 z\)

The limits of the region bounded by the given surface are z = 0 to z = 1, \(y=-\sqrt{4-x^2} \text { to } y=\sqrt{4-x^2}\) and x = -2 to x = 2.

By Gauss’s divergence theorem

⇒ \(\int_S \mathbf{F} \cdot \mathbf{N} d S=\int_V d i v \mathbf{F} d V=\int_V 2 z d V=\int_{x=-2}^{x=2} \int_{y=-\sqrt{4-x^2}}^{y=\sqrt{4-x^2}} \int_{z=0}^{z=1} 2 z d x d y d z\)

⇒ \(\left.=\int_{x=-2}^{x=2} \int_{y=-\sqrt{4-x^2}}^{y=\sqrt{4-x^2}} z^2\right]_{z=0}^{z=1} d x d y=\int_{x=-2}^{x=2} \int_{y=-\sqrt{4-x^2}}^{y=\sqrt{4-x^2}} 1 d x d y\)

⇒ \(\left.\int_{x=-2}^{x=2} y\right] _{y=-\sqrt{4-x^2}}^{y=\sqrt{4-x^2}} d x =\int_{x=-2}^{x=2} 2 \sqrt{4-x^2} d x=4 \int_0^2 \sqrt{4-x^2} d x\)

⇒ \(4\left[\frac{x \sqrt{4-x^2}}{2}+\frac{4}{2} \text{Sin}^{-1} \frac{x}{2}\right]_0^2=4\left[2 \frac{\pi}{2}-0\right]=4 \pi\)

15. If F = x i− y j + (z²−1) k, V is the volume of the cylinder bounded by z = 0, z = 1 and x² +y² = a² and S is the surface of the cylinder, show that \(\int_S\) F . N dS = π a²

Solution: Given=x i− y j + (z²−1)k, Now F₁=x,F₂=−y,F₃=z−1

∴ \(\frac{\partial F_1}{\partial x}=1, \frac{\partial F_2}{\partial y}=-1, \frac{\partial F_3}{\partial z}=2 z . \text{div} \mathbf{F}=\nabla \cdot \mathbf{F}=\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}=1-1+2 z=2 z\)

By the Gauss divergence theorem,

⇒ \(\int_S \mathbf{F} \mathbf{N} d S=\int_v \text{div} \mathbf{F} d V=\int_V 2 z d V=\int_{x=-a}^{x=a} \int_{y=\sqrt{a^2-x^2}}^{y=-\sqrt{a^2-x^2}} \int_{z=0}^{z=1} 2 z d x d y d z\)

⇒ \(\left.\int_{x=-a}^{x=a} \int_{y=-\sqrt{a^2-x^2}}^{y=\sqrt{a^2-x^2}} z^2\right]_{0}^{1} d x d y=\int_{x=-a}^{x=a}\int_{-y=\sqrt{a^2-x^2}}^{y=\sqrt{a^2-x^2}} d x d y \left.= \int_{x=-a}^{x=a} y\right]_{y=-\sqrt{a^2-x^2}}^{y=\sqrt{a^2-x^2}} dx
\)

⇒ \(\left.\int_{x=-a}^{x=a} 2 \sqrt{a^2-x^2} d x=x \sqrt{a^2-x^2}+a^2 \text{Sin}^{-1}(x / a)\right]_{-a}^a=a^2[\pi / 2-(-\pi / 2)]=\pi a^2\)

16. By transforming into triple integral, evaluate \(\int_S\) ( x³dy dz + x²y dz dx + x²z dx dy) where S is the closed surface consisting of the cylinder x²+y² = a² and the circular disc z = 0 and z = b.

Solution:

Let \(F_1=x^3, F_2=x^2 y, F_3=x^2 z. \quad \frac{\partial F_1}{\partial x}=3 x^2, \frac{\partial F_2}{\partial y}=x^2, \frac{\partial F_3}{\partial z}=x^2\)

⇒ \(\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}=3 x^2+x^2+x^2=5 x^2\)

By Gauss’s divergence theorem \(\iint_S\left(x^3 d y d z+x^2 y d z d x+x^2 z d x d y\right)\)

⇒ \(\iiint_V 5 x^2 d x d y d z=4 \int_{x=0}^{x=a} \int_{y=0}^{y=\sqrt{a^2-x^2}} \int_{z=0}^{z=b} 5 x^2 d x d y d z\)

⇒ \(20 \int_{x=0}^{x=a} \int_{y=0}^{y=\sqrt{a^2-x^2}}\left[x^2 z\right]_{z=0}^{z=b} d x d y=20 b \int_{x=0}^a \int_{y=0}^{\sqrt{a^2-x^2}} x^2 d x d y\)

⇒ \(\left.20 b \int_0^a x^2 y\right]_0^{\sqrt{a^2-x^2}}=20 b \int_0^a x^2 \sqrt{a^2-x^2} d x\)

Put x = a sin θ

∴ dx = a cos θ dθ

x = 0 ⇒ θ = 0

x = a ⇒ θ = π/2

⇒ \(20 b \int_0^{\pi / 2} a^2 \sin ^2 \theta \sqrt{a^2-a^2 \sin ^2 \theta} a \cos \theta d \theta=20 a^4 b \int_0^{\pi / 2} \sin ^2 \theta \cos ^2 \theta d \theta\)

⇒ \(20 a^4 b \int_0^{\pi / 2} \sin ^2 \theta\left(1-\sin ^2 \theta\right) d \theta=20 a^4 b\left[\int_0^{\pi / 2} \sin ^2 \theta-\int_0^{\pi / 2} \sin ^4 \theta d \theta\right]\)

⇒ \(20 a^4 b\left[\frac{1}{2} \cdot \frac{\pi}{2}-\frac{3}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2}\right]=20 a^4 b \cdot \frac{\pi}{16}=5 a^4 b \frac{\pi}{4}\)

17. If F = 2xyi +yz²j + xzk and S is a rectangular parallelopiped bounded by x = 0, y = 0,z = 0,x = 2,y= 1 and z = 3 verily Gauss’s divergence theorem.

Solution:  Consider the six faces of the rectangular parallelopiped bounded by x=o,y=0,z=0,x=2,y=1, and z=3.

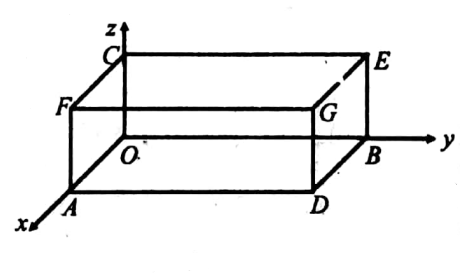
Case (1): For the face OADB, the outward normal

N = -k, z = 0, dS = dx dy.

∴ \(\int_{S_1} \mathbf{F} \cdot \mathbf{N} d S=\int_{x=0}^{x=2} \int_{y=0}^{y=1}\left(2 x y \mathbf{i}+y z^2 \mathbf{j}+x z \mathbf{k}\right) \cdot(-\mathbf{k}) d x d y=\int_{x=0}^{x=2} \int_{y=0}^{y=1}-x z d x d y=0 .\)

Case (2): For the face OBEC, the outward normal, N = -i, x = 0, dS = dx dz.

∴ \(\int_{S_2} \mathbf{F} \cdot \mathbf{N} d S=\int_{y=0}^{y=1} \int_{z=0}^{z=3}\left(2 x y \mathbf{i}+y z^2 \mathbf{j}+x z \mathbf{k}\right) \cdot(-\mathbf{i}) d y d z=\int_{y=0}^{y=1} \int_{z=0}^{z=3} 2 x y d y d z=0\)

Case (3): For the face OCFA, the outward normal, N = -j, y = 0, dS = dz dx

∴ \(\int_{S_3} \mathbf{F} \cdot \mathbf{N} d S=\int_{x=0}^{x=2} \int_{z=0}^{z=3}\left(2 x y \mathbf{i}+y z^2 \mathbf{j}+z x \mathbf{k}\right) \cdot(-\mathbf{j}) d x d z=\int_{x=0}^{x=2} \int_{z=0}^{z=3}-y z^2 d x d z=0\)

Case (4): For the face ADGF, the outward normal, N = I, x = 2, dS = dy dz

⇒ \(\int_{S_4} \mathbf{F} \cdot \mathbf{N} d S=\int_{y=0}^{y=1} \int_{z=0}^{z=3}\left(2 x y \mathbf{i}+y z^2 \mathbf{j}+x z \mathbf{k}\right) \cdot \mathbf{i} d y d z=\int_{y=0}^{y=1} \int_{z=0}^{z=3} 2 x y d y d z\)

⇒ \(\left.\left.=\int_{y=0}^{y=1} \int_{z=0}^{z=3} 4 y d y d z=\int_{y=0}^{y=1} 4 y z\right]_{z=0}^{z=3} d y=\int_0^1 12 y d y=6 y^2\right]_0^1=6\)

Case (5): For the faces BDGE, the outward normal, N = j, y = 1, dS = dz dx

⇒ \(\int_{S_5} \mathbf{F} \cdot \mathbf{N} d S=\int_{x=0}^{x=2} \int_{z=0}^{z=3}\left(2 x y \mathbf{i}+y z^2 \mathbf{j}+x z \mathbf{k}\right) \cdot(\mathbf{j}) d z d x\)

⇒ \(\left.\left.=\int_{x=0}^{x=2} \int_{z=0}^{z=3} y z^2 d z d x=\int_{x=0}^{x=2} \int_{z=0}^{z=3} z^2 d z d x=\int_{x=0}^{x=2} z^3 / 3\right]_0^3 d x=\int_{x=0}^{x=2} 9 d x=9 x\right]_0^2=18\)

Case (6):  For the faces CEGF, the outward normal, N = k, z = 3, dS = dx dy

⇒ \(\int_{S_6} \mathbf{F} \cdot \mathbf{N} d S=\int_{x=0}^{x=2} \int_{y=0}^{y=1}\left(2 x y \mathbf{i}+y z^2 \mathbf{j}+z x \mathbf{k}\right) \cdot \mathbf{k} d x d y\)

⇒ \(\left.\left.\int_{x=0}^{x=2} \int_{y=0}^{y=1} x z d x d y=\int_{x=0}^{x=2} \int_{y=0}^{y=1} 3 x d x d y=\int_{x=0}^{x=2} 3 x y\right]_{y=0}^{y=1} d x=\int_{x=0}^{x=2} 3 x d x=3 x^2 / 2\right]_0^2=6 .\)

∴ \(\int_S \mathbf{F} \cdot \mathbf{N} d S\) sum of the six integrals over the six faces

⇒ 0 + 0 + 0 + 6 + 18 + 6 = 30.

⇒ \(\int_V \nabla \cdot \mathbf{F} d V=\int_V\left[\frac{\partial}{\partial x}(2 x y)+\frac{\partial}{\partial y}\left(y z^2\right)+\frac{\partial}{\partial z}(x z)\right] d V=\int_V\left(2 y+z^2+x\right) d V\)

⇒ \(\int_{x=0}^{x=2} \int_{y=0}^{y=1} \int_{z=0}^{z=3}\left(x+2 y+z^2\right) d x d y d z=\int_{x=0}^{x=2} \int_{y=0}^{y=1}\left[x z+2 y z+\frac{z^3}{3}\right]_{z=1}^{z=3} d x d y\)

⇒ \(\left.\int_{x=0}^{x=2} \int_{y=0}^{y=1}(3 x+6 y+9) d x d y=\int_{x=0}^{x=2}\left[3 x y+3 y^2+9 y\right]\right]_{y=0}^{y=1} d x=\int_0^2(3 x+12) d x\)

∴ \(\left[\frac{3 x^2}{2}+12 x\right]_0^2=6+24=30\) ∴ \(\int_S \mathbf{F} \cdot \mathbf{N} d S=\int_V \nabla \cdot \mathbf{F} d V\)

∴ Gauss’s divergence theorem is verified.

18. Evaluate \(\int_S\)F.N dS where F = 2xy i +yz² +xzk and S is the surface of the parallelopiped formed by x=0 ,  y = 0, z = 0  x = 2,y = 1, z = 3

Solution: Consider the parallelopiped O A B C P Q R S surrounded by x=0,y=0, z=0, x=2,y=1, and z=3.

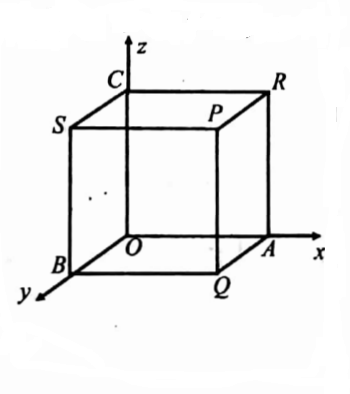
1. For the face PQAR, I is the outward normal.

N = i, x = 2, dS = dy dz.

∴ \(\int_{R_1} \mathbf{F} \cdot \mathbf{N} d S=\int_{y=0}^{y=1} \int_{z=0}^{z=3}\left(2 x y \mathbf{i}+y z^2 \mathbf{j}+x z \mathbf{k}\right) \cdot \mathbf{i} d y d z\)

⇒ \(=\int_{y=0}^{y=1} \int_{z=0}^{z=3} 2 x y d y d z=\int_{y=0}^{y=1}[4 y z]_{z=0}^{x=3} d y=\int_{y=0}^{y=1} 12 y d y=\left[6 y^2\right]_0^1=6\)

2. For the faces OBSC, -i is the outward normal. N = -i, x = 0, dS = dy dz

∴ \(\int_{R_2} \mathbf{F} \cdot \mathbf{N} d S=\iint_{R_2}\left(2 x y \mathbf{i}+y z^2 \mathbf{j}+x z \mathbf{k}\right) \cdot(-\mathbf{i}) d y d z=-\iint_R 2 x y d y d z=0 .\)

3. For the face BQPS, j is the outward normal. ∴ N = j, y = 1 and dS = dx dz.

∴ \(\int_{R_3} \mathbf{F} \cdot \mathbf{N} d S=\iint_{R_3}\left(2 x y \mathbf{i}+y z^2 \mathbf{j}+x z \mathbf{k}\right) \cdot \mathbf{j} d x d z=\iint_{R_3} y z^2 d x d z\)

⇒ \(=\int_{x=0}^{x=2} \int_{z=0}^{z=3} z^2 d x d z=\int_{x=0}^{x=2}\left[\frac{z^3}{3}\right]_{z=0}^{z=3} d x=\int_{x=0}^{x=2} 9 d x=[9 x]_0^2=18\)

4. For the face OARC, -j is the outward normal. ∴ N = -j, y = 0 and dS = dx dz

∴ \(\int_{R_4} \mathbf{F} \cdot \mathbf{N} d S=\iint_{R_4}\left(2 x y \mathbf{i}+y z^2 \mathbf{j}+x z \mathbf{k}\right) \cdot(-\mathbf{j}) d x d z=-\iint_{R_4} y z^2 d x d z=0\)

5. For the face PRCS, k is the outward normal. ∴ N = k, z = 3 and dS = dx dy.

∴ \(\int_{R_5} \mathbf{F} \cdot \mathbf{N} d S=\iint_{R_5}\left(2 x y \mathbf{i}+y z^2 \mathbf{J}+x z \mathbf{k}\right) \cdot \mathbf{k} d x d y=\iint_{R_5} x z d x d y\)

⇒ \(\int_{x=0}^{x=2} \int_{y=0}^{y=1} 3 x d x d y=\int_{x=0}^{x=2}[3 x y]_{y=0}^{y=1} d x=\int_{x=0}^{x=2} 3 x d x=\left[\frac{3 x^2}{2}\right]_0^2=6\)

6. For the face OAQB, -k is the outward normal. N = -k, z = 0 and dS = dx dy

∴ \(\int_{R_6} \mathbf{F} \cdot \mathbf{N} d S=\iint_{R_6}\left(2 x y \mathbf{i}+y z^2 \mathbf{j}+x z \mathbf{k}\right) \cdot(-\mathbf{k}) d x d y=-\iint_{R_6} x z d x d y=0\)

∴\(\int_s \mathbf{F} \cdot \mathbf{N} d S=6+0+18+0+6+0=30\)

19. Evaluate\(\iint_S\) (x dydz +y dzdx + z dxdy) taken over the outer surface of the cube[0,a;0,a;0,a].

Solution:  By Gauss’s Divergence theorem,

⇒ \(\iint_S(x d y d z+y d z d x+z d x d y)=\iiint_v\left[\frac{\partial}{\partial x}\{x\}+\frac{\partial}{\partial y}\{y\}+\frac{\partial}{\partial z}\{z\}\right] d x d y d z\)

⇒ \(\iiint_V(1+1+1) d x d y d z=3 \int_{x=0}^{x=a} \int_{y=0}^{y=a} \int_{z=0}^{z=a} d x d y d z=3 \int_{x=0}^{x=a} \int_{y=0}^{y=a}[z]_{z=0}^{z=a} d x d y\)

∴ \(3 \int_{x=0}^{x=a} \int_{y=0}^{y=a} a d x d y=3 \int_{x=0}^{x=a}[a y]_{y=0}^{y=a} d x=3 \int_{x=0}^{x=a} a^2 d x\left[3 a^2 x\right]_{x=0}^{x=a}=3 a^3\)

20. Evaluate \(\int_S\)F . N dS where F = 2x²y i -y²j + 4xz²k taken over the region in the first octant bounded by y² + z²= 9 and x = 2.

Solution:  \(\int_S\)F . N dS=\(\int_V\)∇.F dV=\(\int_V\)∇.(2x²yi-y²j+4xz² k)dv

⇒ \(\int_v\left[\frac{\partial}{\partial x}\left(2 x^2 y\right)+\frac{\partial}{\partial y}\left(-y^2\right)+\frac{\partial}{\partial z}\left(4 x z^2\right)\right] d V=\int_V(4 x y-2 y+8 x z) d V\)

⇒ \(\int_{x=0}^{x=2} \int_{y=0}^{y=3} \int_{z=0}^{z=\sqrt{9-y^2}}(4 x y-2 y+8 x z) d x d y d z\)

= \(\int_{x=0}^{x=2} \int_{y=0}^{y=3}\left[4 x y z-2 y z+4 x z^2\right]_{=0}^{z=\sqrt{9-y^2}} d x d y\)

⇒ \(\int_{x=0}^{x=2} \int_{y=0}^{y=3}(2 x-1) 2 y \sqrt{9-y^2}+4 x\left(9-y^2\right) d x d y\)

⇒ \(\int_{x=0}^{x=2}\left[(2 x-1) \frac{\left(9-y^2\right)^{3 / 2}}{-3 / 2}+4 x\left(9 y-\frac{y^3}{3}\right)\right]_{y=0}^{y=3} d x=\int_{x=0}^{x=2}\left[4 x(27-9)+\frac{2(2 x-1)}{3} \times 27\right] d x\)

∴ \(\int_0^2[72 x+36 x-18] d x=\int_0^2(108 x-18) d x=\left[54 x^2-18 x\right]_0^2=216-36=180\)

21. Evaluate by Gauss divergence theorem for \(\iint_S\) 4xz dy dz -y² dz dx+yz dx dy where S is the surface of the cube bounded by the planes  x=0,x=1,y=0,y=1,z=0,z=1

Solution:  

Let \(F_1=4 x z, F_2=-y^2, F_3=y z\)

⇒ \(\frac{\partial F_1}{\partial x}=4 z, \frac{\partial F_2}{\partial y}=-2 y, \frac{\partial F_3}{\partial z}=y \cdot \frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}=4 z-2 y+y=4 z-y\)

By Gauss’s divergence theorem, \(\iint_S 4 x z d y d z-y^2 d z d x+y z d x d y\)

⇒ \(\left.\iiint_V(4 z-y) d x d y d z=\int_{x=0}^{x=1} \int_{y=0}^{y=1} \int_{z=0}^{z=1}(4 z-y) d x d y d z=\int_{x=0}^{x=1} \int_{y=0}^{y=1}\left[2 z^2-y z\right]\right]_{z=0}^{z=1} d x d y\)

∴ \(\int_{x=0}^{x=1} \int_{y=0}^{y=1}(2-y) d x d y=\int_{x=0}^{x=1}\left[2 y-\frac{y^2}{2}\right]_{y=0}^{y=1} d x=\int_{x=0}^{x=1} \frac{3}{2} d x=\left[\frac{3 x}{2}\right]_{x=0}^{x=1}=\frac{3}{2} .\)

22. Find the value of \(\int_S\)(F x ∇φ) .N dS, where F = x² i +y²j + z²k,  φ= xy+yz + zx, S is the surface bounded by x = ± 1 ,y = ± 1, z = ± 1.

Solution:

Given \(\mathbf{F}=x^2 \mathbf{i}+y^2 \mathbf{j}+z^2 \mathbf{k}, \varphi=x y+y z+z x . \quad \nabla \varphi=(y+z) \mathbf{i}+(z+x) \mathbf{j}+(x+y) \mathbf{k}\)

⇒ \(\mathbf{F} \times \nabla \varphi=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
x^2 & y^2 & z^2 \\
y+z & z+x & x+y
\end{array}\right|\)

⇒ \(\mathbf{i}\left(x y^2+y^3-z^3-x z^2\right)-\mathbf{j}\left(x^3+x^2 y-y z^2-z^3\right)+\mathbf{k}\left(x^2 z+x^3-y^3-y^2 z\right)\)

∴ \(\nabla \cdot(F \times \nabla \varphi)=\frac{\partial}{\partial x}\left(x y^2+y^3-z^3-x z^2\right)-\frac{\partial}{\partial y}\left(x^3+x^2 y-y z^2-z^3\right)[latex]

+[latex]\frac{\partial}{\partial z}\left(x^2 z+x^3-y^3-y^2 z\right)\)

= \(y^2-z^2-x^2+z^2+x^2-y^2=0\)

By Gauss’s divergence theorem;\(\int_S\)(F×∇φ).N dS=\(\int_V\)∇.(F×∇φ)dV=0.

23. Verify Gauss divergence theorem for F = 4xzi -y²j  +yzk taken over the curve bounded by x = 0, x- 1,y = 0,y= 1,z = 0,z= 1.

Solution:  Consider the cube OABCPQRS surrounded by the following faces.

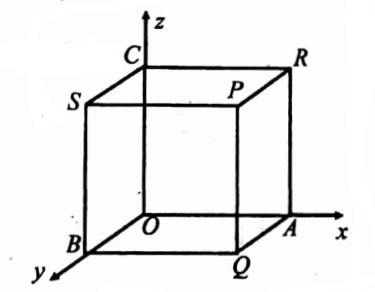
1. For the face PQAR, I is the outward normal.

N = i, x = 1, ds = dy dz.

∴ \(\int_{R_1} \mathbf{F} \cdot \mathbf{N} d S=\int_{y=0}^{y=1} \int_{z=0}^{z=1}\left(4 x z \mathbf{i}-y^2 \mathbf{j}+y z \mathbf{k}\right) \cdot \mathbf{i} d y d z\)

⇒ \(=\int_{y=0}^{y=1} \int_{z=0}^{z=1} 4 x z d y d z=\int_{y=0}^{y=1} \int_{z=0}^{z=1} 4 z d y d z=\int_{y=0}^{y=1}\left[2 z^2\right]_{z=0}^{z=1} d y=\int_{y=0}^{y=1} 2 d y=[2 y]_0^1=2\)

2. For the face OBSC, -i is the outward normal. ∴ N = -i, x = 0, and dS = dy dz

∴ \(\int_{R_2} \mathbf{F} \cdot \mathbf{N} d S=\iint_{R_2}\left(4 x z \mathbf{i}-y^2 \mathbf{j}+y z \mathbf{k}\right) \cdot(-\mathbf{i}) d y d z=-\iint_{R_2} 4 x z d y d z=0\)

3. For the face BQPS, j is the outward normal. ∴ N = j, y = 1, and dS = dx dz

∴ \(\int_{R_3} \mathbf{F} \cdot \mathbf{N} d S=\iint_{R_3}\left(4 x z \mathbf{i}-y^2 \mathbf{j}+y z \mathbf{k}\right) \cdot \mathbf{j} d x d z\)

= \(-\iint_{R_3} y^2 d x d z=-\int_{x=0}^{x=1} \int_{z=0}^{z=1} d x d z=-[x]_0^1[z]_0^1=-1\)

4. For the face OARC, -j is the outward normal. ∴ N = -j, y = 0 and dS = dx dz

∴ \(\int_{R_4} \mathbf{F} \cdot \mathbf{N} d S=\int_{R_4}\left(4 x z \mathbf{i}-y^2 \mathbf{j}+y z \mathbf{k}\right) \cdot(-\mathbf{j}) d S=\iint_{R_4} y^2 d x d z=0\)

5. For the face PRCS, k is the outward normal. ∴ N = k, z = 1, and dS = dx dy

∴ \(\int_{R_5} \mathbf{F} \cdot \mathbf{N} d S=\int_{R_5}\left(4 x z \mathbf{i}-y^2 \mathbf{j}+y z \mathbf{k}\right) \cdot \mathbf{k} d S\)

= \(\iint_{R_5} y z \cdot d x d y=\int_{x=0}^{x=1} \int_{y=0}^{y=1} y d x d y=[x]_0^1 \cdot\left[\frac{y^2}{2}\right]_0^1=\frac{1}{2} .\)

⇒ \(\int_s \mathbf{F} \cdot \mathbf{N} d S=2+0-1+0+\frac{1}{2}+0=\frac{3}{2}\)

⇒ \(\int_s \mathbf{F} \cdot \mathbf{N} d S=2+0-1+0+\frac{1}{2}+0=\frac{3}{2}\)

⇒ \(\int_V \nabla \cdot \mathbf{F} d V=\int_V\left[\frac{\partial}{\partial x}(4 x z)+\frac{\partial}{\partial y}\left(-y^2\right)+\frac{\partial}{\partial z}(y z)\right] d V=\int_V(4 z-2 y+y) d V\)

⇒ \(=\int_{x=0}^{x=1} \int_{y=0}^{y=1} \int_{z=0}^{z=1}(4 z-y) d x d y d z=\int_{x=0}^{x=1} \int_{y=0}^{y=1}\left[2 z^2-y z\right]_{z=0}^{z=1} d x d y=\int_{x=0}^{x=1} \int_{y=0}^{y=1}(2-y) d x d y\)

⇒ \(=\int_{x=0}^{x=1}\left[2 y-\frac{y^2}{2}\right]_{y=0}^{y=1} d x=\int_{x=0}^{x=1}\left(2-\frac{1}{2}\right) d x=\left[3 \frac{x}{2}\right]_{x=0}^{x=1}=\frac{3}{2}\) ∴ \(\int_S F \cdot \mathbf{N} d S=\int_V \nabla \cdot \mathbf{F} d V\)

∴ Gauss’s divergence theorem is verified.

24. Verify Gauss’s divergence theorem to evaluate \(\int_S\){(x³ −yz) i- 2x²yi + zk }. N dS over the surface of a cube bounded by the coordinate planes x=y=z=a.

Solution:

∴ \(\mathbf{F}=\left(x^3-y z\right) \mathbf{i}-2 x^2 y \mathbf{j}+z \mathbf{k} . \quad \text{div} \mathbf{F}=\nabla \cdot \mathbf{F}=3 x^2-2 x^2+1=x^2+1\)

⇒ \(\int_V \text{div} \mathbf{F} d V=\int_V\left(x^2+1\right) d V=\int_{x=0}^{x=a} \int_{y=0}^{y=a} \int_{z=0}^{z=a}\left(x^2+1\right) d x d y d z\)

⇒ \(=\int_{x=0}^{x=a} \int_{y=0}^{y=a}\left[\left(x^2+1\right) z\right]{ }_{z=0}^{z=a} d x d y=\int_{x=0}^{x=a} \int_{y=0}^{y=a} a\left(x^2+1\right) d x d y=\int_{x=0}^{x=a}\left[a\left(x^2+1\right) y\right]_{y=0}^{y=a} d x\)

⇒ \(\left.=a^2 \int_{x=0}^{x=a}\left(x^2+1\right) d x=a^2\left(\frac{x^3}{3}+x\right)\right]_0^a=a^2\left(\frac{a^3}{3}+a\right)=\frac{a^5}{3}+a^3\)

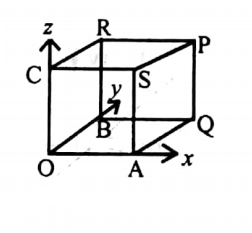
Case (1): For the face OAQB, the outward normal, N = -k, dS = dx dy, z=0

∴ \(\int_{s_1} \mathbf{F} \cdot \mathbf{N} d S=\int_{s_1}\left[\left(x^3-y z\right) \mathbf{i}-2 x^2 y \mathbf{j}+z \mathbf{k}\right] \cdot(-\mathbf{k}) d S=-\int_{s_1} z d S=0\)

Case (2): For the face CSPR, the outward normal, N =k, dS = dx dy, z = a

∴ \(\int_{s_2} \mathbf{F} \cdot \mathbf{N} d S=\int_{S_2}\left[\left(x^3-y z\right) \mathbf{i}-2 x^2 y \mathbf{j}+z \mathbf{k}\right] \cdot \mathbf{k} d S\)

⇒ \(=\int_{S_2} z d S=a \int_{x=0}^{x=a} \int_{y=0}^{y=a} d x d y=a \int_{x=0}^{x=a} [y]_{y=0}^{y=a} d x=a^2 \int_0^a d x=\left[a^2 x\right]_{x=0}^{x=a}=a^3\)

Case (3): For the face OASC, the outward normal, N = -j, dS = dx dy, y = 0

∴ \(\int_{s_3} \mathbf{F} \cdot \mathbf{N} d S=\int_{S_3}\left[\left(x^3-y z\right) \mathbf{i}-2 x^2 y \mathbf{j}+z \mathbf{k}\right) \cdot(-\mathbf{j}) d S=\int_{s_3}\left(2 x^2 y\right) d S=0\)

Case (4): For the face BQPR, the outward normal, N = j, dS = dx dz, y = a

∴ \(\int_{s_4} \mathbf{F} \cdot \mathbf{N} d S=\int_{s_4}\left[\left(x^3-y z\right) \mathbf{i}-2 x^2 y \mathbf{j}+z \mathbf{k}\right) \cdot \mathbf{j} d S=\int_{s_4}-2 x^2 y d S\)

⇒ \(\left.-2 a \int_{x=0}^{x=a} \int_{z=0}^{z=a} x^2 d x d z=-2 a \int_{x=0}^{x=a}\left[x^2 z\right]_{z=0}^{z=a} d x=-2 a^2 \int_0^a x^2 d x=-2 a^2 \frac{x^{3}}{3}\right]_{0}^{a}=-\frac{2 a^5}{3}\)

Case (5): For the face OBRC, the outward normal, N = -i, dS = dy dz, x = 0

∴ \(\int_{s_5} \mathbf{F} \cdot \mathbf{N} d S=\int_{S_5}\left[\left(x^3-y z\right) \mathbf{i}-2 x^2 y \mathbf{j}+z \mathbf{k}\right) \cdot(-\mathbf{i}) d S=-\int_{S_5}\left(x^3-y z\right) d S\)

⇒ \(\left.\int_{y=0}^{y=a} \int_{z=0}^{z=a} y z d y d z=\int_{y=0}^{y=a}\left[y z^2 / 2\right]\right]_{z=0}^{z=a} d y=\frac{a^2}{2} \int_{y=0}^{y=a} y d y=\left[\frac{a^2}{2} \cdot \frac{y^2}{2}\right]_{y=0}^{y=a}=\frac{a^4}{4}\)

Case (6): For the face AQPS, the outward normal, N = i, dS = dy dz, x = a

∴ \(\int_{s_5} \mathbf{F} \cdot \mathbf{N} d S=\int_{s_5}\left[\left(x^3-y z\right) \mathbf{i}-2 x^2 y \mathbf{j}+z \mathbf{k}\right] \cdot \mathbf{i} d S\)

= \(\int_{s_5}\left(x^3-y z\right) d S=\int_{y=0}^{y=0} \int_{z=0}^{y=a}\left(a^3-y z\right) d y d z\)

⇒ \(\int_{y=0}^{y=a}\left[a^3 z-y z^2 / 2\right]_{z=0}^{z=a} d y=\int_{y=0}^{y=a}\left[a^4-\frac{a^2 y}{2}\right] d y=\left[a^4 y-\frac{a^2 y^2}{4}\right]_{y=0}^{y=a}=a^5-\frac{a^4}{4}\)

∴ \(\int_s \mathbf{F} \cdot \mathbf{N} d S=\int_{s_1} \mathbf{F} \cdot \mathbf{N} d S+\int_{s_2} \mathbf{F} \cdot \mathbf{N} d S+\int_{s_3} \mathbf{F} \cdot \mathbf{N} d S+\int_{s_4} \mathbf{F} \cdot \mathbf{N} d S\)

+\(\int_{s_5} \mathbf{F} \cdot \mathbf{N} d S+\int_{s_6} \mathbf{F} \cdot \mathbf{N} d S\)

= \(0+a^3+0-\frac{2 a^5}{3}+\frac{a^4}{4}+a^5-\frac{a^4}{4}=a^3+\frac{a^5}{3}\)

∴ \(\int_V \text{div} \mathbf{F} d V=\int_s \mathbf{F} \cdot \mathbf{N} d S\)

∴ Gauss’s divergence theorem is verified.

25. Verify Gauss’s divergence theorem for F = (x² -yz) i- 2x² y J + 2k taken over the cube bounded by the planes x = 0, x= a, y = 0, y =a, z = 0, z = a.

Solution: 

∴ \(\int_V \text{div} \mathbf{F} d V=\int_V \nabla \cdot \mathbf{F} d V=\int_V\left[\frac{\partial}{\partial x}\left(x^2-y z\right)+\frac{\partial}{\partial y}\left(-2 x^2 y\right)+\frac{\partial}{\partial z}(2)\right] d V\)

⇒ \(\int_V\left(2 x-2 x^2\right) d V=\int_{x=0}^{x=a} \int_{y=0}^{y=a} \int_{z=0}^{z=a}\left(2 x-2 x^2\right) d x d y d z\)

⇒ \(\int_{x=0}^{x=a} \int_{y=0}^{y=a}\left(2 x-2 x^2\right) d x d y [z]_{z=0}^{z=a}=\int_{x=0}^{x=a} \int_{y=0}^{y=a} a\left(2 x-2 x^2\right) d x d y\)

⇒ \(\left.\int_{x=0}^{x=a} a\left(2 x-2 x^2\right) d x \quad y\right]_{y=0}^{y=a}\quad\)

= \(\int_{x=0}^{x=a} a^2\left(2 x-2 x^2\right) d x=a^2\left[x^2-2 x^3 / 3\right]_0^a=a^2\left[a^2-2 a^3 / 3\right]\)

⇒ \(a^4-2 a^5 / 3\)

Case (1): For the face ADGF, N = i, dS = dy dz and x = a

∴ \(\int_{S_1} \mathbf{F} \cdot \mathbf{N} d S=\int_{S_1}\left[\left(x^2-y z\right) \mathbf{i}-2 x^2 y \mathbf{j}+2 \mathbf{k}\right] \cdot \mathbf{i} d S=\int_{S_1}\left(x^2-y z\right) d S\)

⇒ \(\int_{y=0}^{y=a} \int_{z=0}^{z=a}\left(a^2-y z\right) d y d z=\int_{y=0}^{y=a}\left[a^2 z-y z^2 / 2\right]_{z=0}^{z=a}dy\)

⇒ \(\left.\int_0^a\left(a^3-a^2 y / 2\right) d y=a^3 y-a^2 y^2 / 4\right]_0^a=a^4-a^4 / 4=3 a^4 / 4\)

Case (2): For the face OBEC, N = -i, dS = dy dz and x = 0.

∴ \(\int_{S_2} \mathbf{F} \cdot \mathbf{N} d S=\int_{S_2}\left[\left(x^2-y z\right) \mathbf{i}-2 x^2 y \mathbf{j}+2 \mathbf{k}\right] \cdot(-\mathbf{i}) d S=\int_{y=0}^{y=a} \int_{z=0}^{z=a}(0-y z)(-1) d y d z\)

⇒ \(\left.\left.\int_{y=0}^{y=a} \int_{z=0}^{z=a} y z d y d z=\int_{y=0}^{y=a} y z^2 / 2\right]_{z=0}^{z=a} d y=\int_{y=0}^{y=a}\left[a^2 y / 2\right] d y=\frac{a^2 y^2}{4}\right]_0^a=\frac{a^4}{4}\)

Case (3): For the face BEGD, N = I, dS = dx dz and y = a

∴ \(\int_{S_3} \mathbf{F} \cdot \mathbf{N} d S=\int_{S_3}\left[\left(x^2-y z\right) \mathbf{i}-2 x^2 y \mathbf{j}+2 \mathbf{k}\right] \cdot(\mathbf{j}) d S=\int_{x=0}^{x=a} \int_{z=0}^{z=a}-2 a x^2 d x d z\)

⇒ \(\left.\int_{x=0}^{x=a}\left[-2 a x^2 z\right]_{z=0}^{z=a} d x=\int_0^a-2 a^2 x^2 d x=-2 a^2 x^3 / 3\right]_0^a=-2 a^5 / 3 .\)

Case (4): For the face OCFA, N = -j, dS = dx dz, y = 0

∴ \(\int_{S_4} \mathbf{F} \cdot \mathbf{N} d S=\int_{S_4}\left[\left(x^2-y z\right) \mathbf{i}-2 x^2 y \mathbf{j}+2 \mathbf{k}\right] \cdot(-\mathbf{j}) d S=0\)

Case (5): For the face CFGE, N = k, dS = dx dy, z = a

∴\(\int_{S_5} \mathbf{F} \cdot \mathbf{N} d S=\int_{S_5}\left[\left(x^2-y z\right) \mathbf{i}-2 x^2 y \mathbf{j}+2 \mathbf{k}\right) \cdot \mathbf{k} d S\)

⇒ \(\left.\left.\int_{x=0}^{x=a} \int_{y=0}^{y=a} 2 d x d y=\int_{x=0}^{x=a} 2 y\right]_{y=0}^{y=a} d x=\int_{x=0}^{x=a} 2 a d x=2 a x\right]{ }_0^a=2 a^2\)

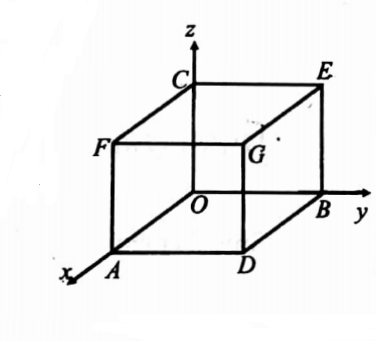
Case (6): for this face OADB, N = -k, dS = dx dy, z = 0.

∴ \(\int_{S_6} \mathbf{F} \cdot \mathbf{N} d S=\int_{S_6}\left[\left(x^2-y z\right) \mathbf{i}-2 x^2 y \mathbf{j}+2 \mathbf{k}\right) \cdot(-\mathbf{k}) d S\)

⇒ \(\left.\left.\int_{x=0}^{x=a} \int_{y=0}^{y=a}(-2) d x d y=\int_{x=0}^{x=a}(-2 y)\right]_{y=0}^{y=a} d x=\int_{x=0}^{x=a}-2 a d x=-2 a x\right]_0^a=-2 a^2\)

∴ \(\mathbf{F} \cdot \mathbf{N} d S=\int_{S_1} \mathbf{F} \cdot \mathbf{N} d S+\int_{S_2} \mathbf{F} \cdot \mathbf{N} d S\)

+ \(\int_{S_3} \mathbf{F} \cdot \mathbf{N} d S+\int_{S_4} \mathbf{F} \cdot \mathbf{N} d S+\int_{S_5} \mathbf{F} \cdot \mathbf{N} d S+\int_{S_6} \mathbf{F} \cdot \mathbf{N} d S\)

= \(3 a^4 / 4+a^4 / 4-2 a^5 / 3+0+2 a^2-2 a^2=a^4-2 a^5 / 3\)

∴ \(\int_V \text{div} \mathbf{F} d V=\int_S \mathbf{F} \cdot \mathbf{N} d S .\)

∴ Gauss’s divergence theorem was verified.

26. State and prove Green’s theorem in a plane.

Solution:   Let S be a closed region in the plane enclosed by a curve C if P and Q are continuous and differentiable scalar functions of x and y in S, then\(\int_C\) P dx + Q dy = \(\iint_S\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\)dx dy,  the line integral being taken along the entire boundary C of S such that S is on the left as one advance along C

Proof: Let any line parallel to either co-ordinate axes cut C in at most two points.

Let S  lie between the lines x=a, x=b,and y=c y=d.

Let y=f(x) be the curve C₁ (AEB) and y=g(x)  be the curve C₂ (ADB) where f(x)≤ g(x)

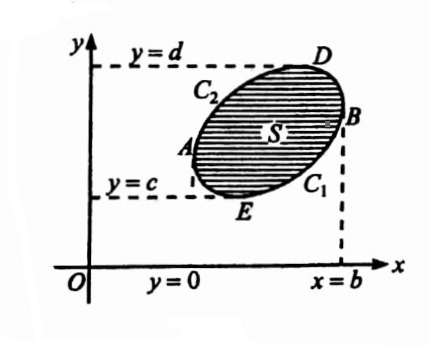
Consider \(\iint_S \frac{\partial P}{\partial y} d x d y=\int_{x=a}^{x=b} \int_{y=f(x)}^{y=g(x)}\left(\frac{\partial P}{\partial y} d y\right) d x\)

= \(=\int_{x=a}^{x=b}[P(x, y)]_{y=f(x)}^{y=g(x)} d x=\int_a^b[P(x, g(x))-P(x, f(x))] d x\)

= \(\int_a^b P(x, g) d x-\int_a^b P(x, f) d x=-\int_{C_1} P(x, y) d x-\int_{C_2} P(x, y) d x=-\int_{c_3} P d x\)

Similarly , we can prove that \(\iint_S\)\(\left(\frac{\partial Q}{\partial x}\right)\)dx dy=\(\int_C\)dy.

∴\(\int_C\) P dx + Q dy = \(\iint_S\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\)dx dy

27. Evaluate \(\oint_C\)(x dy-y dx) around the circle C where C is x² +y²=1.

Solution:

By Green’s theorem, \(\int_c P d x+Q d y=\iint_S\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y\)

Put P = -y, Q = x. Then \(\frac{\partial Q}{\partial x}=1, \frac{\partial P}{\partial y}=-1\)

∴ \(\int_C x d y-y d x=\iint_S[1-(-1)] d x d y=2 \iint_S d x d y\)

= \(2 \text { (Area of the surface } S \text { ) }=2 \pi(1)^2=2 \pi\)

28. If f and g are two continuous and differentiable scalar point functions over the region V enclosed by the surface S, then prove that

1. \(\int_V\left[f \nabla^2 g+\nabla f \cdot \nabla g\right] d V\)=\(=\int_S(f \nabla g) \cdot N d S\)
2. \(\int_V\left(f \nabla^2 g-g \nabla^2 f\right) d V\)=\(=\int_S(f \nabla g-g \nabla f) \cdot \mathbf{N} d S\)

Solution:

1. Let F = f ∇g.

Then \(\nabla \cdot \mathbf{F}=\nabla \cdot(f \nabla g)=f(\nabla \cdot \nabla g)+\nabla f \cdot \nabla g=f \nabla^2 g+\nabla f \cdot \nabla g\)

By Gauss’s divergence theorem, \(\int_V \nabla \cdot \mathbf{F} d V=\int_S \mathbf{F} \cdot \mathbf{N} d S\)

⇒ \(\int_V\left[f \nabla^2 g+\nabla f \cdot \nabla g\right] d V=\int_S(f \nabla g) \cdot \mathbf{N} d S\)

2. From (1); \(\int_V\left(f \nabla^2 g+\nabla f \cdot \nabla g\right) d V=\int_S(f \nabla g) \cdot \mathbf{N} d S\) → (1)

Interchanging f and g in (1), we get \(\int_V\left(g \nabla^2 f+\nabla g \cdot \nabla f\right) d V=\int_s(g \nabla f) \cdot \mathbf{N} d S\) → (2)

(1) – (2) ⇒ \(\int_V\left(f \nabla^2 g-g \nabla^2 f\right) d V=\int_S(f \nabla g-g \nabla f) \cdot \mathbf{N} d S\)

29. Show that the area bounded by a simple closed curve C is given by ½ \(\oint_C\) x dy-y dx and hence find area of ellipse x=a cos θ, y= b sin θ ,0≤θ≤2π.

Solution:

Here P = -y, Q = x. Then \(\frac{\partial Q}{\partial x}=1, \frac{\partial P}{\partial y}=-1\)

By Green’s theorem \(\frac{1}{2} \int_C x d y-y d x=\frac{1}{2} \int_C P d x+Q d y=\frac{1}{2} \iint_S\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y\)

= \(\frac{1}{2} \iint_S[1-(-1)] d x d y=\iint_S d x d y\) = Area of the surface bounded by the curve C.

Equations of ellipse are x = a cos θ, y = b sin θ, 0 ≤ θ ≤ 2π

∴ \(\frac{d x}{d \theta}=-a \sin \theta, \frac{d y}{d \theta}=b \cos \theta\)

∴ Area of the ellipse = \(\frac{1}{2} \int_c x d y-y d x=\frac{1}{2} \int_0^{2 \pi}[(a \cos \theta)(b \cos \theta) {-}(b \sin \theta)(-a \sin \theta)] d \theta\)

= \(\frac{1}{2} \int_0^{2 \pi}\left(a b \cos ^2 \theta+a b \sin ^2 \theta\right) d \theta=\frac{a b}{2} \int_0^{2 \pi} d \theta=\frac{a b}{2}(2 \pi)=\pi a b \text { sq.unit }\)

30. \(\oint_C\) (cos x sin y- xy) dx + sin x cos y dy, by Green’s theorem, where C is the circle x²+y²=1

Solution:  By Green’s theorem\(\int_C\) P dx + Q dy = \(\iint_S\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\)dx dy

Let P = cos x sin y -xy, Q = sin x cos y. \(\frac{\partial P}{\partial y}=\cos x \cos y-x, \frac{\partial Q}{\partial x}=\cos x \cos y\).

The limits of the surface of the circle x² + y² = 1 are x = -1 to x = 1 and \(y=-\sqrt{1-x^2} \text { to } y=\sqrt{1-x^2} \text {. }\)

∴\(\int_c(\cos x \sin y-x y) d x+\sin x \cos y d y=\iint_s(\cos x \cos y-\cos x \cos y+x) d x d y\)

= \(\iint_S x d x d y=\int_{x=-1}^{x=1} \int_{y=-\sqrt{1-x^2}}^{y=\sqrt{1-x^2}} x d x d y=\int_{x=-1}^{x=1} 2 x d x \int_0^{y=\sqrt{1-x^2}} d y=\int_{x=-1}^{x=1} 2 x \sqrt{1-x^2} d x=0\)

31. Evaluate by Green’s theorem \(\oint_C\)(x²– cosh y) + (y + sinx) dy, where C is the rectangle with vertices (0, 0), (π, 0), (π, 1), (0, 1).

Solution:

By theorem \(\int_c P d x+Q d y=\iint_s\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y\)

Let \(P=x^2-\cosh y, Q=y+\sin x \text {.. Then } \frac{\partial P}{\partial y}=-\sinh y, \frac{\partial Q}{\partial x}=\cos x\)

The limits of the surface of integration are x = 0 to x = π and y = 0 to y = 1.

∴ \(\int_C\left(x^2-\cosh y\right) d x+(y+\sin x) d y=\int P d x+Q d y\)

= \(\iint_S\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y=\int_{x=0}^{x=\pi} \int_{y=0}^{y=1}(\cos x+\sinh y) d x d y\)

= \(\int_{x=0}^{x=\pi}[y \cos x+\cosh y]_{y=0}^{y=1} d x=\int_0^{\pi}(\cos x+\cosh 1-1) d x\)

= \([\sin x+x \cosh 1-x]_{x=0}^{x=\pi}=\pi \cosh 1 – \pi=\pi(\cosh 1-1)=\pi\left(\frac{e+e^{-1}}{2}-1\right)\)

32. Using Green’s theorem, evaluate \(\oint_C\)(x² +y²)dx + 3xy² dy where C is the circle x²+y²=4

Solution:

Here \(P=x^2+y^2, Q=3 x y^2\) ∴ \(\frac{\partial P}{\partial y}=2 y, \frac{\partial Q}{\partial x}=3 y^2\). The limits of the surface of integration are x = -2 to x = 2 and \(y=-\sqrt{4-x^2} \text { to } y=\sqrt{4-x^2}\)

By Green’s theorem, \(\int_C\left(x^2+y^2\right) d x+3 x y^2 d y=\iint_S\left(3 y^2-2 y\right) d x d y\)

= \(\int_{x=-2}^{x=2} \int_{y=-\sqrt{4-x^2}}^{y=\sqrt{4-x^2}}\left(3 y^2-2 y\right) d x d y=\int_{x=-2}^{x=2}\left[y^3-y^2\right]_{y=-\sqrt{4-x^2}}^{y=\sqrt{4-x^2}} d x=\int_{x=-2}^{x=2} 2\left(4-x^2\right)^{3 / 2} d x\)

= \(4 \int_0^2\left(4-x^2\right)^{3 / 2} d x=4 \int_0^{\pi / 2}\left(4-4 \sin ^2 \theta\right)^{3 / 2} 2 \cos \theta d \theta \text { where } x=2 \sin \theta\)

= \(64 \int_0^{\pi / 2} \cos ^4 \theta d \theta=64 \times \frac{3}{4} \times \frac{1}{2} \times \frac{\pi}{2}=12 \pi\)

33. Evaluate \(\oint_C\) (3x + 4y) dx + (2x− 3y) dy where ‘C’ is the circle  x²+y²= 4.

Solution:

Here P = 3x + 4y, Q = 2x – 3y. \(\frac{\partial P}{\partial y}=4, \frac{\partial Q}{\partial x}=2\). The limits of the surface of integration are x = -2 to x = 2 and \(y=-\sqrt{4-x^2} \text { to } y=\sqrt{4-x^2}\).

By Green’s theorem, \(\int_C(3 x+4 y) d x+(2 x-3 y) d y\)

= \(\iint_y(2-4) d x d y=\int_{x=-2}^{x=2} \int_{y=-\sqrt{4-x^2}}^{y=\sqrt{4-x^2}}(-2) d x d y=\int_{x=-2}^{x=2}[-2 y]_{y=-\sqrt{4-x^2}}^{y=\sqrt{4-x^2}}\)

= \(\int_{-2}^2-4 \sqrt{4-x^2} d x=-8 \int_0^2 \sqrt{4-x^2} d x=-8\left[\frac{x}{2} \sqrt{4-x^2}+\frac{4}{2} \text{Sin}^{-1} \frac{x}{2}\right]_{0}^{2}=-8\left[2 \frac{\pi}{2}\right]=-8 \pi\)

34. Evaluate by Green’s theorem \(\oint(y-\sin x) d x\)+ cos x dy where C is the triangle enclosed by the lines x=0, x=π/2,  πy=2x.

Solution:

Here P = y – sin x, Q = cos x. ∴ \(\frac{\partial P}{\partial y}=1, \frac{\partial Q}{\partial x}=-\sin x\)

The limits of the surface of integration are x = 0 to \(x=\frac{\pi}{2} ; y=0 \text { to } y=\frac{2 x}{\pi}\)

By Green’s theorem \(\int_C(y-\sin x) d x+\cos x d y=\int_C P d x+Q d y\)

= \(\iint_s\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y=\int_{x=0}^{x=\pi / 2} \int_{y=0}^{y=2 x / \pi}(-\sin x-1) d x d y\)

=\(\int_{x=0}^{x=\pi / 2}[(-\sin x-1) y]_{y=0}^{y=2 x / \pi} d x\)

= \(\int_0^{\pi / 2}(-\sin x-1) \frac{2 x}{\pi} d x=-\frac{2}{\pi} \int_0^{\pi / 2} x(1+\sin x) d x\)

=\(-\frac{2}{\pi}[x(x-\cos x)]_{0}^{\pi /2}-\int_0^{\pi / 2}(x-\cos x) d x\)

= \(-\frac{2}{\pi}\left[\frac{\pi}{2}\left(\frac{\pi}{2}\right)-\left(\frac{x^2}{2}-\sin x\right)_0^{\pi / 2} \right]=-\frac{2}{\pi}\left[\frac{\pi^2}{4}-\frac{\pi^2}{8}+1\right]=-\frac{\pi}{4}-\frac{2}{\pi}\)

35. Compute \(\oint_C\) (x²− 2xy) dx + (x²y + 3) dy around the boundary C of the region defined by y² = 8x and x = 2 by applying Green’s theorem.

Solution:

Here \(P=x^2-2 x y, Q=x^2 y+3\)  ∴ \(\frac{\partial P}{\partial y}=-2 x, \frac{\partial Q}{\partial x}=2 x y\)

The limits of the surface of integration are x = 0 to x = 2 and y = 0 to \(\sqrt{8 x}\).

By Green’s Theorem, \(\oint_c\left(x^2-2 x y\right) d x+\left(x^2 y+3\right) d y=\int_c P d x+Q d y\)

= \(\iint_S\left[\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right] d x d y=\int_{x=0}^{x=2} \int_{y=-\sqrt{8 x}}^{y=\sqrt{8 x}}(2 x y+2 x) d x d y=\int_{x=0}^{x=2}\left[x y^2+2 x y\right]_{y=-\sqrt{8 x}}^{y=\sqrt{8 x}} d x\)

= \(\int_{x=0}^{x=2}(4 x \sqrt{8 x}) d x=\left[8 \sqrt{2} \frac{x^{5 / 2}}{5 / 2}\right]_{x=0}^{x=2}=\frac{128}{5}\)

36. Find the area bounded by x^2/3 +y^2/3 = a^2/3  using Green’s theorem.

Solution:

The parametric equation of \(x^{2 / 3}+y^{2 / 3}=a^{2 / 3} \text { is } x=a \cos ^3 \theta, y=a \sin ^3\) θ and θ variation from 0 to 2π.

By green’s theorem, Area = \(\frac{1}{2} \int_C(x d y-y d x)\)

= \(\frac{1}{2} \int_{\theta=0}^{\theta=2 \pi} a\cos ^3 \theta 3 a \sin ^2 \theta \cos \theta d \theta-a \sin ^3 \theta\left(3 a \cos ^2 \theta\right)(-\sin \theta) d \theta\)

= \(\frac{1}{2} \int_{\theta=0}^{2 \pi} 3 a^2 \cos ^2 \theta \sin ^2 \theta\left(\cos ^2 \theta+\sin ^2 \theta\right) d \theta=\frac{1}{2} \int_0^{2 \pi} 3 a^2 \cos ^2 \theta \sin ^2 \theta d \theta\)

= \(6 a^2 \int_0^{\pi / 2} \sin ^2 \theta \cos ^2 \theta d \theta=6 a^2 \times \frac{1}{4} \times \frac{1}{2}=\frac{3 a^2}{4} \times \frac{\pi}{2}=\frac{3 \pi a^2}{8} \text { sq.unit }\)

37. Verify Green’s theorem in the plane for \(\oint_C\)(3x²– 8y²) dx + (4y- 6xy) dy where C is the region bounded by y = \(\sqrt{x}\)and y = x².

Solution:

P = \(P=3 x^2-8 y^2, Q=4 y-6 x y . \quad \frac{\partial P}{\partial y}=-16 y ; \frac{\partial Q}{\partial x}=-6 y .\)

⇒ \(\int_C\left(3 x^2-8 y^2\right) d x+(4 y-6 x y) d y=\iint_s \left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y\)

= \(\iint_s(-6 y+16 y) d x d y=10 \int_{x=0}^{x=1}\left(\int_{y=x^2}^{y=\sqrt{x}} y d y\right) d x\)

= \(10 \int_{x=0}^{x=1}\left[\frac{y^2}{2}\right]_{y=x^2}^{y=\sqrt{x}} d x \quad=5 \int_0^1\left(x-x^4\right) d x=5\left[\frac{x^2}{2}-\frac{x^5}{5}\right]_0^1=5\left[\frac{1}{2}-\frac{1}{5}\right]=5\left[\frac{5-2}{10}\right]=\frac{3}{2}\)

∴ \(\int_c\left(3 x^2-8 y^2\right) d x+(4 y-6 x y) d y\)

= \(\int_{C_1}\left(3 x^2-8 y^2\right) d x+(4 y-6 x y) d y+\int_{C_2}\left(3 x^2-8 y^2\right) d x+(4 y-6 x y) d y\)

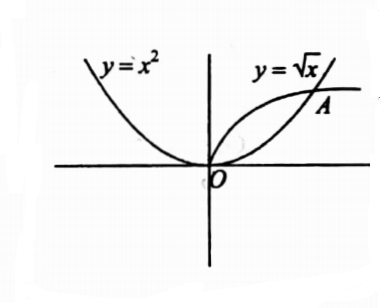
Where c₁ is the curve y = x² from O to A and C₂ is the curve = √x from A to O

= \(\int_0^1\left(3 x^2-8 x^4\right) d x+\left(4 x^2-6 x^3\right) 2 x d x+\int_1^0\left(3 x^2-8 x\right) d x+(4 \sqrt{x}-6 x \sqrt{x}) \frac{d x}{2 \sqrt{x}}\)

= \(\int_0^1\left(3 x^2+8 x^3-20 x^4\right) d x-\int_0^1\left(3 x^2-8 x+2-3 x\right) d x=\int_0^1\left(8 x^3-20 x^4+11 x-2\right) d x\)

= \(\left[2 x^4-4 x^5+\frac{11 x^2}{2}-2 x\right]_0^1=2-4+\frac{11}{2}-2=\frac{3}{2}\)  ∴ Green’s theorem is verified.

38. Verify Green’s theorem in the plane for\(\oint_C\)(xy + y²) dx + x²dy where C is the closed curve of the region bounded by y = x andy = x².

Solution:

Here P = xy + y², Q = x² ∴ \(\frac{\partial P}{\partial y}=x+2 y, \frac{\partial Q}{\partial x}=2 x\)

By Green’s theorem, \(\int_c\left(x y+y^2\right) d x+x^2 d y=\int_c P d x+Q d y=\iint_s\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y\)

= \(\iint_s[2 x-(x+2 y)] d x d y=\iint_s(x-2 y) d x d y=\int_{x=0}^{x=1} \int_{y=x^2}^{y=x}(x-2 y) d x d y\)

= \(\int_{x=0}^{x=1}\left[x y-y^2\right]_{y=x^2}^{y=x} d x=\int_0^1\left[\left(x^2-x^2\right)-\left(x^3-x^4\right)\right] d x=\int_0^1\left(x^4-x^3\right) d x\)

= \(\left[\frac{x^5}{5}-\frac{x^4}{4}\right]_0^1=\frac{1}{5}-\frac{1}{4}=-\frac{1}{20}\)

 

\(\int_c\left(x y+y^2\right) d x+x^2 d y\)

= Line integral along y = x² (from O to A) + line integral along y = x (from A to O)

= \(=\int_0^1\left[x\left(x^2\right)+x^4\right] d x+x^2 \cdot 2 x d x+\int_1^0\left(x^2+x^2\right) d x+x^2 d x\)

= \(\int_0^1\left(3 x^3+x^4\right) d x-\int_0^1 3 x^2 d x=\left[3 \frac{x^4}{4}+\frac{x^5}{5}-x^3\right]_{0}^{1}=\frac{3}{4}+\frac{1}{5}-1=\frac{15+4-20}{20}=-\frac{1}{20}\)

39. Verify Green’s theorem in the plane for \(\oint_C\)(2xy − x²)dx + (x +y²) dy where C is the boundary of the region enclosed by y = x² and y²=x described in the positive sense.

Solution:

Here P = 2xy – x², Q = x² + y².

∴ \(\frac{\partial P}{\partial y}=2 x, \frac{\partial Q}{\partial x}=2 x\)

⇒ \(\iint_S\left[\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right] d x d y=\iint_S(2 x-2 x) d x d y=0\)

⇒ \(\int_c P d x+Q d y\) = Line integral along y = x² (from O to A) + Line integral along y² = x (from A to O) = I₁ + I₂

Now \(I_1=\int_{x=0}^{x=1} P d x+Q d y=\int_0^1\left[2 x\left(x^2\right)-x^2\right] d x+\left(x^2+x^4\right) 2 x d x\)

= \(\left.\int_0^1\left(2 x^3-x^2+2 x^3+2 x^5\right) d x=\int_0^1\left(2 x^5+4 x^3-x^2\right) d x=\frac{x^6}{3}+x^4-\frac{x^3}{3}\right]_0^1=1\)

⇒ \(I_2=\int_{x=1}^{x=0} P d x+Q d y=\int_1^0\left(2 x \sqrt{x}-x^2\right) d x+\left(x^2+x\right) \frac{1}{2 \sqrt{x}} d x\)

= \(\int_1^0\left[2 x \sqrt{x}-x^2+x \sqrt{x} / 2+\sqrt{x} / 2\right] d x=\int_1^0\left[5 x^{3 / 2} / 2-x^2+x^{1 / 2} / 2\right] d x\)

= \(\left.\frac{5}{2} \times \frac{x^{5 / 2}}{5 / 2}-\frac{x^3}{3}+\frac{1}{2} \times \frac{x^{3 / 2}}{3 / 2}\right]_1^0=-1+\frac{1}{3}-\frac{1}{3}=-1\)

∴ \(\int_c P d x+Q d y=I_1+I_2=1-1=0\)

∴ Green’s theorem is verified.

40. Verify Green’s theorem, \(\oint_C\)(3x²– 8y²) dx + (4y- 6xy)dy where C is the boundary enclosed by x = 0,y = x+y= 1.

Solution:

Here P = 3x² – 8y², Q = 4y – 6xy. ∴ \(\frac{\partial P}{\partial y}=-16 y, \frac{\partial Q}{\partial x}=-6 y\)

The limits o the surface of integration are x = 0 to x = 1 and y = 0 to y = 1 – x

By Green’s theorem, \(\oint\left(3 x^2-8 y^2\right) d x+(4 y-6 x y) d y\)

= \(\int_c P d x+Q d y=\iint_S\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y=\int_{x=0}^{x=1} \int_{y=0}^{y=1-x}(-6 y+16 y) d x d y\)

= \(\int_{x=0}^{x=1} \int_{y=0}^{y=1-x} 10 y d x d y=\int_{x=0}^{x=1}\left(5-10 x+5 x^2\right) d x=\int_{x=0}^{x=1}\left[5 y^2\right]_{x=0}^{y=1-x} d x\)

=\(\int_{x=0}^{x=1} 5(1-x)^2 d x\)

= \(\left[5 x-5 x^2+\frac{5 x^3}{3}\right]_{x=0}^{x=1}=5-5+\frac{5}{3}=\frac{5}{3}\)

Given planes x = 0, y = 0 and x + y = 1 from a triangle in xy-plane with vertices O(0,0), A(1,0) and B(0,1).

∴ \(\int_c\left(3 x^2-8 y^2\right) d x+(4 y-6 x y) d y\)

= Line integral along \(\overrightarrow{O A}\) + Line along \(\overrightarrow{A B}\) + Line integral along \(\overrightarrow{B O}\).

1. Line integral along \(\left.\overrightarrow{O A}=\int_0^1 3 x^2 d x=x^3\right]_0^1=1\)

2. Line integral along \(\overrightarrow{A B}\). Here x + y = 1 ⇒ y = 1 – x varies from 1 to 0.

Line integral along \(\overrightarrow{A B}=\int_1^0\left[3 x^2-8(1-x)^2\right] d x+[4(1-x)-6 x(1-x)](-d x)\)

= \(\int_1^0\left(3 x^2-8-8 x^2+16 x\right) d x-\left(4-4 x-6 x+6 x^2\right) d x=\int_1^0\left(-11 x^2+26 x-12\right) d x\)

= \(\left[-\frac{11 x^3}{3}+13 x^2-12 x\right]_1^0=\frac{11}{3}-13+12=\frac{8}{3} .\)

3. Line integral along \(\left.\overrightarrow{B O}=\int_1^0 4 y^2 d y=2 y^2\right]_1^0=-2\)

∴ \(\int_C\left(3 x^2-8 y^2\right) d x+(4 y-6 x y) d y=1+\frac{8}{3}-2=\frac{5}{3}\)

∴ Green’s theorem is verified.

41. State and prove Stake’s theorem.

Solution:  Let S be a surface bounded by a closed non-intersecting curve C. If F is any differentiable vector point function, then

\(\int_C\)F.dr= \(\int_S\) curl F.Nds, where N is the outward drawn unit normal vector to S and C is traversed in the positive direction.

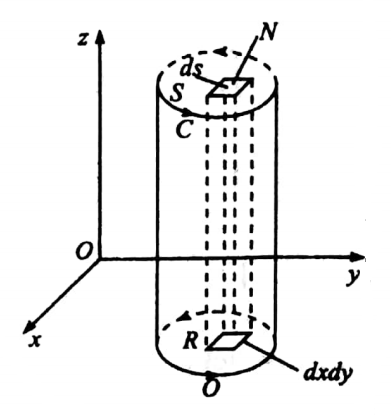
proof: Let S be a surface which is such that its projection on xy,yz,zx or y=h(z,x) where f,g,h are simple valued continuous and differentiable functions. Let F=F₁i+F₂j+F₃k.

Then curl F =∇×F=∇ × (F₁i + F₂j + F₃k)

=∇ × F₁i × F₂j × F₃k

 

Now \(\nabla \times F_1 \mathbf{I}=\left|\begin{array}{ccc}
\mathbf{I} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
F_1 & 0 & 0
\end{array}\right|=\frac{\partial F_1}{\partial z} \mathbf{J}-\frac{\partial F_1}{\partial y} \mathbf{k}\)

⇒ \(\left(\nabla \times F_1 \mathbf{I}\right) \cdot \mathbf{N}=\left[\frac{\partial F_1}{\partial z}(\mathbf{j} \cdot \mathbf{N})-\frac{\partial F_1}{\partial y}(\mathbf{k} \cdot \mathbf{N})\right]\) (1)

Let z = f(x,y) be the equation of S.

For any point in S, r = xi + yj + zk = xi + yi + f(x,y)k…

∴ \(\frac{\partial \mathbf{r}}{\partial y}=\mathbf{j}+\frac{\partial z}{\partial y} \mathbf{k} \text {. Since } \frac{\partial \mathbf{r}}{\partial y} \text { is the tangent vector to } S, \mathbf{N} \cdot \frac{\partial \mathbf{r}}{\partial y}=0\)

⇒ \(\mathbf{N} \cdot \mathbf{J}+(\mathbf{N} \cdot \mathbf{k}) \frac{\partial z}{\partial y}=0 \Rightarrow \mathbf{N} \cdot \mathbf{j}=-(\mathbf{N} \cdot \mathbf{k}) \frac{\partial z}{\partial y}\)

From (1); \(\left(\nabla \times F_1 \mathbf{i}\right) \cdot \mathbf{N}=-(\mathbf{N} \cdot \mathbf{k}) \frac{\partial F_1}{\partial z} \cdot \frac{\partial z}{\partial y}-(\mathbf{N} \cdot \mathbf{k}) \frac{\partial F_1}{\partial y}\)

∴ \(\left[\left(\nabla \times F_1 \mathbf{i}\right) \cdot \mathbf{N}\right] d S=-\left(\frac{\partial F_1}{\partial y}+\frac{\partial F_1}{\partial z} \cdot \frac{\partial z}{\partial y}\right)(\mathbf{N} \cdot \mathbf{k}) d S\)

= \(-\frac{\partial}{\partial y} F_1(x, y, z) \cos \gamma d S=-\frac{\partial F_1}{\partial y} d x d y\)

Let R be the projection of S on xy-plane. Then

∴ \(\int_S\left(\nabla \times F_1 \mathbf{i}\right) \cdot \mathbf{N} d S=\int_R \int-\frac{\partial F_1}{\partial y} d x d y=\int_C F_1 d x\), by green’s theorem

Similarly \(\int_S\left(\nabla \times F_2 \mathbf{j}\right) \cdot \mathbf{N} d S=\int_c F_2 d y \text { and } \int_S\left(\nabla \times F_3 \mathbf{k}\right) \cdot \mathbf{N} d S=\int_c F_3 d z\)

∴ \(\int_S \nabla \times\left(F_1 \mathbf{i}+F_2 \mathbf{j}+F_3 \mathbf{k}\right) \cdot \mathbf{N} d S=\int_c F_1 d x+F_2 d y+F_3 d z\)

∴ \(\int_S(\nabla \times F) \cdot \mathbf{N} d S=\int_c F \cdot d r\)

42. Prove by Stake’s theorem curl grad φ = 0.

Solution:  Let be a  surface enclosed by a simple closed curve C.

∴ By stoke’s theorem, \(\int_s(\text{curl} \text{grad} \varphi) \cdot \mathbf{N} d S\)

= \(\int_s[\nabla \times(\nabla \varphi)] \cdot \mathbf{N} d S=\int_c \nabla \varphi \cdot d \mathbf{r}=\int_c\left(\mathbf{i} \frac{\partial \varphi}{\partial x}+\mathbf{j} \frac{\partial \varphi}{\partial y}+\mathbf{k} \frac{\partial \varphi}{\partial z}\right) \cdot(\mathbf{i} d x+\mathbf{j} d y+\mathbf{k} d y)\)

= \(\left.\int_C\left(\frac{\partial \varphi}{\partial x} d x+\frac{\partial \varphi}{\partial y} d y+\frac{\partial \varphi}{\partial z} d z\right)=\int_C d \varphi=\varphi\right]_P^P=0\)

∴ \(\int_S(\text{curl} \text{grad} \varphi) \cdot \mathbf{N} d S=0 \Rightarrow \text{curl}(\text{grad} \varphi)=0\)

43. Find \(\int_C\)T .dr where T is the unit tangent vector and C is the unit circle in the xy-plane with centre at the origin.

Solution:  By stokes theorem ,\(\int_C\)T.dr=\(\int_S\)(curl T).N dS=\(\int_S\)(∇×T).N dS=\(\int_S\)0 dS=0.

44. Prove that \(\oint_C\)r.dr = 0.

Solution:  By stokes theorem ,\(\int_C\)T.dr=\(\int_S\)(curl r).N dS=\(\int_S\)0. N dS=0.

45. By Stoke’s theorem prove that div curl F = 0.

Solution:  Let S be the surface enclosed by a simple closed curve C

∴ \(\int_s \text{div} \text{curl} \mathbf{F} d S=\int \nabla \cdot \nabla \times \mathbf{F} d S=\int_s \Sigma \mathbf{i} \frac{\partial}{\partial x}(\nabla \times \mathbf{F}) d S=\int_S \Sigma \frac{\partial}{\partial x}[\mathbf{i} \cdot(\nabla \times \mathbf{F})] d S\)

= \(\Sigma \frac{\partial}{\partial x} \int_S(\nabla \times F) \cdot i d S=\Sigma \frac{\partial}{\partial x} \int_C\left(F_2 d y+F_3 d z\right)=0\)

∴ div curl F = 0.

46. Verify Stoke’s theorem to evaluate \(\int_C\)xy dx + xy² dy, where C is the square in the  xy-plane with vertices (1, 0), (- 1, 0), (0, 1), (0,- 1)

.Solution:

Let F = \(x y \mathbf{i}+x y^2 \mathbf{j} . \text{curl} \mathbf{F}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
x y & x y^2 & 0
\end{array}\right|=\left(y^2-x\right) \mathbf{k}\)

⇒ \(\int_c x y d x+x y^2 d y=\oint_C \mathbf{F} \cdot d \mathbf{r}=\int_s \nabla \times \mathbf{F} \cdot \mathbf{N} d S=\int_S\left(y^2-x\right) \mathbf{k} \cdot \mathbf{N} d S\)

Since k. N ds = dx dy and R is the region ABCD in xy-plane,

We have \(\int_S\left(y^2-x\right) \mathbf{k} \cdot \mathbf{N} d S=\iint_R\left(y^2-x\right) d x d y\)

Equation to \(\stackrel{\leftrightarrow}{A B} \text { is } \frac{x}{1}+\frac{y}{1}=1 \Rightarrow y=1-x\)

Equation to \(\stackrel{\leftrightarrow}{B C} \text { is } \frac{x}{-1}+\frac{y}{1}=1 \Rightarrow y=1+x\)

Equation to \(\stackrel{\leftrightarrow}{C D} \text { is } \frac{x}{-1}+\frac{y}{-1}=1 \Rightarrow y=-1-x\)

Equation to \(\stackrel{\leftrightarrow}{D A} \text { is } \frac{x}{1}+\frac{y}{-1}=1 \Rightarrow y=x-1\)

 

⇒ \(\iint_R\left(y^2-x\right) d x d y=\int_{x=0}^{x=1} \int_{y=0}^{y=1-x}\left(y^2-x\right) d x d y+\int_{x=-1}^{x=0} \int_{y=0}^{y=1+x}\left(y^2-x\right) d x d y\)

+ \(\int_{x=-1}^{x=0} \int_{y=-1-x}^{y=0}\left(y^2-x\right) d x d y+\int_{x=0}^{x=1} \int_{y=x-1}^{y=0}\left(y^2-x\right) d x d y\)

= \(\int_{x=0}^{x=1}\left[\frac{y^3}{3}-x y\right]_{y=0}^{y=1-x} d x+\int_{x=-1}^{x=0}\left[\frac{y^3}{3}-x y\right]_{y=0}^{y=1+x} d x\)

+\(\int_{x=-1}^{x=0}\left[\frac{y^3}{3}-x y\right]_{y=-1-x}^{y=0} d x+\int_{x=0}^{x=1}\left[\frac{y^3}{3}-x y\right]_{y=x-1}^{y=0} d x\)

= \(\int_0^1\left[\frac{(1-x)^3}{3}-x(1-x)\right] d x+\int_{-1}^0\left[\frac{(1+x)^3}{3}-x(1+x)\right] d x\)

–\(\int_{-1}^0\left[\frac{(-1-x)^3}{3}-x(-1-x)\right] d x – \int_0^1\left[\frac{(x-1)^3}{3}-x(x-1)\right] d x\)

= \(\int_0^1\left[\frac{(1-x)^3}{3}-x+x^2\right] d x+\int_{-1}^0\left[\frac{(1+x)^3}{3}-x-x^2\right] d x\)

+\(\int_{-1}^0\left[\frac{(1+x)^3}{3}-x-x^2\right] d x-\int_0^1\left[\frac{(x-1)^3}{3}-x^2+x\right] d x\)

= \(\left[\frac{(1-x)^4}{-12}-\frac{x^2}{2}+\frac{x^3}{3}\right]_0^1+\left[\frac{(1+x)^4}{12}-\frac{x^2}{2}-\frac{x^3}{3}\right]_{-1}^0\)

+\(\left[\frac{(1+x)^4}{12}-\frac{x^2}{2}-\frac{x^3}{3}\right]_{-1}^0-\left[\frac{(x-1)^4}{12}-\frac{x^3}{2}+\frac{x^2}{2}\right]_0^1\)

= \(\left[0-\frac{1}{2}+\frac{1}{3}+\frac{1}{12}\right]+\left[\frac{1}{12}-0-0-0+\frac{1}{2}+\frac{1}{3}\right]\)

+\(\left[\frac{1}{12}-0-0-0+\frac{1}{2}-\frac{1}{3}\right]-\left[0-\frac{1}{3}+\frac{1}{2}-\frac{1}{12}+0-0\right]\)

= \(\frac{-6+4+1}{12}+\frac{1+6-4}{12}+\frac{1+6-4}{12}-\frac{-4+6-1}{12}=-\frac{1}{12}+\frac{3}{12}+\frac{3}{12}-\frac{1}{12}=\frac{4}{12}=\frac{1}{3}\).

Case (1): Line integral along AB: y = 1-x, dy = -dx, x varies from 1 to 0.

∴ \(\int_{C_1} x y d x+x y^2 d y=\int_1^0 x(1-x) d x+x(1-x)^2(-d x)=\int_1^0\left(x-x^2-x+2 x^2-x^3\right) d x\)

= \(\int_1^0\left(x^2-x^3\right) d x=\left[\frac{x^3}{3}-\frac{x^4}{4}\right]_1^0=-\left[\frac{1}{3}-\frac{1}{4}\right]=-\frac{1}{12}\)

Case (2): Line integral along BC: y = 1+x, dy = dx, x varies from 0 to -1.

∴ \(\int_{C_2} x y d x+x y^2 d y=\int_0^{-1} x(1+x) d x+x(1+x)^2 d x=\int_0^{-1}\left(x+x^2+x+2 x^2+x^3\right) d x\)

= \(\int_0^{-1}\left(2 x+3 x^2+x^3\right) d x=\left[x^2+x^3+\frac{x^4}{4}\right]_0^1=1-1+\frac{1}{4}=\frac{1}{4}\)

Case (3): Line integral along CD: y = -1, dy = -dx, x varies from -1 to 0.

∴ \(\int_{C_3} x y d x+x y^2 d y=\int_{-1}^0 x(-1-x) d x+x(-1-x)^2(-d x)\)

=\(\int_{-1}^0\left(-x-x^2-x-2 x^2-x^3\right) d x\)

= \(-\int_{-1}^0\left(2 x+3 x^2+x^3\right) d x=-\left[x^2+x^3+\frac{x^4}{4}\right]_0^{-1}=1-1+\frac{1}{4}=\frac{1}{4}\)

Case (4): Line integral along DA: y = x-1, dy = dx, x varies from 0 to 1.

∴ \(\int_{C_4} x y d x+x y^2 d y=\int_0^{1} x(x-1) d x+x(x-1)^2 d x=\int_0^{1}\left(x^2-x+x^3-2 x^2+x\right) d x\)

= \(\int_0^1\left(x^3-x^2\right) d x=\left[\frac{x^4}{4}-\frac{x^3}{3}\right]_0^1=\frac{1}{4}-\frac{1}{3}=-\frac{1}{12}\)

∴ \(\int_S\)xy dx+xy² dy=1/12+1/4+1/4−1/12=1/3

∴  Stoke’s theorem is verified.

47. Verify Stoke’s theorem for the function F =x²i + xy j integrated round the square in the plane z= 0 whose sides are along the line x = 0, y = 0, x = a, y = a.

Solution:

∴ \({F}=x^2 \mathbf{i}+x y \mathbf{j} . \quad \text{curl} \mathbf{F}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
x^2 & x y & 0
\end{array}\right|=\mathbf{i}(0-0)-\mathbf{j}(0-0)+\mathbf{k}(y-0)=y \mathbf{k}\)

F. dr = (x2i + xyj) . (dx i + dy j + dz k) = x2 dx + xy dy

Let N be the unit normal vector to the surface of the square.

By Stoke’s theorem \(\int_S \boldsymbol{F} \cdot d \mathbf{r}=\int_S \text{cur} l \boldsymbol{F} \cdot \mathbf{N} d S\)

Since the surface of the square lies in the xy-plane, N = k.

⇒ \(\int_S \text{curl} \mathbf{F} \cdot \mathbf{N}dS =\int_S y k \cdot{k} d S=\int_S y d S=\int_0^a \int_0^a y d x d y\)

=\(\int_0^a\left[\frac{y^2}{2} \right]_0^a d x=\int_0^a \frac{a^2}{2} d x=\left[\frac{a^2 x}{2}\right]_0^a=\frac{a^3}{2}.\)

Case (1): Along the side OA: y = 0 and x varies from 0 to a.

\(\int_{c_1} F \cdot d \mathbf{r}=\int_{c_1} x^2 d x+x y d y=\int_{x=0}^{x=a} x^2 d x=\left[\frac{x^3}{3}\right]_0^a=\frac{a^3}{3}\)

Case (2): Along the side AB: x = a, dx = 0 and y varies from 0 to a.

\(\int_{c_2} F \cdot d \mathbf{r}=\int_{C_2} x^2 d x+x y d y=\int_{y=0}^{y=a} a y d y=\left[\frac{a y^2}{2} \right]_0^a=\frac{a^3}{2}.\)

Case (3): Along the side BC: y = a, dy = 0 and x varies from a to 0.

\(\int_{C3} \mathbf{F} \cdot d \mathbf{r}=\int_{C3} x^2 d x+x y d y=\int_{x=a}^{x=0} x^2 d x=\left[\frac{x^3}{3}\right]_a^0=-\frac{a^3}{3}\)

Case (4): Along the side CO: x = 0, y varies from a to 0.

\(\int_{C_4} \boldsymbol{F} \cdot d \boldsymbol{r}=\int_{C_4} x^2 d x+x y d y=0\)

∴ \(\int_C \mathbf{F} \cdot d \mathbf{r}=\int_{c_1} \mathbf{F} \cdot d \mathbf{F}+\int_{c_2} \mathbf{F} \cdot d \mathbf{r}+\int_{c_3} \mathbf{F} \cdot d \mathbf{r}+\int_{c_4} \mathbf{F} \cdot d \mathbf{r}=\frac{a^3}{3}+\frac{a^3}{2}-\frac{a^3}{3}+0=\frac{a^3}{2}\)

=\(\int_S\) curl F.NdS

∴ Stoke’s theorem is verified

48. Verify Stoke’s theorem to evaluate \(\oint_C\) F .dr where F =y²i + x² j- (x+ z)k and C is the boundary of the triangle with vertices (0, 0, 0), (1, 0, 0), (1, 1, 0).

Solution:

F = y² i + x² j – (x + z) k.

∴ \(\nabla \times \mathbf{F}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
y^2 & x^2 & -x-z
\end{array}\right|=\mathbf{i}(0-0)-\mathbf{j}(-1-0)+\mathbf{k}(2 x-2 y)=\mathbf{j}+(2 x-2 y) \mathbf{k}\)

Let N be the unit normal vector to the surface of the triangle.

Since the triangle lies in xy-plane, N=k, and dS=dx dy.

In xy -plane, the vertices of the triangle are O(0,0), A(1,0), and B(1,1).

By Stokes theorem,

∴ \(\int_C \mathbf{F} \cdot d \mathbf{r}=\int_S(\nabla \times \mathbf{F}) \cdot \mathbf{N} d S=\int_S[\mathbf{j}+(2 x-2 y) \mathbf{k}] \cdot \mathbf{k} d S\)

= \(\iint_R(2 x-2 y) d x d y=\int_{x=0}^{x=1} \int_{y=0}^{y=x}(2 x-2 y) d x d y\) [∵ Along OB, x = y]

= \(\left.=\int_{x=0}^{x=1}\left[2 x y-y^2\right]{ }_{y=0}^{y=x} d x=\int_0^1\left(2 x^2-x^2\right) d x=\int_0^1 x^2 d x=\frac{x^3}{3}\right]_0^1=\frac{1}{3}\)

∴ \(\int_C \mathbf{F} \cdot d \mathbf{r}=\int_{O A} \mathbf{F} \cdot d \mathbf{r}+\int_{A B} \mathbf{F} \cdot d \mathbf{r}+\int_{B O} \mathbf{F} \cdot d \mathbf{r}\)

1. Along OA, y = 0, z = 0, dy = 0, dz = 0, x varies from 0 to 1

∴ \(\int_{O A} \mathbf{F} \cdot d \mathbf{r}=\int_0^{1} y^2 d x=0\)

2. Along AB, x = 1, z = 0, dx = 0, dz = 0, y varies from 0 to 1

∴ \(\left.\int_{A B} \mathbf{F} \cdot d \mathbf{r}=\int_0^1 x^2 d y=\int_0^1 d y=y\right]_0^1=1\)

3. Along BO, x = y, z = 0, dx = dy and x varies from 1 to 0.

∴ \(\left.\int_{B O} \mathbf{F} \cdot d \mathbf{r}=\int_1^0 y^2 d x+x^2 d y=\int_1 x^2 d x+x^2 d x=\int_1 2 x^2 d x=\frac{2 x^{30}}{3}\right]_1=-\frac{2}{3}\)

∴ \(\int_C F \cdot d \mathbf{F}=0+1-\frac{2}{3}=\frac{1}{3}\)

∴ Stoke’s theorem is verified.

49. Verify Stoke’s theorem for \(\oint_C\) F =- y³i + x³j,  where S is the circular disc x² +y² ≤ 1, z= 0.

Solution:  F=−y³i+x³j.

The boundary of C of S is a circle in xy -plane, x² +y²= 1, z=0

The parametric equations are x=cos θ,y=sin θ,z=0 where 0≤ θ≤2π.

∴ \(\int_c \mathbf{F} \cdot d \mathbf{r}=\int_c-y^3 d x+x^3 d y=\int_{\theta=0}^{\theta=2 \pi}-\sin ^3 \theta(-a \sin \theta) d \theta+\cos ^3 \theta(a \cos \theta) d \theta\)

Put x = sin θ

∴ dx = cos θ dθ

x = 0 ⇒ θ = 0

x = 1 ⇒ θ = π/2

= \(\int_0^{2 \pi}\left(\cos ^4 \theta+\sin ^4 \theta\right) d \theta=\int_0^{2 \pi}\left[\left(\cos ^2 \theta+\sin ^2 \theta\right)^2-2 \cos ^2 \theta \sin ^2 \theta\right] d \theta\)

= \(\int_0^{2 \pi}\left[1-\frac{1}{2} \sin ^2 2 \theta\right] d \theta=\int_0^{2 \pi}\left[1-\frac{1-\cos 4 \theta}{4}\right] d \theta\)

= \(\int_0^{2 \pi}\left[\frac{3+\cos 4 \theta}{4}\right] d \theta=\left[\frac{3 \theta}{4}+\frac{\sin 4 \theta}{16}\right]_0^{2 \pi}=\left[\frac{3 \pi}{2}+0\right]=\frac{3 \pi}{2}\)

∴ \(\nabla \times \mathbf{F}=\left[\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
-y^3 & x^3 & 0
\end{array}\right]=\mathbf{i}(0-0)-\mathbf{j}(0+0)+\mathbf{k}\left(3 x^2+3 y^2\right)=3\left(x^2+y^2\right) \mathbf{k}\)

Let R be the projection of S in the xy-plane.

∴ \(\int_S(\nabla \times \mathbf{F}) \cdot \mathbf{N} d S=\iint_R 3\left(x^2+y^2\right) \mathbf{k} \cdot \mathbf{k} d x d y=3 \iint_R\left(x^2+y^2\right) d x d y\)

= \(3 \int_{x=-1}^{x=1} \int_{y=-\sqrt{1-x^2}}^{y=\sqrt{1-x^2}}\left(x^2+y^2\right) d x d y=12 \int_{x=0}^{x=1} \int_{y=0}^{y=\sqrt{1-x^2}}\left(x^2+y^2\right) d x d y\)

= \(12 \int_{x=0}^{x=1}\left[x^2 y+\frac{y^3}{3}\right]_0^{\sqrt{1-x^2}} d x=12 \int_0^1\left[x^2 \sqrt{1-x^2}+\frac{1-x^2}{3} \sqrt{1-x^2}\right] d x\)

= \(4 \int_0^1\left(1+2 x^2\right) \sqrt{1-x^2} d x=4 \int_0^{\pi / 2}\left(1+2 \sin ^2 \theta\right) \cos \theta \cos \theta d \theta\)

= \(4 \int_0^{\pi / 2}\left(\cos ^2 \theta+2 \sin ^2 \theta \cos ^2 \theta\right) d \theta=4\left[\frac{1}{2} \cdot \frac{\pi}{2}+2 \cdot \frac{1}{4} \cdot \frac{1}{2} \cdot \frac{\pi}{2}\right]=4\left[\frac{\pi}{4}+\frac{\pi}{8}\right]=\frac{3 \pi}{2}\)

∴ \(\int_C \mathbf{F} \cdot d \mathbf{r}=\int_S(\nabla \times \mathbf{F}) \cdot \mathbf{N} d S\)

∴ Stoke’s theorem is verified.

50. Verify Stoke’s theorem for F = (2x-y) i -yz² j -y²zk, where S is the upper half surface of the sphere x² +y² +z²= 1 and C is its boundary.

Solution: The boundary C os S is a circle in xy-plane, i.e…,  x² +y² +z²= 1 z=0.

The parametric equations are x=cos t,y= sin t, 0≤t≤2π

F=(2x-y)i-yz²j+y²zk

r=xi+yj+zk⇒dr=dxi+dyj+dzk

F.dr=(2x-y)dx-yz² dy+y²z dz=(2cos t-sin t) (-sin t)(dt)

=(sin² t-2 cos t sin t)dt=(sin² t-sin 2t)dt.

∴ \(\int_C \mathbf{F} \cdot d \mathbf{r}=\int_0^{2 \pi}\left(\sin ^2 t-\sin 2 t\right) d t=4 \int_0^{\pi / 2} \sin ^2 t d t+\left[\frac{\cos 2 t}{2}\right]_0^{2 \pi}\)

= \(4 \cdot \frac{1}{2} \cdot \frac{\pi}{2}+\frac{1}{2}[\cos 4 \pi-\cos 0]=\pi+\frac{1}{2}(1-1)=\pi\)

Also \(\nabla \times \mathbf{F}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
2 x-y & -y z^2 & -y^2 z
\end{array}\right|=\mathbf{i}(0-0)-\mathbf{j}(0-0)+\mathbf{k}(0+1)=\mathbf{k}\)

Let R be the projection of S in the xy-plane. Then k. N dS = dx dy.

∴ \(\int_S(\nabla \times \mathbf{F}) \cdot \mathbf{N} d S=\int_S \mathbf{k} \cdot \mathbf{N} d S=\iint_R d x d y\)

= \(4 \int_{x=0}^{x=1} \int_{y=0}^{y=\sqrt{1-x^2}} d x d y=4 \int_{x=0}^{x=1}[y]{ }_{y=0}^{y=\sqrt{1-x^2}} d x=4 \int_0^1 \sqrt{\left(1-x^2\right)} d x\)

= \(4\left[\frac{x}{2} \sqrt{1-x^2}+\frac{1}{2} \text{Sin}^{-1} x\right]_0^1=4\left[\frac{1}{2} \times \frac{\pi}{2}\right]=\pi\)

∴ \(\int_C \mathbf{F} \cdot d \mathbf{r}=\int_S(\nabla \times \mathbf{F}) \cdot \mathbf{N} d S\)

∴ Stoke’s theorem is verified.

51. Verify Stoke’s theorem for A = 2 yi + 3xj− z² k where S is the upper half surface of the sphere x²+y² + z² = 9 and C is its boundary.

Solution: The boundary Cof S is a circle in xy-plane  is the circle  x²+y²=9,z=0

The parametric equations are x=3 cos θ,y=3 sin θ , z=0

⇒dx =− 3 sin θ dθ ,dy =3 cos θ dθ,dz=0

∴ \(\int_C\)A.dr=\(\int_C\)(2yi+3xj−z²k).(dxi+dyj+dzk)

= \(\int_c 2 y d x+3 x d y-z d z=\int_0^{2 \pi} 2(3 \sin \theta)(-3 \sin \theta d \theta)+3(3 \cos \theta)(3 \cos \theta d \theta)-0\)

= \(\int_0^{2 \pi}\left[-18 \sin ^2 \theta+27 \cos ^2 \theta\right] d \theta=\int_0^{2 \pi}\left(27-45 \sin ^2 \theta\right) d \theta\)

= \(27(2 \pi-0)-45 \times 4 \times \frac{1}{2} \times \frac{\pi}{2}=54 \pi-45 \pi=9 \pi\)

∴ \(\nabla \times \mathbf{A}=\left|\begin{array}{lll}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
2 y & 3 x & -z^2
\end{array}\right|=\mathbf{i}(0-0)-\mathbf{j}(0-0)+\mathbf{k}(3-2)=\mathbf{k}\)

Let R be the projection of S in the xy-plane.

∴ \(\int_S(\nabla \times \mathbf{A}) \cdot \mathbf{N} d S=\iint_R(\mathbf{k} \cdot \mathbf{N}) d S=\iint_R d x d y\)

= \(\int_{x=-3}^{x=3} \int_{y=-\sqrt{9-x^2}}^{y=\sqrt{9-x^2}} d x d y=4 \int_{x=0}^{x=3} \int_{y=0}^{y=\sqrt{9-x^2}} d x d y\)

= \(4 \int_{x=0}^{x=3}\left[y\right]_{y=0}^{\sqrt{=9-x}} d x=4 \int_{0}^3 \sqrt{9-x^2} d x=4\left[\frac{x}{2} \sqrt{9-x^2}+\frac{9}{2} \text{Sin}^{-1} \frac{x}{3}\right]_0^3=4\left[\frac{9}{2} \times \frac{\pi}{2}\right]=9 \pi\)

∴ \(\int_S(\nabla \times \mathbf{A}) \cdot \mathbf{N} d S=\int_c \mathbf{A} \cdot d \mathbf{r}\)

∴ Stoke’s theorem is verified.

52. Apply Stoke’s theorem to evaluate\(\int_C\) (y dx + z dy+x dz) where C is the curve of intersection of x²+ y² + z²= a² and x + z =a.

Solution:  

For the sphere x² + y² + z² = a², Centre O = (0, 0, 0), radius = a.

Let A be the centre and r be the radius of the circle of intersection of x² + y² + z² = a² and x + z = a.

∴ \(O A=\left|\frac{0+0-a}{\sqrt{2}}\right|=\frac{a}{\sqrt{2}}\)

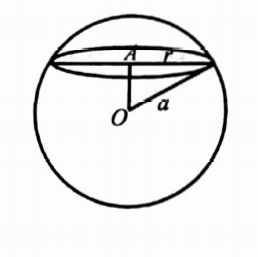
⇒ \(r^2=a^2-O A^2=a^2-\frac{a^2}{2}=\frac{a^2}{2} \Rightarrow r=\frac{a}{\sqrt{2}}\)

Since the plane of the circle is perpendicular to the y-axis, the vector normal to the plane is j.  ∴ N = j.

Let F = yi + zj + xk

∴ \(\nabla \times \mathbf{F}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
y & z & x
\end{array}\right|=\mathbf{i}(0-1)-\mathbf{j}(1-0)+\mathbf{k}(0-1)\)

= – i – j – k

By stoke’s theorem, \(\int_C(y d x+z d y+x d z)=\int_C \mathbf{F} \cdot d \mathbf{r}=\int_S(\nabla \times \mathbf{F}) \cdot \mathbf{N} d S\)

= \(\int_S(-\mathbf{i}-\mathbf{j}-\mathbf{k}) \cdot \mathbf{j} d S=\int_S(-1) d S=-S=-(\text { Area of the circle })={-}\left(\pi a^2 / 2\right)\)

53.Evaluate \(\int_S\)∇xF.N dS using Stoke’s theorem, where F = (2x -y) i -yz²-y²z k and S is tlie upper halfof the sphere x² +y² +z² = 1 and C is its boundary.

Solution:  The boundary C of S is a circle in xy-plane, i.e x² +y² =1,z=0.

The parametric equations are x=cos t, y=sint, 0≤t ≤2π.

F = (2x – y)i – y z j + y z k.

r = xi + yj + zk ⇒ dr = dxi + dyj + dzk.

= \(\mathbf{F} \cdot d \mathbf{r}=(2 x-y) d x-y z^2 d y+y^2 z d z=(2 \cos t-\sin t)(-\sin t)(d t)\)

= \(\left(\sin ^2 t-2 \cos t \sin t\right) d t=\left(\sin ^2 t-\sin 2 t\right) d t\)

By Stoke’s Theorem,

∴ \(\int_S(\nabla \times \mathbf{F}) \cdot \mathbf{N} d s=\int_C \mathbf{F} \cdot d \mathbf{r}=\int_0^{2 \pi}\left(\sin ^2 t-\sin 2 t\right) d t=4 \int_0^{\pi / 2} \sin ^2 t d t+\left[\frac{\cos 2 t}{2}\right]_0^{2 \pi}\)

= \(4 \cdot \frac{1}{2} \cdot \frac{\pi}{2}+\frac{1}{2}[\cos 4 \pi-\cos 0]=\pi+\frac{1}{2}(1-1)=\pi\)

54. Evaluate  \(\int_S\)(∇x F). N dS where F =yi + (x- 2xz) j -xy k and S is the surface S  of the sphere x² +y² + z² = a², above the xy-plane.

Solution:  The boundary C of S is a circle in xy-plane, i.e. x² +y² =1,z=0.

The parametric equations are x=a cos t, y= a sin t,z=0, 0≤t ≤2π. And dx =-a isn’t dt, dy= a cos t dt, dz=0.

∴ \(\int_S \nabla \times \mathbf{F} \cdot \mathbf{N} d S=\int_C \mathbf{F} \cdot d \mathbf{r}=\int_C[y \mathbf{i}+(x-2 x z) \mathbf{j}-x y \mathbf{k}] \cdot d \mathbf{r}\)

= \(\int_C y d x+(x-2 x z) d y-x y d z=\int_{t=0}^{t=2 \pi} a \sin t(-a \sin t) d t+(a \cos t-0) a \cos t d t\)

= \(a^2 \int_{t=0}^{t=2 \pi}\left(\cos ^2 t-\sin ^2 t\right) d t\)

= \(a^2 \int_{t=0}^{t=2 \pi} \cos 2 t d t=\left[\frac{a^2}{2} \sin 2 t\right]_{t=0}^{t=2 \pi}=0\)

55. Prove that \(\oint_C\) f∇g .dr  \(\oint_C\)(∇fx ∇g) .N dS.

Solution: By Stoke’s theorem,

∴ \(\oint_c(f \nabla g) \cdot d \mathbf{r}=\int_S[\nabla \times(f \nabla g)] \cdot \mathbf{N} d S=\int_s[\nabla f \times \nabla g+f \text { curl } \text{grad} g] \cdot \mathbf{N} d S\)

= \(\int_S(\nabla f \times \nabla g) \cdot \mathbf{N} d S\) ∵ curl grad g = 0.

56. Prove that \(\int_S\) curlφ f .dS = \(\int_C\) φ f .dr− \(\int_S\) ∇φ x f.dS.

Solution: Applying Stoke’s theorem to the function φ f.

∴ \(\oint_c(f \nabla g) \cdot d \mathbf{r}=\int_s[\nabla \times(f \nabla g)] \cdot \mathbf{N} d S=\int_s[\nabla f \times \nabla g+f \mathrm{curl} \text{grad} g] \cdot \mathbf{N} d S\)

∴ \(\int_s(\nabla f \times \nabla g) \cdot \mathbf{N} d S .\)

∵ curl grad g = 0.

57.Prove that \(\oint_C\)f∇f.dr = 0.

Solution:

By Stoke’s theorem, \(\int_C(f \nabla f) \cdot d \mathbf{r}=\int_S(c u r l f \nabla f) \cdot \mathbf{N} d S\)

= \(\int_S \phi \text{curl} \mathbf{f} \cdot d \mathbf{S}=\int_C \phi \mathbf{f} \cdot d \mathbf{r}-\int_S \nabla \phi \times \mathbf{f} \cdot d \mathbf{S} .\)