Vector Integration- 4 Exercise−(4)
Solved Problems On Line Surface And Volume Integrals
1. Evaluate \(\int_0^1\)(et + e-2t j + Z k) dt.
Solution:
Given
⇒ \(\left.\left.\left.\int_0^1\left(e^t \mathbf{i}+e^{-2 t} \mathbf{j}+t \mathbf{k}\right) d t=\mathbf{i} \int_0^1 e^t d t+\mathbf{j} \int_0^1 e^{-2 t} d t+\mathbf{k} \int_0^1 t d t=\mathbf{i} e^t\right]_0^1+\mathbf{j} \frac{e^{-2 t}}{-2}\right]_0^1+\mathbf{k} \frac{t^2}{2}\right]_0^1\)
= \(\mathbf{i}(e-1)+\mathbf{j}\left(\frac{e^{-2}}{-2}+\frac{1}{2}\right)+\frac{1}{2} \mathbf{k}=\mathbf{i}(e-1)+\mathbf{j}\left(\frac{1-e^{-2}}{2}\right)+\frac{1}{2} \mathbf{k}\)
2. IfF(Z) = ti + (t2– 2t) j + (3t2 + 3t3) k then find \(\int_0^1\)f(t) dt.
Solution:
⇒ \(\int_0^1 \mathbf{f}(t) d t=\int_0^1\left[t \mathbf{i}+\left(t^2-2 t\right) \mathbf{j}+\left(3 t^2+3 t^3\right) \mathbf{k}\right] d t\)
= \(\int_0^1 t d t+\mathbf{j} \int_0^1\left(t^2-2 t\right) d t+\mathbf{k} \int_0^1\left(3 t^2+3 t^3\right) d t\)
= \(i\left[\frac{t^2}{2}\right]_0^1+\mathbf{j}\left[\frac{t^3}{3}-t^2\right]_0^1+\mathbf{k}\left[t^3+\frac{3 t^4}{4}\right]_0^1=\frac{1}{2} \mathbf{i}-\frac{2}{3} \mathbf{j}+\frac{7}{4} \mathbf{k} . .\)
3. If f(t) = (t−t2) i + 2t3 j- 3k, then find \(\int_1^2\)f(t) dt.
Solution:
⇒ \(\int_1^2 \mathbf{f}(t) d t=\int_1^2\left[\left(t-t^2\right) \mathbf{i}+2 t^3 \mathbf{j}-3 \mathbf{k}\right] d t=\mathbf{i} \int_1^2\left(t-t^2\right) d t+\mathbf{j} \int_1^2 2 t^3 d t-\mathbf{k} \int_1^2 3 a\)
= \(\mathbf{i}\left[\frac{t^2}{2}-\frac{t^3}{3}\right]_1^2+\mathbf{j}\left[\frac{t^4}{2}\right]_1^2-\mathbf{k}[3 t]=\mathbf{i}\left[2-\frac{8}{3}-\frac{1}{2}+\frac{1}{3}\right]+\mathbf{j}\left[8-\frac{1}{2}\right]-\mathbf{k}[6-3]\)
= \(-\frac{5}{6} i+\frac{15}{2} j-3 k\)
4. If f (t) = 2i- J + 2k and f(3) = 4i- 2j + 3k then find\(\int_2^ 3\)f.\(\frac{d f}{d t}\) dt.
Solution:
\(\frac{d}{d t}\left\{f(t)^2\right\}=2 \mathbf{f}(t) \cdot \frac{d \mathbf{f}}{d t} \Rightarrow \int \mathbf{f}(t) \cdot \frac{d \mathbf{f}}{d t} d t=\frac{1}{2} \mathbf{f}(t)^2\)∴ \(\left.\int_2^3\left(\mathbf{f} \cdot \frac{d \mathbf{f}}{d t}\right) d t=\frac{1}{2} \mathbf{f}(t)^2\right]_2^3=\frac{1}{2}\left[\mathbf{f}(3)^2-\mathbf{f}(2)^2\right]=\frac{1}{2}\left[(4 \mathbf{i}-2 \mathbf{j}+3 \mathbf{k})^2-(2 \mathbf{i}-\mathbf{j}+2 \mathbf{k})^2\right]\)
= \(\frac{1}{2}[(16+4+9)-(4+1+4)]=\frac{1}{2}(29-9)=10\)
5. lf f(t) = 5t2i + tj-t3k. find\(\left(f \times \frac{d^2 \mathbf{f}}{d t^2}\right)\)dt.
Solution:
∴ \(\int_1^2\left(\mathbf{f} \times \frac{d^2 \mathbf{f}}{d t^2}\right) d t=\left[\mathbf{f} \times \frac{d \mathbf{f}}{d t}\right]_1^2=\left[-2 t^3 \mathbf{i}+5 t^4 \mathbf{j}-5 t^2 \mathbf{k}\right]_1^2=-14 \mathbf{i}+75 \mathbf{j}-15 \mathbf{k} .\)
6. If \(\frac{d^2 \mathbf{r}}{d t^2}\)= 6ti- 24t2 + 4 sin t k, find r given that r = 2i + j and \(\frac{d r}{d t}\)=−i−3k at t=0
Solution:
\(\frac{d \mathbf{r}}{d t}=\int \frac{d^2 \mathbf{r}}{d t^2} d t=\int\left[6 t \mathbf{i}-24 t^2 \mathbf{j}+4 \sin t \mathbf{k}\right] d t=3 t^2 \mathbf{i}-8 t^3 \mathbf{j}-4 \cos t \mathbf{k}+\mathbf{c}_1\)At \(t=0, \frac{d \mathbf{r}}{d t}=-\mathbf{i}-3 \mathbf{k} \Rightarrow-4 \mathbf{k}+\mathbf{c}_1=-\mathbf{i}-3 \mathbf{k} \Rightarrow \mathbf{c}_1=-\mathbf{i}+\mathbf{k}\)
∴ \(\frac{d \mathbf{r}}{d t}=3 t^2 \mathbf{i}-8 t^3 \mathbf{j}-4 \cos t \mathbf{k}-\mathbf{i}+\mathbf{k}=\left(3 t^2-1\right) \mathbf{i}-8 t^3 \mathbf{j}+(1-4 \cos t)\)
r = \(\left.\int \frac{d \mathbf{r}}{d t} d t=\int\left[\left(3 t^2-1\right) \mathbf{i}-8 t^3 \mathbf{j}+(1-4 \cos t) \mathbf{k}\right)\right] d t=\left(t^3-t\right) \mathbf{i}-2 t^4 \mathbf{j}+(t-4 \sin t) \mathbf{k}+\mathbf{c}_2\)
At \(t=0, \mathbf{r}=2 \mathbf{i}+\mathbf{j} \Rightarrow \mathbf{c}_2=2 \mathbf{i}+\mathbf{j}\)
∴ \(r=\left(t^3-t\right) \mathbf{i}-2 t^4 \mathbf{j}+(t-4 \sin t) \mathbf{k}+2 \mathbf{i}+\mathbf{j}=\left(t^3-t+2\right) \mathbf{i}+\left(1-2 t^4\right) \mathbf{j}+(t-4 \sin t) \mathbf{k}\)
7. lf\(\frac{d^2 \mathbf{r}}{d t^2}\)=−k2r, show that \(\left(\frac{d r}{d t}\right)^2\) = c −k2r2.
Solution:
Given that \(\frac{d^2 \mathbf{r}}{d t^2}=-k^2 \mathbf{r} \Rightarrow 2 \frac{d \mathbf{r}}{d t} \cdot \frac{d^2 \mathbf{r}}{d t^2}=- k^2\left(2 \mathbf{r} \cdot \frac{d \mathbf{r}}{d t}\right)\)
⇒ \(\int\left(2 \frac{d \mathbf{r}}{d t} \cdot \frac{d^2 \mathbf{r}}{d t^2}\right) d t=-k^2 \int\left(2 \mathbf{r} \cdot \frac{d \mathbf{r}}{d t}\right) d t \Rightarrow\left(\frac{d \mathbf{r}}{d t}\right)^2=-k^2 \mathbf{r}^2+\mathbf{c} \Rightarrow\left(\frac{d \mathbf{r}}{d t}\right)^2=\mathbf{c}-k^2 \mathbf{r}^2\)
Vector Integration Line Integral Exercises
8. IfA = ti− t2j+ (t- 1)k, B = 2 t2 + 6tk, find (a)\(\int_1^2\)(A.B) dt (b) \(\int_0^2\) (A x B) dt
Solution:
1. \(\mathbf{A} \cdot \mathbf{B}=\left[t \mathbf{i}-t^2 \mathbf{j}+(t-1) \mathbf{k}\right] \cdot\left[2 t^2 \mathbf{i}+6 t \mathbf{k}\right]=2 t^3+6 t(t-1)=2 t^3+6 t^2-6 t^2\)
∴ \(\int_0^2(\mathbf{A} \cdot \mathbf{B}) d t=\int_0^2\left(2 t^3+6 t^2-6 t\right) d t=\left[\frac{4 t^4}{4}+\frac{6 t^3}{3}-\frac{6 t^2}{2}\right]_0^2=16+16-12=20\)
2. \(\mathbf{A} \times \mathbf{B}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
t & -t^2 & t-1 \\
2 t^2 & 0 & 6 t
\end{array}\right|=\mathbf{i}\left(-6 t^3-0\right)-\mathbf{j}\left(6 t^2-2 t^3+2 t^2\right)+\mathbf{k}\left(0+2 t^4\right)\)
= \(-6 t^3 \mathbf{i}+\left(2 t^3-8 t^2\right) \mathbf{j}+2 t^4 \mathbf{k}\)
⇒ \(\int_0^2(\mathbf{A} \times \mathbf{B}) d t=\int_0^2\left[-6 t^3 \mathbf{i}+\left(2 t^3-8 t^2\right) \mathbf{j}+2 t^4 \mathbf{k}\right] d t=\left[-\frac{6 t^4}{4} \mathbf{i}+\left(\frac{2 t^4}{4}-\frac{8 t^3}{3}\right) \mathbf{J}+\frac{2 t^5}{5} \mathbf{k}\right]_0^2\)
= \(-24 \mathbf{i}+\left(8-\frac{64}{3}\right) \mathbf{j}+\frac{64}{5} \mathbf{k}=-24 \mathbf{i}-\frac{40}{3} \mathbf{j}+\frac{64}{5} \mathbf{k}\)
9. Evaluate \(\int_c\)(x2 +y2) dx, where C is the arc of the parabola y2= 4ax between (0, 0)and (a, 2a).
Solution:
⇒ \(\int_C\left(x^2+y^2\right) d x\)
⇒ \(=\int_{x=0}^{x=a}\left(x^2+4 a x\right) d x\)
⇒ \(=\left[\frac{x^3}{3}+2 a x^2\right]_{x=0}^{x=a}\)
⇒ \(=\frac{a^3}{3}+2 a^3\)
∴ \(\frac{7 a^3}{3}\)
10. Evaluate \(\int_c \frac{d x}{(x+y)}\) , where C is the curve x=at2,y=2at,0≤t≥2
Solution:
⇒ \(\int_C \frac{d x}{x+y}\)
⇒ \(=\int_{t=0}^{t=2} \frac{d\left(a t^2\right)}{a t^2+2 a t}\)
⇒ \(=\int_{t=0}^{t=2} \frac{2 a t d t}{a t^2+2 a t}\)
∴ \(=2 \int_0^2 \frac{d t}{t+2}\)=\(2 \log (t+2)]_0^2\)
11. Show that \(\int_c\)[(x-y)3 dx + (x-y)3 dy] = 3πa4 taken along the circle x2+y2 = a2 in the counter clockwise sense.
Solution:
The parametric equations circle x+y = a are x=a cos θ, y= a sin θ.
dx= -a sin θ dθ, dy= a cos θ dθ and θ varies from 0 to 2π.
⇒ \(\int_C\left[(x-y)^3 d x+(x-y)^3 d y\right]\)
⇒ \(=\int_0^{2 \pi}(a \cos \theta-a \sin \theta)^3(-a \sin \theta d \theta)\)+ \((a \cos \theta-a \sin \theta)^3(a \cos \theta d \theta)\)
⇒ \(a^4 \int_0^{2 \pi}(\cos \theta-\sin \theta)^4 d \theta=a^4 \int_0^{2 \pi}\left(\cos ^4 \theta-4 \cos ^3 \theta \sin \theta+6 \cos ^2 \theta \sin ^2 \theta-4 \cos \theta \sin ^4 \theta+\sin ^4 \theta\right) d \theta\)
⇒ \(a^4 4 \int_0^{\pi / 2}\left(\cos ^4 \theta-0+6 \cos ^2 \theta \sin ^2 \theta-0+\sin ^4 \theta\right) d \theta\)
⇒ \(4 a^4 \int_0^{\pi / 2}\left[\left(\cos ^2 \theta+\sin ^2 \theta\right)^2+4 \cos ^2 \theta \sin ^2 \theta\right] d \theta\)
∴ \(4 a^4 \int_0^{\pi / 2}\left(1+4 \cos ^2 \theta \sin ^2 \theta\right) d \theta=4 a^4\left[\frac{\pi}{2}+4 \times \frac{1}{4} \times \frac{1}{2} \times \frac{\pi}{2}\right]=3 \pi a^4\).
12. Define line integral and explain the Cartesian form of line integral.
Line integral:
An integral which is to be evaluated along a curve is called a ” Line Integral. Suppose r=xi+yj+zk defines a piecewise smooth curve C joining two points A and B. Suppose F is a vector point function defined and continuous along C. If s denotes the arc length of the curve C then \(\frac{d r}{d s}\)= T is a unit vector along the tangent to the curve C at the point r.
The component of the vector F along the tangent is F.\(\frac{d r}{d s}\). The integral of F.\(\frac{d r}{d s}\) along from A to B written as \(\int_A^B\left(F \cdot \frac{d r}{d s}\right)\) ds \(=\int_A^B \mathbf{F} \cdot d \boldsymbol{r}\) \(=\int_C F \cdot d r\) . is an example of a line integral. it is called tangent line integral of F along C.
Cartesian form: If F = F1i +F2 j + F3k then
F.dr =(F1i +F2 j + F3k). (dxi+dyj+dzk)= F1dx+F2dy+F3dz
∴ \(\int_C\)F.dr=\(\int_C\)F1dx+F2dy+F3dz
If the parametric equation of the curve C are x=x(t),y(t), z=z(t) and if t1 at A, t=t2 at B then \(\int_C\)F.dr=\(=\int_{t_1}^{t_2}\left[F_1 \frac{d x}{d t}+F_2 \frac{d y}{d t}+F_3 \frac{d z}{d t}\right]\)dt
13. If F- 3xyi- 5zj + 10xk, evaluate \(\int_c\)F.dr along the curve, x = t2 + 1, y = 2t2, z= t3 from t = 1 to t= 2.
Solution:
Given
F- 3xyi- 5zj + 10xk
Let \(\mathbf{r}=x \mathbf{i}+y \mathbf{J}+z \mathbf{k}=\left(t^2+1\right) \mathbf{i}+2 t^2 \mathbf{j}+t^3 \mathbf{k} \Rightarrow \frac{d \mathbf{r}}{d t}=2 t \mathbf{l}+4 t \mathbf{j}+3 t^2 \mathbf{k} …\)
⇒ \(\mathbf{F}=3 x y \mathbf{i}-5 z \mathbf{j}+10 x \mathbf{k}=3\left(t^2+1\right) 2 t^2 \mathbf{i}-5 t^3 \mathbf{j}+10\left(t^2+1\right) \mathbf{k}\)
⇒ \(6 t^2\left(t^2+1\right) \mathbf{i}-5 t^3 \mathbf{J}+10\left(t^2+1\right) \mathbf{k}\)
⇒ \(\mathbf{F} \cdot \frac{d \mathbf{r}}{d t}=6 t^2\left(t^2+1\right) \cdot 2 t-5 t^3 \cdot 4 t+10\left(t^2+1\right) \cdot 3 t^2\)
⇒ \(12 t^5+12 t^3-20 t^4+30 t^4+30 t^2=12 t^5+10 t^4+12 t^3+30 t^2\)
∴ \(\left.\int \mathbf{F} \cdot d \mathbf{r}=\int\left(\mathbf{F} \cdot \frac{d \mathbf{r}}{d t}\right) d t=\int_1^2\left(12 t^5+10 t^4+12 t^3+30 t^2\right) d t=12 t^6+2 t^5+3 t^4+10 t^3\right]_1^2\)
= 138 + 64 + 48 + 80 – 2 – 2 – 3 – 10 = 320 – 17 = 303.
Volume Integrals Solved Examples
14. If F- 3xyi- 5zj + l0xk, evaluate \(\int_c\)F.dr along the curve, x =t2 , y = 2t2, from z = t3 to t= 1 t=2
Solution:
Given
F- 3xyi- 5zj + l0xk
Let r=xi+yj+zk=t2i+2t2j+t3k ⇒\(\frac{d r}{d t}\)=2ti+4tj+3t2k
F=3xyi-5zj+10xk=3t2(2t2)i-5t3j+10t2k= 6t4i-5t3j+10t2k
⇒ \(\mathbf{F} \cdot \frac{d \mathbf{r}}{d t}=\left(6 t^4 \mathbf{i}-5 t^3 \mathbf{j}+10 t^2 \mathbf{k}\right) \cdot\left(2 t \mathbf{i}+4 t \mathbf{j}+3 t^2 \mathbf{k}\right)\)
⇒ \(\left(6 t^4\right)(2 t)+\left(-5 t^3\right)(4 t)+\left(10 t^2\right)\left(3 t^2\right)=12 t^5-20 t^4+30 t^4=12 t^5+10 t^4\)
∴ \(\left.\int \mathbf{F} \cdot d \mathbf{r}=\int \mathbf{F} \cdot \frac{d \mathbf{r}}{d t}\right) d t=\int\left(12 t^5+10 t^4\right) d t=\left[2 t^6+2 t^5\right]_1^2=(128+64)-(2+2)=188\).
15. Find ∫F .dr where F = xyi+yzj + zxk over the curve Curve r = ti + t2j + t3k, t varying from −1 to 1 .
Solution:
⇒ \(\mathbf{r}=x \mathbf{i}+y \mathbf{j}+3 \mathbf{k}=t \mathbf{i}+t^2 \mathbf{j}+t^3 \mathbf{k} \Rightarrow x=t, y=t^2, z=t^3 \text { and } \frac{d \mathbf{r}}{d t}=\mathbf{i}+2 t \mathbf{j}+3 t^2 \mathbf{k}\)
⇒ \(\mathbf{F}=x y \mathbf{i}+y z \mathbf{j}+z x \mathbf{k}=t^3 \mathbf{i}+t^{\mathbf{5}} \mathbf{j}+t^4 \mathbf{k}\)
∴ \(\int \mathbf{F} \cdot d \mathbf{r}=\int\left(\mathbf{F} \cdot \frac{d \mathbf{r}}{d t}\right) d t=\int_{-1}^1\left(t^3+2 t^5+3 t^5\right) d t=\int_{-1}^1\left(t^3+5 t^5\right) d t=\left[\frac{t^4}{4}+5 \frac{t^7}{7}\right]_{-1}^1\)
⇒ \(\left(\frac{1}{4}+\frac{5}{7}\right)-\left(\frac{1}{4}-\frac{5}{7}\right)=\frac{10}{7}\)
16. Find \(\int_c\)F.dr where C is the arc of y- x2 in xy-plane from (0, 0) to (1, 1) and F=x2i +y2j.
Solution: The equation of the given curve is y= x2⇒ 2x dx. Given F=xi+yj+zk the curve lies in xy plane from (0,0) t0 (1,2) the limits of integration are x=0 to x=1
∴ \(\int_c F \cdot d r\)
⇒ \(=\int_C x^2 d x+y^2 d y\)
⇒ \(=\int_0^1 x^2 d x+x^4(2 x d x)\)
⇒ \(=\int_0^1\left(x^2+2 x^3\right) d x\) \(=\left[\frac{x^3}{3}+\frac{2 x^6}{6}\right]_0^1\)
∴ \(=\frac{1}{3}+\frac{1}{3}=\frac{2}{3}\)
17. If F = 3xy i -y2 j, evaluate \(\int_c\)Fdr where C is the curve y = 2x2 in the xy-plane from (0, 0) to (1, 2).
Solution:
The equation of given curve C is y= x2⇒ 4x dx. The integration was performed in xy- plane along C from (0,0) to (1,2).
∴ x varies from 0 to 1.
⇒ \(\int_C F \cdot d r\)
⇒ \(\int_C\left(3 x y \mathbf{i}-y^2 \mathbf{j}\right) \cdot(d x \mathbf{i}+d y \mathbf{j}+d z \mathbf{k})\)
⇒ \(=\int_C\left(3 x y d x-y^2 d y\right)\)
⇒ \(=\int_{x=0}^{x=1} 3 x \cdot\left(2 x^2\right) d x-4 x^4 \cdot 4 x d x\)
⇒ \(=\int_0^1\left(6 x^3-16 x^3\right) d x\) \(\left.=6 \frac{x^4}{4}-16 \frac{x^6}{6}\right]_0^1\)
⇒ \(=\frac{3}{2}-\frac{8}{3}=\frac{9-16}{6}\)
∴ \(-\frac{7}{6}\).
18. Evaluate \(\int_c\)F.dr, where F = x2y2 i +yj and the curve C is y= 4x in the xy-plane c from (0, 0) to (4, 4).
Solution:
The equation of curve C is y2=4x⇒2y dy =4dx⇒ ydy =2dx.
∴ x varies from 0 to 4.
⇒ \(\int_C F \cdot d r\)
⇒ \(\int_C x^2 y^2 d x+y d y\)
⇒ \(\int_0^4 x^2 \cdot 4 x d x+2 d x\)
⇒ \(\int_0^4\left(4 x^3+2\right) d x\) \(\left.=x^4+2 x\right]_0^4\)
=256+8=264.
19. Evaluate \(\int_c\)F.dr where F = 3x2i + (2xz -y)j + zk along the straight line C from(0,0,0) to (1,2).
Solution:
Equation of the joining (0,0,0) to (2,1,3) are \(\frac{x}{2}=\frac{y}{1}=\frac{z}{3}=t\) (say).
∴ x = 2t, y = t, z = 3t, t varies from 0 to 1. Also \(\frac{d x}{d t}=2, \frac{d y}{d t}=1, \frac{d z}{d t}=3\)
⇒ \(\mathbf{r}=x \mathbf{i}+y \mathbf{j}+z \mathbf{k} \Rightarrow d \mathbf{r}=d x \mathbf{i}+d y \mathbf{j}+d z \mathbf{k}=\left(\frac{d x}{d t} \mathbf{i}+\frac{d y}{d t} \mathbf{j}+\frac{d z}{d t} \mathbf{k}\right) d t=(2 \mathbf{i}+\mathbf{j}+3 \mathbf{k}) d t\)
⇒ \(\mathbf{F}=3 x^2 \mathbf{i}+(2 x z-y) \mathbf{j}+z \mathbf{k}=12 t^2 \mathbf{i}+\left(12 t^2-t\right) \mathbf{j}+3 t \mathbf{k}\)
⇒ \(\int_C \mathbf{F}. d \mathbf{r}=\int_C\left[12 t^2 \mathbf{i}+\left(12 t^2-t\right) \mathbf{j}+3 t \mathbf{k}\right] \cdot(2 \mathbf{i}+\mathbf{j}+3 \mathbf{k}) d t=\int_C\left(24 t^2+12 t^2-t+9 t\right) d t\)
∴ \(\left.\int_0^1\left(36 t^2+8 t\right) d t=12 t^3+4 t^2\right]_0^1=12+4=16\)
Exercises On-Line, Surface, And Volume Integrals With Answers
20. Evaluate \(\int_c\)A.dr where C is the line joining (0,0,0) and (2,1,1), given A = (2y + 3)i + xzj + (yz−x)k.
Solution:
The equations of the line joining (0,0,0) and (2,1,1) are \(\frac{x}{2}=\frac{y}{1}=\frac{z}{3}\) =t.
Then along the line C,x=2t,y=t,z=t.
∴ At (0,0,0,) , t=0 and at (2,1,1,) , t=1.
r=xi+yj+zk=2ti+rj=tk.
∴ dr=(2i+j+k)dt.
∫A.dr=\(\int_C[2(2 y+3)+1(x z)+1(y z-x)] d t\)
=\(\int_0^1[2(2 t+3)+(2 t \cdot t)+(t \cdot t-2 t)] d t\)
∴ \(\left.=\int_0^1\left(2 t^2+2 t+6\right) d t=t^3+t^2+6 t\right]_0^1\)=8.
21. Evaluate \(\oint_c\)F .dr where C is the circle x2+y2 = 1, z = 0 and F =yi + zj +xk.
Solution:
The equation of the circle is x+y+=1,z=0
∴ dz=0.
In parametric form, x=cos θ,y=sin θ, z=0 and θ varies from 0 to 2π.
∴ \(\int_C F \cdot d r\)=\(\int_C(y \mathbf{i}+z \mathbf{j}+x \mathbf{k}) \cdot(\mathbf{i} d x+\mathbf{j} d y+\mathbf{k} d z)\)
⇒ \(\int_C(y d x+z d y+x d z)\)=\(\int_C y d x\)
⇒ \(=\int_{\theta=0}^{2 \pi} \sin \theta(-\sin \theta) d \theta\)
⇒ \(\theta=-4 \int_0^{\pi / 2} \sin ^2 \theta d \theta\)
=4(1/2)(π/2)=−π
22. If F = (3x2 + 6y)i- 14yzi + 20xz2 k, evaluate \(\int_c\)F.dralong the straight line joining (0, 0, 0) to (1, 0, 0) to(l, 1, 0) to (1, 1, 1)5
Solution:
(1) Line integral along the line from (0, 0, 0) to (1, 0, 0): Here y = 0, z = 0, x varies from 0 to 1, dy = 0, dz = 0.
\(\int_{c_1} \mathbf{F} \cdot d r\)=\(\int_0^1 3 x^2 d x\)
=1.
(2) Line integral along the line from (1,0,0) to (1,1,0):
Here x=1, y varies from 0 to 1, z=0; dx=0, dz=0.
∴ \(\int_{c_2} \mathbf{F} \cdot d r\)=\(\int_0^1\)=0
(3) Line integral along the line from (1,1,0) t0 (1,1,1):
Here x=1,y=1, and z varies from 0 to 1. dx=0, dy=0.
⇒ \(\int_{c_3} \mathbf{F} \cdot d r\)=\(\int_0^1 20 z^2 d z\)=\(\frac{20 z^3}{3}\)\(]_0^1\)
⇒ \(\frac{20}{3}\)
∴ \(\int_{c} \mathbf{F} \cdot d r\)\(\)=\(\int_{c_1} \mathbf{F} \cdot d r\)+\(\int_{c_2} \mathbf{F} \cdot d r\)+\(\int_{c_3} \mathbf{F} \cdot d r\)=1+0+\(\frac{20}{3}\)=\(\frac{23}{3}\).
Step-By-Step Solutions To Vector Integration Problems
23. If F =(x2 +y2)i− 2xy j, evaluate \(\oint_c\)F .dr where the curve C is the rectangle in the xy-plane bounded by y = 0,y = b, x = 0, x = a.
Solution:
Since the integration takes place in xy -plane (z=0),
∴ \(\oint_c\)F.dr= \(\oint_c\)F1dx+F2 dy=\(\oint_c\)(x2+y2)dx-2xy dy
(1) Line integral along OP: Here y=0, dy=0 and x varies from o to a. \(\int_{O P} F \cdot d r\)=\(\int_0^a x^2 d x\)=\(\frac{a^3}{3}\)
(2) Line integral along PQ: Here x=a, dx=0, and y changes from 0 to b.
∴ \(\int_{P Q} F \cdot d r\)=\(\int_a^b(-2 a y) d y\)=\(\left.-a y^2\right]_0^b\)=−ab2
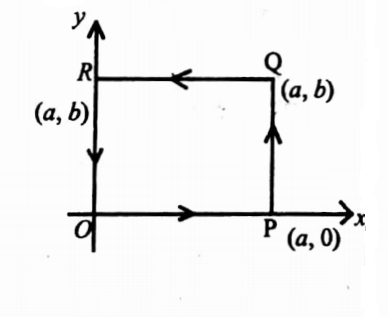
(3) Line integral along QR: Here y=b, dy=0, and x changes from a to 0.
∴\(\int_{Q R} F \cdot d r\)=\(\int_b^0 0\)=0
∴\(=\int_a^0\left(x^2+b^2\right) d x\)
=\(\left[\frac{x^3}{3}+b^2 x\right]_a^0\)
=\(-\frac{1}{3} a^3-a b^2\)
(4) Line integral along RO: Here x=0, dx=0, and y varies from b to 0.
∴ \(\int_{R O} F \cdot d r\)=\(\int_b^0 0\)
∴ \(\oint_c \boldsymbol{F} \cdot d \boldsymbol{r}\)=\(\int_{O P} F \cdot d r\)+ \(\int_{P Q} F \cdot d r\)+\(\int_{Q R} F \cdot d r\)+\(\int_{R O} F \cdot d r\)=\(\frac{a^3}{3}-a b^2-\frac{1}{3} a^3-a b^2\)=-2ab2
24. Find \(\int_c\)y2dx−x2dy, where C the curve represents sides of ΔABC, where A =(1, 0), B = (0, 1), C = (- 1, 0).
Solution:
Equation of \(\overleftrightarrow{A B}\) is \(\frac{y-0}{1-0}\)=\(=\frac{x-1}{0-1}\)⇒ y=1−x
Equation of \(\overleftrightarrow{B C}\) is \(\frac{y-1}{0-1}\)\(=\frac{x-0}{-1-0}\) ⇒ y=1+x.
Equation of \(\overleftrightarrow{C A}\) is y=0.
Case(1): Line integral along \(\overleftrightarrow{A B}\): y=1-x, dy =−dx, x varies from 1 to 0
∴ \(\int_{c_1} y^2 d x-x^2 d y=\int_1^0(1-x)^2 d x-x^2(-d x)=\int_1^0\left(1+x^2-2 x+x^2\right) d x\)
= \(\int_1^0\left(1-2 x+2 x^2\right) d x=\left[x-x^2+\frac{2 x^2}{3}\right]_1^0=-\left(1-1+\frac{2}{3}\right)=-\frac{2}{3}\)
Case(2): Line integral aling \(\overleftrightarrow{B C}\): y=1+x,dy=dx, x varies from 0 to −1
∴ \(\int_{c_2} y^2 d x-x^2 d y=\int_0^{-1}(1+x)^2 d x-x^2 d x=\int_0^{-1}\left(1+2 x+x^2-x^2\right) d x\)
= \(\int_0^{-1}(1+2 x) d x=\left[x+x^2\right]_0^{-1}=-1+1=0\)
Case(3): Line integral along \(\overleftrightarrow{C A}\): y=0,dy=0, x varies from −1 to 1.
∴ \(\int_{c_3} y^2 d x-x^2 d y=\int_{-1}^1 0=0\)
∴ \(\int_C y^2 d x-x^2 d y=\int_{c_1} y^2 d x-x^2 d y+\int_{c_2} y^2 d x-x^2 d y+\int_{c_3} y^2 d x-x^2 d y\)
= \(-\frac{2}{3}+0+0=-\frac{2}{3}\)
25. Find the work done when a force F = (x2 − y2 + x) i− (2xy+y)j moves a particle in xy-plane from (0, 0) to (1, 1) along the parabola y2= x.
Solution:
Given curve is y2=x⇒ 2y dy=dx. Work done by F is \(\int_C F \cdot d r\). the integration is performed in xy-plane and y varies from 0 to 1.
⇒ \(\int_c \mathbf{F} \cdot d \mathbf{r}=\int_c\left(x^2-y^2+x\right) d x-(2 x y+y) d y=\int_0^1\left(y^4-y^2+y^2\right) 2 y d y-\left(2 y^3+y\right) d y\)
⇒ \(\int_0^1\left(2 y^5-2 y^3-y\right) d y=\left[\frac{y^6}{3}-\frac{y^4}{2}-\frac{y^2}{2}\right]_0^1=\frac{1}{3}-\frac{1}{2}-\frac{1}{2}=\frac{2-3-3}{6}=\frac{-4}{6}=\frac{-2}{3}\)
26. If F = (x +y2) i−2xj+ 2yzk, evaluate \(\int_S\) F . N dS where S is the surface of plane 2x +y + 2z = 6 in the first octant.
Solution: Let φ =2x+y=2z-6.
The vector normal to the surfaces S is ∇φ=\(\mathbf{i} \frac{\partial \varphi}{\partial x}+\mathbf{j} \frac{\partial \varphi}{\partial y}+\mathbf{k} \frac{\partial \varphi}{\partial z}\)=2i+j+2k.
Unit normal vector, N \(=\frac{2 i+j+2 k}{\sqrt{4+1+4}}\)=\(=\frac{1}{3}(2 \mathbf{i}+\mathbf{j}+2 \mathbf{k})\).
Let R be the projection of S on xy-plane.
Now R is bounded by the x-axis, y-axis, and the line 2x+y=6z= 0
⇒ \(\mathbf{F} \cdot \mathbf{N}=\left[\left(x+y^2\right) \mathbf{i}-2 x \mathbf{j}+2 y z \mathbf{k}\right] \cdot \frac{1}{3} (2 \mathbf{i}+\mathbf{j}+2 \mathbf{k})=\frac{1}{3}\left[2 x+2 y^2-2 x+4 y z\right]=\frac{2}{3}\left(y^2+2 y z\right)\)
⇒ \(\mathbf{N} \cdot \mathbf{k}=\frac{1}{3}(2 \mathbf{i}+\mathbf{j}+2 \mathbf{k}) \cdot \mathbf{k}=\frac{2}{3}\)
⇒ \(\int_S \mathbf{F} \cdot \mathbf{N} d S=\iint_R \mathbf{F} \cdot \mathbf{N} \frac{d x d y}{|\mathbf{N} \cdot \mathbf{k}|}=\iint_R \frac{2}{3}\left(y^2+2 y z\right) \frac{d x d y}{(2 / 3)}=\iint_R\left(y^2+2 y z\right) d x d y\)
⇒ \(\iint_R\left[y^2+y(6-2 x-y)\right] d x d y=2 \int_{x=0}^{x=3} \int_{y=0}^{y=6-2 x} y(3-x) d x d y\)
⇒ \(2 \int_{x=0}^{x=3}\left[\frac{y^2}{2}(3-x)\right]_{y=0}^{y=6-2 x} d x=\int_{x=0}^{x=3}(3-x)(6-2 x)^2 d x\)
⇒ \(\int_0^3(3-x)\left(36-24 x+4 x^2\right) d x=\int_0^3\left(108-108 x+36 x^2-4 x^3\right) d x\)
∴ \(\left[108 x-54 x^2+12 x^3-x^4\right]_0^3=324-486+324-81=81\)
Vector Integration Solved Problems For Students
27. Evaluate \(\int_S\)F.N dS where F = xy i- x2j + (x + z) k and S is the surface of the planes 2x + 2y + z=6 in the first octant.
Solution:
Let φ =2x+2y=z-6.
The vector normal to the surfaces S is ∇φ=\(\mathbf{i} \frac{\partial \varphi}{\partial x}+\mathbf{j} \frac{\partial \varphi}{\partial y}+\mathbf{k} \frac{\partial \varphi}{\partial z}\)=2i+j+2k.
Unit normal vector, N \(=\frac{2 i+2 j+k}{\sqrt{4+4+1}}\)=\(\frac{1}{3}\)(2i+2j+k).
Let R be the projection of S on xy-plane.
Now R is bounded by x-axis, y-axis, and the line 2x+y=6,z= 0
F.N =[(xyi-x2j+(x+z)K].1/3(2i+2j+k)=\(=\frac{1}{3}\left(2 x y-2 x^2+x+z\right)\).
⇒ \(\mathbf{N} \cdot \mathbf{k}=\frac{1}{3}(2 \mathbf{i}+2 \mathbf{j}+\mathbf{k}) \cdot \mathbf{k}=\frac{1}{3}\)
⇒ \(\int_S \mathbf{F} \cdot \mathbf{N} d S=\iint_R \mathbf{F} \cdot \mathbf{N} \frac{d x d y}{|\mathbf{N} \cdot \mathbf{k}|}=\iint_R \frac{1}{3}\left(2 x y-2 x^2+x+z\right) \frac{d x d y}{(1 / 3)}\)
⇒ \(\iint_R\left(2 x y-2 x^2+x+6-2 x-2 y\right) d x d y=\int_{x=0}^{x=3} \int_{y=0}^{y=3-x}\left(2 x y-2 x^2-x-2 y+6\right) d x d y\)
⇒ \(\int_{x=0}^{x=3}\left[x y^2-2 x^2 y-x y-y^2+6 y\right]_{y=0}^{y=3-x} d x\)
⇒ \(\int_{x=0}^{x=3}\left[x(3-x)^2-2 x^2(3-x)-x(3-x)-(3-x)^2+6(3-x)\right] d x\)
⇒ \(\int_0^3\left(9 x-6 x^2+x^3-6 x^2+2 x^3-3 x+x^2-9+6 x-x^2+18-6 x\right) d x\)
⇒ \(\int_0^3\left(3 x^3-12 x^2+6 x+9\right) d x=\left[\frac{3 x^4}{4}-4 x^3+3 x^2+9 x\right]_0^3=\frac{243}{4}-108+27+27\)
∴ \(\frac{243}{4}-54=\frac{27}{4}\)
28.Evaluate\(\int_S\) F. N dS where F= 18zi- 12J + 3yk and S is the part of the planes 2x + 3y + 6z=12 located in the first octant.
Solution: Let φ =2x+3y+6z-12. The vector normal to the plane is ∇φ=2i+3j+6k.
Unit normal vector, N=\(\frac{2 i+3 j+6 k}{\sqrt{4+9+36}}\)=\(\frac{2 \mathbf{i}+3 \mathbf{j}+6 \mathbf{k}}{7}\).
Let R be the projection of S on xy-plane.
∴ \(\mathbf{F} \cdot \mathbf{N}=(18 z \mathbf{i}-12 \mathbf{j}+3 y \mathbf{k}) \cdot\left(\frac{2 \mathbf{i}+3 \mathbf{j}+6 \mathbf{k}}{7}\right)=\frac{1}{7}(36 z-36+18 y)=\frac{6}{7}(6 z-6+3 y)\)
⇒ \(\mathbf{N} \cdot \mathbf{k}=\frac{1}{7}(2 \mathbf{i}+3 \mathbf{j}+6 \mathbf{k}) \cdot \mathbf{k}=\frac{6}{7} \cdot \quad d S=\frac{d x d y}{|\mathbf{N} \cdot \mathbf{k}|}=\frac{d x d y}{6 / 7}\)
⇒ \(\int_S \mathbf{F} \cdot \mathbf{N} d S=\iint_R \mathbf{F} \cdot \mathbf{N} \frac{d x d y}{|\mathbf{N} \cdot \mathbf{k}|}=\iint_R \frac{6}{7}(6 z-6+3 y) \frac{d x d y}{(6 / 7)}=\iint_R(6 z-6+3 y) d x d y\)
⇒ \(\iint_R(12-2 x-3 y-6+3 y) d x d y=\int_{x=0}^{x=6} \int_{y=0}^{y=(12-2 x) / 3}(6-2 x) d x d y\)
⇒ \(\int_{x=0}^{x=6}[(6-2 x) y]_{y=0}^{y=(12-2 x) / 3} d x=\int_{x=0}^{x=6} \frac{4}{3}(3-x)(6-x) d x=\frac{4}{3} \int_0^6\left(x^2-9 x+18\right) d x\)
∴ \(\frac{4}{3}\left[\frac{x^3}{3}-1 \frac{9 x^2}{2}+18 x\right]_0^6=\frac{4}{3}[72-162+108]=24\)
29. Evaluate \( \int_S\)F.N dS where F =yi + 2xj -zk and S is the surface of the plane s 2x+y = 6 in the first octant, cut of f by the plane z = 4.
Solution: Let φ =2x+y-6.
The vector to the surfaces S is ∇φ =\(i \frac{\partial \varphi}{\partial x}+j \frac{\partial \varphi}{\partial y}+k \frac{\partial \varphi}{\partial z}=\)=2i+j
Unit normal vector to th surface is N \(=\frac{\nabla \varphi}{|\nabla \varphi|}\)=\(\frac{2 \mathbf{i}+\mathbf{j}}{\sqrt{5}}\).
Let r be the projection of S over xz plane.
The boundaries of R is x=0 to x=3 and z-0 to z=4.
∴ \(\int_S \mathbf{F} \cdot \mathbf{N} d S=\iint_R(y \mathbf{i}+2 x \mathbf{j}-z \mathbf{k}) \cdot \frac{2 \mathbf{i}+\mathbf{j}}{\sqrt{5}} \frac{d x d z}{|\mathbf{j} \cdot \mathbf{n}|}\)
⇒ \(\iint_R \frac{2 y+2 x}{\sqrt{5}} \frac{d x d z}{1 / \sqrt{5}}=\iint_R[2(6-2 x)+2 x] d x d z=\int_{x=0}^{x=3} \int_{z=0}^{z=4}(12-2 x) d x d z\)
⇒ \(\left.\int_{x=0}^{x=3}(12-2 x) z\right]{ }_{z=0}^{z=4} d x=\int_{x=0}^{x=3}(12-2 x) 4 d x=4\left[12 x-x^2\right]_0^3=4[36-9]=108\)
Practice Problems Online, Surface, And Volume Integrals
30. Evaluate Evaluate \(\int_S\)F.N dS where F = zi +xj− 3y2 zk and S is the surfaces x2 +y2 = 16 included in the first octant between z = 0 and z = 5.
Solution: Let φ = x2+y2-16
The normal to the surfaces S is grad φ = ∇φ=\(\mathbf{i} \frac{\partial \varphi}{\partial x}+\mathbf{j} \frac{\partial \varphi}{\partial y}+\mathbf{k} \frac{\partial \varphi}{\partial z}\)=2xi+2yj
Unit normal vector, N=\(\frac{2 x i+2 y i}{\sqrt{4 x^2+4 y^2}}\)
=\(\frac{x \mathbf{i}+y \mathbf{j}}{\sqrt{x^2+y^2}}\)
=\(\frac{x \mathbf{i}+y \mathbf{j}}{4}\)
Let R be the projection of S on xy-plane .
In yz- plane, for the surface y varies from 0 to 4 and z varies from 0 to 5.
Then \(\int_S \mathbf{F} \cdot \mathbf{N} d S=\iint_R \mathbf{F} \cdot \mathbf{N} \frac{d y d z}{|\mathbf{N} \cdot \mathbf{i}|}=\int_{y=0}^{y=4} \int_{z=0}^{z=5} \frac{x z+x y}{4} \cdot \frac{d y d z}{x / 4}\)
⇒ \(\int_{y=0}^{y=4} \int_{z=0}^{z=5}(z+y) d y d z=\int_{y=0}^{y=4}\left[z^2 / 2+y z\right]{ }_{z=0}^{z=5} d y=\int_0^4\left[\frac{25}{2}+5 y\right] d y=\left[\frac{25 y}{2}+\frac{5 y^2}{2}\right]_0^4\)
⇒ 50 + 40 = 90.
31. Evaluate \(\int_S\)F.N dS where F = 6z i + (2x +y) j- x k and S is the surface of the region bounded by x2 + z2 = 9, x == 0,y = 0, z = 0 and y = 8.
Solution: Let φ x2 +y2+ z2 − 9
The normal to the surfaces S is ∇φ \(\mathbf{i} \frac{\partial \varphi}{\partial x}+\mathbf{j} \frac{\partial \varphi}{\partial y}+\mathbf{k} \frac{\partial \varphi}{\partial z}\)=2xi+2zk
Unit normal vector, N=\(\frac{2 x i+2 y i}{\sqrt{4 x^2+4 y^2}}\)
=\(\frac{x \mathbf{i}+z \mathbf{k}}{\sqrt{x^2+z^2}}\)
=\(=\frac{1}{3}(x \mathbf{i}+z \mathbf{k})\)
F.N =(6zi+(2x+y)j-xk).\(\frac{1}{3}\) (xi+zk)=1/3 (6xz-xz)=\(\frac{5}{3}\) xz
N.K=\(\frac{1}{3}\) (xi+zk)k. =z/3. Let R be the projection of S on xy-plane.
In xy-plane, for the surfaces x varies from 0 to 3 and y varies from 0 to 8.
∴ \(\int_S \mathbf{F} \cdot \mathbf{N} d S=\iint_R \mathbf{F} \cdot \mathbf{N} \frac{d y d z}{|\mathbf{N} \cdot \mathbf{k}|}=\int_{x=0}^{x=3} \int_{y=0}^{y=8}\left(\frac{5}{3} x z\right) \frac{d x d y}{(z / 3)}\)
\(=\int_{x=0}^{x=3} \int_{y=0}^{y=8} 5 x d x d y\)=\(\int_{x=0}^{x=3} 40 x d x=\left[20 x^{2}\right]_{0}^{3}=180\)
32. Evaluate \(\int_S\)F.N dS, where F =yzi + zxj + xyk. and S is the part ofthe sphere x2 +y2 + z2 = 1 which lies in the first octant.
Solution: Let φ =x2 +y2+ z2−1
Normal vector to the surfaces is ∇φ=2(xi+yj+zk)
Unit normal vector, N=\(\frac{2(x \mathbf{i}+y \mathbf{j}+z \mathbf{k})}{\sqrt{4 x^2+4 y^2+4 z^2}}\)
=\(\frac{x \mathbf{i}+y \mathbf{j}+\mathbf{k}}{\sqrt{x^2+y^2+z^2}}\)
=xi+yj+zk.
F.N (yzi+zxj+xyk).(xi+yj+zk)=xyz+xyz+xyz=3xyz, N.i=x.
Let R be the projection of S on yz-plane.
Then \(\int_S F \cdot N d S\)
=\(\iint_R F \cdot \mathbf{N} \frac{d y d z}{|\mathbf{N} \cdot \boldsymbol{i}|}\)
=\(\iint_R 3 x y z d y d z / x\)
=\(3 \iint_R y z d y d z\)
In yz-plane x=0, the equation of the surface becomes y2+ z2=1
∴ y varies from o to 1 and z varies from o to \(\sqrt{1-y^2}\)
∴ \(\int_s \mathbf{F} \cdot \mathbf{N} d S=3 \int_{y=0}^{y=1} \int_{z=0}^{z=\sqrt{1-y^2}} y z d y d z=3 \int_{y=0}^{y=1}\left[\frac{z^2}{2}\right]_{z=0}^{z=\sqrt{1-y^2}} y d y\)
⇒ \(\frac{3}{2} \int_0^1 y\left(1-y^2\right) d y=\frac{3}{2}\left[\frac{y^2}{2}-\frac{y^4}{4}\right]=\frac{3}{2}\left[\frac{1}{2}-\frac{1}{4}\right]=\frac{3}{8}\)
33. Evaluate \(\int_S\)F.N dS where F =y2z2 i + z2x2 j + x2y2 k and the surfaces x2 +y2 + z2 = 1 above xy-plane.
Solution: Let φ= x2 +y2+ z2−1
Normal vector to the surfaces is ∇φ=2(xi+yj+zk)
Unit normal vector, N=\(=\frac{2(x \mathbf{i}+y \mathbf{j}+z \mathbf{k})}{\sqrt{4 x^2+4 y^2+4 z^2}}\)
=\(\frac{x+y+z k}{\sqrt{x^2+y^2+z^2}}=\)
=xi+yj+zk.
F.N =( y2 z2 i+z2 x2 j+x2 y2 k).(xi+yj+zk)=xy2 z2 +x2 yz2 +x2 y2 z
Let R be the projection of S in xy−plane.
Then \(\int_S F \cdot N d S\)
=\(\iint_R F \cdot \mathbf{N} \frac{d x d y}{|\mathbf{N} \cdot \mathbf{k}|}\)
=\(\iint_R \frac{\left(x y^2 z^2+x^2 y z^2+x^2 y^2 z\right)}{z} d x d y\)
=\(\iint_R\left(x y^2 z+x^2 y z+x^2 y^2\right) d x d y\)
In xy-plane , z=0 and the equation of the surfaces becomes x+y=1.
x varies from -1 to 1 and z varies from
=\(\sqrt{1-x^2}\) to \(\sqrt{1-x^2}\)
∴ \(\int_S F \cdot N d S\)
=\(\iint_R\left(x y^2 z+x^2 y z+x^2 y^2\right) d x d y\)
=\(\iint_R x^2 y^2 d x d y\)
=\(y\int_{x=-1}^{x=1} \int_{y=-\sqrt{1-x^2}}^{y=\sqrt{1-x^2}} x^2 y^2 d x d y\)
⇒ \(4 \int_{x=0}^{x=1} \int_{y=0}^{y=\sqrt{1-x^2}} x^2 y^2 d x d y=4 \int_{x=0}^{x=1}\left[\frac{x^2 y^3}{3}\right]_0^{\sqrt{1-x^2}} d x=\frac{4}{3} \int_{x=0}^{x=1} x^2\left(1-x^2\right)^{3 / 2} d x\)
Put x = sin θ.
Then dx = cos θ dθ
x = 0, 1 ⇒ θ = 0, π/2
⇒ \(\frac{4}{3} \int_{\theta=0}^{0=\pi / 2} \sin ^2 \theta\left(1-\sin ^2 \theta\right)^{3 / 2} \cos \theta d \theta\)
⇒ \(\frac{4}{3} \int_0^{\pi / 2} \sin ^2 \theta \cos ^4 \theta d \theta=\frac{4}{3} \times \frac{1}{6} \times \frac{3}{4} \times \frac{1}{2} \times \frac{\pi}{2}=\frac{\pi}{24}\)
34. Find the surface area of the sphere given by x = a sin θ cos φ, y = a sin θ sin φ , z= a cos θ,0≤θ≤π,0≤φ≤2π.
Solution: x2 +y2 +z2 = a2 sin2 θ cos2 φ+a2 sin2 θ sin2 φ +a2 cos2 θ
= a2 sin2 θ (cos2 φ+sin2 φ)a2 cos2 θ=a2 sin2 θ + a2 cos2 θ= a2( sin2 θ + cos2 θ) =a2
Volume Integrals Practice Problems With Step-By-Step Guidance
35. If F = 4xzi -y2 j+yz k, evaluate ∫F . N dS where S is the surface of the cube bounded by x = 0, x = a ,y = 0, y=a, z = 0, z = a.
Solution:
Consider the cube OABCPQRS surrounded by the following faces:
(1) For the faces PQAR, i is the outward normal:
∴ N=i, x=a, dS=dy dz.
∴ \(\int_{R_1} \mathbf{F} \cdot \mathbf{N} d S=\int_{y=0}^{y=a} \int_{z=0}^{z=a}\left(4 x z \mathbf{i}-y^2 \mathbf{j}+y z \mathbf{k}\right) \cdot \mathbf{i} d y d z\)
⇒ \(\int_{y=0}^{y=a} \int_{z=0}^{z=a} 4 x z d y d z=\int_{y=0}^{y=a} \int_{z=0}^{z=a} 4 a z d y d z\)
⇒ \(\int_{y=0}^{y=a}\left[2 a z^2\right]_{z=0}^{z=a} d y=\int_{y=0}^{y=a} 2 a^3 d y=\left[2 a^3 y\right]_0^a=2 a^4\)
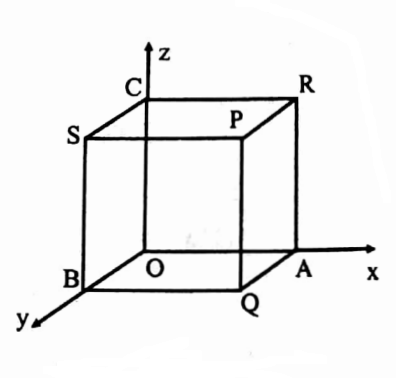
(2) For the faces OBSC,−i is the outward normal:
∴ N=-i,x=0 , and dS =dy dz
∴ \(\int_{R_2} \mathbf{F} \cdot \mathbf{N} d S\)
=\(\iint_{R_2}\left(4 x z \mathbf{i}-y^2 \mathbf{j}+y z \mathbf{k}\right) \cdot(-\mathbf{i}) d y d z\)
=\(-\iint_{R_2} 4 x z d y d z\)=0
(3) For the face BQPS, j is the outward normal:
∴N=j,y=a, and dS=dx dz
∴\(\int_{R_3} \mathbf{F} \cdot \mathbf{N} d S\)
=\(\iint_{R_3}\left(4 x z \mathbf{i}-y^2 \mathbf{j}+y z \mathbf{k}\right)\).j dx dz
=\(-\iint_{R_3} y^2 d x d z\)
=\(-a^2 \int_{x=0}^{x=a} \int_{z=0}^{z=a} d x d z\)
=\(-a^2[x]_0^a[z]_0^a\)
=-a4
(4) For the OARC, -j is the outward normal:
∴ N=-j, y=0 and dS =dx dz
∴ \(\int_{R_4} \mathbf{F} \cdot \mathbf{N} d S\)
=\(\int_{R_4}\)(4xzi-y2j+yzk).(-j) dS
=\(\int_{R_4}\)∫y2 dx dz=0
(5) For the face PRCS, k is the outward normal:
∴ N=k, z=a, and dS= dx dy
∴ \(\int_{R_5} \mathbf{F} \cdot \mathbf{N} d S\)
=\(\int_{R_5}\left(4 x z \mathbf{i}-y^2 \mathbf{j}+y z \mathbf{k}\right) \cdot \mathbf{k} d S\)
=\(\iint_{R_5} y z \cdot d x d y\)
=\(\int_{x=0}^{x=a} \int_{y=0}^{y=a} a y d x d y\)
=\(a[x]_0^a \cdot\left[\frac{y^2}{2}\right]_0^a\)
∴ \(=\frac{a^4}{2}\)
(6) For the face OAQB, -k is the outward normal:
∴ N=-k, z=0 and dS= dx dy
∴ \(\int_{R_6} \mathbf{F} \cdot \mathbf{N} d S\)
=\(\int_{R_6}\left(4 x z \mathbf{i}-y^2 \mathbf{j}+y z \mathbf{k}\right) \cdot(-\mathbf{k}) d S\)
=\(-\iint_{R_6} y z d x d y\)=0
∴ \(\int_S \mathbf{F} \cdot \mathbf{N} d S\)=2a4+0-a4+0+½ a4+0=3/2a4.
36. If F = 2xzi−xj+yk, evaluate ∫F dV where V is the region bounded by the surfaces x = 0, x = 2, y = 0, y = 6, z=x2, z = 4.
Solution:
⇒ \(\int_V \mathbf{F} d V=\int_{x=0}^{x=2} \int_{y=0}^{y=6} \int_{z=x^2}^{z=4}\left(2 x z \mathbf{i}-x \mathbf{j}+y^2 \mathbf{k}\right) d x d y d z\)
⇒ \(i\int_{x=0}^{x=2} \int_{y=0}^{y=6} \int_{z=x^2}^{z=4} 2 x z d x d y d z-\mathbf{j} \int_{x=0}^{x=2} \int_{y=0}^{y=6} \int_{z=x^2}^{z=4} x d x d y d z+\mathbf{k} \int_{x=0}^{x=2} \int_{y=0}^{y=6} \int_{z=x^2}^{z=4} y^2 d x d y d z\)
⇒ \(\left.\left.\left.=\mathbf{i} \int_{x=0}^{x=2} \int_{y=0}^{y=6} x z^2\right]_{z=x^2}^{z=4} d x d y-\mathbf{j} \int_{x=0}^{x=2} \int_{y=0}^{y=6} x z\right]_{z=x^2}^{z=4} d x d y+\mathbf{k} \int_{x=0}^{x=2} \int_{y=0}^{y=6} y^2 z\right]_{z=x^2}^{z=4} d x d y\)
⇒ \(\text { i } \int_{x=0}^{x=2} \int_{y=0}^{y=6}\left(16 x-x^5\right) d x d y-\mathbf{j} \int_{x=0}^{x=2} \int_{y=0}^{y=6}\left(4 x-x^3\right) d x d y+\mathbf{k} \int_{x=0}^{x=2} \int_{y=0}^{y=6}\left(4 y^2-x^2 y^2\right) d x d y\)
⇒ \(\left.\left.=\mathbf{i} \int_{x=0}^{x=2}\left(16 x-x^5\right) y\right]_{y=0}^{y=6} d x-\mathbf{j} \int_{x=0}^{x=2}\left(4 x-x^3\right) y\right]_{y=0}^{y=6} d x+\mathbf{k} \int_{x=0}^{x=2}\left[4 y^3 / 3-x^2 y^3 / 3\right]_{y=0}^{y=6} d x\)
⇒ \(\mathbf{i} \int_0^2\left(96 x-6 x^5\right) d x-\mathbf{j} \int_0^2\left(24 x-6 x^3\right) d x+\mathbf{k} \int_0^2\left(288-72 x^2\right) d x\)
∴ \(\mathbf{i}\left[48 x^2-x^6\right]_0^2-\mathbf{j}\left[12 x^2-3 x^4 / 2\right]_0^2+\mathbf{k}\left[288 x-24 x^3\right]_0^2=128 \mathbf{i}-24 \mathbf{j}+384 \mathbf{k}\)
Solved Examples Of Vector Calculus Integrals
37. Evaluate \(\int_V\)F dV where F =xi +yj + zk and V is the region bounded by x = 0, x =2,y = 0, y = 6, z = 4 and z=x2 .
Solution:
⇒ \(\int_V F d V=\int_{x=0}^{x=2} \int_{y=0}^{y=6} \int_{z=x^2}^{z=4}(x \mathbf{i}+y \mathbf{j}+z \mathbf{k}) d x d y d z\)
⇒ \(i\int_{x=0}^{x=2} \int_{y=0}^{y=6} \int_{z=x^2}^{z=4} x d x d y d z+j\int_{x=0}^{x=2} \int_{y=0}^{y=6} \int_{z=x^2}^{z=4} y d x d y d z+k \int_{x=0}^{x=2} \int_{y=0}^{y=6} \int_{z=x^2}^{z=4} z d x d y d z\)
⇒ \(i \int_{x=0}^{x=2} \int_{y=0}^{y=6}[x z]_{z=x^2}^4 d x d y+\mathbf{j} \int_{x=0}^{x=2} \int_{y=0}^{y=6}[y z]_{z=x^2}^{z=4} d x d y+\mathbf{k} \int_{x=0}^{x=2} \int_{y=0}^{y=6}\left[\frac{z^2}{2}\right]_{z=4}^{x^2} d x d y\)
⇒ \(i \int_{x=0}^{x=2} \int_{y=0}^{y=6}\left(4 x-x^3\right) d x d y+\mathbf{j} \int_{x=0}^{x=2} \int_{y=0}^{y=6}\left(4-x^2\right) y d x d y+\mathbf{k} \int_{x=0}^{x=2} \int_{y=0}^{y=6}\left[8-\frac{x^4}{2}\right] d x d y\)
⇒ \(\mathbf{i} \int_{x=0}^{x=2}\left[\left(4 x-{x}^3\right) y\right]_{y=0}^{y=6} d x+\mathbf{j} \int_{x=0}^{x=2}\left[\left(4 x-x^2\right) \frac{y^2}{2}\right]_{y=0}^{y=6} d x+\mathbf{k} \int_{x=0}^{x=2}\left[\left(8-\frac{x^4}{2}\right) y\right]_{y=0}^{y=6} d x\)
⇒ \(\mathbf{i} \int_{x=0}^{x=2} 6\left(4 x-x^3\right) d x+\mathbf{j} \int_{x=0}^{x=2} 18\left(4-x^2\right) d x+\mathbf{k} \int_{x=0}^{x=2} 6\left(8-\frac{x^4}{2}\right) d x\)
⇒ \(\mathbf{i}\left[12 x^2-\frac{6 x^4}{4}\right]_{x=0}^{x=2}+\mathbf{j}\left[18\left(4 x-\frac{x^3}{3}\right)\right]_{x=0}^{x=2}+\mathbf{k}\left[6\left(8 x-\frac{x^5}{10}\right)\right]_{x=0}^{x=2}\)
⇒ \(\mathbf{i}(48-24)+\mathbf{j}\left[18\left(8-\frac{8}{3}\right)\right]+\mathbf{k}\left[6\left(16-\frac{32}{10}\right)\right]=24 \mathbf{i}+96 \mathbf{j}+\frac{384}{5} \mathbf{k}\)
38. If F = (2x2– 3z) i- 2xy j- 4x k, then evaluate ∫\(\int_V\)∫∇.F dV where V is the closed region bounded by the planes x = 0,y = 0, z = 0 and 2x + 2y + z = 4. Also, Evaluate ∫\(\int_V\)∫∇×F dV.
Solution:
∴ \(\nabla \cdot \mathbf{F}=\left(\mathbf{i} \frac{\partial}{\partial x}+\mathbf{j} \frac{\partial}{\partial y}+\mathbf{k} \frac{\partial}{\partial z}\right) \cdot\left[\left(2 x^2-3 z\right) \mathbf{i}-2 x y \mathbf{j}-4 x \mathbf{k}\right]\)
⇒ \(\frac{\partial}{\partial x}\left(2 x^2-3 z\right)+\frac{\partial}{\partial y}(-2 x y)+\frac{\partial}{\partial z}(-4 x)=4 x-2 x=2 x\)
∴ \(\iiint_V \nabla \cdot \mathbf{F} d V=\iiint_V 2 x d x d y d z=2 \int_{x=0}^{x=2} \int_{y=0}^{y=2-x} \int_{z=0}^{z=4-2 x-2 x} x d x d y d z\)
⇒ \(\left.2 \int_{x=0}^{x=2} \int_{y=0}^{y=2-x} x[z]\right]_{z=0}^{z=4-2 x-2 y} d x d y=2 \int_{x=0}^{x=2} \int_{y=0}^{y=2-x} x(4-2 x-2 y) d x d y\)
⇒ \(\left.2 \int_{x=0}^{x=2}\left[4 x y-2 x^2 y-x y^2\right]\right]_{y=0}^{y=2-x} d x=2 \int_0^2\left[4 x(2-x)-2 x^2(2-x)-x(2-x)^2\right] d x\)
⇒ \(2 \int_0^2\left[x^3-4 x^2+4 x\right] d x=2\left[\frac{1}{4} x^4-\frac{4}{3} x^3+2 x^2\right]_0^2=2\left[4-\frac{32}{3}+8\right]=\frac{8}{3}\)
We have \(\nabla \times \mathbf{F}=\left|\begin{array}{ccc}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\
2 x^2-3 z & -2 x y & -4 x
\end{array}\right|\)
⇒ \(\left[\frac{\partial}{\partial y}(-4 x)-\frac{\partial}{\partial z}(-2 x y)\right] \mathbf{i}-\left[\frac{\partial}{\partial x}(-4 x)-\frac{\partial}{\partial z}\left(2 x^2-3 z\right)\right] \mathbf{j}+\left[\frac{\partial}{\partial x}(-2 x y)-\frac{\partial}{\partial y}\left(2 x^2-3 z\right)\right] \mathbf{k}\)
⇒ \(0 \mathbf{i}-(-4+3) \mathbf{j}+(-2 y) \mathbf{k}=\mathbf{j}-2 y \mathbf{k}\)
∴ \(\iiint_V \nabla \times \mathbf{F} d V=\iiint_V(\mathbf{j}-2 y \mathbf{k}) d x d y d z\)
⇒ \(\int_{x=0}^{x=2} \int_{y=0}^{y=2-x z=4} \int_{z=0}^{-2 x-2 y}(\mathbf{j}-2 y \mathbf{k})dx dy dz =\int_{x=0}^{x=2} \int_{y=0}^{y=2-x}(\mathbf{j}-2 y \mathbf{k})(4-2 x-2 y) d x d y.\)
⇒ \(\int_{x=0}^{x=2}\left[\mathbf{j}\left(4 y-2 x y-y^2\right)-2 \mathbf{k}\left(2 y^2-x y^2-\frac{2}{3} y^3\right)\right]_{y=0}^{y=2-x} d x\)
⇒ \(=\int_{x=0}^{x=2}\left[\mathbf{j}(2-x)(4-2 x-2+x)-2 \mathbf{k}(2-x)^2\left\{2-x-\frac{2}{3}(2-x)\right\}\right] d x\)
⇒ \(\int_0^2\left[(2-x)^2 \mathbf{j}-\frac{2}{3}(2-x)^3 \mathbf{k}\right] d x=\int_0^2\left[(x-2)^2 \mathbf{j}+\frac{2}{3}(x-2)^3 \mathbf{k}\right] d x\)
⇒ \(\left[\frac{(x-2)^3}{3}\right]_0^2 \mathbf{j}+\left[\frac{2}{3} \frac{(x-2)^4}{4}\right]_0^2 \mathbf{k}=\frac{8}{3} \mathbf{j}-\frac{8}{3} \mathbf{k}=\frac{8}{3}(\mathbf{j}-\mathbf{k})\)
39. Evaluate ∫∫∫(2x+y)dV where V is closed region bounded by the cylinder z = 4−x2 and the planes x = 0,y = 0 and y = 2, z = 0.
Solution:
∴ \(\iiint_V(2 x+y) d V=\int_{x=0}^{x=2} \int_{y=0}^{y=2} \int_{z=0}^{z=4-x^2}(2 x+y) d x d y d z=\int_{x=0}^{x=2} \int_{y=0}^{y=2}[(2 x+y) z]\int_{z=0}^{z=4-x^2} d x d y\)
⇒ \(\int_{x=0}^{x=2} \int_{y=0}^{y=2}(2 x+y)\left(4-x^2\right) d x d y=\int_{x=0}^{x=2}\left[\left(4-x^2\right)\left(2 x y+\frac{y^2}{2}\right)\right]_{y=0}^{y=2} d x\)
⇒ \(\int_{x=0}^{x=2}\left(4-x^2\right)(4 x+2) d x=\int_0^2\left(8+16 x-2 x^2-4 x^3\right) d x\)
⇒ \(\left[8 x+8 x^2-\frac{2 x^3}{3}-x^4\right]_0^2=16+32-\frac{16}{3}-16=\frac{80}{3}\)
40. If φ = 45x2y, evaluate ∫\(\int_V\)∫φ dV where V is the closed region bounded by the plane 4x + 2y + z = 8,x = 0,y = 0,z = 0.
Solution:
∴ \(\iiint_V \varphi d V=\iiint_V 45 x^2 y d x d y d z=\int_{x=0}^{x=2} \int_{y=0}^{y=4-2 x} \int_{z=0}^{z=8-4 x-2 y} 45 x^2 y d x d y d z\)
⇒ \(\int_{x=0}^{x=2} \int_{y=0}^{y=4-2 x}\left[45 x^2 y z\right]_{z=0}^{z=8-4 x-2 y} d x d y=\int_{x=0}^{x=2} \int_{y=0}^{y=4-2 x}\left[45 x^2 y(8-4 x-2 y)\right] d x d y\)
⇒ \(\int_{x=0}^{x=2} \int_{y=0}^{y=4-2 x} 45 x^2\left(8 y-4 x y-2 y^2\right) d x d y=\int_{x=0}^{x=2} 45 x^2\left[4 y^2-2 x y^2-\frac{2}{3} y^3\right]_{y=0}^{y=4-2 x} d x\)
⇒ \(\int_{x=0}^{x=2}\left[720 x^2(2-x)^2-360 x^3(2-x)^2-240 x^2(2-x)^3\right] d x\)
⇒ \(120 \int_{x=0}^{x=2}\left[6 x^2\left(4-4 x+x^2\right)-3 x^3\left(4-4 x+x^2\right)-2 x^2\left(8-12 x+6 x^2-x^3\right)\right] d x\)
⇒ \(120 \int_{x=0}^{x=2}\left(24 x^2-24 x^3+6 x^4-12 x^3+12 x^4-3 x^5-16 x^2+24 x^3-12 x^4+2 x^5\right) d x\)
⇒ \(120 \int_{x=0}^{x=2}\left(8 x^2-12 x^3+6 x^4-x^5\right) d x=120\left[\frac{8 x^3}{3}-3 x^4+\frac{6 x^5}{5}-\frac{x^6}{6}\right]_0^2\)
= 2560 – 5760 + 4608 – 1280 = 128.
41. Evaluate I=∫∫∫\sqrt{\left(a^2 b^2 c^2-b^2 c^2 x^2-c^2 a^2 y^2-a^2 b^2 z^2\right)} dx dy dz taken throughout the domain \(\left\{(x, y, z): \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2} \leq 1\right\}\)
Solution: The limits of integration are ;x varies from -a to a; y varies from -b\(\sqrt{1-x^2 / a^2}\) to b\(\sqrt{1-x^2 / a^2}\) and z varies from -c \(\sqrt{1-x^2 / a^2-y^2 / b^2}\) to c \(\sqrt{1-x^2 / a^2-y^2 / b^2}\)
∴ \(I=\iiint \sqrt{\left(a^2 b^2 c^2-b^2 c^2 x^2-c^2 a^2 y^2-a^2 b^2 z^2\right)} d x d y d z\)
⇒ \(a b c \int_{x=-a}^{x=a} \int_{y=-b \sqrt{1-x^2 / a^2}}^{y=b \sqrt{1-x^2 / a^2}} \quad \int_{z=-c \sqrt{1-x^2 / a^2-y^2 / b^2}}^{z=c \sqrt{1-x^2 / a^2-y^2 / b^2}} \sqrt{\left(1-\frac{x^2}{a^2}-\frac{y^2}{b^2}-\frac{z^2}{c^2}\right)} d x d y d z\)
⇒ \(8a b c \int_{x=-a}^{x=a} \int_{y=0}^{y=b \sqrt{y=1-x^2 / a^2}} \quad \int_{z=0}^{z=c \sqrt{z=1-x^2 / a^2-y^2 / b^2}} \sqrt{\left(1-\frac{x^2}{a^2}-\frac{y^2}{b^2}-\frac{z^2}{c^2}\right)} d x d y d z\)
⇒ \(=8 a b c^2 \int_{x=0}^{x=a} \int_{y=0}^{y=b \sqrt{y=1-x^2 / a^2}}\left[0+\frac{1}{2}\left(1-\frac{x^2}{a^2}-\frac{y^2}{b^2}\right)\left(\frac{\pi}{2}-0\right)\right] d x d y\)
⇒ \(8 a b c^2 \frac{\pi}{4} \int_{x=0}^{x=a} \int_{y=0}^{y=b \sqrt{1-x^2 / a^2}}\left[\left(1-\frac{x^2}{a^2}\right)-\frac{y^2}{b^2}\right] d x d y\)
⇒ \(2 a b c^2 \pi \int_{x=0}^{x=a}\left[\left(1-\frac{x^2}{a^2}\right) y-\frac{y^3}{3 b^2}\right]_{y=0}^{y=b \sqrt{1-x^2 / a^2}} d x\)
⇒ \(2 a b c^2 \pi \int_0^a b\left(1-\frac{x^2}{a^2}\right)^{3 / 2}-\frac{1}{3 b^2} b^3\left(1-\frac{x^2}{a^2}\right)^{3 / 2} d x\)
Put x = a sin θ.
Then dx = a cos θ dθ.
x = 0, a ⇒ θ = 0, π/2
⇒ \(2 a b c^2 \pi \int_0^a \frac{2 b}{3}\left(1-\frac{x^2}{a^2}\right)^{3 / 2} d x=\frac{4 a b^2 c^2 \pi}{3} \int_0^{\pi / 2}\left(1-\sin ^2 \theta\right)^{3 / 2}(a \cos \theta d \theta)\)
∴ \(\frac{4 a^2 b^2 c^2 \pi}{3} \int_0^{\pi / 2} \cos ^4 \theta d \theta=\frac{4 a^2 b^2 c^2 \pi}{3} \frac{3}{4} \times \frac{1}{2} \times \frac{\pi}{2}=\frac{a^2 b^2 c^2 \pi^2}{4}\)
42. Find the volume of a sphere of radius ‘a’.
Solution: The equation of the sphere with the center origin and radius a is x2+y2+z2=a2
The volume of the sphere V \(=\int_V d V\)
The limits of integration are x=± a,y=±\(\sqrt{a^2-x^2}\),z=±\(\sqrt{a^2-x^2-y^2}\)
∴ \(V=\int_{v}dv=\int_{x=-a}^{x=a} \int_{y=- \sqrt{a^2 – x^2}}^{y= \sqrt{a^2+x^2}} \int_{z=- \sqrt{a^2-x^2-y^2}}^{z= \sqrt{a^2-x^2-y^2}}d x d y d z\)
⇒ \(8 \int_{x=0}^{x=a} \int_{y=0}^{y=\sqrt{a^2-x^2}} \int_{z=0}^{z=\sqrt{a^2-x^2-y^2}} d x d y d z=8 \int_{x=0}^{x=a} \int_{y=0}^{y=\sqrt{a^2-x^2}}[z]_{z=0}^{z=\sqrt{a^2-x^2-y^2}} d x d y\)
⇒ \(8 \int_{x=0}^{x=a} \int_{y=0}^{y=\sqrt{a^2-x^2}} \sqrt{a^2-x^2-y^2} d x d y\)
⇒ \(8 \int_{x=0}^{x=a}\left[\frac{y}{2} \sqrt{a^2-x^2-y^2}+\frac{a^2-x^2}{2} \text{Sin}^{-1} \frac{y}{\sqrt{a^2-x^2}}\right]_{y=0}^{y=\sqrt{a^2-x^2}} d x\)
⇒ \(8 \int_{x=0}^{x=a}\left(\frac{a^2-x^2}{2}\right) \frac{\pi}{2} d x=2 \pi\left[a^2 x-\frac{x^3}{3}\right]_0^a=2 \pi\left[a^3-\frac{a^3}{3}\right]=\frac{4 \pi a^3}{3}\)
